A Continuous-Binding Cross-Linker Model for Passive Airway Smooth Muscle

Abstract

Although the active properties of airway smooth muscle (ASM) have garnered much modeling attention, the passive mechanical properties are not as well studied. In particular, there are important dynamic effects observed in passive ASM, particularly strain-induced fluidization, which have been observed both experimentally and in models; however, to date these models have left an incomplete picture of the biophysical, mechanistic basis for these behaviors. The well-known Huxley cross-bridge model has for many years successfully described many of the active behaviors of smooth muscle using sliding filament theory; here, we propose to extend this theory to passive biological soft tissue, particularly ASM, using as a basis the attachment and detachment of cross-linker proteins at a continuum of cross-linker binding sites. The resulting mathematical model exhibits strain-induced fluidization, as well as several types of force recovery, at the same time suggesting a new mechanistic basis for the behavior. The model is validated by comparison to new data from experimental preparations of rat tracheal airway smooth muscle. Furthermore, experiments in noncontractile tissue show qualitatively similar behavior, suggesting support for the protein-filament theory as a biomechanical basis for the behavior.

Introduction

Passive airway smooth muscle (ASM) exhibits strain-induced fluidization (see, e.g., Fabry et al. (1) and Trepat et al. (2)). That is, in response to imposed strain, the mechanical properties of the passive tissue are altered such that it is more fluidlike, in this case generating a reduced force. This is a particular phenomenon of interest in ASM due to its implications for asthma and deep inspirations in that both tidal breathing and deep inspirations are expected to create conditions of increased strain. Thus, dynamic models of asthma may need to account for the passive dynamic properties of ASM. There are several existing modeling approaches for passive soft tissue rheology, most notably, for example, viscoelastic theory employing a combination of springs and dashpots (3,4), soft glassy materials with strain-induced state transitions (1,2), and so-called wormlike chain (WLC) models (5–8). However, the existing models leave an incomplete picture of the underlying biomechanical basis for the observed behaviors. For example, though WLC-type models certainly suggest a biophysical interpretation of folding and unfolding of WLCs, the necessary metastable energy landscapes still largely resist direct connections with underlying mechanistic behaviors (8).

One hypothesis for the mechanistic source underlying this behavior is the interaction between protein filaments. For instance, the cell is spanned by actin filaments, whereas the extracellular matrix is rich in collagen and elastin fibers (9). These filaments are interconnected via cross-linker proteins such as fibronectin, filamin, and α-actinin (see, e.g., Winder and Ayscough (10)). It has been shown that stress causes partial unfolding and detachment of cross-linkers (11–16); this detachment reduces stress in the filament network and thus causes stress relaxation. Indeed, cross-linked F-actin networks reconstituted in vitro have mechanical properties similar to those of the living cell (17), indicating that such networks contribute substantially to cell mechanical properties, and experimental work in actin gels suggests that they exhibit fluidization-like behavior attributed to cross-linker proteins (18). Mathematical models have previously been used to relate network structure and cross-linker properties to static mechanical properties (19,20).

We propose a model of passive airway smooth muscle (ASM) based on the protein-filament hypothesis, using an extension of sliding filament theory and the Huxley cross-bridge model (21). The central idea is that strain on the filament network causes detachment of the cross-linkers, and thus relaxation. The original cross-bridge model described the attachment and detachment of actin and myosin filaments moving relative to one another; these rate functions were asymmetric functions reflecting the directional sense of contractile tissue. In passive tissue, we will assume that these rate functions are symmetric functions. The model also allows a continuum of cross-linker binding sites (22), rather than the commonly used discrete binding model.

We validate the model with experiments in rat tracheal ASM. The model exhibits strain-induced fluidization, as well as force recovery after and between transient stretches, in excellent agreement with the experimental data. Furthermore, we show that the results are in qualitative agreement with experimental data in noncontractile tissues (tendon and skin), suggesting that the mechanistic basis for strain-induced fluidization may lie with attachment and detachment of protein filaments.

Experimental Methods

All procedures were approved by the McGill University Animal Care Committee and complied with the guidelines of the Canadian Council on Animal Care. Lewis rats (n = 8) aged 8–11 weeks with a ranging in body mass from 255 to 320 g (ssNHsd, Harlan Sprague Dawley, Indianapolis, IN) were euthanized by overdose of pentobarbital sodium. An area of skin overlying the abdomen was shaved and marked, so that the craniocaudal direction could be identified, and removed. The trachea and a portion of the tibialis anterior tendon were dissected out. All tissues were placed in ice-cold, calcium-free Krebs-Henseleit solution (in mM, 118.0 NaCl, 4.5 KCl, 2.5 MgSO₄, 1.2 KH₂ PO₄, 25.5 NaHCO₃, and 10.0 glucose, pH 7.4) that had been aerated with 95% O₂/5% CO₂ for at least 30 min. Loose connective tissue was removed from the trachea, which was then cut transversely to separate out a single cartilage ring with adjoining muscle tissue. In situ muscle length was measured to the nearest 0.1 mm by holding a scale next to the ring under 45× magnification. The muscle strip was cut out of the ring with ∼1.5 mm cartilage at each end. A strip of skin was cut with its long axis in the craniocaudal direction. The lower layers of skin were cut away, leaving the epidermis and a small amount of dermis. A strip of tendon was cut parallel to the long axis of the tendon. Aluminum foil clips were folded around the ends of the skin and tendon strips, and around the cartilage at the ends of the muscle strips, to allow them to be attached to the experimental apparatus. The tissue strips were mounted in a horizontal tissue bath by placing the foil clips over hooks attached to a length controller (model 322C-I, Aurora Scientific, Ottawa, Ontario, Canada) and a force transducer (model 404A, Aurora Scientific). Calcium-free Krebs-Henseleit solution was stored in an adjacent reservoir, where it was aerated with 95% O₂/5% CO₂, and was circulated through the tissue bath at ∼3 ml/min throughout the experiment. A water jacket maintained the bath at ∼37°C.

The effect of length oscillation on force during stress relaxation was determined by stretching the tissue strips by $\Delta L$, holding length constant for 10 s, and then oscillating length sinusoidally at 2 Hz for 1 min. Stretch amplitudes ($\Delta L$) were 0.17 $L_{ref}$ for muscle, 0.125 $L_{ref}$ for skin, and 0.02 $L_{ref}$ for tendon. Oscillation amplitudes of 0, 0.2, 0.1, and 0.4 $\Delta L$ were tested, in that order, with 15- to 20-min rest periods at $L_{ref}$ between trials. Despite these rest periods, the force increase upon stretch often decreased during this experiment. To account for this, the initial pretrial force was subtracted and the force data were normalized to the force immediately before oscillation.

To quantify force recovery between transient stretches, a quick stretch followed by return to $L_{ref}$ was performed (half-sinusoid, 0.25-s duration). An identical stretch and return was performed 0.5–200 s later, and the ratio of the maximal force in response to the second stretch to the maximal force in response to the first stretch was calculated. Eight different time intervals were used in randomized order. Trials with a peak-to-peak time interval of 0.25 s were later excluded from analysis, because force did not return to baseline between stretches, so that the increase in force in response to the second stretch could not be accurately calculated. These amplitudes were chosen, based on preliminary experiments, to allow recovery of baseline force and tissue stiffness during the subsequent 15-min rest period. However, systematic increases or decreases in stiffness did sometimes occur over the course of the experiment. The influence of these changes was minimized by performing the trials in random order.

Model

We model the density of attached cross-linkers $n\left(y,t\right)$ according to sliding filament theory (21,23) as

$$\frac{\partial n}{\partial t}=\alpha \left(y\right)\left(1-N\left(t\right)\right)-\beta \left(y\right)n+v\left(t\right)\frac{\partial n}{\partial y},$$ (1)

where y is the cross-linker strain. Here, $\alpha \left(y\right)$ is the cross-linker attachment function, $\beta \left(y\right)$is the detachment function, $v\left(t\right)$is the relative filament velocity, and $N\left(t\right)$ is the total fraction of bound cross-linkers,

$$N\left(t\right)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}n\left(y,t\right)dy.$$

It is assumed here that the binding sites are continuously distributed (22).

The cross-linker-generated force is

$$\varphi \left(t\right)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\rho \left(y\right)n\left(y,t\right)dy,$$

where $\rho \left(y\right)$ is the relationship between cross-linker force and strain. We take the force function as

$$\rho \left(y\right)=\{\begin{array}{c}{\rho }^{2}y2+{\rho }^{3}y3,y\ge 0\\ 0,y<0\end{array}$$ (2)

under the assumption that displaced cross-linkers produce a nonlinear force response to stretch but do not push against shortening. The implications of this assumption are discussed at length later in this section and in the Discussion. To account for static elastic properties, we include a linear spring in parallel with the cross-linker, so that the total force is

$$F\left(t\right)=\varphi \left(t\right)+F_0+k_1\Delta L\left(t\right),$$

where F₀ is the basal force, k₁ is the spring modulus, and $\Delta L$ is the tissue displacement relative to the initial length. The proportionality of the cross-linker displacement and tissue displacement is given by $\Delta y\left(t\right)=\gamma \Delta L\left(t\right)$, where γ depends upon the length of the cross-linkers and their arrangement within the tissue, assuming an essentially 1D arrangement of the cross-linkers.

The attachment function $\alpha \left(y\right)$ is taken to be

$$\alpha \left(y\right)=\{\begin{array}{cc}{\alpha }_1,& y\in \left[-1,1\right]\\ 0,& \left|y\right|>1\end{array}$$

under the assumption that there is a defined, constant binding region, which we have normalized to $\left(-1,1\right)$. The detachment function $\beta \left(y\right)$ is

$$\beta \left(y\right)={\beta }_1+{\beta }_2\frac{{\left|y\right|}^m}{y_{max}^m+{\left|y\right|}^m}.$$ (3)

Here, the detachment function is highly nonlinear, with $m=14.4$; thus, the detachment rate is small within the binding region and increases rapidly for larger displacements. The parameter y_max is given and describes the inflection point of the sigmoidal curve. Although for large m, Eq. 3 resembles a step function with a value of β₁ for $\left|y\right|<y_{max}$ and β₂ otherwise, at this value of m, there remains a significant difference between this form of β and a step function. The Hill equation form here is not meant to be indicative of positive cooperativity; the form of $\beta \left(y\right)$ is merely taken to be sigmoidal.

That said, the forms of α, β, and ρ are largely unknown and the assumptions made here are based only on intuition to give reasonable agreement with the observed data (please see the Discussion for more details).

Following from above, the steady-state solution of Eq. 1 is

$$n_s\left(y\right)=\frac{\alpha \left(y\right)}{\beta \left(y\right)}\left(1-N_s\right),$$

where

$$N_s=\frac{1}{1+1/{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\alpha \left(y\right)/\beta \left(y\right)dy}$$

and the steady-state solution is taken as the initial condition for the simulations. The net force at steady state is then

$${\varphi }_s=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\rho \left(y\right)n_s\left(y\right)dy=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\rho \left(y\right)\left(\frac{\alpha \left(y\right)}{\beta \left(y\right)}\left(1-N_s\right)\right)dy>0,$$ (4)

as $\alpha \left(y\right)$ and $\beta \left(y\right)$ are nonnegative, even functions and $\rho \left(y\right)$ is zero for $y<0$ and positive otherwise. Note that this nonzero steady-state force implies an internal tension at all times; an alternative assumption is that $\rho \left(y\right)$ is an odd function, resulting in zero steady-state force. However, such an arrangement allows negative force generation, which is unrealistic; under shortening, the muscle goes slack rather than pushing against the shortening. Additional comment on this important point can be found in the Discussion.

The tissue displacement $L\left(t\right)$ is specified for each simulation, according to the experimental protocols. We use the sign convention that v is negative when the tissue is being stretched and positive when the tissue is shortened, and thus $v\left(t\right)=-\gamma L^{\prime }\left(t\right)$.

A simple illustration of cross-linker model function is as follows: imposed tissue velocity creates a displacement in the established steady-state distribution of bound cross-linkers. Such a displacement will move some bound cross-linkers into an unbinding region, and likewise move regions without bound cross-linkers into the binding region. The displaced cross-linkers initially generate a force according to the displacement. However, bound cross-linkers in the unbinding region begin to detach, and cross-linkers in the binding region begin to attach, and eventually the steady state is reattained. This behavior is illustrated in Fig. 1 for a tissue strip undergoing a single transient stretch. For the first 0.5 s, the tissue is unstretched and the steady state persists. Between 0.5 and 0.75 s, a half-sinusoidal stretch of 17% of reference length is imposed; during this stretch, cross-linkers are displaced out of the binding region into areas of unbinding. Thus, cross-linkers at the leading edge (positive y) are detached, bringing N below 1 and allowing binding within the binding region. At the conclusion of the stretch, these newly bound cross-linkers at the trailing edge (negative y) then exert no force and, thus, a reduction in total force. This persists until the steady state is reattained at long time (not shown).

Figure 1.

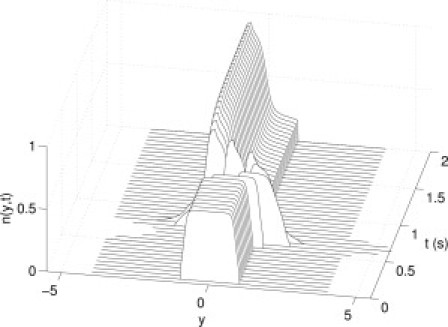
Illustration of cross-linker function. Here the distribution of bound cross-linkers is given for a single half-sinusoidal stretch of 17% of reference length for 0.25 s, beginning at 0.5 s. The steady-state distribution persists for the first 0.5 s, followed by the single transient stretch displacing the bound cross-linkers. After the stretch, recovery toward steady state begins.

The parameter values used are ${\alpha }_1=4.16$ (1/s), $y_{max}=1.58$, ${\beta }_1=0.01$ (1/s), ${\beta }_2=34.6$(1/s), $m=14.4$, ${\rho }_2=1.74$ mN, ${\rho }_3=0.36$mN, $F_0=0.055$mN, $k_1=0.17$mN, and $\gamma =9.3$. Model parameters were fitted to the experimental data by least-squares optimization using the Nelder-Mead simplex method fminsearch in MATLAB. The governing partial differential equation (Eq. 1) is reduced to a family of ordinary differential equations via the method of characteristics, which are in turn solved numerically by forward Euler integration with timestep $\delta t=0.005$ s. The spatial discretization is $\delta y=0.01$. The nonlocal term was integrated at each timestep by the trapezoidal rule.

Results

We demonstrate the predictions of the model in comparison to the experimental data for strain-induced fluidization and force recovery after and between transient stretches.

Strain-induced fluidization

To examine strain-induced fluidization, the following protocol is applied in both model and experiment: tissue at steady state is prestretched, and the force is allowed to decay for 10 s. At this point, length oscillations begin and continue with 2 Hz frequency for 60 s, with amplitudes of 0%, 10%, 20%, and 40% of the prestretch. The force is then recorded for a further 30 s after the oscillations subside. The prestretch amplitudes were 17%, 12.5%, and 2% of the reference length for ASM, skin, and tendon, respectively.

In Fig. 2, we give the time course of the force generated for each oscillation amplitude in both ASM and in the model, normalized by the force at 10 s. The mean effect is given in the lower panel, averaged with a 0.5-s moving average to suppress the oscillations. Up to 10 s, each case is identical as oscillations have not begun. During the oscillation phase, the size of the force oscillations increases with the amplitude of the length oscillations. After the oscillations end, the remaining force is decreased depending upon the oscillation amplitude; this demonstrates that the expected fluidization effect is seen in both model and experiment. Here, the model reproduces very well the experimental data for both the time course and mean behavior of this protocol. Qualitatively similar behavior is also seen in both skin and tendon (Fig. 3).

Figure 2.

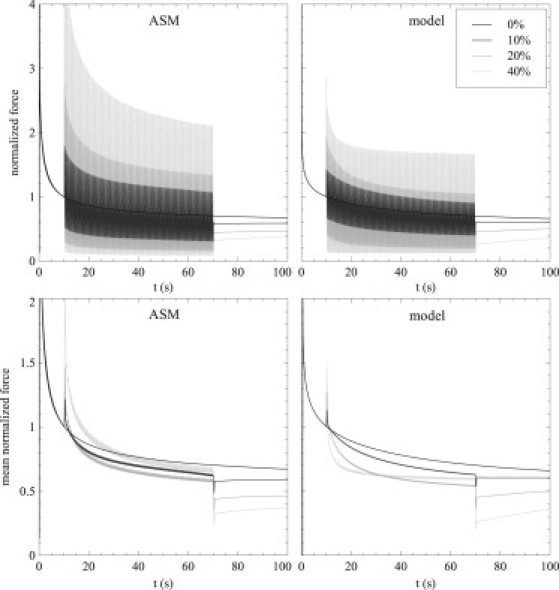
Time courses of strain-induced fluidization. Tissue is stretched by 17% from reference length and held for 10 s; then, 2-Hz oscillations of 0% (baseline), 10%, 20%, and 40% of the stretch amplitude occur for 60 s. Recording continues for a further 30 s after the stretch. Experimental data (left) and model predictions (right) for the full oscillatory time course (upper) and the mean data averaged with a 0.5-s moving average to show the mean effect of the oscillations (lower).

Figure 3.

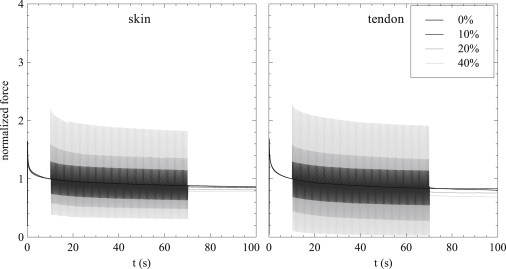
Time courses of strain-induced fluidization (layout as in Fig. 2) for skin and tendon, with initial stretch amplitudes of 12.5% and 2%, respectively.

Fluidization may be measured more closely by examining the decrease in force induced by the oscillations. We thus measure the force after the conclusion of the oscillations $\left(F_{osc}\right)$, at 70 s, and the corresponding force in the nonoscillatory case $\left(F_{con}\right)$ for each of the specified oscillation amplitudes for the model and ASM (Fig. 4, left) experimental data, with equivalent results for noncontractile skin and tendon (Fig. 4, right). With the exception of the smallest amplitude of oscillation for tendon, force after oscillation always decreased as oscillation amplitude increased, in both the experiments and the model. The model predictions for final force reduction due to strain-induced fluidization agree very well with the experimental data.

Figure 4.

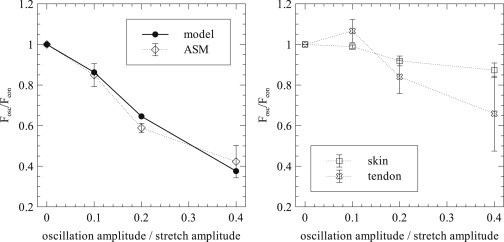
Final values for strain-induced fluidization. The ratio of force after oscillations (F_osc) to force during stress relaxation without oscillation (F_con) for the data in Fig. 2, (left), and equivalent data for skin and tendon (right). Errors are given as ± 1 SD.

Force recovery between transient stretches

To examine the reattachment of cross-linkers, we also measure the recovery in force between transient stretches by beginning with tissue at steady state and applying two transient stretches with amplitude 17% of the reference length and duration 0.25 s. The time between the two transient stretches is varied from 0.5 s to 200 s. We measure the baseline force before any stretch, F_b, as well as the maximum force during each transient stretch, F₁ and F₂, respectively. The ratio $\left(F_2-F_b\right)/\left(F_1-F_b\right)$ indicates the force recovery between stretches: at short times, there will be a significant force drop; at long times, the tissue will return to steady state between the stretches, and the ratio will approach 1. The results for model predictions and ASM experiment are given in Fig. 5.

Figure 5.

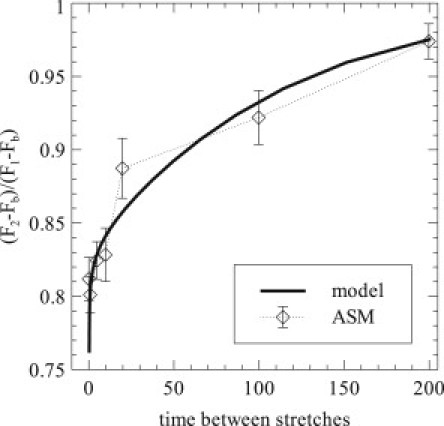
Force recovery between transient stretches. Tissue at equilibrium is subject to a transient stretch of 17% of reference length lasting 0.25 s, followed by a rest period and a second, identical stretch. The ratio between peak forces above baseline is measured as a function of the time between stretches. Data are given for both the model prediction and ASM experiment, with errors shown as ± 1 SD.

Here, the model predicts well the experimental results in ASM, although the long-time recovery is slightly slower in the model than in the experiment. Experimental data in skin and tendon exhibited a smaller initial drop in force and a much faster recovery (data not shown).

Force recovery after transient stretch

After a single transient stretch, when the tissue is returned to the reference length, there is initially a force drop, which slowly decays as the tissue returns to steady state. This force drop and recovery is measured by experiment and model simulation (Fig. 6) using the same protocol as for force recovery between transient stretches but with only the initial stretch and the data normalized to the drop in force. Here, $F_{drop}$ is the minimum force obtained, with F_b the baseline force as before. Again the model reproduces very well the experimental data. The time constants associated with the force recovery are ${\tau }_{ASM}=55.1$ s and ${\tau }_{model}=69.2$ s, fit from $t=5$ s onward.

Figure 6.

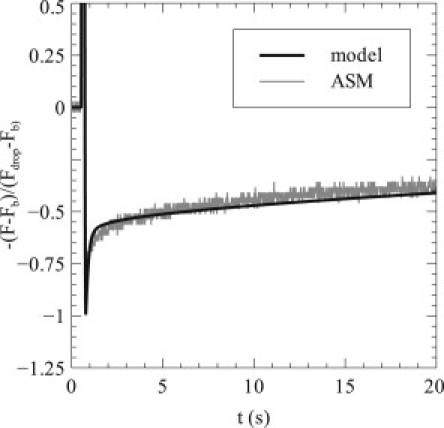
Recovery of force after a transient stretch. Tissue is stretched by 17% of reference length for 0.25 s, half-sinusoidally, generating a drop in basal force upon return to L_ref and subsequent recovery. Results are given both for the ASM experiment (gray line) and model predictions (black line).

Discussion

We have demonstrated that a continuous-binding cross-linker model can accurately reproduce dynamic behaviors in ASM by way of comparison with experimental data for fluidization and force recovery after and between transient stretches. The model is based on a continuous-binding extension of the sliding-filament Huxley cross-bridge model for active muscle, and provides a mechanistic basis for the dynamic, passive properties observed previously. The model is primarily intended to agree qualitatively with ASM, and it provides good agreement with the experimental data found from rat tracheal smooth muscle preparations. Moreover, the experimental data in skin and tendon give some qualitative agreement with the model and ASM results; these phenomena in noncontractile tissue support the hypothesized protein-filament mechanistic basis.

Sliding-filament theory has been widely used in many studies; most models employ the standard single-binding-site assumption. However, the possibility of multiple, discrete binding sites was explored by Schoenberg (24), who employed a cross-bridge model with seven binding sites spaced by $\sim 5.5$ nm. Here, we use the extended idea of a continuum of binding sites (22), such that in principle cross-linkers may be bound at any displacement.

As mentioned previously, the assumption of an asymmetric force function bears further examination. The negative force generated by cross-bridges with negative y is crucial for the Huxley model in active muscle, in that it allows the observed force-velocity curve. However, in this model of passive muscle, there is a crucial difference: if the imposed length decreases quickly, the muscle does not push (i.e., generate negative force), it just goes slack. As such, there is no force-velocity curve for passive muscle, and thus, asymmetric force generation is an appropriate assumption for passive muscle. One consequence of this assumption is that cross-linkers exert a positive force at steady state (Eq. 4). However, the idea that such tissue is under internal tension at steady state is consistent with recent evidence suggesting that living cells are out of equilibrium and under prestress (25–27).

Alternately, one may assume that Eq. 2 is an odd function of y, resulting in zero force at steady state. However, such a construction allows negative values of both the cross-linker force, $\varphi \left(t\right)$, and the total force, $F\left(t\right)$, under sufficient shortening. One may crudely rectify this by simply enforcing $F\left(t\right)\ge 0$, i.e., that the model is no longer valid under such shortening. Under such a modified model, parameters may be found that approximate the experimental data reasonably well. However, the small-force behavior under oscillations is poor and the force-recovery timescales do not match well. On balance, the asymmetric force model is vastly superior in terms of agreement with this experimental data set.

A number of other modeling approaches have exhibited some of the phenomena illustrated here, including viscoelastic models (springs, dashpots, and Maxwell bodies), soft glassy materials (transitions between metastable energy states), and WLC models. The strength of the cross-linker model is that it exhibits many of the desired experimental behaviors, particularly strain-induced fluidization, at the same time suggesting a new biomechanical basis for the behavior. This is not to say that existing models are entirely without mechanistic basis; for example, WLC models certainly imply the underlying behavior of stiff and semiflexible fibers. However, as noted in a previous study (8), the necessary energy landscapes still largely resist direct connections with underlying mechanistic behaviors, and there are questions about the microscopic basis of viscoplastic phenomenology (28). In fact, the cross-linker model may contribute meaningfully to the interpretation of phenomenological aspects of these existing models by providing one possible explanation for this behavior.

The cross-linker model functions at a fundamental level by the displacement-induced detachment and subsequent reattachment of cross-linkers. At steady state, there are bound cross-linkers (nonzero n) only within the binding region. This steady-state distribution is an even function of y. When the tissue is displaced ($\Delta L$), the cross-linker distribution is displaced according to $v\left(t\right)$; the cross-linker distribution is no longer symmetric about $y=0$ and the generated force is increased correspondingly. Bound cross-linkers that have been moved outside the binding region then undergo detachment, bringing the total number of attached cross-linkers below 1 and triggering attachment within the binding region.

Fluidization occurs in a similar manner. The oscillations encourage detachment of cross-linkers by creating a larger displacement from the binding region and thus triggering rebinding. Upon return to the original displacement (i.e., the mean of the oscillations), the bound cross-linkers are preferentially located in the center of the bound distribution, as this region has undergone less displacement into the detachment region. As a result, less cross-linker force is generated.

The model behavior depends on a number of parameters, particularly in the attachment, detachment, and force functions. In fact, little is known about the assumed forms of the attachment function, $\alpha \left(y\right)$, the detachment function, $\beta \left(y\right)$, or the force generating function, $\rho \left(y\right)$. The parameter set used here was determined by trial and error to give reasonable agreement with the experimental data presented for ASM. However, the primary goal is to demonstrate qualitative agreement between the cross-linker model and experiment to support the hypothesis that these observed phenomena can be explained on a biomechanical basis in cross-linker protein dynamics. Further knowledge of α, β, and ρ, as well as appropriate parameters, would greatly aid the further development of this model.

The model does fail to capture one aspect of the experimental data; principally, it does not capture the full amplitude of the force oscillations in the oscillatory regime (Fig. 2) and consequently underestimates somewhat the mean behavior. It is possible to rectify this by applying a higher-order, or perhaps exponential, force-generating function, $\rho \left(y\right)$, but we feel that at this time, such a modification would be purely phenomenological and complicate the model unnecessarily.

One observation about the model results is that the stress relaxation behavior is not precisely described by a power law. Many studies have shown that biological tissues exhibit power-law stress relaxation (2,4,29), sometimes spanning durations of several orders of magnitude (30,31). Stress relaxation in our model is dominated by two time constants, and it thus exhibits multiexponential rather than true power-law behavior. In the model, as described, these exponentials blend reasonably well toward quasi-power-law behavior: see Fig. 7 for the time course of stress relaxation for a held stretch of 10% L_ref. This certainly suggests the possibility of blending exponentials to provide power-law stress relaxation; while a single cross-linker does exhibit multiexponential behavior, a distribution of lengthscales across many cross-linkers could create an ensemble that generates power-law relaxation. A similar approach has previously been demonstrated for viscoelastic elements (4). An alternate explanation is that cell rheology in fact exhibits terminal relaxation rather than true power-law behavior, an observation supported by intracelluar, rather than extracellular, measurements (32,33); such observations are broadly consistent with the plateau in stress relaxation seen here. Another possibility is that the attachment, detachment, and force-generation functions used here are inaccurate and, as such, do not fully capture the underlying behavior.

Figure 7.

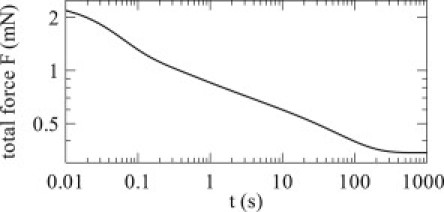
Stress relaxation. The cross-linker is stretched by 10% of the reference length and held for 1000 s. Although the relaxation is multiexponential, across these five decades of time the behavior is a reasonable approximation to a power law.

Another limitation of the model is the assumption that cross-linker strain can be related to tissue displacement by a single parameter (γ). Although this is a reasonable assumption when considering a 1D arrangement, disordered tissues may be difficult to capture in this manner. However, this may be both a limitation and an opportunity: it may be that a single γ, rather than a more detailed treatment of the distribution of γ across multiple cross-linkers, is the limitation that prevents sufficient exponential blending into power-law stress relaxation.

That said, the cross-linker model does an excellent job of reproducing the dynamic, passive properties of ASM, especially strain-induced fluidization. In particular, this will be of use in assessing the potential impact of strain-induced fluidization in terms of asthma and the cyclic strains associated with tidal breathing and deep inspirations. Moreover the cross-linker model suggests a new biomechanical basis for strain-induced fluidization, which may help with the interpretation of behavior underlying the phenomenological aspects of existing models.