Statistics of Active Transport in Xenopus Melanophores Cells

Abstract

The transport of cell cargo, such as organelles and protein complexes in the cytoplasm, is determined by cooperative action of molecular motors stepping along polar cytoskeletal elements. Analysis of transport of individual organelles generated useful information about the properties of the motor proteins and underlying cytoskeletal elements. In this work, for the first time (to our knowledge), we study collective movement of multiple organelles using Xenopus melanophores, pigment cells that translocate several thousand of pigment granules (melanosomes), spherical organelles of a diameter of ∼1 μm. These cells disperse melanosomes in the cytoplasm in response to high cytoplasmic cAMP, while at low cAMP melanosomes cluster at the cell center. Obtained results suggest spatial and temporal organization, characterized by strong correlations between movement of neighboring organelles, with correlation length of ∼4 μm and pair lifetime ∼5 s. Furthermore, velocity statistics revealed strongly non-Gaussian velocity distribution with high velocity tails demonstrating exponential behavior suggestive of strong velocity correlations. Depolymerization of vimentin intermediate filaments using a dominant-negative vimentin mutant or actin with cytochalasin B reduced correlation of behavior of individual particles. Based on our analysis, we concluded that steric repulsion is dominant, but both intermediate filaments and actin microfilaments are involved in dynamic cross-linking organelles in the cytoplasm.

Introduction

Fundamental aspects of active transport and emergent behavior in biomolecular systems consisting of polar filaments and protein motors are at the center of research in both the biology and physics communities. Recent in vivo and in vitro experiments (1–4), simulations, and continuum theories (5–7) have revealed a rich variety of active transport and highly-organized structures formed spontaneously in model biomolecular systems composed of a few types of purified proteins (such as cytoskeletal filaments and associated motor proteins) and supplemented with ATP. These structures include radial asters assembled from microtubules, rotating vortices, and various kinds of oriented bundles and networks of actin filaments with motors and crosslinkers.

A related fundamental problem is active transport of cargo on cytoskeletal networks in a cell and its dependence on the cooperation between different kinds of motor proteins and polar network organization (8–10). It is known that due to the polar nature of cytoskeletal filaments, the transport of cell cargo (vesicles, organelles) is greatly enhanced by the activity of molecular motors moving directly along their filament tracks rather than diffusion throughout the cytoplasm. The relationship between transport and filamentous network structure, and more importantly, cooperative dynamics between various classes of molecular motors, is poorly understood. Large-scale network organization will strongly influence active transport, and the self-assembled structures such as microtubular asters and bundles could provide a mechanism for transporting and concentrating molecular factors of interest over macroscopic distances in a highly efficient manner.

Here we focus on active transport in a simplified yet nontrivial biological model system. Melanophores are pigment cells found in many lower vertebrates responsible for allowing rapid color change in these animals. To accomplish this task, pigment granules called melanosomes are transported en masse along microtubules and actin filaments in response to hormonal signals, resulting in darkening or lightening of the skin. The advantage of this system for biophysical study is that primary biological mechanisms of melanosome transport are well characterized.

In Xenopus laevis melanophores, microtubule motors kinesin-II and cytoplasmic dynein transport melanosomes away from or toward the cell center, respectively (11), while myosin V is responsible for actin-based motility of melanosomes (12). Regulation of melanosome transport is mediated by cAMP-dependent protein kinase (PKA) (13). Transport toward the cell center (referred to as aggregation) occurs in response to factors that act to ultimately lower cAMP levels and decrease PKA activity, such as melatonin. Conversely, factors that act to increase cAMP and PKA activity, such as melanocyte-stimulating hormone, induce dispersion of melanosomes throughout the cell (see Fig. 1).

Figure 1.

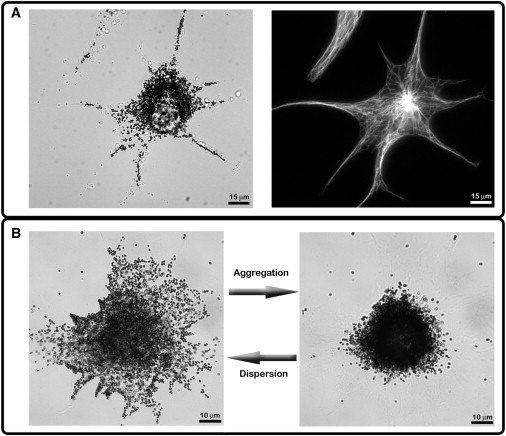
Xenopus melanophore cell. (A) Bright-field image of the cell (left). Epifluorescence imaging of the same cell stained with a monoclonal antibody against α-tubulin (right). (B) Bright-field images of fully dispersed (left) and aggregated (right) melanophore cells. See also Movie S1 and Movie S2 in the Supporting Material.

Using a variety of image tracking tools and sophisticated correlation analysis, we clearly demonstrate that active transport of melanosomes exhibits spatial and temporal organization, manifested by non-Maxwellian velocity distribution functions, clustering of the particles, and enhanced correlations between neighboring organelles. We hypothesize that the correlations arise due to two primary mechanisms: steric repulsion between neighboring organelles and cross-linking of neighboring organelles by cytoskeletal filaments, such as vimentin and actin.

Results

In this study, we employed one- and two-particle statistics to characterize the collective motility of melanosomes with high resolution. Single-particle analysis includes velocity distribution functions P(V). Two-particle analysis includes the time correlation function of the distance between melanosome pairs and pair fluctuations as a function of distance, pair lifetime, and cluster size distribution. Our particle-tracking procedures, with subpixel resolution (14), allowed us to effectively track thousands of melanosomes in the course of their aggregation, dispersion, and in the resting state, and over a long interval of time with sufficient resolution to accumulate reliable statistical information.

One-particle statistics

We tracked several thousand particles over a 10-min period with a camera acquisition rate of five frames per second. This allowed us to accumulate significant statistics of instantaneous (frame-to-frame) velocity V probability distribution of individual melanosomes, P(V), typically ∼10⁶ sample points. These measurements were performed in cell processes where the direction of movement (toward or away from the cell center) can be easily determined and melanosomes can be continuously tracked for a long time.

Representative trajectories of individual melanosomes at the rest state, dispersion, and aggregation are shown in Fig. 2; the insets illustrate projections of instantaneous velocities on the average velocity along the trajectory in question. As one sees from Fig. 2, at the rest state the melanosome executes a type of random walk. In the case of dispersion and aggregation, they move predominantly along the processes in a certain direction, with relatively rare direction reversals. The results for the melanosome velocity distributions are shown in Fig. 3. The average rate of movement toward the center during aggregation is ∼0.19 μm/s and that away from the cell center during dispersion is ∼0.063 μm/s.

Figure 2.

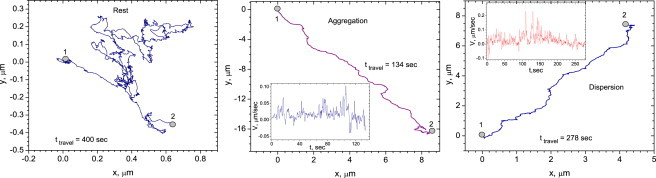
Representative trajectories of individual melanosomes in rest state, dispersion, and aggregation. (Insets) Instant velocity of melanosomes projected on average velocity along the trajectory for aggregation and dispersion.

Figure 3.

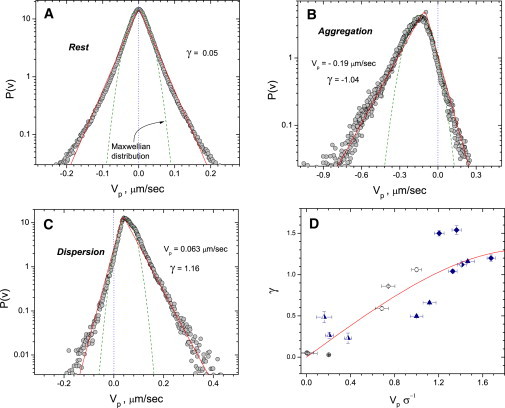
Typical velocity distribution P(V) of melanosomes in a melanophore cell in the rest state (A), aggregation (B), and dispersion (C). (Solid lines) Fit to solution of Eq. 4 for η = 0.1 and F₀ = 0 for panel A and F₀ = 0.7 for panels B and C. (Dashed lines) Fit to the Maxwell distribution P(V) ∼ exp((V/V₀)²). (D) Skewness γ of the velocity distribution P(V) as a function of normalized average transport velocity in melanophore processes. Mean velocity V is normalized by the standard deviation σ of the corresponding velocity distribution. (Diamonds) Aggregation data. (Stars) Dispersion. (Circles) Rest condition. Data shown for different cells. (Half-solid symbols) Cells with depolymerized actin subsystem. (Crossed symbols) Data for cells with depolymerized vimentin network. Solid curve is obtained by solving Eq. 4 in the range of forces F₀.

To characterize the degree of deviation from the Gaussian distribution, we used dispersion of the velocity

$$D=\langle V^2\rangle -{\langle V\rangle }^2$$

and higher normalized central moments of the distribution functions, such as skewness γ and kurtosis K:

$$\begin{array}{l}\gamma =\frac{\langle {\left(V-\langle V\rangle \right)}^3\rangle }{D^{3/2}},\\ K=\frac{\langle {\left(V-\langle V\rangle \right)}^4\rangle }{D^2}.\end{array}$$ (1)

Skewness characterizes asymmetry of the distribution while kurtosis measures the symmetric deviation from the Gaussian distribution (the size of a distribution's tails). For the Gaussian distribution, both skewness and kurtosis are equal to zero. The results of our statistical analysis summarized in Fig. 3 showing that melanosome velocities are more widely distributed than the Gaussian, with kurtosis in all cases larger than 2. Remarkably, the skewness of the distribution (measure of asymmetry) is nonzero in the case of both aggregation and dispersion and essentially zero in the steady-state case. This means that the asymmetry of the velocity distribution is directly related to the bias between molecular motors that results in overall motion of the melanosomes toward or away from the cell center.

The skewness appears to be a monotonically increasing function of normalized mean velocity of melanosomes (Fig. 3 D). This indicates that the primary cause of skewness is the bias between molecular motors. We believe that the nonzero skewness of distribution could be explained by correlative behavior of individual particles (15) and dissipation in the case of directed motion (aggregation or dispersion). The most likely source of dissipation is the viscous drag and friction that is experienced by melanosomes moving through the crowded environment of the cytoplasm. This drag is also a likely source of the large overpopulated tails of the distribution. As we show below, the shape of this distribution function can be described by a simple model that incorporates isotropic fluctuations, viscous dissipation, and constant biased force (see Fig. 3, A–C).

The tails of the distribution behave approximately as an exponent, i.e.,

$$P\left(V\right)\sim \exp \left(-\left|V\right|/a_{\pm }\right),$$

where a_± expressions are the decay constants for V → ∞ and V → −∞, correspondingly. In the resting state (Fig. 3 A), the constants are

$$a_{+}\approx a_{-}=0.027\pm 0.002\mu m/s,$$

which is comparable to the typical speed of moving melanosomes. Importantly, both tails have the same decay constant. In the case of dispersion or aggregation, however, the asymptotic constants a_± are markedly different between tails. For example, in the dispersion case shown in Fig. 3 C, the constants are

$$\begin{array}{l}{a}_{+}=0.027\pm 0.003\mu \text{m}/\text{s},\\ a_{-}=0.0346\pm 0.0003\mu \text{m}/\text{s}.\end{array}$$

This is consistent with the observation that the distribution has nonzero skewness.

Multiparticle statistics

So far, we have described the behavior of individual melanosomes. Next, we analyzed whether aggregating or dispersing melanosomes move independently of each other or if their behavior is correlated. To examine correlation, we measured the distance between all pairs of melanosomes contained in a single cellular process during the course of aggregation, dispersion, and at the steady state, typically ∼1500 particles. We then determined the following characteristics: standard deviation and correlation of distance between two particles versus time, pair lifetime (i.e., how long the particles are in contact), and melanosome cluster size distribution.

To analyze correlation effects on melanosome transport we tracked melanosomes in the cell and determined the standard deviation, δ, of fluctuations of the distance R(t) at time t between pair of melanosomes over the entire time of transport:

$$\delta =\sqrt{\langle R^2\rangle -{\langle R\rangle }^2}.$$ (2)

The averaging is done over time. These pair distance fluctuations were calculated for all pairs of melanosomes involved in transport within a specific cell's processes.

The distance R is calculated only for moving melanosomes; the particles which had displacement smaller than the radius of melanosome over the duration of experiment were excluded. Because melanosomes are moving with roughly the same velocity, the distance R exhibits relatively slow fluctuation. However, a significant difference in the value of standard deviation δ between different cells is likely due to the difference in physiological conditions, such as bias between the motors, configuration of actin/microtubules networks, and other factors.

Evolution of the pair distance standard deviation δ as a function of pair distance R is shown in Fig. 4, A–C, for aggregation, dispersion, and for the resting state. One sees from this figure that melanosome pair fluctuations are significantly suppressed at distances below 4 μm regardless of type of transport; this is a clear manifestation of correlated motion. The data suggest a correlation length (i.e., length associated with suppressed fluctuations) of a melanosome to be ∼4–5 melanosome diameters. Because this correlation length does not depend on the net direction of transport (associated with different types of motors), we conclude that the main contribution to the correlation effects come from physical factors such as steric repulsion and/or crosslinking by other cytoskeletal elements, rather than the identity of the motor proteins transporting the melanosomes.

Figure 4.

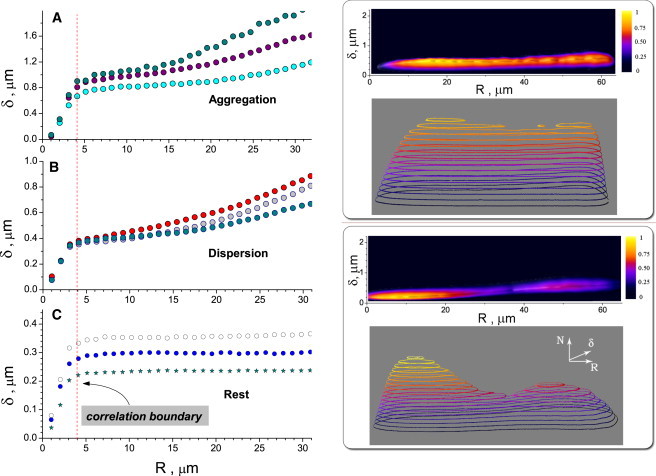
Pair distance correlation statistics. Plots A–C illustrate typical distance standard deviation δ between pair of melanosomes as a function of distance between the pair R for aggregation (A), dispersion (B), and in the steady state (C). Representative data for three different cells is shown in each plot. In all cases the pair fluctuations δ are suppressed at distances under 4 μm. Dashed lines in the plot indicates a distance correlation boundary. Error bars are within the size of the symbols. The noise level due to the uncertainty of a particle position determination is 0.06 μm. Plots D and E show probability distribution f(R,δ) to find a pair at the distance R with the distance fluctuation δ. Plot D shows data for aggregation and E for dispersion. (Upper panel) f(R,δ) in pseudocolor representation and lower plots in surface-contour representation. Note a peak for small (R,δ) on the plot E corresponding to higher probability of correlated motion in the case of dispersion.

Fig. 4, D and E, shows probability f(R,δ) to find a pair at the distance R with the standard deviation of distance fluctuations δ. There is a noticeable difference between the data for aggregation and dispersion (compare Fig. 4, panel D to Fig. 4, panel E). The peak in Fig. 4 E indicates a larger tendency toward correlated motion of dispersing melanosomes. In the case of dispersion, more pairs of melanosomes form tightly-bound states with reduced fluctuations of the pair distance. This differs from the case of aggregation, where we do not see large populations of correlated particles.

The transport of melanosomes is, in general, a nonstationary stochastic process. In the case of dispersion/aggregation, the motion of individual melanosomes can be described as a random walk with nonzero drift velocity. Correspondingly, the distance between pairs R(t) can be presented as

$$R\left(t\right)={\int }_0^t\Delta v\left(t^{\prime }\right)d{t}^{\prime },$$

where Δv(t) is the difference in instant velocity of two melanosomes. Because, in general, 〈Δv〉 ≠ 0 (the mean velocity measurements of melanosomes are not identical), the distance 〈R(t)〉 ∼ 〈Δv〉 t will diverge for large times (note that R(t) is only the difference-stationary stochastic process). Consequently, the standard autocorrelation function

$$K\left(\tau \right)=\langle R\left(\tau \right)R\left(t+\tau \right)\rangle -{\langle R\left(t\right)\rangle }^2$$

will diverge for t→∞ and, therefore, cannot be used. To analyze the time correlation T_corr between melanosome pairs, we calculated instead a normalized autocovariance function

$$C\left(\tau ,t\right)=\frac{\langle R\left(t\right)R\left(t+\tau \right)\rangle -\langle R\left(t\right)\rangle \langle R\left(t+\tau \right)\rangle }{\langle R{\left(t\right)}^2\rangle -{\langle R\left(t\right)\rangle }^2}.$$ (3)

For the difference-stationary processes, the autocovariance does not depend on the second argument. Select autocovariance functions C(t) for individual pairs for the rest state, dispersion, and aggregation are shown in Fig. 5. In Fig. 6, the dependence of correlation time versus distance is shown for several different cells. Here the averaging procedure is taken over time and all pairs of melanosomes in the same process. Correlation time is determined from the condition

$$C\left(T_{\text{corr}}\right)=\left(C\left(0\right)-\min C\left(t\right)\right)/2.$$

Typical pair correlation times are shown in Fig. 6 as a function of distance between the particles.

Figure 5.

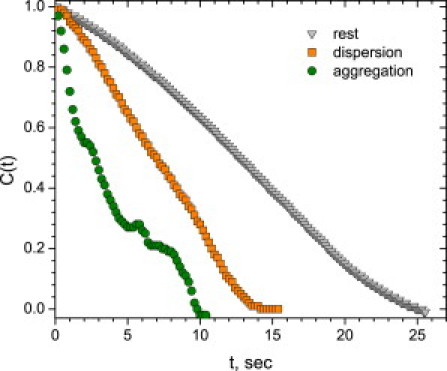
Select autocovariance functions C(t) for pair distance for rest state, dispersion, and aggregation.

Figure 6.

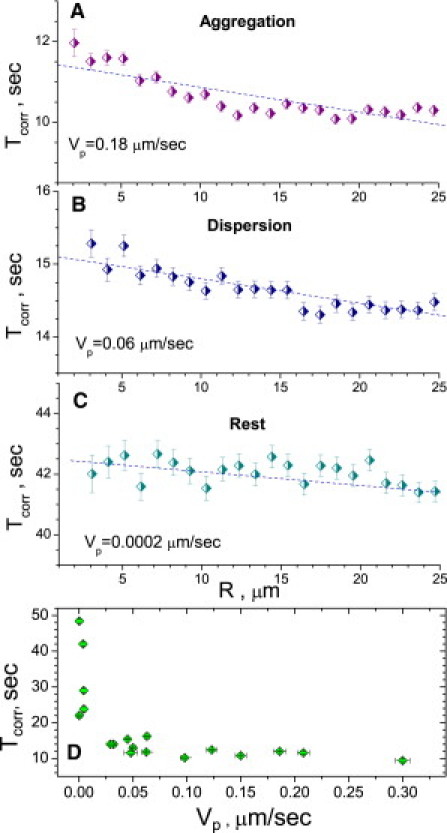
Pair correlation times T_corr as a function of distance for aggregation (A), dispersion (B), and in the steady state (C). Pair time correlation decreases with the distance and depends on average transport velocity in the processes, V_p: lower value of the average velocity produces longer pair correlation times. (D) Correlation time T_corr versus average transport velocity in the processes, V_p. For all cells studied (including cells with depolymerized actin and vimentin filaments), correlation time decreases with the averaged velocity V_p.

For all transport events (aggregation, dispersion, and resting state), the pair correlation time T_corr decreases with the distance between melanosomes R. The magnitude of correlation, however, depends on the average transport velocity in the cell processes (Fig. 6 D). We observed that the higher transport velocities correspond to smaller pair correlation times, suggesting that heterogeneity of cytoskeletal networks impeding motion of melanosomes is a primary factor for the decay of pair correlation. We also calculated from our data the average pair lifetime, T_life. This is the time during which the distance between two melanosomes stays on the order of the average melanosome diameter, i.e., 1 μm. For most of our measurements, we observed that the lifetime is on the order of T_life ∼ 5–6 s, both for dispersion and aggregation.

Contribution of other cytoskeletal networks

To investigate the role of different cellular components on the statistical properties of transport, we compared measurements taken from control melanophores with those taken from cells whose actin or intermediate filament networks have been disrupted. Melanophores were treated with Latrunculin B to depolymerize actin microfilaments, then subjected to particle tracking analysis as previously described; fluctuations of the pair distances are shown in Fig. 7, A and B. Fluctuations are suppressed at distances <3 μm, compared to 4 μm in untreated cells. This suggests the smaller correlations between melanosomes when actin filaments are depolymerized. Corresponding values of the transport velocities, V_p (index p denotes averaging over many processes of the cell) were decreased in these cells, leading to an increase in time correlation.

Figure 7.

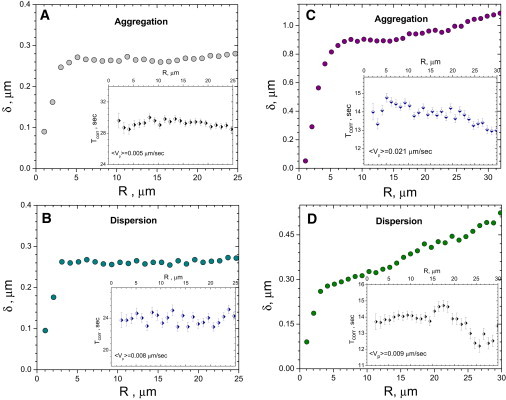
Pair distance correlation statistics for the cells with depolymerized actin (A and B) and vimentin (C and D). (Main plots) Distance fluctuations δ versus distance R. (Insets) Correlation times T_corr versus R. Error bars are within the size of the symbols. Depolymerization of the actin subnetwork leads to decrease of melanosome's distance correlations. Pair time correlations are significantly increased for both aggregation (A) and dispersion (B) due to significant decrease of the transport velocity for the system with depolymerized actin.

To investigate the effect of the intermediate filament network on melanosome transport, we performed particle-tracking and analysis on melanophores transfected with a dominant-negative vimentin construct (16) to disrupt vimentin polymer formation. Pair fluctuations in these cells have not shown considerable deviations with respect to wild-type cells for aggregation or dispersion (Fig. 7, C and D). This fact suggests that while vimentin may provide short-range linking of melanosomes, as demonstrated in Fig. 8 A, these events are rather rare and do not significantly effect the global statistics of melanosome transport. In addition, we calculated a cluster size distribution. The cluster is defined as an assembly of particles with the distance between neighbors not exceeding critical distance of the order of mean particle diameter. While the clusters move together for a long time, the number of particles in the cluster is not necessarily conserved: particles leave/join the cluster with a certain rate, as it is characterized by the averaged pair lifetime.

Figure 8.

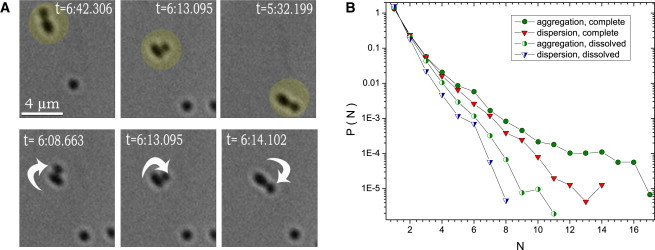
(A) Example of composite rotational and translational motion of two permanently bound melanosomes in complete system during aggregation process. (Upper row of images) Drift of rotating melanosome pair. (Lower row) Rotation of the pair in a moving frame. Correlation time for this pair is ∼70 s. Averaged over the entire system, the pair time correlation is only 12 s and averaged pair lifetime is T_life ∼ 5–6 s. Melanosomes in the dimer can rotate with respect to each other without breaking the contact as demonstrated in the middle sequence of images. See also Movie S3 in the Supporting Material. (B) Cluster size probability function P(N),where N is the number of melanosomes in the cluster, for the complete system (solid symbols), and the system with depolymerized vimentin intermediate filaments (half-solid symbols).

The comparison for cells with disrupted vimentin network and corresponding distributions taken in wild-type cells is shown in Fig. 8 B. As one can see, cells with a disrupted vimentin network demonstrate suppressed cluster size distributions P(N). This effect becomes more pronounced for large clusters (number of particles in the cluster N > 4), while for small clusters (N ∼ 2–3), which are the core contributors to transport, all curves practically coincide.

Mathematical model

To understand single-particles statistics, we apply the generalization of a well-known statistical model for dissipative gases, the so-called inelastic Maxwell model, studied in the context of granular materials (17,18). To analyze the evolution of the velocity probability distribution density P(V), we consider the following model of the melanosome transport: the melanosomes experience random fluctuations, nonzero bias force, and viscous-type relaxation of the velocity. The model is described by linear nonlocal Fokker-Planck equation for P(V) (17,18):

$$\frac{\partial P\left(V\right)}{\partial t}=D_0\frac{{\partial }^{2}P\left(V\right)}{\partial V^2}-F_0\frac{\partial P\left(V\right)}{\partial V}+\frac{1}{\eta }P\left(\frac{V}{\eta }\right)-P\left(V\right).$$ (4)

The first term describes random forcing acting on melanophore due to motor fluctuations, approximated for simplicity by the white noise with intensity D₀ (in the following D₀ can be set to 1); the second term describes the bias force F₀ due to action of motors. The last two terms describe, on the phenomenological level, changes in the velocity due to viscous dissipation and other mechanisms of velocity relaxation (e.g., friction with actin/vimentin filament networks, etc.). Note that this form of Eq. 4 conserves the total number of particles,

$$\int dVP\left(V\right).$$

Equation 4 does not provide information on two-particle statistics and time correlation. It would require a significantly more complicated and essentially nonstationary model.

Equation 4 is different from that considered in Kohlstedt et al. (17) and Harting et al. (18) in the context of granular media by the presence of bias force F₀. Stationary (∂P/∂t = 0) solution, which describes steady-state transport of melanosomes as the mean drift velocity 〈V〉 is not zero due to the bias, can be obtained by means of Fourier transformation:

$$F\left(k\right)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}dV{e}^{-ikV}P\left(V\right)=\prod _{m=0}^{\mathrm{\infty }}\frac{1}{1+k^2{\eta }^{2m}-i{F}_{0}k{\eta }^m}.$$ (5)

For |V| → ∞ , the term

$$\frac{1}{\eta }P\left(\frac{V}{\eta }\right)$$

in Eq. 4 can be neglected (compare to the equation term in Kohlstedt et al. (17)); the asymptotic behavior is then exponential,

$$P\left(V\right)\sim \exp \left(-\left|V\right|/a_{\pm }\right),$$

with asymptotic exponents

$$a_{\pm }=1/|F_0/2\pm \sqrt{F_0^2/4+1}|\text{.}$$

Obviously, a₊ ≠ a₋ for F₀ ≠ 0.

The results obtained from theoretical model are in excellent agreement with the experiment. For nonzero bias, the F₀ solution to Eq. 4 closely resembles the experimental curve: exponential tails and asymmetry (see Fig. 3, A–C). Moreover, the dependence of the skewness γ on F₀ (and, correspondingly, the mean velocity of drift

$$\langle V\rangle =\int dVVP\left(V\right)$$

lays within experimental data (see Fig. 3 D). It strongly supports our assumption that the asymmetry of distribution function is the effect of directed transport and dissipation rather than the difference between the motors pulling back and forth.

Discussion

In this study, we characterized the collective transport of pigment-containing organelles in Xenopus melanophores. Our analysis revealed that the motility of neighboring melanosomes exhibits a strong correlation, manifested by increased correlation time, decreased intensity of pair distance fluctuations, and clustering of particles. We suggest that two major mechanisms are responsible for the increase of correlations: steric repulsion between the neighboring particles and cross-linking by cytoskeletal filaments.

The evidence that cytoskeletal filaments provide short-range linking of melanosomes is demonstrated in Fig. 8 A. The sequence of images shows a spinning pair of melanosomes (a dimer) found in complete systems. Such spinning configuration may exist only if the melanosomes are permanently bound, and cannot be explained by steric repulsion alone.

Crosslinking of melanosomes by cytoskeletal filaments is likely responsible for different shapes of distribution functions f(R,δ) in the course of dispersion and aggregation in wild-type melanophores (compare Fig. 4, D and E). As one sees from Fig. 4 E, there is an increased probability to observe a cluster of particles in the course of dispersion, manifested by a peak in the probability distribution. No similar peak was observed for aggregation. The difference is likely due to the fact that dispersion starts with closely-packed configuration of melanosomes, and those can be more readily crosslinked by cytoskeletal filaments. In contrast, aggregation starts with particles that are relatively far away from each other, making it more difficult to be crosslinked by short filaments.

We ask, what is the biological significance of correlation in melanophore transport? We think that crosslinking increases the collective mobility of melanosome trains in highly crowded cell environment that, in turn, significantly increases the efficiency of the melanosomes transport.