Abstract
Understanding the role of electrostatics in protein stability requires knowledge of these interactions in both the folded and unfolded states. Electrostatic interactions can be probed experimentally by characterizing ionization equilibria of titrating groups, parameterized as pKa values. However, pKa values of the unfolded state are rarely accessible under native conditions, where the unfolded state has a very low population. Here, we report pKa values under nondenaturing conditions for two unfolded fragments of the protein G B1 domain that mimic the unfolded state of the intact protein. pKa values were determined for carboxyl groups by monitoring their pH-dependent 13C chemical shifts. Monte Carlo simulations using a Gaussian chain model provide corrections for changes in electrostatic interactions that arise from fragmentation of the protein. Most pKa values for the unfolded state agree well with model values, but some residues show significant perturbations that can be rationalized by local electrostatic interactions. The pH-dependent stability was calculated from the experimental pKa values of the folded and unfolded states and compared to experimental stability data. The use of experimental pKa values for the unfolded state results in significantly improved agreement with experimental data, as compared to calculations based on model data alone.
Abbreviations used: HSQC, heteronuclear single quantum coherence; NA, Avogadro's number
Introduction
Electrostatic interactions are important for protein solubility (1) and function, e.g., catalysis and proton transport (2–5), and modulate protein stability (6,7). Experimental information on electrostatic interactions is accessible by measurement of protonation equilibria of ionizable groups, which are typically reported as pKa values. NMR spectroscopy offers a direct and site-specific method to determine pKa values by measuring chemical shifts as a function of pH (8,9), providing a rich source of data (10,11). Significant perturbations away from the intrinsic values in short peptides are seen in many proteins (12). Perturbed pKa values report on long-range electrostatic interactions (13,14), specific interactions such as salt bridges (15), and the functional importance of catalytic groups in enzyme active sites (3).
The pH-dependent stability of a protein can be calculated if the pKa values of all ionizable groups are known (16). Since protein stability is determined from the free-energy difference between the unfolded and folded states, the pKa values of both states need to be known (Fig. 1). However, it is not straightforward to measure pKa values of the unfolded state, because it normally has a very low population under native conditions. To date, there has been only a single report where pKa values were determined experimentally for an unfolded state under nondenaturing conditions (17). Indirect methods use denaturing conditions, and the pKa values of the unfolded state under native conditions are estimated by extrapolation to zero denaturant (18). This approach has the drawback that the unfolded state may have different characteristics under native and denaturing conditions (19). The unfolded state has also been assessed through stability data for mutants of the N-terminal domain of protein L9, barnase, and CI2, where strong electrostatic interactions persist in the unfolded state (20–22). Calculated pKa values for random-coil-like models of unfolded proteins have given good agreement with experimental stability data in a number of cases (6,23–28). Here, we take an alternative experimental approach and use intrinsically unfolded fragments as a model for the unfolded state of the intact protein (29–32).
Figure 1.
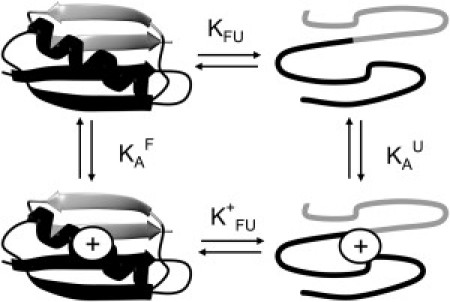
A thermodynamic cycle links the equilibria for protein folding in the charged and uncharged states of a protein. For PGB1-QDD, the equilibrium to the left was previously studied (33) and the equilibrium to the right is determined indirectly in this study by using fragments (N41 (black) and C16 (gray)) as models for the unfolded state. The upper and lower equilibria were studied at various pH values using thermal denaturations (34).
Recently, we determined the pKa values for the folded state of a variant of the B1 domain of Streptococcal protein G with mutations T2Q, N8D, and N37D (PGB1-QDD) (Fig. 2) (33). Based on the experimental pKa values for the folded state and a Gaussian chain model of the unfolded state, we calculated the pH-dependent stability and compared it with that determined by denaturation at a series of pH values (34). The results revealed deviations between the calculated and experimental stability curves (35), indicating that the unfolded state includes electrostatic interactions that are not adequately described by the Gaussian chain model. To refine the description of the unfolded state, we have measured pKa values for two PGB1 fragments, comprising residues 1–41 and 41–56, respectively, which are unfolded under nondenaturing conditions and serve as a model of the unfolded state of the intact protein (36,37). The fragments were derived from a highly stable PGB1 variant denoted PGB1-QDD (34) that contains the T2Q mutation to avoid N-terminal degradation (38) and the N8D and N37D mutations to avoid heterogeneity due to deamidation (39). Side-chain carboxyl 13C chemical shifts were monitored as a function of pH to yield pKa values of all acidic groups in the unfolded fragments. We carried out Monte Carlo (MC) simulations of the electrostatic interactions in the unfolded states of intact PGB1-QDD and the two fragments to assess to what extent cleavage of the peptide chain affects the pKa values. Furthermore, we performed molecular dynamics (MD) simulations to gain structural insights into some highly shifted pKa values observed for the folded state. Using the experimental pKa values, the pH dependent stability was calculated and compared to experimental denaturation data. The agreement is significantly improved compared to the previous calculations based purely on a Gaussian chain model of the unfolded state.
Figure 2.

Primary and secondary structure of intact PGB1-QDD. The arrow indicates the point of fragmentation. The acidic residues are in bold.
Materials and Methods
Cloning, expression, and purification of 13C- and 15N-labeled PGB1 fragments
Detailed description about cloning, expression, and purification of PGB1-QDD fragments can be found elsewhere (see Bauer et al. (36) and Supporting Material). In short, the fragments were expressed in minimal medium containing 13.7 mM 15NH4Cl and 12.5 mM 13C-glucose, purified on chitin matrix, cleaved from the intein and chitin-binding domain by dithiothreitol, further purified by gel filtration and desalted. Purified peptides were analyzed using matrix-assisted laser desorption/ionization mass spectrometry to confirm peptides of correct size. Far-UV CD spectra (Fig. S1 in the Supporting Material) indicate that the fragments are unfolded over the pH range.
NMR spectroscopy
NMR spectra were recorded on a 500-MHz Varian Unity Plus spectrometer at 25°C. Data processing was performed using the NMRPipe program suite (40), and Sparky (T. Goddard and T. Kneller, unpublished results) was used for assignment and peak analysis. All spectra needed for peak assignment were recorded using samples of 1 mM 13C-15N-labeled N41 (the N-terminal fragment of PGB1-QDD covering residues 1–41) or C16 (the C-terminal fragment of PGB1-QDD covering residues 41–56) at pH 5.0 in 90% H2O/10% D2O, 0.1 mM NaN3, and 0.1 mM 2,2-dimethyl-2-silapentane-5-sulfonic acid. Assignments were based on SO-FAST versions (42) of HNCA, HNCACO, HNCO, HNCOCA, HNCACB (43–48), together with CCONH (49) and 15N-HSQC (50,51) spectra recorded using BioPack (Varian, Palo Alto, CA). The side-chain carboxyl groups were assigned from an H(C)CO experiment (52) or by correlating the side-chain carboxyl 13C chemical shifts with the backbone amide proton chemical shift of the following residue (17).
pH titration
13C-15N-labeled N41 or C16 was dissolved in 90% H2O/10% D2O containing 0.1 mM NaN3 and 0.1 mM 2,2-dimethyl-2-silapentane-5-sulfonic acid to a protein concentration of 0.3 mM. The sample did not include any added NaCl, but the counterion concentration should amount to ∼1 mM. The initial pH was 5.42 for the N41 sample and 6.48 for the C16 sample. The N41 sample was split into two separate samples to obtain a common starting point for upward and downward titrations.
The pH was measured using an MP225 pH meter equipped with a U402-M3-S7/200 combination electrode, calibrated with standard solutions of pH 4.01, 7.00, and 9.21 (Mettler Toledo, Columbus, OH). The pH was adjusted with microliter additions of 0.2 M HCl or NaOH. The concentration of added salt at the end of each titration amounted to 0.03 M. The pH was corrected by 0.04 units to account for the 10% D2O in the sample (53). Spectra were collected in steps of ∼0.25 pH units from pH 1.5–13 for N41 and from pH 2–6.5 for C16.
The titration of acidic groups in N41 was followed by correlating the side-chain carboxyl carbon with the backbone amide proton (17). Spectra were recorded using 2048 and 64 complex points in ω2 (1H) and ω1 (13C), respectively. The spectral widths were 8012 and 1320 Hz for the 1H and 13C dimensions, respectively. For C16, which contains only four carboxyl groups, the titration was followed using an H(C)CO experiment in which the side-chain carboxyl carbon is correlated with the Hβ and Hγ protons of Asp and Glu, respectively (52). At each pH value a H(C)CO spectrum was recorded using 1024 and 64 complex points in ω2 (1H) and ω1 (13C), respectively. The spectral widths were 8012 and 1250 Hz for the 1H and 13C dimensions, respectively. A 15N HSQC spectrum was recorded at each pH value to verify that the sample remained intact and to detect structural changes. All spectra were processed with a cosine window function in both dimensions and zero-filled before Fourier transformation.
Data analysis
The Henderson-Hasselbalch equation with an added Hill parameter (nH) (54) (Eq. 1) was fitted to the side-chain 13C chemical shift data.
| (1) |
where δobs is the observed chemical shifts at a given pH, and δHA and δA- are the chemical shifts of the protonated and deprotonated states, respectively. pH, pKa, and the acid dissociation constant, Ka are defined as follows:
| (2) |
| (3) |
| (4) |
With the assumption ==1, the acid dissociation constant can be written as
| (5) |
Nonlinear least-squares regression analysis of Eq. 1 was performed using Kaleidagraph (Synergy Software, Essex Junction, VT). The standard errors from the fit are presented in Table 1 and the uncertainty in pH was estimated to be ±0.05 pH units. The proton binding capacitance (33,55) was obtained from the derivative of normalized titration data using Grace (http://plasma-gate.weizmann.ac.il/Grace/). The proton binding capacitance of the whole protein was obtained by summing up the capacitance from all residues.
Table 1.
Residue-specific pKa values and Hill parameters in the folded and unfolded states of PGB1-QDD
| Residue | pKa Folded∗ | nH Folded∗ | pKa Unfolded† | nH Unfolded† | pKa Unfolded corrected‡ | nH Unfolded corrected‡ | pKa Folded§ |
|---|---|---|---|---|---|---|---|
| D8 | 4.91 ± 0.02 | 0.67 ± 0.02 | 3.74 ± 0.01 | 0.92 ± 0.02 | 3.72 | 0.90 | 3.22 |
| E15 | 4.63 ± 0.01 | 0.88 ± 0.02 | 4.40 ± 0.01 | 0.89 ± 0.02 | 4.41 | 0.86 | 3.77 |
| E19 | 3.90 ± 0.02 | 1.02 ± 0.03 | 4.45 ± 0.01 | 0.84 ± 0.02 | 4.46 | 0.80 | 3.59 |
| D22 | 2.99 ± 0.05 | 1.05 ± 0.09 | 3.87 ± 0.02 | 0.86 ± 0.02 | 3.87 | 0.83 | 3.29 |
| E27 | 4.81 ± 0.01 | 0.83 ± 0.02 | 4.44 ± 0.01 | 0.86 ± 0.02 | 4.47 | 0.82 | 3.30 |
| D36 | 4.20 ± 0.02 | 0.82 ± 0.03 | 4.11 ± 0.02 | 0.76 ± 0.02 | 4.11 | 0.71 | 3.92 |
| D37 | 6.51 ± 0.02 | 1.11 ± 0.04 | 4.18 ± 0.02 | 0.76 ± 0.02 | 4.20 | 0.69 | 3.93 |
| D40 | 4.12 ± 0.02 | 0.72 ± 0.02 | 4.24 ± 0.02 | 0.71 ± 0.02 | 4.24 | 0.63 | 4.01 |
| E42 | 4.81 ± 0.01 | 0.73 ± 0.02 | 4.39 ± 0.01 | 0.88 ± 0.02 | 4.90 | 0.72 | 4.92 |
| D46 | 3.84 ± 0.02 | 0.90 ± 0.03 | 3.98 ± 0.02 | 0.89 ± 0.03 | 4.10 | 0.77 | 3.59 |
| D47 | 3.15 ± 0.02 | 0.92 ± 0.03 | 3.92 ± 0.02 | 0.89 ± 0.03 | 4.03 | 0.78 | 3.31 |
| E56 | 3.81 ± 0.05 | 0.56 ± 0.02 | 4.73 ± 0.02 | 0.78 ± 0.02 | 4.83 | 0.70 | 5.37 |
| C-term | 3.13 ± 0.04 | 0.69 ± 0.03 | 3.58 ± 0.06 | 0.74 ± 0.05 | 3.58 | 0.66 | 3.69 |
Values previously determined (33).
Values obtained by fitting Eq. 1 to side-chain 13C chemical shift data. The standard errors from the fit are shown and the errors in pH are estimated to be ± 0.05 units.
Values obtained by correcting for cleavage into fragments.
Values obtained from MC simulations of pair-wise electrostatic interactions.
Calculation of pH-dependent stability using generated pKa values
Assuming that the charge state of the protein does not affect its structure, the pH-dependent stability of a protein is expected to be a direct function of the difference in charge between the native and unfolded states and can hence be calculated from pKa values for both states (16). The free energy of unfolding, , for a protein depends on the charge of its residues in the folded and unfolded states according to
| (6) |
where and represent the fractional charges of residue i in the folded and unfolded states, respectively, which can be calculated from the pKa values according to
| (7) |
where Q denotes the formal charge of the ionized group (–1 for acidic residues and +1 for basic ones).
The stability curve calculated from Eqs. 6 and 7 reflects pH-dependent contributions only; therefore, a constant offset (baseline stability) was added to qualitatively compare the curves to the previously determined pH-dependent stability of PGB1-QDD (34). The offset was determined by minimizing the root-mean-square deviation (RMSD) between the two stability curves.
MD simulations on intact, folded PGB1-QDD
Atomistic MD simulations of intact PGB1-QDD, protonated according to pH 7, were performed in the isobaric-isothermal ensemble (NPT) using explicit solvent and the Amber 9 program (56) with the ff99 nonpolarizable force field. The temperature was kept at 298 K using the Anderson thermostat, and the Berendsen barostat was used to maintain a constant external pressure of 1 atm. The protein and counterions were solvated in 3300 SPC/E water molecules (57) in a cubic simulation box with periodic boundaries. A spherical cut-off of 12 Å was applied for all nonbonded interactions and the particle-mesh Ewald summation method was used to take into account long-range electrostatics. After 1 ns equilibration, production runs were sampled for 15 ns with a 2-fs timestep. Ensemble averages of the solvent-accessible surface area (SASA) were sampled for each residue by rolling a ball (radius 1.5 Å) over the fluctuating protein surface. The starting structure for the simulations was generated using the pdb file 1pgb, where T2Q, N8D, and N37D mutations were introduced using Swiss model (58). Intrinsic pKa values were used to determine the charge state of titratable residues.
Gaussian chain model to correct for cleavage
Differences in electrostatic interactions between the intact chain and fragments are due to introduction of new termini and changes in long-range Coulombic interactions due to loss of the complementary part of the chain. The Gaussian chain model (28) should be a good model to capture these differences and was used to evaluate the difference in pKa values between unfolded intact protein and unfolded fragments. The model is presented in depth elsewhere (see Lindman et al. (35) and Supporting Material) and accounts for direct Coulombic interactions. At each pH, the average charges of all negative residues and C-termini in the intact protein and in N41 and C16 were obtained. Titration curves were obtained by performing the simulations at pH values 1–8, and Eq. 7 was fit to data to obtain pKa values.
Experimental pKa values of the fragments were corrected for cleavage and introduction of new N- and C-termini. From MC simulations, using the Gaussian chain model, the pKa values of unfolded, intact chain and unfolded fragments could be calculated. The corrected values were calculated as
| (8) |
MC simulations on intact, folded PGB1-QDD
Coarse-grained Metropolis Monte Carlo simulations of a single PGB1-QDD molecule in a salt solution were performed in the canonical ensemble (NVT) at 298 K using the freely available Faunus framework (59). The procedure and parameters used have been described in detail elsewhere (60,61). In short, amino acid residues in the protein are reduced to single spheres that can be either charged or neutral, depending on the residue type and protonation state. Salt particles are explicitly described by mobile, charged particles, whereas the solvent is treated as a dielectric continuum. Coordinate space is sampled over all salt positions, protonation states, and—if the protein is flexible—backbone configurations. In the case of flexible proteins, neighboring residues are connected via a harmonic potential, , with the spring constant f = 0.1 Å−2 and an equilibrium distance req = 4.9 Å (average amino acid mass center separation in the PDB). Statistical mechanical ensemble averages of the charge state, zi, of all titratable residues are sampled as a function of pH and fitted to Eq. 7 to obtain acid dissociation constants and Hill parameters.
Results
The charge states of all carboxyl groups in the N-terminal fragment (residues 1–41) (N41) and the C-terminal fragment (residues 41–56) (C16) of PGB1-QDD (for sequence details, see Fig. 2) could be monitored using the chemical shift of the 13C carboxyl nucleus as a reporter. The two Asp and two Glu residues in C16 were resolved and assigned using the H(C)CO experiment (52), in which each crosspeak links a side-chain carboxyl carbon to the Hβ (Asp) or Hγ (Glu) of the same residue. The five Asp and three Glu residues in N41 were assigned by correlating the chemical shift of the carboxyl 13C with the amide proton of the following residue (17). All 12 side-chain carboxyl groups and the C-terminus were thus identified and showed pH-dependent chemical shifts (Fig. 3). We note that a few residues (most notably D40) display different pKa values for 1H and 13C (nonlinear titrations in Fig. 3). We showed previously that side-chain 13C gives more reliable pKa values (33), whereas 1H probably reflects titration also of nearby residues. Fig. 4 shows the side-chain chemical shifts versus pH together with the fitted modified Henderson-Hasselbalch model (Eq. 1). The obtained residue-specific pKa values and Hill parameters are listed in Table 1. The Hill parameter is commonly introduced to get improved fit to nonideal titration data (8,54) but also has a physical meaning (33). For a Hill parameter of <1, the titrating group senses repulsion that changes linearly with pH, and a Hill parameter of >1 means that the attraction changes linearly with pH. For nH = 1, the electrostatic energy is constant throughout the titration.
Figure 3.
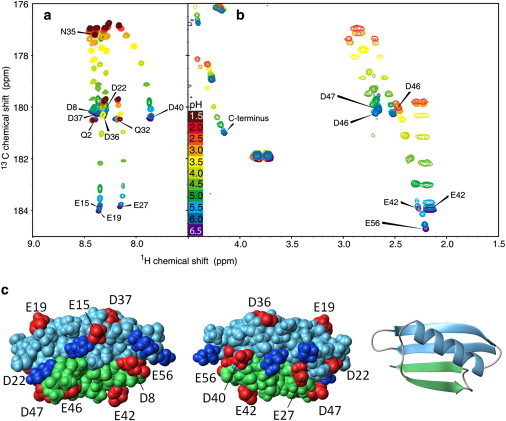
(a) Overlay of spectra at pH 1.5–6.5 for the N41 fragment. The side-chain carboxyl carbon for Asp and Glu is correlated with the amide proton of the following residue (17). (b) Overlay of spectra at pH 2–6.5 for the C16 fragment. The side-chain carboxyl carbon for Asp and Glu is correlated with the β- or γ-protons respectively (52). Some residues show distinct proton chemical shifts for the two hydrogens, indicating slightly different chemical environments. (c) Space filling and ribbon model of PGB1 with residues 1–40 in blue, 41–56 in green, acidic side chains in red, and basic side chains in blue. The two space filling models are related by a 180° rotation around the y axis, with the right one in the same orientation as the ribbon model.
Figure 4.
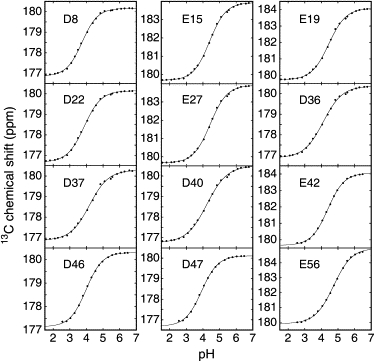
Titration curves for the seven Asp and five Glu residues in the PGB1-QDD fragments. Data points are shown as solid circles and the fit of Eq. 1 to data as solid lines.
In Fig. 5, the pKa values of the unfolded state are compared to model values and to those for the folded state. In general, the experimental pKa values for the unfolded state agree well with the model values, i.e., 4.0 for Asp and 4.4 for Glu (62). Most of the residue-specific shifts in pKa value occur in the same direction as in the folded protein, whereas the pKa values of D8 and E56 are shifted in opposite directions in the folded and unfolded states. Deprotonation of D8 is unfavorable in the folded protein with a pKa value of 4.9, but it seems to be favorable in the unfolded fragment where the pKa value is reduced to 3.7. E56 has a downshifted pKa of 3.8 in the folded state despite being the C-terminal residue with an additional carboxyl group. This observation is rationalized by the presence of a hydrogen bond between K10 and E56 in the folded state, which cannot exist in the fragment. Indeed, in the unfolded fragment the expected repulsion between the two carboxylates is noticeable, causing the pKa value of E56 to increase to 4.7. D36, D37, and D40 form a cluster of negatively charged residues, which may focus the attraction of protons and cause an increase in pKa values. D36, D37, and D40 also show low values of the Hill parameter, indicating that these residues are electrostatically coupled. In the folded protein, D37 has a highly upshifted pKa value of 6.5, whereas in the unfolded fragment, this residue has a marginally upshifted pKa value of 4.2.
Figure 5.
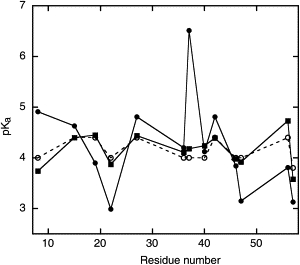
Comparison of pKa values determined in the full-length folded protein (solid circles) with those in the unfolded fragments (solid squares). These values are also compared with model values (open circles) (62). Lines connecting symbols are inserted to help guide the eye.
Proton binding capacitance curves (33,55,63) offer a convenient means of comparing the pH-dependent variation in charge states between the folded and unfolded states. In Fig. 6, the derivatives of the normalized titration data are plotted. The derivative for an isolated residue would have a maximum peak height of 0.57 at pH = pKa. A lower and broader capacitance curve signifies electrostatic coupling, but the area below the curve is retained. Fig. 6 reveals that the proton binding capacitance curves are sharpest for the unfolded state, with peak heights closer to the ideal value of 0.57. Fig. 7 compares the total proton binding capacitances of the intact, folded protein and the unfolded fragments. It is clear that the capacitance curves for the unfolded fragments are closer to ideal than are those for the folded protein. Together, Figs. 5–7 indicate that most of the electrostatic coupling is removed in the unfolded state so that each residue titrates more or less independently of the others. This is in stark contrast to the folded state, where broad and asymmetric capacitance curves reflect significant electrostatic coupling between residues.
Figure 6.
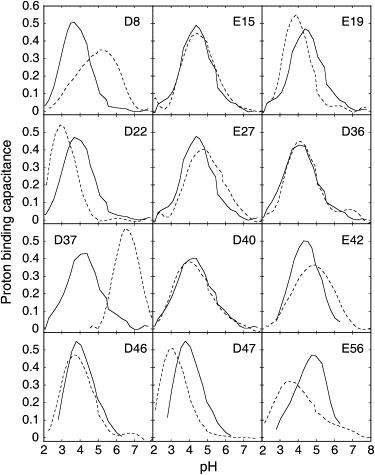
Proton binding capacitance curves for carboxyl residues in intact folded PGB1-QDD (33) (dashed line) and in unfolded fragments (solid line). Lower and extended curves indicate greater electrostatic coupling with surrounding charges.
Figure 7.
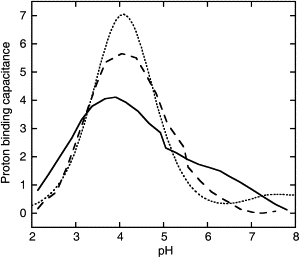
Total proton binding capacitance curves for PGB1-QDD obtained by summing up the capacitance for all residues in the intact folded protein (solid line), unfolded fragments (dashed line), and model (62) (dotted line).
Cleaving the protein and separating the fragments necessarily alters the electrostatic interactions to some extent. The shift in pKa values due to fragmentation and separation, were estimated by MC simulations of a Gaussian chain model as a function of pH followed by fitting of Eq. 7. The calculated difference between fragments and intact protein reports on the effect of new charged termini and loss of long-range interactions with the other fragment and were used to correct the experimental pKa values measured for the fragments (Eq. 8). Although the Gaussian chain model does not reproduce accurately the charge distribution of the unfolded state (35), we believe that it is accurate in capturing the difference in pKa values between unfolded intact protein and fragments. Although the pKa value of E42 is shifted by 0.5 pH units, most residues are not significantly affected by fragmentation (Table 1). It is reasoned that the E42 shift stems from the favorable interaction with the introduced N-terminus at G41. The remaining three side-chain carboxyl groups in C16 have pKa values shifted by 0.1 pH unit. The pKa value of D40 seems to be unaffected by the new C-terminus at G41, which probably compensates for the removal of E42.
The coarse-grained MC simulations of intact PGB-QDD predict small pKa downshifts, but neglect the solvation penalty of burial. Thus, the experimentally observed upshifts do not seem to originate from site-site electrostatics, but are more likely due to desolvation effects associated with side-chain burial. Therefore, we performed atomistic MD simulations of the intact chain, sampling the SASA involving the side-chains of aspartates and glutamates. SASA for the aspartic acids varies between 61 and 105 Å2 (Table 2). The upshifted pKa values measured for D8 and D37 may reflect partial burial of these residues. Although the average SASA values for D8 and D37 are not significantly different from those of D22, D46, and D47, the fluctuations in SASA around the mean values, , of D8 and D37 are up to 10 times greater than for the other aspartates. Statistical mechanical perturbation theory (64) shows that the fluctuation amplitude is related to the free energy of perturbing (burial or exposure) the side chain away from its mean solvent accessibility, i.e., . We conclude that D8 and D37 populate conformations with low SASA and that these populations are expected to increase upon protonation (no net charge on the side chain).
Table 2.
Average side-chain SASA and SASA fluctuations for glutamates and aspartates in intact folded PGB1-QDD as obtained from atomic-scale MD simulations
| Residue | SASA |
|
|---|---|---|
| (Å2) | (Å4) | |
| D8 | 65 | 301 |
| D22 | 64 | 45 |
| D36 | 98 | 60 |
| D37 | 54 | 297 |
| D40 | 105 | 67 |
| D46 | 61 | 32 |
| D47 | 67 | 59 |
| E15 | 87 | 188 |
| E19 | 110 | 72 |
| E27 | 49 | 111 |
| E42 | 125 | 141 |
| E56 | 116 | 274 |
Discussion
The work presented here provides pKa values in a model of the unfolded state of a protein under nondenaturing conditions. The results imply that in the unfolded state, most residues have pKa values close to the model values and charge capacitance curves close to ideal. The approach of measuring pKa values in fragments has the advantage that the unfolded state can be studied under nativelike conditions without the addition of denaturants.
A thermodynamic cycle links the equilibria of protein folding in the charged and uncharged states (Fig. 1). The pH-dependent stability of the protein can be calculated from the difference in pKa values between the folded and unfolded states (Eq. 6), based on the assumption that the structural ensembles of the folded and unfolded states are unaffected by changes in electrostatic charge. Here, we present the results of such calculations based on experimental pKa values for the intact folded protein and for the unfolded fragments and compare these to experimental denaturation data (Fig. 8). We observe a significant improvement in the agreement (RMSD 4.3 kJ/mol) compared with previous results based on calculated pKa values for the unfolded state using a Gaussian chain model (RMSD 6.8 kJ/mol) (35). When pKa values for the unfolded state are corrected for the change in electrostatic interactions due to protein fragmentation, the agreement between the calculated and experimental stability is further improved across the entire pH range (RMSD 2.4 kJ/mol) (Fig. 8). In our previous article (35), we outlined two extreme scenarios that would explain the pH-dependent stability; either the pKa values for all residues in the unfolded state are upshifted by 0.2 pH units or the pKa value for one residue (D37) is upshifted by 1.9 pH units. The results from the unfolded fragments support the first scenario. The residual deviations may be due to changes in the structures of the folded and/or unfolded states in response to altered electrostatics during the pH titration. This may yield additional pH-induced changes in stability of non-Coulombic origin. Furthermore, the experimental stability data are based on thermal denaturation, which involves extrapolation from high temperature. Again, the conformational ensembles may be affected by changes in temperature. Finally, cleaving the unfolded chain into fragments will result in disruption of any residual tertiary interactions, as discussed above.
Figure 8.
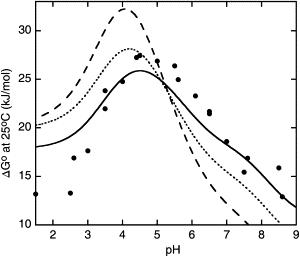
Comparison of experimental with calculated pH-dependent stability curves for PGB1-QDD. Curves represent experimental stability data at different pH values from denaturation studies (34) (solid circles); calculated stability based on experimental pKa values for the folded (33) and unfolded (this study) states (dotted line); calculated stability based on experimental pKa values for the folded state and corrected pKa values for the unfolded state, determined from the difference between the intact protein and cleaved fragments in their electrostatic interactions, as obtained from MC simulations using a Gaussian chain model (solid line); calculated stability based on experimental pKa values in the folded state (33) and calculated pKa values in the unfolded state assuming a Gaussian chain, as reported previously (35) (dashed line). The curves were shifted vertically to minimize the RMSD.
The pKa values measured for the unfolded fragments also enable us to deduce mechanistic details underlying the pKa shifts in the folded protein. In the case of PGB1-QDD, the largest pKa shifts are seen for D8, D37, D47, E56, and E19, which we discuss briefly below. It is apparent from our results obtained for the fragments that the pKa values of the mutated residues D8 and D37 in the folded state are not shifted due to repulsion inherent in the sequence, but must be a consequence of partial burial upon folding. This conclusion is further strengthened by the results from MD simulations. The low pKa value of E56 in the folded state is not maintained in the unfolded fragment, indicating that local electrostatic attractions are not the cause of the downshift; rather, it appears that the effect is due to the hydrogen bond to K10. In the case of D22, the downshifted pKa value is maintained to some extent in the unfolded fragment, indicating that part of the large downshift in the folded state is due to local electrostatic interactions. However, the major part of the downshift is probably caused by the hydrogen bond to T25 (65). The same effect is seen for D47, where the downshifted pKa value can be traced partly to a hydrogen bond between the Y45 and D47 side chains (65). E19 is proximal to the N-terminus in the folded protein, but this interaction is removed in the fragment where the side chain has a pKa close to the ideal value and the charge capacitance is decreased.
The results obtained in this and previous studies of PGB1-QDD reiterates the conclusion that electrostatic interactions on the protein surface cause minor pKa shifts relative to shifts arising from desolvation or specific hydrogen bonds (11,66). The analysis of proton binding capacitance curves adds insight into the origin of pKa shifts, and pure electrostatic interactions can be detected.
In conclusion, unfolded fragments of PGB1-QDD serve as a useful model for the unfolded state of the intact protein under nondenaturing conditions. The accuracy is improved when correcting for changes in electrostatic interactions caused by cleavage of the protein. Moreover, the analysis of proton binding capacitance reveals that even in this highly charged protein, most of the electrostatic interactions are largely diminished in the unfolded state.
Acknowledgments
We thank Dr. Ingemar André for helpful comments on the manuscript.
This work was supported by the Swedish Research Council (S. Linse and M.A.) and its Linneaus Center, Organizing Molecular Matter (S. Linse and M.L.), the Knut and Alice Wallenberg Foundation (M.A.), the Göran Gustavsson Foundation for Research in Natural Sciences and Medicine (M.A.), and the Royal Physiographic Society in Sweden (S. Lindman).
Supporting Material
References
- 1.Lawrence M.S., Phillips K.J., Liu D.R. Supercharging proteins can impart unusual resilience. J. Am. Chem. Soc. 2007;129:10110–10112. doi: 10.1021/ja071641y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Warshel A. Electrostatic origin of the catalytic power of enzymes and the role of preorganized active sites. J. Biol. Chem. 1998;273:27035–27038. doi: 10.1074/jbc.273.42.27035. [DOI] [PubMed] [Google Scholar]
- 3.Harris T.K., Turner G.J. Structural basis of perturbed pKa values of catalytic groups in enzyme active sites. IUBMB Life. 2002;53:85–98. doi: 10.1080/15216540211468. [DOI] [PubMed] [Google Scholar]
- 4.Tõugu V., Kesvatera T. Role of ionic interactions in cholinesterase catalysis. Biochim. Biophys. Acta. 1996;1298:12–30. doi: 10.1016/s0167-4838(96)00128-8. [DOI] [PubMed] [Google Scholar]
- 5.Luecke H., Richter H.T., Lanyi J.K. Proton transfer pathways in bacteriorhodopsin at 2.3 Å resolution. Science. 1998;280:1934–1937. doi: 10.1126/science.280.5371.1934. [DOI] [PubMed] [Google Scholar]
- 6.Akke M., Forsén S. Protein stability and electrostatic interactions between solvent exposed charged side chains. Proteins. 1990;8:23–29. doi: 10.1002/prot.340080106. [DOI] [PubMed] [Google Scholar]
- 7.Sali D., Bycroft M., Fersht A.R. Stabilization of protein structure by interaction of α-helix dipole with a charged side chain. Nature. 1988;335:740–743. doi: 10.1038/335740a0. [DOI] [PubMed] [Google Scholar]
- 8.Markley J.L. Observation of histidine residues in proteins by means of NMR spectroscopy. Acc. Chem. Res. 1975;8:70–80. [Google Scholar]
- 9.Bradbury J.H., Scheraga H.A. Structural studies of ribonuclease. XXIV. Application of Nuclear Magnetic Resonance spectroscopy to distinguish between histidine residues of ribonuclease. J. Am. Chem. Soc. 1966;88:4240–4246. [Google Scholar]
- 10.Grimsley G.R., Scholtz J.M., Pace C.N. A summary of the measured pK values of the ionizable groups in folded proteins. Protein Sci. 2009;18:247–251. doi: 10.1002/pro.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pace C.N., Grimsley G.R., Scholtz J.M. Protein ionizable groups: pK values and their contribution to protein stability and solubility. J. Biol. Chem. 2009;284:13285–13289. doi: 10.1074/jbc.R800080200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Thurlkill R.L., Grimsley G.R., Pace C.N. pK values of the ionizable groups of proteins. Protein Sci. 2006;15:1214–1218. doi: 10.1110/ps.051840806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kesvatera T., Jönsson B., Linse S. Measurement and modelling of sequence-specific pKa values of lysine residues in calbindin D9k. J. Mol. Biol. 1996;259:828–839. doi: 10.1006/jmbi.1996.0361. [DOI] [PubMed] [Google Scholar]
- 14.Kesvatera T., Jönsson B., Linse S. Focusing of the electrostatic potential at EF-hands of calbindin D(9k): titration of acidic residues. Proteins. 2001;45:129–135. doi: 10.1002/prot.1132. [DOI] [PubMed] [Google Scholar]
- 15.Anderson D.E., Becktel W.J., Dahlquist F.W. pH-induced denaturation of proteins: a single salt bridge contributes 3–5 kcal/mol to the free energy of folding of T4 lysozyme. Biochemistry. 1990;29:2403–2408. doi: 10.1021/bi00461a025. [DOI] [PubMed] [Google Scholar]
- 16.Tanford C. Protein denaturation. C. Theoretical models for the mechanism of denaturation. Adv. Protein Chem. 1970;24:1–95. [PubMed] [Google Scholar]
- 17.Tollinger M., Forman-Kay J.D., Kay L.E. Measurement of side-chain carboxyl pK(a) values of glutamate and aspartate residues in an unfolded protein by multinuclear NMR spectroscopy. J. Am. Chem. Soc. 2002;124:5714–5717. doi: 10.1021/ja020066p. [DOI] [PubMed] [Google Scholar]
- 18.Quijada J., López G., Tasayco M.L. On the NMR analysis of pKa values in the unfolded state of proteins by extrapolation to zero denaturant. Biophys. Chem. 2007;129:242–250. doi: 10.1016/j.bpc.2007.06.004. [DOI] [PubMed] [Google Scholar]
- 19.Marti D.N. Apparent pKa shifts of titratable residues at high denaturant concentration and the impact on protein stability. Biophys. Chem. 2005;118:88–92. doi: 10.1016/j.bpc.2005.06.011. [DOI] [PubMed] [Google Scholar]
- 20.Cho J.-H., Sato S., Raleigh D.P. Thermodynamics and kinetics of non-native interactions in protein folding: a single point mutant significantly stabilizes the N-terminal domain of L9 by modulating non-native interactions in the denatured state. J. Mol. Biol. 2004;338:827–837. doi: 10.1016/j.jmb.2004.02.073. [DOI] [PubMed] [Google Scholar]
- 21.Oliveberg M., Arcus V.L., Fersht A.R. pKA values of carboxyl groups in the native and denatured states of barnase: the pKA values of the denatured state are on average 0.4 units lower than those of model compounds. Biochemistry. 1995;34:9424–9433. doi: 10.1021/bi00029a018. [DOI] [PubMed] [Google Scholar]
- 22.Tan Y.-J., Oliveberg M., Fersht A.R. Perturbed pKA-values in the denatured states of proteins. J. Mol. Biol. 1995;254:980–992. doi: 10.1006/jmbi.1995.0670. [DOI] [PubMed] [Google Scholar]
- 23.Spencer D.S., Xu K., Zhou H.X. Effects of pH, salt, and macromolecular crowding on the stability of FK506-binding protein: an integrated experimental and theoretical study. J. Mol. Biol. 2005;351:219–232. doi: 10.1016/j.jmb.2005.05.029. [DOI] [PubMed] [Google Scholar]
- 24.Zhou H.X. Residual electrostatic effects in the unfolded state of the N-terminal domain of L9 can be attributed to nonspecific nonlocal charge-charge interactions. Biochemistry. 2002;41:6533–6538. doi: 10.1021/bi025580m. [DOI] [PubMed] [Google Scholar]
- 25.Zhou H.X. Residual charge interactions in unfolded staphylococcal nuclease can be explained by the Gaussian-chain model. Biophys. J. 2002;83:2981–2986. doi: 10.1016/S0006-3495(02)75304-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhou H.X. Direct test of the Gaussian-chain model for treating residual charge-charge interactions in the unfolded state of proteins. J. Am. Chem. Soc. 2003;125:2060–2061. doi: 10.1021/ja0298491. [DOI] [PubMed] [Google Scholar]
- 27.Zhou H.X. Polymer models of protein stability, folding, and interactions. Biochemistry. 2004;43:2141–2154. doi: 10.1021/bi036269n. [DOI] [PubMed] [Google Scholar]
- 28.Zhou H.X. A Gaussian-chain model for treating residual charge-charge interactions in the unfolded state of proteins. Proc. Natl. Acad. Sci. USA. 2002;99:3569–3574. doi: 10.1073/pnas.052030599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Horng J.C., Moroz V., Raleigh D.P. Characterization of large peptide fragments derived from the N-terminal domain of the ribosomal protein L9: definition of the minimum folding motif and characterization of local electrostatic interactions. Biochemistry. 2002;41:13360–13369. doi: 10.1021/bi026410c. [DOI] [PubMed] [Google Scholar]
- 30.Pujato M., Bracken C., Tasayco M.L. pH dependence of amide chemical shifts in natively disordered polypeptides detects medium-range interactions with ionizable residues. Biophys. J. 2005;89:3293–3302. doi: 10.1529/biophysj.105.060384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Pujato M., Navarro A., Tasayco M.L. The pH-dependence of amide chemical shift of Asp/Glu reflects its pKa in intrinsically disordered proteins with only local interactions. Biochim. Biophys. Acta. 2006;1764:1227–1233. doi: 10.1016/j.bbapap.2006.04.014. [DOI] [PubMed] [Google Scholar]
- 32.Marti D.N., Bosshard H.R. Inverse electrostatic effect: electrostatic repulsion in the unfolded state stabilizes a leucine zipper. Biochemistry. 2004;43:12436–12447. doi: 10.1021/bi048771t. [DOI] [PubMed] [Google Scholar]
- 33.Lindman S., Linse S., André I. Electrostatic contributions to residue-specific protonation equilibria and proton binding capacitance for a small protein. Biochemistry. 2006;45:13993–14002. doi: 10.1021/bi061555v. [DOI] [PubMed] [Google Scholar]
- 34.Lindman S., Xue W.-F., Linse S. Salting the charged surface: pH and salt dependence of protein G B1 stability. Biophys. J. 2006;90:2911–2921. doi: 10.1529/biophysj.105.071050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lindman S., Linse S., André I. pK(a) values for side-chain carboxyl groups of a PGB1 variant explain salt and pH-dependent stability. Biophys. J. 2007;92:257–266. doi: 10.1529/biophysj.106.088682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bauer M.C., Xue W.F., Linse S. Protein GB1 folding and assembly from structural elements. Int. J. Mol. Sci. 2009;10:1552–1566. doi: 10.3390/ijms10041552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kobayashi N., Honda S., Munekata E. Complement assembly of two fragments of the streptococcal protein G B1 domain in aqueous solution. FEBS Lett. 1995;366:99–103. doi: 10.1016/0014-5793(95)00503-2. [DOI] [PubMed] [Google Scholar]
- 38.Smith C.K., Withka J.M., Regan L. A thermodynamic scale for the β-sheet forming tendencies of the amino acids. Biochemistry. 1994;33:5510–5517. doi: 10.1021/bi00184a020. [DOI] [PubMed] [Google Scholar]
- 39.Reissner K.J., Aswad D.W. Deamidation and isoaspartate formation in proteins: unwanted alterations or surreptitious signals? Cell. Mol. Life Sci. 2003;60:1281–1295. doi: 10.1007/s00018-003-2287-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Delaglio F., Grzesiek S., Bax A. NMRPipe: a multidimensional spectral processing system based on UNIX pipes. J. Biomol. NMR. 1995;6:277–293. doi: 10.1007/BF00197809. [DOI] [PubMed] [Google Scholar]
- 41.Reference deleted in proof.
- 42.Schanda P., Van Melckebeke H., Brutscher B. Speeding up three-dimensional protein NMR experiments to a few minutes. J. Am. Chem. Soc. 2006;128:9042–9043. doi: 10.1021/ja062025p. [DOI] [PubMed] [Google Scholar]
- 43.Bax A., Ikura M. An efficient 3D NMR technique for correlating the proton and nitrogen-15 backbone amide resonances with the α-carbon of the preceding residue in uniformly nitrogen-15 to carbon-13 enriched proteins. J. Biomol. NMR. 1991;1:99–104. doi: 10.1007/BF01874573. [DOI] [PubMed] [Google Scholar]
- 44.Farmer B.T., 2nd, Venters R.A., Müller L. A refocused and optimized HNCA: increased sensitivity and resolution in large macromolecules. J. Biomol. NMR. 1992;2:195–202. doi: 10.1007/BF01875530. [DOI] [PubMed] [Google Scholar]
- 45.Grzesiek S., Bax A. Improved 3D triple-resonance NMR techniques applied to a 31-kDa protein. J. Magn. Reson. 1992;96:432–440. [Google Scholar]
- 46.Kay L.E., Ikura M., Bax A. 3-Dimensional triple-resonance NMR-spectroscopy of isotopically enriched proteins. J. Magn. Reson. 1990;89:496–514. doi: 10.1016/j.jmr.2011.09.004. [DOI] [PubMed] [Google Scholar]
- 47.Wittekind M., Mueller L. HNCACB, a high-sensitivity 3D NMR experiment to correlate amide-proton and nitrogen resonances with the α-carbon and β-carbon resonances in proteins. J. Magn. Reson. B. 1993;101:201–205. [Google Scholar]
- 48.Clubb R.T., Thanabal V., Wagner G. A constant-time 3-dimensional triple-resonance pulse scheme to correlate intraresidue H-1(N), N-15, and C-13(′) chemical-shifts in N-15-C-13-labeled proteins. J. Magn. Reson. 1992;97:213–217. [Google Scholar]
- 49.Grzesiek S., Anglister J., Bax A. Correlation of backbone amide and aliphatic side-chain resonances in C13/N15-enriched proteins by isotropic mixing of C-13 magnetization. J. Magn. Reson. B. 1993;101:114–119. [Google Scholar]
- 50.Bodenhausen G., Ruben D.J. Natural abundance nitrogen-15 NMR by enhanced heteronuclear spectroscopy. Chem. Phys. Lett. 1980;69:185–189. [Google Scholar]
- 51.Marion D., Ikura M., Bax A. Rapid recording of 2D NMR spectra without phase cycling. Application to the study of hydrogen exchange in proteins. J. Magn. Reson. 1989;85:393–399. [Google Scholar]
- 52.Yamazaki T., Yoshida M., Nagayama K. Complete assignments of magnetic resonances of ribonuclease H from Escherichia coli by double- and triple-resonance 2D and 3D NMR spectroscopies. Biochemistry. 1993;32:5656–5669. doi: 10.1021/bi00072a023. [DOI] [PubMed] [Google Scholar]
- 53.Glasoe P.K., Long F.A. Use of glass electrodes to measure acidities in deuterium oxide. J. Phys. Chem. 1960;64:188–190. [Google Scholar]
- 54.Markley J.L. Nuclear magnetic resonance studies of trypsin inhibitors. Histidines of virgin and modified soybean trypsin inhibitor (Kunitz) Biochemistry. 1973;12:2245–2250. doi: 10.1021/bi00736a010. [DOI] [PubMed] [Google Scholar]
- 55.Lund M., Jönsson B. On the charge regulation of proteins. Biochemistry. 2005;44:5722–5727. doi: 10.1021/bi047630o. [DOI] [PubMed] [Google Scholar]
- 56.Case D.A., Cheatham T.E., 3rd, Woods R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Berendsen H.J.C., Grigera J.R., Straatsma T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987;91:6269–6271. [Google Scholar]
- 58.Guex N., Peitsch M.C. SWISS-MODEL and the Swiss-PdbViewer: an environment for comparative protein modeling. Electrophoresis. 1997;18:2714–2723. doi: 10.1002/elps.1150181505. [DOI] [PubMed] [Google Scholar]
- 59.Lund M., Trulsson M., Persson B. Faunus: an object oriented framework for molecular simulation. Source Code Biol. Med. 2008;3:1. doi: 10.1186/1751-0473-3-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Jönsson B., Lund M., da Silva F.L.B. Electrostatics in macromolecular solutions. In: Dickinson E., E. Leser M., editors. Food Colloids: Self-Assembly and Material Science. Royal Society of Chemistry; London: 2007. pp. 129–153. [Google Scholar]
- 61.Lund M., Jönsson B., Woodward C.E. Implications of a high dielectric constant in proteins. J. Chem. Phys. 2007;126:225103. doi: 10.1063/1.2741543. [DOI] [PubMed] [Google Scholar]
- 62.Nozaki Y., Tanford C. Examination of titration behavior. Methods Enzymol. 1967;11:715–734. [Google Scholar]
- 63.Di Cera E., Gill S.J., Wyman J. Binding capacity: cooperativity and buffering in biopolymers. Proc. Natl. Acad. Sci. USA. 1988;85:449–452. doi: 10.1073/pnas.85.2.449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.McQuarrie D.A. Harper Collins; New York: 1976. Statistical Mechanics. [Google Scholar]
- 65.Khare D., Alexander P., Orban J. pKa measurements from nuclear magnetic resonance for the B1 and B2 immunoglobulin G-binding domains of protein G: comparison with calculated values for nuclear magnetic resonance and x-ray structures. Biochemistry. 1997;36:3580–3589. doi: 10.1021/bi9630927. [DOI] [PubMed] [Google Scholar]
- 66.Castañeda C.A., Fitch C.A., García-Moreno B.E. Molecular determinants of the pKa values of Asp and Glu residues in staphylococcal nuclease. Proteins. 2009;77:570–588. doi: 10.1002/prot.22470. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


