Abstract
In developing and self-renewing tissues, terminally differentiated (TD) cell types are typically specified through the actions of multistage cell lineages. Such lineages commonly include a stem cell and multiple progenitor (transit-amplifying) cell stages, which ultimately give rise to TD cells. As the tissue reaches a tightly controlled steady-state size, cells at different lineage stages assume distinct spatial locations within the tissue. Although tissue stratification appears to be genetically specified, the underlying mechanisms that direct tissue lamination are not yet completely understood. Herein, we use modeling and simulations to explore several potential mechanisms that can be utilized to create stratification during developmental or regenerative growth in general systems and in the model system, the olfactory epithelium of mouse. Our results show that tissue stratification can be generated and maintained through controlling spatial distribution of diffusive signaling molecules that regulate the proliferation of each cell type within the lineage. The ability of feedback molecules to stratify a tissue is dependent on a low TD death rate: high death rates decrease tissue lamination. Regulation of the cell cycle lengths of stem cells by feedback signals can lead to transient accumulation of stem cells near the base and apex of tissue.
Introduction
Multistage cell lineages, typically comprised of a stem cell stage and several subsequent progenitor cell stages (also referred to as transit-amplifying or TA cells), underlie the production of different (terminally differentiated; TD) cell types within a tissue. Genetic studies and tissue culture experiments have shown that control of stem or progenitor cell proliferation and differentiation which ultimately control the TD cell number is mediated by secreted molecules through feedback regulation. Examples are liver cell regeneration (1), myogenesis (2), neurogenesis (3,4), and skin epidermis development (5). Results from studies utilizing mathematical modeling also suggest the necessity of feedback regulation in multistage cell lineages for maintaining homoeostasis (6–8).
Most of these studies, however, consider the regulation of cells as populations, disregarding the spatial aspects of the system within the tissue. With rising interest in the “stem cell niche”, a term that generally refers to the microenvironment where stem cells reside and self-renew (9,10), more attention has been paid to the spatial aspects of cell lineage. This microenvironment typically provides a protective environment for stem cells to enhance their survival, and the factors within it may provide diverse signals that regulate stem cells and their daughter cells (11). In vertebrates, examples of stem cell niches can be found in the hematopoietic system (12), hair follicles (13), and intestinal epithelia (14).
In particular, in many epithelia such as olfactory epithelium and the cerebral cortex, the cells in different stages of the lineage are organized into layers (11,15,16). Within the skin, for example, keratinized epithelial cells lie apical to the proliferative progenitor cells that are found in the innermost cell layer (17). In the developing cortex, differentiating cells migrate away from the ependymal layer to more apical regions (18). Importantly, epithelial layering suggests that secreted molecules, commonly produced by TD cells, may exist in the tissue as gradients (19). Furthermore, depending on the location in the layer, stem and progenitor cells may be exposed to different levels of those molecules, due to diffusion or other transport mechanisms. As a result, they may exhibit different proliferation and differentiation capabilities at different spatial locations, leading to spatial stratification of different types of cells and direct formation of the stem cell niche (see Fig. 1 A for illustration).
Figure 1.
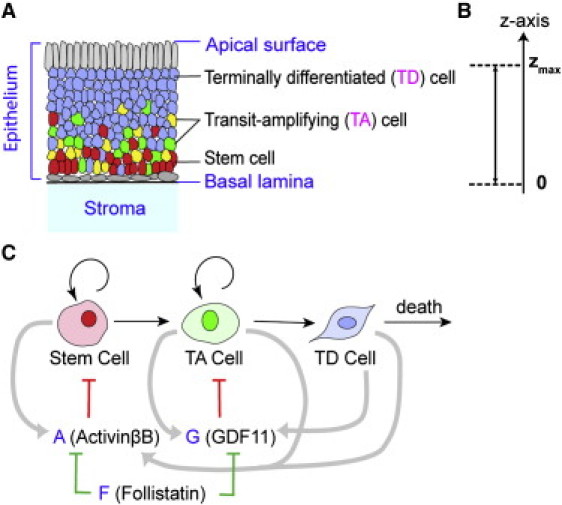
Multistage cell lineage and tissue stratification. (A) A cartoon of general epithelia and relative locations of cells at different lineage stages (red, stem cells; yellow and green, TA cells, blue, TD cells). The connective tissue underlying the basal lamina is stroma. (B) One-dimensional coordinate along the apical-basal axis (z axis). The origin z = 0 is aligned with the basal lamina, and the top of epithelium, which moves due to the growth of the tissue, is denoted by zmax. (C) A schematic diagram of a single cell lineage and associated regulatory molecules. Cells proliferate, differentiate to the next lineage stage or undergo death. The terms A, G, and F represent secreted molecules, which are analogous to molecules ActivinβB, GDF11, and Follistatin in OE, respectively. The secreted molecules A and G inhibit the population of stem and TA cells, respectively (red barred arrow), and they are both inhibited by F (green barred arrow). (Gray arrows) Molecule production: A is produced by all cells, and G is produced by TA and TD cells.
We explore these questions regarding the spatial organization of cells using a model system of regenerating epithelia: the olfactory epithelium (OE) of the mouse, in which the identities of the cells and secreted molecules that regulate lineage progression have been extensively studied (20). The principal TD cell type within the OE is the olfactory receptor neuron (ORN), whose lineage is thought to derive from a stem cell that can be identified by its expression of transcription factor Sox2. Expression of proneural transcription factor Mash1 is thought to commit this type of cell to the neuronal lineage. Early-stage Mash1+ TA cells give rise to late-stage TA cells termed immediate neuronal precursor (INP) cells marked by expression of proneural transcription factor Ngn1 (21–23). Cells in the OE lineage exhibit spatial heterogeneity: Sox2+, Mash1+ cells, and INPs occupy the two basalmost layers of the OE, and apical to this are ORN cell bodies. This layering is necessary for olfactory function because ORN dendrites require access to the nasal cavity to bind incoming odorant molecules.
Secreted molecules of the transforming growth factor β (TGF-β) superfamily regulate ORN number. For example, absence of growth differentiation factor 11 (GDF11), which is produced by INPs and ORNs (3), leads to an increased number of INPs and ORNs (3), and ActivinβB, which is produced by all cells of the neuronal lineage, regulates Sox2+ (stem) and Mash1+ (early progenitor) cells, the cells that give rise to INPs (K. K. Gokoffski, H.-H. Wu, C. Beites, J. Kim, M. Matzuk, E.J. Kim, J. Johnson, A. Lander, and A. L. Calof, unpublished). In addition, ActivinβB and GDF11 are antagonized by follistatin, another secreted protein produced mostly by cells in the underlying stroma (3,25,26). Interactions among the three diffusive molecules ActivinβB, GDF11, and follistatin, such as diffusion of ActivinβB and GDF11 across the basal lamina into the stroma and binding of follistatin to ActivinβB and GDF11, may facilitate development of OE (K. K. Gokoffski, H.-H. Wu, C. Beites, J. Kim, M. Matzuk, E.J. Kim, J. Johnson, A. Lander, and A. L. Calof, unpublished).
In this article, we use the OE as a model system to explore biologically plausible potential mechanisms that would enable tissue stratification of different cell types (Fig. 1 A).
Our spatial models explicitly take into consideration:
-
1.
A cell lineage comprised of stem, TA, and TD cells.
-
2.
Diffusive signaling molecules produced by those cells or neighboring tissues.
-
3.
Regulation of cell proliferation and differentiation rates by these secreted molecules.
-
4.
The growing tissue.
Based on the OE example, the simulations suggest that the diffusion of signaling molecules, which regulate cell proliferation, from the tissue into the stroma, and repression of these signaling molecules within the tissue by inhibitors produced in the stroma, are two basic mechanisms for producing stratification from a cell lineage. In addition, the death rate of TD cells affects the quality of stratification. Moreover, regulation of stem cell cycle length can lead to transient accumulations of stem cells at both the base and apex of the epithelium.
Material and Methods
The calculations for Figs. 2–5 were carried out using FORTRAN 77 with plots generated by MATLAB 7 (The MathWorks, Natick, MA). Details of numerical approximations are described in the Supporting Material.
Figure 2.
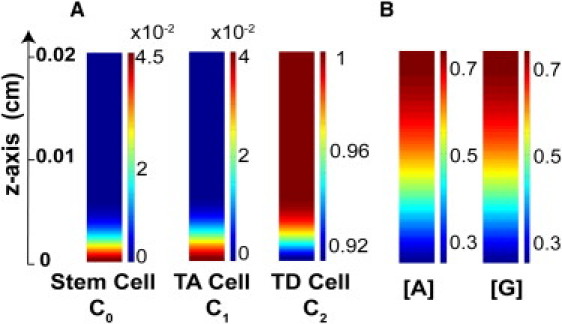
Distribution of different cell types and molecule concentrations along the apical-basal axis in epithelia. (A) Cell volume fractions of each lineage stage, with color bars for the scales. (B) Normalized molecule concentrations of A and G. Parameters used are listed in Table S1 in the Supporting Material.
Figure 3.
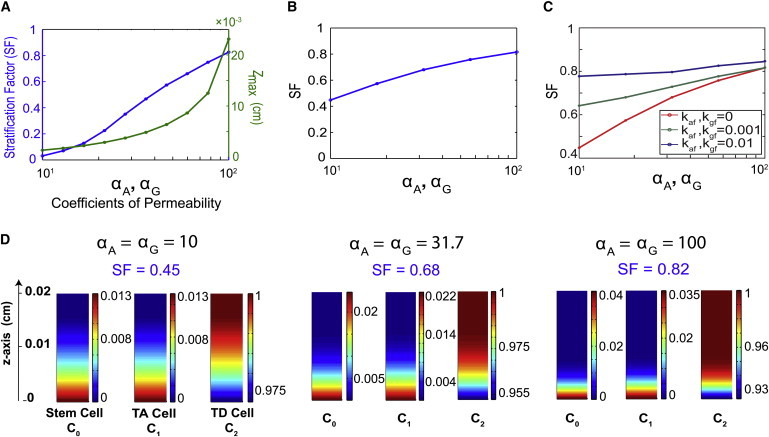
Correlation between permeability coefficients αA and αG with SF of stem cell and zmax. (A) (Blue) Permeability coefficients αA and αG in Eq. 8 (log scale) versus stratification factor (SF) defined in Eq. 9; (Green) permeability coefficients versus epithelium thickness. (B) Coefficients αA and αG versus SF with a fixed epithelium thickness. In the simulations, zmax is fixed to be 0.02 cm, which can be achieved by adjusting one of γA and γG. (C) αA = αG is varied from 10 to 100 with different binding rates (kaf = kgf = 0, 0.01, 0.1). In these simulations, the epithelium thickness zmax is fixed to be 0.02 cm by adjusting γA. (D) Cell distributions with three sets of parameters with different coefficient values of αA and αG. The parameters associated with the above simulations are listed in Table S1 and Table S2.
Figure 4.
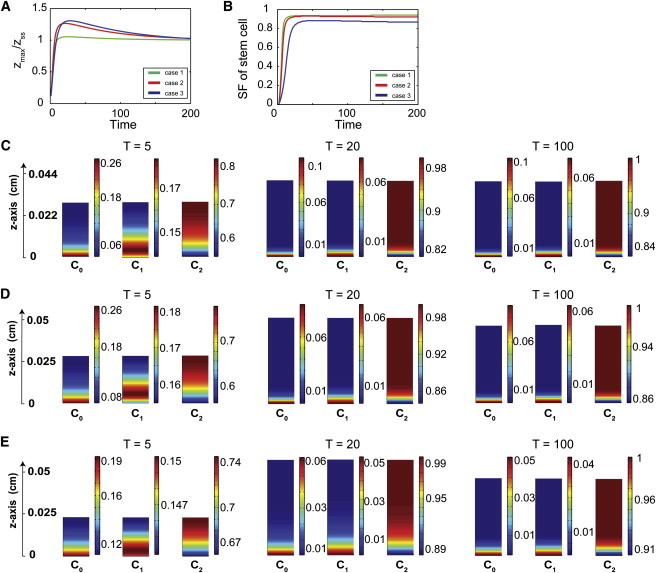
Dynamics of epithelium thickness and dynamics of tissue stratification. Three cases are plotted: 1), rapid uptake of A and G in the stroma, with the intraepithelial binding with F; 2), slow uptake of A and G in the stroma, with the intraepithelial binding with F; and 3), rapid uptake of A and G in the stroma, without the intraepithelial binding with F. These cases are referred to in the figures as cases 1, 2, and 3 (and in panels A and B they are distinguished by colors green, red, and blue, respectively). The corresponding parameter sets are listed in Table S1 and Table S2. (A) Time versus the epithelium thickness (zmax) normalized by the steady-state thickness (zss). (B) Time versus the stem cell stratification measured by SF. (C) Distribution of cells for case 1. (D) Distribution of cells for case 2. (E) Distribution of cells for case 3.
Figure 5.
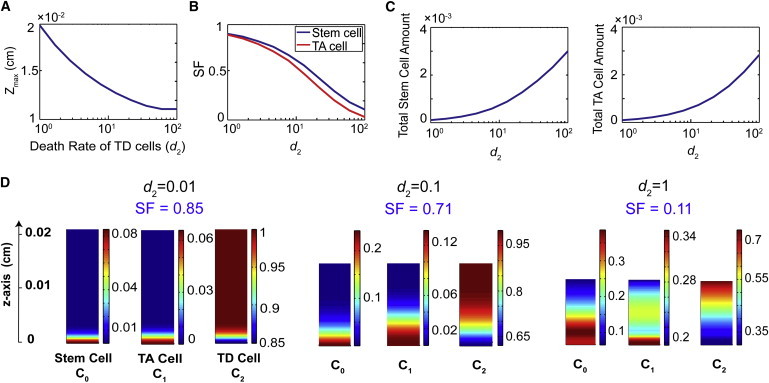
Tissue stratification and thickness as functions of the death rate of TD cells. (A) Death rate of TD cells (d2 in unit of per-cell cycle length) versus the thickness of the epithelium (zmax). (B) The value d2 versus stratification factor (SF) of stem cells (blue) and TA cells (red). (C) Relationship between d2 and the total stem cell (left) and TA cell (right panel) populations (arbitrary unit). (D) Cell distributions with d2 = 0.01, 0.1, and 1. All other parameters are listed in Table S1 and Table S2.
Results
A spatial model of multistage cell lineage
We consider a simplified lineage with only three stages consisting of stem cells, TA cells, and TD cells, similar to the nonspatial models described elsewhere (6,7), with volume fractions or cell densities C0, C1, and C2 for each stage, respectively. In space, only the apical-basal direction is considered, with z = 0 representing the basal lamina and zmax for the top of the epithelium, a time-dependent moving boundary due to tissue growth (Fig. 1 B). If we let V(z,t) represent the tissue growth velocity driven by proliferation and differentiation of cells, then C0, C1, and C2 are governed by
| (1) |
| (2) |
| (3) |
In these equations, pi represents the replication probability of each cell type (also termed as renewal probability), and vi is the inverse of the cell cycle length multiplied by ln 2. TD cells do not proliferate or differentiate but undergo death (apoptosis), at the rate d2. For simplicity, we neglect death of stem and TA cells. With the assumption that the volume of substance between cells is negligible and the overall cell population tends to maintain a uniform density as cells proliferate or differentiate, we have C0 + C1 + C2 = 1, up to normalization, for any spatial location z and at any time t. Summing Eqs. 1–3 and using C0 + C1 + C2 = 1, we obtain the equation for growth velocity
| (4) |
The dynamics of the epithelium thickness (zmax) is then governed by the velocity at that point as
In this model, the spatial heterogeneity of cell dynamics arises from the fact that pi and/or vi are spatially and temporally regulated by secreted molecules produced by stem, TA, and TD cells located at different locations. In OE, two of the molecules for such spatial regulation are GDF11 and ActivinβB. Experimental data indicate that GDF11, secreted by INPs (TA cells) and ORNs (TD cells), inhibits the proliferation of INPs (3) while ActivinβB, which appears to be produced by all cells in the lineage, inhibits proliferation of the stem cell (K. K. Gokoffski, H.-H. Wu, C. Beites, J. Kim, M. Matzuk, E.J. Kim, J. Johnson, A. Lander, and A. L. Calof, unpublished). Both molecules seem to reduce the rates at which their target cells divide, and increase the probability that the products of those divisions differentiate into cells at the next lineage stage (Fig. 1 C), leading to regulated proliferation probabilities modeled by
| (5) |
Here, A and G represent ActivinβB and GDF11, respectively; is the maximal replication probability; γA and γG are reciprocal of the corresponding EC50; and m and n are Hill coefficients. In this article, we choose m = n = 2 for modeling nonlinear and saturated responses.
For Eqs. 1–5, needs to be >0.5 and needs to be <0.5 to ensure a nonzero stem cell and TA cell population. For any number of intermediate progenitors, a constant replication probability (i.e., ) of the stem cells has to be exactly equal to 0.5 for a tissue to reach a finite size with a nonzero stem cell population (see an analytical study in the section titled SII.A in the Supporting Material). Spatial and temporal regulation through A and G on the replication probability may provide robust controls for homeostasis and spatial arrangement of cells.
Two potential mechanisms for a “stem cell niche” and tissue stratification
In epithelia that exhibit stratification, the stem cell niche usually refers to a cluster or a layer of stem cells (15,27). In the OE, this region spans 5–10% of the OE thickness from the basal lamina. The tissue exhibits stratification of cell types, with TD cells mainly occupying the remainder of the epithelia. Although the OE produces another differentiated cell type, the sustentacular cell, whose cell bodies lie apical to ORNs, we chose to ignore this population of cells for simplicity. Intuitively, the spatial distribution of stem, TA, and TD cells from the basal lamina to the apical surface should intimately depend on the spatial distribution of the diffusive molecules A and/or G, as a result of Eq. 5. A desirable distribution in the OE system seems to require the two secreted molecules GDF11 and ActivinβB to possess gradients which are low near the basal lamina, and high at the apical surface. We identified two potential mechanisms that can lead to gradients of such shape, for the observed formation of stem cell niche and tissue stratification.
Rapid uptake of regulatory molecules in the underlying stroma can lead to tissue stratification
Epithelia are usually open systems, and molecules produced by epithelia may leak into their neighboring microenvironment. Usually the basal lamina is a permeable boundary across which molecules can diffuse freely, whereas the apical surface is a closed boundary with tight junctions between epithelial cells preventing molecules from escaping the apical surface (28,29). Such one-directional leakage at the basal lamina may lead to formation of desirable gradients of A and G, as well as tissue stratification. The dynamics of A and G may be described by a system of convection-diffusion equations,
| (6) |
| (7) |
with each type of molecule assuming individual effective diffusion rates DA and DG. The removal of molecules due to degradation or binding with other molecules is assumed linearly proportional to the concentration of molecule, with a rate constant adeg or gdeg, and the synthesis of A or G is assumed to be proportional to the density of the cell types that produce A or G with rates μj or ηj. We also explored a nonlinear model that additionally includes the species of the membrane ligand-binding receptors and the bound receptor-ligand complex that may lead to saturation of binding and nonlinear degradation of molecules (see SI.A in the Supporting Material). As we show below, the boundary conditions of those molecules play an important part in the homeostasis and dynamics of the tissue. In particular, the uptake of A and G due to the leakage and binding with other molecules in the stroma is modeled by leaky boundary conditions at z = 0,
| (8) |
where αG and αA are coefficients of permeability. Note that the coefficients αG and αA here are not approximating the physical permeability of the basal lamina, but the ratios of the decay lengths, the average distance that a molecule travels, across the basal lamina (SII.B in the Supporting Material). At the apical surface, no-flux conditions are imposed for both A and G at z = zmax.
In the system Eqs. 6 and 7, the convection timescale due to the tissue growth is L/V and the diffusion timescale is L2/D, where L represents the length scale, V the average velocity, and D the diffusion rate. The ratio between these two timescales is D/(VL). The steady-state epithelium thickness zmax is ∼0.02 cm, and the cell cycle length is ∼17 h (6). As a result, the ratio is usually large (e.g., 15.3 in this case) and we can neglect the convection terms in the equations. Moreover, because the typical timescales of cell cycle lengths and tissue growth are days, whereas the timescale for molecule interactions is typically hours (30), we use a quasi-steady-state approximation for Eqs. 6–8 to allow faster computation (see SI.A in the Supporting Material for more details).
To explore stratification systematically and quantitatively, we define a quantity termed the “stratification factor (SF)” to measure the level of stratification for cell type j:
| (9) |
According to this definition, θ is between 0 and 0.8 zmax if the cell density Cj is a decreasing function along the z axis, and SF is between 0 and 1. The quantity estimates the ratio between the tissue thickness and the length where 80% of the cells accumulate from the basal lamina. The value SF = 0 corresponds to cells being uniformly distributed, and SF = 1 corresponds to an extreme polarization of the tissue.
First, we studied how stratification and the epithelium thickness depend on the permeability coefficients. Fig. 2 is a typical simulation, which is consistent with the experimental observation in OE, showing stratified epithelium in terms of the spatial distribution of stem, TA, and TD cells. As the permeability increases, the tissue stratification measured by SF becomes larger and the epithelium becomes thicker (Fig. 3 A). This is due to a rapid uptake of A and G, which leads to sharper gradients of A and G within the epithelium, resulting in a more stratified tissue. In addition, as more molecules at the basal lamina leak to the stroma, their inhibition on stem cell proliferation gets weaker, triggering an increase in stem cell population, and leading to a larger total cell population and a thicker tissue. Both thickness and stratification are relatively sensitive to permeability constants: when αA and αG coefficient values are as small as 10, the cells are not very stratified (SF = 0.05); but a 10-fold increase in αA and αG (from 10 to 100) raises SF up to 0.8 while the thickness increases ∼10-fold.
To understand how uptake of molecules affects stratification given that a tissue needs to achieve a desired fixed thickness at steady state, we conducted similar simulations by adjusting one of the EC50 numbers γA and γG to ensure same overall tissue thickness (Fig. 3 B). The value SF is still found to be an increasing function of the coefficients of permeability; in particular, SF is doubled as αj varied from 10 to 100. The distributions of three cell types with SF are displayed in Fig. 3 D. All considered, our simulations show that the uptake of the epithelial molecules by the underlying stroma is sufficient to give rise to tissue stratification.
Simulations under various parameters and conditions suggest that as long as permeability αA is positive, the stem cell population will never go extinct. An analytical study of the model demonstrates that the leaky boundary condition for A can prevent the stem cell population from extinction, leading to the formation of a stem cell niche (SII.C in the Supporting Material). In short, when αA is positive, [A] at the basal lamina is shown to be bounded by a constant multiple of zmax at the steady state. Therefore, if the thickness becomes very small, [A] becomes close to zero, which makes the replication probability of the stem cells p0 close to its maximum (>0.5), resulting in a rapid proliferation of the stem cells and preventing the stem cells from extinction.
Diffusive inhibitors in the stroma enhance tissue stratification
In many epithelial systems, molecules produced in the underlying stroma diffuse into the epithelia, and inhibit intraepithelial molecules by binding to them and preventing subsequent binding to their receptors (26,31,32). In OE, a diffusive molecule follistatin expressed in the stroma acts as an inhibitor of GDF11 and ActivinβB and regulates the cell lineage (3,33). In principle, the distribution of this type of molecule, denoted by F, is graded within the tissue along the basal-apical axis because F is only produced in the stroma, making reversed gradients of G and A. This interaction can be modeled through modifying the model for A and G proposed in the previous section, in which the interaction was approximated through boundary conditions, to include binding of A and G with F,
| (10) |
| (11) |
| (12) |
where kaf and kgf are the binding rates, and DF and fdeg are diffusion and degradation rates, with an assumption that those binding events are irreversible (26,31,32) and the resultant complexes are neglected, for simplicity. Because G is only produced by TA and TD cells, in Eq. 11 we take η0 to be zero. The influx of F to the epithelium is assumed to be a constant in time:
| (13) |
At the apical surface, F takes a no-flux boundary condition like A and G.
The simulations show that binding of F with G and A within the tissue improves tissue stratification (Fig. 3 C). To compare stratification between cases, we adjust feedback strength such that cases presented have a fixed tissue thickness in the simulations. It seems that the stronger that F binds with A and G, the stronger the stratification for any fixed permeability, and the stratification improves with stronger permeability for any fixed binding rate (Fig. 3 C). The fact that permeability of the basal lamina enhances stratification becomes more obvious with a smaller binding rate: without intraepithelial binding of A and G by F, a 10-fold decrease in permeability results in a nearly 50% decrease in stratification; and with binding rates of 0.001 and 0.01, the change becomes 30% and 10% under a 10-fold decrease in permeability, respectively. This occurs because when the binding rate is large, most of G and A near the basal lamina is removed by F, and the permeability becomes less important. Overall, the intraepithelial binding of F with G and A provides another mechanism, in addition to the leaky boundary, by which tissue stratification could be controlled.
Tissue stratification affects dynamics of tissue growth
To study how the dynamics of tissue growth may depend on stratification, we investigated three sets of parameters representing three typical cases:
-
1.
Rapid uptake of A and G in the stroma, with the intraepithelial binding with F (green curves in Fig. 4, A and B).
-
2.
Slow uptake of A and G in the stroma, with the intraepithelial binding with F (red curves in Fig. 4, A and B).
-
3.
Rapid uptake of A and G in the stroma, without the intraepithelial binding with F (blue curves in Fig. 4, A and B).
The dynamics of zmax, normalized by the steady-state thickness, is shown in Fig. 4 A, and the dynamics of stem cell stratification measured by SF is displayed in Fig. 4 B. The cell distributions for these three cases are displayed in Fig. 4, C, D, and E, respectively.
For the case of rapid uptake of A and G in the stroma, with the intraepithelial binding with F (Fig. 4 A), the epithelium thickness monotonically increases to reach the steady state. For the other two cases, the tissue thickness first increases and then slowly decreases as it approaches the steady state, taking a longer time to reach steady state than for the first case. Such overgrowth has been observed in studies for nonspatial models (6,7). The simulations in Fig. 4, A and B, together suggest that the dynamics of tissue growth may correlate with the tissue stratification. When the stratification is set up earlier, such as in the first case, the tissue growth may not exhibit overgrowth, unlike the other two cases that tend to develop stratification later. It seems that the early setup of tissue stratification, which strongly depends on spatial distribution and temporal dynamics of inhibitors, plays an important role in the overall dynamics of the cell population at a later time.
Lower death rate of TD cells further enhances stratification
Tissue homeostasis requires a balance between cell proliferation and cell death. Because regulation of cell proliferation by secreted molecules impacts homeostasis and spatial dynamics, cell death (e.g., apoptosis or other processes removing cells from the system) may also significantly affect dynamics of homeostasis and the spatial arrangement of cells within a tissue. In our model, the only loss of cells is through a cell removal term for TD cells. Our simulations show that increasing the TD cell death rate reduces tissue thickness (Fig. 5 A). For example, a 100-fold increase of d2 results in an almost twofold decrease in tissue thickness. Intuitively, the increased death rate of TD cells, which constitute the majority of the epithelium, should greatly reduce the production of A and G in the tissue, leading to increased proliferation of stem and TA cells, which ultimately make more TD cells. However, the regeneration of TD cells does not seem to be fast enough to compensate for the loss of TD cells, resulting in a thinner tissue.
Unlike tissue thickness, it is less intuitive how cell death may affect tissue stratification. It is observed that distributions of both stem and TA cells become less stratified as the death rate increases (Fig. 5, B and D). A 10-fold increase in death rate results in an approximately twofold decrease in the tissue stratification factor for both types of cells. Interestingly, as tissue stratification decreases in both stem and TA cells, the total amount of stem and TA cells at steady state (calculated by integrating the cell density along the z axis) is found to increase dramatically when the cell death rate is increased (Fig. 5 C). This again confirms that loss of TD cells can lead to less A and G, resulting in larger proliferation probabilities of stem and TA cells.
These observations are consistent with the mammalian OE. In normal OE, ORNs (TD cells) are constantly dying in low numbers (due to disease, injury, or apoptosis) (3). A higher death rate can be induced by unilateral olfactory bulbectomy, which is the surgical removal of one olfactory bulb, the synaptic target of ORNs of the OE (34,35). In adult mice subjected to unilateral bulbectomy, it has been found that the thickness of OE decreases as cells degenerate. Despite the fact that cells in the basal compartment of the OE then proliferate and new ORNs are generated, the OE never reaches its original thickness in the absence of its synaptic target tissue (22,34,36). In such tissue, progenitor cell stratification appears to be decreased relative to unoperated control OE (K. K. Gokoffski, H.-H. Wu, C. Beites, J. Kim, M. Matzuk, E.J. Kim, J. Johnson, A. Lander, and A. L. Calof, unpublished observations).
Prolonged cell cycle length of stem cells allows a transient peak of stem cells to form at the apical surface
In the models considered, diffusive molecules regulate only proliferation probabilities of cells. We showed that such spatial regulation alone is sufficient for the epithelium to reach a homeostasis with an appropriate size and tissue stratification. However, experiments in the OE also suggest that signaling molecules can regulate the system through prolonging cell cycle length (K. K. Gokoffski, H.-H. Wu, C. Beites, J. Kim, M. Matzuk, E.J. Kim, J. Johnson, A. Lander, and A. L. Calof, unpublished). Although the performance objectives of regulating cell cycle lengths are not yet completely understood, previous nonspatial models (6,7) provide some hints: feedback on cell cycle length tends to have a larger effect on the dynamics, rather than on the homeostasis of a system.
To model regulation of cell cycle length, we use a Hill function to represent the inverse of the cell cycle length,
where is the maximal cell division rate and k is taken to be 2. It is observed that such regulation can lead to important different spatial and temporal cell distributions compared to regulation of proliferation probabilities alone. In particular, the stem cell distribution is no longer a simple decreasing function in space (Fig. 6).
Figure 6.
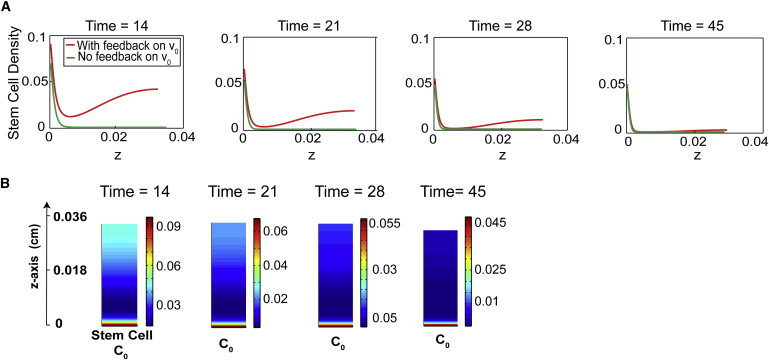
Feedback on the cell cycle length of stem cells induces transient peaks of stem cell density. (A) Time course of stem cell distribution from the basal (z = 0) to apical direction is presented at four time points: 14, 21, 28, and 45 (cell cycles/ln 2). In each figure, the green-colored curve represents the stem cell density without any feedback on the cell cycle lengths (β = 0). The density of stem cells is graded monotonically from the basal lamina, with the stem cell niche established at T = 14. The red-colored curve is the stem cell density with molecule A regulating the cell cycle length of stem cells (β = 3). Two local maxima of stem cell density, one at the basal lamina, and the other at the apical surface, appear by T = 14, and the peak at the apical surface vanishes eventually, after T = 45. (B) Stem cell distributions at time points T = 14, 21, 28, and 45.
Taking an initial state (T = 0) with a stem cell thickness of 0.006 cm (Fig. 6), the number of TA and TD cells immediately start to increase. At a later time (T = 14), the epithelium has two spatial peaks of stem cell density: near the basal lamina and at the apical surface. The height of these two spatial peaks gradually decrease (e.g., T = 21, 28), while stem cells in between the two peaks are vanishing. Eventually, the accumulation of stem cells at the apical surface vanishes (∼T = 45), after which the stem (TA) cell niche is established and maintained at the basal compartment. Exploration of systems under various conditions show that as long as there is feedback on stem cell cycle length, both the basal and apical peaks of stem and TA cell density will always be observed. In addition, the time for the apical peak to disappear positively correlates with the parameter β, the EC50 in the feedback regulation.
Similar spatial and temporal dynamics have actually been observed for the Sox2-expressing cells in the developing OE. Experiments have shown that during development, the distribution of cells expressing Sox2, a marker for the stem cells, are initially uniform, and then start to exhibit two peaks at the apical and the basal compartments. Apical Sox2+ cells differentiate into sustentacular cells while the basal cells make up the stem cell compartment (20,37). The function and mechanisms behind the formation of the peak of stem cells at the apical surface are still elusive and require further exploration. Our numerical results thus provide a possible explanation, suggesting that the transient presence of two peaks of stem cell density may be due to the regulation of the cell cycle length of stem cells.
Discussion
Cell lineages underlie the growth and development of most tissues. An important aspect of tissue function is the heterogeneous spatial distribution of cells at different lineage stages within a tissue. For many epithelial systems, the tissues are stratified in the apical-to-basal axis in terms of stem, TA, and TD cells. Mechanisms such as secreted factors, adhesive molecules between cells or between cells and the basal lamina, and the mechanical properties induced by adhesion are proposed to potentially affect the formation and maintenance of spatial heterogeneity. In this article, we focused on studying how diffusive molecules produced by cells within the tissue or in the neighboring microenvironment may regulate cell proliferation and produce tissue stratification.
Based on modeling of the OE lineage system, we found that negative regulation of cell proliferation by diffusive molecules produced at different cell lineage stages together with the spatial control of molecules could give rise to desirable spatial patterning of cell distributions. In particular, uptake of molecules across the basal lamina due to their diffusion to the stroma or their diffusive inhibitors produced in the stroma could generate tissue stratification. Although such biological tools are currently not available, it would be interesting to test whether tissue lamination would change in an OE that has an altered ActivinβB and GDF11 gradient.
For example, would changing the binding affinity between follistatin and ActivinβB or GDF11, without changing their signaling properties, lead to a change in the slope of the ActivinβB and GDF11 gradient? Moreover, would this produce a change in OE lamination? Alternatively, would changing the source of GDF11 and ActivinβB, for example, if it were produced in the stroma, in the absence of follistatin, lead to a change in OE lamination?
We also showed that tissue stratification is limited by ORN death rate: the larger death rate of TD cells, the thinner and the less stratified the epithelium becomes. In theory, this can be tested via bulbectomy experiments where surgical removal of the olfactory bulb, the synaptic targets of ORNs, leads to a sustained increase in ORN death (34). In response to bulbectomy-induced ORN-death, the number of proliferating cells increases (22,35). Quantification of the distribution of stem and TA cells could help elucidate the influence of TD death rate on tissue stratification. In addition, prolonged stem cell cycle length regulated by the diffusive molecules might lead to two transient spatial peaks of the stem cell cluster: one near the basal lamina and the other near the apical surface. These findings, based on this modeling study, are either consistent with the existing experimental data for the OE system, or are experimentally testable.
The model presented herein can be extended to include additional space dimensions. This model only accounts for the one-dimensional growth along the apical-basal direction, neglecting its expansion parallel to the basal membrane. The inclusion of horizontal expansion is likely to affect spatial and temporal dynamics of the epithelium. For example, the observed overgrowth of epithelium in our simulations (Fig. 4), which is also observed in nonspatial models, may no longer exist for two- or three-dimensional models.
It would be interesting to investigate more intermediate stages in the cell lineage or/and branched cell lineages and their effects on tissue stratification. More cell lineages can be easily incorporated into our current model. Taking the OE system as an example, the Sox2+ cell not only gives rise to the neuronal lineage, which is the only lineage considered in our model, but also gives rise to another lineage which ultimately leads to the sustentacular cells lying at the uppermost layer the OE. Inclusion of a second branch may result in a better understanding of the generation of sustentacular cells, and their potential interaction with the apical peak of stem cell population observed in our simulations.
Finally, the model presented herein provides a generic modeling framework for spatial dynamics involving stem cells and multistate cell lineages. Other biological systems such as the colonic crypt (38), and tumor growth involving cancer stem cells (39,40), may be modeled and studied under this framework.
Acknowledgments
This work was supported by the National Institutes of Health grants GM76516 (to A.D.L., A.L.C., Q.N., and F.W.) and DC03580 (to A.L.C.) and National Science Foundation grant DMS0917492 (to Q.N.). K.K.G. was supported by training grants from the National Institutes of Health (NS07444 and GM08620) and the medical science training program of the University of California, Irvine. Y.T.Z. is supported by National Science Foundation grant (DMS-0810413). C.S.C. is supported by National Science Foundation grant (DMS-1020625).
Supporting Material
References
- 1.Strain A.J. Transforming growth factor-β: the elusive hepatic chalone? Hepatology. 1992;16:269–270. doi: 10.1002/hep.1840160139. [DOI] [PubMed] [Google Scholar]
- 2.McPherron A.C., Lawler A.M., Lee S.J. Regulation of skeletal muscle mass in mice by a new TGF-beta superfamily member. Nature. 1997;387:83–90. doi: 10.1038/387083a0. [DOI] [PubMed] [Google Scholar]
- 3.Wu H.H., Ivkovic S., Calof A.L. Autoregulation of neurogenesis by GDF11. Neuron. 2003;37:197–207. doi: 10.1016/s0896-6273(02)01172-8. [DOI] [PubMed] [Google Scholar]
- 4.Seuntjens E., Nityanandam A., Tarabykin V. Sip1 regulates sequential fate decisions by feedback signaling from postmitotic neurons to progenitors. Nat. Neurosci. 2009;12:1373–1380. doi: 10.1038/nn.2409. [DOI] [PubMed] [Google Scholar]
- 5.Chuong C.M., Widelitz R.B. The river of stem cells. Cell Stem Cell. 2009;4:100–102. doi: 10.1016/j.stem.2009.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lander A.D., Gokoffski K.K., Calof A.L. Cell lineages and the logic of proliferative control. PLoS Biol. 2009;7:e15. doi: 10.1371/journal.pbio.1000015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lo W.C., Chou C.S., Nie Q. Feedback regulation in multistage cell lineages. Math. Biosci. Eng. 2009;6:59–82. doi: 10.3934/mbe.2009.6.59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Reeves G.T., Fraser S.E. Biological systems from an engineer's point of view. PLoS Biol. 2009;7:e21. doi: 10.1371/journal.pbio.1000021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Watt F.M., Hogan B.L.M. Out of Eden: stem cells and their niches. Science. 2000;287:1427–1430. doi: 10.1126/science.287.5457.1427. [DOI] [PubMed] [Google Scholar]
- 10.Moore K.A., Lemischka I.R. Stem cells and their niches. Science. 2006;311:1880–1885. doi: 10.1126/science.1110542. [DOI] [PubMed] [Google Scholar]
- 11.Rizvi A.Z., Wong M.H. Epithelial stem cells and their niche: there's no place like home. Stem Cells. 2005;23:150–165. doi: 10.1634/stemcells.2004-0096. [DOI] [PubMed] [Google Scholar]
- 12.Wilson A., Trumpp A. Bone-marrow hematopoietic-stem-cell niches. Nat. Rev. Immunol. 2006;6:93–106. doi: 10.1038/nri1779. [DOI] [PubMed] [Google Scholar]
- 13.Ohyama M. Hair follicle bulge: a fascinating reservoir of epithelial stem cells. J. Dermatol. Sci. 2007;46:81–89. doi: 10.1016/j.jdermsci.2006.12.002. [DOI] [PubMed] [Google Scholar]
- 14.Yen T.H., Wright N.A. The gastrointestinal tract stem cell niche. Stem Cell Rev. 2006;2:203–212. doi: 10.1007/s12015-006-0048-1. [DOI] [PubMed] [Google Scholar]
- 15.Smart I.H. Location and orientation of mitotic figures in the developing mouse olfactory epithelium. J. Anat. 1971;109:243–251. [PMC free article] [PubMed] [Google Scholar]
- 16.Frantz G.D., McConnell S.K. Restriction of late cerebral cortical progenitors to an upper-layer fate. Neuron. 1996;17:55–61. doi: 10.1016/s0896-6273(00)80280-9. [DOI] [PubMed] [Google Scholar]
- 17.Blanpain C., Horsley V., Fuchs E. Epithelial stem cells: turning over new leaves. Cell. 2007;128:445–458. doi: 10.1016/j.cell.2007.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cooper J.A. A mechanism for inside-out lamination in the neocortex. Trends Neurosci. 2008;31:113–119. doi: 10.1016/j.tins.2007.12.003. [DOI] [PubMed] [Google Scholar]
- 19.Pesold C., Impagnatiello F., Caruncho H.J. Reelin is preferentially expressed in neurons synthesizing γ-aminobutyric acid in cortex and hippocampus of adult rats. Proc. Natl. Acad. Sci. USA. 1998;95:3221–3226. doi: 10.1073/pnas.95.6.3221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Beites C.L., Kawauchi S., Calof A.L. Identification and molecular regulation of neural stem cells in the olfactory epithelium. Exp. Cell Res. 2005;306:309–316. doi: 10.1016/j.yexcr.2005.03.027. [DOI] [PubMed] [Google Scholar]
- 21.D'Arcangelo G. Reelin mouse mutants as models of cortical development disorders. Epilepsy Behav. 2006;8:81–90. doi: 10.1016/j.yebeh.2005.09.005. [DOI] [PubMed] [Google Scholar]
- 22.Gordon M.K., Mumm J.S., Calof A.L. Dynamics of MASH1 expression in vitro and in vivo suggest a non-stem cell site of MASH1 action in the olfactory receptor neuron lineage. Mol. Cell. Neurosci. 1995;6:363–379. doi: 10.1006/mcne.1995.1028. [DOI] [PubMed] [Google Scholar]
- 23.Calof A.L., Chikaraishi D.M. Analysis of neurogenesis in a mammalian neuroepithelium: proliferation and differentiation of an olfactory neuron precursor in vitro. Neuron. 1989;3:115–127. doi: 10.1016/0896-6273(89)90120-7. [DOI] [PubMed] [Google Scholar]
- 24.Reference deleted in proof.
- 25.Schneyer A., Schoen A., Sidis Y. Differential binding and neutralization of activins A and B by follistatin and follistatin like-3 (FSTL-3/FSRP/FLRG) Endocrinology. 2003;144:1671–1674. doi: 10.1210/en.2002-0203. [DOI] [PubMed] [Google Scholar]
- 26.Schneyer A.L., Sidis Y., Krasney P.A. Differential antagonism of activin, myostatin and growth and differentiation factor 11 by wild-type and mutant follistatin. Endocrinology. 2008;149:4589–4595. doi: 10.1210/en.2008-0259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cuschieri A., Bannister L.H. The development of the olfactory mucosa in the mouse: light microscopy. J. Anat. 1975;119:277–286. [PMC free article] [PubMed] [Google Scholar]
- 28.Dowd C.J., Cooney C.L., Nugent M.A. Heparan sulfate mediates bFGF transport through basement membrane by diffusion with rapid reversible binding. J. Biol. Chem. 1999;274:5236–5244. doi: 10.1074/jbc.274.8.5236. [DOI] [PubMed] [Google Scholar]
- 29.Tang J., Tang J., Liang F. Juxtanodin in the rat olfactory epithelium: specific expression in sustentacular cells and preferential subcellular positioning at the apical junctional belt. Neuroscience. 2009;161:249–258. doi: 10.1016/j.neuroscience.2009.03.051. [DOI] [PubMed] [Google Scholar]
- 30.DeHamer M.K., Guevara J.L., Calof A.L. Genesis of olfactory receptor neurons in vitro: regulation of progenitor cell divisions by fibroblast growth factors. Neuron. 1994;13:1083–1097. doi: 10.1016/0896-6273(94)90047-7. [DOI] [PubMed] [Google Scholar]
- 31.Amthor H., Nicholas G., Patel K. Follistatin complexes Myostatin and antagonizes Myostatin-mediated inhibition of myogenesis. Dev. Biol. 2004;270:19–30. doi: 10.1016/j.ydbio.2004.01.046. [DOI] [PubMed] [Google Scholar]
- 32.de Winter J.P., ten Dijke P., van den Eijnden-van Raaij A.J. Follistatins neutralize activin bioactivity by inhibition of activin binding to its type II receptors. Mol. Cell. Endocrinol. 1996;116:105–114. doi: 10.1016/0303-7207(95)03705-5. [DOI] [PubMed] [Google Scholar]
- 33.Feijen A., Goumans M.J., van den Eijnden-van Raaij A.J. Expression of activin subunits, activin receptors and follistatin in postimplantation mouse embryos suggests specific developmental functions for different activins. Development. 1994;120:3621–3637. doi: 10.1242/dev.120.12.3621. [DOI] [PubMed] [Google Scholar]
- 34.Holcomb J.D., Mumm J.S., Calof A.L. Apoptosis in the neuronal lineage of the mouse olfactory epithelium: regulation in vivo and in vitro. Dev. Biol. 1995;172:307–323. doi: 10.1006/dbio.1995.0025. [DOI] [PubMed] [Google Scholar]
- 35.Costanzo R.M., Graziadei P.P. A quantitative analysis of changes in the olfactory epithelium following bulbectomy in hamster. J. Comp. Neurol. 1983;215:370–381. doi: 10.1002/cne.902150403. [DOI] [PubMed] [Google Scholar]
- 36.Schwartz Levey M., Chikaraishi D.M., Kauer J.S. Characterization of potential precursor populations in the mouse olfactory epithelium using immunocytochemistry and autoradiography. J. Neurosci. 1991;11:3556–3564. doi: 10.1523/JNEUROSCI.11-11-03556.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kawauchi S., Kim J., Calof A.L. Foxg1 promotes olfactory neurogenesis by antagonizing Gdf11. Development. 2009;136:1453–1464. doi: 10.1242/dev.034967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Johnston M.D., Edwards C.M., Chapman S.J. Mathematical modeling of cell population dynamics in the colonic crypt and in colorectal cancer. Proc. Natl. Acad. Sci. USA. 2007;104:4008–4013. doi: 10.1073/pnas.0611179104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ganguly R., Puri I.K. Mathematical model for the cancer stem cell hypothesis. Cell Prolif. 2006;39:3–14. doi: 10.1111/j.1365-2184.2006.00369.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Visvader J.E., Lindeman G.J. Cancer stem cells in solid tumors: accumulating evidence and unresolved questions. Nat. Rev. Cancer. 2008;8:755–768. doi: 10.1038/nrc2499. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


