Structural and Magnetic Effects of meso-Substitution in Alkyl-Substituted Metalloporphyrinate π-Cation Radicals: Characterization of [Fe-(TalkylP^.)(Cl)]SbCl₆ (alkyl = ethyl and n-propyl)

Abstract

We report the preparation and characterization of two meso-alkyl substituted porphyrin π-cation radical derivatives, [Fe(TalkylP^.)(Cl)]SbCl₆ (alkyl = ethyl or propyl). Both complexes have been characterized by UV/vis/near-IR, IR and Mössbauer spectroscopy, temperature-dependent solid-state magnetic susceptibility measurements and X-ray structure determinations. All data for both oxidized species are consistent with the formulation of the complexes as ring-oxidized iron(III) porphyrin species. The molecular structures of the two five-coordinate species have the typical square-pyramidal coordination group of high-spin iron(III) derivatives. The crystal structures also reveal that the species form cofacial π–π dimers with lateral shifts of 1.44 Å and 3.22 Å, respectively, for the propyl and ethyl radical derivatives. Both radicals exhibit porphyrin cores with alternating bond distance patterns in the inner 16-membered ring. In addition, [Fe(TEtP^.)(Cl)]SbCl₆ and [Fe(TPrP^.)(Cl)]SbCl₆ have been characterized by temperature-dependent (6–300K) magnetic susceptibility studies, the best fitting of the temperature-dependent moments reveal strong coupling between iron spins and porphyrin radical, and a smaller magnitude of antiferromagnetic coupling between ring radicals, which are opposite to those found in the five-coordinate iron(III) OEP radicals. The differences in structure and properties of the cation radical meso-alkyl and β-alkyl derivatives possibly reflect differences in properties of a _1u- and a _2u-forming radicals.

Introduction

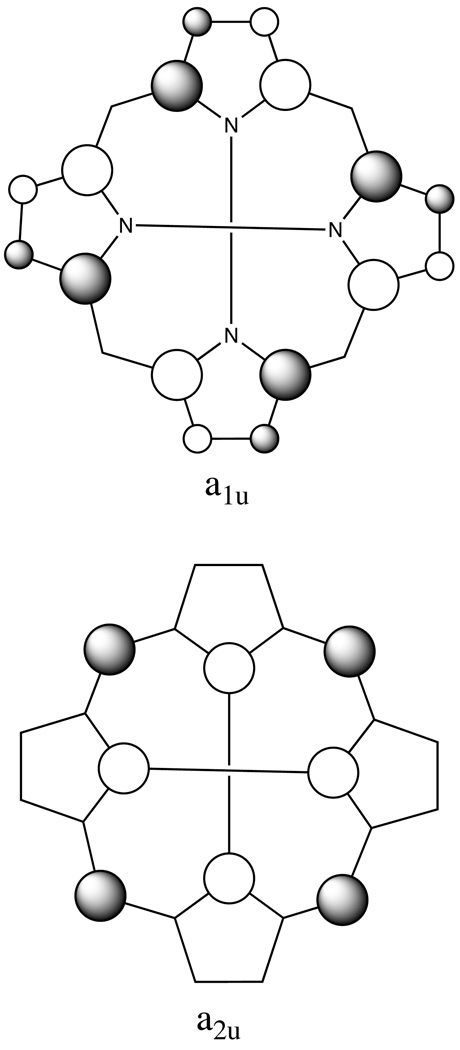
The oxidation of metalloporphyrin derivatives leads to two limiting types of π-cation derivatives: metallo derivatives of octaethylporphyrin (MOEP¹) yield an a_1u type of cation radical whereas metallo derivatives of tetraphenylporphyrin (MTPP) yield a_2u type cation radicals (Scheme 1). The two radical types are distinguished by the localization of the unpaired spin density in the radical as shown in Scheme 1. One issue associated with the two types of radicals is bond length alternation–short and long values–in the inner 16-membered ring. The bond alternation phenomenon was first observed in strongly interacting dimeric radicals of [Zn(OEP^.)(OH₂)]ClO₄.² There are two unusually distinct sets of C_a–N and C_a–C_m bond distances in the inner 16-membered ring, the values for the C_a–N bond type are 1.342 and 1.384 Å and those for the C_a–C_m bond type are 1.372 and 1.416 Å. So far the alternating bond distance pattern has been seen mostly in the a_1u cation radicals; it seems to be related to the strongly interacting dimeric structures, since the sterically unencumbered OEP cation radicals formed rather tight dimers in all four and five-coordinated complexes structurally characterized. Another possible reason might lie in orbitals of a_1u and a_2u symmetry; a_1u radicals have high spin density at the β carbons, whereas a_2u radicals localize unpaired spin density at the nitrogens and meso carbons. Therefore a clearer explanation for the bond alternation may evolve as additional high-precision determinations of π-cation radicals become available.

Scheme 1.

Plots of HOMOs of a_1u and a_2u symmetry. The magnitude of the orbital coefficients are depicted by the size of the circles with shaded/unshaded indicating the sign.

In earlier work on metalloporphyrin π-cation radicals, spin coupling between the metal ion and the oxidized porphyrin ring in a number of derivatives that differed in metal ion, axial ligation, and/or porphyrin ligand were investigated.^2–10 The nature of this coupling is dependent on the extent of porphyrin core overlap and orientation of the dimeric π-cation-radical derivatives, i.e., directly related to the porphyrin ligands. For example, in [Fe(OEP^.)(Cl)]SbCl₆,⁹ the complex forms a very strongly coupled dimer, in [Fe(oxoOEC^.)(Cl)]SbCl₆,^1;10 however, one gem-diethyl group on one side of one radical cation inhibits the approach of the second radicalcation, even so, there is still a weak intermolecular antiferromagnetic interaction between the radical spins in the dimeric unit. To more completely explore the notion that the magnitude of the inter-ring coupling is proportional to the degree of overlap between two porphyrin cores, we attempted to prepare two meso-alkyl substituted (chloro)iron(III) porphyrinate π-cation derivatives.

Molecular structures of three neutral meso-alkyl substituted (chloro)iron(III) porphyrinate derivatives with the meso-substituents ethyl, [Fe(TEtP)(Cl)], n-propyl, [Fe(TPrP)(Cl)], and n-hexyl, [Fe(THexP)(Cl)] revealed that the degree of the inter-ring interactions depends on the meso-substituted groups.¹¹ The magnitude of the inter-ring coupling decreases in the order: [Fe(TEtP)(Cl)] > [Fe(TPrP)(Cl)] ≥ [Fe(THexP)(Cl)]. Unexpectedly, the inter-ring coupling in the solid state is stronger in π-cation [Fe(TPrP^.)(Cl)]⁺ than in [Fe(TEtP^.)(Cl)]⁺ cation upon oxidation. We report herein on our characterization of the chloro derivatives [Fe(TalkylP^.)(Cl)]SbCl₆ (alkyl = ethyl and propyl), including UV-vis, near-IR, IR, and Mössbauer spectra, magnetic susceptibilities, and X-ray crystal structures.

Experimental Section

General Information

All manipulations were carried out under argon using a double manifold vacuum line, Schlenkware, and cannula techniques. Dichloromethane was distilled over CaH₂, and hexanes was distilled over sodium benzophenone. All other chemicals were used as received from Aldrich or Fisher. meso-Tetra-n-propylporphyrin (H₂TPrP) was prepared according to Neya’s method,¹² while meso-tetraethylporphyrin (H₂TEtP) was prepared according to Lindsey’s method.¹³ The chloroiron(III) derivatives [Fe(TPrP)(Cl)] and [Fe(TEtP)(Cl)] were synthesized by literature methods.¹⁴

Preparation of [Fe(TPrP^.)(Cl)]SbCl₆]

[Fe(TPrP)(Cl)] (15 mg, 0.0265 mmol) and tris(p-bromophenyl)aminium hexachloroantimonate (22 mg, 0.0269 mmol) were placed in a 100-mL Schlenk flask, and dichloromethane (~20 mL) was added. The solution was stirred for 1 h and transferred into two 10mL beakers. These were each placed in a crystallizing bottle with hexanes to induce crystallization by slow vapor diffusion in a refrigerator (4°C). Dark-purple crystals formed after ~5 days. UV-vis and IR spectra were measured on samples comprised of selected crystals. UV-vis/near-IR (CH₂Cl₂ solution): λ_max: 378, 408, 518, 618, 721,1327 nm. IR(KBr): ν(TPrP^.) 1283 cm⁻¹ (s), ν(Sb–Cl stretch) 341 cm⁻¹.

Bulk samples were prepared for magnetic susceptibility and Mössbauer measurements by the following procedure: [Fe(TPrP)(Cl)] (100 mg, 0.176 mmol) and tris(p-bromophenyl)aminium hexachloroantimonate (146 mg, 0.1788 mmol) were dissolved in dichloromethane in a 100-mL Schlenk flask. The solution was stirred for 1h, and filtered/transferred into another 100-mL Schlenk flask. The filtered solution was layered with hexanes. After several days, the crystals were filtered and washed with hexanes.

Preparation of [Fe(TEtP^.)(Cl)]SbCl₆

The same procedures as above were used for [Fe(TEtP^.)(Cl)]SbCl₆. Single crystals of [Fe(TEtP^.)(Cl)]SbCl₆ were obtained by slow diffusion of hexanes into a CH₂Cl₂ solution. UV-vis/near-IR (CH₂Cl₂ solution): λ_max: 377, 409, 518, 614, 722, 1432 nm. IR(KBr): ν(TEtP^.) 1283 cm⁻¹ (s), ν(Sb–Cl stretch) 341 cm⁻¹.

X-Ray Structure Determinations

X-ray diffraction data for both complexes were collected on a Nonius FAST area-detector diffractometer. Our detailed methods and procedure for small molecular X-ray data collection have been described previously.¹⁵

Both structures were solved by direct methods.¹⁶ The structures were refined against F² using SHELXL-93,¹⁷ in which all data collected were used including negative intensities. Hydrogen atoms of the porphyrin ligands and the solvent molecules were idealized with the standard SHELXL-93 idealization methods. The absorption correction program DIFABS¹⁸ and extinction were applied for [Fe(TPrP^.)(Cl)]SbCl₆]. There are three disordered units in [Fe(TEtP^.)(Cl)]SbCl₆. The first is a CH₂Cl₂ molecule, the C atom of which occupies two sites (the occupancy factors were refined to be 0.52 and 0.48). The ${\text{SbCl}}_6^{-}$ ion appears to have a small rotational disorder around the Cl(6)–Cl(3) axis. Only the disordered Cl(2) atom was resolved and occupies two sites with refined occupancies of 0.66 and 0.34; the disorder of the remaining three chlorides was taken up in the thermal motion. One ethyl group was disordered over two sites (up and down with respect to the porphyrin plane). For [Fe(TPrP^.)(Cl)]SbCl₆], C(32) and C(33) were found to be disordered over two positions with refined half-occupation factors. Brief crystal data are listed in Table 1. Complete details of both structure determinations are available in the Supporting Information.

Table 1.

Crystallographic details

	[Fe(TEtP.)(Cl)]SbCl6	[Fe(TPrP.)(Cl)]SbCl6
Formula	C28H28Cl7FeN4Sb·CH2Cl2	C32H36Cl7FeN4Sb·CH2Cl2
FW	931.22	987.32
a, Å	9.768(2)	10.0407(1)
b, Å	13.585(3)	14.4882(6)
c, Å	14.508(3)	15.7601(9)
α, deg	76.90(3)	111.079(5)
β, deg	87.32(3)	103.848(7)
γ, deg	71.77(3)	101.504(5)
V, Å3	1780.2(6)	1971.21(14)
Z	2	2
Space group	P1̅	P1̅
Dc, g/cm3	1.737	1.663
F(000)	924	988
µ, mm−1	1.870	1.694
Radiation (λ, Å)	0.71073
Temperature, K	130(2)
Final R indices [I > 2 σ(I)]	R1 = 0.0516; wR2 = 0.1213	R1 = 0.0497; wR2 = 0.1227
Final R indices [for all data]	R1 = 0.0632; wR2 = 0.1286	R1 = 0.0571; wR2 = 0.1338

Physical Characterization

UV/visible/near-IR spectra were recorded on a Perkin-Elmer Lambda 19 spectrometer and IR spectra on a Perkin-Elmer model 883 or on a Perkin-Elmer Paragon 1000 as KBr pellets. Mössbauer velocity scales are referred to the centroid of the room temperature spectrum of a metallic iron foil. Magnetic susceptibility measurements were obtained on ground samples in the solid state over the temperature range 6–300 K on a Quantum Design MPMS SQUID susceptometer. All samples were immobilized in Dow Corning silicone grease. Measurements at two fields (2 and 20 kG) showed that no ferromagnetic impurities were present. χ_M was corrected for the underlying porphyrin ligand diamagnetism according to previous experimentally observed values;²⁰ all remaining diamagnetic contributions (χ_dia) were calculated using Pascal’s constants.^21,22 All measurements included a correction for the diamagnetic sample holder and diamagnetic immobilizing agent. Magnetic susceptibility and Mössbauer spectroscopic measurements were taken on portions from the same sample preparation.

Results and Discussion

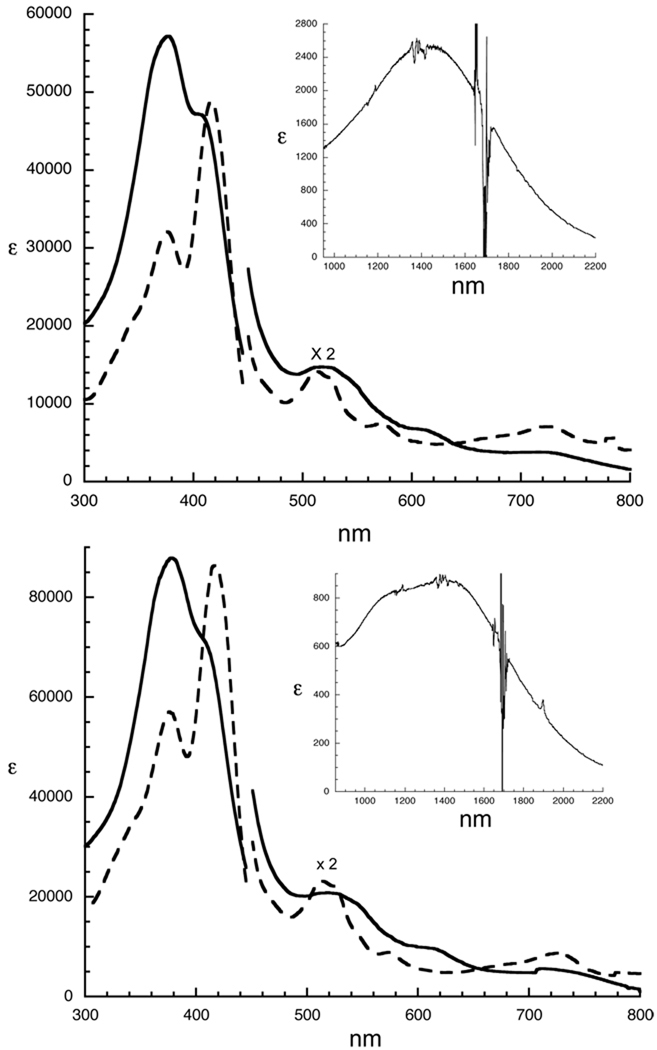
We have characterized the π-cation radical derivatives of two meso-alkyl substituted iron por-phyrinates, [Fe(TEtP^.)(Cl)]SbCl₆ and [Fe(TPrP^.)(Cl)]SbCl₆, using UV/vis/near-IR, IR and Mössbauer spectra, and magnetic susceptibilities as well as determining the solid-state structures. All data for both oxidized species are consistent with the formulation of the complexes as ring-oxidized iron(III) porphyrin species. Typically, the electronic spectrum characteristics of a radical cation species are a broadened α, β region, a new band at low energy, and a dramatically broadened, low-intensity, blue-shifted Soret band relative to the unoxidized species.²⁵ As seen in Figure 1 and Table 2, both spectra of the oxidized species have the characteristic features of radical formation. Interestingly, we note that there are two Soret bands with one showing an increased intensity and the other a lower intensity relative to those of the parent complexes. This spectral feature is not present in [Fe(TPP^.)(Cl)]SbCl₆ ³ and [Fe(OEP^.)(Cl)]SbCl₆.⁹

Figure 1.

UV-vis spectra of [Fe(TEtP)(Cl)] (- - -) and [Fe(TEtP^.)(Cl)]SbCl₆ (—)(Top), and [Fe(TPrP)(Cl)] (- - -) and [Fe(TPrP^.)(Cl)]SbCl₆] (—) (Bottom) in CH₂Cl₂ solution. Insets in both sets of spectra display the near-IR band of [Fe(TEtP^.)(Cl)]SbCl₆ (top) and [Fe(TPrP^.)(Cl)]SbCl₆ (bottom).

Table 2.

UV-visible and near-IR Spectral Data(λ_max;, nm (logε)) in CH₂Cl₂ at room temperature.

Complex	Soret bands		Visible bands				Near-IR band
[Fe(TEtP)(Cl)]	376(4.51)	416(4.69)	513(3.85)	524(3.82)	573(3.57)	723(3.55)
Fe(TPrP)(Cl)]	378(4.76)	418(4.94)	513(4.06)	524(4.04)	573(3.65)	726(3.64)
[Fe(TEtP.)(Cl)]SbCl6	377(4.76)	408(4.67)	518(3.87)	614(3.52)	723(3.28)		1432(3.09)
Fe(TPrP.)(Cl)]SbCl6]	378(4.94)	408(4.85)	518(4.02)	618(3.67)	713(3.45)		1327(2.92)

Moreover, as shown in the insets to Figure 1, [Fe(TEtP^.)(Cl)]SbCl₆ and [Fe(TPrP^.)(Cl)]SbCl₆ both display a broad near-IR absorption band. Such near-IR bands have been seen in a number of other metalloporphyrin π-cation radical derivatives.^{8, 10, 26, 27, 28} The near-IR band in a number of these derivatives is associated with the formation of dimeric π-cation radical derivatives of OEP, ${[\mathrm{M}({\text{OEP}}^{·})]}_2^{2+}$, ^{26, 27, 28} or in one case, an oxoOEC species, ${[\text{Cu}({\text{oxoOEC}}^{·})]}_2^{2+}$ ⁸. The near-IR band in these derivatives shows a sensible dependence on concentration, consistent with dimerization. However, there is no dimerization-type concentration dependence for the near-IR bands of [Fe(TEtP^.)(Cl)]SbCl₆ and [Fe(TPrP^.)(Cl)]SbCl₆. We were able to obtain near-IR spectra at several concentrations that span a range of better than one order of magnitude. This Beer’s law concentration dependence of the near-IR bands has been observed for only one other radical species, [Fe(oxoOEC^.)(Cl)]SbCl₆,¹⁰ also an iron derivative. Although the sample is not as extensive as one might like, we can tentatively conclude that the likely origin for this near-IR band is an iron to porphyrin radical charge transfer band.

Porphyrin π-cation radicals exhibit a diagnostic infrared marker band.²⁹ This band is found at ~1280 cm⁻¹ for TPP and other tetraaryl derivatives and at ~1550 cm⁻¹ for OEP and related species. The position of the marker band is thought to reflect whether the half-filled radical MO is predominantly that of a_2u or a_1u symmetry. Both [Fe(TEtP^.)(Cl)]⁺ and [Fe(TPrP^.)(Cl)]⁺ π-cation radicals display a marker band at 1283 cm⁻¹, close to that of ~1290 cm⁻¹ observed in the [Fe(TPP^.)(Cl)]⁺ cation²⁹ and presumably reflects that the half-filled MO has predominant a_2u character.

The Mössbauer spectra for [Fe(TEtP^.)(Cl)]SbCl₆ and [Fe(TPrP^.)(Cl)]SbCl₆ provides compelling evidence that oxidation has occurred at the porphyrin ring. The observed isomer shift and quadrupole splitting values in the oxidized species at 4.2 K are ΔE_Q = 0.75 mm/s and δ = 0.42 mm/s for [Fe(TEtP^.)(Cl)]SbCl₆, and ΔE_Q = 0.44 mm/s and δ = 0.41 mm/s for [Fe(TPrP^.)(Cl)]SbCl₆, consistent with those observed for five-coordinate high-spin iron(III) porphyrins (ΔE_Q = 0.4–1.0 mm/s; δ = 0.25–0.43 mm/s).^3,9,30

The coordination environments of the iron atom in [Fe(TEtP^.)(Cl)]SbCl₆ and [Fe(TPrP^.)-(Cl)]SbCl₆ are very similar. Both porphyrin cores are slightly saddled, the displacement of the iron atoms for each complex is 0.46 Å from the 24-atom porphyrin mean plane. Both of the species have identical average Fe–N_p bond lengths (2.068(5) Å), the Fe–Cl distances are similar to each other (2.1634(11) vs 2.1700(7) Å), comparable to the distances observed in high-spin [Fe(TTP^.)(Cl)]⁺ cation³ ( Fe–N_p = 2.07(1) Å and Fe–Cl = 2.168(5) Å ) and [Fe(OEP^.)(Cl)]⁺ cation⁹ (Fe–N_p = 2.058(5) Å and Fe–Cl = 2.186(1) Å). The Fe–Cl distances in π-cation radical derivatives are shorter than the distances typically observed in neutral five-coordinate chloroiron species.²⁴ The slight contraction of the Fe—Cl distance is consistent with the increased positive charge of the complexes.

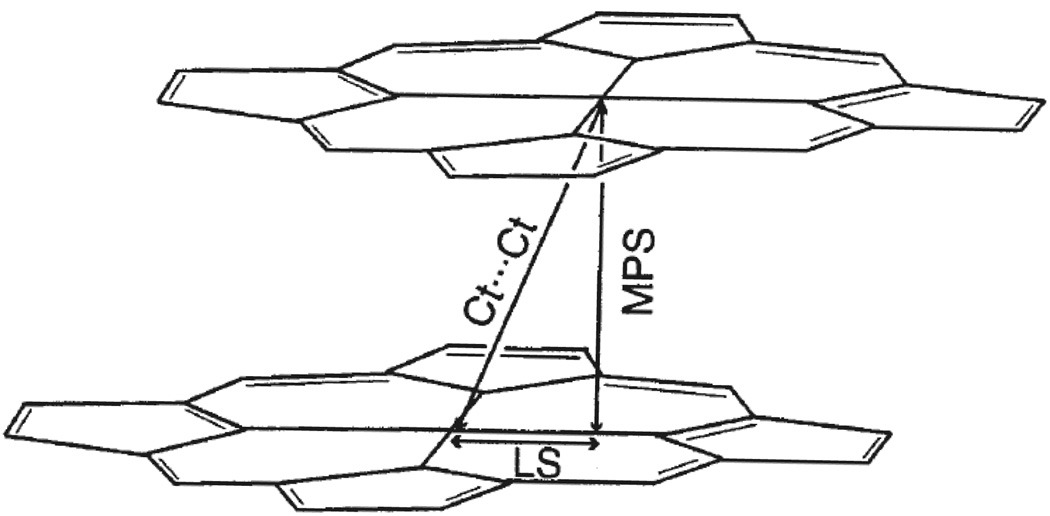
Table 3 lists a number of structural parameters²³ for [Fe(TEtP^.)(Cl)]SbCl₆ and [Fe(TPrP^.)-(Cl)]SbCl₆. The inter-ring geometry changes more dramatically upon oxidation for [Fe(TPrP)(Cl)] relative to that of [Fe(TEtP)(Cl)] (Figures 4 and 5). For [Fe(TEtP^.)(Cl)]SbCl₆, the Fe· · ·Fe distance is 5.26 Å, the Ct· · ·Ct distance is 4.58 Å, the mean plane separation is 3.25 Å and the lateral shift is 3.22 Å, while the corresponding values found in [Fe(TEtP)(Cl)] are 5.56 Å, 5.04 Å, 3.34 Å and 3.79 Å. Thus, the inter-ring parameters do not change significantly upon oxidation. In marked contrast, there are very large changes in these values between [Fe(TPrP)(Cl)] and [Fe(TPrP^.)(Cl)]SbCl₆]. More specifically, the lateral shift decreases by 2.85 Å and the Ct· · ·Ct distance by 1.99 Å upon oxidation of [Fe(TPrP)(Cl)] to [Fe(TPrP^.)(Cl)]SbCl₆.

Table 3.

Structural, Mossbauer, and Magnetic Measurement data for π-Cation Radical Porphinatoiron(III) Complexes

complex	Fe⋯Fea	Ct⋯Cta	MPSa, b	LSa, c	−2JFe–rd	−2Jr–rd	−2JFe–Fed	−2JFe–r′d	Dd	ΔEqe	δe	ref
[Fe(TPrP.)(Cl)]SbCl6	4.51	3.65	3.35	1.44	−225	−36	0.5	−0.5	7	0.44	0.41	this work
[Fe(TEtP.)(Cl)]SbCl6	5.26	4.58	3.25	3.22	−193	−24	0.4	−0.4	11	0.75	0.42	this work
[Fe(OEP.)(Cl)]C104	4.11	3.25	3.24	0.2						0.59	0.41	9
[Fe(OEP.)(Cl)]SbCl6 f					−90	−278	1		3	0.71	0.42	9
[Fe(OEP.)(Br)]SbCl6 f					−118	−348	3		1	0.77	0.41	9
[Fe(oxoOEC.)(Cl)]SbCl6	10.03	10.03	4.82	8.70	−76	−13	−0.14		6	0.70	0.50	10
[Fe(TPP.)(Cl)]SbCl6					−100	−16	–g		3	0.56	0.39	37
[Fe(TTP.)(Cl)]SbCl6	5.39	4.70	3.68	3.13								3
[Fe(TEtP)(Cl)]	5.56	5.04	3.34	3.79			0.45		7			11
[Fe(TPrP)(Cl)]	6.44	5.64	3.66	4.29			0.17		7			11

^aValues in Å.

^bMPS = mean plane separation.

^CLS = lateral shift of two porphyrin rings.

^dValues in cm⁻¹

^eValues in mm/s.

^fModel B.(Ref. ⁹)

^gDistinction between radical–radical and Fe–Fe coupling is indeterminate.

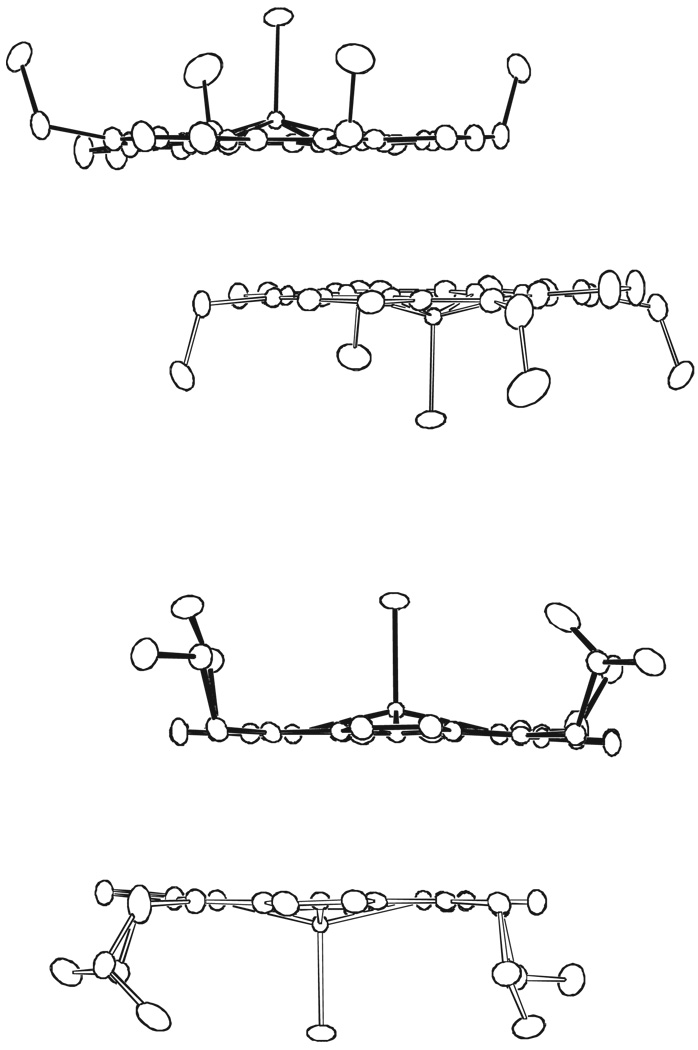
Figure 4.

Edge-views of the dimeric units of [Fe(TEtP^.)(Cl)]⁺ (top) and [Fe(TPrP^.)(Cl)]⁺ (bottom). 50% probability ellipsoids are shown. The scale of this figure and Figure 5 are identical.

Figure 5.

Top-views of the dimeric units of [Fe(TEtP^.)(Cl)]⁺ (top) and [Fe(TPrP^.)(Cl)]⁺ (bottom). (50% probability ellipsoids).

An interesting question of why [Fe(TPrP^.)(Cl)]SbCl₆ forms an apparently stronger inter-ring interaction than [Fe(TEtP^.)(Cl)]SbCl₆ does is addressed by these data above. The answer may lie in a conformational effect of the macrocycles that drives the dimerization of the porphyrin rings. The core conformation of [Fe(TEtP)(Cl)] is basically planar with two adjacent ethyl groups pointing up and two pointing down in an orientation to favor inter-ring overlap.¹¹ Upon oxidation of [Fe(TEtP)(Cl)], the macrocycle becomes slightly saddle-shaped. However, the macrocyclic conformations change significantly upon oxidation of [Fe(TPrP)(Cl)]. The macrocycle of [Fe(TPrP)(Cl)] is ruffled with alternating up and down meso-substituents as to hinder inter-ring overlap,¹¹ while the macrocycle of the [Fe(TPrP^.)(Cl)]⁺ cation becomes slightly saddled with all the propyl groups pointing away from the center of the dimers (Figure 4 and Figure 5). Thus, there is a larger conformational driving force upon the oxidation of [Fe(TPrP)(Cl)] than upon oxidation of [Fe(TEtP)(Cl)]. Scheidt has pointed out²³ that the saddled distortion allows more extensive intermolecular interactions between radicals than a planar porphyrin would.

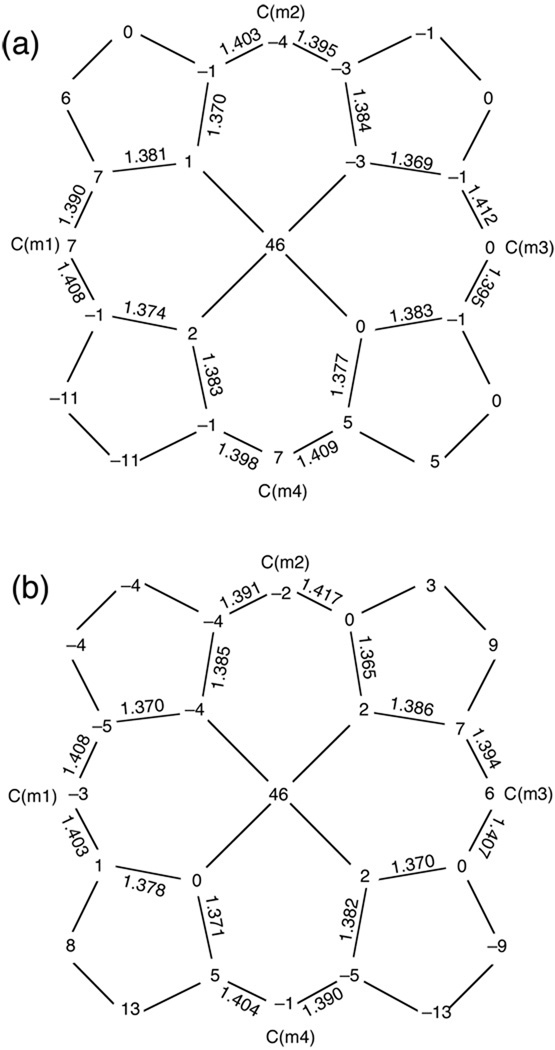
Although average N–C and C–C distances in porphyrins and porphyrin π-cation radicals tend to be similar,³¹ specific classes of bonds change upon oxidation for [Fe(TEtP)(Cl)] and [Fe(TPrP)(Cl)]. As shown in Figure 6, bond distances in the inner 16-membered ring exhibit a quite unusual pattern of alternating shorter and longer bonds. The average N–C_a distances of two classes are 1.373(4) Å and 1.382(4) Å for [Fe(TEtP^.)(Cl)]SbCl₆, and 1.369(3) Å and 1.383(3) Å for [Fe(TPrP^.)(Cl)]SbCl₆; the average values of the C_a–C_m bond lengths are 1.395(3) Å and 1.408(4) Å, and 1.394(6) Å and 1.409(6) Å for [Fe(TEtP^.)(Cl)]SbCl₆ and [Fe(TPrP^.)(Cl)]SbCl₆, respectively. The same pattern was present in most dimeric OEP radicals assigned an a_1u ground state,^9,32 but the trend is not universal in all a_2u radicals.³³

Figure 6.

Formal diagrams of the porphinato core displaying perpendicular displacements, in units of 0.01Å, of the core atoms from the 24-atom mean plane. Also entered on the diagrams are the values of the individual bond distances in the inner 16-membered rings. Note the alternating short-long pattern of the N–C_a and C_a–C_m bond distances. [Fe(TEtP^.)(Cl)]SbCl₆ (top), [Fe(TPrP^.)(Cl)]SbCl₆ (bottom).

Scheidt has addressed the issue of whether the bond alternation phenomenon is a result of the formation of cofacial dimers,³⁴ since this feature was observed mostly in the strongly interacting dimeric OEP derivatives. As shown in Figures 4 and 5, both of the radicals form cofacial dimers but with lateral shifts much larger than the analogous OEP species. Therefore it is clear, from density functional theory (DFT) calculation³⁵ along with other data³⁶ that dimerization in itself does not necessarily lead to an alternating bond distance pattern.

One of the major objectives of this study was to obtain detailed information on the nature of the spin-coupling in these two a_2u radical species. We expected to obtain significant useful information on this issue by determination of the temperature-dependent magnetic susceptibilities and fitting the data to an appropriate coupling model. The structural data show that both radical cation derivatives display pairwise interactions in the solid state. Hence the treatment of the magnetic susceptibility data is expected to require consideration of a four-spin coupling system. This model would include intra- and inter-molecular coupling between the unpaired electrons on the two iron atoms and the radical spin on the two porphyrin rings. The centrosymmetric relationship of the dimeric species simplifies the coupling model to a radical–radical coupling in the dimer, −2J _r–r, two identical iron–radical interactions, −2J _Fe–r, possibly two identical iron–radical (each from the different porphyrin) interactions, −2J _Fe–r′, and a possible interaction between the two high-spin iron atoms. Fits of the experimental magnetic susceptibility data for the radicals using the model described above were then attempted. The exact spin Hamiltonian used is

$$H=D[(S_z^2-1/3S(S+1))+({S\prime }_z^2-1/3S\prime (S\prime +1))]+g\beta \overrightarrow{H}\cdot (\overrightarrow{S}+\overrightarrow{S\prime }+\overrightarrow{s}+\overrightarrow{s\prime })-2J_{\text{Fe}-\mathrm{r}}(\overrightarrow{S\prime }\cdot \overrightarrow{s}+\overrightarrow{S\prime }\cdot \overrightarrow{s}\prime )-2J_{\text{Fe}-\text{Fe}}(\overrightarrow{S}\cdot \overrightarrow{S\prime })-2J_{\mathrm{r}-\mathrm{r}}(\overrightarrow{s}\cdot \overrightarrow{s}\prime )-2J_{\text{Fe}-\mathrm{r}\prime }(\overrightarrow{S}\cdot \overrightarrow{s}\prime +\overrightarrow{S\prime }\cdot \overrightarrow{s})$$

We initially experienced difficulties in obtaining reliable, temperature-dependent magnetic susceptibility data on both radical cation samples. The problem appears to be the result of exceptionally difficult preferential sample alignment problems, apparent impurities present in “bulk” samples, solvent loss. We believe that the difficulties have definitely been overcome for [Fe(TEtP^.)(Cl)]SbCl₆ and [Fe(TPrP^.)(Cl)]SbCl₆ samples. All magnetic data used was acquired from single crystal samples selected to make up an adequate sized sample; solvent loss for [Fe(TPrP^.)(Cl)]SbCl₆ was 50 %, whereas [Fe(TEtP^.)(Cl)]SbCl₆ loses solvent more readily and complete loss of solvent was assumed for the magnetic measurement.

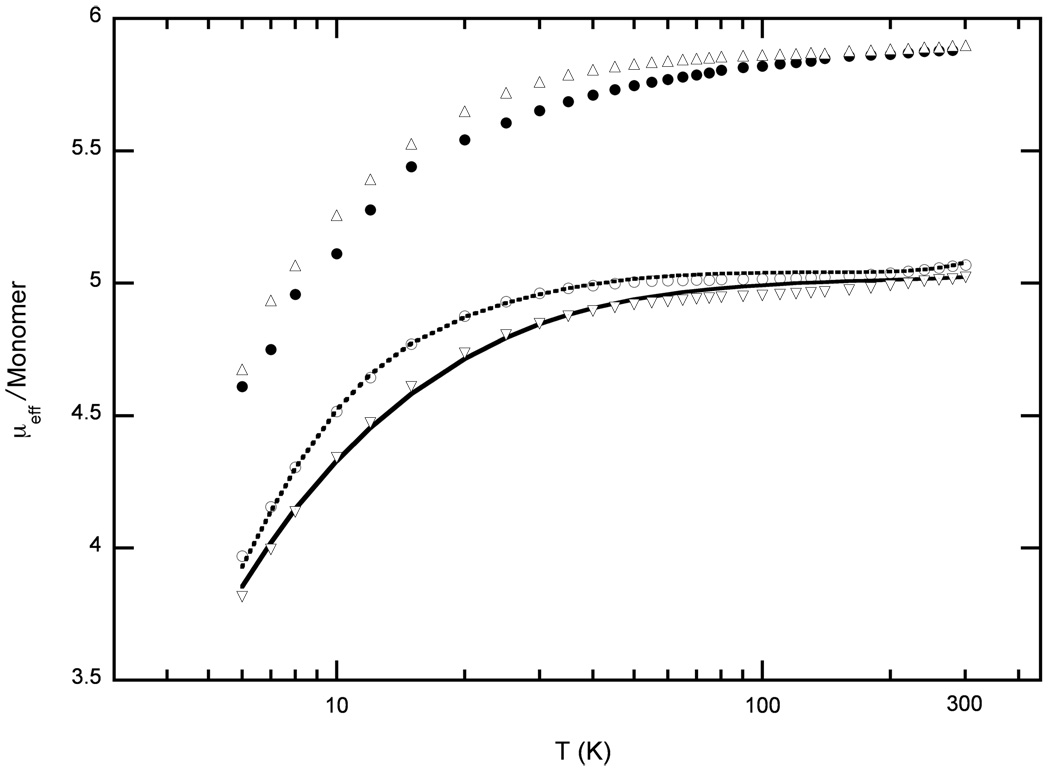
We have been able to obtain satisfactory fits of the experimental magnetic susceptibility data for both radicals, [Fe(TEtP^.)(Cl)]SbCl₆ and [Fe(TPrP^.)(Cl)]SbCl₆, using the model described above. A comparison of the experimental data and the calculated fit is given in Figure 7. The values obtained from the fitting analysis are given in Table 3. Also tabulated in Table 3 are the results of magnetic fitting for all other five-coordinate porphinatoiron(III) π-cation radical derivatives available.^{9, 10, 37} We have also tabulated several relevant geometric factors for these derivatives. In several cases, closely related species must be considered as a group in order to provide for both magnetic results and the structural patterns.

Figure 7.

Comparison of observed and calculated values of µ_eff/monomer vs T for [Fe-(TEtP^.)(Cl)]SbCl₆ (○) and [Fe(TPrP^.)(Cl)]SbCl₆] (▽). The lines (solid or dashed) are model calculations assuming pairwise spin coupling. The fit parameters used are given in Table 3. Also shown in the figure are the T-dependent magnetic susceptibilities for the precursors [Fe(TPrP)(Cl)] (●) and [Fe(TEtP)(Cl)] ((△) that have been described previously.¹¹

The magnitude of the antiferromagnetic coupling between ring radicals (−2J _r–r) shows a sensible dependence on the interaction between pairs of rings in the cofacial dimers (as measured by the lateral shift and ring center to ring center distance). The observed coupling between the two TPrP^. rings in [Fe(TPrP^.)(Cl)]SbCl₆] is larger than that seen in [Fe(TEtP^.)(Cl)]SbCl₆, but both values are significantly smaller than that seen in the analogous OEP^. derivative where the two ring display almost no lateral shift between pairs of rings. Although the data are limited, it appears that there is no obvious relationship between −2J _r–r and whether the radical derivative is of the a_2u or a_1u type. The inter-ring coupling is thus seen to be closely related only to the degree of the ring overlap.

However, the coupling between the iron spins and the porphyrin radical (−2J _Fe–r) does appear to show significant differences between the two radical types. The derived iron–radical coupling constants for [Fe(TEtP^.)(Cl)]SbCl₆ and [Fe(TPrP^.)(Cl)]SbCl₆ (a_2u radicals) are significantly larger than the two values available for [Fe(OEP^.)(X)]SbCl₆ species (a_1u type radicals). The pattern continues when the value of this variable is examined for [Fe(TPP^.)(Cl)]SbCl₆ (a_2u) and [Fe(oxoOEC^.)(Cl)]SbCl₆ (a_1u). The magnitudes of the iron–radical couplings reflect differences in the location of significant unpaired density in the singly occupied radical m.o. The a_2u radical wave function has large amplitude at the pyrrole nitrogens, whereas the a_1u wave function has nodes at the pyrrole nitrogen atoms. Therefore, it is natural to expect the a_2u orbital to overlap more strongly than a_1u with the iron d-orbitals, and which will result in a larger iron-radical contact coupling. It should be emphasized that this pattern is seen independent of the magnitude of the radical–radical coupling. It is to be noted that differences in the magnituve of the iron-radical coupling in the TPP and T(n-alkyl)P derivatives is larger than might be expected since both are a_2u radicals. This might be related to differing electron density distributions, especially at the nitrogen atoms. No theoretical calculations are currently available, but NMR shjifts of the β-pyrrole protons show modest differences in shifts for [Fe(Por)Cl], Por = TPP (shift 70.2),³⁸ TEtP (shift = 88.6), and TMeP (shift 87.6)³⁹ consistent with sin density differences in the pyrrole ring. A final possibility for observed differences is simply that the a_1u/a_2u distinction is too simple. This has been suggested in a somewhat different context by Ghosh et al.³⁵

What are the similarities and differences between a_1u and a_2u radicals of iron(III) porphyrinates that we have found? The sample data are limited, but some distinct differences or trends seem evident. In the a_2u radicals, relatively weak inter-ring coupling of π-cation radicals is observed, while the a_1u type radicals show exceptionally strong inter-ring coupling. The differences in the magnitude of the spin coupling are correlated with inter-ring structure, with relatively large inter-ring coupling constants being associated with the formation of tight cofacial π-π dimers. On the other hand, the large iron-radical coupling observed in the a_2u type radicals arises from the high concentration of spin density at the coordinating nitrogen atoms of the iron(III) porphyrin radicals. For the structurally similar iron(III) complexes with the a_1u-type radicals, the iron-radical coupling shows much smaller constants because the a_1u-type radicals have high concentration of spin density at the β-pyrrole carbon atoms, remote from the the iron center.

Summary

The molecular structures and magnetic susceptibility of [Fe(TEtP^.)(Cl)]SbCl₆ and [Fe(TPrP^.)(Cl)]SbCl₆ are reported. The structural analysis shows that there is a stronger cofacial dimer interaction in [Fe(TPrP^.)(Cl)]SbCl₆] than in [Fe(TEtP^.)(Cl)]SbCl₆, unlike those found in their parent complexes; this is a result of the changes of the core conformation upon oxidation. Both radicals are a_2u radicals, and display cores with the bond alternation in the inner 16-membered ring. Magnetic exchange coupling between radical spins in a dimeric unit are in accord with the trend in structural inter-ring geometries.

Figure 2.

ORTEP diagram of [Fe(TEtP^.)(Cl)]SbCl₆ displaying the atom labeling scheme. Thermal ellipsoids of all atoms are contoured at the 50% probability level. Hydrogen atoms have been omitted for clarity.

Figure 3.

ORTEP diagram of [Fe(TPrP^.)(Cl)]SbCl₆ displaying the atom labeling scheme. Thermal ellipsoids of all atoms are contoured at the 50% probability level. Hydrogen atoms have been omitted for clarity.

Scheme 2.

Diagram illustrating structural features found in cofacial porphyrin dimers. Quantities displayed include the mean plane separation, MPS, the center to center distance, Ct⋯Ct, and the lateral shift of the two ring centers, LS.