Multiscale molecular dynamics using the matched interface and boundary method

Abstract

The Poisson-Boltzmann (PB) equation is an established multiscale model for electrostatic analysis of biomolecules and other dielectric systems. PB based molecular dynamics (MD) approach has a potential to tackle large biological systems. Obstacles that hinder the current development of PB based MD methods are concerns in accuracy, stability, efficiency and reliability. The presence of complex solvent-solute interface, geometric singularities and charge singularities leads to challenges in the numerical solution of the PB equation and electrostatic force evaluation in PB based MD methods. Recently, the matched interface and boundary (MIB) method has been utilized to develop the first second order accurate PB solver that is numerically stable in dealing with discontinuous dielectric coefficients, complex geometric singularities and singular source charges. The present work develops the PB based MD approach using the MIB method. New formulation of electrostatic forces is derived to allow the use of sharp molecular surfaces. Accurate reaction field forces are obtained by directly differentiating the electrostatic potential. Dielectric boundary forces are evaluated at the solvent-solute interface using an accurate Cartesian-grid surface integration method. The electrostatic forces located at reentrant surfaces are appropriately assigned to related atoms. Extensive numerical tests are carried out to validate the accuracy and stability of the present electrostatic force calculation. The new PB based MD method is implemented in conjunction with the AMBER package. MIB based MD simulations of biomolecules are demonstrated via a few example systems.

1 Introduction

Since most biological processes, such as gene regulation, signal transduction, and protein-protein interaction occur in aqueous environment, the solvent-solute interactions are important to biological processes. The solvation process is typically described by explicit models and implicit models. Explicit atomistic description of biomolecules and their aqueous environment, including solvent, co-solutes, and mobile ions, is prohibitively expensive for large biomolecular systems, although a variety of advanced computational methods, such as Ewald summations, Euler summations, periodic images and reaction field theory, have been developed for molecular dynamics in the past few decades. In fact, our central interest in most biomolecular studies is the behavior of biomolecules and their interactions, instead of water molecules. As such, implicit solvent models [5, 21] that treat the solvent as an electrostatic continuum while admit an atomistic description for biomolecules, are attractive multiscale approaches for the quantitative understanding of large scale biological systems [16, 23, 32, 55, 58, 62, 65, 71]. These approaches have become increasingly popular in the biophysical and biochemical community since the earlier work by Warwicker and Watson in the early 1980s [65], and Honig in the 1990s [32]. The most commonly used implicit solvent models include the Poisson-Boltzmann equation (PBE) [5], generalized Born (GB) [22] and polarizable continuum approaches. The most attractive feature of these methods is their combination of atomic details of the biomolecule and a mean field approximation of the solvent. The PBE describes the electrostatic potential under a given charge assignment of the biomolecule and a Boltzmann distribution of the ionic concentration in the solvent. The coulomb gauge for electrostatic potential, the Gauss’s divergence theorem and law for the electric field are utilized to derive the PBE. The GB theory is simple and is usually regarded as an approximation to the PBE.

The PBE has a wide range of applications, including the estimation of electrostatic solvation free energies [24, 36, 59], pK_α values [26, 49, 64], and the electrostatic analysis of interaction surfaces. There has been a great deal of effort in developing PBE based electrostatic force calculations for molecular dynamics (MD) [28, 42, 43, 45, 50, 58] in the past two decades. The basic theoretical foundation for such calculations was established by Gilson et al. [28] based on the free energy functional derived by Sharp and Honig [58].

Most implicit solvent models, such as the Poisson-Boltzmann (PB) and GB models, utilize a solvent-molecule interface to separate the continuum domain from that of the biomolecule. Various biomolecular surface models, including the van der Waals surface, the solvent accessible surface [37], the molecular surface (MS) [53], minimal molecular surface [6] and more general geometric flow based biomolecular surfaces [7] are often employed for the application of the PB method. Recently, smoothed molecular surfaces have been proposed for implicit solvent models [14, 66, 27, 76]. Variational approaches are utilized to determine the profile of smoothed surfaces [14, 66]. It was argued that care is required when use atomic centered dielectric functions in implicit solvent models for solvation free energy calculations [60, 63]. However, as shown by Swanson et al. [61] and in our differential geometry based models [14, 66], a simple reparameterization of van der Waals radii can lead to accurate solvation calculations from smoothed surface definitions. Therefore, at a coarse level of approximation, sharp surfaces and smoothed surfaces produce similar results for many PB applications. Thus, the selection of a surface is often dictated by the numerical convenience.

Nevertheless, the numerical instability of the sharp interface becomes a severe problem in the calculation of solvation forces. In molecular dynamics simulations, solvation force has to be evaluated for tens of millions of times. As such, numerical stability is particularly important. To avoid the electrostatic force calculation involving the sharp solvent-solute interfaces, Im et al. presented a smoothed dielectric boundary approach [33]. Using a smooth surface approach, Lu and Luo demonstrated that PBE based methods can be successfully and consistently applied to stable and efficient dynamics simulation of unconstrained biomolecules [43]. Remarkably, Prabhu et al. reported a smooth-permittivity finite difference PB method that is up to eight times faster than the explicit water simulations [50]. However, so far, no force calculation and MD simulation have been carried out based on any sharp molecular surface definition, although sharp molecular surfaces are widely used in all other PB applications.

The instability of the solvation force evaluation is inherently associated with the instability in the numerical solution of the PBE. The use of sharp molecular surface has certainly contributed to the instability. Many numerical methods have been used to solve the PBE, including finite element methods [3, 4, 16, 30, 67], and boundary integral methods [8, 9, 10, 34, 39, 62, 71, 44]. The most commonly used PB solvers in the field are usually based on finite difference methods [23, 32, 42, 43, 45, 58, 65, 33]. Many popular software packages, such as DelPhi [35, 54], UHBD [18], MEAD [54], APBS [30, 31, 2], AMBER [13] and CHARMM [12, 46], adopt finite difference schemes, which offer the best combination of speed, accuracy, and efficiency [5]. Although van der Waals surfaces, solvent accessible surfaces and molecular surfaces were often used in popular software packages, most traditional PB solvers neglect interface flux continuity conditions at the solvent-solute interfaces. As a result, these methods may suffer from instability and slow convergence when directly admit molecular surfaces or van der Waals surfaces. Therefore, stability enhancement and convergence acceleration are pressing technical issues in the development of PB methods.

Mathematically, the aforementioned problem is originated from elliptic equations with discontinuous coefficients and singular sources. This is a very challenging problem in applied mathematics and scientific computing. There has been much research interest in this class of problems since Peskin’s pioneer work on immersed boundary method (IBM) [51]. A number of elegant mathematical methods have been introduced in the past two decades, including finite element formulations [1, 11, 40], the ghost fluid method (GFM) [20, 41], coupling interface method [15], and integral equation approach [47]. A remarkable contribution was due to LeVeque and Li [38], who proposed the first second order accurate immersed interface method (IIM). Their method has been applied to the PBE in two spatial dimensions [52], among a variety of other interesting applications. These methods have not been applied to the PBE in biomolecular context. An important problem in computational mathematics is that many existing interface schemes may not work in biomolecular context, due to the complexity in three-dimensional (3D) geometry and geometric singularities.

Recently, we have proposed a high order method, the matched interface and boundary (MIB) method, for elliptic interface problems [72, 73, 74]. We have demonstrated fourth and sixth order MIB schemes for curved interfaces in 2D [73, 74] and 3D [69] applications. More recently, we have developed three generations of MIB based PB solvers, MIBPB-I, MIBPB-II, and MIBPB-III. The MIBPB-I presents a rigorous interface treatment for arbitrarily complex biomolecular interfaces [75] by carefully implementing the flux continuity conditions. However, it cannot maintain the targeted second order convergence because the presence of geometric singularities, such as cusps and self-intersecting surfaces in protein molecular surfaces [17, 19, 29, 56]. To overcome this difficulty, we have developed an MIB method that is able to solve elliptic equations with geometric singularities [68, 69]. This MIB scheme based PB solver, called MIBPB-II, is able to deliver the second order accuracy in solving the PBE with molecular surface singularities [70]. The state of the art MIB method is described in our recent paper [69].

Another problem in the development of advanced PB solvers is point charges in proteins, which are represented by Dirac delta functions. As distributions, delta functions reduce the regularity of the solution of the PBE. In most existing PB solvers, Dirac delta functions in the PBE, or singular charges in a molecule, are redistributed to their neighboring grid points. This approach is compatible with the neglect of interface flux continuity conditions in commonly used PB solvers. However, in the MIBPB-II, accuracy reduction occurs when a grid point has both redistributed charge contribution and interface condition contribution. This typically happens when the mesh size approaches half of the van der Waals radius, i.e., about 0.6Å, for smallest atoms in a protein. To overcome this difficulty, a regularization procedure that separates the solution of the PBE into a regular part and an irregular part was employed in our MIBPB-III [25]. The irregular part consists of the Green’s function, which is the solution to the Poisson equation with the singular charges. The MIBPB-III was found to be a few orders of magnitude more accurate and up to three times faster than commonly used PB solvers in achieving the same accuracy [25].

The work described in this paper is a continuation of our endeavor in developing mathematical methods for problems in molecular biology. The objective of the present work is to develop stable and accurate algorithms for electrostatic force calculations based on the sharp molecular surfaces. The MIBPB technique is utilized to solve the PBE with molecular surfaces. The present work offers a number of new features. First, the present force calculation is based on the molecular surface [53] or the minimal molecular surface [6], without resorting to any surface preprocessing, such as the geometric smoothening and/or the dielectric smoothening. Additionally, to directly evaluate solvation forces with sharp interfaces, force density expressions, particularly the dielectric boundary force density, are derived. The theoretical approach used in our present derivation is similar to that used in our differential geometry based multiscale models [66]. Yet, the resulting force density involves the evaluation of limiting values of the first order derivatives of the electrostatic potential from both inside and outside the interface. Moreover, the molecular surface interface contains reentrant surfaces which are detached from individual atomic spheres. Therefore, forces from reentrant surfaces need to be distributed to nearby atoms, which touch the probe when it forms the reentrant surface. Furthermore, accurate surface integrations are required for the evaluation of dielectric boundary forces and ionic forces. These evaluations are to be carried out along the complex interface and in the Cartesian grid. Finally, a PB solver that is able to handle sharp interface without numerical instability is needed. This is done with our MIBPB-II method.

The rest of this paper is organized as the follows. Theory and algorithm are presented in Section 2. The derivation of electrostatic force density functions is based on a free energy functional. Derivation of the density functions is discussed with respect to sharp interfaces and molecular surfaces. A number of numerical algorithms, including the evaluation of the force density as limiting values at the interface, accurate surface integrations in Cartesian grids, and the distribution of dielectric boundary forces to the individual atoms, are developed. Validation and numerical experiments are described in Section 3. The method of accurate integration in Cartesian grid is tested with the area of molecular surfaces. The proposed force algorithms are tested over many polyatomic systems. Section 4 is devoted to the molecular dynamics applications. The present electrostatic forces are implemented in conjugation with the AMBER force fields [13], particularly, in place of the AMBER PB module [43, 45] for molecular dynamics simulations. Three small biomolecules are used in our demonstration. This paper ends with concluding remarks summarizing the results.

2 Theory and algorithm

This section describes the basic theories and algorithms that are required for the construction of the proposed MIBPB based MD method. Electrostatic free energy functional and electrostatic force were presented by Sharp and Honig [58], and Gilson et al. [28], respectively. In the present work, we present new derivations that are appropriate for sharp solvent-solute interfaces. Section 2.1 is devoted to the free energy functional for electrostatic problems. In Section 2.2, we present a new derivation of electrostatic forces. Force expressions for surface integrations are given in Section 2.3. These new force expressions involve left and right gradients of the electrostatic potential on the molecular surface, which are to be computed by using the MIBPB method. To establish notation, Section 2.4 gives a brief review of the MIBPB method. Finally, Section 2.5 provides details for calculating dielectric boundary forces. Such calculations involve three techniques: gradient evaluation, surface integral on Cartesian grid, and the distribution of force elements to related atoms.

2.1 Free energy functional

Consider an open domain Ω ∈ ℝ³. Let Γ be the interfaces which divides Ω into two disjoint open subdomains, Ω = Ω⁻ ∪ Ω⁺ ∪ Γ. Here Ω⁻ is the biomolecular domain, and Ω⁺ is the solvent domain. The starting point for the implicit solvent theory is a given set of atomic coordinates for a molecule in ℝ³. The charge density of the molecule ρ_m(r) can therefore be obtained by assigning charge to each atom according to its type and environment

$${\rho }_m=4\pi \sum _{i=1}^{N_m}{Q}_i\delta (\mathbf{r}-{\mathbf{r}}_i),$$ (1)

where Q_i is the partial charges of ith atom, and N_m is the number of charged atoms. The positions of the charge r_i is determined from experiments, such as X-ray crystallography, nuclear magnetic resonance and computations. We introduce the biomolecular domain characteristic function

$${\lambda }^{-}(\mathbf{r})=\{\begin{array}{ll}1\hfill & \mathbf{r}\in {\mathrm{\Omega }}^{-}\cup \mathrm{\Gamma };\hfill \\ 0\hfill & \mathbf{r}\in {\mathrm{\Omega }}^{+}.\hfill \end{array}$$ (2)

Obviously, λ⁺ = (1 − λ⁻) characterizes the solvent domain Ω⁺. The permittivity ε(r)

$$\epsilon (\mathbf{r})={\lambda }^{-}{\epsilon }^{-}+{\lambda }^{+}{\epsilon }^{+}$$ (3)

is a function of position r ∈ ℝ³, and its value in the molecular domain (Ω⁻) differs from that in the solvent domain (Ω⁺). Note that Eqs. (2) and (3) present a simplified treatment of the ion domain. More appropriate treatment should include an additional ion exclusion zone outside the biomolecular domain [25].

The charge density of the solvent ρ_s(φ(r)) is a function of the electrostatic potential φ. In case of a multi-species system, a commonly used ionic density is the Boltzmann distribution and is given by

$${\rho }_s=\sum _{j=1}^N{q}_j{c}_j{e}^{-q_j\phi /kT},$$ (4)

where N is the number of ionic species, c_j’s are the bulk concentration of each ionic species, and q_j’s are charges of each ionic species. The free energy of the electrostatic system can be expressed as an integral

$$G^{\text{elec}}=\underset{\mathrm{\Omega }}{\int }{g}^{\text{elec}}(x,y,z,\phi ,{\phi }_x,{\phi }_y,{\phi }_z)d\mathrm{\Omega },$$ (5)

where g^elec is the free energy functional or energy density

$$g^{\text{elec}}={\lambda }^{-}{\rho }_m\phi -{\lambda }^{-}\frac{{\epsilon }^{-}}{2}{\mid \nabla \phi \mid }^2-{\lambda }^{+}\frac{{\epsilon }^{+}}{2}{\mid \nabla \phi \mid }^2+{\lambda }^{+}{\overline{\rho }}_s.$$ (6)

Here ρ̄_s(φ) = ∫ ρ_s(φ)dφ and ρ̄_s(0) = 0. If ρ_s(f) is given by Eq. (4), then we have

$${\overline{\rho }}_s=-kT\sum _{j=1}^N[c_j(e^{-q_j\phi /kT}-1)].$$ (7)

To minimize the free energy, the energy functional g^elec(x, y, z, φ, φ_x, φ_y, φ_z) must satisfy the Euler-Lagrange equation

$$\frac{\partial g^{\text{elec}}}{\partial \phi }-\left[\frac{\partial }{\partial x}\frac{\partial g^{\text{elec}}}{\partial {\phi }_x}+\frac{\partial }{\partial y}\frac{\partial g^{\text{elec}}}{\partial {\phi }_y}+\frac{\partial }{\partial z}\frac{\partial g^{\text{elec}}}{\partial {\phi }_z}\right]=0,$$ (8)

which gives rise to the PBE,

$$-\nabla ·\epsilon (\mathbf{r})\nabla \phi (\mathbf{r})={\lambda }^{-}{\rho }_m+{\lambda }^{+}{\rho }_s.$$ (9)

Obviously, there are flexibilities in the selection of ρ_s. In particular, the present choice does not account for the effect of ionic correlation and ion-macromolecule interaction near the interface.

For a sharp interface Γ, the permittivity values ε (r) at molecular domain Ω⁻ and the solvent domain Ω⁺ are different, as shown in Eq. (3). In most calculations, ε⁻ and ε⁺ are set to 1 and 80, respectively. This jump in permittivity gives rise to discontinuous coefficients in the PBE (9). To ensure the uniqueness of the solution, the PBE is to be solved with the following continuity conditions at the interface

$$[\phi ]={\phi }^{+}(\mathbf{r})-{\phi }^{-}(\mathbf{r})=0,$$ (10)

$$[\epsilon {\phi }_{\mathbf{n}}]={\epsilon }^{+}(\mathbf{r})\nabla {\phi }^{+}(\mathbf{r})·\mathbf{n}-{\epsilon }^{-}(\mathbf{r})\nabla {\phi }^{-}(\mathbf{r})·\mathbf{n}=0,$$ (11)

where n = (n_x, n_y, n_z) is the outer normal direction and φ^± are the limiting values at the interface Γ. Here [φ] = 0 and [εφ_n] = 0 for the PBE therefore [φ_n] are non-zero. The interface normal can be computed from given interfaces, such as the molecular surface of a given protein.

2.2 Electrostatic forces

The electrostatic force at a reference point, say the origin, denoted as F^elec, can be expressed as the volume integral of the gradient of the free energy density g^elec

$${\mathbf{F}}^{\text{elec}}=-\underset{\mathrm{\Omega }}{\int }\nabla g^{\text{elec}}d\mathrm{\Omega }.$$ (12)

In this treatment, we assume that the system is at equilibrium so that the temperature T, the ion concentration c_i and their charge q_i are position independent quantities. From Eqs. (6) and (7), we have

$${\mathbf{F}}^{\text{elec}}=-\underset{\mathrm{\Omega }}{\int }\left({\lambda }^{-}\phi \nabla {\rho }_m+\phi {\rho }_m\nabla {\lambda }^{-}-\frac{1}{2}{\mid \nabla \phi \mid }^2\nabla \epsilon -kT\sum _{j=1}^N[c_j(e^{-q_j\phi /kT}-1)]\nabla {\lambda }^{+}+{\lambda }^{-}{\rho }_m\nabla \phi -\epsilon \nabla \phi ·\nabla \nabla \phi +{\lambda }^{+}\sum _{j=1}^N[q_j{c}_j{e}^{-q_j\phi /kT}\nabla \phi ]\right)d\mathrm{\Omega }.$$ (13)

The first term on the right hand side of Eq. (13) can be integrated by parts

$${\int }_{\mathrm{\Omega }}{\lambda }^{-}\phi \nabla {\rho }_{m}d\mathrm{\Omega }=-{\int }_{\mathrm{\Omega }}{\rho }_m\nabla ({\lambda }^{-}\phi )d\mathrm{\Omega },$$ (14)

where the product φρ_m vanishes at infinity. Using the product rule on the sixth term of Eq. (13), we have

$$\underset{\mathrm{\Omega }}{\int }(\epsilon \nabla \phi )·(\nabla \nabla \phi )d\mathrm{\Omega }=\underset{\mathrm{\Omega }}{\int }\nabla ·(\epsilon \nabla \phi \nabla \phi )d\mathrm{\Omega }-\underset{\mathrm{\Omega }}{\int }(\nabla \phi )\nabla ·(\epsilon \nabla \phi )d\mathrm{\Omega }.$$ (15)

The first term on the right vanishes as a surface integral at infinity. The resulting force expression becomes

$${\mathbf{F}}^{\text{elec}}=-{\int }_{\mathrm{\Omega }}\left(-{\rho }_m\nabla ({\lambda }^{-}\phi )+\phi {\rho }_m\nabla {\lambda }^{-}-\frac{1}{2}{\mathbf{E}}^2\nabla \epsilon -kT\sum _{j=1}^N{c}_j(e^{-q_j\phi /kT}-1)\nabla {\lambda }^{+}+\left[{\lambda }^{-}{\rho }_m+\nabla ·(\epsilon \nabla \phi )+{\lambda }^{+}\sum _{j=1}^N{q}_j{c}_j{e}^{-q_j\phi /kT}\right](\nabla \phi )\right)d\mathrm{\Omega },$$ (16)

where E = −▽φ is the electrostatic field vector. Recognizing that the terms in the square bracket vanish because of the PBE (9), one arrives at the force expression

$$\begin{array}{l}{\mathbf{F}}^{\text{elec}}=-{\int }_{\mathrm{\Omega }}\left(-{\rho }_m\nabla ({\lambda }^{-}\phi )+\phi {\rho }_m\nabla {\lambda }^{-}-\frac{1}{2}{\mathbf{E}}^2\nabla \epsilon -kT\sum _{j=1}^N{c}_j(e^{-q_j\phi /kT}-1)\nabla {\lambda }^{+}\right)d\mathrm{\Omega }\\ ={\int }_{\mathrm{\Omega }}{\mathbf{f}}^{\text{elec}}d\mathrm{\Omega },\end{array}$$ (17)

where the force density is

$${\mathbf{f}}^{\text{elec}}={\rho }_m\nabla ({\lambda }^{-}\phi )-\phi {\rho }_m\nabla {\lambda }^{-}+\frac{1}{2}{\mathbf{E}}^2\nabla \epsilon +kT\sum _{j=1}^N{c}_j(e^{-q_j\phi /kT}-1)\nabla {\lambda }^{+}.$$ (18)

This expression is to be further simplified for practical calculations.

Since ▽λ⁻ gives rise to a Dirac delta function at the solvent-solute interface, the second term φρ_m▽ λ⁻ vanishes because ρ_m consists of delta functions away from the interface. Similarly, the first term can be simplified as λ⁻ ρ_m▽φ. Therefore, the total force can be broken into three contributions F^elec = F^RF + F^DB + F^IB. The first term is the reaction field force at the reference point and is often evaluated at the charge locations

$$\begin{array}{l}{\mathbf{F}}^{\text{RF}}={\int }_{\mathrm{\Omega }}{\lambda }^{-}{\rho }_m\nabla \phi d\mathrm{\Omega }\\ ={\int }_{{\mathrm{\Omega }}^{-}}{\rho }_m\nabla \phi d\mathrm{\Omega }\\ =4\pi \sum _{i=1}^{N_m}{\int }_{{\mathrm{\Omega }}^{-}}{Q}_i\delta (\mathbf{r}-{\mathbf{r}}_i)\nabla \phi d\mathrm{\Omega }\\ =4\pi \sum _{i=1}^{N_m}{Q}_i(\nabla \phi ){\mid }_{\mathbf{r}={\mathbf{r}}_i}.\end{array}$$ (19)

In practical computations, F^RF corresponding to the solvation is evaluated as the difference of the solution gradients in solvent and in vacuum

$$\begin{array}{l}{\mathbf{F}}^{\text{RF}}=4\pi \sum _{i=1}^{N_m}{Q}_i[(\nabla {\phi }_s){\mid }_{\mathbf{r}={\mathbf{r}}_i}-(\nabla {\phi }_v){\mid }_{\mathbf{r}={\mathbf{r}}_i}]\\ =\sum _{i=1}^{N_m}{\mathbf{F}}_i^{\text{RF}},\end{array}$$ (20)

where ${\mathbf{F}}_i^{\text{RF}}$ is the reaction field force at ith atom, φ_s is the potential for solvated molecule and φ_v is the that of molecule in vacuum. Note that it is ${\mathbf{F}}_i^{\text{RF}}$, instead of F^RF, that is evaluated and used in molecular dynamics. The second term in Eq. (17) is the dielectric boundary force at the reference point

$${\mathbf{F}}^{\text{DB}}={\int }_{\mathrm{\Omega }}\frac{1}{2}{\mathbf{E}}^2\nabla \epsilon d\mathrm{\Omega }.$$ (21)

The last term in Eq. (17) is the ionic boundary force at the reference point

$${\mathbf{F}}^{\text{IB}}={\int }_{\mathrm{\Omega }}kT\sum _i^N{c}_i(e^{-q_i\phi /kT}-1)\nabla {\lambda }^{+}d\mathrm{\Omega }.$$ (22)

Both the dielectric boundary force and the ionic boundary force are to be evaluated on the surface of the biomolecule.

2.3 Force expressions involving sharp interfaces

For the dielectric boundary force, the force expression involves the gradients of the characteristic functions

$$\nabla \epsilon (\mathbf{r})={\epsilon }^{-}\nabla {\lambda }^{-}+{\epsilon }^{+}\nabla {\lambda }^{+}.$$ (23)

According to Eq. (2), these gradients vanish away from the interface Γ. Let R(Γ) be a general position vector on the interface Γ, and

$${\mathbf{R}}^{\pm }(\mathrm{\Gamma })=\underset{\epsilon \to 0}{lim}\mathbf{R}(\mathrm{\Gamma })\pm \epsilon \widehat{\mathbf{n}},$$ (24)

where n̂ is the unit normal vector at R(Γ). Note that R^±(Γ) vary only along the positive and the negative n̂ directions. We therefore have

$$\nabla {\lambda }^{\pm }(\mathbf{r})=\{\begin{array}{ll}\pm \widehat{\mathbf{n}}\delta (r-{\mathbf{R}}^{\pm }(\mathrm{\Gamma }))\hfill & \mathbf{r}\text{near}\mathrm{\Gamma };\hfill \\ \mathbf{0}\hfill & \mathbf{r}\text{away}\text{from}\mathrm{\Gamma },\hfill \end{array}$$ (25)

where r is the position variable in the unit normal direction. The dielectric boundary force at the reference point is

$${\mathbf{F}}^{\text{DB}}={\int }_{\mathrm{\Gamma }}\int \frac{1}{2}{\mathbf{E}}^2[{\epsilon }^{+}\delta (r-{\mathbf{R}}^{+}(\mathrm{\Gamma }))-{\epsilon }^{-}\delta (r-{\mathbf{R}}^{-}(\mathrm{\Gamma }))]\widehat{\mathbf{n}}\mathit{drdS}.$$ (26)

By carrying out the integration over r, we have

$${\mathbf{F}}^{\text{DB}}={\int }_{\mathbf{\Gamma }}{\mathbf{f}}^{\text{DB}}dS$$ (27)

$$={\int }_{\mathbf{\Gamma }}\frac{1}{2}({\epsilon }^{+}{\mid {\mathbf{E}}^{+}\mid }^2-{\epsilon }^{-}{\mid {\mathbf{E}}^{-}\mid }^2)d\mathbf{S},$$ (28)

where dS = n̂dS is pointed at the surface normal direction n and ${\mathbf{f}}^{\text{DB}}=\frac{1}{2}({\epsilon }^{+}{\mid {\mathbf{E}}^{+}\mid }^2-{\epsilon }^{-}{\mid {\mathbf{E}}^{-}\mid }^2)\widehat{\mathbf{n}}$ is the dielectric boundary force density. Here, E^± = −▽φ^± are to be evaluated at the interface Γ. It is noted that the full-scale integration of Eq. (28) will not be pursued. It is the local forces at all intersecting points of the interface and meshlines that are needed. Such forces are evaluated by $\frac{1}{2}({\epsilon }^{+}{\mid {\mathbf{E}}^{+}\mid }^2-{\epsilon }^{-}{\mid {\mathbf{E}}^{-}\mid }^2)\widehat{\mathbf{n}}\mathrm{\Delta }S$, where ΔS is the area of the surface element in a given mesh.

For the ionic boundary force F^IB, since λ⁺ has its non-zero value only in the solvent, ▽λ⁺ contributes to a delta function evaluated at points on the interface where the mesh lines and the interface intersect. Consequently, the ionic boundary force is

$${\mathbf{F}}^{\text{IB}}={\int }_{\mathbf{\Gamma }}{\mathbf{f}}^{\text{IB}}dS$$ (29)

$$={\int }_{\mathbf{\Gamma }}kT\sum _{j=1}^N{c}_j(e^{-q_j{\phi }^{+}/kT}-1)d\mathbf{S},$$ (30)

where φ⁺ is to be evaluated at the interface Γ and ${\mathbf{f}}^{\text{DB}}=kT{\displaystyle \sum _{j=1}^N}{c}_j(e^{-q_j{\phi }^{+}/kT}-1)\widehat{\mathbf{n}}$ is the ionic boundary force density. At these intersecting points, the values of φ⁺ can be obtained by the interpolation of two grid points outside the interface and a fictitious point inside the interface. When singular geometry occurs, interpolation using one grid point outside the interface and two fictitious points inside can provide an alternative.

Here we mention that when a more appropriate ion exclusion zone is included, the notation will become more complicated, but the derivation of the ionic boundary force is the same. The calculation of the ionic boundary force is very similar to that of the dielectric boundary force technically but it has less impact on the total electrostatic solvation force. Therefore, we just mention this aspect briefly here without providing further consideration and numerical results.

In this paper, we carry out dielectric boundary force evaluations by using technique based on sharp molecular surfaces, which is developed in the next subsection. The molecular surface is generated by using the MSMS [56]. A technique developed in Ref. [75] is used to convert the triangle surface representation from the MSMS into the required Cartesian representation.

2.4 The MIB solution of the Poisson Boltzmann equation

Rigorous interface technique, the MIB method, has been described in a series work for the solution of Eq. (31) [25, 70, 75]. To establish notation, we present a brief description of our MIB based PB solvers.

Assume that an interface Γ divides a domain Ω into two disjoint parts, a molecular subdomain Ω⁻ and a solvent subdomain Ω⁺. The outer boundary of Ω⁺ is chosen to be regular. Without loss of generality, let us consider the linearized Poisson Boltzmann equation (PBE) of the form

$$-\nabla ·(\epsilon (\mathbf{r})\nabla \phi (\mathbf{r}))+{\kappa }^2(\mathbf{r})\phi (\mathbf{r})=4\pi {\lambda }^{-}\sum _{i=1}^{N_m}{Q}_i\delta (\mathbf{r}-{\mathbf{r}}_i),$$ (31)

where the ionic strength κ(r) is defined as ${\kappa }^2=\frac{{\lambda }^{+}(\mathbf{r})}{\epsilon kT}{\sum }_{j=1}^N{c}_j{q}_j^2$. The continuity conditions of the solution and its flux across the interface are given by Eqs. (10) and (11), respectively. In the MIB method, these conditions are to be implemented rigorously in order to obtain the highly accurate and fast convergent solution to the PBE. Dirichlet far-field boundary condition φ (∞) = 0 is used for Eq. (31).

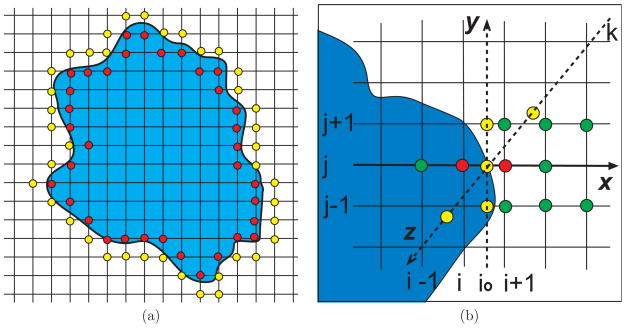
The essence of MIBPB solvers is the treatment of interface continuity conditions Eqs. (10) and (11) in the Cartesian grid. The standard finite difference schemes cannot maintain the designed order of convergence due to the discontinuity in the flux. To restore the convergence, we compute the derivatives in the PBE near the interface without directly using the function values across the interface. Instead, we use only function values on the same side of the interface and their smooth extensions across the interface, which are often called fictitious values, see Fig. 1. A fictitious value is needed when a finite difference scheme reaches across the interface. To determine fictitious values, we make use of continuity conditions at the interface. This in turn enforces the continuity conditions.

Figure 1.

An illustration of MIB schemes. The horizontal and vertical axes are the x and y directions, respectively. (a) The grid extension near the interface in a second order scheme; (b) An intersecting point at (i_o, j, k)

The MIB method takes the dimension splitting approach which reduces a multidimensional interface problem into 1D ones. Therefore, unlike the IIM, the MIB method normally does not use multidimensional interpolation or multidimensional Taylor expansion. Consequently, the MIB method simplifies the local topological relation near an interface, which is crucial for 3D problems with complex interface geometries.

Consider a case where the interface Γ intersects the grid in the x-direction at a point (i_o, j, k), which has two nearest neighbor grid points (i, j, k) and (i + 1, j, k). Fictitious values f⁺(i, j, k) and f⁻(i + 1, j, k) are required in a second order finite difference scheme in the x-direction near the intersecting point. In general, at every intersecting point of the interface and mesh lines, there are two original interface conditions and two additional first order interface conditions. These four conditions can in principle determine four fictitious values. However, these four interface conditions involve six first order derivatives ${\phi }_x^{+},{\phi }_x^{-},{\phi }_y^{+},{\phi }_y^{-},{\phi }_z^{+}$, and ${\phi }_z^{-}$. The evaluation of these derivatives can be very difficult for a complex geometry. In the MIB method, we simultaneously determine as few fictitious values around an intersecting point as possible so that we have the maximal flexibility in avoiding the determination of many first order derivatives, which are often difficult to evaluate due to the geometric constraint. Nevertheless, we have to determine at least two fictitious values so that both of the original two interface conditions can be implemented directly or indirectly. Consequently, we determine only two fictitious values around an intersecting point and thus, use two interface conditions to eliminate two first order derivatives. The remaining four derivatives are to be approximated using appropriate grid function values near the intersecting point.

In order to derive two additional conditions, we define a local coordinate (ξ,η, ζ) such that ξ is along the normal direction, and η is in the x – y plane. Two coordinates are connected by the transformation

$$\left[\begin{array}{c}\xi \\ \eta \\ \zeta \end{array}\right]=\left[\begin{array}{ccc}sin\psi cos\theta & sin\psi sin\theta & cos\psi \\ -sin\theta & cos\theta & 0\\ -cos\psi cos\theta & -cos\psi sin\theta & sin\psi \end{array}\right]\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\mathbf{p}·\left[\begin{array}{c}x\\ y\\ z\end{array}\right],$$ (32)

where θ and ψ are the azimuth and zenith angles with respect to the normal direction ξ, respectively. Two additional continuity conditions are generated by differentiating Eq. (10) along two tangential directions, η and ζ

$$[{\phi }_{\eta }]=({\phi }_x^{+}{p}_{21}+{\phi }_y^{+}{p}_{22}+{\phi }_z^{+}{p}_{23})-({\phi }_x^{-}{p}_{21}+{\phi }_y^{-}{p}_{22}+{\phi }_z^{-}{p}_{23})$$ (33)

$$[{\phi }_{\zeta }]=({\phi }_x^{+}{p}_{31}+{\phi }_y^{+}{p}_{32}+{\phi }_z^{+}{p}_{33})-({\phi }_x^{-}{p}_{31}+{\phi }_y^{-}{p}_{32}+{\phi }_z^{-}{p}_{33}),$$ (34)

where p_ij is the ijth component of the transformation matrix p. From Eq. (32) we have [φ_ξ, φ_η, φ_ζ]^T = p · [φ_x, φ_y, φ_z]^T, where T denotes the transpose. Three flux continuity conditions, Eqs. (11), (33) and (34) can be cast in the form

$$\left[\begin{array}{c}[\epsilon {\phi }_{\xi }]\\ [{\phi }_{\eta }]\\ [{\phi }_{\zeta }]\end{array}\right]=\mathbf{C}·\left[\begin{array}{c}{\phi }_x^{+}\\ {\phi }_x^{-}\\ {\phi }_y^{+}\\ {\phi }_y^{-}\\ {\phi }_z^{+}\\ {\phi }_z^{-}\end{array}\right],$$ (35)

where

$$\mathbf{C}=\left[\begin{array}{c}{\mathbf{C}}_1\\ {\mathbf{C}}_2\\ {\mathbf{C}}_3\end{array}\right]=\left[\begin{array}{cccccc}{p}_{11}{\epsilon }^{+}& -p_{11}{\epsilon }^{-}& p_{12}{\epsilon }^{+}& -p_{12}{\epsilon }^{-}& p_{13}{\epsilon }^{+}& -p_{13}{\epsilon }^{-}\\ p_{21}& -p_{21}& p_{22}& -p_{22}& p_{23}& -p_{23}\\ p_{31}& -p_{31}& p_{32}& -p_{32}& p_{33}& -p_{33}\end{array}\right],$$ (36)

where C_i represents the ith row of matrix C. As discussed above, there are six derivatives, ${\phi }_x^{+},{\phi }_x^{-},{\phi }_y^{+},{\phi }_y^{-},{\phi }_z^{+}$, and ${\phi }_z^{-}$, in restricted subdomains. Some of these conditions are very difficult to evaluate for complex biomolecular interface geometries. Therefore, in the MIB method, we eliminate two derivatives as the follows. In Fig. 1(b) we illustrate a case where the ${\phi }_y^{-}$ is difficult to compute and is to be eliminated. In general, after the elimination of the lth and mth elements of the array [ ${\phi }_x^{+},{\phi }_x^{-},{\phi }_y^{+},{\phi }_y^{-},{\phi }_z^{+},{\phi }_z^{-}$], Eq. (35) becomes

$$a[\epsilon {\phi }_{\xi }]+b[{\phi }_{\eta }]+c[{\phi }_{\zeta }]=({a\mathbf{C}}_1+b{\mathbf{C}}_2+c{\mathbf{C}}_3)·\left[\begin{array}{c}{\phi }_x^{+}\\ {\phi }_x^{-}\\ {\phi }_y^{+}\\ {\phi }_y^{-}\\ {\phi }_z^{+}\\ {\phi }_z^{-}\end{array}\right],$$ (37)

where

$$\begin{array}{l}a=C_{2l}{C}_{3m}-C_{3l}{C}_{2m}\\ b=C_{3l}{C}_{1m}-C_{1l}{C}_{3m}\\ c=C_{1l}{C}_{2m}-C_{2l}{C}_{1m}.\end{array}$$ (38)

Finally, Eqs. (10) and (37) are used to determine two fictitious values near the interface, together with the evaluation of four partial derivatives. This procedure is systematically repeated to determine fictitious values along other mesh lines and at other intersecting points. This dimension splitting approach effectively reduces a 3D interface problem into 1D-like ones locally.

For the situation depicted in Fig. 1(b), after elimination of ${\phi }_y^{-}$, we compute ${\phi }_y^{+}$. However, on the line passing through (i_o, j, k) in the y-direction, there is no grid point. Therefore, ${\phi }_y^{+}$ has to be evaluated by using interpolation schemes with solution values from the neighboring points. Specifically, ${\phi }_y^{+}$ at (i_o, j, k) will be interpolated by using values at points (i_o, j − 1, k), (i_o, j, k) and (i_o, j + 1, k). Because these three points are not normal grid points, we have to further obtain the values at (i_o, j − 1, k) by interpolation using grid values at (i + 1, j − 1, k), (i + 2, j − 1, k) and (i + 3, j − 1, k), and the value at (i_o, j + 1, k) by using grid values at (i + 1, j + 1, k), (i + 2, j + 1, k) and (i + 3, j + 1, k). For the value at (i_o, j, k), the fictitious value at (i, j, k) and grid values at (i + 1, j, k) and (i + 2, j, k) will be employed for the interpolation.

There are some simple principles for the selection of two derivatives to be eliminated and for the selection of the interpolation strategy. One is the feasibility of the scheme and the other is matrix optimization. We eliminate those derivatives that are difficult to evaluate. For a given local geometry, we will choose to compute one of two partial derivatives, ${\phi }_z^{+}$ and ${\phi }_z^{-}$, such that the evaluation in the x – z plane can be easily carried out. We select an appropriate interpolation strategy such that the resulting MIB matrix is optimally symmetric and diagonal for arbitrarily complex solvent-molecule interfaces with geometric singularities. A detailed discussion of the matrix optimization and 3D MIB methods for geometric singularities can be found in Ref. [69]. A rigorous validation of MIB based PB solver, MIBPB-II, for molecular surface singularities can be found in Ref. [70]. For a detailed treatment of charge singularities, the reader is referred to Ref. [25].

2.5 Dielectric boundary force calculation

There are two features in the present work that differ from any of the previous work in electrostatic force calculation. First, our force calculation is based on the rigorous treatment of the PBE with discontinuous solvent-solute interfaces. Therefore, our evaluation of the dielectric boundary force density is to be based on Eq. (28), instead of Eq. (21), for sharp interfaces. Second, due to the use of molecular surfaces, instead of van der Waals surfaces, the distribution of reentrant surface effects in the dielectric boundary force to individual atoms is a new issue. In the present calculation of the dielectric boundary force, three issues are to be resolved. First, one needs to evaluate E^± in Eq. (28), which involves partial derivatives at the interface. Second, one needs to numerically carry out the surface integral Eq. (28) along the interface. Finally, one needs to distribute the calculated boundary forces from reentrant surfaces to individual atoms. For the first issue, the calculation of the surface density function is actually at the intersecting points of the interface and the meshlines. Some of these intersecting point values are actually computed in solving PBE, and by modifying part of our MIB schemes. Derivatives of φ with respect to x, y and z-directions on these points in both inside and outside of the interface can be conveniently computed. For the surface integration, we employ the method developed by Smereka [57] with a minor modification. In this method, the numerical surface integral is calculated by volume integral with integrand supported by discrete delta functions defined only on grid points close to the interface. For the issue of force distribution, since our numerical integral is in the form of the summation of the product of the force density and curved small area, we can distribute the force to individual atoms based on the location of the force density. The details of surface density evaluation, surface integration and force distribution are given in the following three subsections.

2.5.1 Evaluation of dielectric boundary force density on the interface

The dielectric boundary force on the interface as discussed in the previous section is given by Eq. (28). To compute E⁺ and E⁻, we need to evaluate the gradient of φ on the interface from both inside of the biomolecule denoted as “−”, and outside of the biomolecule but in the solvent denoted as “+”, i.e., ${\phi }_y^{-},{\phi }_z^{+},{\phi }_z^{-},{\phi }_x^{+},{\phi }_x^{-}$ and ${\phi }_y^{+}$.

Having obtained the solution φ to the PBE in the entire domain and supposing now one wants to evaluate these partial derivatives at (x_o, y_j, z_k) from Fig. 1(b), ${\phi }_x^{+}$ can be interpolated by values of φ at (i − 1, j, k) and (i, j, k), and the fictitious value of φ at (i+1, j, k), which is the linear combination of values at some grid points. Meanwhile ${\phi }_x^{-}$ can be interpolated by the values of φ at (i + 1, j, k) and (i, j, k), and the fictitious value of at (i − 1, j, k). In our MIB scheme, two of ${\phi }_y^{+},{\phi }_y^{-},{\phi }_z^{+}$ and ${\phi }_z^{-}$ can also be interpolated by values at one fictitious point, two grid points and six auxiliary points (actually just regular grid points). Here, we only need one derivative from these two, i.e., ${\phi }_y^{+}$. Then, one can use Eq. (35) to compute ${\phi }_y^{-},{\phi }_z^{+}$ and ${\phi }_z^{-}$.

To this end, one rewrites Eq. (36) into the following form by block matrices

$$\mathbf{J}=\left[\begin{array}{c}[\epsilon {\phi }_{\xi }]\\ [{\phi }_{\eta }]\\ [{\phi }_{\zeta }]\end{array}\right]={\mathbf{C}}_{\mathbf{A}}·\left[\begin{array}{c}{\phi }_x^{+}\\ {\phi }_x^{-}\\ {\phi }_y^{+}\end{array}\right]+{\mathbf{C}}_{\mathbf{B}}·\left[\begin{array}{c}{\phi }_y^{-}\\ {\phi }_z^{+}\\ {\phi }_z^{-}\end{array}\right]$$ (39)

where C_A and C_B are the first three and last three columns of C, respectively. With this setting, one can obtain the three unknown partial derivatives by

$$\left[\begin{array}{c}{\phi }_y^{-}\\ {\phi }_z^{+}\\ {\phi }_z^{-}\end{array}\right]={\mathbf{C}}_{\mathbf{B}}^{-\mathbf{1}}·\left(\mathbf{J}-{\mathbf{C}}_{\mathbf{A}}·\left[\begin{array}{c}{\phi }_x^{+}\\ {\phi }_x^{-}\\ {\phi }_y^{+}\end{array}\right]\right).$$ (40)

Note that under some rare situations, matrix C_B could be singular, and one needs to first compute four of six partial derivatives of φ by an interpolation with grid point and fictitious values, and then use the interface jump conditions to solve the remaining two. Moreover, if an intersecting point is exactly a grid point, some special treatments are required as described in the MIB schemes [68, 69]. These treatments are implemented in our software package. Their description is lengthy and is omitted here.

2.5.2 Numerical surface integration in Cartesian grids

According to Smereka, the surface integral of a density function in Cartesian grids can be approximated by [57]

$${\int }_{\mathrm{\Gamma }}f(x,y,z)dS={\int }_{\mathrm{\Omega }}f(x,y,z)\delta (d(x,y,z))d\mathrm{\Omega }\approx \sum _{i,j,k}f(x_i,y_j,z_k){\stackrel{\sim }{\delta }}_{i,j,k}{h}^3$$ (41)

where (x_i, y_j, z_k) is the coordinate of grid point (i, j, k), d(x, y, z) is the distance of a point (x, y, z) defined in Ω from Γ, and f(x, y, z) is the surface density function defined in Γ. With Φ as the level set function such that Φ = 0 defines the interface, i.e. Γ = {(x, y, z): Φ(x, y, z) = 0}, the first order discrete delta function at (i, j, k) is given by [57]

$${\stackrel{\sim }{\delta }}_{i,j,k}={\stackrel{\sim }{\delta }}_{i,j,k}^{(+x)}+{\stackrel{\sim }{\delta }}_{i,j,k}^{(-x)}+{\stackrel{\sim }{\delta }}_{i,j,k}^{(+y)}+{\stackrel{\sim }{\delta }}_{i,j,k}^{(-y)}+{\stackrel{\sim }{\delta }}_{i,j,k}^{(+z)}+{\stackrel{\sim }{\delta }}_{i,j,k}^{(-z)},$$ (42)

where

$$\begin{array}{l}{\stackrel{\sim }{\delta }}_{i,j,k}^{(+x)}=\{\begin{array}{ll}\frac{\mid {\mathrm{\Phi }}_{i+1,j,k}{D}_x^0{\mathrm{\Phi }}_{i,j,k}\mid }{h^2\mid D_x^{+}{\mathrm{\Phi }}_{i,j,k}\mid \mid {\nabla }_0^{\epsilon }{\mathrm{\Phi }}_{i,j,k}\mid }\hfill & \text{if}{\mathrm{\Phi }}_{i,j,k}{\mathrm{\Phi }}_{i+1,j,k}\le 0;\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\\ {\stackrel{\sim }{\delta }}_{i,j,k}^{(-x)}=\{\begin{array}{ll}\frac{\mid {\mathrm{\Phi }}_{i-1,j,k}{D}_x^0{\mathrm{\Phi }}_{i,j,k}\mid }{h^2\mid D_x^{-}{\mathrm{\Phi }}_{i,j,k}\mid \mid {\nabla }_0^{\epsilon }{\mathrm{\Phi }}_{i,j,k}\mid }\hfill & \text{if}{\mathrm{\Phi }}_{i,j,k}{\mathrm{\Phi }}_{i-1,j,k}<0;\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\\ {\stackrel{\sim }{\delta }}_{i,j,k}^{(+y)}=\{\begin{array}{ll}\frac{\mid {\mathrm{\Phi }}_{i,j+1,k}{D}_y^0{\mathrm{\Phi }}_{i,j,k}\mid }{h^2\mid D_y^{+}{\mathrm{\Phi }}_{i,j,k}\mid \mid {\nabla }_0^{\epsilon }{\mathrm{\Phi }}_{i,j,k}\mid }\hfill & \text{if}{\mathrm{\Phi }}_{i,j,k}{\mathrm{\Phi }}_{i,j+1,k}\le 0;\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\\ {\stackrel{\sim }{\delta }}_{i,j,k}^{(-y)}=\{\begin{array}{ll}\frac{\mid {\mathrm{\Phi }}_{i,j-1,k}{D}_y^0{\mathrm{\Phi }}_{i,j,k}\mid }{h^2\mid D_y^{-}{\mathrm{\Phi }}_{i,j,k}\mid \mid {\nabla }_0^{\epsilon }{\mathrm{\Phi }}_{i,j,k}\mid }\hfill & \text{if}{\mathrm{\Phi }}_{i,j,k}{\mathrm{\Phi }}_{i,j-1,k}<0;\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\\ {\stackrel{\sim }{\delta }}_{i,j,k}^{(+z)}=\{\begin{array}{ll}\frac{\mid {\mathrm{\Phi }}_{i,j,k+1}{D}_z^0{\mathrm{\Phi }}_{i,j,k}\mid }{h^2\mid D_z^{+}{\mathrm{\Phi }}_{i,j,k}\mid \mid {\nabla }_0^{\epsilon }{\mathrm{\Phi }}_{i,j,k}\mid }\hfill & \text{if}{\mathrm{\Phi }}_{i,j,k}{\mathrm{\Phi }}_{i,j,k+1}\le 0;\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\\ {\stackrel{\sim }{\delta }}_{i,j,k}^{(-z)}=\{\begin{array}{ll}\frac{\mid {\mathrm{\Phi }}_{i,j,k-1}{D}_z^0{\mathrm{\Phi }}_{i,j,k}\mid }{h^2\mid D_z^{-}{\mathrm{\Phi }}_{i,j,k}\mid \mid {\nabla }_0^{\epsilon }{\mathrm{\Phi }}_{i,j,k}\mid }\hfill & \text{if}{\mathrm{\Phi }}_{i,j,k}{\mathrm{\Phi }}_{i,j,k-1}<0;\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\end{array}$$ (43)

where $D_{\alpha }^{+}{\mathrm{\Phi }}_{i,j,k},D_{\alpha }^{-}{\mathrm{\Phi }}_{i,j,k}$ and $D_{\alpha }^0{\mathrm{\Phi }}_{i,j,k}$ are upwind, downwind and central finite difference schemes in the α-direction (α = x, y, z), respectively, and $\mid {\nabla }_0^{\epsilon }{\mathrm{\Phi }}_{i,j,k}\mid =\sqrt{{(D_x^0{\mathrm{\Phi }}_{i,j,k})}^2+{(D_y^0{\mathrm{\Phi }}_{i,j,k})}^2+{(D_z^0{\mathrm{\Phi }}_{i,j,k})}^2+\epsilon }$ with ε = 10⁻¹⁰.

In our case, the function values are available only on the interface. Therefore, a modification of the above formalism is required. After some derivation, we have the following integral expression

$${\int }_{\mathrm{\Gamma }}f(x,y,z)dS\approx \sum _{(i,j,k)\in I}\left(f(x_o,y_j,z_k)\frac{\mid n_x\mid }{h}+f(x_i,y_o,z_k)\frac{\mid n_y\mid }{h}+f(x_i,y_j,z_o)\frac{\mid n_z\mid }{h}\right)h^3,$$ (44)

where (x_o, y_j, z_k) is the intersecting point of the interface and the x meshline that passes through (i, j, k), and n_x is the x component of the unit normal vector at (x_o, y_j, z_k). Similar relations exist between (x_i, y_o, z_k) and n_y, and between (x_i, y_j, z_o) and n_z, respectively. We here define irregular grid points as points with neighbor from the other side of the interface. Since Eq. (44) has already taken into account for the contribution from irregular grid points outside the interface, the summation is restricted to I, the set of irregular grid points inside or on the interface. Based on Eq. (41), the derivation of Eq. (44) is quite straightforward, and is illustrated with ${\stackrel{\sim }{\delta }}_{i,j,k}^{(+x)}$.

1. In the expression of ${\stackrel{\sim }{\delta }}_{i,j,k}^{(+x)},\left|\frac{{\mathrm{\Phi }}_{i+1,j,k}}{D_x^{+}{\mathrm{\Phi }}_{i,j,k}}\right|$ and $\left|\frac{D_x^0{\mathrm{\Phi }}_{i,j,k}}{{\nabla }_0^{\epsilon }{\mathrm{\Phi }}_{i,j,k}}\right|$ are numerical approximations of $h_x^{+}=(x_{i+1}-x_o)$ and |n_x|, which can be analytically evaluated since one knows the interface location and normal information of the molecular surface at its intercepting point.

2. For grid point (i, j, k) inside the interface with a negative Φ value, if its neighboring point, e.g., (i+1, j, k), has a positive Φ value, the discrete delta function at (i, j, k) will have a component corresponding to ${\stackrel{\sim }{\delta }}_{i,j,k}^{(+x)}$ in Eq. (43). Meanwhile, the discrete delta function at (i + 1, j, k) will have a component corresponding to ${\stackrel{\sim }{\delta }}_{i+1,j,k}^{(-x)}$ in Eq. (43). The sum of the two components at (i, j, k) and (i + 1, j, k) is exactly $\frac{\mid n_x\mid }{h}$.

3. For a sharp interface, it is possible that both sides of (i, j, k, ) have positive Φ values, then Eq. (44) will have two terms in the x-direction at ( $x_o^{+}$, y_j, z_k) and ( $x_o^{-}$, y_j, z_k).

4. In Eq. (41), the density function f is evaluated at grid point (x_i, y_j, z_k). For our application, the density function is defined only on the interface, therefore we use interface values f(x_o, y_j, z_k), f (x_i, y_o, z_k) and f(x_i, y_j, z_o) instead. In fact, the results of surface integration evaluated at the interface are better than those evaluated at grid points, according to our numerical tests.

5. Eq. (44) is also valid for the case where the interface exactly crosses a grid point.

2.5.3 The distribution of dielectric boundary forces to individual atoms

In the previous two subsections, we discuss the evaluations of numerical surface integral and dielectric boundary force. To compute dielectric forces on individual atoms, we need to distribute each unit dielectric boundary force, i.e., the force density multiplied by the associated area element, to related neighboring atoms and then collect all the forces on each specific atom. This procedure requires to classify the interfaces points into several categories since different treatments will be applied.

Fig. 2(a) shows an example of the molecular surface for a small system composed of 5 atoms. The red dots denote the centers of the probe, the “+” denote the centers of atoms, and the capital letters denote the contacting points between the atoms and the probe. The molecular surface consists of three type of facets. The contact surfaces are parts of atomic surfaces that directly contact the probe. The toric surfaces are the collection of the curves on the probe connecting two contact points, when the probe rolls over two contacted atoms, as shown by the curved face CEDB on the graph. The reentrant surfaces are the curved facet on the probe when it contacts more than three atoms, shown as ABC or DEF on the graph. It is worth mentioning that conventionally both the reentrant surface and toric surfaces are called an reentrant surface. Here, we differentiate them due to the need of different numerical treatments.

Figure 2.

Dielectric boundary force calculation. (a) Illustration of reentrant surfaces, e.g. ABC and DEF, and toric surfaces, e.g. CEDB in green, on the molecular surface; (b) Force distribution from a reentrant surface to related atoms.

We first classify interface points as two types, on-atom points and off-atom points. For molecular surfaces, an on-atom point is a point that is on a contact surface while an off-atom point is a point that is on a toric surface and/or a reentrant surface. For the first type, we just need to find points which are within the distance of the atom radius from the center of an atom, and attributing it to the atom. For the second type, we need to find out which atoms the probe contacts with. Our method is to locate the probe center by a distance of the probe radius from the interface point in the surface normal direction. If the distance between an atomic center and the probe center is approximately the sum of atomic radius and probe radius, then the probe is regarded as contacting this atom. For numerically generated MSs, a small tolerance (threshold) is used to classify interface points. In case of the MSMS surface, the results of the classification can be checked by those reported by the MSMS program [56]. Approximately, the optimal threshold is 0.013 when the MSMS density is set to 10, and 0.0013 for density 100.

The integral method described in previous section can give a force element on a small part of the molecular surface. A force element is directly attribute to an atom if the corresponding interface point is an on-atom point. However, if an interface point is on a toric or reentrant surface, we need to attribute the force element to all the contacted atoms.

For a toric surface, the normal direction of a surface element is in the same plane with directions pointed from the centers of the two atoms to the center of the probe, the distribution of the force element to two atoms can be calculated by

$${\mathbf{F}}_{\mathbf{1}}=\frac{\mathbf{F}·{\mathbf{f}}_{\mathbf{1}}-\mathbf{F}·{\mathbf{f}}_{\mathbf{2}}({\mathbf{f}}_{\mathbf{1}}·{\mathbf{f}}_{\mathbf{2}})}{1-{({\mathbf{f}}_{\mathbf{1}}·{\mathbf{f}}_{\mathbf{2}})}^{\mathbf{2}}}{\mathbf{f}}_{\mathbf{1}}$$ (45)

$${\mathbf{F}}_{\mathbf{2}}=\frac{\mathbf{F}·{\mathbf{f}}_{\mathbf{2}}-\mathbf{F}·{\mathbf{f}}_{\mathbf{1}}({\mathbf{f}}_{\mathbf{2}}·{\mathbf{f}}_{\mathbf{1}})}{1-{({\mathbf{f}}_{\mathbf{2}}·{\mathbf{f}}_{\mathbf{1}})}^{\mathbf{2}}}{\mathbf{f}}_{\mathbf{2}}$$ (46)

where F is the force from the surface point to the probe center, which will be distributed into two forces F₁ and F₂ pointing from the two atom centers to the probe center, respectively. Here, f, f₁ and f₂ are corresponding unit force vectors.

For reentrant surfaces, the probe might contact more than three atoms at a time. These situations are dealt with as the following. First, if the probe contacts only three atoms, the force vector is decomposed into three vectors pointing from each atomic center to the probe center. The magnitudes of three components are computed by solving the following linear system

$$\left[\begin{array}{ccc}{f}_1(1)& f_2(1)& f_3(1)\\ f_1(2)& f_2(2)& f_3(2)\\ f_1(3)& f_2(3)& f_3(3)\end{array}\right]\left[\begin{array}{c}{F}_1\\ F_2\\ F_3\end{array}\right]={\mathbf{F}}^T,$$ (47)

where f_i(j), i, j = 1, 2, 3, is the jth component of the unit force vector f_i, F₁, F₂, and F₃ are the magnitude of the distributed force.

If the probe contacts more than three atoms, we need to distribute the force into more than three directions. However, this distribution is not unique, except that all atoms have the same distance from the probe. In the latter case, the force can be equally distributed. Otherwise, the force will be distributed to three atoms that are closest to the force element. Fig. 2(b) illustrates this scheme. Here, the interface point locates at point O, which belongs to the probe surface ABCD, i.e., the reentrant surface, when the probe contacts four atoms at points A, B, C and D. To avoid the difficulties of decomposing force vector P O to four directions, we choose the closest three atoms at points B, C and D, and distribute the vector P O into components P B, P C and P D. Our numerical experiments indicate this scheme is a very good approximation.

3 Validation

In this section, we validate our surface integration in Cartesian grids and overall force calculation scheme.

3.1 Validation of the surface integration in Cartesian grids

The overall accuracy, stability and reliability of dielectric boundary force calculations depend on the quality of PB solvers, the evaluation of six derivatives of the potential on the interface, the numerical surface integration and the distribution of forces to related atoms. The accuracy of MIBPB solvers has been extensively verified in the previous papers [70] and [25]. The same MIB algorithm is modified to rigorously evaluate the six partial derivatives at the interface. The basic numerical integration algorithm in Cartesian grids was validated in [57]. However, this algorithm is modified so that it can be applied to our situation. A major difference is that the density function values are defined and computed on the interface, instead of on irregular grid points. Moreover, there is no analytical result for the surface area of molecular surfaces in general. Therefore, we validate our Cartesian-grid surface integration algorithm by calculating molecular surface areas of sphere, two-atom, three-atom and eighteen-atom systems. Table 1 shows the validation of the surface integration with spheres of radii 2 and 4Å. Numerical results are compared with exact values. It is seen that errors essentially depend on the grid resolution. Change in the curvature does not affect the result very much. Approximately, second order convergence is observed, although the method was designed as a first order one.

Table 1.

Integration errors for spherical surfaces

Mesh	Radius 2Å			Radius 4 Å
h	Area	Error	Order	Area	Error	Order
1	41.77	8.50	-	192.94	8.12	-
0.5	48.23	2.03	2.07	198.67	2.40	1.76
0.25	49.67	0.60	1.76	200.58	0.49	2.30
0.125	50.14	0.12	2.30	200.92	0.14	1.78
0.0625	50.23	0.04	1.78	201.03	0.03	1.95
Exact	50.265			201.062

For two- or multi-atomic systems, a common probe radius of 1.4Å with density 10 triangles per Ų is used in molecular surface generations except specified. Our results are compared with those of the MSMS [56]. We also plot the molecular surfaces of the diatomic, three-atom and eighteen-atom systems as illustrated in Fig. 3. Test cases conducted on these systems will be provided in the later sections. The locations and atomic van der Waals radii are (x y z r_vdW) = (1.500 0.4 0.4 1.6) and (−3.000 0.0 0.0 2.0) for the two-atom system, and (2.000 0.0 0.0 2.0), (0.000 −1.0 0.0 2.0) and (0.000 1.0 0.0 2.0) for the three-atom system.

Figure 3.

Molecular Surface generated from MSMS for (a) a diatomic system (b) a three-atom system; and (c) Cyclohexane (18 atoms).

Table 2 gives the results of our numerical integration. It is seen from the table that when the mesh is refined, the computed total areas converge to those of the MSMS, which validates the numerical integration carried out at the intersecting points of the interface and meshlines, and using the corresponding normal directions. However, the areas of contact surface, toric surface, and reentrant surface do not show a similar level of consistency with those of the MSMS. This is due to the fact that the MSMS surface was not analytically given but was in the triangular representation. We have used a threshold to categorize the MSMS molecular surface points into contact surface, toric surface and reentrant surface. For different cases, the best threshold may vary, which leads to errors. However, our tests indicate that the error in classification does not substantially affect our force calculation because the projection of a surface force element into atomic center directions is insensitive to the element classification.

Table 2.

Comparison of surface areas calculated from numerical integrations and from the MSMS

	Two-atom				Three-atom				18-atom
h	total	cont.	toric	reen	total	cont.	toric	reen	total	cont.	toric	reen
0.5	82.73	70.08	12.46	0.00	90.85	76.01	13.35	0.99	132.05	64.16	51.56	15.99
0.25	83.82	70.79	12.98	0.00	92.88	76.76	14.88	1.11	131.01	65.50	49.13	16.30
0.125	84.32	71.57	12.73	0.00	93.92	78.30	14.39	1.19	130.99	65.76	48.73	16.41
0.0625	84.44	71.63	12.84	0.00	93.98	77.94	14.73	1.21	131.16	65.46	48.71	16.91
MSMS	84.41	70.71	13.70	0.00	94.03	75.61	17.68	0.74	131.32	64.17	52.61	14.32

3.2 Validation of force calculations

3.2.1 Methods of validation

The validation of electrostatic force calculations is a difficult issue because of the lack of analytical values even for small molecular systems. However, there are two ways to evaluate electrostatic forces and to examine the consistency of force calculations. In the first approach, an atom in a molecule is moved forward (or backward) along an axis by a small distance, e.g., 0.005Å, at a time. The electrostatic free energy of each configuration is evaluated and the electrostatic force corresponding to each movement can be computed. For example, the force due to a small displacement δ in the x-direction on the ith atom centered at (x_i, y_i, z_i) can be calculated as

$$F(\mathrm{\Delta }G)=\frac{\mathrm{\Delta }G(x_i+\delta ,y_i,z_i)-\mathrm{\Delta }G(x_i-\delta ,y_i,z_i)}{2\delta }.$$ (48)

The other way is to obtain electrostatic solvation forces of the same movement by summing over components

$$F(\text{Sum})=F(\text{RXN})+F(\text{DB})+F(\text{IB})$$ (49)

where F(Sum) is the total force, and F(RXN), F(DB), and F(IB) are the reaction field, dielectric boundary, and ionic boundary forces, respectively. The consistency of the electrostatic forces calculated in two independent approaches, F(ΔG) and F(Sum), can be used to validate force schemes. As the accuracy of the MIBPB solvers has been extensively validated [75, 70, 25], the consistency in two independent force calculations provides a reliable check for the proposed method of electrostatic force evaluation.

3.2.2 Test on molecules

Here we consider a few test examples to validate our force calculation scheme. Normally, we let one atom of a molecule to move along an axis and compute the corresponding reaction field forces and dielectric boundary forces. Molecular surfaces are generated with the MSMS program at density 10, with a probe radius of 1.4Å, except for Case 1, where the molecular surface is analytical.

Case 1: Two-atom system

The two-atom system is a benchmark test for the validation of electrostatic force calculations [28, 33]. Im et al. have provided a detail analysis for this system using their PBEQ, the CHARMM PB solver, with smoothed dielectric functions [33]. There is a tradeoff between accuracy and simplicity as these two methods are compared. In the present project, we provide MIBPB based test results. We have set the ionic strength to 0. The MIBPB-II is employed in our force evaluation.

Consider two atoms of radius 2.0Å. Each atom has a unit charge located at its atomic center. One atom is fixed at (−3, 0, 0) and the other moves from (−3,0,0) to (4,0,0). The reason for us to move the atom up to (4,0,0) is that at about (3.2,0,0), the MS breaks up into two pieces and admits two cusps.

Fig. 4 depicts the results generated with MIBPB at different mesh size (h = 0.21Å for (a) and (c), and h = 0.42Å for (b) and (d)). The units for the force are kcal/mol/e_c and the probe radius of 1.4Å is used to generate molecular surfaces. At different position of the center of the moving atom, the total forces calculated by differentiating electrostatic free energies Eq. (48) are given in red solid line. Meanwhile, the total forces calculated by summing of forces components Eq. (49) are given in blue solid line. As in (a) and (b), the sums of forces include the reaction field forces Eq. (20) in dashed green line and dielectric boundary forces Eq. (28) in dotted-dashed brown line, which is decomposed into the contact forces in dotted black line and reentrant forces in dotted-dashed pink line as shown in (c) and (d). From these pictures, we could draw the following conclusions. 1) Total forces calculated by two different approaches confirm each other, therefore validate the present method for this test case; 2) The reaction field forces, as the leading component of electrostatic forces, are smooth even for coarse mesh; 3) The dielectric boundary forces are composed of contact forces, toric forces and reentrant forces (=0 for this case), suffers from numerical instability, especially when the mesh is coarse. However, in the view of an entire system, the dielectric boundary forces are important components with acceptable perturbation; 4) The pattern of both the reaction field forces and the dielectric boundary forces are consistent with the physical interpretation of this test model.

Figure 4.

Electrostatic forces calculated for two separating charged atoms. The horizontal axis is the position of the moving atom in unit Å and the vertical axis is the forces. (a) h = 0.21Å with summed dielectric boundary forces; (b) h = 0.42Å with summed dielectric boundary forces; (c) h = 0.21Å with decomposed dielectric boundary forces; (d) h = 0.42Å with decomposed dielectric boundary forces.

We also provided the detailed comparisons of the results from MIBPB and PBEQ, the PB solver in CHARMM as given in Fig. 5. Mesh size h = 0.21 is used to test these methods. The results calculated by the PBEQ with smoothed dielectric boundaries and by the MIBPB with sharp molecular surfaces are illustrated with dotted blue lines and shown with solid red lines, respectively. From Fig. 5(a), one sees a similar pattern of the solvation free energy, which confirms the reliability of two methods. We also noticed that there are about 30 kcal/mol energy difference in two results, which is due to the fact that the PBEQ uses a smoothed dielectric interface as discussed by [60, 61, 63].

Figure 5.

Comparison of electrostatic forces on the moving atom of a two-atom systems obtained at h = 0.21Å. The horizontal axis is the position of the moving atom in unit Å. Red solid line: present MIB based method with molecular surfaces; Blue dotted line: PBEQ with smooth interface. (a) Solvation free energy of the system; (b) Total force on the moving atom calculated from the summation of reaction force and dielectric boundary force; (c) Reaction force; (d) Dielectric boundary forces;

The total forces obtained by the force density approaches are given in Figs. 5(b) for the PBEQ and the MIBPB. The force curve from the MIBPB is almost completely smooth and monotonically decay. The smoothness indicates that the present method is highly stable. The monotonically decay in the total force curve is consistent with underlying physics of two separating charged spheres.

Fig. 4(c) gives a comparison of the reaction field forces obtained with two methods. These forces obtained from two methods have similar patterns. However, the peak force value of the PBEQ is about 40% higher than that of the MIBPB. This is consistent with what reported in the literature that the smoothed dielectric boundaries result in 10–40% over-estimation of solvation energies and forces [63, 60].

It is difficult to obtain stable dielectric boundary forces as shown in Fig. 5. Physically, we expect a smooth decay of the dielectric boundary forces as two atoms separate from each other. The dielectric boundary forces of the MIBPB shown in Fig. 5(d) have a monotonically decaying pattern, which leads to the same pattern in the total force calculation. The dielectric boundary forces of the PBEQ shown in Fig. 5(d) slightly undulate over the coordinate from −3 to 1.

Case 2: Three-atom system

Since molecular surfaces admit reentrant surfaces, it is important to further validate our algorithm for a 3-atom system. In this case, one atom is moved from (−2,0,0) to (2,0,0) in the x-direction while the other two atoms are fixed at (0,−1,0) and (0,1,0), respectively. All atoms have radius 2.0Å and charge 1.0e_c. From Fig. 6-(a), it is seen a good consistency of the x-direction forces on the moving atom obtained by two different methods. The forces of contact surfaces (F(Contact)) are separated from those of toric and reentrant surfaces (F(Toric+Reen)). The symmetric pattern about x = 0 confirms the symmetric setup of the testing system. It is worth mentioning that the forces calculated by electrostatic free energies show more oscillations, which in fact largely depend on the quality of the MSMS surface generation. These oscillations can be observed with different settings of the MSMS parameters. In contrast, the total forces calculated by the summation of force components are much smoother and more stable. This is important for PB based molecular dynamics simulations.

Figure 6.

Forces calculated for (a) a three-atom system and (b) Cyclohexane. The horizontal axis is the position of the moving atom in unit Å and the vertical axis is the forces.

Case 3: Eighteen-atom system

As seen in Fig. 3, the eighteen-atom system, Cyclohexane, is composed of 6 carbon atoms and 12 hydrogen atoms. The partial charges of these atoms are artificially assigned to the atomic centers as 1 e_c. In this test, we fixed the coordinates of atom 2–18 while move the first one, a carbon atom located at (0.9540 −0.6510 1.7), in the x-direction forward and backward 1 Å. In Fig. 6-(b), electrostatic forces on the first atom obtained by the two different methods show a good consistency.

Case 4: A biomolecule example: a Low-density lipoprotein receptor (PDB: 1ajj)

The final example is chosen as the molecular surface of a Low-density lipoprotein receptor (PDB: 1ajj) with 37 residues and 519 atoms. Fig. 7(a) shows its structure. We move the outmost nitrogen natively located at (−0.169, 7.698, 13.415) along the positive and negative direction of the x-axis for a distance of 0.25Å. This movement cannot be too large, or it will violate the physical limitation. The calculation results are shown in Fig. 7(b) where the confirmation of results from two methods has been achieved.

Figure 7.

A low-density lipoprotein receptor 1ajj: (a) Illustration of the molecule and the atom that is moved; (b) Electrostatic forces. The horizontal axis is the position of the moving atom in unit Å and the vertical axis is the forces.

3.2.3 Force correlation test

Finally, we provide an alternative way to confirm the convergence of the resulting forces from our method. In Fig. 8, we plot the correlation of forces obtained at different mesh sizes, i.e., 0.25Å, 0.5 Å and 1.0 Å, for 1ajj. All the forces in x, y and z directions for each atom are plot here. From the figure, we can see a good convergence of reaction field forces at mesh sizes of 1.0Å and 0.5 Å compared with that obtained at 0.25 Å. For dielectric boundary forces, as well as their toric and reentrant components, their accuracy is significantly reduced at the mesh size of 1.0Å, because of the error in the surface integration conducted at such a coarse mesh. However, at 0.5Å, the convergence is good as seen in Figs. 8(c)–(e).

Figure 8.

Correlations of forces obtained at different mesh sizes by the MIBPB for protein 1ajj. (a) Reaction field forces between mesh sizes of 0.25 and 0.5Å; (b) Reaction field forces between mesh sizes of 0.25 and 1.0Å; (c) Toric forces between mesh sizes of 0.25 and 0.5 Å, (d) Reentrant forces between mesh sizes of 0.25 and 0.5Å, (e) Dielectric boundary forces between mesh sizes of 0.25 and 0.5Å.

4 Application to molecular dynamics simulations

4.1 The implementation of MIBPB based PB forces in the AMBER package

The present MIBPB calculates the electrostatic potential and provides electrostatic forces asserted on each individual atoms for solvated biomolecules. However, to perform the molecular dynamics simulation, it takes more computational modules such as other components of the force field, initialization, randomness, time evolution and so on. In this work, we implement the MIBPB in the AMBER package. Specifically, we replace the original PB solver and force driver in the AMBER [43, 45] with our MIBPB solver and MIBPB force driver, respectively. We use igb = 8, a value currently not being used by AMBER-GB modules, to switch the implicit solvent model to the MIBPB. We modified a few files and included all the necessary files of MIBPB in the sander package of AMBER. We plan to contact the authors of AMBER/CHARMM to see if they would officially contain our package after our method becomes more stable and efficient.

It is also necessary for us to point out that the MIBPB, as still in the early stage of its development, does not provide many options for the user. The molecular surface is obtained by running the MSMS [56]. Charges are treated by trilinear interpolations which distribute the charge at a location to its closest eight grid points with weights decided by the distance between the original charge location and the grid point. The FFT is used to solve the PBE in vacuum, and a preconditioned biconjugate method is used to solve PBE in solution.

In summary, to run the MIBPB module embedded in the AMBER, we change the algorithm in providing reaction field forces, dielectric boundary forces, ionic boundary forces, and electrostatic solvation energy while keep the force fields of bond, angle, dihedral, van der Waals, Coulomb and all others intact.

4.2 Molecular dynamics simulations

In this subsection, we demonstrate MD simulations using the MIBPB based PB approach in conjugation with the AMBER package. Three biomolecular systems are considered in our study. To ensure the reliability of the PB results, all simulations are conducted at the mesh size of 0.3Å. Time increment is set to 10⁻¹⁵s. All MD data, including the configuration for computing RMSDs, are collected at each 50 time steps.

Case 1: Alanine dipeptide

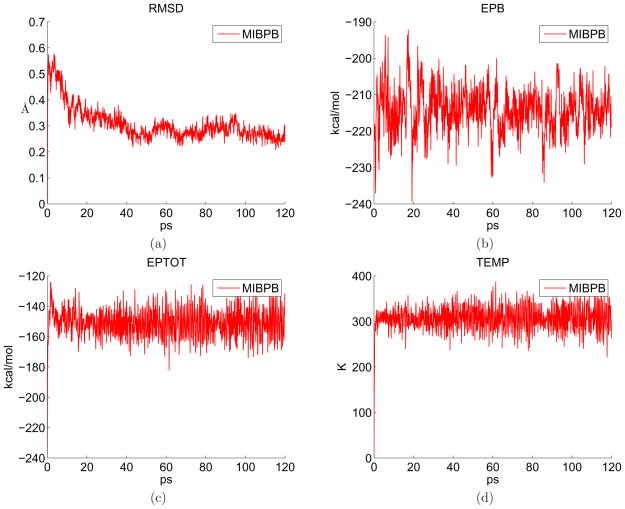
The first system is the alanine dipeptide with 22 atoms, which was studied by Im et al [33]. As suggested by the AMBER tutorial, we started from a pdb file with the first atoms (C,C,N) of the three residue/terminal (ACE, ALA, NME), and used leap, one of the functional modules of the AMBER to generate parameters and structure, and to add other 19 atoms. We relaxed the system with the graphic tools provided by leap and minimized it with 200 steps of steepest descent runs and 300 steps of conjugate gradient runs. After that, we run 300ps MD (i.e., 300,000 steps) simulations. We use the AMBER option to remove translational and rotational motions after every 500 steps. The results are given in Fig. 9. From the results, it is seen that the RMSD reduces after some initial steps but keeps certain level of irregular oscillations, which are due to the small size of the system. And later, with increased size of the system, we will seen more and more stable results.

Figure 9.

300 ps MD simulations of the alanine dipeptide obtained with MIBPB based methods. The horizontal axis is time in unit of picosecond (ps). (a) RMSD; (b) Solvation free energies; (c) Total potential energies; (d) Temperature.

Case 2: WW domain binding protein-1

The other biomolecular system used is the WW domain binding protein-1, the peptide bound to 65 KDA yes-associated protein. The structure is obtained from the complex (1jmq) and has 10 residues (GTPPP-PYTVG), 138 atoms. We follow the AMBER procedure to obtain the pdb file and add hydrogens by using the leap. The minimization and MD simulation have been run in the same setup as that of the first system. The translational and rotational motions are removed after every 100 steps. From Fig. 10, one can see that RMSDs shown in (a) and temperature shown in (d) are more stable due to the increased size of the system. Most of ten residues in the chain are non-polar, and a few of them are polar. There is no charged residue in the system. This kind of polymer chains in the water will tend to fold due to the hydrophobicity, as confirmed by the trajectory in VMD. It is found that structures obtained by the MIBPB based MD simulations stay mostly in folded morphologies. We further verified our conjecture by checking the averaged distances between all C_α atoms at the end of each 50 steps are plotted in Fig. 11(a). The MIBPB based MD method predicts smaller C_α distances with time until convergence, indicating a more compact packing of residues.

Figure 10.

A 120 ps MD simulation of the WW domain binding protein-1 obtained with the MIBPB based PB method. The horizontal axis is time in unit of picosecond (ps). (a) RMSD; (b) Solvation free energy; (c) Total potential energy; (d) Temperature.

Figure 11.

A comparison of the averaged C_α atom distances. The horizontal axis is time in unit of picosecond (ps) and the vertical axis is distance. The red line is the simulation result and the blue line is that from NMR data. Results of the MIBPB are illustrated in red lines. (a) The averaged C_α atom distances for WW domain binding protein-1 (Case 2); (b) The averaged C_α atom distances for Trp-cage miniprotein (Case 3).

Case 3: Trp-cage miniprotein (1L2Y)

We further consider a Trp-cage miniprotein (1L2Y) which has 95% folded structures in water at physiological pH [48]. This molecule has 20 residues and 340 atoms, representing a novel fold, designated as the ‘Trp-cage’ motif. It is known to be significantly more stable than other miniproteins reported [48]. The folding of this miniprotein is synergic and is hydrophobically driven by the encapsulation of a Trp side chain in a sheath of Pro rings. As a small protein-like molecule, this Trp-cage miniprotein was advocated as a benchmark test for both experimental studies and computational predictions of protein folding and unfolding pathways [48].

Our simulations were carried out in the same procedure as described in the last case. As shown in Fig. 12, the biomolecule approaches to stabilized solvation energy and RMSD. The averaged distances between all C_α atoms at the end of each 50 steps are plotted in Fig. 11(b), which confirms the folding and stabilizing procedure. Typical structures obtained from NMR experiments, as the initial structure of MD simulation and that from the MIBPB based MD simulation are also illustrated in Fig. 13. The molecule folded after the MD simulation and this can be associated with the polarity and charge distribution of residues of the molecule.

Figure 12.

250 ps MD simulations of the Trp-cage miniprotein (1L2Y) obtained with the MIBPB method. The horizontal axis is time in unit of picosecond (ps). (a) RMSD; (b) Solvation free energy; (c) Total potential energy; (d) Temperature.

Figure 13.

A comparison of typical Trp-cage miniprotein structures obtained from NMR experiments and from MIBPB MD simulations. (a) Obtained from NMR experiments as the initialization structure; (b) Obtained from the MIBPB based MD simulation as the final structure.

Finally, we point out that compared with the AMBER PB module, the present MIBPB based MD method is a few times slower. There are a few reasons that hinder the efficiency of the present method. First, at each time step, MIBPB based MD simulations require the generation of the molecular surface by the MSMS, which is the bottleneck at present. Additionally, AMBER typically has a seven-diagonal matrix, whereas to better resolve jump singularity and geometric singularity, the MIBPB based PB solver has a more complicated matrix structure. Furthermore, the force computations in MIBPB based MD simulations use more complicated algorithms. However, in this paper, we have provided a sufficient evidence to demonstrate the advantage in accuracy and stability of the current method. We hope this could arouse the attention from the mathematical community to further develop powerful mathematical algorithms to improve the efficiency of implicit solvent models.

5 Concluding remarks

Multiscale implicit solvent models have attracted much attention in the past decade due to its efficiency in reducing computational cost by modeling the solvent and mobile ions as continuum. The Poisson-Boltzmann (PB) equation is a primary implicit solvent model and has been widely applied in molecular biology and material sciences. PB based molecular dynamics (MD) methods have a potential to tackle large biomolecules and have been extensively studied in the past few decades. However, no interface based technique has been applied to any of the existing PB based MD methods. The present work presents the first development of an interface technique based MD method via the PB formalism. The matched interface and boundary (MIB) method [68, 69, 72, 73, 74] is developed to handle the sharp molecular surface (MS) in the PB based MD approach. This work is a natural extension of our previous endeavor on the development of MIB based PB solvers [25, 70, 75].

An MIB based PB solver, MIBPB-II [70], is employed to obtain electrostatic potentials. To calculate the electrostatic forces associated with the use of sharp MSs, new force density expressions are derived. To compute dielectric boundary forces, a complete set of potential gradients are required at all the intersecting points of the interface and meshlines. These gradients are calculated by extending our earlier MIBPB scheme. The surface integration in the Cartesian grid is a crucial issue in the dielectric boundary force calculation that often limits the accuracy and convergence. To this end, an advanced surface integration technique developed by Smereka [57] is adopted with a minor modification. Unlike the van der Waals surface where each facet belongs uniquely to an atom, the MS admits reentrant surfaces which do not uniquely belong to a single atom. Therefore, forces from the reentrant surfaces have to be assigned to related atoms. A set of force distribution schemes are introduced. The resulting electrostatic forces due to the displacements of atoms are carefully validated by a comparison with those obtained by differentiating the electrostatic free energy. A large test set, including a diatomic system, a triatomic system, a cyclohexane, and a low-density lipoprotein receptor, is utilized in our validation. Correlations of results obtained at different mesh sizes are plotted to verify the convergence of the present method. The correlation patterns indicate good convergence of reaction field forces at mesh sizes as coarse as 1.0Å. For dielectric boundary forces, good convergence can be obtained at the mesh size of near 0.5Å. The MIBPB solver and its force calculation are then interfaced with the AMBER MD package, Sander, parallelizing to its original finite difference based PB solver [43, 45].

As our first attempt, the present MIBPB based MD package is far from mature and can be improved in a number of ways. First, the MIBPB-III method [25] which employs the Green’s function to alleviate charge singularity should be able to provide accurate electrostatic potentials at much coarser meshes. Additionally, the current numerical surface integral scheme is of first order in convergence and can be improved. The accuracy of dielectric boundary forces is a limiting fact at large grid sizes in the present method. Moreover, MSs are generated in triangular meshes by using the MSMS program [56] and converted to Cartesian meshes by a scheme developed in our earlier work [75]. This setup is normally stable during the MD simulation but does cause a stability problem on a very rare basis. Furthermore, the preconditioned bi-conjugate solver is used in solving PB equation and its matrix system has been optimized in MIBPB-II. However, the choice of a precondition matrix and even the decision about which linear system solver is to be used is still worthy of further exploration. Finally, the most time-consuming part is the molecular surface generation. There is a pressing need to speed up the molecular surface construction in the Cartesian domain. Due to these reasons, the present MIBPB based MD package can only meet the speed requirement of small-scale systems in relatively short simulation time.