Musical intervals and relative pitch: Frequency resolution, not interval resolution, is special

Abstract

Pitch intervals are central to most musical systems, which utilize pitch at the expense of other acoustic dimensions. It seemed plausible that pitch might uniquely permit precise perception of the interval separating two sounds, as this could help explain its importance in music. To explore this notion, a simple discrimination task was used to measure the precision of interval perception for the auditory dimensions of pitch, brightness, and loudness. Interval thresholds were then expressed in units of just-noticeable differences for each dimension, to enable comparison across dimensions. Contrary to expectation, when expressed in these common units, interval acuity was actually worse for pitch than for loudness or brightness. This likely indicates that the perceptual dimension of pitch is unusual not for interval perception per se, but rather for the basic frequency resolution it supports. The ubiquity of pitch in music may be due in part to this fine-grained basic resolution.

INTRODUCTION

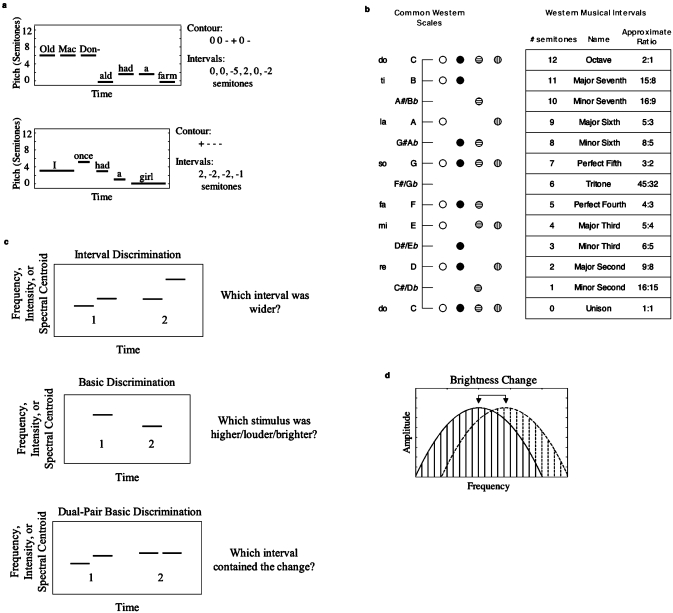
Music is made of intervals. A melody, be it Old MacDonald or Norwegian Wood, is defined not by the absolute pitches of its notes, which can shift up or down from one rendition to another, but by the changes in pitch from one note to the next [Fig. 1a]. The exact amounts by which the notes change—the intervals—are critically important. If the interval sizes are altered, familiar melodies become much less recognizable, even if the direction of the pitch change between notes (the contour) is preserved (Dowling and Fujitani, 1971; McDermott et al., 2008).

Figure 1.

(a) Pitch contour and intervals for two familiar melodies (top: Old MacDonald; bottom: Norwegian Wood). (b) Scales and intervals, described using the nomenclature of Western music (white circles—major scale; black circles—minor scale; circles with horizontal lines—Phrygian scale; circles with vertical lines—pentatonic scale). (c) Schematic description of the three tasks. Each plot depicts the stimuli for a single trial. (d) Schematic of stimulus used in brightness tasks, with two “notes” with different brightness values shown simultaneously. The frequency components composing the two “notes” were the same, but their amplitudes were altered, producing a shift in the spectral envelope.

Interval patterns are also integral to scales—the sets of notes from which music is composed. Scales as diverse as the Western diatonic scales, the pelog scale of Indonesian gamelan, and the pentatonic scales common to much indigenous music, are all defined by arrangements of different interval sizes [Fig. 1b]. It is believed that the interval sizes are encoded by the auditory system and used to orient the listener in the scale, facilitating musical tonality (Balzano, 1982; Trehub et al., 1999). Listeners can also associate patterns of intervals with types of music and circumstance. Music composed from different scales tends to evoke different moods (Hevner, 1935), with the major typically sounding bright and happy, the minor darker and sad, and the Phrygian evoking the music of Spain, for example. The importance of intervals in music has motivated a large body of perceptual research (Dowling and Fujitani, 1971; Cuddy and Cohen, 1976; Siegel and Siegel, 1977; Burns and Ward, 1978; Zatorre and Halpern, 1979; Maher, 1980; Edworthy, 1985; Rakowski, 1990; Peretz and Babai, 1992; Smith et al., 1994; Schellenberg and Trehub, 1996; Burns, 1999; Deutsch, 1999; Russo and Thompson, 2005; McDermott and Oxenham, 2008).

The ubiquitous role of pitch intervals in music is particularly striking given that other dimensions of sound (loudness, timbre etc.) are not used in comparable fashion. Melodies and the intervals that define them are almost exclusively generated with pitch, regardless of the musical culture, even though one could in principle create similar structures in other dimensions (Slawson, 1985; Lerdahl, 1987; McAdams, 1989; Schmuckler and Gilden, 1993; Marvin, 1995; Eitan, 2007; McDermott et al., 2008; Prince et al., 2009). Notably, the functions of intervals in music are predicated on our ability to represent intervals at least partially independent of their pitch range. A major second (two semitones), for instance, retains its identity regardless of the pitch range in which it is played, and remains distinct from a minor third (three semitones), even when they are not in the same register (Maher, 1980). One obvious possibility is that this capacity is unique to pitch (McAdams and Cunibile, 1992; Patel, 2008). Indeed, the brain circuitry for processing pitch intervals has been proposed to be specialized for music (Peretz and Coltheart, 2003; McDermott, 2009), and has been of considerable recent interest (Peretz and Babai, 1992; Schiavetto et al., 1999; Trainor et al., 1999; Trainor et al., 2002; Fujioka et al., 2004; Schön et al., 2004; Stewart et al., 2008). In previous work we found that contours could be perceived in dimensions other than pitch (McDermott et al., 2008), indicating that one aspect of relative pitch is not special to pitch. However, intervals involve the step size from note to note in addition to the step direction, and it seemed plausible that these fine-grained representations would be pitch-specific.

To measure the fidelity of interval perception, we used a simple discrimination task. Listeners were presented with two pairs of sequentially presented “notes,” and had to judge which pair was separated by the wider interval [Fig. 1c]. This task is readily performed with stimuli varying in pitch (Burns and Ward, 1978; Burns and Campbell, 1994), and is easily translated to other dimensions of sound. An adaptive procedure was used to measure the threshold amount by which intervals had to differ to achieve a criterion level of performance (71% correct in our procedure). These thresholds were measured for intervals in pitch, loudness, and brightness [a key aspect of timbre, as is altered by the treble knob on a stereo; Fig. 1d]. To compare thresholds across dimensions, we translated the interval thresholds into units of basic discrimination thresholds (JNDs), measured in the same subjects [Fig. 1c]. Our expectation was that interval thresholds expressed in this way might be lower for pitch than for other dimensions of sound, indicating a specialized mechanism for pitch intervals. To maximize the chances of seeing high performance for pitch, we included conditions with canonical musical intervals, and tested highly trained music students in addition to nonmusicians.

Contrary to our expectation, we found no evidence that the fidelity of pitch interval perception was unusually high. In fact, relative to basic discrimination thresholds, interval thresholds for pitch were consistently worse than those in other dimensions, even for highly trained musicians. Our results suggest that the importance of pitch may instead derive in large part from advantages in basic discriminability.

METHOD

Subjects performed three different two-alternative forced-choice tasks in each of three dimensions (pitch, loudness, and brightness). The first was an interval discrimination task, as described above [Fig. 1c, top]. The second was a standard basic discrimination task, in which subjects judged which of two sounds was higher in pitch, loudness, or brightness [Fig. 1c, middle]. The third was a “dual-pair” basic discrimination task—a task with the same format as the interval-discrimination task, but with a base interval of zero [such that one interval contained a stimulus difference and the other did not; Fig. 1c—bottom]. This allowed us to measure basic discrimination using stimuli similar to those in the interval task.

For the pitch tasks, the stimuli were either pure or complex tones (separate conditions), the frequency or fundamental frequency (F0) of which was varied. For the loudness tasks, the stimuli were bursts of broadband noise, the intensity of which was varied. For the brightness tasks, the stimuli were complex tones, the spectral envelope of which was shifted up or down on the frequency axis [Fig. 1d].

Procedure

Thresholds were measured with a standard two-down, one-up adaptive procedure that converged to a stimulus difference yielding 70.7% correct performance (Levitt, 1971). For the basic discrimination task, the two stimuli on each trial had frequencies∕F0s, intensities, or spectral centroids of S and S+ΔS, where S was roved about a standard value for each condition (160, 240, and 400 Hz for pitch, 40, 55 and 70 dB SPL for loudness, and 1, 2, and 4 kHz for brightness). The extent of the rove was 3.16 semitones for the pitch task, 8 dB for the loudness task, and 10 semitones for the brightness task, which was deemed sufficiently high to preclude performing the task by learning an internal template for the standard (Green, 1988; Dai and Micheyl, 2010). A run began with ΔS set sufficiently large that the two stimuli were readily discriminable (3.16 semitones for the pitch task, 8 dB for the loudness task, 4 semitones for the brightness task). On each trial subjects indicated whether the first or the second stimulus was higher. Visual feedback was provided. Following two consecutive correct responses, ΔS was decreased; following an incorrect response it was increased (Levitt, 1971). Up to the second reversal in the direction of the change toΔS, ΔS was decreased or increased by a factor of 4 (in units of % for the pitch and brightness tasks, and in dB for the loudness task). Then up to the fourth reversal, ΔS was decreased or increased by a factor of 2. Thereafter it was decreased or increased by a factor of√2. On the tenth reversal, the run ended, and the discrimination threshold was computed as the geometric mean of ΔS values at the last 6 reversals.

The procedure for the interval tasks was analogous. The two stimulus pairs on each trial were separated (in frequency, intensity, or spectral centroid) by I and I+ΔI; I was fixed within a condition. A run began with ΔI set to a value that we expected would render the two intervals easily discriminable. On each trial subjects indicated whether the first or second interval was larger; visual feedback was provided. ΔI was increased or decreased by 4, 2, or√2, according to the same schedule used for the basic discrimination experiments.

To implement this procedure, it was necessary to assume a scale with which to measure interval sizes and their increments. Ideally this scale should approximate that which listeners use to assess interval size. We adopted logarithmic scales for all dimensions. Support for a logarithmic scale for frequency comes from findings that listeners perceive equal distances on a log-frequency axis as roughly equivalent (Attneave and Olson, 1971), and that the perceived size of a pitch interval scales roughly linearly with the frequency difference measured in semitones (Russo and Thompson, 2005), with one semitone equal to a twelfth of an octave. This scale was used for both pitch and brightness; in the latter case we took the difference between spectral envelope centers, in semitones, as the interval size. A logarithmic scale for intensity derives support from loudness scaling—loudness approximately doubles with every 10 dB increment so long as intensities are moderately high (Stevens, 1957), suggesting that intervals equal in dB would be perceived as equivalent.

Intervals were thus measured in semitones for the pitch and brightness tasks, and in dB for the loudness task. ΔI was always initialized to 11.1 semitones for the pitch task, 12 dB for the loudness task, and 11.1 semitones for the brightness task, and I was set to different standard values in different conditions (1, 1.5, 2, 2.5, and 3 semitones for pitch, 8, 12, and 16 dB for loudness, and 10, 14, and 18 semitones for brightness). The pitch conditions included intervals that are common to Western music (having an integer number of semitones) as well as some that are not; the non-integer values were omitted for the complex-tone conditions. The integer-semitone pitch intervals that we used are those that occur most commonly in actual melodies (Dowling and Harwood, 1986; Vos and Troost, 1989). The interval sizes for loudness and brightness were chosen to be about as large as they could be given the roving (see below) and the desire to avoid excessively high intensities∕frequencies. These interval sizes were also comparable to those for pitch when converted to units of basic JNDs (estimated from pilot data to be 0.2 semitones for pitch, 1.5 dB for loudness, and 1 semitone for brightness). This at least ensured that the intervals were all well above the basic discrimination threshold.

To ensure that subjects were performing the interval task by hearing the interval, rather than by performing some variant of basic discrimination, two roves were employed. The first sound of the first interval was roved about a standard value (pitch: a 3.16-semitone range centered on 200 Hz; loudness: a 6-dB range centered on 42 dB SPL; brightness: a 6-semitone range centered on 1 kHz), and the first sound of the second interval was shifted up relative to the first sound of the first interval by a variable amount (pitch: 2–10 semitones; loudness: 7–12 dB; brightness: 6–12 semitones). These latter ranges were chosen to extend substantially higher than the expected interval thresholds, such that subjects could not perform the task by simply observing which pair contained the higher second sound. Computer simulations confirmed that the extent of the roves were sufficient to preclude this possibility. The sounds of the second interval thus always occupied a higher range than those of the first, as shown in Fig. 1c, but the larger interval was equally likely to be first or second. The roving across trials meant that there was no consistent implied key relationship between the pairs.

The parameters of the dual-pair basic discrimination task were identical to those of the interval discrimination task, except that the base interval was always zero semitones or dB, and the first sound of the first interval was roved about either 160 and 400 Hz (pitch), 40 and 55 dB (loudness), or 1000 and 1414 Hz (brightness). We omitted the complex-tone pitch conditions for this task.

For each dimension, subjects always completed the interval task first, followed by the two basic discrimination tasks. Five subjects did not complete the dual-pair task (three of the five nonmusicians, and two of the three amateur musicians; see below). The stimulus dimension order was counterbalanced across subjects, spread as evenly as possible across the subject subgroups (see below); for each dimension, each subgroup contained at least one subject who completed it first, and at least one subject who completed it last. Within a task block, conditions (differing in the magnitude of the standard) were intermixed. Subjects completed 8 runs per condition per task. Our analyses used the median threshold from these 8 runs. All subjects began by completing 4 practice runs of the adaptive procedure in each condition of each task.

Subjects performed the experiments seated in an Industrial Acoustics double-walled sound booth. Responses were entered via a computer keyboard. Feedback was given via a visual signal on the computer screen.

Stimuli

In all conditions the sounds were 400 ms in duration, including onset and offset Hanning window ramps of 20 ms. The two sounds in each trial of the basic discrimination task were separated by 1000 ms. The two sounds of each interval in the interval and dual-pair tasks were played back to back, with the two intervals separated by 1000 ms. In the pitch and brightness tasks the rms level of the stimuli was 65 dB SPL. The complex tones in the pitch task contained 15 consecutive harmonics in sine phase, starting with the F0, with amplitudes decreasing by 12 dB per octave. An exponentially decaying temporal envelope with a time constant of 200 ms was applied to the complex tones (before they were Hanning windowed) to increase their similarity to real musical-instrument sounds. The pure tones had a flat envelope apart from the onset and offset ramps. In the loudness tasks the stimuli were broadband Gaussian noise (covering 20–20,000 Hz). Noise was generated in the spectral domain and then inverse fast Fourier transformed after coefficients outside the passband were set to zero. The tones used in the brightness task were the same as those used in an earlier study (McDermott et al., 2008). They had an F0 of 100 Hz and a Gaussian spectral envelope (on a linear frequency scale) whose centroid was varied. To mirror the logarithmic scaling of frequency, the spectral envelope was scaled in proportion to the center frequency—the standard deviation on a linear amplitude scale was set to 25% of the centroid frequency. The temporal envelope was flat apart from the onset and offset ramps. Sounds were generated digitally and presented diotically through Sennheiser HD580 headphones, via a LynxStudio Lynx22 24-bit D∕A converter with a sampling rate of 48 kHz.

Participants

Five subjects (averaging 28.4 years of age, SE=7.1, 3 female) described themselves as non-musicians. Three of these had never played an instrument, and the other two had played only briefly during childhood (for 1 and 3 years, respectively). None of them had played a musical instrument in the year preceding the experiments. The other six subjects (averaging 20.2 years old, SE=1.4, 3 female) each had at least 10 years experience playing an instrument; all were currently engaged in musical activities. Three of these were degree students in the University of Minnesota Music Department.

Analysis

For analysis purposes, we divided our subjects into three groups: five non-musicians, three amateur musicians, and three degree students. All statistical tests were performed on the logarithm of the thresholds expressed in semitones or dB, or on the logarithm of the threshold ratios. Only those subjects who completed the dual-pair task in all three dimensions were included in the analysis of the threshold ratios derived from that task.

RESULTS

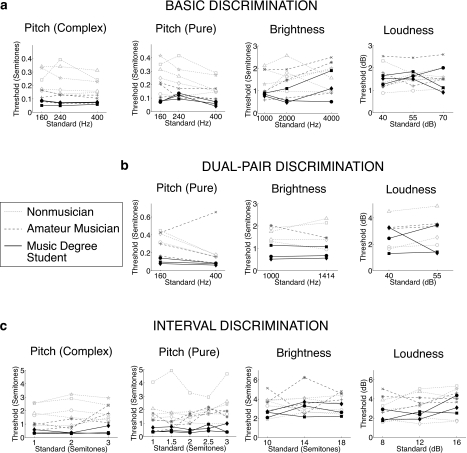
Figure 2 displays the thresholds measured in the three tasks for each of the three dimensions. The basic discrimination thresholds we obtained were consistent with many previous studies (Schacknow and Raab, 1976; Jesteadt et al., 1977; Wier et al., 1977; Lyzenga and Horst, 1997; Micheyl et al., 2006b) and, as expected from signal detection theory (Micheyl et al., 2008), thresholds measured in the dual-pair task were somewhat higher than in the basic discrimination task. As has been found previously (Spiegel and Watson, 1984; Kishon-Rabin et al., 2001; Micheyl et al., 2006b), pitch discrimination thresholds were lower in subjects with more musical experience than in those with less, both for complex [F(2,8)=14.12, p=0.002] and pure [F(2,8)=10.79, p=0.005] tones, though this just missed significance for the dual-pair experiment, presumably due to the smaller subject pool[F(2,6)=5.08, p=0.051]. The trend for brightness discrimination thresholds to be higher in subjects with more musical experience was not statistically significant [basic: F(2,8)=1.95, p=0.2; dual-pair: F(2,5)=5.59, p=0.053].

Figure 2.

Basic discrimination, dual-pair discrimination, and interval discrimination thresholds for pitch, brightness, and loudness. Thresholds for each subject are plotted with the line style denoting their level of musical training (fine dash, open symbols—nonmusician; coarse dash—amateur musician; solid line, filled symbols—music degree student). Values given for the brightness standards in (a) and (b) are spectral centroids.

Although previous reports of pitch interval discrimination focused primarily on highly trained musicians (Burns and Ward, 1978; Burns and Campbell, 1994), our results nonetheless replicate some of their qualitative findings. In particular, pitch interval thresholds were relatively constant over the range of interval sizes tested, and were no lower for canonical musical intervals than for non-canonical intervals. For both pure and complex tones, the modest effect of interval size [complex tones: F(2,16)=4.09, p=0.04; pure tones: F(4,32)=3.63, p=0.015] was explained by a linear trend [complex tones: F(1,8)=7.4, p=0.03; pure tones: F(1,8)=6.56, p=0.034], with no interaction with musicianship [complex tones: F(4,16)=1.82, p=0.175; pure tones: F(8,32)=2.18, p=0.056].

Our most experienced musician subjects yielded pitch interval thresholds below a semitone, on par with musicians tested previously (Burns and Ward, 1978). However, these thresholds were considerably higher for subjects with less musical training, frequently exceeding a semitone even in amateur musicians, and producing a main effect of musicianship for both complex [F(2,8)=19.72, p=0.001] and pure [F(2,8)=12.25, p=0.004] tone conditions. For listeners without musical training, the size of the smallest discriminable change to an interval was often on the order of the interval size itself (1–3 semitones). These results are consistent with previous reports of enhanced pitch interval perception in musicians compared to nonmusicians (Siegel and Siegel, 1977; Smith et al., 1994; Trainor et al., 1999; Fujioka et al., 2004).

To our knowledge, interval thresholds for loudness and brightness had not been previously measured. However, we found that subjects were able to perform these tasks without difficulty, and that the adaptive procedure converged to consistent threshold values. These thresholds did not differ significantly as a function of musicianship [brightness: F(2,8)=2.8, p=0.12; loudness: F(2,8)=1.15, p=0.37], and, like pitch, did not vary substantially with interval size: there was no effect for brightness[F(2,16)=0.33, p=0.72]; the effect for loudness [F(2,16)=3.68, p=0.049] was small, and was explained by a linear trend[F(1,8)=5.9, p=0.041].

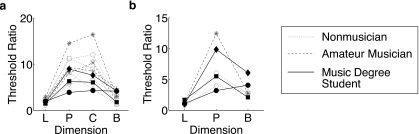
To compare interval acuity across dimensions, we expressed the interval thresholds in units of basic JNDs, using the JNDs measured in each subject. Because neither the interval thresholds nor the basic JNDs varied much across interval size or magnitude of the standard, we averaged across conditions to get one average threshold per subject in each of the tasks and dimensions. We then divided each subject’s average interval threshold in each dimension by their average basic discrimination and dual-pair thresholds in that dimension.

As shown in Fig. 3, this analysis produced a consistent and unexpected result: interval thresholds were substantially higher for pitch than for both loudness and brightness when expressed in these common units. This was true regardless of whether the JND was measured with the standard basic discrimination task or with the dual-pair task, producing a main effect of dimension in both cases [basic: F(3,24)=45.09, p<0.0001; dual-pair: F(2,6)=23.65, p=0.001]. In both cases, pairwise comparisons revealed significant differences between interval thresholds for the pitch conditions and the brightness and loudness conditions, but not between loudness and brightness, or pure- and complex-tone pitch (t-tests, 0.05 criterion, Bonferroni corrected). There was no effect of musicianship in either case [basic: F(2,8)=2.3, p=0.16; dual-pair: F(2,3)=1.48, p=0.36], nor an interaction with dimension [basic: F(6,24)=0.99, p=0.46; dual-pair: F(4,6)=0.7, p=0.62]. Musicians were better at both interval and basic discrimination, and these effects apparently cancel out when interval thresholds are viewed as threshold ratios. For both musicians and nonmusicians, interval perception appears worse for pitch than for loudness and brightness when expressed in units of basic discriminability.

Figure 3.

Interval thresholds expressed in basic JNDs. Each data point is the interval discrimination threshold for a subject divided by their basic discrimination threshold (a), or the dual-pair discrimination threshold (b), for a given dimension—loudness (L), pure tone pitch (P), complex tone pitch (C), or brightness (B). Line styles and symbols are consistent with Fig. 2.

DISCUSSION

Pitch intervals have unique importance in music, but perceptually they appear unremarkable, at least as far as acuity is concerned. All of our listeners could discriminate pitch intervals, but thresholds in nonmusicians tended to be large compared to the size of common musical intervals, and listeners could also readily discriminate intervals in other dimensions. Relative to basic discriminability, interval acuity was actually worse for pitch than for the other dimensions we tested, contrary to the notion that pitch intervals have privileged perceptual status. This was true even when basic discrimination was measured using a variant of the interval task (the “dual-pair” task).

One potential explanation for unexpectedly large interval thresholds might be a mismatch between the scale used by listeners and that implicit in the experiment (as would occur if listeners were not in fact using logarithmic scales to estimate interval sizes). Could this account for our results? The effect of such a mismatch would be to increase the number of incorrect trials—trials might occur where the two measurement scales yield different answers for which of the two intervals was larger, in which case the listener would tend to answer incorrectly more often than if using the same scale as the experiment. An increase in incorrect trials would drive the adaptive procedure upwards, producing higher thresholds. However, the choice of scale is the least controversial for pitch, where there is considerable evidence that listeners use a log-frequency scale. Since we found unexpectedly high thresholds for pitch rather than loudness or brightness, it seems unlikely that measurement scale issues are responsible for our results. Rather, our pitch interval thresholds seem to reflect perceptual limitations.

In absolute terms, pitch-interval acuity was not poor—thresholds were about half as large as those for brightness, for instance, measured in semitones. However, these thresholds were not as good for pitch as would be predicted from basic discrimination abilities. For most subjects, loudness and brightness interval thresholds were a factor of 2 or 3 higher than the basic JND, whereas for pitch, they were about a factor of 8 higher. This result was the opposite of what had seemed intuitively plausible at the outset of the study.

Calculating the ratio between interval and basic discrimination thresholds allowed a comparison across dimensions, but in principle is inherently ambiguous. Large ratios, such as those we obtained for pitch, could just as well be due to abnormally high interval thresholds as to abnormally small basic JNDs. In this case, however, there is little reason to suppose that pitch interval perception is uniquely impaired; the apparent poor standing relative to other dimensions (Fig. 3) seems best understood as the product of a general capacity to perceive intervals coupled with unusually low basic JNDs for pitch.

The notion that basic pitch discrimination is unusual compared to that in other dimensions may relate to recent findings that listeners can detect frequency shifts to a component of a complex tone even when unable to tell if the component is present in the tone or not (Demany and Ramos, 2005; Demany et al., 2009). Such findings suggest that the auditory system may possess frequency-shift detectors that could produce an advantage in fine-grained basic discrimination for pitch compared to other dimensions. The uniqueness of basic pitch discriminability is also evident in comparisons of JNDs to the dynamic ranges of different dimensions. The typical pitch JND of about a fifth of a semitone is very small compared to the dynamic range of pitch (roughly 7 octaves, or 84 semitones); intensity and brightness JNDs are a much larger proportion of the range over which those dimensions can be comfortably and audibly varied.

It seems that the basic capacity for interval perception measured in our task is relevant to musical competence, because pitch-interval thresholds were markedly lower in musicians than nonmusicians. However, it is noteworthy that for all but the most expert musicians, pitch-interval thresholds generally exceeded a semitone, the amount by which adjacent intervals differ in Western music [Fig. 1b]. This is striking given that many salient musical contrasts, such as the difference between major and minor scales, are conveyed by single semitone interval differences [Fig. 1b]. In some contexts, interval differences produce differences in sensory dissonance that could be detected without accurately encoding interval sizes, but in other settings musical structure is conveyed solely by sequential note-to-note changes (a monophonic melody, for instance). Perceiving the differences in mood conveyed by different scales in such situations requires that intervals be encoded with semitone-accuracy.

How, then, do typical listeners comprehend musical structure? It appears that we depend critically on relating our auditory input to the over-learned pitch structures that characterize the music of our culture, such as scales and tonal hierarchies (Krumhansl, 2004; Tillmann, 2005). Even listeners lacking musical training are adept at spotting notes played out of key (Cuddy et al., 2005), though such notes often differ from in-key notes by a mere semitone. However, listeners rarely notice changes to the intervals of a melody if it does not obey the rules of the musical idiom to which they are accustomed (Dowling and Fujitani, 1971; Cuddy and Cohen, 1976), suggesting that the perception of pitch interval patterns in the abstract is typically quite poor. A priori it might seem that this failure could reflect the memory load imposed by an extended novel melody, but our results suggest it is due to a more basic perceptual limitation, one that expert musicians can apparently improve to some extent, but that non-expert listeners overcome only with the aid of familiar musical structure. This notion is consistent with findings that nonmusicians reproduce familiar tunes more accurately than isolated intervals (Attneave and Olson, 1971) and distinguish intervals more accurately if familiar tunes containing the intervals are used as labels (Smith et al., 1994). The importance of learned pitch patterns was also emphasized in previous proposals that listeners map melodies onto scales (Dowling, 1978).

The possibility of specialized mechanisms underlying musical competence is of particular interest given questions surrounding music’s origins (Cross, 2001; Huron, 2001; Wallin et al., 2001; Hagen and Bryant, 2003; McDermott and Hauser, 2005; Bispham, 2006; Peretz, 2006; McDermott, 2008; Patel, 2008), as specialization is one signature of adaptations that might enable musical behavior (McDermott, 2008; McDermott, 2009). Relative pitch has seemed to have some characteristics of such an adaptation—it is a defining property of music perception, it is effortlessly heard by humans from birth (Trehub et al., 1984; Plantinga and Trainor, 2005), suggesting an innate basis, and there are indications that it might be unique to humans (Hulse and Cynx, 1985; D'Amato, 1988), just as is music. These issues in part motivated our investigations of whether contour and interval representations—two components of relative pitch—might be the product of specialized mechanisms. Previously, we found that listeners could perceive contours in loudness and brightness nearly as well as in pitch (McDermott et al., 2008; Cousineau et al., 2009), suggesting that contour representations are not specialized for pitch. Our present results suggest that the same is true for pitch intervals—when compared to other dimensions, basic pitch discrimination, not pitch interval discrimination, stands out as unusual. It thus seems that the two components of relative pitch needed for melody perception are not in fact specific to pitch, and are thus unlikely to represent specializations for music. Rather, they appear to represent general auditory abilities that can be applied to other perceptual dimensions.

If the key properties of relative pitch are not specific to pitch, what then explains the centrality of pitch in music? Other aspects of pitch appear distinctive—listeners can hear one pitch in the presence of another (Beerends and Houtsma, 1989; Carlyon, 1996; Micheyl et al., 2006a; Bernstein and Oxenham, 2008), and the fusion of sounds with different pitches creates distinct chord timbres (Terhardt, 1974; Parncutt, 1989; Huron, 1991; Sethares, 1999; Cook, 2009; McDermott et al., 2010). These phenomena do not occur to the same extent in other dimensions of sound, and are crucial to Western music as we know it, in which harmony and polyphony are central. However, they are probably less important in the many cultures where polyphony is the exception rather than the rule (Jordania, 2006), but where pitch remains a central conveyor of musical structure.

A simpler explanation for the role of pitch in music may lie in the difference in basic discriminability suggested by our results. Although pitch changes in melodies are typically a few semitones in size, well above threshold levels, the fact that basic pitch JNDs are so low means that melodic step sizes are effortless for the typical listener to hear, and can probably be apprehended even when listeners are not paying full attention. These melodic step sizes (typically a few semitones) are also a tiny fraction of the dynamic range of pitch, providing compositional freedom that cannot be achieved in other dimensions. Moreover, near-threshold pitch changes sometimes have musical relevance—the pitch inflections commonly used by performers to convey emotional subtleties are often a fraction of a semitone (Bjørklund, 1961). Thus, the widespread use of pitch as an expressive medium may not be due to an advantage in supporting complex structures involving intervals and contours, but rather in the ability to resolve small pitch changes between notes.