Adaptive auditory feedback control of the production of formant trajectories in the Mandarin triphthong ∕iau∕ and its pattern of generalization

Abstract

In order to test whether auditory feedback is involved in the planning of complex articulatory gestures in time-varying phonemes, the current study examined native Mandarin speakers' responses to auditory perturbations of their auditory feedback of the trajectory of the first formant frequency during their production of the triphthong ∕iau∕. On average, subjects adaptively adjusted their productions to partially compensate for the perturbations in auditory feedback. This result indicates that auditory feedback control of speech movements is not restricted to quasi-static gestures in monophthongs as found in previous studies, but also extends to time-varying gestures. To probe the internal structure of the mechanisms of auditory-motor transformations, the pattern of generalization of the adaptation learned on the triphthong ∕iau∕ to other vowels with different temporal and spatial characteristics (produced only under masking noise) was tested. A broad but weak pattern of generalization was observed; the strength of the generalization diminished with increasing dissimilarity from ∕iau∕. The details and implications of the pattern of generalization are examined and discussed in light of previous sensorimotor adaptation studies of both speech and limb motor control and a neurocomputational model of speech motor control.

INTRODUCTION

Auditory feedback of the sound of a speaker’s own speech is an integral part of normal speech production. Previous studies that used artificially introduced perturbations of speakers’ auditory feedback during production have generally shown that speakers compensate for such perturbations by modifying their production in the direction opposite to that of the perturbation. These studies have explored a variety of acoustic parameters, including vocal intensity (Lane and Tranel, 1971; Liu et al., 2007), fundamental frequency (Liu et al., 2009; Burnett et al., 1998; Burnett and Larson, 2002; Jones and Munhall, 2000, 2002; Donath et al., 2002; Xu et al., 2004; Larson et al., 2000, 2008), the first and second formant frequencies (F1 and F2) of vowels (Houde and Jordan, 1998, 2002; Purcell and Munhall, 2006b, 2006a; Villacorta et al., 2007; Tourville et al., 2008; Munhall et al., 2009; MacDonald et al., 2010), and more recently the spectrum of the fricative ∕ʃ∕ (Shiller et al., 2009). These studies can be divided into two categories according to the experimental design. One category, which we call the “unexpected perturbation paradigm,” involves the introduction of perturbations during a randomly selected subset of the trials. The findings of such studies address the role of auditory feedback in the online, moment-by-moment control of production of speech sounds (e.g., Purcell and Munhall, 2006b). In the second category of studies, which we refer to as the “sustained perturbation paradigm,” perturbations occur repeatedly on a relatively large number of trials and are aimed at examining long-term modification of speech motor programs in response to altered auditory feedback. These studies probe sensorimotor adaptation of the speech motor system (e.g., Houde and Jordan, 1998, 2002; Purcell and Munhall, 2006a; Villacorta et al., 2007; Munhall et al., 2009; Shiller et al., 2009; MacDonald et al., 2010).

Both types of experimental design elicit compensatory responses, indicating that an important component of goals for speech motor planning is in the auditory domain. This concept has been implemented in a computational model of speech production called DIVA (Guenther et al., 2006). This model proposes that during the execution of a pre-learned speech motor program, a speech sound map located in left ventral premotor cortex not only reads out a pre-learned syllabic motor program via the primary motor cortex, but also provides auditory cortical areas with information about anticipated auditory outcome of the motor execution, i.e., the auditory target. The auditory areas monitor the auditory afferent signal, and compare it with the target. Mismatches between the target and auditory feedback are detected as production errors. To minimize these errors in subsequent productions, the brain uses the error information to modify the feedforward commands for subsequent movements. With the appropriate selection of a small set of parameters, the DIVA model is able to generate quantitatively accurate predictions of online compensation to unexpected perturbations (Tourville et al., 2008) and sensorimotor adaptation to sustained perturbations (Villacorta et al., 2007) of formant frequencies of vowels.

Previous studies of auditory feedback control of formant frequencies focused on steady-state vowels (i.e., monophthongs) (Houde and Jordan, 1998, 2002; Purcell and Munhall, 2006a; Villacorta et al., 2007; Tourville et al., 2008; Munhall et al., 2009; MacDonald et al., 2010). The monophthongs are characterized by relatively static formant frequencies, and many of the above-cited formant perturbation experiments (e.g., Houde and Jordan, 1998; Villacorta et al., 2007; Tourville et al., 2008) explicitly instructed subjects to prolong the monophthongs, which exaggerated the static quality of these vowels. However, time-varying sounds are pervasive in speech. Articulatory movements, which lead to changing vocal tract shapes and formant values, can be found in time-varying vowels such as diphthongs and triphthongs, as well as in transitions between consonants and vowels. In comparison, prolonged static gestures like those used in the previous studies occur rarely in natural running speech. Thus, understanding the role of auditory feedback in the control of the time-varying speech movements is important for reaching a more comprehensive understanding of the properties of the speech motor system.

To our knowledge, no previous studies have examined whether or how time-varying formants produced with articulatory gestures are influenced by auditory feedback. However, the role of auditory feedback has been studied within the context of the control of time-varying fundamental frequency (F0) using unexpected perturbation paradigms. Such studies have shown that when producing utterances with time-varying F0 contours, Mandarin (Xu et al., 2004) and English (Chen et al., 2007) speakers show online, short-latency compensatory F0 adjustments in response to unexpected F0 perturbations. It has been observed that the magnitudes of these compensatory responses were different during time-varying and static multisyllabic tonal sequences (Xu et al., 2004; Liu et al., 2009). These results indicate that the functional properties of the auditory feedback control system may depend on whether the production goal is quasi-static or time-varying. The role of auditory feedback in the control of time-varying formant trajectories has not yet been investigated. In addition, because the above-mentioned studies of auditory feedback control of time-varying F0 trajectories all used unexpected perturbations, they did not shed light upon whether the compensatory motor corrections caused by the auditory errors could be incorporated into the feedforward motor commands of time-varying sounds, as observed previously in longer-term sensorimotor adaptation for steady state sounds.

A second aspect of sensorimotor adaptation addressed by the current study concerns generalization of adaptation to sounds not encountered during perturbation training. Generalization, also called transfer, refers to changes observed in movements not exposed to perturbations accompanying and∕or following adaptation to perturbations of the “trained” movements. Patterns of generalization can often provide valuable insights into the organizational principles of sensorimotor systems and provide constraints for models of those systems. For example, patterns of generalization of adaptation to untrained reaching movements have been used to guide the development of neural models of transforms between visual and motor coordinates (e.g., Ghahramani et al., 1996; Krakauer et al., 2000). Only a few studies have examined generalization of auditory-motor adaptations (Houde, 1997; Villacorta et al., 2007). Although these studies show generalization to untrained sounds, the amount of generalization and its relationship to the similarity between the trained and untrained sounds remains unclear. Nevertheless, such patterns of generalization can potentially reveal additional properties of the speech motor system. For example, generalization of auditory-motor adaptations among vowels with different temporal or serial characteristics (e.g., monophthongs and triphthongs) could reveal principles by which the speech motor system plans and controls complex, time-varying movements. One possible principle is that the system performs auditory-to-motor mappings separately for time-varying and quasi-static vowels, which leads to the prediction that little generalization should be observed between these two different categories of vowels. Alternatively, the system could have a shared auditory-motor mapping between non-time-varying and time-varying vowels, in which case generalization across these categories of vowels is predicted. Following the same logic, more detailed properties of these mappings could be studied by examining generalization of adaptation across time-varying vowels with different numbers of serial components (e.g., diphthong ∕ia∕ and triphthong ∕iau∕) and time-varying vowels with different serial order (e.g., triphthongs ∕iau∕ and ∕uai∕).

Against this background, the aims of the current study are as follows. First, we aim to examine whether perturbations of time-varying formant frequency trajectories can induce adaptive changes in articulation. For this purpose, we chose, as the “training” stimulus, the triphthong ∕iau∕ in Mandarin, which requires active control of multiple articulators (tongue, jaw and lips; see explanation in Sec. 2B), and we manipulated its F1 trajectory in the auditory feedback provided to the speakers. The second aim of the current study is to explore the pattern of generalization of any compensatory adaptation found in response to perturbations of the F1 trajectory in the triphthong to untrained vowels with different formant trajectories and temporal characteristics.

MATERIALS AND METHODS

Participants

Forty adult native speakers of Mandarin Chinese (20 male) participated in this study. These volunteers were recruited from around the Boston area through poster and Internet advertisements in Chinese. Inclusion criteria included: 1) began speaking Standard Mandarin before the age of 5, 2) had Standard Mandarin as the primary language of instruction throughout elementary and secondary education (1st–12th grades), 3) reported no history of hearing, speech, or neurological disorders, and 4) had pure-tone hearing thresholds better than 20 dB HL at 0.5, 1, and 2 kHz as confirmed by an audiometric test. This study was approved by the MIT Committee on the Use of Humans as Experimental Subjects.

Stimulus utterances

The triphthong ∕iau∕ in Mandarin has a long average duration (250 ms on average in running speech, Yamagishi et al., 2008) and spans a large area in the F1×F2 space. As an oral vowel, its formants can be modeled relatively reliably with autoregressive (AR) analysis. Also, its occurrence in Mandarin is frequent. These properties make ∕iau∕ an optimal phonemic target for examining sensorimotor adaptation to time-varying auditory perturbations.

The utterances used as stimuli in this experiment were divided into two categories: training utterances and test utterances. Each of the 10 training utterances, which were produced when auditory feedback was available, consisted of a consonant followed by the triphthong ∕iau∕ in its first (i.e., high-flat) tone, denoted as ∕ iau₅₅∕ (Table 1, left column). Ten test utterances, pronounced only under loud masking noise, were included to study the generalization of the sensorimotor adaptation across phonemes and phonemic categories; they comprised a mixture of different vowels (Table 1, right column). These included the same triphthong ∕ iau₅₅∕ as in the training set, the triphthongs ∕ iou₅₅∕ and ∕ uai₅₅∕, the diphthongs ∕ ia₅₅∕ and ∕ au₅₅∕, and the monophthong ∕ a₅₅∕. A fourth-tone (i.e., high-falling) variant of ∕iau∕, namely ∕ iau₅₁∕, was also included in order to examine the transfer of the adaptation across tones. All the characters (i.e., syllables) in the stimulus list were verbs in Mandarin.

Table 1.

List of stimulus utterances and their IPA transcriptions. The left half of the list shows the training utterances, during which auditory feedback of speech was played through the earphones. The right half shows the test utterances, which were masked by noise (see text for details).

The syllables containing ∕iau∕ or the other vowels were embedded in the carrier phrase ∕ Ciau₅₅ ʈʂɣ∕, with C representing an onset consonant (see Table 1). Figure 1 shows an example spectrogram of a training utterance produced by a male subject. Semantically, the second syllable ∕ʈʂɣ∕ denotes continuous aspect of the verb in the first syllable (similar to the English suffix “-ing”). This embedding increased the naturalness of the production; it also facilitated the online detection of the end of the vowels (see Sec. 2D). Since all but one vowel used in the current experiment had the first tone, the phonetic subscripts for the first tone (∕₅₅∕) are omitted in the following, for simplicity of notation.

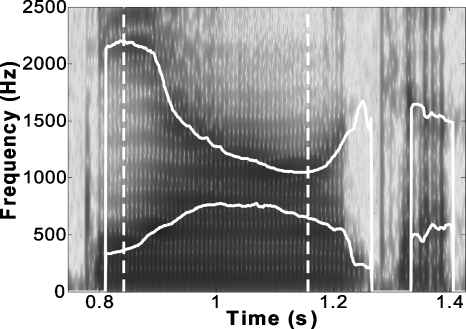
Figure 1.

Spectrogram and parsing of the training utterance. A spectrogram of the utterance ∕ tiau₅₅ ʈʂɣ∕ spoken by a male speaker is overlaid with F1 and F2 tracks estimated online by the experimental apparatus. The two vertical dashed lines indicate the beginning and end of the triphthong ∕ iau₅₅∕, automatically delineated online using heuristics described in Sec. 2D.

Apparatus for formant estimation and shifting

Experimental sessions were conducted in a sound-attenuating audiometric booth (Eckel Acoustic). The subject was seated comfortably in front of a computer monitor, on which the stimulus utterances were displayed at a rate of once per 2.5–2.75 s. The inter-trial intervals were randomized to help reduce boredom due to repeated presentation of the same set of stimuli. The subject wore a headband, to which a condenser microphone (Audio-Technica AT803) was attached and was positioned at a fixed distance of approximately 10 cm from the mouth. Auditory feedback to the subject of his or her own speech was delivered through a pair of insertion earphones (Etymotic Research ER-3A), which provided attenuation of air-conducted sound by approximately 25–30 dB.

During pronunciation of the utterances, frequencies of the first and second formants (F1 and F2) were estimated in near-real time using AR-based linear predictive coding (LPC). LPC was performed only during the voiced portions of the speech, as detected with a short-time root-mean-square (RMS) threshold. The LPC analysis was calculated over 17.3-ms windows. LPC orders of 13 and 11 were used for male and female speakers, respectively. To improve the quality of formant estimation for high-pitched speakers, low-pass cepstral liftering and dynamic-programming formant tracking (Xia and Espy-Wilson, 2000) were performed in conjunction with the LPC. The tracked formant frequencies were then smoothed online with a 10.67-ms window. This smoothing used a weighting of the samples with the instantaneous RMS amplitude of the signal, which effectively emphasized the closed phase of the glottal cycles and reduced the impact of the sub-glottal resonances on the formant estimates.

As in previous studies of vowel formant frequency perturbation (Purcell and Munhall, 2006a; Villacorta et al., 2007), frequency shifting of F1 was achieved by digital filtering which substituted pole pairs on the z-plane. However, unlike in previous formant perturbation studies, which used filters that shifted formant frequency by fixed ratios, the filters used for perturbation in the current study were time-varying and tailored to the time-varying characteristics of the triphthong ∕iau∕. They shifted the formant frequencies on a frame-by-frame basis in specific ways that alter the F1×F2 curvature of the trajectory of the triphthong ∕iau∕ (see Sec. 2G for details). Direct measurements indicated that the feedback delay of this system was 14 ms.

Automatic extraction of the triphthong ∕iau∕

The triphthongs ∕iau∕ in the stimulus phrase ∕Ciau ʈʂɣ∕ were extracted online using the following set of heuristic rules on the frequency of F1 and F2 and their respective formant velocities (dF1∕dt and dF2∕dt). A triphthong ∕iau∕ was considered to begin when the following speaker-independent criteria were satisfied (See the first dashed line in Fig. 1):

$$200\text{Hz}<F1<800\text{Hz};\text{and}800\text{Hz}<F2<3000\text{Hz},$$ (1)

$$dF1∕dt>375\text{Hz}∕\text{s},dF2∕dt<375\text{Hz}∕\text{s},\text{and}dF1∕dt-dF2∕dt>375\text{Hz}∕\text{s}.$$ (2)

Criterion (1) ensures that the values of F1 and F2 are in a region appropriate for ∕i/, while Criterion (2) stipulates that the directions of changes in F1 and F2 are appropriate for an ∕i/-to-∕a/ transition. Once a triphthong starts, the end of the triphthong occurs if and only if the following exit criterion is met (the second dashed line in Fig. 1),

$$dF2∕dt>750\text{Hz}∕\text{s}.$$ (3)

This criterion can effectively detect the cessation of the ∕iau∕ because the ∕u/ component of the triphthong, which has a low F2, was followed by the retroflex affricative ∕ʈʂ∕, which has a relatively high F2 (see Fig. 1 for an example).

Experiment design

As illustrated in Fig. 2, an experimental session was divided into seven phases. Each phase consisted of a number of blocks. Each block contained a single repetition of each of the 10 training utterances in its first half, followed by the 10 test utterance in the second half. The order of the training and test utterances were randomized within each half of the block. During the training utterances, the subject received auditory feedback through the earphones. The level of the feedback was 16.5 dB greater than the level at the microphone, which strengthened the masking of the natural auditory feedback via bone- and air-conduction. During the test utterances, the subjects heard speech-shaped masking noise at a level of 90 dBA SPL, which adequately masked auditory feedback of vowel quality. Therefore the subject effectively produced the test utterances in the absence of meaningful auditory feedback.

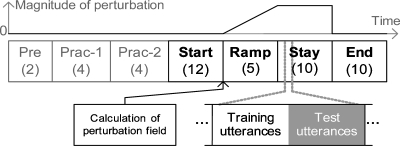
Figure 2.

Experimental design. The experiment was divided into seven phases. The first three phases, Pre, Prac-1 and Prac-2, were for familiarization purposes. The next four phases, Start, Ramp, Stay and End, comprised the main experimental stages. The Start phase served as a no-perturbation baseline, at the end of which a subject-specific perturbation field was calculated (see Sec. 2F for details). Perturbation of auditory feedback was present only in the Ramp and Stay phases. Each phase consisted of a number of blocks. The numbers of blocks are shown in the brackets. Each block was divided into two parts, the first of which contained ten training phrases, the second of which contained ten test utterances.

The first three phases of the experiment (Pre, Prac-1, and Prac-2) were preparatory in nature. In the Pre phase, the subject was familiarized with the experimental procedure and the stimulus utterances. In the Prac-1 phase, the subject was trained to produce the vowels in the training utterances within a level range of 78±4 dBA SPL. In the Prac-2 phase, feedback of duration of the vowel was given in an analogous way in order to train the subject to produce the vowels with a duration between 302 and 398 ms. It was discovered in pilot studies that the above-listed level and duration ranges for the training phrases were too stringent for the noise-masked test utterances due to the Lombard effect. Hence we relaxed the level ranges for the test utterances by 20%.

The Start, Ramp, Stay and End phases constituted the main portion of the experiment. Feedback about the level and duration were no longer provided in these phases, but the subject was notified when the level or duration ranges were not met. In this way, we ensured that relatively constant vocal intensity and speaking rate were maintained throughout the course of the experiment, and that these values were relatively constant across subjects.

In the Start phase, the subject received unperturbed auditory feedback. The productions of the training utterances in this phase were used to make baseline measures of vowel formants in the subject’s natural productions, which provided the basis for computing subject-specific perturbation fields (see Sec. 2F). In successive blocks of the Ramp phase, the magnitude of the perturbation was linearly ramped from zero to maximum. The perturbation was maintained at the maximum magnitude (Fig. 2, top) throughout the Stay phase. In order to study the after-effects of any sensorimotor adaptation that occurred, the perturbation was discontinued for the End phase.

After the experiment, the subject was interviewed in written form about whether he∕she was aware of any perturbations to the speech auditory feedback.

Construction of the perturbation fields

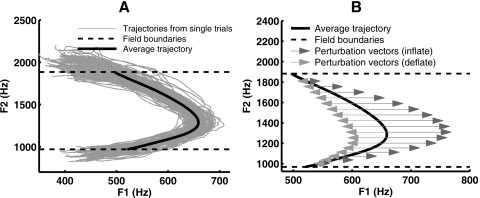
The basis of the time-varying perturbation used in this study was the perturbation field, a region in the F1-F2 space where shifting of the formant frequencies occurred. Since the detailed shape and location of the F1-F2 trajectory of the triphthong ∕iau∕ varied across speakers, perturbation fields were designed to be subject-dependent. As exemplified in Fig. 3A, for each subject, a set of F1-F2 trajectories of ∕iau∕ was automatically extracted and gathered from the Start (baseline) phase. Two iso-F2 lines formed the boundary of the perturbation field. The F2 value of an upper boundary, F2_U, was defined as the highest F2 through which 80% of the ∕iau∕ trajectories passed. Similarly, a lower boundary, F2_L, was defined as the lowest F2 value through which 80% of the trajectories passed.

Figure 3.

Design of the perturbation fields. An example from a single subject is shown. (A) Formant trajectories from 120 repetitions of ∕iau∕ were extracted and gathered from the Start phase and were used as the basis for calculating the average trajectory and the field boundaries. (B) Inflate and Deflate perturbation fields. The perturbation vectors were parallel to the F1 axis. The magnitudes of the vectors followed a quadratic function of F2, and were zero at the boundaries and greatest near the center of the field (see text for details).

Only F1 was perturbed in the subject’s auditory feedback. The amount of this perturbation was implemented in terms of a set of perturbation vectors, V, which defined a perturbation field. The perturbation field was a mapping between locations in the F1×F2 plane to perturbation vectors. Since F1 was the only perturbed formant, all perturbation vectors were parallel to the F1 axis. We took advantage of the fact that F2 varied monotonically in ∕iau∕, and let V be a function of F2 only. We used two different types of perturbation fields, namely Inflate fields and Deflate fields.

In the Inflate fields [Fig. 3B, darker gray arrows], the perturbation vectors point to the right and hence increased the values of F1. The magnitudes of the vectors M follow a quadratic function of F2 which satisfied the following:

$$M\left(F{2}_L\right)=0,M\left(F{2}_U\right)=0,M\left(F{2}_M\right)=0.6\cdot \Delta F1,$$

where F2_M is the average F2 value at which the maximum F1 occurred, and ΔF1 is the range of F1 in the average ∕iau∕ trajectory from the start phase [e.g., the thick solid curves in Fig. 3A].

The Deflate field [Fig. 3B, light gray arrows] was similar to the Inflate field, but its vectors point to the left, and hence caused a decrease in F1. The Deflate field is defined formally as:

$$M\left(F{2}_L\right)=0,M\left(F{2}_U\right)=0,M\left(F{2}_M\right)=0.375\cdot \Delta F1.$$

Subjects were assigned pseudo-randomly to Inflate and Deflate groups.

Data analysis and statistical procedures

The produced tracks of F1 and F2 versus time were smoothed by 41.3-ms Hamming windows. The track for every utterance was inspected manually. Utterances that contained production errors and∕or gross errors in automatic estimations of F1 and F2 were excluded from subsequent analyses. Overall, the excluded utterances comprised 6.3% of the training utterances and 5.0% of the test utterances.

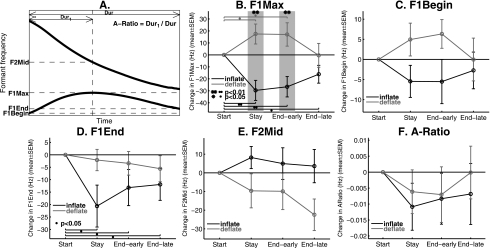
Several parameters that quantify the shape and time course of the formant trajectories of ∕iau∕ were extracted automatically. These include 1) F1Max, defined as the maximum F1 during the triphthong, 2) F1Begin, the F1 at the beginning of the triphthong, 3) F1End, the F1 at the end of the triphthong, 4) F2Mid, the value of F2 at the time when F1Max occurs, and 5) A-Ratio, the ratio between the time when F1Max occurs and the total duration of the triphthong [see Fig. 6A].

Figure 6.

Quantification of adaptive changes in several trajectory parameters for the training vowel ∕iau∕. In A, the definitions of the parameters of the F1 and F2 trajectories of the triphthong ∕iau∕ are shown schematically (see text for details). (B) The change of F1Max (maximum F1 during ∕iau∕) from the Start-phase mean in the Stay and End phases. The End phase is subdivided into “End-early” and “End-late,” in order to show the after-effect of the adaptation in the Stay phase and its decay. The End-early and End-late phases included the first two and the last eight blocks of the End phase, respectively. The error bars show mean±1 SEM across all 18 subjects in each group. The brackets with dots indicate significant change of F1Max from the Start-phase baseline. The gray-shaded regions with asterisks indicate significant differences between the Inflate and Deflate groups according to two-sample t-tests. (C)–(F) The changes re Start-phase mean in F1Begin, F1End, F2Mid and A-Ratio are shown in the same format as Panel B.

To compute average formant trajectories across multiple subjects, each subject’s F1 and F2 trajectories were normalized linearly to [0,1] intervals, respectively. Normalization of F2 was done between F2_L and F2_U as defined in Sec. 2F; normalization of F1 was done between F1_L and F1_U. F1_L was defined as the minimum value of the F1 in the average trajectory of the training vowel ∕iau∕ between F2_L and F2_U in the Start phase; F1_Uwas defined as the maximum value of F1 of the same average trajectory.

For the vowels in the test utterances, the parameter F1Max was defined in the same way and extracted automatically, with exception of the monophthong ∕a/, for which F1Max was defined as the average F1 between the 40% and 60% points of normalized time.

To test for the significance of adaptation of a parameter in the training vowel ∕iau∕, data from a subject were averaged across all blocks and all trials within the Start and Stay phases, respectively, as well as within the End-early and End-late phases. The End-early phase was defined as the first two blocks of the End phase, in order to capture the after-effect of the adaptation following the cessation of the perturbations. The End-late was defined as the final eight blocks of the End phase, in order to quantify the decay toward the baseline production.

These data were then subject to repeated measures analyses of variance (RM-ANOVA) with Huynh-Feldt correction. The RM-ANOVA contained a between-subjects factor: Group ({Inflate, Deflate}), and a within factor: Phase ({Start, Stay, End-early, End-late}). For post hoc comparisons, we followed the least significant difference test paradigm of Fisher (1935) (see also Keppel, 1991) in controlling family-wise errors. For each vowel and trajectory measure, two types of post hoc analyses were undertaken: 1) within-group comparisons between phases were performed only if the main effect of Phase is significant in that group(α=0.05); and 2) between-group comparisons within a phase were performed only if the omnibus test indicates a significant interaction between Group and Phase(α=0.05). Whereas the first approach is the most straightforward way of testing the significance of adaptation and after-effects, the second approach is more statistically sensitive and less susceptible to non-perturbation-related trends of changes than the first one. One-tailed t-tests (α=0.05) were used for these post hoc comparisons [Figs. 6B, 9A, 9B, 9F, 9G, 9H]. The one-tailed test was justified by the existence of a set of a priori hypotheses based on previous findings (e.g., Houde, 1997; Houde and Jordan, 2002; Purcell and Munhall, 2006a; Villacorta et al., 2007) regarding the directions of the changes in the trajectory measures: that on average across the subjects, they should change in the direction opposite to that of the auditory feedback perturbation.

Figure 9.

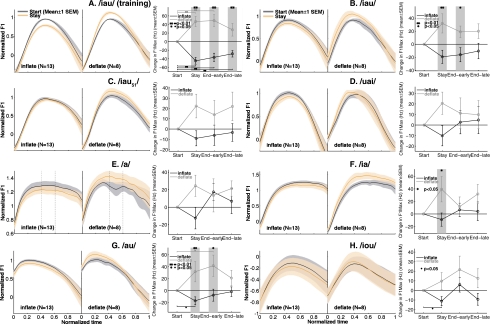
Generalization of the auditory-motor adaptation to the test utterances. Data from the 13 subjects in the Inflate group and the eight subjects in the Deflate group who showed significant Stay-phase adaptation in the training utterance. Panel A shows the average time- and frequency-normalized F1 trajectories of the training vowel /iau/ from the Inflate (Left) and Deflate (right) groups in the Start and Stay phases (color online). The right-hand plot in Panel A shows the average F1Max changes from baseline in the Stay phase and early and late parts of the End phase. The format of this plot is the same as Fig. 6B, in which brackets with filled dots show significant within-group, between-phase changes, and gray shading with asterisks show significant between-group differences. Panels B–H have the same layout as A; they show the data from the seven test vowels: /iau/, / iau₅₁/, /uai/, /a/, /ia/, /au/, and /iou/, respectively. The dashed vertical lines in panel E show the time intervals from which F1Max was calculated.

RESULTS

Adaptation to the perturbation of auditory feedback

Of the 40 subjects who participated, data from 36 were used in subsequent analyses. The data from the other four subjects were judged to contain high proportions of trials with suboptimal formant estimation according to an automatic objective procedure,1 and were excluded from further analysis. Of the 36 subjects, eighteen (mean age mean±SD:26.7±4.1, 10 males) comprised the Inflate group and eighteen (mean age±SD:28.2±6.9, 10 males) the Deflate group. None of the 36 subjects reported being aware of any perturbation to their auditory feedback in an interview after the experiment.

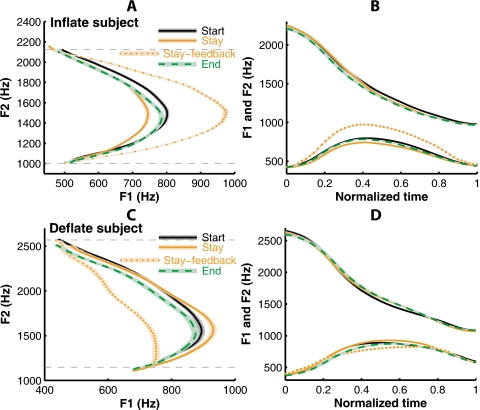
Representative results from one of the subjects (IH) who experienced the Inflate perturbation are shown in Figs. 4A, 4B. Panel A shows average trajectories for the training vowel, ∕iau∕, in the F1-F2 space; panel B shows those trajectories vs. normalized time. In Panel A, the difference between the average trajectories from the Stay phase productions and auditory feedback (dotted curve) shows the effect of the Inflate perturbation, which increased the maximum F1 (F1Max) of the triphthong without altering the values of F1 at the beginning (F1Begin) or end (F1End) of the triphthong. During the Stay phase, the curvature of the F1-F2 trajectories in the auditory feedback was increased: compared to the average trajectory in the Start phase, the average Stay-phase trajectory showed a marked decrease in F1Max (indicative of compensation for the perturbation), while the F1 values at the beginning and end of the triphthong were changed by much smaller amounts. This pattern of F1 change led to a reduced curvature of the produced F1-F2 trajectory in the Stay phase. The subject made this adjustment as if to bring the shape of the formant trajectory in the auditory feedback toward its pre-perturbation baseline. However, this adjustment only partially compensated for the effect of the perturbation. If the compensation were complete, the auditory feedback in the Stay phase would have overlapped with the average Start-phase trajectory. The average trajectory from the End phase (after cessation of the perturbation) lay roughly between the trajectories from the Start and Stay phases, which indicated (1) a significant after-effect of articulatory compensation and (2) a decay of this after-effect toward the pre-perturbation baseline. There were changes in the F2 trajectory over the three phases of the experiment [Fig. 4B], but these changes were small compared to the compensatory changes in F1.

Figure 4.

Adaptive changes in the formant trajectories of the training vowel /iau/ in representative subjects. The F1-F2 trajectories produced by subject IH of the Inflate group are plotted (A) in the formant plane and (B) as functions of time. Different line patterns (color version online) indicate different phase of the experiment (see legend). The dashed curves show the perturbed auditory feedback. The shading surrounding the curves show ±3 SEM. The profiles of F1 and F2 in panel B are normalized in time. Panels C and D show analogous results from subject DF of the Deflate group.

Figures 4C, 4D show representative results from a subject in the Deflate group (DF). As the dashed curves show, the Deflate perturbation decreased the F1 value in the subject’s auditory feedback for the part of the trajectory that passes near the target for the vowel ∕a/ while preserving F1 at the initial and final components of the triphthong. The subject responded to this perturbation in the Stay phase by increasing the extent of movement of F1 in her production, such that F1 in the most perturbed region near the center of the perturbation field was selectively increased. By comparison, the changes in F1 at the two boundaries of the perturbation field, i.e., at the beginning and end of the vowel, remained essentially unaltered. As with the previous subject, who received the Inflate perturbation, this compensation had a comparatively small magnitude and effectively cancelled only a small fraction of the Deflate perturbation. However, unlike in the previous example, in this subject an average End-phase after-effect was not evident, due to a rapid decay of the after-effect.

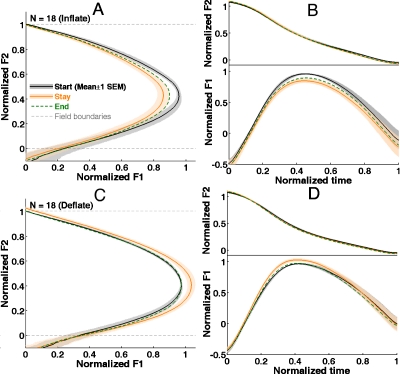
The group average trajectories in the Start, Stay and End phases are shown in Fig. 5. These trajectories are normalized by the subject-specific bounds of F1 and F2 (see Methods, Sec. 2G) and then averaged across all subjects in each perturbation group. The shading around the mean curves shows ±1 standard error of the mean (SEM) across the subjects. The SEMs of the End-phase averages are omitted for the sake of visualization; otherwise, they would partially obscure the other trajectories. Significant changes in the formant trajectory of the triphthong ∕ iau₅₅∕ in the Stay phase in both groups are evident in Fig. 5. These changes were in directions opposite to the auditory perturbations. In the Inflate group, the peak F1 and the curvature of the trajectory deceased during the Stay phase, whereas in the Deflate group, it increased in the Stay phase. The differences in the temporal profiles of F2 between the Start and Stay phases were substantially smaller compared to the F1 changes. They are hardly visible in the time-normalized plots [top parts of Figs. 5B, 5D] and didn’t reach statistical significance for either group, indicating that the compensatory changes in production were mainly specific to F1. In both groups, the End-phase average trajectory was situated roughly midway between the Start- and Stay-phase trajectories. Overall, these observations indicate that at the group level, there were modifications of the subjects’ feedforward motor commands for ∕iau∕, which were manifested as after-effects.

Figure 5.

Group-average formant trajectories of the training vowel /iau/. F1 and F2 were normalized with respect to the perturbation-field boundaries. (A) The mean F1-F2 trajectories of the Inflate group (color online). (B) The time-normalized trajectories of F1 (bottom) and F2 (top) of the Inflate group. Panels C and D analogous results for the Deflate group. The shading shows ±1 SEM of the mean across subjects. The SEM is not shown for the End-phase trajectory for visualization purposes.

A notable feature of the group-average compensatory responses is that these articulatory changes mirrored the time-varying effect of the perturbation field throughout the triphthong movement. The most pronounced effect of the perturbations of F1 values occurred at its peak value (F1Max). The changes at F1Begin (where normalized F2=1) and at F1End (where normalized F2=0) were appreciably smaller compared to the changes in F1Max. This adaptation pattern is indicative of a movement controller capable of subtle spatiotemporal modifications of articulator trajectories (or motor programs) in response to sustained, selective modifications of the sensory consequences of highly practiced movement patterns (in this case, for triphthongs).

To quantify the changes in these trajectory parameters, we performed repeated measures analysis of variance (RM-ANOVA) on F1Max, F1Begin and F1End. The RM-ANOVA contained a between-subjects factor (Group) and a within factor (Phase). For F1Max, the two-way interaction Group×Phase was significant (F(3,102)=9.56, p<0.0001, Huynh-Feldt correction),2 which indicated that the two types of perturbations resulted in changes in the subjects’ productions in different manners and with appropriately opposite directions across the experimental phases. Figure 6B shows the changes in F1Max from the Start-phase baseline to the Stay phase and then the early and late parts of the End phase. Between-group post hoc t-tests of the amounts of F1Max change (from Start-phase baseline) in the Stay, End-early and End-late phases indicated significant differences between the two groups in the Stay and End-early phases [asterisks in Fig. 6B]. In addition, the main effect of Phase was significant in both groups (Inflate: F(3,51)=7.90, p<0.001; Deflate: F(3,51)=3.29, p<0.05). Post hoc comparison within the Inflate group indicated that significant decreases of F1Max from its Start-phase baseline occurred in Stay(p<0.01), End-early(p<0.01), and End-early (p<0.05) phases. In the Deflate group, the same post hoc comparison revealed significant changes from the Start-phase baseline in the Stay and End-early phases(p<0.05), but not in the End-late phase [dots in Fig. 6B].The above pattern of statistical results confirmed the significance of the compensatory response in F1Max in the Stay phase, and of the after-effect of this response in the End-early phase. The lack of significant between-group difference in the End-late phase was most likely due to the gradual decaying of the after-effects following the return of the auditory feedback to the unperturbed condition.

By contrast, the RM-ANOVA on F1Begin didn’t indicate a significant Group×Phase interaction [F(3,102)=2.11, p>0.1, Fig. 6C]. The main effect of Phase was not significant in either group(p>0.25). The Group×Phase interaction for F1End merely approached significance (F(3,102)=3.02, p=0.055). The main effect of Phase was significant only in the Inflate group [see Fig. 6D]. These results indicate that, although on average there are some compensatory adjustments to the value of F1 at the upper and lower boundaries of the perturbation field, these changes are smaller and statistically weaker compared to the change of F1Max at the center of the field. Therefore, the adaptive corrections subjects made to their formant trajectories were primarily a change in the shape of the trajectory, rather than a simple “translational” movement of the entire trajectory in the direction opposite to the perturbation. This is consistent with the observations of the group-average trajectories which indicate that the compensations in the subjects’ productions reflected the time-varying nature of the perturbation magnitude.

In contrast to the significant effects of the perturbations on F1 trajectory of the triphthong, the F2 trajectory didn’t show statistically significant alterations. As Fig. 6E shows, the changes in F2Mid (the value of F2 at the time when F1Max occurs) across the phases were small. The RM-ANOVA on F2Mid indicated neither a significant Group×Phase interaction (p>0.1) nor a significant main effect of Phase in either group(p>0.05).

The analyses discussed so far are only concerned with the spatial (magnitude) aspects of the formant trajectories, and were not directly concerned with the temporal properties of the ∕iau∕ trajectory. We also analyzed whether any change in the relative timing of the trajectory peak as it passes through the target region for ∕a/ was elicited by the perturbations. As Fig. 6F shows, A-Ratio, which quantifies the relative timing of the peak F1 in the triphthong [see definition in Fig. 6A], didn’t show substantial changes across the experimental phases in either group. The Group×Phase interaction for A-Ratio was very weak and non-significant(p>0.9), and so was the main effect in both groups(p>0.5). In fact, given the very small magnitude of the changes in A-Ratio (<2%normalized time) in both groups, it can be seen that the relative timing of the F1 peak was preserved rather strictly when the compensatory responses occurred.

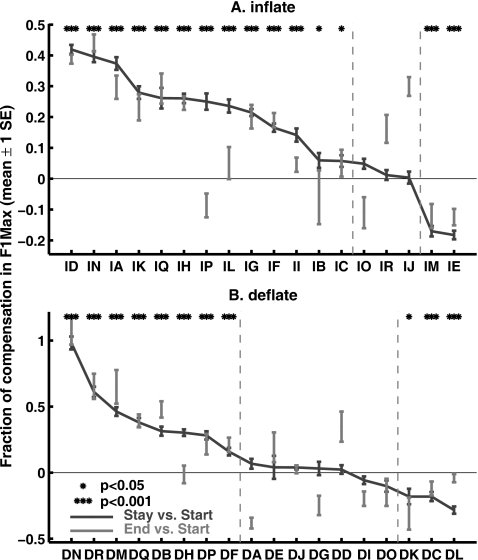
The F1-F2 trajectories and the temporal profiles in Fig. 5 show group-average trends in adapting to the auditory perturbations. To illustrate the variability of responses among individual subjects to the time-varying auditory perturbation, Fig. 7 shows fractions of compensation to the F1Max perturbations in the Stay phase for each subject. Fraction of compensation is defined as the fraction of the auditory perturbations that was cancelled by the compensatory changes in production. In both panels of Fig. 7, positive values indicate compensatory adjustments to productions, while negative ones correspond to production changes that followed the perturbations. The subjects in these plots are arranged in descending order of the fraction of compensation. The plots show that there is substantial variability of compensatory responses among the subjects. In the Inflate group, 13 of the 18 subjects showed significant adaptations to the perturbation in the Stay phase; three did not show significant Stay-phase responses; while two other subjects showed articulatory changes that followed the direction of the perturbation (t-test of the values of F1Max in the Start and Stay phases, α=0.05uncorrected). It can also be seen from the gray bars in Fig. 7A that almost all of the Inflate-group subjects who compensated for the perturbation in the Stay phase demonstrated significant after-effects in the early End phase. A similar pattern was seen in the Deflate group, in which eight of the 18 subjects compensated for the perturbation in the Stay phase; seven showed no changes; and three others followed the perturbation in their productions. As in the Inflate group, all but one of the Deflate subjects who showed significant Stay-phase compensation showed significant after-effects in the early End phase. The average fraction of Stay-phase compensation in the Inflate and Deflate groups were 15.7% and 16.1%, respectively (about equal).

Figure 7.

Amount of adaptation for the training vowel ∕iau∕ in individual subjects. Fractions of compensation in F1Max with respect to the auditory perturbations are shown. The upper and lower panels show the subjects in the Inflate and Deflate groups, respectively. Positive values in both panels indicate compensatory changes, i.e., changes in productions in the direction opposite to the auditory perturbations. A value of 1.0 corresponds to complete compensation. In each group, the subjects are shown in descending order. The error bars show mean±1 SEM across the trials. The asterisks show significance Stay-phase changes from the Start phase (two-sample t-test). Most of the subjects who showed significant compensatory responses in the Stay phase demonstrated a significant after-effect of these responses in the early End phase, as indicated by the gray bars. In each panel, the vertical dashed gray lines divide the subjects into three subgroups: a group that showed significant adaptation in F1Max, a group that showed no change, and a group that followed the auditory perturbation in their F1Max.

Transfer of the adaptive responses to the test utterances

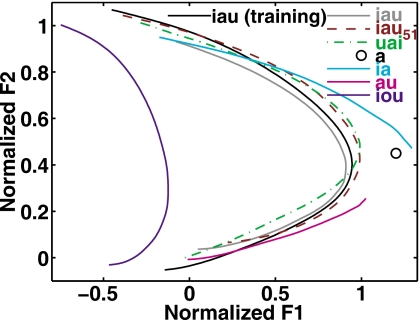
To study the pattern of generalization of the auditory-motor adaptation trained with the triphthong ∕iau∕ to other vowels, the production of utterances containing ∕iau∕ were interleaved with utterances containing the vowels ∕iau∕, ∕ iau₅₁∕, ∕uai∕, ∕a/, ∕ia∕, ∕au∕, and ∕iou∕, which were produced only under auditory masking. Because the test of generalization requires significant adaptation on the training vowel ∕iau∕ as a precondition, the subsequent analyses included the data from only the 21 subjects (13 Inflate, 8 Deflate, see Fig. 7) who showed significant Stay-phase compensation. Figure 8 illustrates the relationships between these test vowels and the training vowel by showing the frequency-normalized Start-phase trajectories of plotted in the same F1-F2 plane. For comparison, the trajectory of the training vowel ∕iau∕ (pronounced without masking noise) is plotted in the same figure as the thick solid curve.

Figure 8.

The relations of the test vowels to the training vowel in formant space. Data in this plot are from the baseline (i.e., Start-phase) productions of all the 21 subjects (13 Inflate, 8 Deflate) who showed significant compensatory adjustment to the auditory perturbation in the training utterances (see Fig. 7). The average Start-phase trajectories of the vowels in the test utterances are plotted in the same formant plane to illustrate their relationship to the trajectory of the training vowel /iau/.

It can be seen that the locations and shapes of the average trajectories of ∕iau∕ and ∕ iau₅₁∕ in the test utterances closely resembled that of ∕iau∕ in the training utterances. Furthermore, the trajectory of the triphthong ∕uai∕, the serially reversed version of ∕iau∕, nearly overlapped the trajectories of the ∕iau∕-type triphthongs. The two diphthongs ∕ia∕ and ∕au∕ had formant trajectories partially overlapping those of the ∕iau∕-type triphthongs near the regions of ∕i/ and ∕u/, which are the beginning and end points of these two diphthongs, respectively. However, their trajectories had slightly higher F1 values in the ∕a/ portions than the triphthongs, which is not unexpected because ∕a/, a via-point for ∕iau∕, is an end point for each of the diphthongs. For a similar reason, the monophthong ∕a/ had a greater F1 than the F1Max of ∕iau∕. The trajectory of the triphthong ∕iou∕ (in the leftmost part of Fig. 8) had a curved shape that resembled the bow shape of the trajectory of ∕iau∕. In particular, ∕iou∕ has a monotonically decreasing F2 similar to that of ∕iau∕ and a rise-fall trend in F1. However, the absolute F1 values at all the three components of ∕iou∕ were lower than those of ∕iau∕, making it the test vowel most distant from the training vowel (∕iau∕) in F1-F2 space.

A three-way RM-ANOVA was performed on the F1Max measure for all the test vowels. This RM-ANOVA included one between-subject factor Group, and two within-subject factors, namely Phase ({Start, Stay, End-early and End-late}) and Vowel ({∕iau∕, ∕ iau₅₁∕, ∕uai∕, ∕a/, ∕ia∕, ∕au∕, ∕iou∕}). The only significant main effect was Vowel (F(6,114)=170.6, p≈0), which was not surprising given the distinct peak F1 values in the different test vowels (see Fig. 8). The two-way interaction Group×Phase reached significance (F(3,57)=4.45, p<0.02), indicating that under the between-group comparison, when all the test vowels are considered as a whole, there was significant generalization of the adaptations from the training vowel ∕iau∕. Within the individual groups, the main effect of Phase was significant in the Deflate group (F(3,21)=4.26, p<0.05) but was not significant in the Inflate group(p>0.2). Therefore, it can be seen that the generalization of the adaptation is statistically less significant than the adaptation itself (see Sec. 3A)

To reveal the fine structure in the generalization patterns, we next examined the generalization to each of the individual test vowels. The perturbation-induced changes in the time-normalized F1 trajectories of the test vowels are summarized in the curve plots in Figs. 9B, 9C, 9D, 9E, 9F, 9G, 9H. For comparison, the average Start- and Stay-phase F1 trajectories of the training vowel ∕iau∕ from the 21 subjects are plotted in Fig. 9A. Because these subjects constituted the subgroups that showed significant adaptations, the differences between the average Start- and Stay-phase trajectories in Fig. 9A are larger than the whole-group results shown in Figs. 5B, 5D. The test vowel ∕iau∕ [Fig. 9B] was the same vowel as the training vowel, but was produced under masking noise. Compared to the changes in the training vowel ∕iau∕ shown in Fig. 9A, the test vowel ∕iau∕ showed smaller changes from baseline in the Stay phase [Fig. 9B]. The main effect of Phase approached significance in the Deflate group(p=0.056), but failed to reach significance in the Inflate group(p>0.1). However, there was a significant Group×Phase interaction (F(3,57)=4.91, p<0.01). Furthermore, the post-hoc t-tests between the two groups reached significance for both the Stay and End-early phases [Fig. 9B]. Therefore, although the adaptation was transferred only partially from the unmasked training condition to the masked test condition, the transfer was significant if the between-group difference was considered.

The generalization across the tonal difference is illustrated in Fig. 9C. Compared to the transfer to the same-tone triphthong ∕iau∕ [Fig. 9B], the transfer to the fourth (high-falling) tone ∕ iau₅₁∕ was slightly smaller in magnitude. Due to this weaker effect, the RM-ANOVA on F1Max of ∕ iau₅₁∕ didn’t show a significant Group×Phase interaction or significant main effect of Phase in either group(p>0.1). In other words, transfer of the auditory-motor adaptation across tonal boundary was not observed.

To investigate the effect of temporal reversal of the articulatory trajectory on generalization of the adaptation, the triphthong ∕uai∕ was included in the set of test vowels. As Fig. 9D shows, the changes in F1Max of ∕uai∕ across the experiment phases were consistent with the trends shown by ∕iau∕ and ∕ iau₅₁∕; however, the magnitude of these changes were smaller than the changes in ∕iau∕. There was not a significant Group×Phase interaction for F1Max of ∕uai∕ (F(3,57)=1.68, p>0.2), nor a significant main effects of Phase in the individual groups(p>0.3). Thus, transfer of the sensorimotor adaptation from ∕iau∕ to its temporally reversed version ∕uai∕ was not observed.

The generalization pattern to the monophthong ∕a/ is shown in Fig. 9E. As with the other test vowels, both groups showed changes in F1Max from baseline in the Stay phases that were in directions opposite to the auditory perturbations. However, the small extent of the changes didn’t reach the threshold for statistical significance (F(3,57)=1.73, p=0.18).

For the two diphthongs ∕ia∕ and ∕au∕, the generalization of the adaptation in F1Max from the training vowel ∕iau∕ was significant when between-group differences were examined (Group×Phase interaction: F(3,57)=3.82, p<0.05for ∕ia∕; F(3,57)=4.80, p<0.01for ∕au∕). Post-hoc t-tests revealed a significant between-group difference in the Stay phase for both vowels, but a significant difference in the early End phase for ∕au∕ only [Figs. 9F, 9G]. But this generalization in the diphthongs was not sufficiently strong to reach statistical significance under the more stringent within-group, between-phase comparisons in all cases. The diphthong ∕ia∕ did not show significant between-phase changes [Fig. 9F]; and ∕au∕ showed significant between-phase change only in the Inflate group. These results indicate that when between-group difference was considered, generalization of the F1Max adaptation did occur for the diphthongs ∕ia∕ and ∕au∕, unlike for ∕a/, which didn’t show significant generalization.

A noteworthy aspect of the generalization is that the patterns of change in the average F1 trajectories of the diphthongs ∕ia∕ and ∕au∕ [Figs. 9F, 9G] were very similar to the pattern of change in triphthong ∕iau∕’s F1 trajectory [Figs. 9A, 9B]. The Start-to-Stay changes in the low F1 value near the beginnings of ∕iau∕ and ∕ia∕ were both small, while the changes at the peak F1 were the greatest for both the vowels. Similarly, both ∕iau∕ and ∕au∕ showed minimal changes in F1 near the end of the vowels, and showed greatest changes around the peak F1. Therefore it appears that the detailed spatiotemporal articulatory pattern of adaptation was transferred from the triphthong to the diphthongs with considerable fidelity.

As observed above, the formant trajectory of the triphthong ∕iou∕ had a similar curved shape as that of ∕iau∕, but the magnitude of F1 was much smaller in ∕iou∕ than in ∕iau∕. In Fig. 9H, it can be seen that the generalization to the triphthong ∕iou∕ was smallest in absolute magnitude among all the test vowels. This vowel failed to show a significant Group×Phase interaction(p>0.25). Significant between-phase change was observed only in the Inflate group [Fig. 9H].

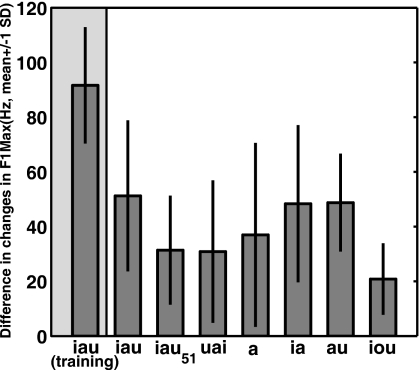
In order to better visualize the pattern of generalization to the seven test vowels, the difference in the changes in F1Max between the two groups, a measure of the strength of generalization, are shown in Fig. 10, along with the data from the training vowel ∕iau∕ (the left most column). It can be seen that the amount of generalization was not uniform across different test vowels. Not surprisingly, the test vowel that demonstrated the greatest transfer was the same triphthong ∕iau∕ as the training vowel. This was followed by the diphthongs ∕au∕ and ∕ia∕, which have formant trajectories very similar to the lower and upper halves of the trajectory of ∕iau∕ in the F1-F2 plane. The transfer from the triphthong to diphthongs indicated that generalization does occur across the boundaries of time-varying vowels with different numbers of serial components, given that the trajectories overlap substantially in the formant space. In comparison with the diphthongs, the transfer from the triphthong to the monophthong ∕a/ was much weaker, despite the fact that the F1Max of ∕a/ was very similar to that of the diphthong ∕ia∕. It can be inferred from this pattern of generalization that increasing dissimilarity in the number of serial components contained by a vowel (1 for monophthongs, 2 for diphthongs, and 3 for triphthongs) leads to weaker generalization of the adaptation. In addition to the number of serial components, the failure to observe that generalization to the triphthong ∕uai∕ indicated that the serial order of the components in a time-varying vowel also plays a role in determining the strength of generalization. It may be inferred that the more dissimilar the serial orders are, the weaker the generalization will be. The especially weak generalization from ∕iau∕ to ∕iou∕ indicates that the generalization also decays with increasing distance in the formant space.

Figure 10.

Quantification of transfer of the adaption to the test vowels. Each bars shows the difference between the Inflate and Deflate group in the changes in F1Max from the Start-phase baseline to the Stay-phase value. From left to right are the results for the training vowel ∕iau∕ (leftmost column) and the seven test vowels.

DISCUSSION

In this study, we imposed time-varying perturbations to speakers’ auditory feedback of the trajectory of F1 in the Mandarin triphthong ∕iau∕ and observed that, after sustained exposure to this perturbation, subjects altered their productions in ways which specifically and partially canceled the auditory perturbation. These observations support the hypothesis that, as with the quasi-static formant trajectories in monophthongs (Houde and Jordan, 1998, 2002; Purcell and Munhall, 2006a; Villacorta et al., 2007), auditory feedback plays an important role in the planning of articulatory gestures involved in producing time-varying formant trajectories. In addition, the compensatory adjustments to the F1 trajectory of the triphthong ∕iau∕ generalized to some other vowels which had not been subject to auditory perturbations. The pattern of generalization was examined in detail. It was found that the generalization showed a weak and decaying pattern with respect to the spatial and temporal similarities between the training vowel and the test vowels. In the following, we discuss the implications of the adaptation and generalization findings.

Compensatory responses

The compensatory responses observed for the Mandarin triphthong, ∕iau∕, in the current study, namely the production changes that partially counteracted the auditory perturbations and the significant but decaying after-effects that followed the cessation of the perturbation, were qualitatively similar to the compensatory changes observed on English monophthongs in earlier formant perturbation studies (Houde and Jordan, 2002; Purcell and Munhall, 2006a; Villacorta et al., 2007; Munhall et al., 2009). The current study is the first demonstration of the role of auditory feedback in the planning of time-varying articulatory gestures, thus generalizing these previous findings to time-varying segments of speech. In the task-dynamics model of Saltzman and Munhall (1989), articulatory trajectories were hypothesized to be formed through temporal patterning of a set of tract-variables. These tract-variable parameters emphasized goals in terms of the biomechanical∕somatosensory configuration of the vocal tract, and did not explicitly address the role of auditory goals or auditory feedback in the planning of articulatory gestures. The results of the current study argue that, even within a time-varying articulatory gesture, auditory feedback plays a significant role in the calibration and adaptation of articulatory movements. This indicates that tract-variable parameters as posited in the task-dynamics framework cannot be “fixed;” instead, they would have to be modifiable in order to reduce errors in the auditory domain in face of perturbed auditory feedback. These findings lend further support to the hypothesis that the primary goals for articulatory movement planning, at least for vowels, reside in the auditory domain (Guenther et al., 1998, 1999, 2006)

Similar to previous observations made for English monopthongs, the magnitude of the compensatory responses varied substantially across subjects in the current study. While the majority (∼60%) of subjects showed statistically significant compensatory responses, a small fraction of the remaining subjects showed production changes that followed the direction of the perturbations. The fraction of the significant “following” subjects in our study was 5 out of 36 (i.e., 14%, Fig. 7), which is slightly higher than the proportion observed in the monophthong studies (e.g., 2 of 20 in Villacorta et al., 2007; 1 of 18 in the “naïve” group of Munhall et al., 2009). A related observation is that the mean fraction of the auditory perturbation canceled by the compensatory adjustment to the production was lower in the current study (about 16% for both Inflate and Deflate perturbations) than in the monophthong studies, which ranged from about 40% (Villacorta et al., 2007) to 54% (Houde and Jordan, 2002).

There are a few possible explanations for these weaker compensatory responses for the Mandarin triphthong. First, since we are aware of no previous study on formant perturbation during the production of Mandarin monophthongs, it cannot be ruled out that the auditory feedback control system is engaged to a lesser degree in Mandarin speakers than in English speakers. This is not unlikely given that the vowel space is not as crowded in Mandarin, with its seven monophthongs, as it is in English, which has about 10 monophthongs. For example, a previous study (Perkell et al., 2001) showed that in Spanish, a language with only five monophthongs, the distance among the vowels in the formant spaces were significantly greater than in English. It is possible that auditory goal regions (Guenther, 1995; Guenther et al., 1998) for individual vowels are larger (i.e., less stringent) in Mandarin than in English, due to the less crowded vowel space. Hence, it may be the case that the same amount of perturbation would induce a smaller auditory error signal and a smaller compensatory change in production of Mandarin.

A second possible explanation for the weaker compensation observed in the triphthong ∕iau∕ is that time-varying articulatory gestures may be inherently less dependent on auditory feedback than quasi-static gestures as used in the previous monophthong studies. In the framework of the DIVA model (Guenther et al., 2006), the somatosensory feedback system also plays a role in the online control of articulation and in the error-based updating of the articulatory commands. Empirical evidence has been found for the role of proprioceptive feedback in planning articulatory movements (Tremblay et al., 2003, 2008; Nasir and Ostry, 2008). Production of the triphthong ∕iau∕ involves movements of the jaw, tongue and lips. During such articulatory movements, both positional and velocity information is available from the discharge of the muscle afferents of the oral facial muscles, whereas during prolonged monophthongs, only static positional information is supplied to the central nervous system. It is possible that the feedback system adaptively adjust the weights for the auditory and somatosensory subsystems according to the relative amount of afferent information coming through the two sensory modalities in order to optimize its performance. This interpretation appears to be consistent with the results from a recent study (Larson et al., 2008); the magnitude of an online compensatory response to auditory F0 perturbations was greater when the surface somatosensation of the vocal folds was blocked by lidocaine than under normal kinesthesia.

Response specificity

The observed pattern of compensation was specific to the perturbed auditory parameter. There are two aspects of this specificity. First, subjects responded to the auditory perturbations with corrections to the trajectory of F1 that reflected the non-uniformity of the perturbation fields in F1×F2 space. Corrections to F1Max (i.e., F1 of ∕a/) were much greater than corrections to F1 at the beginning and end of the triphthong (Fig. 5). However, there were small but appreciable changes in F1 near the two end points of ∕iau∕. For example, in the Inflate group [Figs. 5A, 6D], it can be seen that F1End (near ∕u/) was slightly decreased in the Stay phase with respect to the Start phase; also, in the Deflate group [Figs. 5C, 6C], F1Begin (near ∕i/) was increased slightly in the Stay phase. These small exceptions to the spatial specificity of the compensation may reflect incomplete sensorimotor learning, or they may be due to an interplay between efforts to minimize auditory error and economy of effort. In the DIVA model (Guenther et al., 2006), the auditory goal regions are hypothesized to be time-varying multidimensional regions, rather than point targets. This implementation of goal regions enables the DIVA model to predict widely observed phenomena in speech motor control such as anticipatory coarticulation (Guenther, 1995). This hypothesis is also consistent with the positive cross-subject correlation between auditory acuity to formant frequency differences and the strength of auditory-motor adaptation found by Villacorta et al. (2007). According to the finite-width goal region hypothesis, during adaptation to non-uniform perturbation fields, F1 values for ∕i/ and ∕u/ have some room for variation without causing auditory errors. Since a greater extent of F1 movements would correspond to larger articulatory movements, the control system may have exploited the width of the target regions to conserve effort during the compensatory adjustments, which could explain the observed small changes in F1Begin and F1End.

The second aspect of the specificity of the compensatory responses concerns the fact that no significant changes occurred to the F2 trajectories [Figs. 5B, 5D]. The compensatory adjustments to the F1 trajectory are likely to have involved modifications of the movement trajectories of the jaw, tongue and possibly also lips, all of which would have affected the values of F2 (c.f. the F2 changes concomitant to F1 corrections reported by Purcell and Munhall, 2006b). Therefore, it is noteworthy that the system maintained unchanged values of F2 (the unperturbed parameter) with high precision during this process. This formant specificity was consistent with the perturbation-specific compensatory responses shown by previous monophthong adaptation studies (Houde and Jordan, 2002; Villacorta et al., 2007).

Generalization to unperturbed sounds

In our analyses of the generalization patterns, it was observed that transfer of the adaptation to even the same triphthong (∕iau∕) under masked auditory feedback was incomplete and reached statistical significance only under between-group comparisons. As the first two columns of Fig. 10 show, the F1Max correction in the test vowel ∕iau∕ was only about 56% of that in the training vowel ∕iau∕. Similar partial generalization to the training vowel as produced under auditory masking was reported previously (Houde and Jordan, 2002; Villacorta et al., 2007). Houde and Jordan (2002) showed that while the compensation in F1 and F2 of the monophthong ∕ɛ∕ was 54% with auditory feedback, the compensation of the same vowel was only 35% without feedback, which amounted to a transfer ratio of 65%. Villacorta et al. (2007) also showed partial (∼50%) generalization to the same vowel under noise masking (c.f. their Figs. 34, p. 2310). In this regard, the same-vowel transfer ratios found in the current study are consistent with the ones found previously. As Houde and Jordan (2002) pointed out, this partial transfer may reflect the absence of a contribution from an online, closed-loop auditory feedback-mediated control system, which could not function under masking. The function of such a system was demonstrated by the previously cited studies that unexpectedly perturbed the same English monophthong (Purcell and Munhall, 2006b; Tourville et al., 2008).

However, it is also noteworthy that the fraction of the online compensation shown previously (just 3%–7% at 300 ms after the onset of the perturbation in Purcell and Munhall, 2006b; Tourville et al., 2008) was much smaller than would be needed to make up for the mismatch between the compensation with and without auditory feedback (54%−35%=19%, Houde and Jordan 2002). Therefore it is likely that additional factors contribute to the incompleteness of the transfer. Perkell et al. (2007) showed that under low signal-to-noise ratio caused by high-level masking noise, English speakers reduce their average vowel spacing. Therefore one possible factor is an effect of the high-level masking noise used in the current and previous studies to block feedback.

This incomplete transfer of the adaptation from non-masked to the masked condition may be a potential confound in interpreting pattern of generalization to the test vowels. But this potential confound is more likely to cause an underestimation of the generalization than an overestimation. Indeed, none of the test vowels showed generalization that was strong enough to reach statistical significance under the between-group comparison and the within-group comparisons in both groups. However, the fact that a test vowels (∕au∕) showed significant generalization under the between-group comparison and under the within-group comparison in at least one of the two groups indicates that generalization did occur on certain test vowels. In addition, the pattern of the relative strength of generalization should be less affected by this potential confound.

We observed a rather broad pattern of generalization to untrained, test vowels. In fact, for all the test vowels, the average trends were consistently for the Inflate group to decrease F1Max and for the Deflate group to increase it in the Stay phase (Fig. 9). Analyses of variance showed that this broad generalization was significant under the between-group contrast, despite the fact that post hoc analysis on some individual test vowels failed to reach significance.

The non-uniformity of the pattern of generalization is indicated by the observation that only a subset of the test vowels (∕ia∕ and ∕au∕) demonstrated statistically significant transfer. Among the test vowels, ∕ia∕ and ∕au∕, along with the training vowel ∕iau∕, showed the greatest transfer of adaptation (Fig. 10). This was followed by ∕a/, a monophthong close to the center of the perturbation field. The temporally reversed triphthong ∕uai∕ and different-tone triphthong ∕ iau₅₁∕ showed the next strongest transfer, while the triphthong ∕iou∕ showed the least amount of generalization. The following set of proximity rules for the generalization can be inferred from these observations:

• (1)Dissimilarity of formant velocities (as opposed to position in formant space) leads to reduced strength of generalization, supported by the stronger generalization to the diphthongs ∕ia∕ and ∕au∕ than to the monophthong ∕a/ and the reverse triphthong ∕uai∕.
• (2)Generalization is negatively related to distance in the formant space, as indicated by the very weak transfer to ∕iou∕.
• (3)Tone difference also weakens the generalization (c.f. ∕ iau₅₁∕).

Further comments are warranted with respect to rule (1) above. Although the generalization pattern reveals a partially shared auditory-to-motor mapping between the triphthong, diphthongs and monophthong, the incompleteness of the generalization from ∕iau∕ to the diphthongs and the monophthong indicate that the formant trajectory in the triphthong ∕iau∕ cannot be viewed as a straightforward concatenation of the trajectories of ∕ia∕ and ∕au∕, nor as a simple traversing of the monophthongs ∕i/, ∕a/ and ∕u/. In other words, the articulatory trajectory of ∕iau∕ appears not be planned piece-by-piece in the temporal domain, but done in a more holistic fashion. This idea mirrors theories of limb motor control in which movement trajectories are planned as a whole (e.g., Flash and Hogan, 1985). In addition to this specificity to serial order and velocity, rule (3) above also indicates that control of speech movements is specific to the tonal context, and is not based on a more general mappings between auditory targets and articulation.

The broad but decaying pattern of generalization (within a tonal category) indicates that the auditory-to-motor transformation used by the auditory feedback control system does not encode different vowels as separate entities. Otherwise the auditory-based error correction of movements for one vowel would not have affected the production of different vowels. We can infer that vowels with different serial and spectral properties must share some aspect of the mechanism responsible for computing articulatory trajectories from the auditory target, such that modification of the mapping for one vowel leads to substantial changes in the articulatory programming for other vowels. Similar patterns of generalization have been observed previously in visuomotor adaptation (Bedford, 1993; Ghahramani et al., 1996; Vetter et al., 1999). The current version of the DIVA model (Guenther et al., 2006) treats different utterances as separate entities in a “look-up-table” structure which stores the feedforward articulatory commands for different vowels separately and hence cannot account for the generalization of auditory-motor adaptation across different vowels. Future iterations of the model will need to allow prediction of the generalization patterns observed in Houde and Jordan (1998), Villacorta et al. (2007), and the current study.

The generalization pattern observed in the current study may be also comparable to the visuomotor rotation adaptation reported by Krakauer et al. (2000). The generalization of visuomotor rotational adaptation observed in that study was broadly decaying with increasing angular difference with respect to the trained direction. The Inflate and Deflate perturbations used in the current study may be considered as auditory-motor “rotations” in the two-dimensional formant plane. For example, the Inflate perturbation can be seen as a counterclockwise rotation between ∕i/ and ∕a/, followed by a clockwise rotation between ∕a/ and ∕u/ [see Fig. 3B]. The test vowels (∕ia∕, ∕au∕, ∕uai∕ and ∕iou∕) can be seen as trajectories with directions different from the trained directions of formant movements in ∕iau∕. While the differences in directions were quite small between ∕iau∕ and the two diphthongs (∕ia∕ and ∕au∕), the directions were very dissimilar between ∕iau∕ and the other test vowels, including ∕uai∕ and ∕iou∕ (Fig. 8). Interestingly, the generalization to ∕ia∕ and ∕au∕ was greater than the generalization to ∕uai∕ and ∕iou∕, a result similar to the finding of Krakauer and colleagues in the visuomotor domain. Therefore it appears that 1) F1 and F2 movements in the formant plane during time-varying vowels are analogous to 2-dimensiontal end-effector movements in limb reaching; and 2) the visuomotor and the auditory-motor systems obey similar sets of rules when generalizing adaptations to rotational perturbations in their respective task spaces.

Indeed, there appear to be many similarities between the auditory-motor system for speech production and the visuomotor system for reaching and pointing movements. Both systems have many degrees of freedom in their controlled effector systems, and both are goal-directed, in that the commands to the effectors need to be finely programmed in order for the end-effector to reach desired sensory goal regions. In the case of the visuomotor system, the end-effector is usually the hand or an object manipulated by the hand, which needs to be directed precisely to a small target zone in two- or three-dimensional space defined in terms of visual coordinates. In the speech system, the “end-effectors” are the set of independently controllable articulatory parameters with acoustic consequences. The target zones are specified as time-varying regions in the multidimensional space defined by those acoustic parameters (Guenther, 1995; Guenther et al., 2006). In other words, as indicated by the theoretical and experimental speech studies reviewed above, articulatory movements are controlled in such a way as to achieve targets defined in auditory perceptual space. It may also be noted that the speech motor compensations in response to altered auditory trajectory feedback found in the current study is very similar in form to the limb motor compensations induced by visual trajectory perturbations found by Wolpert et al. (1995). Considering the above-mentioned similarities between the speech and reaching systems, useful insights might be gained by comparing the properties of the two systems (see for example Guenther et al., 1998).

Finally, it is noteworthy that a previous study of adaptation to mechanical (somatosensory) perturbations (Tremblay et al., 2008) observed generalization patterns there were very different from results of the current study and previous ones (Houde, 1997; Villacorta et al., 2007). Tremblay and colleagues introduced perturbation of horizontal displacement to the jaw during the jaw lowering movement in the utterance ∕siæs∕ without introducing any observable concomitant changes in the acoustic formant frequencies. Nearly complete compensatory adjustment in jaw movement trajectory was observed after training; a negative after-effect was seen after the cessation of the force perturbation. However, no after-effect was observed in a test utterance with different vowels but the same jaw movement trajectory ∕suæs∕ or in another test utterance (∕siæis∕) with only one added vowel. There are several possible explanations for the discrepant generalization patterns observed by in the current study and by Tremblay et al. First, it cannot be ruled out that different experimental designs could have led to the different generalization patterns. While the test and training utterances were interleaved throughout the entire experiment in our study, Tremblay and colleagues used a paradigm in which the test stimuli were not presented during the training phase, but only given after the completion of the training. The absence of generalization of the adaptation may be attributable to the fact that the horizontal movement profile of the jaw has little effect on acoustic outcome of articulation, and has a relatively low-level supporting role in relation to the acoustically important movements of the tongue. Pile et al. (2007) studied the generalization of auditory-motor adaptation across different vowels using a design similar to that of Tremblay et al. (2008) and observed no generalization from the vowel ∕ɛ∕ to ∕ɪ∕ and ∕e/. This discrepancy with the current study may be attributable to the interleaving of training and test stimuli in the current study, or to the fact that the current study employed multiple utterances that contained the training vowel (see Table 1), whereas Pile and colleagues used only one training utterance. The issues related to the effects of experimental paradigm on generalization of the sensorimotor adaptations in speech movements remain to be resolved by future studies.

CONCLUSIONS

The results of the current study demonstrate that when producing time-varying formant trajectories in the Mandarin triphthong ∕iau∕, speakers on average made significant but incomplete compensatory adjustments to their productions in response to a perturbation to the F1 trajectory in their auditory feedback. The compensations were specific to the perturbed formant and conformed to the time-varying characteristics of the perturbation. These findings further elucidate the important role of auditory feedback in the planning of complex time-varying articulatory gestures. In addition, we observed that adaptation was generalized relatively weakly and in a broad and decaying fashion to untrained vowels, shedding new light on the internal organization of the auditory-to-motor transformation performed by the speech system.