Auditory spectral integration in the perception of diphthongal vowels

Abstract

This study considers an operation of an auditory spectral integration process which may be involved in perceiving dynamic time-varying changes in speech found in diphthongs and glide-type transitions. Does the auditory system need explicit vowel formants to track the dynamic changes over time? Listeners classified diphthongs on the basis of a moving center of gravity (COG) brought about by changing intensity ratio of static spectral components instead of changing an F2. Listeners were unable to detect COG movement only when the F2 change was small (160 Hz) or when the separation between the static components was large (4.95 bark).

INTRODUCTION

Formant frequencies are undeniably a primary determinant of vowel identity, as shown in experimental and modeling efforts over the past fifty years (see Bladon and Lindblom, 1981; Ito et al., 2001; Hillenbrand and Houde, 2003, for reviews of formant theory). However, a widely recognized complication with formant representation involves tracking individual formants in highly variable natural speech, which Hillenbrand and Houde (2003) call “the unresolved and quite possibly unresolvable problem” (p. 1045).

Today, the nature of the underlying auditory mechanisms and processes responsible for extracting and processing the acoustic cues for formants in the identification of vowels still awaits explanation. Recognizing the complexity of auditory processing of speech signals, this study considers an operation of an auditory spectral integration mechanism which may be involved in perceiving dynamic time-varying changes in speech sounds like those found in diphthongs and glide-type transitions.

The recurring interest in auditory integration mechanisms (e.g., Assmann, 1991; Beddor and Hawkins, 1990; Xu et al., 2004) acknowledges the limitations of formant theory in vowel perception, especially in relation to the levels of auditory phonetic processing. Although the path from the initial output of auditory periphery to the highest levels of neural patterns is complex, a summation (or integration) of spectral information at more central levels of auditory processing is highly plausible. One early proposal that addressed such possibility in speech was the center of gravity (COG) hypothesis advanced by Chistovich and her colleagues (e.g., Chistovich and Lublinskaja, 1979; Chistovich et al., 1979). It was proposed that, within the integration bandwidth of about 3.5 bark, the changes to the relative amplitude ratios between two closely spaced formants of a static vowel affected their combined spectral COG (i.e., the equivalent of its perceived formant frequency). Listeners were sensitive to COG changes when two formants were close enough in frequency to allow spectral integration. The COG effect ceased when the frequency separation was larger than 3.5 bark.

Although this proposal encountered numerous criticisms, it suggested the possibility that formant frequencies are not paramount in phonetic processing and that the auditory system also uses other spectral cues such as proximity of formants and their amplitudes (including amplitude ratios) in processing sound energy distributed across the frequency domain. The COG effect suggested an increased sensitivity to formant amplitude ratios when the formants were close in frequency so that it was the combined energy in this part of the spectrum and not individual formants to which the auditory system was hypothesized to attend in making phonetic quality decisions. In a subsequent experiment, Lublinskaja (1996) showed that systematically modifying only the amplitude ratios of two formants over time induces listeners to hear a glide-like transition that follows the dynamically changing COG.

The present study extends this research and examines the integration of spectral components other than formants in listeners’ classification of vowels. That is, given the dynamic character of speech, does the auditory system need formants exclusively to track the dynamic information over time? This study is also an extension of an earlier work which found that a dynamically changing COG can be used as a cue to place distinction in stop consonants in syllables ∕da∕-/ga∕ and ∕ta∕-/ka∕ (Fox et al., 2008). The COG movement simulated a brief 50-ms consonant-vowel F3 transition whose direction (rising or falling) led to the percept of velar and alveolar stop, respectively. The COG change in this short transition affected the percept of a stop consonant (and not the vowel) and it occurred regardless of whether the stop was voiced or voiceless. The dynamic COG movement in the diphthongal vowels in the present experiment is longer (150 ms) and a combination of longer signal duration and variable extent of a diphthongal rise or fall may unveil further details about the auditory spectral integration. It is important to examine these effects before drawing firmer conclusions as to their potential role in speech processing.

METHODS

Listeners classified tokens as either a diphthongal vowel ∕ui∕ (upward F2 glide), ∕iu∕ (downward F2 glide) or a stationary F2 ∕i/ or ∕u/. The experiment used two types of synthetic vowel-like signals which manipulated (1) F2 frequency or (2) the intensity ratio (i.e., the spectral COG) of two pairs of sine waves which replaced F2. The question was whether listeners can form the percept of an F2 on the basis of intensity weighting across the sine waves, responding to their spectral COG.

The stimuli for the first type of signals were three-formant synthetic series created using HLSyn (.kld option, parallel synthesis). The F0 was set at 160 Hz (appropriate for a low female voice) and the duration of each token was 150 ms (on- and off-ramped over 20 ms). F2 onsets and offsets were manipulated while F1 and F3 were held constant at 350 and 3200 Hz, respectively. F2 onset and offset frequencies were either 1920, 2080, 2240, 2400 or 2560 Hz (increased or decreased in 160-Hz steps). There were 10 stimuli for the upward F2 glide ∕ui∕ whose offsets were either 160, 320, 480 or 640 Hz higher in frequency than the onsets (creating differences in F2 rise: 4 offsets at 1920 Hz-onset, 3 offsets at 2080-Hz onset, 2 offsets at 2240-Hz onset, 1 offset at 2400-Hz onset) and 10 stimuli for the downward F2 glide ∕iu∕ (4 offsets at 2560-Hz onset, 3 offsets at 2400 Hz-onset, 2 offsets at 2240-Hz onset, 1 offset at 2080 Hz-onset). In addition, five stationary vowels were created whose F2 was either 1920, 2080, 2240, 2400 or 2560 (the lower end point corresponded to an ∕u/ and the higher end point to an ∕i/). The formant synthesizer’s values for the bandwidths of the three formants were set at 80, 100 and 150 Hz, respectively and their amplitudes were set at 60 dB, respectively.

Next, from this original series three additional series were created in which F1 and F3 remained intact and F2 was “removed” from the signal by setting the amplitude of F2 to zero. This two-formant series was used as the base for the creation of the second type of stimuli, which we call here “virtual F2” tokens. The virtual F2 was constructed by adding to the base two pairs of steady-state sine waves, lower and higher in frequency than the removed F2 whose frequencies were whole-numbered multiples of the F0. The decision to use pairs of sine waves rather than single sine waves was based on informal listening to the stimuli (tone pairs produced a more natural-sounding synthetic vowel than did single tones). Table 1 lists the frequencies of the sine waves along with their separations (in bark) which were either well within the 3.5 bark bandwidth in the first series (V1), a little above it in the second (V2) and largely exceeded it in the third (V3).

Table 1.

Frequencies of individual sine waves, their means (MF) and intensity ratios in creation of “virtual F2” series. For each virtual F2 frequency (either upward glide, downward glide or steady-state), the intensity ratios of MF corresponded to the spectral COG which matched the frequency of F2. The intensity values of the glide were changed linearly between the end points to match the changing F2 frequency in the actual F2 series.

Virtual stimulus series	Bark∕ERB difference	Sine wave pair (lower∕higher) (Hz)	Mean frequency of the pair (Hz)	Virtual F2 frequency (COG) and the corresponding intensity ratio
				1920	2080	2240	2400	2560
		L: 1760 1920	1840	0.900	0.700	0.500	0.300	0.100
V1	2.90∕3.62	H: 2560 2720	2640	0.100	0.300	0.500	0.700	0.900
		L: 1600 1760	1650	0.714	0.571	0.429	0.286	0.143
V2	3.90∕4.88	H: 2720 2880	2800	0.286	0.429	0.571	0.714	0.857
		L: 1440 1600	1520	0.667	0.556	0.444	0.333	0.222
V3	4.95∕6.19	H: 2880 3040	2960	0.333	0.444	0.556	0.667	0.778

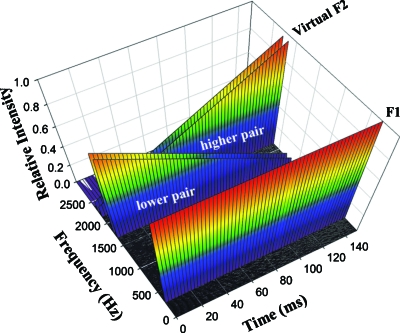
The rise or fall of the virtual F2 producing the percepts of ∕ui∕ or ∕iu∕ was created by dynamically modifying the intensity ratios of the inserted sine waves. The intensity ratios were selected to match the spectral mean (or COG) of the composite which was computed as an intensity-weighted average of the center frequencies of the sine wave pairs. The COG followed the actual F2 changes (over the entire 150 ms signal duration) in the original three-formant synthetic series. For each glide series, the intensity ratios in the course of a glide changed linearly between the end points (onset and offset), thus changing the spectral COG of the composite over time. Table 1 provides further details and Fig. 1 shows a schematic of a virtual F2 token. For the stationary virtual F2 stimuli (∕i/ or ∕u/), the intensity ratio for each virtual series listed in Table 1 was held constant, i.e., did not change linearly between the end points.

Figure 1.

Schematic of a rising virtual F2 glide producing the percept of /ui/. The frequencies of each pair of sine waves remained unchanged throughout the duration of the token. The virtual F2 glide was produced by changing the intensity ratio of the two pairs of sine waves (see Table 1 for more details).

The stimuli were presented diotically via Sennheiser HD600 headphones at a comfortable listening level to a participant seated in sound-attenuated booth. A single-interval 4AFC identification task was used. Listeners were instructed to identify each sound by clicking on one of the four response choices ∕i/ “ee,” ∕u/ “oo,” ∕iu∕ “you” and ∕ui∕ “we” displayed on the computer monitor. They were told that the stimuli varied in their sound quality and some of them would sound more “synthetic” than others. At the beginning of testing, they were given a 20-item practice on the use of the interface and for familiarization with the types of stimuli to ensure they can perform the task. Listeners were tested in two sessions, responding to 300 trials in one session for a total of 600 (25 stimuli consisting of 10 with rising F2, 10 with falling F2 and 5 with stationary F2×4 sets×3 repetitions×2 sessions). The three-formant stimuli and the three virtual F2 series were randomized and presented in the same run. There were 14 listeners (19–28 years old). All were native speakers of American English and students in the Department of Speech and Hearing Science at The Ohio State University. They had pure-tone thresholds better than 15-dB HL at octave frequencies from 250 Hz to 8000 Hz in both ears.

RESULTS

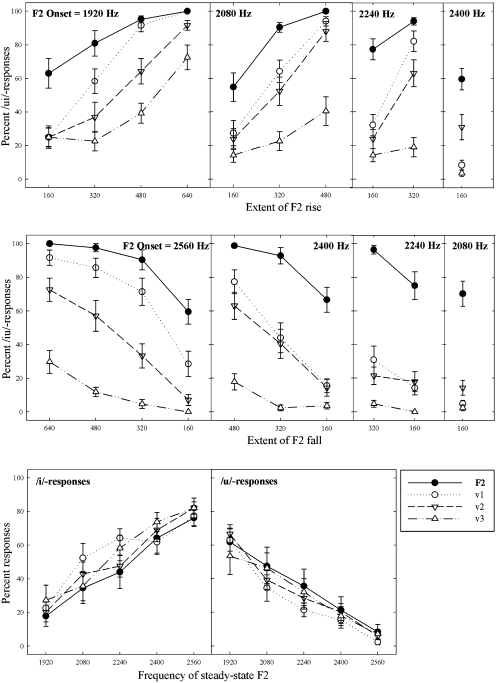
Four different scores were computed: percent ∕ui∕-responses, percent ∕iu∕-responses, and percent stationary ∕i/- and ∕u/-responses. The mean values for these scores are shown in Fig. 2 as a function of the extent of the F2 rise (top), F2 fall (middle) and steady-state F2 (bottom). The scores are plotted for the four series: the original (actual F2) and three virtual F2 series (V1, V2, V3). The results for ∕ui∕ in the actual F2 series show classification scores at the ceiling for the largest F2 rises of 640 and 480 Hz, somewhat lower for the 320-Hz rise, and the lowest for the 160-Hz rise, indicating that the greater the extent of F2 change the higher the classification rate. The responses to the virtual F2 series followed this general pattern although the scores were lower and decreased with each larger separation between the sine wave pairs. However, despite the general reduction of expected responses, listeners were still able to integrate even widely separated acoustic components, most clearly for the greatest extent of F2 change. As for the smallest F2 rise (160 Hz), the percentage of ∕ui∕-responses was below 20% for all virtual glide series, indicating that listeners were unable to track accurately the COG movement, hearing mostly a stationary vowel rather than a glide.

Figure 2.

Classifications of rising F2 glides as ∕ui∕ (top panels), falling F2 glides as ∕ui∕ (middle panels) and steady-state tokens as ∕i∕ and ∕u∕ (bottom panels). Shown are mean responses (with standard errors) to actual F2 series (F2) and to three virtual F2 series in which frequency separation between the two sine wave pairs differed (V1=2.9 bark, V2=3.9 bark, and V3=4.95 bark). The panels display separately the responses for each actual and virtual F2 onset for the rising∕falling glide and for frequency of steady-state F2.

The results for ∕iu∕ are generally in accord with those for ∕ui∕ for the actual F2 tokens. However, for the virtual F2 series, the low scores for the largest separation between the sine waves (V3) and for the F2 onset at 2240 Hz indicate that listeners failed to integrate the spectral components in these testing conditions. Consistent with their responses to the rising glide, the smallest 160-Hz fall yielded mostly ∕u/-responses, indicating that listeners were unable to track the COG movement. ANOVA results verified that the differences arising from the extent of F2 rise (or fall) and F2 stimulus type were significant for each onset condition. For each analysis, the main effect of either F2 extent or stimulus type was significant at the 0.001 level showing a large effect size as evidenced by the high partial eta squared (η²) values summarized in Table 2. The interactions between the two factors were mostly significant although the effect sizes were much smaller (η²values ranged from 0.260 to 0.442). Comparing the results for the steady-state tokens with those for the glides, we find that the classifications of the virtual F2 tokens as either ∕i/ or ∕u/ did not generally change with increased frequency separation between the sine waves. Consequently, the main effect of stimulus type was not significant for either ∕i/ or ∕u/. This suggests that, for steady-state signals, the integration bandwidth may be larger than for dynamically changing sounds. However, there was a significant effect of F2 frequency for ∕i/ (F(4,52)=43.47, p<0.001, η²=0.770) and for ∕u/(F(4,52)=56.98, p<0.001, η²=0.814), verifying that, with higher F2 values, identifications as ∕i/ generally increased and identifications as ∕u/ decreased.

Table 2.

Summary of significant main effects of stimulus type and F2 extent for each onset condition from repeated measures ANOVAs. Shown are partial eta squared values(η²).

	∕ui∕-F2 onset				∕iu∕-F2 onset
	1920	2080	2240	2400	2560	2400	2240	2080
Stimulus type	0.634	0.712	0.770	0.694	0.874	0.841	0.863	0.791
F2 extent	0.875	0.839	0.816	-	0.903	0.826	0.658	-

DISCUSSION

Overall, listeners responded well to a movement of spectral COG (upward and downward) when it corresponded to a large F2 change (640 or 480 Hz) and when the frequency separation between the static spectral components (here: two pairs of sine waves) was relatively small (2.9 and 3.9 bark). They were unable to detect COG movement when the F2 change was small (160 Hz) or, especially for the falling glide, when the separation between the sine waves was large (4.95 bark). For all three virtual series, the number of classifications as a rising glide was greater than as a falling glide, a result similar to what Gordon and Poeppel (2002) found for detecting the direction of upward and downward FM sweeps. However, in the present study, this asymmetry was found only when listeners responded to the movement of the spectral COG and not to actual F2 changes.

The inclusion of the tokens with steady-state F2 allowed us to observe how well listeners responded to a spectral COG in forming a percept of static vowel as compared to their responses to the dynamic COG. The results show that while classifications as ∕i/, although somewhat lower in general, increased with each F2 frequency increase, classifications as ∕u/ were already low at the lowest F2 end point (1920 Hz), reaching only about 60%. This outcome may be expected given that the combination of formant frequencies at 350 Hz (F1) and 1920 Hz (F2) is already ambiguous for a native speaker of American English as an instance of the vowel ∕u/, whose F2 should be much lower, close to 1100–1200 Hz (compare Hillenbrand et al., 1995). This higher F2 did not match well with ∕u/ as one of the four response choices and listeners responded more often as hearing an ∕i/. Despite this ambiguity, however, it is important to note that the sound they reported hearing, either ∕u/ or ∕i/, was a steady-state vowel and not a glide. This suggests an operation of a common spectral integration mechanism which can be used to evoke a percept of a stationary sound or a glide.

This study used a restricted response set of four vowel choices rather than an open-set. It may be argued that the nature of the task made it impossible to determine that perception of the unaltered and virtual stimuli is qualitatively similar, particularly for the small extent of frequency rise of 160 Hz. However, the present results confirmed an earlier finding in Fox et al. (2008) where listeners’ classification of virtual formant transition as “rising” dropped to about 30% for two smallest rises of 265 and 159 Hz. For these small rises, listeners were unable to assign even a non-linguistic label “rising sound,” suggesting that a stationary sound was all they heard (and the responses to unaltered stimuli for these small rises were comparatively higher). As an extension of that study, the current experiment was not as much concerned with what the actual linguistic percept was in terms of vowel category but whether listeners were able to perceive a dynamic frequency change at all, given synthesis parameter specifications appropriate for either ∕ui∕ or ∕iu∕. A natural follow-up and elaboration of the current finding will be inclusion of unrestricted responses to several types of stimulus manipulations.

CONCLUSION

The main conclusion is that, for longer durations of 150 ms, listeners are able to attend to a change in the spectral COG in forming a gliding F2 percept. Otherwise, there is no explanation for why they heard a dynamic change if the frequency of spectral components was held constant. However, this effect is limited by both integration bandwidth and extent of spectral change. Within an integration bandwidth of about 3.9 Bark, intensity weighting contributed a cue which normally is attributed to the percept of a formant. However, no demonstrable integration effects were seen when COG movement corresponded to a small (160 Hz) F2 rise or fall. There was also only limited evidence for auditory integration when the frequency separation between the static spectral components was large (4.95 bark). This experiment demonstrates that changes in the frequency of a formant peak, per se, are not necessary to perceive a diphthongal change because auditory system can be flexible enough to use a variety of auditory cues. This implies that phonetic processing may be independent of the method used to elicit perception of frequency change. The occurrence of COG effects in synthetic signals, first noted in the late 1970s, seems to be a manifestation of an auditory spectral integration mechanism whose potential role in speech processing needs to be yet verified. This mechanism may be useful in estimating frequency from intensity of individual formants. At present, we have demonstrated that auditory system can form a percept of a speechlike diphthongal glide on the basis of changing intensity ratios of static components in the most relevant part of the spectrum.