Abstract
Color, lightness, and glossiness are perceptual attributes associated with object reflectance. For these perceptual representations to be useful, they must correlate with physical reflectance properties of objects, and not be overly affected by changes in illumination or the viewing context. Color and lightness constancy have received much attention in past investigations, but little is known about the perception of glossiness under changing lighting conditions. We employed a matching paradigm to investigate the perception of lightness and glossiness under geometric changes in illumination. Stimuli were computer simulations of scenes with spheres displayed on a high-dynamic-range display. Observers matched the specular and diffuse reflectance of a test sphere to match the appearance of a reference sphere simulated under a different light field. Observers were veridical in their diffuse component matches across geometric changes in light fields. In contrast, surface specularity was either overestimated or underestimated relative to the reference sphere depending on the light field comparison. The effect of changing light field geometry on perceived glossiness and lightness was independent of surface diffuse and specular reflectance and approximately independent of the roughness of the specular component. Luminance histogram statistics (standard deviation, skewness, kurtosis) were not good predictors of the specular component matches.
1 Introduction
Color, lightness, and glossiness are perceptual attributes associated with object reflectance. For these perceptual representations to be useful, they must correlate with physical reflectance properties of objects, and not be overly affected by changes in illumination or the viewing context provided by surrounding objects. Because the light reflected from objects to the eyes confounds reflectance and illumination, generating stable perceptual correlates of object reflectance is not trivial. Despite this difficulty, however, judgments of object color and lightness are known to exhibit considerable constancy across changes of illumination, at least for flat objects with matte reflectance (e.g., Brainard, 2004; Smithson, 2005; Shevell & Kingdom, 2008). Less is known about the constancy of other perceptual correlates of surface reflectance, such as glossiness, although this issue has recently begun to receive experimental attention (e.g., Nishida & Shinya, 1998; Fleming, Dror, & Adelson, 2003; Doerschner, Boyaci, & Maloney, 2010).
Object surface reflectance is characterized by the bidirectional reflectance distribution function (BRDF), which defines the amount and direction of light reflected from a surface as a function of the angles of the incoming and reflected light, relative to the surface normal. The BRDFs of natural surfaces can be quite complex (Oren & Nayar, 1994; Dana, van Ginneken, Nayar, & Koenderink, 1999; Alldrin, Zickler, & Kreigman, 2008). None-the-less, simple parametric models of the BRDF are widely used in computer graphics and capture salient features of the variation in object surface reflectance (e.g., Yu, Debevec, Malik, & Hawkins, 1999). In the work reported here, we will employ the isotropic Ward (1992) reflectance model. This model characterizes reflectance as the sum of a diffuse component and a specular component. Intuitively, the diffuse component describes how much light the object reflects in a non-directional fashion while the specular component describes the strength and spread of mirror-like reflection. Objects with purely diffuse reflection typically appear as matte, whereas objects with a strong specular reflection component are likely to be perceived as glossy.
The majority of studies on the perception of object color and lightness have considered the appearance of matte flat objects. For three-dimensional objects with both diffuse and specular reflectance components, there is considerably more richness in the relation between object reflectance, illumination, and the light reflected to the eye. In particular, because the specular component is directional, the geometric structure of the light field impinging on the object can have a large effect on the reflected light. In addition to overall variation in the intensity and spectrum of the illumination, this geometric structure varies from scene to scene (Debevec, 1998). This fact in turn raises the question of how well the visual system stabilizes object appearance across variation in the geometry of the light field and how this stabilization depends on the object BRDF. These are the broad questions we address in this paper.
As we seek to extend our understanding of object surface perception to the case of three-dimensional objects with realistic BRDFs viewed under geometrically complex lighting, we must manage the fact that the number of experimental conditions increases geometrically with the number of stimulus parameters. To make progress, it is useful to identify and test principles that allow measurements of a small number of stimulus configurations to predict what will happen for a large number of combinations. The focus of the experiments presented here is to test whether geometrical changes in illumination act independently on perceived object lightness and glossiness.
2 Methods
The purpose of this experiment was to measure how changing the geometrical structure of the light field affects the perceived glossiness and lightness of a three-dimensional object, across variations in both diffuse and specular components of the object’s reflectance. To this end, we employed an asymmetric matching procedure, in which the observer adjusted the reflectance of a test object seen under one light field so that its glossiness and lightness matched that of a reference object seen under a second light field. As a control condition, we also measured matches when the objects were seen under the same light field. As part of the experiment, we explored the effect of the complexity of the surrounding scene on the matches.
2.1 Observers
Three naive observers participated in the experiment. Observers VIL and BNW observed in all conditions, while observer MVI ran two out of three conditions. Visual acuity and stereo vision were assessed with the Keystone VS-II vision screener. Color vision was assessed with the Ishihara color plates. Uncorrected (VIL, MVI) or corrected (BNW) visual acuity was at least 20/20 for all observers. All observers had normal stereo acuity and normal color vision.
2.2 Stimuli
The test and reference objects were grayscale spheres; examples are shown in Figure 1. We used the isotropic Ward model to render spheres with different surface reflectance properties (Ward, 1992). In the model, surface reflectance is defined by three parameters: ρd controls the diffuse component (“albedo”), ρs controls the strength of the specular component (“glossiness”), and α controls the spread of the specular component (“roughness”). All scenes were rendered with the RenderToolbox package for Matlab (http://rendertoolbox.org). RenderToolbox acts as an interface to the RADIANCE rendering software (Ward, 1994), allowing scenes to be rendered independently at different monochromatic wavelengths (hyperspectral rendering). This ensures that the spectral interaction between illuminants and surfaces is simulated in a physically correct manner. This feature was not critical here because the stimuli were grayscale, but it remained convenient to use this software.
Figure 1.
Example stimuli rendered under the campus light field. A) Stimuli with the roughness parameter α set to 0.001. The two levels of diffuse reflectance are shown in rows, and the three specularities in columns. B) Stimuli with the same parameters for diffuse and specular reflectance, but with α set to 0.1. The images shown here were created as described in Methods, after which they were scaled, tone-mapped and gamma corrected so that they looked reasonable when viewed on a conventional display or in print. Images shown in subsequent figures were created similarly.
To provide spectral input to the RenderToolbox routines, the objects were assumed to have reflectance that did not vary with wavelength. We used two levels of diffuse reflectance (ρd = [0.15 0.35]) and three levels of specularity (ρs = [0 0.06 0.12]) for the reference stimuli. One set of spheres was rendered with a smooth specular component (α = 0.001), while another was rendered with a rough specular component (α = 0.1).
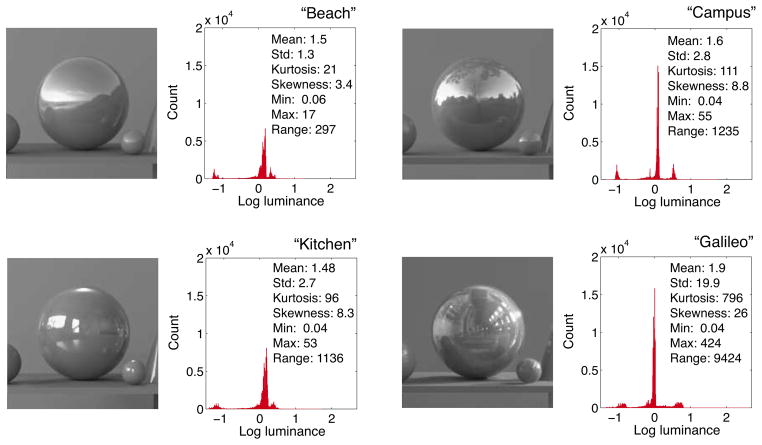
Stimuli were rendered under four real-world light fields measured by Debevec (1998). These are illustrated in Figure 3, which also shows luminance histograms for the image pixels corresponding to the sphere. We chose light fields measured both indoors and outdoors. The original light field measurements were reported in color, with separate values for nominal red, green, and blue (RGB) planes. To render the scenes spectrally within the RenderToolbox environment, the RGB light field images had to be converted to images that represented image intensity as a function of wavelength. This was done as follows. First, we converted the RGB values of the images at each pixel to XYZ values on the assumption that the RGB values represented linearized RGB primary intensities with respect to the sRGB standard (International Electrotechnical Comission, 1999). A three-dimensional linear model for surface reflectance, computed in our lab from measurements of 462 Munsell papers (Newhall, Nickerson, & Judd, 1943; Nickerson & Wilson, 1950; Nickerson, 1957), was then used to convert the XYZ values of each pixel to spectra. This was done by forming a 3 by 3 transformation matrix between XYZ values and linear model weights, using standard linear model methods (see e.g. Brainard, 1995). Spectra were produced by multiplying the basis functions by the obtained weights. This resulted in an n × m × 31 image for each light field, each plane corresponding to one wavelength band. The particular choice of linear model was not of deep theoretical significance and was motivated primarily by convenience; we currently know little about the spectral variation of real world light fields. For the current experiment, only the 500 nm band resulting from this process was used. This single plane was replicated to produce identical red, green, and blue image planes for display. Although the conversion to spectral light fields was not necessary here, we implemented it in preparation for planned future experiments where the spectral properties of the stimuli will be manipulated.
Figure 3.
The left hand images in each panel show a cutout of a scene rendered under the four different light fields used in this study. The histograms on the right from the images show the distribution of log luminances across the sphere. The insets list basic linear luminance statistics of the spheres.
For the observer to perform the matching task, we needed to rapidly render scenes containing spheres of different reflectances. Because re-rendering the entire scene using Radiance was too slow, we generated scenes containing spheres of different reflectances by adjusting and combining three pre-rendered basis images (Griffin, 1999; Xiao & Brainard, 2008). Each basis image contained a sphere, and across the three basis images the sphere varied in reflectance. One basis image contained a matte sphere, one a smooth glossy sphere and one a rough glossy sphere. By taking the difference between the glossy and matte basis images, we could extract a difference image that represented the effect of adding a specular component to the sphere’s reflectance. To generate stimuli with different levels of specularity, we then combined the matte sphere basis image with either the smooth or the rough difference image, and varied the weight on the difference image to simulate the effect of varying the strength of the specular component. To simulate different levels of diffuse reflectance, we extracted the image pixels corresponding to the sphere in the matte basis image, scaled these, and reinserted them. This was done prior to adding in the specular component. We verified that images rendered in this manner provided a good pixel-by-pixel approximation to directly rendered scenes. For the three light fields and two sphere specularities we checked, the mean pixelwise difference between generated and directly rendered images was at most 3% of the mean pixel value in the rendered image.
Two scene contexts were used. The spheres could either be embedded in the scene in which they were rendered (complex context), or against a simple checkerboard background (simple context). For each light field, the checkerboard background was created so that it had the same mean luminance and contrast as the corresponding complex background. A key difference between the two contexts is that the complex context was rendered using the same light field as its sphere and thus carried information about the geometry of the light field, while the simple context only varied with light field in terms of its mean luminance and contrast, and thus did not provide information about lighting geometry. Figure 2 shows a stimulus pair embedded in simple contexts in the upper row and the same pair embedded in complex contexts in the lower row.
Figure 2.
Experimental scenes. Upper row shows an example of a stimulus pair rendered under the beach (left) and the kitchen (right) light fields and presented against the checkerboard background. Lower row shows the same sphere pair embedded in the corresponding complex scene.
The light fields were scaled so that the mean luminance reflected from the matte sphere basis image was the same for each. A common scale factor was then applied to all of the rendered images so that as a set they were mapped into the luminance range of the display.
2.3 Apparatus
The stimuli were displayed on a custom high-dynamic-range (HDR) display, designed along the lines reported by Seetzen et al. (2004). The HDR display consisted of an LCD screen (ViewSonic 19″) where the commercial backlight was replaced by a projector (Panasonic DLP PT-D7600U) that illuminated the LCD screen with a projected image. The largest difference between our HDR display and a conventional transmissive LCD display is thus that the light pattern of the projector can be modulated in concert with spatial modulation provided by the LCD panel. This makes the LCD screen into a spatio-chromatic filter for the projector image, and provides an overall dynamic range that is the product of that provided by the projector and LCD in isolation. Both display devices were driven at a pixel resolution of 1280 by 1024 and at a refresh rate of 60 Hz through a dual-port video card (NVIDIA GeForce GT 120). The host computer was an Apple Macintosh G5.
The displays were arranged so that the LCD panel was enclosed in a box that prevented stray light within the experimental room from reaching the front of the panel and reflecting back to the observer. Visible surfaces within this box were lined with light absorbing black cloth. The observer viewed the LCD panel monocularly from a distance of 73 cm through a circular aperture (6.1 cm in diameter) at the end of the enclosing box. The observer’s head was stabilized with a chin rest, which could be adjusted so that the eye was centered in the circular aperture. Interposed between the observer and LCD panel was a black reduction screen (44 cm from the viewing aperture, square aperture of dimensions 16 × 16 cm; 20.6 × 20.6 degrees of visual angle), which prevented stray light from the projection system from reaching the observer’s eye.
To display calibrated high-resolution images on the HDR display, it is necessary both to align the projector image with the LCD panel and to map desired stimulus values to appropriate RGB inputs for the video card. These tasks were accomplished using custom software, following the general methods outlined by Seetzen et al. (2004). To control the chromaticity and luminance of the overall display system, we used a spectroradiometer (Pho-toResearch, Inc., PR-650) to characterize the properties of the projector and LCD panel separately. This was done in situ, with the radiometer placed at the observer’s eye position. First we characterized the projector, which we used as a grayscale device so that its RGB input values were always set with R=B=G. We set the RGB input values of the LCD panel to their maximum level (corresponding to maximum transmission through the panel) and measured the relation between the R=G=B input values to the projector and luminance output for a series of input values. We then splined these to produce a full gamma curve for the projector. Second, we set all projector pixels to their maximum input values (full light output) and measured separately the gamma curves of the R, G, and B channels of the LCD panel, as well as the transmitted spectrum for each channel. For any desired display luminance and chromaticity, the characterization data were used to compute an R=G=B value for the projector and R, G, and B values for the LCD panel that produced the desired output.
The maximum luminance of the display was 423.5 cd/m2. The minimum luminance was below the measurement range of our radiometer, but at least a factor of 10, 000 below the maximum luminance. There were some deviations between desired and displayed chromaticity, due primarily to shifts in the chromaticity of the nominally neutral projected light as a function of luminance. These shifts were not corrected for by the display control software, but were not readily apparent in the displayed images. Through analysis of the calibration data, we estimate that mean chromaticity of the scenes (i.e. the neutral point of the display) was x=0.306, y=0.353 across all input RGB values and changed gradually as a function of luminance from x=0.307, y=0.338 to x=0.302, y=0.375 as luminance varied between 0.025 and 423.5 cd/m2, with additional shifts at very low luminances.
2.4 Procedure
On each trial of the experiment, the observer viewed a pair of side by side images, one containing the reference sphere and one containing the test sphere (see Figure 2). Each image subtended 9.8 × 9.8 degrees on the display, with the test and reference spheres subtending 1.85 degrees. The two images were separated horizontally by 0.4 degrees; the distance between the centers of the reference and test spheres was 10 degrees. The observer adjusted the diffuse and specular parameters of the test sphere so that it appeared to be made out of the same material (i.e. have the same reflectance properties) as the reference sphere. The exact instructions provided to the observers are provided in the supplemental material available at http://color.psych.upenn.edu/supplements/glossiness_lightness. The reference image was always presented on the left side of the display, and the test image on the right side. Adjustments were made by pushing one of four buttons on a button box. One pair of buttons increased/decreased the specular component of the test sphere, while the other two increased/decreased the diffuse component. Observers could cycle between four different step sizes by pressing a fifth button on the controller. Subjects were required to adjust the test at least once at one of the two smallest step sizes to be able move to the next trial. When the observer was satisfied with the match, he or she pushed a final button to accept it and move to the next trial.
Observers set matches in blocks of 20 trials each. A block was defined by a choice of two light fields and 10 reference stimuli. In symmetric matching blocks, observers set symmetric matches for each of the symmetric reference stimuli/light field pairs. In asymmetric matching blocks, observers set asymmetric matches for each reference stimulus, with each of the two light fields serving as the reference. Different background conditions (simple/complex) and adjustment tasks (symmetric/asymmetric) were run in separate blocks. Within each block, the 20 possible trial types were presented in random order. Observers were allowed to rest between trials and between blocks. Each block type was repeated three times over the course of the experiment, with 2–4 (MVI) or 4–7 (VIL, BWN) blocks per session. Across the experiments blocks were ordered so that all blocks for one pair of light fields were completed before the observer moved on to the blocks for the next light field pair. The order of light field pairs was the same for all observers: kitchen/beach, kitchen/campus and kitchen/galileo.
3 Results
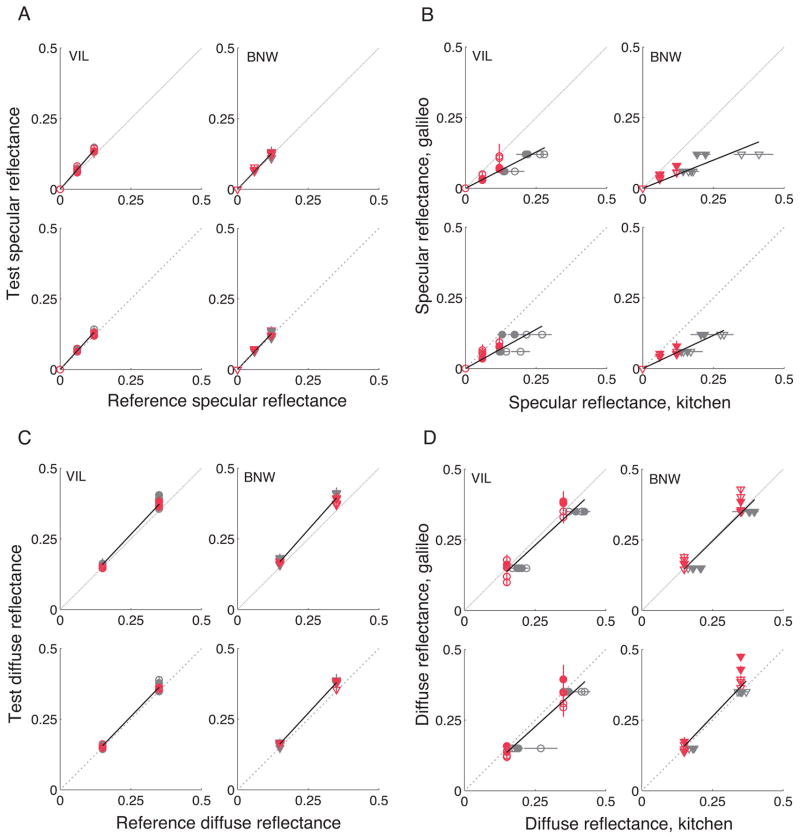
Observers’ symmetric specular matches were close to veridical. Such matches from two observers are shown in Figure 4A for the kitchen/kitchen and galileo/galileo comparisons. Data for both simple (top row of panel) and complex (bottom row of panel) contexts are shown. In all cases the data fall close to the unity line; the slopes of fitted regression lines ranged between 0.97 and 0.99.
Figure 4.
A) Specular matches for observers VIL (left) and BNW (right) for the simple (top row) and complex (bottom row) symmetric cases. Specular values for the kitchen tests are plotted against specular values for the kitchen references in gray, and specular values for the galileo tests are plotted against specular values for the galileo references in red. Settings for smooth surfaces are shown with open symbols and for rough surfaces with filled symbols. The unity line is shown with a black dotted line. Error bars show the standard error of the mean over three matches. Black solid lines are regression lines fitted through the data points. Here one line was fit to the mean data shown in each panel and the lines were constrained to include the origin. Data shown include matches for reference spheres with different levels of diffuse reflectance. To avoid excessive clutter in the figure, these differences are not indicated explicitly. B) Asymmetric specular matches for the same two observers for the simple (top row) and complex (bottom row) contexts. The specular value for the sphere seen under the kitchen illuminant is always plotted on the x-axis, whether that sphere served as the reference (red) or the test (gray). Similarly, the specular value for the sphere seen under the galileo illuminant is always plotted on the y-axis. Error bars show one standard error of the mean and are plotted vertically for the red symbols and horizontally for the gray symbols. Panels C) and D) show diffuse matches in the same format as A and B do for the specular matches.
Asymmetric matches were not always veridical. That is, changing the geometric structure of the light field had an effect on the appearance of the spheres. Figure 4B shows asymmetric specular matches for the same observers for the kitchen/galileo comparison. Matches for tests in the galileo context against references in the kitchen context are plotted with red symbols. Matches for tests in the kitchen context against references in the galileo context are plotted with gray symbols. The latter data have been flipped such that the match values (kitchen) are shown on the x-axis and the reference (galileo) values on the y-axis. This allows direct comparison between the two cases. The broad effect in the data is that the points fall well below the unity line. The slopes of the regression lines shown in Figure 4B for the simple context were 0.51 and 0.40, and for the complex context 0.55 and 0.45 for VIL and BNW, respectively.
In an experiment similar to ours, Doerschner et al. (2010) reported differences in asymmetric specular matching depending on which of two light fields served as the reference. This effect would show up in Figure 4B as a divergence of the red and gray plotted points, and is not readily apparent in the data shown. We have, however, observed such effects in preliminary experiments that employed a larger parameter range than those reported here.
Symmetric matches for the diffuse component were also close to veridical. In addition, the change in the geometric structure of the light field did not have a large effect on the diffuse component of the asymmetric matches. These data are shown also in Figure 4. Panels C and D plot the symmetric (C) and asymmetric (D) diffuse component matches for the same observers and conditions as in panels A and B. For the symmetric matches, the slopes of the regression lines fit to the data in panel C ranged between 0.97 and 0.99. The slopes for the asymmetric matches (panel D) were also close to 1 (range 0.92–1.05). The asymmetric diffuse matches do, however, appear to be more variable than the symmetric ones. The fact that the diffuse component asymmetric matches are close to veridical may arise because we scaled all of the light fields to reflect the same luminance from a purely diffuse sphere. We did this because our interest here is in the effect of changing the geometric structure of the light field, not in overall effects of changing light field luminance.
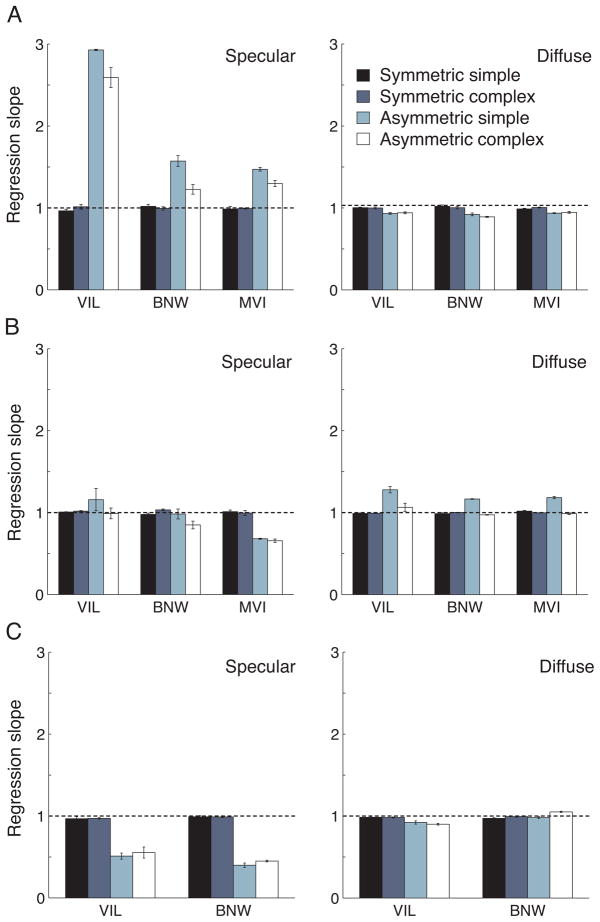
The type of data shown in each panel of Figure 4 may be summarized by the slope of the fitted regression line. Figure 5 provides the slopes of the fitted regression lines for all three light field comparisons. Here lines were fit separately to the data from each session, with the reported slopes representing the mean of the three fits and the error bars representing the standard error of this mean. The left panels show the specular matches. A number of features of the data emerge from this plot. First, the slopes for all of the symmetric conditions were close to one for all observers (range .97–1.02). This confirms that our observers reliably perform the underlying matching task. Second, for each light field comparison the slopes for asymmetric specular matches deviated from one, at least for some observers. This deviation was most apparent for the kitchen/beach (A) and kitchen/galileo comparisons (C), where it is shown by all observers. It is also clearly present for observer MVI in the kitchen/campus comparison; for this comparison there is not much effect for observers VIL and BNW. The sign of the deviation is a matter of convention (depending on which light field is defined as the reference), but given this is consistent across observers in all cases. Third, there was little overall effect of changing from simple to complex background. Although for some conditions (panel A, all observers) the deviations of the slope from unity were larger for the simple background, there was essentially no effect in other cases. If there is a systematic effect of background, further experiments would be needed to document it persuasively. Fourth, there were some individual differences in the strength of the effects. For observer VIL in panel A, the slopes for the asymmetric matches were between 2.5 and 3, meaning that she had to adjust the specularity of the test sphere under the beach illuminant to over two times that of the sphere under the kitchen illuminant. For the two other observers, the effect was considerably smaller. Despite the differences in magnitude, the direction of the effects was the same for all observers.
Figure 5.
A) Regression slopes for the kitchen/beach comparison. The left panel shows the slopes for the specular component matches; the right panel shows the slopes for the diffuse component matches. The three sets of bars in each panel are for the three observers. The bars in each group are from left to right: simple symmetric, complex symmetric, simple asymmetric, complex asymmetric. Slopes plotted were obtained by fitting the data for each of the three replications separately and taking the mean; error bars show the standard error of this mean. The horizontal black lines indicate veridical matches. B) and C) show the slopes for the kitchen/campus comparison and for the kitchen/galileo comparison, respectively. In C), data for two observers are shown. Otherwise, details are as in A).
The right panels in Figure 5 show the corresponding slopes for the diffuse matches. Here the matches were always close to veridical (slope range 0.89 – 1.28, means 0.97, 1.05, 0.97 for A, B, C).
3.1 Component Independence
We analyzed the data to ask whether the effects of light field could be characterized independently for specular and diffuse components, and whether these effects were modulated by surface roughness. To the extend that such independence principles hold, the experimental enterprise of characterizing the effect of light field is greatly simplified, since it is not then necessary to measure the effect separately for all possible combinations of the reflectance components (see e.g., Brainard & Wandell, 1992).
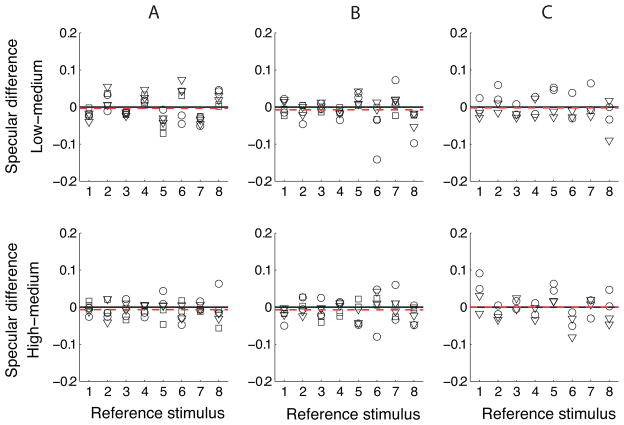
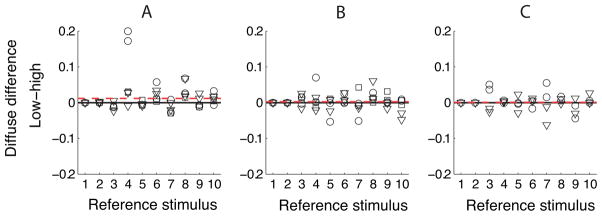
Diffuse component matches were independent of surface specularity. This is illustrated in Figure 6A–C, which shows the difference between the diffuse component matches for the low and medium specularities in the top panels and the difference between the matches for the high and medium specularities in the bottom panels. Figure 6A shows this for the kitchen/ beach comparison. Differences were scattered around zero for all observers and reference stimuli, which indicates that there were no systematic effects of stimulus specular reflectance on diffuse component matches. Figure 6B shows the differences for the kitchen/campus comparison, and Figure 6C for the kitchen/galileo comparison. For these two comparisons, differences were also scattered around zero. Bonferroni corrected t-tests confirmed that none of the differences for the light field comparisons were significantly different from zero (the six uncorrected p-values ranged from 0.05 to 0.93).
Figure 6.
Effect of specularity on diffuse component matches. A) The top panel shows the difference between diffuse component matches for the low and medium reference specularity for the kitchen/beach comparison. The differences are plotted on a nominal x-axis with 8 levels (2 levels of diffuse reflectance × 2 levels of roughness × 2 light fields). The bottom panel shows the differences between diffuse component matches for the high and medium reference specularity for the same comparison. Symbols indicate different observers as follows: circle=VIL, triangle=BNW, square=MVI. The black solid line indicates zero difference. The red dashed line indicates the mean difference across reference stimuli. B) and C) show differences in diffuse component matches for the kitchen/campus and the kitchen/galileo comparisons, respectively. Details are as in A).
Specular component matches were also independent of diffuse reflectance. Figure 7A shows differences between specular component matches for the two different levels of diffuse reflectance for the beach/kitchen comparison. Except for two data points from observer VIL, the differences scatter around zero. Bonferroni corrected t-tests confirmed that none of the differences shown in Figure 7 were significantly different from zero (3 tests; uncorrected p-values of 0.02, 0.36 and 0.78 for panels A, B, and C respectively). We attribute the significant uncorrected p-value for panel A to the outliers in the data.
Figure 7.
Effect of diffuse reflectance on specular component matches. A) Differences between specular component matches for the high and low reference diffuse reflectance for the kitchen/beach comparison. The differences are plotted on a nominal x-axis with 10 levels (3 levels of specular reflectance × 2 levels of roughness × 2 light fields taken as reference; but since the diffuse sphere is the same for both levels of roughness there are a total of only 10 levels). Symbols indicate different observers as follows: circle=VIL, triangle=BNW, square=MVI. The black solid line indicates zero difference. The red dashed line indicates the mean difference across reference stimuli. B) and C) show specular component matches for the kitchen/campus and the kitchen/galileo comparisons, respectively. Details are as in A).
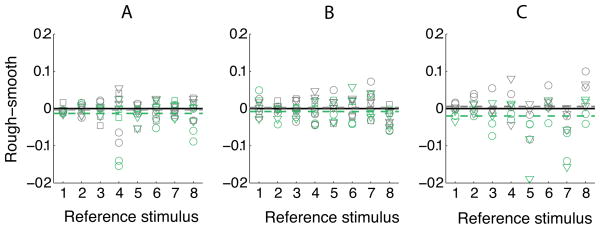
Finally, diffuse component matches for smooth surfaces were similar to the diffuse matches for rough surfaces. Specular component matches, however, were somewhat different for smooth and rough surfaces. This is illustrated in Figure 8, which shows the differences between specular matches for smooth and rough surfaces (green symbols) and the differences between the diffuse component matches for smooth and rough surfaces (gray symbols). The differences for the diffuse component matches were scattered around zero, whereas the differences for the specular component matches were on average below zero, especially for the kitchen/galileo comparisons (panel C). The latter fact indicates that surface roughness modulated the effect of light field on specular matches. Bonferroni corrected t-tests confirmed that the differences for either the specular or diffuse matches were not significantly different from zero for the data in Figure 8A and B (6 tests; uncorrected p-values between 0.01–0.50). For the comparison shown in Figure 8C, the differences for specular matches were significantly different from zero (uncorrected p=0.004).
Figure 8.
Effect of surface roughness on diffuse and specular matches. A) Gray symbols show the differences between diffuse component matches for rough and smooth surfaces for the kitchen/beach comparison. Green symbols show the same differences for specular matches. Black solid line indicates zero difference. The gray and green dashed lines indicate mean differences over reference stimuli for diffuse and specular matches, respectively. Symbols indicate different observers as follows: circles=VIL, triangles=BNW, squares=MVI. B) and C) show the same for the kitchen/campus and kitchen/galileo comparison, respectively.
4 Discussion
4.1 Summary
The primary goal of the experiments reported here was to measure the effects of geometric changes in the light field on perceived lightness and glossiness, and to test independence principles that can simplify the problem of characterizing these effects. In our hands, changing the light field has a substantial effect on perceived glossiness: for many of our conditions the asymmetric matches differed from veridical. We also found that several independence principles hold to good approximation. The effect of changing light field geometry on perceived glossiness is independent of the diffuse component of surface reflectance; the effect of changing light field geometry on perceived lightness is independent of the specular component of surface reflectance; and the effect of changing light field geometry on both perceived lightness and perceived glossiness is approximately independent of the roughness of the specular reflectance component; for one light field pair, there was a small but statistically significant effect of roughness on the specular matches. In this section, we expand on these conclusions and relate them to the prior literature.
4.2 Prior Measurements of Effect of Light field
Several studies have investigated glossiness perception for 3D surfaces under a single illuminant (Beck & Prazdny, 1981; Blake & Bülthoff, 1990; Pellacini, Ferwerda, & Greenberg, 2000; Berzhanskaya, Swaminathan, Beck, & Mingolla, 2005; Wendt, Faul, & Mausfeld, 2008). The constancy of gloss perception under varying illumination, however, has only recently begun to receive attention (Fleming et al., 2003; Obein, Knoblauch, & Viénot, 2004; te Pas & Pont, 2005; Pont & te Pas, 2006; Doerschner et al., 2010).
In a seminal paper, Fleming et al. (2003) used asymmetric matching to measure perceived gloss for spheres rendered under either real-world light fields or geometrically simple illuminants. Our methods are similar to theirs. Fleming et al.’s broad conclusion was that observers’ matches were quite veridical when the light fields were geometrically complex, although this veridicality broke down for geometrically simple illuminants. Their data, however, do show some light field comparisons where there is a definite effect of light field (see for example the top middle panel of their Figure 12). We see the difference between their conclusion and ours as primarily one of emphasis. As we will discuss below, the question of how to evaluate whether a deviation from veridical matching in this type of experiment is large or small is subtle. Doerschner et al. (2010) also studied the effect of light field changes on perceived glossiness. They abandoned asymmetric matching in favor of forced choice comparisons of perceived glossiness across light fields, and found deviations from gloss constancy for almost all light field comparisons. In this regard, our data for specular component matches agree well with those of Doerschner et al.
te Pas and Pont (2005) and Pont and te Pas (2006) studied the perception of material properties under geometrically varying illumination. They used a discrimination paradigm, and asked how well observers could discriminate between changes of illumination and changes of object reflectance. They did this both for computer rendered stimuli (Pont & te Pas, 2006) and for photographs of real objects (te Pas & Pont, 2005). Their conclusion was that the rendered stimuli did not support discrimination, while above-chance performance was possible with the photographed stimuli. Although their data are not directly comparable with ours, their results do sound a cautionary note about the generality of data obtained using computer rendered stimuli.
Obein et al. (2004) used a difference scaling method to derive the relation between perceived gloss and the specular reflectance component of black papers. Their observers viewed physical samples presented in a light booth under directional illumination, and they varied the direction of the light source in relation to the samples. Obein et al. found a monotonic but nonlinear relationship between physical surface specularity and perceived gloss, and the shape of this relation was very similar for the two illuminant directions employed. Because the scales for each light direction were derived from difference scaling data collected only within that condition, however, their data are silent with respect to any shifts in the absolute magnitude of perceived gloss across the two light directions. That is, the "gloss constancy" they report is a constancy of relative perceived glossiness within single light field conditions, and their data do not make predictions about whether asymmetric matches across a light field change would be veridical.
4.3 Luminance Histogram Statistics
Several papers have suggested that simple statistics (e.g., mean, skewness) extracted from the luminance histograms of objects may provide key cues used by the visual system to determine object lightness and glossiness (Nishida & Shinya, 1998; Motoyoshi, Nishida, Sharan, & Adelson, 2007; Sharan, Li, Motoyoshi, Nishida, & Adelson, 2008). This broad conclusion has been criticized, however, on the grounds that the stimulus conditions employed did not sufficiently dissociate variation in histogram statistics from variation in object material properties (Anderson & Kim, 2009). Some of our light field manipulations had a large effect on the luminance histogram of the rendered spheres, even when their reflectance was held constant (see Figure 3). It is thus of topical interest to ask whether our observers’ matches are predicted by simple luminance histogram statistics.
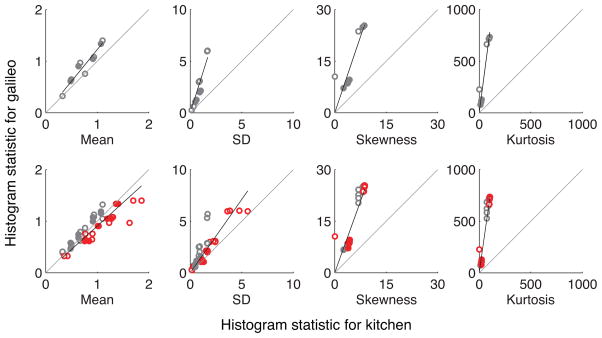
The panels in the top row of Figure 9 show the mean, standard deviation, skewness, and kurtosis of reference spheres under the kitchen light field (x-axis) against the same statistics for the same spheres under the galileo light field (y-axis). As noted above, there was little effect of light field geometry on the histogram means because of the way we normalized light field intensities. For the other three statistics the change in light field has a large effect on the histogram statistics. The bottom panels show the same statistics, but rather than computing them from the same physical spheres across the light field change, we computed them from the asymmetric matches. Each point represents the statistic value for a pair of spheres judged to match across the illuminant change.
Figure 9.
Statistics for spheres under the kitchen light field are shown against statistics for spheres under the galileo light field. The top row shows histogram statistics (from left to right mean, standard deviation, skewness, and kurtosis) across the stimulus set under the kitchen light field on the x-axis against the same statistics for the stimulus set under the galileo light field on the y-axis. Open symbols stand for smooth spheres, and closed symbols stand for rough spheres. The bottom row shows statistics of test and reference stimuli under the kitchen light field against the statistics of test and reference stimuli under the galileo light field. The plotting convention is the same as in the data figures above: gray symbols represent the cases where stimuli under kitchen were matched to stimuli under galileo, and the red symbols represent the reverse case. See supplemental materials for similar figures for the other light field comparisons.
For an observer who matched spheres based on one of these statistics, the data in the bottom panel for that statistic would fall along the positive diagonal of the plot. This pattern is approximated only for the histogram mean, and this is not diagnostic since there was very little variation in the mean produced by the light field change. For the other three statistics, the data deviate strongly from the positive diagonal. Specifically, these data falsify the hypothesis that glossiness matches are predicted by luminance histogram skewness (second panel from right).
Note that for an observer who judged the same physical sphere to have the same lightness and glossiness across the illuminant change, the data in the bottom four panels would fall along the same lines as the data in the corresponding top four panels. Although as shown in Results this is not exactly what occurs, the data do tend in this direction relative to the positive diagonal.
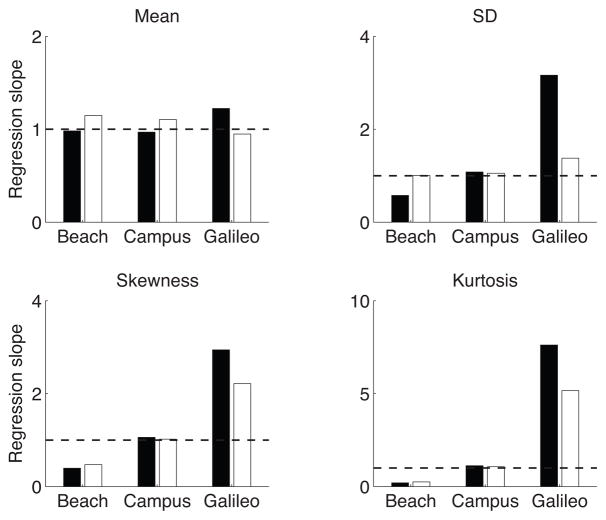
The supplemental material provides additional figures in this same format for all of our light field comparisons, and examination of these figures supports the same conclusions that we draw from Figure 9. To present this in summary format, Figure 10 shows the slopes of the regression lines from each panel of each figure. What is clear is that for each statistic other than the mean, the slopes obtained from the asymmetric matches can deviate substantially from unity, and are in general close to those obtained from the analysis of physically constant spheres.
Figure 10.
Slopes of the regression lines fitted through luminance histogram statistics for each pair of light fields. Each panel is for one statistic. The three sets of bars in each panel are for each of the three light field comparisons. The names under the bars indicate one of the light fields in a pair; the other one was always the kitchen light field. Black bars indicate slopes between reference statistics for a pair of light fields; white bars indicate slopes between matched and reference statistics for a pair of light fields. Dashed black lines mark slope of 1.
In their work arguing for the causal role of luminance histogram skewness in the perception of glossiness and lightness, Motoyoshi et al. (2007) acknowledged that the spatial structure of the judged objects could also be important, and demonstrated this by showing pixel scrambled versions of their stimuli (see also Sharan et al., 2008). Pixel scrambling perfectly preserves the luminance histogram but has a large effect on how a surface is perceived. In this context, Anderson and Kim (2009) showed a set of image manipulations less extreme than pixel scrambling and across which the predictive value of skewness is low. Indeed, Anderson and Kim (2009) rotated and translated highlights in photographs relative to the underlying object and then applied a pointwise luminance nonlinearity to keep the luminance histogram skew constant. They showed that apparent glossiness was strongly affected by their manipulation. They also pointed out that changing the light field can have a large effect on the luminance histogram of the light reflected from an object, and showed images where changes in the direction of a light source had a large effect on the histogram skew of a matte object, but where the object continued to appear matte across the light field changes (see their Figure 9). Our data are consonant with the conclusions of Anderson and Kim (2009): we show that when histogram statistics vary due to naturally occurring changes in illuminants, perceived glossiness is not predicted by histogram skew.
The fact that we draw a different conclusion from Motoyoshi et al. (2007) about the role of luminance histogram skewness in the perception of glossiness is not driven by a contradiction in the data. Although the experiments are not directly comparable, in that Motoyoshi et al. had observers rate glossiness and lightness and we had observers perform asymmetric matches, the fact that the data shown for skewness in the lower right panel of Figure 9 cluster along a single line is consistent with the hypothesis that when light field is held fixed, perceived glossiness increases monotonically with skewness. Motoyoshi et al. held the light field fixed in their experiments, and although Sharan et al. varied the light field somewhat, these variations did not have a large effect on the luminance histogram when the surfaces were held fixed. It is only when we introduce a geometric light field change that the relation between skewness and glossiness perception breaks down, and on this point we are consistent with the observations of Anderson and Kim (2009).
4.4 Independence Principles
A focus of this paper has been on formulating and testing independence principles that would allow us to reduce the number of conjoint experimental manipulations that need to be explored to develop an empirical foundation for object surface perception in natural scenes. Because of the explosion of stimulus parameters that must be considered when one considers object BRDF, shape and light field geometry, there are many such principles that could and should be explored. Other labs have conducted complementary studies that consider other aspects of independence.
Pellacini et al. (2000) used multi-dimensional scaling to derive a two-dimensional model of how the specular component of object reflectance is represented perceptually. They described these dimensions as contrast gloss and distinctness-of-image gloss, and noted that objects also have perceived lightness. They then examined whether each of these three dimensions was the perceptual correlate of a single easily described stimulus variable, by varying object reflectance within the Ward (1992) BRDF model. Asking this type of question is motivated by the same broad considerations that motivated us to test independence principles: a positive conclusion allows simplification of future empirical studies. Pellacini et al. concluded that distinctness-of-image gloss was affected primarily by the roughness parameter of the Ward model and that lightness was affected primarily by the diffuse reflectance component. Contrast gloss, however, was affected both by the strength of the specular reflectance component and by the diffuse reflectance component. Note that our data do not speak to the principles assessed by Pellacini et al., since they examined the perceptual representation of object reflectance within a single light field context. We, on the other hand, looked at how the effect of light field depended on various stimulus parameters.
In their asymmetric matching experiments across changes of light field, Fleming et al. (2003) included conditions where observers matched either the strength of the specular component or the roughness of the specular component. They note in passing that specular component matches were independent of surface roughness, and that roughness matches were independent of surface specularity. Our data are consistent with their first conclusion. Although for one light field pair there we found a small effect of roughness on the specular matches, the approximation that specular matches are independent of roughness is quite good. Since we did not ask observers to match surface roughness, our data are silent with respect to their second conclusion.
4.5 Consistency Across Sets of Asymmetric Matches
The generality of conclusions drawn from experiments that rely on perceptual comparisons across stimuli viewed in different contexts rests on the assumption that data collected for a set of such pairwise comparisons are self-consistent. One type of consistency is that asymmetric matches should not depend on which object is adjusted. Violations of this type of consistency were reported by Fleming et al. (2003) and Doerschner et al. (2010). In the latter case some of the violations were large. Both Fleming et al. and Doerschner et al. attribute the inconsistencies to a nonspecific response bias. Because of the inconsistencies, Doerschner et al. abandoned asymmetric matching for their main experiments and turned to a forced-choice method in which observers indicated which of two objects appeared most glossy.
The data reported here do not show large inconsistencies in the matching data when the roles of test and reference context were reversed, and the summary statistics we analyzed represent aggregation across paired conditions in which each light field served as reference. Because any inconsistencies in our matching data were small and because we measured asymmetric matches in both directions for each pair of light fields, we believe that our data suffer at most minor contamination from any matching response bias. We have observed larger inconsistencies of the sort reported by Fleming et al. (2003) and Doerschner et al. (2010) in preliminary experiments that extend the range of stimulus parameters studied. For the same conditions, we found that changing to a forced-choice procedure substantially reduced these asymmetries, in agreement with (Doerschner et al., 2010). We plan to use forced-choice methods for future experiments.
Doerschner et al. (2010) also examined whether pairwise comparisons across light fields satisfied a second important consistency property referred to as transitivity. Suppose we have measurements of the effect of changing light field from A to B and measurements of the effect of changing light field from B to C. Transitivity means that the effect of changing from A to C is predicted by the concatenation of the effect of A to B and B to C. Doerschner et al. concluded that transitivity holds well for glossiness judgments, a reassuring result.
4.6 Limitations
We note here a few limitations of our current study.
We used a high-dynamic-range display so that our stimuli captured the full range of luminances representative of specular stimuli presented under real-world light fields. Although we were able to present a high dynamic range, there were limits on the maximum luminance of the display. This in turn meant that the mean luminance of our stimuli was rather low, around 1.5 cd/m2. Whether performance is invariant with mean luminance is an aspect that requires future exploration.
We have tested several independence principles, but by no means all possible such principles. One important addition to our current paradigm would be to vary roughness in addition to glossiness and lightness. Other aspects of interest are the overall intensity of the light fields, their spectral properties, and the spectral properties of the objects’ reflectances. Extending the range of stimulus parameters over which the principles are probed will also be of interest.
4.7 Constancy
The specular component matches of our observes deviated from those that would be obtained had they veridically matched object reflectance parameters. In this sense, our observers failed to show what might be termed glossiness constancy. Deviations from perfect constancy are also found reliably in the lightness and color literature (for a review see e.g. Brainard, 2004). In those literatures, it is common to quantify the degree of constancy using an index, where the index is based on a comparison of the data to two reference points. One reference point is the constancy prediction, obtained by positing that observers match object reflectance. The other reference point is a no constancy prediction, obtained by positing the the visual system makes no adjustment for a change in viewing context. Here the prediction is made on the basis of equating the photometric and colorimetric properties of the test stimuli in the image. That is, a no constancy prediction is made by assuming that observers make their matches by equating image properties rather than object properties. The use of the two reference points provides a natural scale against which to judge deviations from constancy. Although the use of constancy indices provide only a broad strokes summary, they have proved valuable for framing the nature of performance (Arend, Reeves, Schirillo, & Goldstein, 1991; Lucassen & Walraven, 1996; Brainard, Brunt, & Speigle, 1997; Kraft & Brainard, 1999; Smithson & Zaidi, 2004; Hansen, Walter, & Gegenfurtner, 2007).
Here, it also seems desirable to find an index that provides a sense of whether the deviations from constancy are large or small. This has proved difficult, however, because it is not clear what to use as the no constancy reference point. When the light field is changed, there is no matching stimulus that is identical to the reference stimulus. For this reason, it is not clear how to scale the deviations from physical matching and thus to decide whether we should view performance as close to constant or far from it.
This noted, we can use matching based on luminance histogram statistics as a proxy for how a visual system with no constancy would perform. Recall that the positive diagonals in the top panels of Figure 9 and corresponding supplemental figures predict asymmetric matches for observers who match luminance histogram statistics. These positive diagonals can thus be regarded as a no constancy prediction. The regression lines in the same panels show how the same statistics would be matched if observers made veridical matches. By comparing the top and bottom panels of this figure (see also Figure 10), we see that observer data (bottom panels), expressed in terms of the histogram statistic values at the match, are in general closer to the predictions of constancy than to the predictions of no constancy. This is particularly true for histogram skewness, which is known to be highly correlated with the strength of the specular reflectance component when the light field is held constant (Motoyoshi et al., 2007; Anderson & Kim, 2009). One could choose a particular statistic and use it to compute a quantitative index. We have declined to do so, however, as we regard the use of luminance histogram statistics in this way as a fairly speculative idea.
Acknowledgments
This work was supported by the NIH grants RO1 EY10016, P30 EY001583 and by a young investigator grant to KMO from the Emil Aaltonen foundation.
References
- Alldrin N, Zickler T, Kreigman D. Photometric stereo with non-parametric and spatially-varying reflectance. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; Anchorage, AK. June 23–28.2008. [Google Scholar]
- Anderson BL, Kim J. Image statistics do not explain the perception of gloss and lightness. Journal of Vision. 2009;9(11):10.1–1017. doi: 10.1167/9.11.10. Available from http://dx.doi.org/10.1167/9.11.10. [DOI] [PubMed]
- Arend LE, Reeves A, Schirillo J, Goldstein R. Simultaneous color constancy: paper with diverse munsell values. Journal of the Optical Society of America A. 1991;8(4):661–672. doi: 10.1364/josaa.8.000661. [DOI] [PubMed] [Google Scholar]
- Beck J, Prazdny S. Highlights and the perception of glossiness. Perception and Psychophysics. 1981;30(4):407–410. doi: 10.3758/bf03206160. [DOI] [PubMed] [Google Scholar]
- Berzhanskaya J, Swaminathan G, Beck J, Mingolla E. Remote effects of highlights on gloss perception. Perception. 2005;34(5):565–575. doi: 10.1068/p5401. [DOI] [PubMed] [Google Scholar]
- Blake A, Bülthoff H. Does the brain know the physics of specular reflection? Nature. 1990;343(6254):165–168. doi: 10.1038/343165a0. Available from http://dx.doi.org/10.1038/343165a0. [DOI] [PubMed]
- Brainard DH. Colorimetry. In: Bass M, editor. OSA Handbook of Optics. Vol. 1. New York: MacGraw-Hill; 1995. pp. 26.1–26.54. [Google Scholar]
- Brainard DH. Color constancy. In: Chalupa L, Werner J, editors. The Visual Neurosciences. MIT Press; 2004. pp. 948–961. [Google Scholar]
- Brainard DH, Brunt WA, Speigle JM. Color constancy in the nearly natural image. I. Asymmetric matches. Journal of the Optical Society of America A. 1997;14:2091–2110. doi: 10.1364/josaa.14.002091. [DOI] [PubMed] [Google Scholar]
- Brainard DH, Wandell BA. Asymmetric color matching: how color appearance depends on the illuminant. Journal of the Optical Society of America A. 1992;9:1433–1448. doi: 10.1364/josaa.9.001433. [DOI] [PubMed] [Google Scholar]
- Dana KJ, van Ginneken B, Nayar SK, Koenderink JJ. Reflectance and texture of real-world surfaces. ACM Transactions on Graphics. 1999;18(1):1–34. [Google Scholar]
- Debevec P. Rendering synthetic objects into real scenes: bridging traditional and image-based graphics with global illumination and high dynamic range photography. SIGGRAPH ’98: Proceedings of the 25th annual conference on Computer graphics and interactive techniques; New York, NY, USA: ACM; 1998. pp. 189–198. [Google Scholar]
- Doerschner K, Boyaci H, Maloney LT. Estimating the glossiness transfer function induced by illumination change and testing its transitivity. Under review. 2010 doi: 10.1167/10.4.8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleming RW, Dror RO, Adelson EH. Real-world illumination and the perception of surface reflectance properties. Journal of Vision. 2003;3(5):347–368. doi: 10.1167/3.5.3. [DOI] [PubMed] [Google Scholar]
- Griffin LD. Partitive mixing of images: a tool for investigating pictorial perception. Journal of the Optical Society of America A. 1999;16(12):2825–2835. Available from http://josaa.osa.org/abstract.cfm?URI=josaa-16-12-2825.
- Hansen T, Walter S, Gegenfurtner KR. Effects of spatial and temporal context on color categories and color constancy. Journal of Vision. 2007;7(4):2, 1–15. doi: 10.1167/7.4.2. [DOI] [PubMed] [Google Scholar]
- International Electrotechnical Comission. International electrotechnical comission standard 61966-2-1. 1999. [Google Scholar]
- Kraft JM, Brainard DH. Mechanisms of color constancy under nearly natural viewing. Proceedings of the National Academy of Sciences of the United States of America. 1999;96(1):307–312. doi: 10.1073/pnas.96.1.307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lucassen MP, Walraven J. Color constancy under natural and artificial illumination. Vision Research. 1996;36(17):2699–2711. doi: 10.1016/0042-6989(95)00346-0. [DOI] [PubMed] [Google Scholar]
- Motoyoshi I, Nishida S, Sharan L, Adelson EH. Image statistics and the perception of surface qualities. Nature. 2007;447(7141):206–209. doi: 10.1038/nature05724. Available from http://dx.doi.org/10.1038/nature05724. [DOI] [PubMed]
- Newhall S, Nickerson D, Judd D. Final report of the O.S.A. subcommittee on the spacing of Munsell Colors. Journal of the Optical Society of America. 1943;33:385–412. [Google Scholar]
- Nickerson D. Spectrophotometric data for a collection of munsell samples (Tech Rep) U.S. Department of Agriculture; 1957. (Spectropho-tometric data for a collection of Munsell samples) [Google Scholar]
- Nickerson D, Wilson DH. Munsell reference colors now specified for nine illuminants. Illumination Engineering. 1950;45:507–517. [Google Scholar]
- Nishida S, Shinya M. Use of image-based information in judgments of surface-reflectance properties. Journal of the Optical Society of America A. 1998;15(12):2951–2965. doi: 10.1364/josaa.15.002951. [DOI] [PubMed] [Google Scholar]
- Obein G, Knoblauch K, Viénot F. Difference scaling of gloss: nonlinearity, binocularity, and constancy. Journal of Vision. 2004;4(9):711–720. doi: 10.1167/4.9.4. Available from http://dx.doi.org/10:1167/4.9.4. [DOI] [PubMed]
- Oren M, Nayar SK. Generalization of Lambert’s reflectance model; SIGGRAPH ’94: Proceedings of the 21st annual conference on Computer graphics and interactive techniques; New York, NY, USA: ACM; 1994. pp. 239–246. [Google Scholar]
- Pellacini F, Ferwerda JA, Greenberg DP. Toward a psychophysically-based light reflection model for image synthesis. SIGGRAPH ’00: Proceedings of the 27st annual conference on computer graphics and interactive techniques; New York, NY, USA: ACM; 2000. pp. 55–64. [Google Scholar]
- Pont SC, te Pas SF. Material-illumination ambiguities and the perception of solid objects. Perception. 2006;35(10):1331–1350. doi: 10.1068/p5440. Available from http://www.hubmed.org/display.cgi?uids=17214380. [DOI] [PubMed]
- Seetzen H, Heidrich W, Stuerzlinger W, Ward G, Whitehead L, Trentacoste M, et al. High dynamic range display systems. SIGGRAPH ’04: Proceedings of the 31st annual conference on Computer graphics and interactive techniques; New York, NY, USA: ACM; 2004. pp. 760–768. [Google Scholar]
- Sharan L, Li Y, Motoyoshi I, Nishida S, Adelson EH. Image statistics for surface reflectance perception. Journal of the Optical Society of America A. 2008;25(4):846–865. doi: 10.1364/josaa.25.000846. [DOI] [PubMed] [Google Scholar]
- Shevell SK, Kingdom FAA. Color in complex scenes. Annual Review of Psychology. 2008;59:143–166. doi: 10.1146/annurev.psych.59.103006.093619. [DOI] [PubMed] [Google Scholar]
- Smithson H. Sensory, computational and cognitive components of human color constancy. Philosophical Transactions of the Royal Society B. 2005;360:1329–1346. doi: 10.1098/rstb.2005.1633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smithson H, Zaidi Q. Colour constancy in context: roles for local adaptation and levels of reference. Journal of Vision. 2004;4(9):693–710. doi: 10.1167/4.9.3. [DOI] [PubMed] [Google Scholar]
- te Pas SF, Pont SC. A comparison of material and illumination discrimination performance for real rough, real smooth and computer generated smooth spheres. APGV ’05: Proceedings of the 2nd symposium on Applied perception in graphics and visualization; New York, NY, USA: ACM; 2005. pp. 75–81. [Google Scholar]
- Ward GJ. Measuring and modeling anisotropic reflection. In: Glassner A, editor. SIGGRAPH 92: Proceedings of the 19th annual conference on computer graphics and interactive techniques; New York: ACM, ACM Press; 1992. pp. 459–472. [Google Scholar]
- Ward GJ. The radiance lighting simulation and rendering system. In: Glassner A, editor. SIGGRAPH 94: Proceedings of the 21st annual conference on computer graphics and interactive techniques; New York: ACM, ACM Press; 1994. pp. 459–472. [Google Scholar]
- Wendt G, Faul F, Mausfeld R. Highlight disparity contributes to the authenticity and strength of perceived glossiness. Journal of Vision. 2008;8(1):14.1–1410. doi: 10.1167/8.1.14. Available from http://dx.doi.org/10.1167/8.1.14. [DOI] [PubMed]
- Xiao B, Brainard DH. Surface gloss and color perception of 3D objects. Visual Neuroscience. 2008;25(3):371–385. doi: 10.1017/S0952523808080267. Available from http://dx.doi.org/10.1017/S0952523808080267. [DOI] [PMC free article] [PubMed]
- Yu Y, Debevec P, Malik J, Hawkins T. Inverse global illumination: recovering reflectance models of real scenes from photographs; SIGGRAPH ’99: Proceedings of the 26th annual conference on Computer graphics and interactive techniques; New York, NY, USA: ACM Press; 1999. pp. 215–224. [Google Scholar]