Bifactor Models and Rotations: Exploring the Extent to which Multidimensional Data Yield Univocal Scale Scores

Abstract

The application of psychological measures often results in item response data that arguably are consistent with both unidimensional (a single common factor) and multidimensional latent structures (typically caused by parcels of items that tap similar content domains). As such, structural ambiguity leads to seemingly endless “confirmatory” factor analytic studies, in which the research question is whether scale scores can be interpreted as reflecting variation on a single trait. An alternative to the more commonly-observed unidimensional, correlated-traits, or second-order representations of a measure's latent structure is a bifactor model. Bifactor structures, however, are not well understood in the personality assessment community and, thus, rarely are applied. To address this, herein we: a) describe issues that arise in conceptualizing and modeling multidimensionality, b) describe exploratory (including Schmid-Leiman and target bifactor rotations) and confirmatory bifactor modeling, c) differentiate between bifactor and second-order models, d) suggest contexts where bifactor analysis is particularly valuable (e.g., for evaluating the plausibility of subscales, determining the extent to which scores reflect a single variable even when the data are multidimensional, and evaluating the feasibility of applying a unidimensional item response theory measurement model). We emphasize that the determination of dimensionality is a related but distinct question from either determining the extent to which scores reflect a single individual difference variable or determining the effect of multidimensionality on IRT item parameter estimates. Indeed, we suggest that in many contexts, multidimensional data can yield interpretable scale scores and be appropriately fitted to unidimensional IRT models.

Chen, West, and Sousa (2006, p. 189) write, “Researchers interested in assessing a construct often hypothesize that several highly related domains comprise the general construct of interest.” As a consequence, factor analytic evaluations of such measures often reveal some evidence of a general factor running through the items (e.g., a relatively large first eigenvalue) but also some evidence of multidimensionality (e.g., an interpretable multidimensional solution that arises due to parcels of items that tap similar content domains). These common findings invariably spark the age-old debate among researchers whether a given construct is unitary or multi-faceted. Does scale score variation primarily reflect variation on a single construct (and, thus, scale scores are unambiguously interpretable) or reflect multiple non-ignorable sources of variance (and, thus, subscales need to be formed)?

Consider, for example, the substantial amount of confirmatory factor analytic research devoted to investigating the dimensionality of data from the Anxiety Sensitivity Index (Lilienfeld, Turner, & Jacob, 1993; Zinbarg, Barlow, & Brown, 1997), Dispositional Hope Scale (Brouwer, et al., 2008), Self-Monitoring Scale (Briggs, Cheek, & Buss, 1980), Life Orientation Test (Robinson-Whelen, et al., 1997), Penn State Worry Questionnaire (Hazlett-Stevens, Ullman, & Craske, 2004), Center for Epidemiologic Studies Depression Scale (Golding & Aneshensel, 1989), Beck Depression Inventory-II (Dozois & Dobson, 1989), Hamilton Depression Rating Scale (Bagby et al., 2004), a self concept scale (Byrne & Shavelson, 1996), and the Toronto Alexithymia Scale-20 (Gignac, Palmer, & Strough, 2007). For all of these instruments, at issue is whether they measure a single construct or whether item responses are best thought of as reflecting multiple, more or less correlated, individual differences.

The above-cited research represents only a very small percentage of the studies of instrument structure and ultimately interpretability. One reason why the dimensionality issue appears to cause such consternation is clear; researchers typically write self-report items to assess a single construct. Nevertheless, they also recognize that constructs are substantively complex (e.g., depression); that is, indicators of the construct are diverse (in the case of depression, for example, cognitive-affective versus somatic-performance symptoms). Consequently, to validly represent the construct, items with heterogeneous content need to be included in the measure. This places personality assessment researchers in the vexing position of trying to measure one thing while simultaneously measuring diverse aspects of this same thing.

With that in mind, it is unsurprising that in many psychometric investigations, it is common to observe evidence for a single dimension, and at the same time, to uncover evidence of multidimensionality. Here are two examples from our own work. First, Reise and Haviland (2005) in considering the application of a unidimensional item response theory (IRT; Embretson & Reise, 2000) model analyzed a 25-item measure of cognitive problems. They reported a 1st to 2nd eigenvalue ratio of 13.29 to 1.5, evidence of a very strong general factor. Yet, they also reported that up to seven additional factors could be extracted from the data, that these factors were interpretable, and that they led to an improved statistical “fit.” In Smith and Reise (1998), a 23-item measure of stress reaction also was considered for application of a unidimensional IRT model to explore hypotheses of differential item functioning. Again, a very large 9.59 to 0.97 ratio of the 1st to 2nd eigenvalues was observed, strongly suggesting unidimensionality. Due to content parcels included within the scale for content validity purposes (see Tellegen & Waller, 2008), however, five interpretable correlated factors could be extracted and interpreted.

In the above two examples, the authors argued that the evidence for the essential unidimensionality of the measures was clear and that any observed multidimensionality due to item content parcels (or mere doublets) was ignorable. They argued that it would be indefensible, for example, to break the cognitive problems scale into seven super-homogeneous subscales. With many other measures, however, the dimensionality and the scale score interpretability issues seldom will be put to rest so clearly. To address such impasses, to evaluate the psychometric properties of substantively complex measures, we propose that a bifactor latent structure may be an excellent alternative to the more commonly-used unidimensional, correlated-traits, or second-order representations of a measure's latent structure. Bifactor latent structures appear not to be well understood in the personality assessment community, however, and, thus, they rarely are applied.

In the present paper, we: a) describe issues that arise in conceptualizing and modeling multidimensionality, b) describe exploratory (including the Schmid-Leiman and target bifactor rotations) and confirmatory bifactor modeling, c) differentiate between bifactor and second-order models, and d) suggest contexts where bifactor analysis is particularly valuable (e.g., for evaluating the plausibility of subscales, determining the extent to which scores reflect a single variable even when the data are multidimensional, and evaluating the feasibility of applying an IRT model). To accomplish these objectives, we make reference throughout to an observer report measure of alexithymia (described below). This measure is an excellent example because it has parcels of item content, but typically it is scored as reflecting a single common construct.

The Observer Alexithymia Scale (OAS)

The Observer Alexithymia Scale (OAS, Haviland, Warren, & Riggs, 2000; Haviland, Warren, Riggs, & Gallacher, 2001; Haviland, Warren, Riggs, & Nitch, 2002) is a 33-item, observer-rated alexithymia measure; each item is rated on a four-point scale: 0 = never, not at all like the person; 1 = sometimes, a little like the person; 2 = usually, very much like the person; and 3 = all of the time, completely like the person. OAS scores, thus, can range from 0 to 99. Item content was taken from the California Q-set Alexithymia Prototype (CAQ-AP; Haviland & Reise, 1996). In CAQ-AP terms, the prototypic alexithymic person has difficulties experiencing and expressing emotion; lacks imagination; and is literal, socially conforming, and utilitarian. Moreover, alexithymic individuals are not insightful, are humorless, have not found personal meaning in life, and anxiety and tension find outlet in bodily symptoms. These various characteristics are a mix of what some call “core” features of alexithymia (Taylor, 2000) and observable expressions or consequences of being alexithymic. Specific OAS items were written to correspond to the most and least characteristic items in the CAQ-AP. This approach to generating an item pool differs from the more-common method; that is, to specify broad features in advance and write several nearly identical items to represent that feature.

Exploratory and confirmatory factor analytic studies (Haviland, Warren, & Riggs, 2000; Haviland, Warren, Riggs, & Gallacher, 2001; Berthoz, Haviland, Riggs, Perdereau, & Bungener, 2005; Yao, Yi, Shu, & Haviland, 2005) provide modest evidence that the OAS has a five (correlated) factor structure: distant (unskilled in interpersonal matters and relationships), uninsightful (lacking good stress tolerance and insight or self-understanding), somatizing (having health worries and physical problems), humorless (colorless and uninteresting), and rigid (too self-controlling). It is important to note here that the subscale labels are terms of convenience and to underscore that these features were not specified a priori.

In tests of substantive hypotheses, researchers use total, and not subscale, scores (e.g., Mueller, Alpers, & Reim, 2006; Perrin, Heesacker, & Shrivastav, 2008). In other words, as with many scales, the multidimensional structure caused by clusters of items with similar content is ignored in practice. One objective of this paper is to explore the extent to which this practice can be justified empirically. In the following section, we provide a foundation for bifactor modeling by introducing two distinct views of multidimensionality. Data (N=1,495) for the various illustrative analyses are from four OAS (English-translation) studies: ratings of people-in-general (close friends and relatives) by undergraduate, graduate, and professional students (Haviland, Warren, & Riggs, 2000; Riggs & Haviland, 2004) and outpatients being treated by Ph.D.-level clinical and counseling psychologists (Haviland, Warren, Riggs, & Gallacher, 2001; Haviland, Warren, Riggs, & Nitch, 2002).

Conceptualizing and Modeling Multidimensionality

To illustrate the examples that follow, we display in Figure 1 four alternative structural models. Model A is easily recognized as a unidimensional model – each item is influenced by a single common factor (the target construct – alexithymia) and a uniqueness term that reflects both systematic and random error components. Note that Model A does not state that there is only one reliable or systematic source of variance for each item, rather it states that there is only one common source. For any item, it is likely that dozens of random and systematic factors affect item performance, including response sets and reading proficiency, for example. Importantly, Model A is neutral as to the size of the common factor; a model with all loadings of .20 (and error variances of .96) and a model with all loadings of .70 (and error variances of .51) both are unidimensional models. This is an important point because the size of a loading on a single factor often is taken incorrectly as an indicator of “unidimensionality.” Of course, sizeable loadings are necessary to reliably distinguish between individuals using a reasonable number of items.

Figure 1.

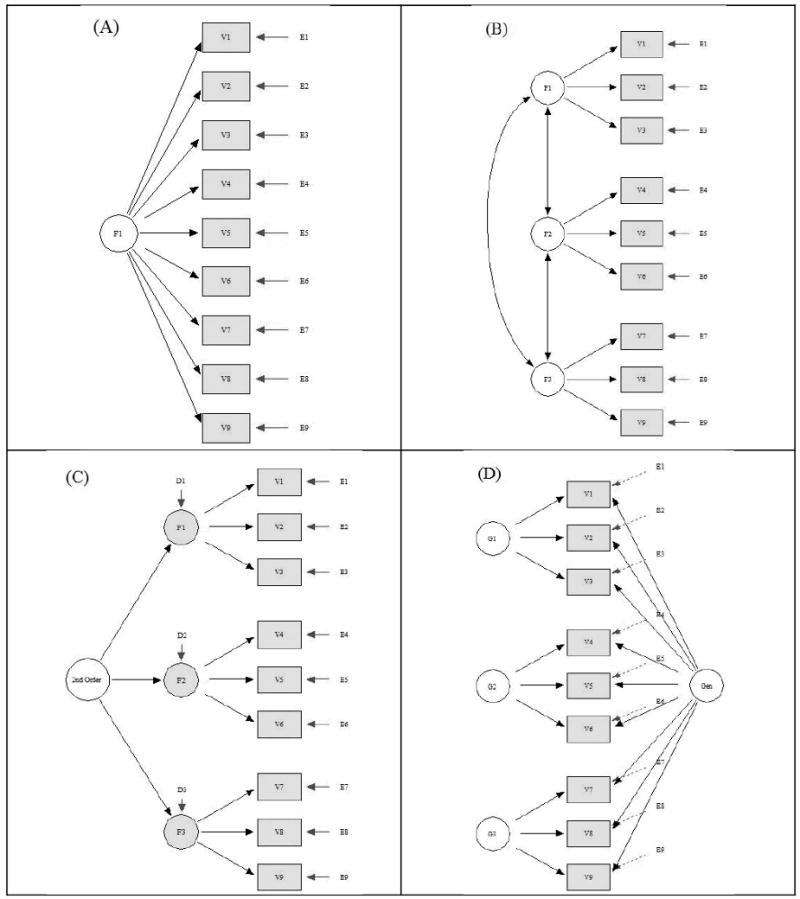
Model A, A Unidimensional Model; Model B, A Correlated Traits Model; Model C, A Second-Order Model; Model D, A Bifactor Model

Model A in Figure 1 is the data structure assumed by all unidimensional IRT models (Embretson & Reise, 2000) for either dichotomous or polytomous items. It also is the model that scale developers hope is reasonably true, so that a summed score provides an unambiguous interpretation of individual differences on the target construct. In terms of the present data, Model A suggests that variation on each OAS item is affected by variation on alexithymia (the target latent variable) and no other common variable. Unfortunately, strictly speaking, McDonald (1981, p. 102) has noted that in regard to the prospect of finding perfectly unidimensional assessment data, “Such a case will not occur in application of theory.” When researchers believe that the restrictions in Model A are violated severely, alternative multidimensional structures often are proposed.

To the degree that Model A is implausible, alternative multidimensional structures must be found, and Models B through D in Figure 1 represent three alternatives. Herein, we refer to the familiar and commonly-applied Model B as the “correlated traits” model. In this model, a construct domain is broken apart into its separate, distinct/correlated elements (sometimes called “primary” traits). Specifically, the variance of each item is assumed to be a weighted linear function of two or more common factors. In exploratory factor analysis, the weights can change depending on rotation choice. This model is most reasonable when a scale is composed of multiple item parcels with similar content, such that the correlation among items within a cluster is substantially larger than the average inter-item correlation. In such cases, multiple (and interpretable) factors always can be extracted and, depending on the degree of correlation among the factors, arguments for forming a single aggregate versus scoring subscales can be made.

Model B, however, is not a measurement model per se. Specifically, in Model B there is no one common target dimension (i.e., alexithymia) to be measured or that directly affects item variance. In contrast to Model B, Model C places a measurement structure onto the correlations among the factors. That is, the factors are correlated because they share a common cause. In other words, this second-order model states that the target construct (alexithymia) is a “second-” or “higher-order” dimension that explains why three or more “primary” dimensions are correlated. Notice that as drawn in Figure 1, there is no direct relationship between the item and the target construct, but rather the relationship between alexithymia and each item is mediated through the primary factor (i.e., an indirect effect).

To determine the item variance due to the second-order factor, one must multiply the loading of the item on the primary factor by the loading of the primary factor on the second-order factor (see example below). Each item also is a function of the disturbance (i.e., that part of the primary factor that is unexplained by or independent of the second-order factor). To determine how much item variance is due uniquely to the primary trait (controlling for the second-order factor), one must multiply the loading of the item on the primary trait by the square root of the disturbance (also shown below).

Finally, the remaining Model D in Figure 1 is a bifactor model (Holzinger & Swineford, 1939; Schmid & Leiman, 1957). As shown, a bifactor model is a latent structure where each item loads on a general factor. This general factor reflects what is common among the items and represents the individual differences on the target dimension that a researcher is most interested in (i.e., alexithymia). Moreover, a bifactor structure specifies two or more orthogonal “group” factors. These group factors represent common factors measured by the items that potentially explain item response variance not accounted for by the general factor. In some applications of the model, the group factors are termed “nuisance” dimensions – factors arising because of content parcels that potentially interfere with the measurement of the main target construct. Group factors are analogous to disturbances in the second-order model.

In what we refer to as a “restricted” bifactor model (Gibbons & Hedeker, 1992), each item loads on a single general factor, and at most on one additional orthogonal group factor. The restricted bifactor model assumes that the items all measure a common latent trait (i.e., alexithymia), but that the variance of each item also is influenced by an additional common factor caused by parcels of items tapping similar aspects of the trait. Thus, a chief virtue of the bifactor model is that it allows researchers to retain a goal of measuring a single common latent trait, but also models, and thus controls for, the variance that arises due to additional common factors. In other words, the bifactor model, in theory, allows one to directly explore the extent to which items reflect a common target trait and the extent to which they reflect a primary or subtrait.

From the above model descriptions, it should be clear that if a researcher intends to both recognize multidimensionality and simultaneously retain the idea of a single important target construct, the second-order or bifactor models are the only choices. As we will explain in detail subsequently, in some ways there is no meaningful distinction to be made between these two models, whereas in other ways, they are vastly different. One difference is that second-order models are fairly common in the literature and in textbooks (e.g., Bryne, 2006), whereas bifactor models are not. Beyond this applied difference, another difference lies in how multidimensionality is conceptualized under the two models.

Underlying the application of both Models B and its nested cousin C is the assumption that common variance on an item can be partitioned into a weighted function of variation on two or more correlated primary traits. Thus, under the correlated traits framework (and its extension to a second-order model), the “target” latent trait is what a sample of more basic elements, primary traits (or subdomains) have in common, not what items have in common. In contrast, the bifactor model specifies that there is a single (general) trait explaining some proportion of common item variance for all items, but that there also are group traits explaining additional common variance for item subsets. The general and group factors are on equal conceptual footing and compete for explaining item variance – neither is “higher” or “lower” than the other. With this viewpoint, the target latent variable is what is in common among the items (i.e., the common latent trait approach).

Both the correlated traits and the common latent trait approaches are reasonable conceptual models for understanding multidimensionality in some contexts. Reckase (2009), for example, has written an entire book on the utility of multidimensional IRT models of the correlated-traits type in educational assessment contexts. We believe, however, that the common trait perspective (and its corresponding bifactor structural model) is more amenable to conceptualizing and studying: a) whether scale items measure a single common dimension, b) how well the scale items measure a single common dimension, c) the effect of multidimensionality on scale scores and, d) the feasibility of applying a unidimensional IRT model in the presence of multidimensional data. We summarize and comment on our arguments in the final sections of this paper.

Independent Clusters and Cross-Loadings

In what follows, we describe and illustrate both exploratory and confirmatory bifactor modeling. Throughout, we make reference to the idea of items being factorially simple (loading on one and only one factor) versus complex (having cross-loadings on two or more factors). We also make use of the concepts of independent cluster structure (IC) and independent cluster basis (ICB). McDonald (1999, p. 460) provides precise definitions of these concepts:

• ICB: “a factor pattern in a confirmatory factor/multidimensional item response model in which each common factor is identified by two or more factorially simple variables (for correlated factors) or by three or more factorially simple variables (for uncorrelated factors).” (italics in original)

• IC: “in a confirmatory factor/item response model, a model in which each variable loads on just one factor. In an exploratory factor model, each variable has a nonnegligible loading on just one factor.” (italics in original)

These concepts play two critical roles in bifactor modeling. First and more generally, they provide a set of rules for identifying and meaningfully interpreting factors in the common factor model (e.g., the correlated traits model). If a structure has an IC basis (and that basis is more than just mere doublets), for example, we can justify substantively interpreting the factors, and items that cross-load on multiple factors can be viewed as blends of two or more dimensions (McDonald, 1999; 2000). Second, and more directly related to bifactor modeling, both restricted second-order and bifactor models are viable to the degree that a given dataset has an IC structure (i.e., no cross-loadings in a correlated traits solution). When data violate IC structure, restricted models will display poor statistical “fit,” and more importantly, parameter estimates (e.g., factor loadings or IRT discriminations) may be seriously distorted.

Software Programs

Many of the analyses that we present require software beyond the most widely-available packages. Thus, it may be helpful to review the options available to researchers interested in performing such analyses or replicating our results. The R Statistical Package (R Development Core Team, 2010) is perhaps the most versatile existing statistical package. This program can be freely downloaded from: http://cran.r-project.org/

Many of the exploratory analyses conducted herein used R software, including polychoric correlation estimation, ordinary exploratory factor analysis, and Schmid-Leiman factor rotation (all from the psych package; Revelle, 2009).

For target factor rotation (described below), we used the Comprehensive Exploratory Factor Analysis program (CEFA; Browne et al., 2004), available free at: http://faculty.psy.ohio-state.edu/browne/programs.htm

CEFA is capable of exploratory factor analysis using multiple extraction methods. We used standard ML extraction on polychoric correlation matrices.

Finally, ordinary confirmatory factor analytic techniques do not apply to dichotomous or polytomous data (Bryne, 2008). Instead, special estimation procedures are required (Wirth & Edwards, 2008). There basically are three options for working with polytomous item response data. The first is to compute a polychoric matrix and then apply standard factor analytic methods (see Knoll & Berger, 1991). A second option is to use full-information item factor analysis (Gibbons & Hedeker, 1992). The third is to use limited information estimation procedures designed specifically for ordered data, such as weighted least squares with mean and variance adjustment (MPLUS, Muthen & Muthen, 2009). For all confirmatory factor analyses, we used EQS (v6.1; Bentler & Wu, 2003) to conduct maximum likelihood (ML) estimation with robust standard errors (Satorra & Bentler, 1994) based on a polychoric correlation matrix. Thus, any fit indices reported herein are “robust” indices. This is important to recognize because traditional benchmarks for structural equation modeling fit indices do not necessarily apply when working with dichotomous or polytomous item response data and so their interpretation must be treated with extreme caution (see Cook & Kallen, 2009).

Exploratory Factor Analyses of the OAS

As a lead into exploratory bifactor analysis, we first present alternative exploratory factor representations of the models described above. Table 1 shows the unidimensional (ML extraction) and five-factor correlated-traits (ML extraction, oblimin rotation) OAS solutions (loadings < .20 not shown). The loading pattern in the unidimensional solution shows a great deal of variation, with a few items having loadings greater than .70 (e.g., #1, #4, #7, #16, #24, and #28) and a few items loading below .30 (#11 and #14). The former items have the largest average inter-item correlations (and, thus, the highest estimated communalities), whereas the latter have the lowest (the lowest estimated communalities), meaning it is the former that disproportionally define the latent variable. The highest loading items appear to be predominantly drawn from the distant content domain.

Table 1.

Exploratory Factor Analysis of the Observer Alexithymia Scale

Item	Subscale	Uni	5-Factor Exploratory (Oblique Rotation)
			1	2	3	4	5
1	Distant	0.73	0.77
2	Uninsightful	0.54		0.69
3	Somatizing	0.42			0.78
4	Humorless	0.76				0.74
5	Rigid	0.46					0.73
6	Distant	0.64	0.84
7	Distant	0.73	0.60	0.25
8	Uninsightful	0.42		0.69
9	Somatizing	0.40			0.76
10	Humorless	0.62				0.92
11	Rigid	0.29	-0.20				0.72
12	Distant	0.55	0.85
13	Uninsightful	0.49		0.59
14	Somatizing	0.30			0.72
15	Humorless	0.75				0.68
16	Rigid	0.71	0.24				0.61
17	Distant	0.63	0.56				0.21
18	Distant	0.45	0.46		-0.22
19	Uninsightful	0.40		0.60
20	Distant	0.62	0.26			0.48
21	Uninsightful	0.51	0.25	0.51
22	Somatizing	0.48			0.66	0.20
23	Humorless	0.68				0.35	0.33
24	Distant	0.74	0.29	0.20		0.24	0.23
25	Distant	0.63	0.46			0.23
26	Uninsightful	0.64	0.21	0.56		0.23
27	Somatizing	0.39		0.29	0.49
28	Humorless	0.71	0.21			0.28	0.35
29	Distant	0.56	0.37			0.29
30	Uninsightful	0.38		0.55
31	Rigid	0.52	0.26				0.51
32	Uninsightful	0.58		0.55		0.21
33	Rigid	0.46					0.47
2nd-Order Loadings:			0.59	0.57	0.38	0.58	0.71

The five-factor oblique solution in Table 1 demonstrates that for the most part, items fall cleanly into their respective content domains. The solution is far from a perfect IC structure (each item loading on one and only one factor), and whether the solution has an IC basis depends on what cross-loading value a researcher judges to be meaningful. McDonald (1999) cites a criterion of .30 for a meaningful (cross) loading, and by this standard, each (correlated) factor does have at least two items that load uniquely on that factor. Thus, the factors are meaningfully interpretable. On the other hand, if one uses a more stringent criterion of .20 for a significant (cross) loading, then factor five (rigid) is questionable, given that there are only two items (#5, #33) loading simply on it.

Although not shown in Table 1, the factor correlations ranged from r = .07 (distant and somatizing) to r = .49 (Distant and Humorless), and the average was approximately r = .30. The size of these factor correlations suggests a common dimension of modest strength¹ among the primary factors. Clearly, the size of the factor correlations does not suggest that the content domains are fungible indicators of a single construct. To model the factor inter-correlations, the last row of Table 1 shows the loadings of the five primary traits on the general factor, alexithymia. These loadings were derived by simply conducting a factor analysis of the correlations among the primary traits. That is, these loadings in the bottom of Table 1 represent the relationships between the second-order factor and the primary traits in a second-order factor model. Note that disturbances for each of the primary traits are equal to one minus the loading squared. In this model, factor five (rigid) has the highest loading (.71), whereas factor three (somatizing) has the lowest. These results suggest that it is highly questionable whether somatizing relates to alexithymia in the same way that the other features do (a point that we return to after more testing).

Exploratory Bifactor Modeling

The term exploratory implies that no restrictions are placed on a solution. In terms of bifactor structures, exploratory means that items are free to load on the general and any number of group factors. Familiar exploratory factor analytic rotation methods are designed to identify simple structure solutions, but in a bifactor structure, items are free to load on a general and a set of group factors. In short, researchers will not be able to identify an exploratory bifactor structure using standard factor rotation methods such as oblimin or promax (however, see Jennrich & Bentler, under review). There are two alternatives, each with its own strengths and weaknesses, which we describe next.

Schmid-Leiman (SL) Orthogonalization

One method to obtain a bifactor solution is the SL procedure (Schmid & Leiman, 1957). For the SL bifactor solutions, we used the schmid routine included in the psych package (Revelle, 2009) of the R software program (R Development Core Team, 2008). The schmid procedure works as follows. Given a tetrachoric or polychoric correlation matrix, schmid:

1. extracts (e.g., minres, ML) a specified number of primary factors,

2. performs an oblique factor rotation (e.g., oblimin),

3. extracts a second-order factor from the primary factor correlation matrix, and

4. performs an SL orthogonalization of the second-order factor solution to obtain the loadings for each item on uncorrelated general and group factors.

Specifically, assuming that an item loads on only one primary factor, an item's loading on the general factor simply is its loading on the primary factor multiplied by the loading of the primary factor on the general factor. In real data where loadings are never exactly zero, an item's loading on the general factor is found by summing the products of the item's loading on a primary factor with the primary factor's loading on the second-order. For Item #1, for example, the actual loadings in Table 1 are .774, .013, .070, .104, and .060. In turn, the loadings of the five primaries on the second-order are: .590, .574, .377, .713, and .575. The sum of the products

$$.774\times .590+.013\times .574+.070\times .377+.104\times .713+.060\times .575=.585$$

is the loading on the general factor for Item #1.

An item's loading on a group factor simply is its loading on the primary factor multiplied by the square root of the disturbance (the disturbance is variance of the primary factor that is not explained by the general factor). For Item #1 and group factor 1 this value would be:

$$.774\times sqrt(1-{.590}^2)=.625$$

The loadings for this item on the remaining four factors follow a similar logic.

SL is a transformation of a second-order factor pattern, which in turn, is a function of a correlated traits solution. Unsurprisingly then, to the extent that the items have IC loading patterns (i.e., no cross-loadings) on the oblique factors in the correlated traits solution, the items will tend to load on one and only one group factor in the SL. To the extent that the items lack an IC structure in an oblique rotation, the loadings in the SL become more complicated to predict. Moreover, to the degree that the primary factors are correlated, loadings on the general dimension in the SL will tend to be high.

To perform a SL, a measure should contain at least two (if the primary factors are constrained to be equally related with the second-order) but preferably three parcels (so that the primary factor correlation matrix can be factor analyzed). The loadings derived from a SL: a) are affected by both the factor extraction and oblique rotation method selected, and importantly, b) contain proportionality constraints (see Yung, Thissen, & McLeod, 1999). The proportionality constraints emerge because the group and general factor loadings in the SL are functions of common elements (i.e., the loading of the primary factor on the second-order factor, and the square root of the primary factor disturbance).

Although the SL is easy to implement, there is a critical problem: because of the proportionality constraints, the factor loadings produced from a SL typically are biased estimates of their corresponding population values. In other words, if one were to assume that in the population, the factor loading matrix had a bifactor structure, the SL only can recover the precise loadings in real data if: a) the data have a perfect IC structure and b) the ratio of an item's group to general factor loading is equal for items within each cluster (thus, retaining proportionality). When these conditions are not met, the loadings in the SL may not accurately reflect the true population loadings, even in models that display an excellent “fit” to the data.

To demonstrate, in the top portion of Table 2, we display (from left to right) three true bifactor population loading patterns. For each of these patterns, we computed the implied population correlation matrix and then conducted a SL orthogonalization. In the first set of columns, it is clear that the SL will recover the population loading matrix with perfect accuracy when the group and general factor loadings are proportional. The middle column displays the SL's lack of accuracy when group factor loadings vary in their relation to the item's general factor. Most important, the third set of columns shows the distorting effect of cross-loadings. Specifically, for the items with cross-loadings, the SL overestimates the loadings on the general factor and underestimates the loadings on the group factors. Despite this obvious limit of the SL, the distortions in the SL are generally not of great concern if a researcher is primarily interested in identifying the pattern of salient and non-salient loadings as opposed to estimating their specific value in the population.

Table 2.

Schmid-Leiman Orthogonalization Under Three Conditions

Item	True Population Structure
	IC: Proportional				IC: Not Proportional				IC: Basis
	Gen	G1	G2	G3	Gen	G1	G2	G3	Gen	G1	G2	G3
1	0.50	0.60			0.40	0.27			0.50	0.60	0.50
2	0.50	0.60			0.40	0.68			0.50	0.60
3	0.50	0.60			0.40	0.65			0.50	0.60
4	0.50	0.60			0.40	0.21			0.50	0.60
5	0.50	0.60			0.40	0.65			0.50	0.60
6	0.50		0.50		0.40		0.43		0.50		0.50	0.50
7	0.50		0.50		0.40		0.51		0.50		0.50
8	0.50		0.50		0.40		0.29		0.50		0.50
9	0.50		0.50		0.40		0.27		0.50		0.50
10	0.50		0.50		0.40		0.19		0.50		0.50
11	0.50			0.40	0.40			0.61	0.50	0.50		0.40
12	0.50			0.40	0.40			0.13	0.50			0.40
13	0.50			0.40	0.40			0.46	0.50			0.40
14	0.50			0.40	0.40			0.64	0.50			0.40
15	0.50			0.40	0.40			0.53	0.50			0.40
Schmid-Leiman
Item	Gen	G1	G2	G3	Gen	G1	G2	G3	Gen	G1	G2	G3
1	0.50	0.60			0.33	0.32	0.09	0.05	0.65	0.49	0.36	0.11
2	0.50	0.60			0.41	0.67	0.01	0.01	0.49	0.61	0.01	0.02
3	0.50	0.60			0.40	0.65	0.00	0.00	0.49	0.61	0.01	0.02
4	0.50	0.60			0.31	0.27	0.10	0.06	0.49	0.61	0.01	0.02
5	0.50	0.60			0.40	0.65	0.00	0.00	0.49	0.61	0.01	0.02
6	0.50		0.50		0.41	0.01	0.41	0.01	0.61	0.05	0.40	0.38
7	0.50		0.50		0.43	0.02	0.45	0.02	0.50	0.01	0.50	0.03
8	0.50		0.50		0.37	0.02	0.33	0.02	0.50	0.01	0.50	0.03
9	0.50		0.50		0.36	0.02	0.32	0.03	0.50	0.01	0.50	0.03
10	0.50		0.50		0.33	0.04	0.27	0.05	0.50	0.01	0.50	0.03
11	0.50			0.40	0.41	0.01	0.01	0.60	0.56	0.45	0.05	0.33
12	0.50			0.40	0.30	0.07	0.12	0.20	0.42	0.05	0.04	0.48
13	0.50			0.40	0.38	0.02	0.03	0.48	0.42	0.05	0.04	0.48
14	0.50			0.40	0.42	0.01	0.02	0.63	0.42	0.05	0.04	0.48
15	0.50			0.40	0.39	0.01	0.01	0.54	0.42	0.05	0.04	0.48

Target Pattern Rotation

If the proportionality constraints of the SL are a concern, a clear alternative is to estimate an even less restricted model, such as a rotation to a target matrix. Rotation of a factor pattern to a partially-specified target matrix (Browne, 1972a, b; 2001) only is recently gaining popularity due to the availability of software packages to implement target and other types of non-standard rotation methods (e.g., MPLUS; Asparouhov & Muthen, 2008; comprehensive exploratory factor analysis, CEFA; Browne, Cudeck, Tateneni, & Mels, 2004). In this study, we use the freeware CEFA program exclusively. This program allows the user to specify a target pattern matrix where each element in the target factor pattern is treated as either specified (0) or unspecified (?). Extracted factors then are rotated to this target.

The target matrix in a targeted rotation, “reflects partial knowledge as to what the factor pattern should be” (Browne, 2001, p. 124). It forms the basis for a rotation that minimizes the sum of squared differences between the target and the rotated factor pattern. The use of targeted bifactor rotations raises two important questions. The first is how to form an initial target, empirically or theoretically. Empirical preliminary analyses, for example, such as a SL or cluster analysis, could be used to suggest the number of group factors and a bifactor target structure. Alternatively, one may rely on theory to determine the number of factors and which items belong to the various content parcels. In either case, the target pattern matrix will consist of unspecified elements (?) in the first column to represent the fact that the general trait is related to every item and that each item will have zero (which means that the item is a pure marker of the general trait) or one or more unspecified elements on the group factors.

One potential (and likely) challenge of target rotations is that a researcher must correctly specify the target matrix. Unfortunately, there is no research on the robustness of target bifactor rotations to initial target misspecification. The second question is, given a correctly specified target pattern, how well can a targeted rotation to a bifactor structure recover the true population loadings? The answer presently is not known. In Table 3, using the examples from Table 2, we show that when an initial target matrix is correctly specified, a target rotation will recover the true population loadings perfectly, thus avoiding the problems in the SL. On the other hand, the recovery of bifactor loadings in the context of target rotations has not been thoroughly explored under a variety of conditions. Although Reise, Moore, and Maydeu-Olivares (under review) suggest reasonable accuracy with sample sizes greater than 500 if the data are well structured and if the target matrix is correct, accuracy tests under other conditions are needed.

Table 3.

Target Rotation Under Three Conditions

Item	True Population Structure
	IC: Proportional				IC: Not Proportional				IC Basis
	Gen	G1	G2	G3	Gen	G1	G2	G3	Gen	G1	G2	G3
1	0.50	0.60			0.40	0.27			0.50	0.60	0.50
2	0.50	0.60			0.40	0.68			0.50	0.60
3	0.50	0.60			0.40	0.65			0.50	0.60
4	0.50	0.60			0.40	0.21			0.50	0.60
5	0.50	0.60			0.40	0.65			0.50	0.60
6	0.50		0.50		0.40		0.43		0.50		0.50	0.50
7	0.50		0.50		0.40		0.51		0.50		0.50
8	0.50		0.50		0.40		0.29		0.50		0.50
9	0.50		0.50		0.40		0.27		0.50		0.50
10	0.50		0.50		0.40		0.19		0.50		0.50
11	0.50			0.40	0.40			0.61	0.50	0.50		0.40
12	0.50			0.40	0.40			0.13	0.50			0.40
13	0.50			0.40	0.40			0.46	0.50			0.40
14	0.50			0.40	0.40			0.64	0.50			0.40
15	0.50			0.40	0.40			0.53	0.50			0.40
Targeted Rotation
Item	Gen	G1	G2	G3	Gen	G1	G2	G3	Gen	G1	G2	G3
1	0.50	0.60			0.40	0.27			0.50	0.60	0.50
2	0.50	0.60			0.40	0.68			0.50	0.60
3	0.50	0.60			0.40	0.65			0.50	0.60
4	0.50	0.60			0.40	0.21			0.50	0.60
5	0.50	0.60			0.40	0.65			0.50	0.60
6	0.50		0.50		0.40		0.43		0.50		0.50	0.50
7	0.50		0.50		0.40		0.51		0.50		0.50
8	0.50		0.50		0.40		0.29		0.50		0.50
9	0.50		0.50		0.40		0.27		0.50		0.50
10	0.50		0.50		0.40		0.19		0.50		0.50
11	0.50			0.40	0.40			0.61	0.50	0.50		0.40
12	0.50			0.40	0.40			0.13	0.50			0.40
13	0.50			0.40	0.40			0.46	0.50			0.40
14	0.50			0.40	0.40			0.64	0.50			0.40
15	0.50			0.40	0.40			0.53	0.50			0.40

Exploratory Bifactor Rotations With The OAS

Table 4 displays two five-group-factor exploratory bifactor rotations of the OAS. Columns 2-7 show the SL, and columns 8-13 show the target rotation output from CEFA (loadings less than .20 are not shown). The target pattern matrix for the target rotation was built according to the proposed OAS structure, meaning that the results of the SL were not used to suggest which elements should be (non-)specified in the target matrix. In the present data, the results of the SL and the target rotation are very similar with one notable exception. Namely, the loadings on the general factor almost always are higher in the target rotation than in the SL, and thus, loadings on the group factors almost always are lower in the target rotation relative to comparable values in the SL. Notice also that in each solution, there are items that display cross-loadings on the group factors. This is not a major concern in these exploratory analyses; they potentially are a major source of model misfit and item parameter estimation distortion in restricted models, which we consider next.

Table 4.

Exploratory Bifactor Analyses of the Observer Alexithymia Scale

Item	Schmid-Leiman Orthogonalization						Targeted Rotation
	Gen	G1	G2	G3	G4	G5	Gen	G1	G2	G3	G4	G5
1	0.59	0.63					0.62	0.59
2	0.48		0.57				0.57		0.52
3	0.38			0.72			0.51			0.62
4	0.68				0.52		0.57	0.33			0.57
5	0.43					0.60	0.47					0.57
6	0.50	0.68					0.56	0.60
7	0.59	0.49	0.20				0.62	0.47
8	0.37		0.57				0.49		0.51
9	0.36			0.71			0.52			0.58
10	0.59				0.65		0.42				0.74
11	0.29					0.59	0.31					0.59
12	0.42	0.69					0.48	0.58				-0.24
13	0.44		0.49				0.51		0.47	0.24
14	0.27			0.66			0.41			0.58
15	0.66				0.47		0.53	0.39			0.51
16	0.61					0.50	0.69					0.38
17	0.51	0.45					0.48	0.51
18	0.34	0.37		0.21			0.35	0.37		-0.26
19	0.35		0.49				0.41		0.45
20	0.53	0.21			0.33		0.48	0.31			0.36
21	0.42	0.20	0.41				0.52		0.33			-0.22
22	0.43			0.61			0.49			0.54
23	0.59				0.24	0.27	0.76				0.32
24	0.63	0.23					0.59	0.35				0.22
25	0.51	0.37					0.47	0.45
26	0.53		0.46				0.48	0.31	0.48
27	0.36		0.23	0.45			0.43		0.25	0.46
28	0.61					0.29	0.85			-0.21	0.25
29	0.46	0.30			0.20		0.39	0.43
30	0.31		0.45				0.42		0.32
31	0.43	0.21				0.41	0.51					0.32
32	0.48		0.45				0.44	0.26	0.43
33	0.41					0.39	0.45					0.35

Note: G1=distant; G2=uninsightful; G3=somatizing; G4=humorless; G5=rigid

Confirmatory Latent Structures

The above analyses involved models that were either completely unrestricted (e.g., correlated traits) or partially restricted (Schmid-Leiman). In this section, we now shift and consider highly restricted or (confirmatory) models. These multidimensional models are highly restrictive because they assume that each item loads on a single factor or, in the bifactor, loads only on the general and one and only one group factor. Table 5 shows parameter estimates (standardized solution) based on fitting a unidimensional model to the matrix of polychoric correlations using ML estimation in EQS. This model was identified by fixing the variance of the latent factor to 1.0. Note that this solution is exactly the same as the unidimensional solution in Table 1 (with only one factor, of course, there is no distinction between the exploratory and confirmatory models).

Table 5.

Unidimensional and Correlated-Traits Solutions of the Observer Alexithymia Scale

Item	Correlated Traits							Correlations Among Factors
	Uni	G1	G2	G3	G4	G5		G1	G2	G3	G4	G5
1	0.73	0.84					G1	1
2	0.53		0.79				G2	0.35	1
3	0.41			0.79			G3	0.19	0.40	1
4	0.76				0.86		G4	0.56	0.36	0.26	1
5	0.46					0.67	G5	0.35	0.28	0.24	0.41	1
6	0.65	0.79
7	0.73	0.78
8	0.40		0.73
9	0.39			0.81
10	0.62				0.77
11	0.29					0.54
12	0.55	0.71
13	0.48		0.72
14	0.29			0.70
15	0.75				0.82
16	0.71					0.83
17	0.63	0.71
18	0.45	0.53
19	0.39		0.61
20	0.62	0.61
21	0.50		0.61
22	0.47			0.75
23	0.68				0.72
24	0.73	0.67
25	0.63	0.67
26	0.63		0.63
27	0.38			0.68
28	0.71				0.73
29	0.56	0.60
30	0.37		0.47
31	0.51					0.61
32	0.57		0.55
33	0.46					0.58

Note: G1=distant; G2=uninsightful; G3=somatizing; G4=humorless; G5=rigid

Unsurprisingly, the fit of this model by conventional benchmarks (which may or may not apply) is not acceptable: overall model chi-square is 12,407 on 495 DF p. < .01, CFI = .83 and RMSEA = .13. Also not surprising, the modification indices suggest that additional dimensions need to be specified; specifically, items within a parcel have correlated residuals (the three largest are between #14 and #3; #28 and #23; #12 and #6). As noted in the previous section, the OAS includes five item content parcels and, thus, it is understandable that SEM fit indices would lead to the rejection of such a model. These fit values, however, do not necessarily imply either that a unidimensional IRT model is impossible to meaningfully fit to the data or that a researcher cannot measure a single common “alexithymia” construct using these items. We will address both of these issues below.

Table 5 shows the loadings and factor intercorrelations for a five-factor solution, where each item is restricted to load on one and only one primary trait. For identification, each factor variance was fixed to 1.0. The fit of this model is “acceptable” and much improved relative to the unidimensional model: model chi-square is 4,447 on 485 DF p. < .01, CFI = .94 and RMSEA = .07. Modification indices reveal that for several items, the restriction that they load on a single primary trait was responsible for the lack of fit; for example, we needed to free up the loading (i.e., allow cross-loadings) for #24 on rigid and #s 26 and 32 on distant. Finally, the estimated correlations among the primary factors range between .76 (distant and humorless) and .29 (distant and somatizing). These values are much larger than comparable values in the exploratory analysis.

Table 6 displays the loadings of the OAS in a second-order model where each item is restricted to load on a single primary factor. Model chi-square is 4,818 on 490 DF p. < .01, CFI = .94 and RMSEA = .08. The modification indices are a little more complicated in this model due to all the restrictions. Modification indices suggested that we needed to free up the direct effect between item #24 and the second-order factor (alexithymia). Moreover, the second-order factor does not completely explain the correlation among primary traits as evidenced by the need to free up the correlation between uninsightful and somatizing. As in Model B, a number of cross-loadings still need to be estimated to reduce the overall model chi-square. Finally, inspections of the paths among the second-order and primary traits reveal that distant, humorless, and rigid are the most highly related to the second-order trait.

Table 6.

Second-Order and Bifactor Solutions of the Observer Alexithymia Scale

Item	Second-Order Model						Bifactor Model
	F1	F2	F3	F4	F5	Gen	F1	F2	F3	F4	F5
1	.85					.70	.50
2		.78				.45		.68
3			.80			.33			.73
4				.86		.74				.47
5					.66	.44					.61
6	.79					.60	.62
7	.78					.71	.31
8		.71				.31		.75
9			.81			.31			.75
10				.77		.58				.70
11					.53	.26					.65
12	.71					.48	.70
13		.71				.39		.63
14			.70			.20			.70
15				.81		.76				.35
16					.84	.70					.38
17	.71					.66	.21
18	.52					.47	.22
19		.60				.33		.51
20	.60					.63	.09
21		.61				.47		.37
22			.76			.43			.63
23				.73		.69				.14
24	.67					.71	.08
25	.67					.65	.15
26		.65				.62		.26
27			.67			.31			.58
28				.73		.71				.09
29	.59					.58	.11
30		.48				.35		.31
31					.61	.49					.34
32		.58				.58	.20
33					.57	.45					.37
2nd-Order Loadings:	.81	.67	.49	.89	.79
Sum of λ Squared						292.07	8.94	13.76	11.49	3.06	5.52

Note: G1=Distant; G2=Uninsightful; G3=Somatizing; G4=Humorless; G5=Rigid

Table 6 also displays the loadings for the confirmatory bifactor model where each item loads on the general and one and only one group factor. To highlight the items providing the best discrimination on the general factor, we put the 15 items loading greater than .50 on the general factor in boldface type. These items are mostly from the distant and humorless content domains. Moreover, we put in boldface type the loadings on the group factors that were larger than an item's loading on the general factor. These items are relatively better measures of the specific group factor construct than they are of alexithymia. Note that some items (e.g., #6) are fairly good measures of both general and group factors.

The fit of the bifactor model (see Table 6) also is adequate: overall model chi-square is 3,152 on 462 DF p. < .01, CFI = .96, RMSEA = .06. The rescaled chi-square difference test showed that the bifactor model is a statistically significant improvement over the second-order model in terms of overall model chi-square. In other words, restricting the direct effects among the second-order factor and the items to be zero in the second-order model significantly worsens the fit. In the restricted bifactor model, the three highest modification indices were due to: a) the restriction that uninsightful and somatizing group factors be uncorrelated, which suggests a model misspecification in the form of correlated group factors even after controlling for the general factor, b) item #20 needed a cross-loading path to humorless group factor, and c) #13 requires a cross-loading on the rigid group factor. These needed cross-loadings undermine our confidence in the parameter estimates; if these paths were freed, the magnitude of the loadings could change meaningfully.

Bifactor Compared to Correlated Traits and Second-Order Models

When a measure contains multiple subdomains of item content (i.e., multidimensionality reflecting the heterogeneous manifestations of the trait), the second-order and the bifactor models are alternative structural representations. Chen, West, and Sousa (2006, p. 189), for example, refer to the bifactor and second-order factor analytic models as “alternative approaches for representing general constructs comprised of several highly related domains.” Historically, second-order confirmatory factor models frequently are used in non-cognitive domains, whereas bifactor models seldom are used. Of late, however, psychopathology and personality researchers also have been making good use of these models (Brouwer, Meijer, Weekers, & Baneke, 2008; Chernyshenko, Stark, & Chan, 2001; Simms, Gros, Watson, & O'hara, 2007; Steer et al., 1995; Zinbarg, & Barlow, 1996).

Despite these publications, there remains a great deal of confusion in the literature regarding the bifactor approach and when and how it differs from the second-order method; thus, in this section, we will explain some of the consequential differences. For lengthier summaries, see Yung, Thissen, and McLeod (1999); Gustafsson and Balke (1993); Chen, West, and Sousa (2006); and Rindskopf and Rose (1988). To begin, from the exploratory section, it should be clear that there are no real differences between a second-order model and a SL orthogonalization, due to the fact that the latter simply is a transformation of the former. In the case of target bifactor rotations, there is no meaningful comparison to an analogous second-order model because there is no such thing as a rotation to a second-order solution.

Although as detailed above, we believe that the second-order model and the bifactor are distinct ways of representing a single construct (i.e., item variance explained by a weighted combination of primary traits, as opposed to item variance explained by a general factor and group factors). Gustafsson and Balke (1993) argue that the differences between second-order and bifactor models rest more in appearance than in substance. They assert that, whereas in the second-order model it may appear that the second-order factor is further removed from the items and at a “higher level” of abstraction, this really is not the case. They believe that the only real difference between second-order and primary factors is the range of variables they affect. This perspective suggests that the difference between partitioning the general and group factors in the bifactor and partitioning the second-order and primary dimensions in the second-order model is minor. Gustafsson and Balke (1993) do point out differences in the models, however, and in fact, they favor use of the bifactor in their studies of human abilities.

The main difference between the bifactor and second-order models emerges in confirmatory models that compare Models C and D. First, the traditional second-order model is nested within the bifactor model, and thus, the more general bifactor can be used to evaluate the decrement in fit resulting from placing the restrictions inherent in the correlated traits, second-order, and unidimensional models. Consider the OAS with 33 items and five group factors in a restricted bifactor model. After fixing all factor variances to one, factor correlations to one, and factor inter-correlations to zero, 99 parameters are estimated for the bifactor — 33 loadings on the general factor, 33 loadings on the group factors, and 33 error variances — leaving 462 degrees of freedom (561 - 99 = 462 df).

For the second-order model, with one second-order and five primary factors, fixing the factor variances to one, 24 parameters are estimated — 5 loadings of primary on secondary, 33 loadings of items on primary, 33 error variances, and 5 disturbance terms — leaving 490 degrees of freedom (561 - 71 = 490 df). Notice, however, that in the traditional second-order model, there are no direct effects specified between the second-order factor and the items (i.e., the only effects are indirect). If in the OAS data, one were to specify the 28 possible direct paths (33 items minus 5 primary factors), then the second-order and bifactor are equivalent models (see Chen, West, & Sousa, 2006, for a demonstration).

Finally, in terms of application, Chen, West, and Sousa (2006) list seven advantages of the confirmatory bifactor relative to the second-order model:

1. Because it is the most general model, the bifactor can be used as a foundational model for testing more constricted models.

2. The bifactor model allows the correct separation of general and domain specific factors, whereas the second-order model “forces” a primary trait to be a domain specific factor. In other words, even if a researcher mistakenly specifies a content parcel that ostensibly is unique in regards to the general trait, this easily would be identified in the bifactor (group factor loadings would be zero, and the items would load only on the general) but difficult to identify in the second-order model (where an artificial separation between the primary trait and the general is forced on the model).

3. The relation between items and group factors can be directly modeled by the bifactor.

4. In the bifactor, the contribution of the group factors to prediction of an external variable can be studied independently of the general factor. This would be difficult to do with the second-order model because it is difficult to estimate paths between disturbances and external variables.

5. The bifactor model allows for tests of measurement invariance at both the general and group factor levels. In the second-order, measurement invariance is studied at the general factor level only.

6. In the bifactor model, group mean differences can be studied at both general and group factor levels.

Applications

In this section, we demonstrate how the bifactor can be used to address important issues that routinely arise in psychometric analysis of personality and psychopathology measures. Specifically, using the OAS data, we demonstrate the utility of bifactor analyses for: a) evaluating the plausibility of subscales, b) determining the degree to which sum scores reflect a single factor, and c) evaluating the feasibility of applying a unidimensional IRT measurement model. Finally, in the conclusion, we review the strengths and limits of bifactor modeling.

The Plausibility of Subscales and General Factor Dominance

Arguments whether a measure should be scored as reflecting a single construct or broken down into subscales are very common in both cognitive and non-cognitive measurement contexts. Typically, the technical details of this argument are sidestepped in the applied literature in favor of simply reporting scores (and sometimes standard errors) for both subscales and the total aggregate. Yet, this apparently pleasing compromise is problematic in several ways.

First, if the OAS (and like scales) were broken down into (correlated) subscales, multicollinearity would interfere with our ability to judge the unique contribution of each of the subscales in predicting some important outcome. In turn, if a heterogeneous aggregate score were formed to represent alexithymia, we would not be confident that any external correlates truly reflect the common trait of alexithymia rather than the effect of one or more components of alexithymia. Second, and related to the first, a common argument for breaking a measure into subscales is that the subscales may have differential correlates with external variables. This is technically true but weak justification for “cutting up” a measure. Indeed, any two items that are not perfectly correlated potentially have different correlations with external variables, yet it would be silly to argue that one should investigate external correlates for each item separately. Why, for example, would one break apart two correlated parcels to create two unreliable specific measures that, when combined, can provide a reliable measure of one thing?

Third, a seldom recognized problem with computing subscales is that from a bifactor perspective, subscale scores reflect variation on both a general trait (alexithymia) and a more specific trait (rigidity). The effect of this is that the subscale may appear to be reliable, but in fact that reliability is a function of the general trait, not the specific subdomain. Finally, as argued in Sinharay and Puhan (2007), subscales often are so unreliable compared to the composite score, that the composite score actually is a better predictor of an individual's true score on a subscale than is the subscale score. For this reason, these authors develop the argument that subscale scores are seldom, if ever, empirically justified (although they may be necessary for political/policy reasons).

Given that traditional psychometric practices fail to truly inform on the general score versus subscale score issue, we argue that the bifactor model gives some guidance to argue for one approach over the other (see also Gustafsson & Aberg-Bengtsson, 2010). At the most simple level of analysis, because the general and group factors are uncorrelated in a bifactor model, a simple inspection of the factor loadings on the general and group is informative. To the degree that the items reflect primarily the general factor and have low loadings on the group factors, subscales make little sense. In the case that the items have substantial loadings on both group and general factors, a researcher should consider the computation of factor scores for all factors. In either case, at the very least, the bifactor representation potentially provides one with a clear view of the extent to which the items truly reflect a general construct (free of the multidimensionality) and to what extent they reflect a more conceptually narrow construct (controlling for the general).

In the present case, inspection of the loadings in Table 6 reveals that under the second-order model, one could easily be fooled into thinking that there are five well defined and scoreable subscales. Inspection of the bifactor results, on the other hand, clearly shows that after controlling for the general factor, the group factor loadings generally are lower. As a consequence, it would be difficult to squeeze out meaningful variation for some of these subscales. For group factors #'s 1, 2, 3, and 5 in Table 6, for example, it would be hard to argue that the number of items with high loadings supports computation of a factor score (or creation of a subscale). Factor 1, for example, is defined by only two items with loadings > .50. On the other hand, group factor #2 (uninsightful) has four items with loadings greater than .50. Although some researchers may find this acceptable, our general advice for use of the OAS in practice/research is to not estimate group factor scores or form subscale scores.

Relatedly, a second important issue that arises in psychometrics is the question, despite the heterogeneity of item content, to what degree do scores reflect a single construct? When data are perfectly unidimensional (Model A), coefficient alpha provides a direct index of general factor saturation. In other words, under unidimensionality, coefficient alpha reflects the percent of variance in sum scores explained by a single factor. When data are multidimensional, Cronbach's alpha can be very misleading in regard to interpreting how well a measure reflects a single construct (Cortina, 1993). This is simple to understand if one recognizes that in classical test theory, the true score reflects all reliable sources of variance (including general, group, and item specific sources). In short, under multidimensionality, coefficient alpha can lead a researcher into a false sense of security as to how well a single construct is being measured.

Coefficient omega hierarchical (Zinbarg et al., 1997; 2005), on the other hand, is a statistic based on a bifactor model representation that estimates the proportion of variance in raw scores attributable to a single general target trait. In this framework, variation in scores attributable to group and specific factors are treated as nuisance variance or error in measurement. Specifically, given the results of a bifactor solution, coefficient omega can be calculated as:

$${\omega }_h=\frac{{(\sum {\lambda }_{\mathit{\text{Gen}}})}^2}{\mathit{\text{VAR}}(X)}$$ (1)

Where λ are the “unstandardized” loadings of the items on the general factor in a bifactor model, and VAR(X) is simply the variance of (unweighted) raw scores. Note that some debate exists in regard to whether VAR(X) should be based on the estimated covariance matrix or model reproduced covariance matrix (Bentler, 2009).

Coefficient omega hierarchical is not a pure “unidimensionality” index per see (see below). Nevertheless, the difference between the coefficients alpha and omega hierarchical is the extent to which the reliability estimate is influenced by allowing group factors to figure into true score variation. Moreover, Gustafsson and Aberg-Bengtsson (2010) demonstrate how indices such as omega hierarchical can be used to argue that scores on achievement tests, despite being clearly multidimensional in content, still reflect primarily a single dimension. Gustafsson and Aberg-Bengtsson (2010) also argue that the effect of a factor on raw score variance is related to the square of the number of items loading on a factor.

If a researcher were interested in a cleaner index of “unidimensionality”, defined as the percent of unweighted raw score variance attributable to the general factor, then Equation 2 is appropriate (explained common variance, EVC; ten Berge & Sočan, 2004; Bentler, 2009).

$$\mathit{\text{ECV}}=\frac{(\sum {\lambda }_{\mathit{\text{Gen}}}^2)}{(\sum {\lambda }_{\mathit{\text{Gen}}}^2)+(\sum {\lambda }_{G1}^2)+(\sum {\lambda }_{G2}^2)····(\sum {\lambda }_{\mathit{\text{GK}}}^2)}$$ (2)

In Equation 2, the factors are assumed uncorrelated, and the denominator contains the sum of the (unstandardized) loadings, squared, for all the K common factors including both general and group. This is a superior unidimensionality index because it represents how much reliable variance in unweighted raw scores is attributable to a single general factor.

Given the above, we now can see how the bifactor model guides us in interpreting the OAS as an index of a single score. First, in terms of variance explained, in the confirmatory analysis (Table 6), the general factor explains 30% total variance, and the five group factors explain, 4%, 6%, 7%, 3%, and 3%, with 47% error. Thus, the general factor accounts for nearly 57% of the common variance extracted. Again, using the confirmatory bifactor results (Table 6), if a composite were formed based on summing the OAS items, coefficient omega hierarchical = .82 and EVC = .87^2,3 (see bottom row Table 6 for bifactor model); thus we conclude that 82% of the variance of this composite could be attributable to variance on the general factor. The group factors would account for 3%, 4%, 3%, 1%, and 2% (5% error in the aggregate). Thus, in our view, despite the empirical fact that the data are multidimensional, scores derived from the OAS primarily reflect a single common source, alexithymia (depending, of course, on further construct validity work). We recommend continuing the practice of using total, not subscale, scores. We also recommend reporting a reliability of approximately .80 as opposed to the somewhat deceptive reported alphas, which generally are > .90.

Judging the Feasibility of an IRT Model

Dimensionality issues are of paramount concern to researchers who wish to apply unidimensional IRT (Embretson & Reise, 2000) measurement models. These models assume unidimensionality (i.e., one and only one common factor underlies item responses) and local independence (i.e., no correlated residuals -- after extracting a single common factor, item responses are uncorrelated). Because, a) most IRT models used today assume unidimensionality, and b) data are never truly unidimensional, there is constant debate in the psychometric literature about how best to respond. Researchers have explored the robustness of unidimensional IRT model parameter estimates to multidimensionality violations (e.g., Drasgow & Parsons, 1983; Reckase, 1979), and one conclusion is that if the data have a “strong” common factor or multiple highly correlated factors, then IRT item parameter estimates are not seriously distorted.

Accordingly, over the years researchers have developed a variety of schemes and rules-of-thumb for judging whether a dataset is unidimensional enough for IRT model application, including use of SEM fit statistics, inspection of residuals after fitting a one-factor model, and comparing the ratio of 1st to 2nd eigenvalues. This is not the place to point out the strengths and weaknesses of these “unidimensional enough” indices. Rather, suffice it say that the ultimate goal of measurement is to assess individuals on the common construct underlying the items. If data truly are multidimensional, then the general trait in the bifactor model is the most reasonable approximation to that common construct. In turn, the ultimate goal of a unidimensional IRT analysis is to correctly estimate the item parameters (e.g., item discrimination) linking items with this common latent variable, even in the presence of violations of perfect unidimensionality.

One method of exploring this issue is as follows: if one fit a unidimensional factor model and a bifactor model to the same dataset, any discrepancy among the general factor loadings in the bifactor model and the loadings in the unidimensional model are, by definition, an indicator of problems with the unidimensional model parameter estimates. That is, if the two sets of loadings are different, the loadings in the unidimensional model are ipso facto distorted by virtue of forcing inherently multidimensional data into a unidimensional framework. Thus, given that the factor analytic model easily can be transformed into an IRT model, Reise, Morizot, and Hays (2007) and Reise, Cook, and Moore (under review) propose that in any application of a unidimensional IRT model, a corresponding bifactor IRT model should be reported so that reviewers can more readily tell whether multidimensionality seriously distorts the parameter estimates in the unidimensional model.

Although not demonstrated here, note that it is quite possible a unidimensional IRT model may well be adequate even in the presence of multidimensional data. One needs to be mindful that the most important issue in applying an IRT model is not absolute “fit” of a unidimensional model or whether a multidimensional model provides a superior relative fit. Rather, the most important considerations are: a) is there a common factor running among the items, b) is the common latent trait identified correctly; that is, does it reflect what is in common among all the items or distorted by multidimensionality, and c) to what degree do the item parameters reflect the relation between the common latent trait (purified of multidimensionality) and the item responses. When items load highly on the general factor in a bifactor model, and content (group) factors are roughly similar in size and item-intercorrelation, it may well be the case that multidimensionality, indeed, is mere nuisance in terms of fitting a unidimensional IRT model. In the present case, for example, notice that the loadings in the unidimensional model (Table 5) are very similar to those on the general factor in the bifactor (Table 6).

Strengths and Limits of the Bifactor Model

We believe that a fair reading of the personality assessment literature supports the following: when a scale is subjected to “confirmatory” factor analyses, the conclusion is, almost without exception, that the data are multidimensional (or at the least, correlated residuals need to be specified to achieve acceptable fit). In fact, authors of almost all the CFA articles cited in the beginning of this manuscript reach this conclusion. On the other hand, when a scale is being considered for IRT modeling, the conclusion almost always is that the item responses are “unidimensional enough” (see Reise & Waller, 2009, for a review of IRT applications). Perhaps the mostly frequently encountered phrase in published IRT applications is, “Some evidence of multidimensionality was found, but we concluded there was a strong single common factor, and thus, the data are unidimensional enough for an IRT model.”

How the assessment community arrived at this point and why scale developers, critics, and users remain somewhat at odds is beyond the scope of this paper. Suffice it to say, given the challenges inherent in writing a set of scale items that: a) measure a single target construct but are not entirely redundant (i.e., the same question asked over and over), b) are heterogeneous enough to validly represent the diverse manifestations of the construct, and c) provide acceptable reliability, it is not surprising that psychological test data often are consistent with multiple models. Thus, by judicious selection of fit statistics and rules-of-thumb, and by deciding whether to parcel items or allow correlated residuals, informed researchers basically can conclude whatever they wish regarding dimensionality, the applicability of latent variable models such as unidimensional IRT models, and the ultimate interpretability of scale scores.

How, then, are instruments best scored in real-world clinical and research settings, and what guidance can we offer clinicians and applied researchers? Clearly, a central question we have raised is whether more frequent and better use of a bifactor model can help resolve these issues. In this regard, part of the problem in the traditional psychometric evaluation of scales is that the wrong default model is used. That is, Model A (the unidimensional) not only is the model required for application of unidimensional IRT models, it also is used as an “ideal” in exploratory and confirmatory factor analytic investigations. Yet, item response data drawn from substantively complex measures never will be strictly unidimensional. Moreover, it has long been recognized (e.g., Humphreys, 1959) that even if achievable, Model A is not necessarily desirable. To achieve Model A, one essentially has to write a set of items with very narrow conceptual bandwidth (i.e., the same item written over and over in slightly different ways), which results in poor predictive power or theoretical usefulness.

Given that the goal of measurement almost always is to scale individuals on a single common dimension, perhaps the use of Model A as the default standard has been a mistake. Maybe the bifactor model – which contains a single common trait but also allows for multidimensionality due to item content diversity – provides a better foundational model for conceptualizing dimensionality and for understanding what factors are influencing scores derived from a psychological measure. Of course, we have not provided conclusive evidence for this assertion; however, as argued above, among the advantages of adopting the bifactor model are that it:

1. allows researchers to scale individuals on a single trait but at the same time control for the distorting effects of multidimensionality caused by item content clusters,

2. provides a framework for the computation of informative statistics, such as coefficient omega. These statistics reflect the interpretability of scale scores as insular constructs,

3. assists in the study of the distorting effects of forcing multidimensional data into a unidimensional model by comparing the results of a bifactor model with a unidimensional model, and

4. makes it possible for one to study the unique contribution of the general and group factors to the prediction of external variables.

Outside of cognitive testing, however, the bifactor model mostly has been poorly received by personality, psychopathology, and health outcomes researchers. One obvious reason is that there has never been a “bifactor” command on standard statistical software packages (but see Wolf & Preising, 2005; Jennrich & Bentler, under review). Beyond this convenience factor, however, our experience tells us that researchers view bifactor structures with great suspicion. In what follows, we consider three broad reasons: a) interpretation, b) specification, and c) restrictions.

Interpretation

One issue with the bifactor structure is the conceptualization itself, that is, the view that there is a general common trait, plus additional traits, and that all of these are orthogonal. One colleague asked recently, what does it mean to say a task is mostly accounted for by intelligence (general) but also accounted for by working memory that is “independent of” intelligence? In what sense can there be a working memory that is independent of general intelligence? Cast in present terms, what does it mean to propose a group factor of “rigidity” or “humorless” that partially reflects alexithymia but also has a specific component that is independent of alexithymia? In short, some researchers are skeptical that the model itself makes any sense. Clearly one is free to ask such a question, but a perfectly reasonable response is to ask, in what sense is the correlated traits model a more plausible or valid reflection of the nature of psychological traits and behavior? In our view, the next generation of neuro-biological based personality research may well provide insights into these issues.

Model Specification

Imagine a researcher considering the application of bifactor models to his/her item response data as in the present study. The first questions that would need to be addressed are: how many group factors should the model have, and once this is known, how and how well can the model's parameters be estimated? The “number of factors to extract” has always been a vexing problem in traditional factor analysis, and it can become even more complicated in bifactor analysis. One reason is that, for a bifactor model, it would be wise to have at least three group factors, for the group factors to be balanced in terms of the numbers of items, and for each group factor to have at least three items loading simply.

What should a researcher do when the construct suggests only two conceptually meaningful clusters, such as dispositional hope (see Brouwer et al. 2008)? What should be done in the analysis of an existing measure when one content domain is represented by twelve items, a second is represented by four, and a third appears to only have two potential marker items? Can the bifactor still recover the “true” common latent dimension under these conditions? Moreover, in applied data analysis, often it is very challenging to tell whether there is a group factor or if a cluster of items is more a doublet or triplet (same item content stated in slightly different ways). In the presence of such doublets and triplets, McDonald (1999) concludes a data set cannot have any identifiable dimensionality and most certainly cannot have even an IC basis. Finally, being the most general model, the bifactor contains the most paths to estimate and thus the fewest degrees of freedom. Some would argue such a solution represents an overdetermination of the data and is too clumsy for routine use in structural modeling.

Restrictions

Beyond the major assumption of orthogonality, the bifactor model also has restrictive assumptions that need to be met for group factors to be identified, substantively interpreted, and have parameters that are properly estimated. For a group factor to be identified, for example, there must be at least three items that load on the general and only one group factor. More important, although items displaying cross-loadings on the group factors are allowable in exploratory solutions, such items lead to distorted and untrustworthy item parameter estimates in restricted bifactor solutions. (This also is true of second-order models, but this has not adequately been addressed/acknowledged in the literature.) Stated differently, a restricted bifactor model demands not only that the data be multidimensional but also that the multidimensionality be well structured (i.e., each item measures a general trait and one and only one subtrait). Lest one claim the second-order provides relief on this front, Wolff and Preising (2005, p. 49) note, “When a variable is factorially complex – that is, it loads on several factors – problems of interpretation are aggravated. In this case, higher order FA does not yield total effects.”

Conclusion

“We have already concluded that one possible approach that could be used to deal with the problem of representing aspects of constructs with different degrees of generality is hierarchical factor-analytic modeling…. Still, the impact on practical applications has been limited.” (Gustafsson & Aberg-Bengtsson, 2010, p. 104).

The above quote illustrates the point that many researchers over the years have made; that is, models such as the bifactor provide an excellent framework for studying how measures containing heterogeneous item content still can be understood as primarily measuring one construct. We agree with Gustafsson and Aberg-Bengtsson that the bifactor model is poorly understood and seldom used by applied researchers. This is unfortunate because, when working with substantively complex constructs, a bifactor model can serve as an informative psychometric tool as we have demonstrated throughout the present paper. Despite a promising future, we believe that research is needed to further explore a) the strengths and weaknesses of target (Browne 2001) and direct (Jennrich & Bentler, under review) bifactor rotation methods, b) the issue of cross-loadings, and their potentially distorting effects on restricted models, c) the robustness of the model to differential group factor strength, and d) how this model can best be used to inform scale development, interpretations, and revisions.