Dynamics and Heterogeneity in the Process of Human Frailty and Aging: Evidence From the U.S. Older Adult Population

Abstract

Objectives.

This study investigated the dynamics and heterogeneity of the frailty index (FI) conceived as a systemic indicator of biological aging in the community-dwelling older adult population in the United States.

Methods.

We used panel data on multiple birth cohorts from the Health and Retirement Survey 1993–2006 and growth curve models to estimate age trajectories of the FI and their differences by sex, race, and socioeconomic status (SES) within cohorts.

Results.

The FI for cohorts born before 1942 exhibit quadratic increases with age and accelerated increases in the accumulation of health deficits. More recent cohorts exhibit higher average levels of and rates of increment in the FI than their predecessors do at the same ages. Females, non-Whites, and individuals with low education and income exhibit greater degrees of physiological deregulation than their male, White, and high-SES counterparts at any age. Patterns of sex, race, and SES differentials in rates of aging vary across cohorts.

Discussion.

Adjusting for social behavioral factors, the analysis provides evidence for physiological differences in the aging process among recent cohorts of older adults, points to the need for biological explanations of female excess in general system damage, and reveals the insufficiency of any single mechanism for depicting the racial and SES differences in the process of physiological deterioration.

THE concept of frailty has long been used to study aging-related processes in human populations. Early frailty models developed in the tradition that conceptualized differences in susceptibility to disease and death among individuals as fixed individual frailty during the life course (Vaupel, Manton, & Stallard, 1979). Over the past two decades, the notion of frailty has acquired a more physiological meaning in studies of factors and processes associated with individual biological aging. A variable frailty concept has appeared that considers frailty a specific physiological state of increased nonspecific vulnerability to stressors due to decreased physiological reserves and deregulation of multiple biological systems that typically increases at late ages. This results in difficulty maintaining homeostasis in response to “normal” perturbations that would not create such problems at younger ages (Fried, Ferrucci, Darer, Williamson, & Anderson, 2004).

Empirical tests of the theoretical concept of individual frailty were undertaken by various groups in different settings (e.g., Bortz, 2002; Lally & Crome, 2007; Manton, Woodbury, & Stallard, 1995). Although the stochastic and multidimensional formulation of the aging processes yields more insight into the variability of frailty (Manton et al.), its reliance on complex mathematical models and the large number of variables prevents broad applications (Gavrilov & Gavrilova, 1991). The current view of frailty as a systemic disorder manifested through aging-associated health problems suggests an alternative approach using a small number of generalized variables that capture major physiological dimensions of the human organism through summaries of various signs, symptoms, or abnormalities (Fried et al., 2004; Mitnitski, Mogilner, MacKnight, & Rockwood, 2002; Seeman, McEwen, Rowe, & Singer, 2001; Strawbridge, Shema, Balfour, Higby, & Kaplan, 1998). The frailty index (FI) is one such generalized variable that was developed to measure aging-associated health disorders and deficits that have accumulated within individuals; it is quantified as the proportion of deficits present, including symptoms, disabilities, and disease classifications for a given person at a given age (Mitnitski et al., 2002; Rockwood, Hogan, & MacKnight, 2000). This approach to individual frailty and aging moves beyond the conventional approach seeking single markers of aging and aims to characterize integrative and systemic changes in aging organisms. It extends earlier work by Strawbridge and colleagues that conceived frailty as a syndrome typically evidenced in multiple areas and as general vulnerability to environmental challenge. Consistent with the notion of “allostatic load,” which emphasizes the biological complexity of the comorbidity process and the cumulative nature of biological deregulation across multiple systems with aging (Seeman et al.), the FI assesses frailty by simultaneously incorporating multiple domains of deficits and offers more precise estimation of physiological reserves.

Since the introduction of the FI (Mitnitski et al., 2002; Rockwood et al., 2000), a number of studies have been conducted to test its utility as a composite measure of individual frailty in different populations. The FI has been shown to have good construct and criterion validities and to be compatible with the view of frailty as the failure to integrate the complex responses required to maintain function (Mitnitski, Song, & Rockwood, 2004). Although similar constructs such as allostatic load or index of phenotypic frailty (Fried et al., 2004) require detailed biomarker measures based on clinical examinations, the FI is based on conventional self-reported data that are more readily available in demographic and health surveys. In addition, studies using the FI largely replicate findings based on clinical databases (Goggins, Woo, Sham, & Ho, 2005; Mitnitski et al., 2004) and show it can more precisely characterize susceptibility to death and predict survival and longevity because it assesses a broader spectrum of disorders than specific clinical syndromes and physiological risk factors (Kulminski, Ukraintseva, Kulminskaya, et al., 2008). Another important advantage of the FI is that it can be constructed using the set of deficits available in any specific study. For instance, it is found that even a restricted set of deficits (about 20) that occur with reasonable frequency and variability can represent a wide variety of impairments (Mitnitski et al., 2002) and can characterize frailty by their aggregate ability rather than the substance of the individual disorders (Kulminski, Arbeev, et al., 2008; Mitnitski et al., 2004). Furthermore, the statistical properties of the FI, such as age distributions and its effect on other outcomes such as mortality, are largely insensitive to differences in the study designs and the number and selection of the variables that were used (Mitnitski et al., 2005). In fact, this property holds even for random compositions of the deficits in the FI (Rockwood, Mitnitski, Song, Steen, & Skoog, 2006). The consistency and robustness of the construct, therefore, provides a sound empirical basis for future research using the FI. In sum, the FI is found to perform well in characterizing individual heterogeneity in frailty by age and sex in population-based studies, serving as an alternative to chronological age for characterizing the overall burden of senescence, and can be an efficient and robust measure of biological aging and general system damage (Kulminski, Arbeev, et al.; Mitnitski et al., 2002; Woo, Tang, Suen, Leung, & Leung, 2008).

Although the FI has attracted increasing attention in gerontology, epidemiology, and clinical studies as a systemic measure of aging, there remains a lot to be learned about the nature and heterogeneity of the process by which health disorders and deficits accumulate and accelerate as individuals move through the life course. This study examines three remaining questions.

First, the relationship between frailty and aging is not clear due to a lack of longitudinal studies on the age trajectory of the FI. It is essential to understand this relationship because it can be used to characterize the dynamics of the aging process and the rate of biological aging. The concept of frailty as a physiological state of nonspecific vulnerability to stressors holds that individuals will likely accumulate deficits when stresses exceed the limits of an organism’s stress resistance (Fried et al., 2004). Constant stress load corresponds to a linear change in the FI with age due to its cumulative nature, whereas increases in stress load with age corresponds to accelerated increases in the FI (Kulminski et al., 2006). The age pattern of the FI, therefore, sheds light on the process by which compromises in individuals’ viability with age accumulate and shows the utility of the FI as a systemic indicator of aging. Extant evidence of a nonlinear increase in the FI with age largely comes from cross-sectional data that lack cross-time linkages within individuals (e.g., Kulminski et al., 2006; Mitnitski et al., 2004). In addition, the implicit assumption of previous studies is that no confounding of aging with birth cohort effects exists. This assumption may not be tenable in light of cohort changes in health. Although studies documented improvements in health capital and survival across historical cohorts (Finch & Crimmins, 2004; Yang, 2008), more recent cohorts may have worse health than their predecessors do at the same ages that can be attributed to a variety of social behavioral factors such as smoking and an earlier onset of debilitating conditions (such as obesity and diabetes) in more recent cohorts (Finch, 2007; Soldo, Mitchell, Tfaily, & McCabe, 2006; Yang & Lee, 2009). Only one study of age patterns of the FI used longitudinal cohort-specific data (Kulminski et al., 2007), but its comparisons of wave-specific means are descriptive in nature and begs further analysis using multivariate regression models. The known age pattern needs to be validated with an analysis of within-cohort true age changes in frailty before it can definitively represent the aging process.

Second, even less is known about population heterogeneity than dynamics of frailty with aging. Sex-specific patterns of frailty indicate that women have higher levels of frailty at all ages. However, the sex difference is statistically significant in some studies (Goggins et al., 2005; Mitnitski et al., 2004) but not in others (Kulminski et al., 2006; Strawbridge et al., 1998). Few extant studies examined race differences, largely because they are based on racially homogeneous populations. One study that did suggest no significant ethnic difference, but it is based on a small sample from one geographic area (Alameda County, CA), which precluded analyses by ethnicity (Strawbridge et al.). The focus of previous studies on statistical distributions and properties of the FI in the overall population also obscures the possible socioeconomic stratification of frailty within the population. In all cases, investigations of social heterogeneity in age trajectories of frailty and hence in rates of deficit accumulation are conspicuously absent. It is well established that low socioeconomic status (SES) and the lower social status of racial minorities are associated with greater exposure to adversity in life and to a range of negative environmental factors (such as toxins, crime, smoking, and poor diet) but less access to protective and effective coping resources (such as social integration, knowledge, and safe areas to exercise; Link & Phelan, 1995). Therefore, the cumulative lifetime adversity and disadvantage experienced by individuals of lower status means that they are likely to exhibit higher degrees of loss in physiological reserve at any given age and incur physiological deterioration at earlier ages. A recent study on the Canadian population indeed suggests that social vulnerability—which encompasses a variety of social risk factors such as social support, living situation, and SES—is moderately correlated with the FI (Andrew, Mitnitski, & Rockwood, 2008). The finding relates to distributions of social vulnerability and frailty in the aggregate data. How individuals from different SES strata accumulate age-associated deficits at different rates merits an additional study.

Third, there is a need to extend prior analyses to larger samples of community-residing adults across a larger segment of the life course in the United States. The utility and properties of the FI have been mostly tested in Canadian (e.g., Mitnitski et al., 2004) and Chinese populations (Goggins et al., 2005) that are ethnically and culturally distinct from the U.S. population and share different health care systems. There have been U.S.-based studies of frailty measures. Apart from the analysis using the relatively small Alameda County Study (Strawbridge et al., 1998), recent analyses of the FI based on the National Long Term Care Survey (NLTCS) are especially useful for understanding aging-related processes for disabled and institutionalized populations (Kulminski et al., 2006, 2007), and those based on the Cardiovascular Health Study and Framingham Heart Study focused on specific risk factors and the development of heart disease and stroke (Kulminski, Arbeev, et al., 2008; Kulminski, Ukraintseva, Kulminskaya, et al., 2008). These findings need to be corroborated in other large-scale nationally representative longitudinal studies of community samples that potentially have different trajectories and structures of heterogeneity in frailty. Previous studies are also largely limited to older adults (65+ years). Incorporation of younger adults (middle-aged) may provide more insights into the cumulative nature of frailty. In all, comparisons across settings can contribute to a more general understanding of the characteristics and processes of human frailty and aging.

This study aims to fill the above gaps in our knowledge about frailty and aging by investigating age trajectories of cumulative health deficits and disorders summarized by the FI in a nationally representative longitudinal sample of community-dwelling older adults in the United States. It further explores the population heterogeneity in age trajectories of the FI and assesses how the rate of deficits accumulation with age and hence the acceleration of the aging process differs by sex, race, and SES.

DATA AND METHODS

Data

We used data from the Health and Retirement Survey (HRS), which is a nationally representative longitudinal survey of the U.S. older population conducted every 2 years from1992 to 2006 that includes several birth cohorts with different entry years. This study used the RAND HRS Data file and includes the maximum number of waves for each of the four birth cohorts for whom data on the FI are available: the Study of Assets and Health Dynamics Among the Oldest Old (AHEAD) cohort (born before 1924) surveyed in 1993, 1995, and 1998–2006; Children of Depression (CODA) cohort (born 1924–1930); HRS cohort (born 1931–1941); and War Baby (WB) cohort (born 1942–1947) surveyed in 1996–2006. We did not include the youngest cohort—the Early Baby Boomers (EBB) cohort—because it entered the survey in 2004 and did not have sufficient data on age trajectories over time. The cohort membership is based on the actual birth year variable (RACOHBYR). The analytic samples for all cohorts exclude small numbers of respondents who had missing data on any covariates used in the regression analysis. The numbers of person-year observations pooling all waves for the AHEAD, CODA, HRS, and WB cohorts are 25,207, 13,446, 37,137, and 12,327, respectively, which include observations contributed by respondents who were present at all waves, respondents who died at follow-ups (ranging from 4% for the WB cohort to 47% for the AHEAD cohort), and those who were nonrespondents at follow-ups (about 11% for all).

Construction of the FI is based on the subset of health deficits most similar to those assessed in the original studies from the Canadian Study of Health and Aging (CSHA) and includes symptoms, disabilities or impaired functions, disease classifications, and health attitudes (Mitnitski et al., 2002, 2004). Specifically, we include 30 questions available across waves: 8 chronic illnesses respondents ever had, including high blood pressure, diabetes, cancer, lung disease, heart problems, stroke, psychological problems, arthritis; 5 disabilities in activities of daily living (ADL), including difficulty in walking across room, dressing, bathing or showering, eating, getting in/out of bed; 7 disabilities in instrumental activities of daily living (IADL), including difficulty in using a map, the toilet, telephone, managing money, taking medications, shopping for groceries, and preparing hot meals; 8 depressive symptoms as measured by the Center for Epidemiological Studies-Depression (CES-D) scale, including felt depressed, everything an effort, sleep was restless, felt lonely, sad, could not get going, enjoyed life, was happy; self-rated health; and obesity (body mass index ≥ 30). All but one variable are binary, with 1 indicating the presence and 0 indicating the absence of the deficit. Self-rated health was a 5-point ordinal scale and was mapped into the [0, 1] interval: 0 (excellent), 0.25 (very good), 0.5 (good), 0.75 (fair), and 1 (poor). Because six of seven IADL items and most of the frailty associated items were not available for the calculation of the FI in the 1992 and 1994 surveys, respectively, we had to omit the data for those two waves for the HRS cohort. Following extant practice, we define the FI as a count of deficits for any given person divided by the total number of possible deficits. With no missing data, the denominator would be the theoretical maximum for all individuals (30 in this study). In our study, although the majority of respondents had complete measures of all 30 items, the exclusion of respondents with missing answers would decrease the sample size substantially. We therefore included respondents who had data on at least 25 of the 30 conditions. For instance, if a respondent was administered 30 questions and responded positively (there is a deficit) to 4 and negatively (no deficit) to 23 of them, then the FI for this person is 4/27. Previous research shows no difference in the use of the full set of 30 or so deficits and a reduced set of 26 deficits (Kulminski et al., 2006). We confirmed this finding in our own supplemental analysis by comparing the results based on the reduced sample whose respondents had no missing items and the current sample whose respondents had at most five missing items. We report analysis from the latter sample with a larger number of observations. The FI ranges between 0 and 0.9 and averages between 0.14 and 0.18 across cohorts (Table 1).

Table 1.

Weighted Summary Statistics of All Variables in the Analysis: HRS 1993–2006

		All (N = 88,117)		AHEAD (N = 25,207)		CODA (N = 13,446)		HRS (N = 37,137)		WB (N = 12,327)
Variable	Description and coding	M/%	SD	M/%	SD	M/%	SD	M/%	SD	M/%	SD
FI	Frailty index	0.16	0.13	0.18	0.13	0.17	0.13	0.14	0.12	0.14	0.13
Age	Chronological age	67.75	10.06	80.06	5.47	73.51	3.31	63.52	4.52	56.35	3.26
Female	Respondent’s sex 1 =  female; 0 = male	56%	0.50	60%	0.49	56%	0.50	54%	0.50	53%	0.50
Non-White	Respondent’s race 1 =  non-White; 0 = White	12%	0.32	8%	0.28	11%	0.32	13%	0.33	15%	0.36
Education:  low	Years of schooling 1 =  0–11; 0 = 12+	26%	0.44	36%	0.48	29%	0.45	23%	0.42	16%	0.37
Poverty	Family income 1 = below  poverty level; 0 = above	10%	0.29	12%	0.34	10%	0.26	9%	0.29	9%	0.28
Died	Attrition type at follow-up  1 = deceased; 0 = others	19%	0.39	47%	0.50	16%	0.36	8%	0.27	4%	0.19
Nonresponse	Attrition type at follow-up  1 = nonresponse; 0 = others	11%	0.32	11%	0.31	9%	0.29	12%	0.33	12%	0.32
Not married	Marital Status 1 = not currently  married; 0 = currently married	37%	0.48	53%	0.50	40%	0.49	30%	0.46	28%	0.45
Ever smoked	1 = ever smoked; 0 = never	67%	0.47	56%	0.50	69%	0.46	71%	0.45	73%	0.45

Notes: The N’s presented above reflect the unweighed sample sizes. The weighted sample sizes are slightly smaller due to unavailability of weights for some respondents and are 84,878 for all, 24,635 for AHEAD, 12,065 for CODA, 36,953 for HRS, and 11,225 for WB. This discrepancy is not relevant to subsequent regression analysis that was unweighed. AHEAD = Assets and Health Dynamics Among the Oldest Old; CODA = Children of Depression; HRS = Health and Retirement Survey; WB = War Baby.

Age at first entrance into the samples ranges from 70+ for the AHEAD cohort, 66–82 for the CODA cohort, 55–75 for the HRS cohort, and 49–64 for the WB cohort. At each follow-up, respondents in each cohort aged together, yielding age trajectories of the FI. Other key variables include sex (female = 1 and male = 0), race (non-White = 1 and White = 0), and SES, which is represented by levels of education (low or 0–11 years = 1 and high or 12+ years = 0) and family income (below poverty level = 1 and above poverty level = 0). The RAND HRS data file includes a measure of poverty beginning in 2002 that uses the poverty threshold levels from the U.S. Census Bureau and family composition to determine the poverty status of an HRS family. Using the same method and the Census Bureau’s poverty threshold levels for corresponding years, we constructed this variable for the earlier waves. We combined Blacks and other races into the non-White group due to a lack of statistical significance between these groups in regression analysis. We explored other operational definitions of SES using categorical and continuous variable specifications. Because they yielded less significant coefficients and inferior model fits than the dichotomous specification, we use the latter in the final analysis. The analysis accounts for selection due to attrition by controlling for attrition status: died (= 1 if deceased at follow-up) and nonresponse (= 1 if nonrespondent at follow-up). Marital status (not married = 1 and married = 0) and smoking (ever smoked = 1 and never smoked = 0) are controlled to take into account the effects of social integration, solidarity, and a key health behavior.

The HRS oversamples racial minorities such as Hispanics and Blacks and provides weighting variables to make it representative of the community-based population. Table 1 summarizes the weighted descriptive statistics of all variables by birth cohort. Regression analysis presented below is unweighed because it controls for variables on which weights were based and did not produce significantly different results from analyses using weights (Winship & Radbill, 1994).

Analytic Methods

We employ the hierarchical linear model (HLM) for the regression analysis (Raudenbush & Bryk, 2002). The two-level HLM applied to longitudinal data is also termed the growth curve model because it depicts the growth trajectory with age within individuals (Level 1 observation) and heterogeneity in these trajectories across individuals (Level 2 observation). The model specification is the following:

Level 2 model:

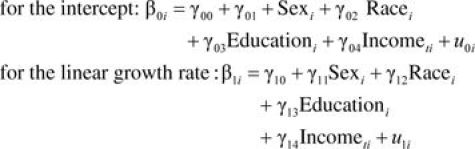The Level 1 model characterizes within-individual change with age. In this model, the FI for person i at time t is modeled as a function of within-individual time-varying covariates, including a quadratic function of age. Other parametric forms of the age–FI association such as linear and log linear functions were also tested. The current parameterization was chosen based on superior model fit. The Level 2 model assesses individual differences in change with age and determines the associations between the change with age and individual-level characteristics. Accordingly, the intercept and age coefficients or growth rates are modeled as functions of sex, race, and SES (indicated by education and income). The model for the quadratic growth rate was tested but omitted here due to lack of statistical significance and no improvement in model fit. The coefficients γ₀₀–γ₀₄ represent the effects on mean level of FI, and the coefficients γ₁₁–γ₁₄ represent the effects on the linear rate of change with age in the FI. In addition, we add control variables in the final model to adjust for the gross effects. We assess model fit by generalized model fit statistics for nonnesting models—Bayes Information Criterion (BIC).

The theoretical focus of this research is on changes in the FI with age and the heterogeneity therein. We note, however, that better inference can be achieved by considering FI changes with age in a cohort-specific context. It is likely that the four cohorts in the HRS study differ in either levels or rate of change of the FI or both. They may also differ in the pattern of heterogeneity in the age trajectories. A major strength of the current study is that it uses the accelerated longitudinal panel design that follows multiple birth cohorts for multiple waves. This design allows a more rapid accumulation of information with age for multiple cohorts than does a single longitudinal cohort design, and it makes cohort analysis possible. Formal methodological (Miyazaki & Raudenbush, 2000; Raudenbush & Bryk, 2002) and substantive studies (Willson, Shuey, & Elder, 2007; Yang, 2007; Yang & Lee, 2009) have illustrated the estimation of cohort differences in age trajectories for such a research design using the HLM approach. Although some ages cannot be observed for all cohorts, the models yield significance tests of at least overlapping segments of the life course for adjacent cohorts. As waves of data accumulate, age and cohort will become less and less confounded, making it increasingly possible to estimate stable cohort-specific age trajectories. This HRS study builds upon these studies and uses more waves of data, which provide higher power for testing hypotheses. In addition, we adopt the analytic strategy of using centered age variables: Age is grand mean centered in the model for all cohorts combined and cohort median centered in cohort-specific models (see, e.g., Raudenbush & Bryk). Age centering eases the interpretation of the intercept, stabilizes estimation, and prevents the bias in the estimate that arises from systematic variation in mean age across the cohorts, hence eliminating the confounding of age and cohort variables. We also divided the age variable by 10 to make coefficients more visible.

We conducted a likelihood ratio test that compares models to examine whether cohort-specific trajectories can actually be represented by a single mean-age trajectory (convergence test). We rejected the convergence hypothesis that there are no cohort differences in age trajectories based on the presence of significant cohort effect coefficients and the likelihood ratio test (LR = 3,522 (14), p < .001). Given the apparent cohort variations in health, we further estimate the growth curve models separately for each cohort to reveal more detailed patterns within cohorts. We test cohort differences in the regression coefficients in these cohort-specific models with the Wald chi-squared test. All statistical analyses are performed using Stata 10.0.

RESULTS AND FINDINGS

The growth curve model estimates for all and by birth cohort are presented in Table 2, which includes fixed effect coefficients, significance tests, and model fit statistics. All models presented control for all covariates and are the final and best-fitting models for each sample considered.

Table 2.

Growth Curve Models of Frailty and Aging by Cohort

	All (49+ years)	AHEAD (70+ years)	CODA (66–82 years)	HRS (55–75 years)	WB (49–64 years)	Cohort difference
Variable	Coefficients (z score)	Coefficients (z score)	Coefficients (z score)	Coefficients (z score)	Coefficients (z score)	Wald test, p Value
For intercept, β0i
Intercept, γ00	0.087*** (46.54)	0.121*** (28.70)	0.103*** (24.56)	0.087*** (33.11)	0.089*** (20.93)	.000
Female, γ01	0.025*** (14.98)	0.027*** (7.61)	0.026*** (6.79)	0.029*** (12.26)	0.022*** (5.64)	.837
Non-White, γ02	0.033*** (15.55)	0.022*** (4.93)	0.015** (2.72)	0.024*** (8.26)	0.037*** (7.68)	.015
Education: low, γ03	0.046*** (26.33)	0.036*** (11.26)	0.052*** (13.12)	0.061*** (23.17)	0.078*** (15.82)	.000
Poverty, g04	0.016*** (15.07)	0.012*** (5.82)	0.012*** (4.27)	0.014*** (9.82)	0.018*** (6.71)	.016
For linear growth rate, β1i
Intercept, γ10	0.045*** (38.13)	0.101*** (30.67)	0.074*** (17.39)	0.048*** (22.38)	0.043*** (9.33)	.000
Female, γ11	0.000 (−0.33)	−0.002 (−0.57)	0.003 (0.48)	0.001 (0.50)	0.011* (2.05)	.027
Non-White, γ12	−0.006** (−2.98)	−0.003 (−0.63)	−0.021* (−2.43)	−0.006† (−1.66)	0.005 (0.74)	.173
Education: low, γ13	−0.009*** (−5.62)	−0.005 (−1.40)	0.018** (2.93)	−0.001 (−0.22)	0.004 (0.62)	.973
Poverty, γ14	−0.003** (−3.06)	−0.003 (−0.87)	0.000 (−0.06)	−0.006† (−1.94)	0.014† (1.93)	.987
Quadratic growth rate, β2i	0.014*** (29.80)	0.017*** (8.56)	0.018*** (3.80)	0.008*** (4.41)	−0.002 (−0.48)	.000
Control variables
Died	0.018*** (9.48)	0.040*** (12.96)	0.075*** (17.64)	0.074*** (21.46)	0.104*** (12.84)	.000
Not married	0.022*** (19.57)	0.014*** (6.45)	0.027*** (9.93)	0.024*** (14.29)	0.020*** (6.31)	.033
Ever smoked	0.027*** (16.70)	0.025*** (7.77)	0.010** (2.63)	0.016*** (6.66)	0.007† (1.91)	.003
Goodness of fit (BIC)	−173,001.3	−43,276.8	−27,701.5	−80,921.9	−25,616.0
N	88,117	25,207	13,446	37,137	12,327

Notes: Estimates presented above are fixed effect coefficients; random effect variance components are all significant but omitted. AHEAD = Assets and Health Dynamics Among the Oldest Old; BIC = Bayes Information Criterion; CODA = Children of Depression; HRS = Health and Retirement Survey; WB = War Baby.

†p < .10; *p < .05; **p < .01; ***p < .001 (two-tailed test).

We find quadratic age trajectories of the FI for all, indicating accelerated increases in the accumulation of health deficits and disorders with age, which can be considered as rates of biological aging. Specifically, the estimated mean value of the FI is 0.087 at the age of 68 years (grand mean age of the pooled sample), and both the linear and quadratic age coefficients (growth rates) are highly significant, indicating an average rate of increment in the FI of 0.045 (p < .001) that increases at the rate of 0.014 (p < .001) with each additional 10 years of age (49+). In earlier analyses, the nonresponse type of attrition was also controlled, but its effect was not statistically significant in any models or samples (so those who dropped out due to nonresponse did not differ from those who had complete observations) and thus was omitted in the final models.

The reduced model for all cohorts combined may not represent cohort-specific patterns. We therefore turn to the estimates for the four cohorts. The general quadratic age pattern appears to apply to the AHEAD, CODA, and HRS cohorts. The most recent cohort, the WB cohort, shows only a linear trajectory with no significant rate of acceleration with age. The age trajectory estimates (means, rates of increase, and rates of acceleration) shown in Table 2 pertain to cohort-specific age ranges. To further examine cohort differences at the same ages, we compared predicted age trajectories of the FI (described in the note to Figure 1 and not shown separately) across cohorts. We found that more recent cohorts had higher levels of and steeper growth rates in frailty than earlier cohorts at the same ages, controlling for other factors, including sex and race compositions, SES, mortality, marital status, and smoking. The Wald test suggests that cohort differences in these age patterns of the FI are highly significant (p < .001).

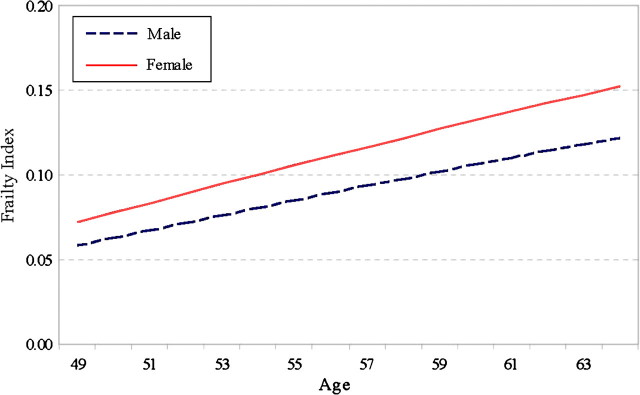
Figure 1.

Age trajectories of the frailty index (FI) by sex: War Baby cohort. Note. We calculated the predicted value of FI based on the model estimates as follows: 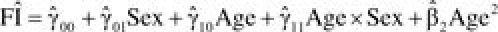which indicates the expected FI score when all the other variables are held constant (set at 0) or for the reference group. For women (sex = 1) at the age of 49, for instance, $\text{F}\widehat{\text{I}}=0.089+0.022+0.043\times \left(\right(49-56)/10)+0.011\times \left(\right(49-56)/10)-0.002\times {\left(\right(49-56)/10)}^2=0.072,$where (49–56) means the age value is centered around the cohort median age of 56, which is further divided by 10, as described in the text. Subsequent figures are constructed similarly.

We also find substantial heterogeneity in the aging trajectories of the FI by social status. First, the effects of sex, race, education, and income are all highly significant on the intercepts or means of the FI. In the model for all, being female is associated with a 0.025 unit higher FI on average, net of other factors. The effect of race is stronger than that of sex: A non-White has a 0.033 unit higher FI on average. And the effect of education is the strongest of all: Having less than a high school education increases the FI by 0.046. Poverty similarly increases one’s FI score by 0.016. The stratification patterns are also observed in each within-cohort model, suggesting that females, non-Whites, and low-SES groups suffer from a greater degree of physiological reserve loss at any given age than their male, White, and higher SES counterparts. There are cohort differences in the race, education, and income effects. The disadvantages of non-Whites and those that have a low level of education and are in poverty seem to be more pronounced in more recent cohorts, such as the HRS and WB cohorts.

Second, the linear (but not quadratic) growth rate of the FI also differs significantly by social status. The specific patterns of heterogeneity vary somewhat depending on the birth cohort considered. The sex difference in the aging trajectory is only significant for the WB cohort: Women show a faster rate of increase in the FI with age than men (0.011, p < .05), which translates into diverging predicted aging trajectories of the FI for the two sexes, as depicted in Figure 1. In the WB cohort, women not only have higher average frailty (lower average physiological capacities) but also a faster rate of aging than men. The racial difference in the rate of aging is significant for all and the CODA and HRS cohorts: Non-Whites show slower rates of increase in the FI with age than Whites (CODA: −0.021, p < .05; HRS: −0.006, p < .10). Figure 2 shows the predicted trajectories of the FI for Whites and non-Whites that converge with age in both the CODA and HRS cohorts and slightly cross over for the oldest ages in the CODA cohort. To the extent that the FI was found to predict mortality well (Mitnitski et al., 2004), the frailty crossover for Whites and non-Whites corresponds to the well-known racial mortality crossover (Nam, 1995).

Figure 2.

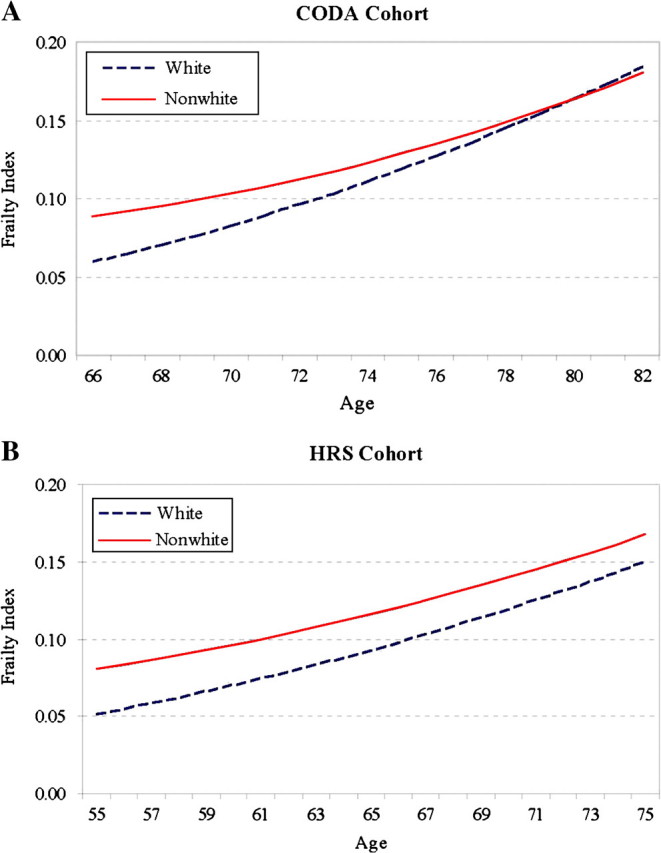
Age trajectories of the frailty index (FI) by race. 2A: CODA = Children of Depression; 2B: HRS = Health and Retirement Survey.

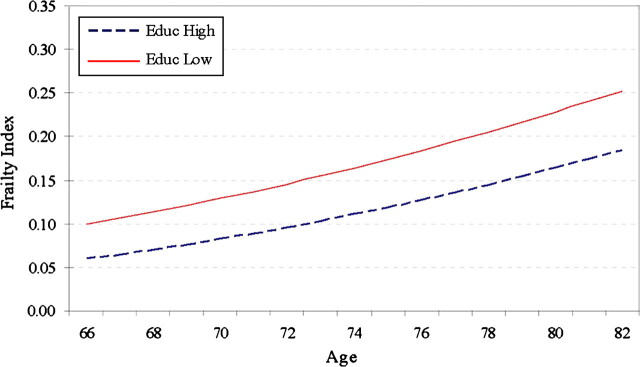
The educational difference in the growth rate of the FI is significant for all and for the CODA cohort. For the total sample, the low-education group shows a slightly slower rate of increment in frailty than the high-education group (−0.009, p < .001). For the CODA cohort, however, the low-education group shows a much faster rate of increment in frailty (0.018, p < .01), leading to a divergence in the trajectories of the FI for the two education groups (as shown in Figure 3). The corresponding results regarding income effects show a significantly slower rate of aging for the poverty group than for the higher income group in the HRS cohort (as shown in Figure 4A) but a faster rate of aging for the poverty group than for the higher income group in the WB cohort (as shown in Figure 4B). Combining the above results on the intercept models suggests two possible scenarios for the low-SES groups. One is that they are particularly worse off because they not only have higher levels of frailty but also experience faster rates of increase in frailty, as shown in the CODA and WB cohorts. The other is that their higher average levels of frailty are tempered somewhat by slightly slower rates of increase in frailty, as shown in the HRS cohort. The Wald tests show that the cohort differences in the race, education, and income effects on the linear growth rate of the FI are not statistically significant. The coefficients in the model for all suggest the dominance of the second scenario in which non-Whites and those of low SES are more frail on average but incur physiological declines at lower rates as they age.

Figure 3.

Age trajectories of the frailty index (FI) by education: Children of Depression cohort.

Figure 4.

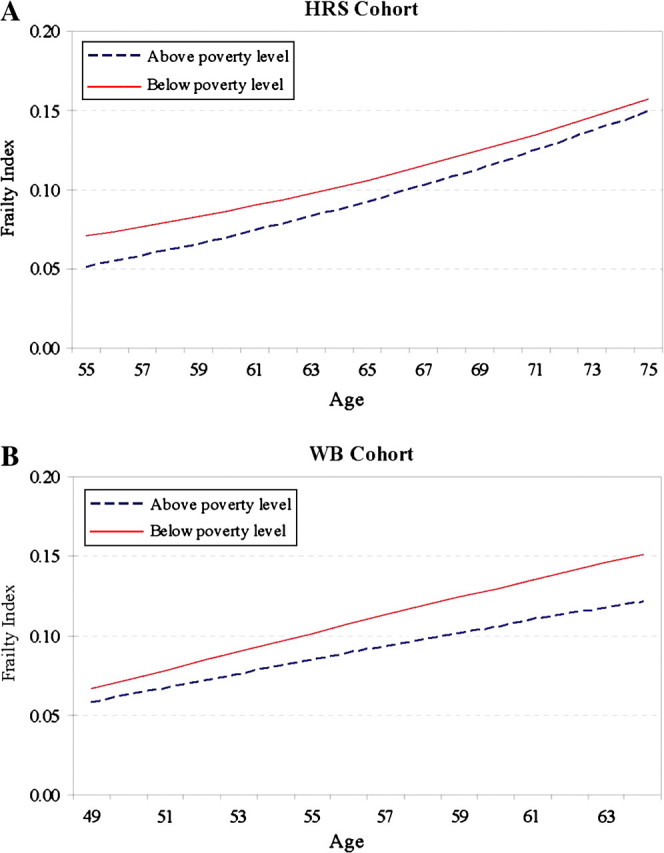
Age trajectories of the frailty index (FI) by poverty status. 4A: HRS = Health and Retirement Survey; 4B: WB = War Baby.

DISCUSSION AND CONCLUSIONS

A growing number of studies of the aging process focus on simultaneous and potentially cumulative physiological effects depicted by the concept of frailty that bears resemblance to allostatic load. The FI developed along this line of research has become one major indicator that can be used to capture the variability in individual rates of biological aging. There is evidence that the FI generally increases with age and exhibits characteristic of an integrative marker of aging. The favorable properties of the FI as a systemic measure of biological aging and aging-associated processes, however, have been established mostly in cross-sectional studies that at best only approximate true age changes over time. This study further examines the dynamics of the FI by modeling within-cohort aging trajectories with longitudinal data. It also extends the current framework of frailty and aging by considering heterogeneity in the way frailty changes with age.

We show that the patterns of FI change with age for cohorts of older adults born before 1942 exhibit nonlinear increases, that is, quadratic increases or acceleration of increments with age. This corroborates the findings from previous studies in various national settings (Goggins et al., 2005; Kulminski et al., 2006; Rockwood et al., 2006) and further supports the view that the FI can serve as a systemic measure of aging. However, we also find variations in rates of aging across these cohorts and even an exception. In the most recent cohort examined (WB cohort born 1942–1947), the age pattern appears linear with no acceleration, suggesting that one does not accumulate more deficits per year as one ages. Because various, albeit not all, social behavioral factors that can contribute to the cohort differences are controlled, this can be regarded as provisionary evidence for physiological differences in the aging process in these cohorts. An alternative explanation, which may not be mutually exclusive to the above interpretation, is that the life history of this younger cohort has yet to unfold. This precludes observation of the frailty acceleration that more likely accompanies transitions to older ages in which stress loads are elevated. Our analysis cannot test this possibility due to lack of data for all adult ages and invites future research to further investigate alternative trajectories of frailty accumulation across a wider range of ages. In any case, the existence of differences in the shapes of cohort-specific trajectories cautions against the universal application of the quadratic parameterization of the FI age pattern to any population and highlights the relevance of historical context and stages of the life course.

We also find that more recent cohorts exhibit higher degrees of loss in physiological reserve and faster increases in frailty than their predecessors do at the same ages. This is consistent with an earlier study by Soldo and colleagues (2006) using the HRS data that show that, at the verge of retirement (aged 51–56 years), EBB and War Babies had poorer health (e.g., more pain and chronic conditions) than earlier cohorts born in 1926–1941. The eroding health of middle-aged persons in the United States has been noted by Banks Marmot, Oldfield, and Smith (2006); their study shows that adults aged 50 years and older in Britain have superior health than those in America. A recent study by Yang and Lee (2009) also indicates that successive cohorts in the United States have higher levels of disability than earlier cohorts at the same ages. Whereas previous studies used only a few domain-specific health indicators and limited waves of longitudinal data, the present study provides additional evidence of cohort change in health using a summary index of physiological deterioration across multiple systems and over longer follow-ups.

Consistent with extant findings, this analysis demonstrates a sex difference in the dynamics of the FI. What is new from this longitudinal study is that this difference hinges mostly on the mean levels of frailty rather than the rates of aging. On average, women bear a larger burden of deficits and disorders than men at any given age. The size of this difference is smaller than that estimated by earlier studies of another elderly sample (Kulminski et al., 2006, 2007) because the sex effect is attenuated by race, SES, and other factors in this analysis. For all but one cohort, we found that men and women accumulate deficits at the same rate, which is equivalent to constant female excess in frailty and parallel sex-specific trajectories of frailty increment with age. In the WB cohort, the rate at which deficits are accumulated is larger for women so that the female excess in frailty increases with age. All evidence points to the overwhelming trend that women exhibit a greater average degree of physiological deregulation and vulnerability to stress relative to men and such disadvantage does not lessen with age.

This finding contradicts the speculation in some studies that the sex health paradox (i.e., women have higher risks of morbidity yet live longer than men) may be explained by a greater number of deficits in women but slower rates of aging or deficit accumulation than in men (Kulminski et al., 2007; Nakamura & Miyao, 2008), and it points to alternative explanations. First, because the sex difference in morbidity can be attributed in large part to sex differences in social roles, SES, lifestyle, and psychosocial stressors, the significant female excess after the adjustment of these social factors then suggests the existence of biological differences between the two sexes (Verbrugge, 1989). Second, previous studies on the sex health and survival paradox mostly considered individual health traits that have small, insignificant, or inconsistent effects on mortality risks. An integrative cumulative measure of frailty, on the other hand, can capture the aggregate effect of these health deficits for a better understanding of sex differences in physiological aging (Kulminski, Culminskaya, et al. 2008). In addition, the paradox may be produced by potentially different impacts of frailty on mortality for the two sexes, as shown by a larger relative contribution of the FI to the risk of death for male than for female older adults (Kulminski, Culminskaya, et al.). All these explanations suggest the importance for future research to systematically incorporate biological assumptions for understanding females’ superior tolerance to general system damage.

We found substantially higher degrees of loss in physiological reserve at any given age for non-Whites and the low-SES group on average, adjusting for all other factors. Although consistent with the widely documented inverse relationship between social status and the risk of illness (Link & Phelan, 1995), the racial and SES gaps in mean FI levels also provide new evidence that social adversity exerts strong effects on multiple domains of deficit accumulation simultaneously and on the complex process of physiological deregulation. The findings on racial and SES heterogeneity in rates of biological aging indicated by the growth rates of the FI are more varied. In some birth cohorts (CODA and WB), individuals with low education or income exhibit higher rates of aging and incur faster physiological deterioration. The resulting diverging SES-specific trajectories of frailty can be depicted by the cumulative disadvantage process over the life course (O’Rand, 2006) in which the excess in health deficits for the disadvantaged increases with age. In other cohorts, non-Whites (CODA and HRS) and individuals in poverty (HRS) show slower rates of aging, resulting in converging race- and income-specific trajectories of frailty. The prevailing explanation for decreasing disparities with age is the age-as-leveler process, which occurs because of the equalization of resources in later life and the selective survival of elites who have acquired immunity against hardships (Preston, Hill, & Drevenstedt, 1998). In still other cohorts, there are no racial or SES differences in the rates of aging, indicating constant frailty disparities across the life course. The data for all cohorts combined show significantly lower growth rates of frailty with age, but this does not necessarily constitute evidence for the age-as-leveler process that emphasizes intracohort heterogeneity (as does the cumulative disadvantage process).

The lack of consistent relationships between the rates of aging, race, and SES across cohorts and the absence of significant intercohort differences in these relationships preclude any straightforward characterization of social heterogeneity in the dynamics of frailty and aging. We further note that there are potential measurement limitations of the study, such as the dichotomous racial group categorization, which may obscure an even more complex pattern of inequality over the life course and necessitate future research. The only clear conclusion that can be drawn at this point is that the expression of biological aging and the accumulation of general system damage do not follow the same path under different circumstances within a human population. In fact, individuals’ slopes of change with age are sensitive to social conditions in which they are embedded. This, we believe, is the most important finding that has emerged from this study. It challenges a prevailing assumption in many medical and genetic studies that there exist common paths and determinants of health declines and aging across individuals. It provides another example of the powerful interplay between biological and environmental forces that shape the divergent developmental paths of aging organisms (Finch, 2007). And it emphasizes the important role of individual-specific health care interventions for achieving longer and healthier lives for all population subgroups.

Due to data availability, the FI used in this analysis includes similar but not identical items of health deficits as those included in earlier analyses of Canadian (CSHA), Chinese, and other U.S. samples. For instance, we have not included problems with eyesight, hearing, nose, or skin but have more detailed items on depressive symptoms. The total number of deficits included is smaller than some previous studies but is not substantially smaller than others using data sets, such as the CSHA (19–26 deficits) and NLTCS (32 deficits; e.g., Kulminski et al., 2007; Kulminski, Ukraintseva, Kulminskaya, et al., 2008; Mitnitski et al., 2002). Although the FI used here by no means includes an exhaustive list of age-associated deficits, the similarity of the findings on age changes of the FI supports its robustness as a summary measure of multiple domains and also supports the notion that it is the proportion of deficits that is important in the aging process rather than the nature of the deficits. The assumption of equality of deficits, however, should be tested in future research. If, given the same number of deficits, some deficits have greater influence on biological vitality than others do, then the assumption does not hold. The equal weight assumption may not pose problems in data sets with a sufficient number of age-related disorders as used here (Goggins et al., 2005; Mitnitski et al., 2004). In the case of only a few indicators, it might be necessary to apply different weights to deficits through statistical means, such as principal components analysis.

FUNDING

This research is supported by a P30 AG-12857 National Institutes on Aging, National Opinion Research Center Pilot Award.