Novel sequence-based method for identifying transcription factor binding sites in prokaryotic genomes

Abstract

Motivation: Computational techniques for microbial genomic sequence analysis are becoming increasingly important. With next-generation sequencing technology and the human microbiome project underway, current sequencing capacity is significantly greater than the speed at which organisms of interest can be studied experimentally. Most related computational work has been focused on sequence assembly, gene annotation and metabolic network reconstruction. We have developed a method that will primarily use available sequence data in order to determine prokaryotic transcription factor (TF) binding specificities.

Results: Specificity determining residues (critical residues) were identified from crystal structures of DNA–protein complexes and TFs with the same critical residues were grouped into specificity classes. The putative binding regions for each class were defined as the set of promoters for each TF itself (autoregulatory) and the immediately upstream and downstream operons. MEME was used to find putative motifs within each separate class. Tests on the LacI and TetR TF families, using RegulonDB annotated sites, showed the sensitivity of prediction 86% and 80%, respectively.

Availability: http://ural.wustl.edu/∼gsahota/HTHmotif/

Contact: stormo@wustl.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

There are more bacterial species than from any other kingdom, but only a few have been studied in much detail. Their relatively small genomes make them readily amenable to sequencing and they now constitute the most abundant genome sequences in the public databases. Projects such as the Human Microbiome Project (Turnbaugh et al., 2007) and other metagenomic sequencing projects (Riesenfeld et al., 2004) promise to significantly increase the amount of genomic sequence from bacterial species. For most of these species, the genome sequence is the only available information so computational approaches are essential to learning more about their characteristics and capabilities.

Most current computational analyses focus on sequence assembly (Pop, 2009; Ye and Tang, 2009), the phylogenetic distributions of species (Hamady et al., 2009; Pei et al., 2009), functional classification of gene (Qin et al., 2010; Selengut et al., 2010) and metabolic network reconstruction (Ye and Doak, 2009). Many of these analyses are accomplished through the identification of homologous proteins with known function and the inference of functional conservation in the newly sequenced species. As of yet, there has been little computational work focused on transcriptional regulation in these prokaryotic systems. In this article, we present a novel sequence-based method to infer the specificities of prokaryotic transcription factors (TFs) through the comparisons of their DNA-binding domains and applying a motif-finding algorithm to likely binding regions.

Most prokaryotic TFs contain a helix-turn-helix (HTH) fold, where the second helix, also known as the recognition helix, primarily contacts DNA (Harrison, 1991; Perez-Rueda and Collado-Vides, 2000; Santos et al., 2009). Using crystal structures of protein–DNA complexes, we can determine a set of residues that is important for defining the specificity of the protein, the ‘critical residues’. Commonly, these HTH TFs bind as homodimers with palindromic DNA specificities. Previous studies have utilized those features to identify regulatory motifs in related bacterial species but in those cases the TF that binds the motif was not identified except in cases where the motif corresponded to one for a known TF (McCue et al., 2002; Qin et al., 2003). In general, when the binding motif for a specific TF is known, and orthologous TFs are identified in other species, one can transfer the knowledge about the motif and predict genes that are regulated by the TF in the new species (Alkema et al., 2004; Gelfand et al., 2000b; Tucker et al., 2004; Yu et al., 2004). Making connections between novel motifs and the TFs that bind them can also be accomplished by taking into account additional information (Tan et al., 2005). In that study, the most useful information for identifying the TF that bound to a specific motif was the proximity of the TF, within the genome, to the locations of the predicted binding sites. In a similar approach, motifs for orthologous TF were predicted based on the assumption of autoregulation (Sorokin et al., 2009). In an earlier study of the Escherichia coli transcriptome, ∼55% of the TFs analyzed were estimated to be autoregulated (Martínez-Antonio and Collado-Vides, 2003). Our analysis using RegulonDB 6.7 (Gama-Castro et al., 2008) indicates that this value increases to 78% if one also includes the promoters of neighboring operons.

Motif finders typically depend on having at least one of two types of data. In a ‘phylogenetic footprinting’ approach one has orthologous genes from a set of species and attempts to find the conserved binding site motifs that control their expression (Berezikov et al., 2004; Blanchette and Tompa, 2002; Cliften et al., 2003; Wang and Stormo, 2005). Using such data one can often find potentially functional regulatory motifs, but the TFs that bind to them are frequently unknown. The other general approach uses sets of sequences within one species for which experimental data suggest they contain common binding sites. This may be the promoters (or other regulatory regions) that are known to be regulated by a common TF, or sets of genes that are found to be co-regulated, perhaps by unknown TFs (Bailey and Elkan, 1994; Buhler and Tompa, 2002; Down and Hubbard, 2005; Hertz and Stormo, 1999; Liu et al., 2001; Pavesi et al., 2001; Thompson et al., 2003). More recently ChIP-chip and ChIP-Seq methods have been used to identify genomic regions that bind to a specific TF. Both kinds of data can be used simultaneously, where sets of genes within one species are thought to be co-regulated, or at least co-bound by the same TF, and one also has the orthologous regions from multiple species from which to focus on the conserved sites (Gelfand et al., 2000a; Jensen et al., 2005; Kellis et al., 2003; Moses et al., 2004; Prakash et al., 2004; Siddharthan et al., 2005; Sinha, 2007; Wang and Stormo, 2003). But for the vast majority of sequenced bacterial species, data that can be used to identify the binding sites for specific TFs is not available. There is generally no experimental data from which to identify co-regulated genes, and frequently bacterial TFs, such as LacI, only regulate one gene so that canonical motif finding would not work. While motifs can be found for orthologous genes across multiple species that often works only for relatively closely related species and not for the entire distribution of bacterial genomes that are sequenced (Lozada-Chávez et al., 2006; Price et al., 2007). In analyzing metagenomic data, the definition of orthologous genes also becomes quite difficult because one only has partial genome sequences. It also does not identify the TF that binds to the motif, which is necessary to be able to begin determining the regulatory networks across bacteria.

The approach we take in this article relies on three types of information. The first is the identification of bacterial TFs that contain HTH domains and their classification into subfamilies based on the primary protein sequence signatures within the HTH domain using Pfam (Finn et al., 2010). These subfamilies are not necessarily functionally related, as many times the functions of a specific protein are determined by a separate effector domain, but proteins within the same subfamily are likely to interact with DNA very similarly, and in particular to use the same critical residues for determining the binding specificity of the TF (Contreras-Moreira and Collado-Vides, 2006; Morozov and Siggia, 2007; Siggers et al., 2005). The second type of information is the structure of the DNA–protein complex for at least one member of the subfamily, which is obtained from PDB (Dutta et al., 2009). There are 22 subfamilies of bacterial HTH TFs that have at least one known crystal structure from which we can determine the protein residues, within the HTH domain, that determine the binding specificity. We cluster together TFs from the same subfamily that also contain the same critical residues as we expect them to bind to identical, or at least very similar, motifs whether or not they are orthologous TFs. The third type of information we need in order to assign motifs to each TF cluster is a set of likely binding regions. For this we rely on the fact, mentioned above, that most bacterial TFs regulate themselves and/or adjacent operons. Therefore, we only need short contigs, containing the TF and its promoter as well as adjacent promoters, to have a high likelihood of having regions that contain binding sites for the TFs. Although there are currently many complete bacterial genomes in the database, there are also many genomes represented only by whole-genome shotguns (WGS) in which the contigs are considerably shorter, and the large-scale microbiome projects that are beginning will also generate large datasets with much smaller contigs. The approach we apply in this article will be able to leverage that type of data to identify the binding motifs for many uncharacterized bacterial TFs, which opens the way to start modeling regulatory networks. We demonstrate this approach on two HTH subfamilies, TetR and LacI which are large HTH subclasses with protein–DNA crystal structures and palindromic specificities. Initially, this large size will be important in order to have enough sequences within each specificity class to confidently find motifs.

2 METHODS

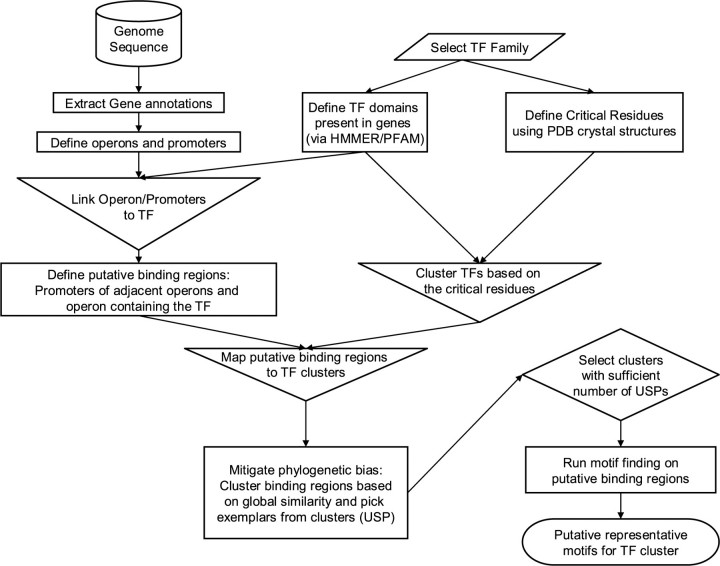
A conceptual overview of the method is shown in Figure 1. The implementation was via a series of Perl scripts, using inline C code for the pairwise sequence alignment for speed.

Fig. 1.

Flowchart describing overall method. The shapes are standard flowchart shapes, with the disk showing a database, parallelograms showing user input, the rectangle showing processes, inverted triangles showing merging, diamonds showing selection and the rounded box showing the terminating state.

2.1 Processing genomes

Four main types of genomic data were selected from the NCBI ftp site for this project: completed bacterial genomes, completed plasmid genomes, completed phage genomes and bacterial WGS projects. For the former three datasets, the genbank DNA sequence (gbk), the protein translation tables (ptt) and rna translation tables (rnt) and the protein fasta sequence (faa) files were retrieved. For the plasmids and the phages (retrieved as viruses), they were filtered to only contain bacterial or phage sequences, respectively. In the case of the WGS sequences, these subfiles were generated from the genbank flat file (gbff). The downloaded files were validated for correct file format structure and the gbk files were used to recreate the ptt and rnt files when errors were found. Each separate gbk file, with its ptt and rnt annotations, was further processed into operon and promoters using distance cutoffs similar to those used previously (Liu et al., 2008; Price et al., 2005; Tan et al., 2005): a 50 bp intergenic cutoff for determining operon membership and a 400 bp maximum promoter length relative the first gene of the operon. The minimum promoter size was required to be 50 bp. Circular sequences were appropriately handled both in defining the operons as well as their respective promoters.

2.2 Determining critical residues

To classify the proteins into their respective HTH subfamilies, HMMER v3.0rc2 (Eddy, 2009) and Pfam v24.0 were used. The PDB files for each Pfam entry were used to determine the critical residues for that subfamily (ie. residues that contact DNA). This was achieved using a modified version of PDB2PQR v1.5 (Dolinsky et al., 2007) to find all protein residues within 3.5 Å of a DNA base pair (excluding backbone atoms) that may form van der Waals contacts or hydrogen bonds, where the distance cutoff was 3.4 Å and 30° maximal angle between the acceptor, donor and donor hydrogen atoms. A maximum of two hydrogen bonded bridging waters were allowed between the protein and DNA base. The union of all of these sets of potential contacts yielded the critical residues.

2.3 Finding TF family members

The hidden markov model (HMM) for the Pfam entry was used to search through the fasta sequences using hmmsearch. TFs containing multiple domains of an HTH subfamily were removed. The resulting domains were then aligned using hmmalign. In order to try to maintain a similar binding mechanism, no gaps/insertions were allowed in the alignment within the range bounded by the critical residues unless the same gaps/insertions had also been seen in the PDB structures. Critical residues were also constrained to fall within the boundaries of the HMM domain.

2.4 Defining putative binding regions

Under the assumption that prokaryotic TFs regulate nearby operons, for every TF, the upstream promoter and the two promoters of the neighboring operon in either direction were concatenated to generate a ‘super-promoter’, which potentially contains a binding site for the TF. The WGS sequence data was in the form of contigs rather than finished full-length sequences; thus, there was no guarantee that all three component promoters would be part of the same contig. In these cases where the contigs did not contain all of the specified promoters, the subset of present relevant promoters was used to define the super-promoter.

2.5 Clustering TFs and generating USPs

For each HTH subfamily, these critical residue (CR) sets, which will be referred to as CR tags, were used to cluster the TF protein sequences. These clusters of TFs needed be mapped into clusters of putative binding regions in order to proceed with motif finding. Given the biased distribution of sequenced genomes and the potential for non-unique genomes in the procedure above, a simple mapping of the TFs to their super-promoters would not be sufficient to generate an approporiate dataset for motif finding. Instead, a subset, known as unique super-promoters (USPs), was defined as described.

To compare two super-promoters, the component promoter sequences were compared. To mitigate differences due to promoter shuffling or varying sizes of super-promoters, an all-by-all comparison was performed, using a trimmed Needleman–Wunsch (NW; Needleman and Wunsch, 1970) alignment (1/-1, -2 score scheme for match/mismatch, gap, respectively, excluding the trailing gaps). The alignment score for each pair of promoters was normalized to fall between 0 and 1. The Hungarian algorithm (Kuhn, 2005) optimization was applied to the normalized NW scores to determine the best pairs of related promoter sequences. The ‘super-promoter’ weighting score was defined as the average of the best component pairwise scores. These weighting scores were used to generate a hierarchical complete linkage tree via the perl module Algorithm-Cluster version 1.4.6 and using a threshold of 90% of the theoretical maximum score, this tree was cut to define clusters of sequences. Each resulting cluster of promoter sequences was considered one effective sequence and the sequence closest to the center of the cluster was chosen as the exemplar. If multiple sequences were equidistant from the center, ties were broken using the length of the sequence and the species of origin. This set of exemplar sequences was the USP set for each TF cluster and used for the motif finding procedure described below.

2.6 Motif finding

An expectation maximization (EM) based algorithm, specifically Multiple Em for Motif Elicitation (MEME) v4.3.0 (Bailey and Elkan, 1994) was used to determine the motifs of these USP sets. Only TF clusters with a minimum of 10 USPs were used in motif finding. A maximum of three motifs were reported for each cluster. MEME was run allowing zero or one site per sequence (zoops); the sites were required to be palindromic and the motif width was restricted to be between 15 and 25 bp. For further analysis, motifs were required to have an e-value of <1. The result of motif finding was a set of motifs that likely contained the true representative binding site of the CR tag cluster members.

2.7 Validation

All TFs and promoter sequences from E.coli K12 MG1655 (genbank code NC_000913) along with the corresponding promoter sequence cluster members were excluded from the motif discovery sets so that they could be used as independent test sets for evaluating the effectiveness of this procedure to identify true motifs for bacterial TFs. In order to validate the predicted motifs, a Z-score-based metric was used to search the sites defined in RegulonDB 6.7. The position weight matrix (PWM) was calculated from the frequency matrix as has been described earlier, using a pseudocount of 1 (Hertz et al., 1990). The weighted mean and variance was determined for each column (position) of the PWM, weighting by the relative background frequencies for each base. The mean and variance of the PWM were calculated as the sum of the means and variances of the individual columns. The standard deviation was calculated as the square root of the summed variance. Sequences were scored using an additive model as the sum of the PWM elements for each sequence position. The threshold Z-score of 5, corresponding to roughly one match in the E.coli genome by chance, was used to specify whether the RegulonDB site matched the motif. A motif was considered correct if any of the RegulonDB sites for that TF exceeded this threshold. The quality measure is the sensitivity of finding a correct motif, (TP) / (TP+FN).

3 RESULTS

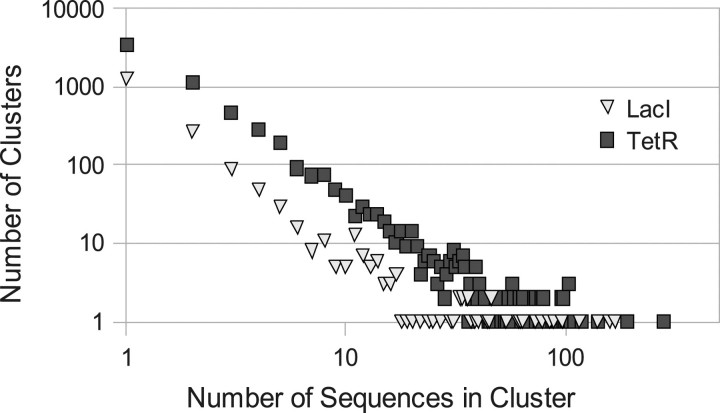
Between releases 176 and 177, Genbank contained 1056 complete bacterial genomes and 634 WGS datasets as well as 2011 plasmid and 543 phage genomes. In this study, we have focused on the LacI (PF00356) and TetR (PF00440) Pfam HTH subfamilies (Table 1). These two subfamilies comprise roughly 1/10 of the HTH domains in the Pfam clan CL0123. From that set of DNA sequences, for LacI there are 5989 domains. When filtered to remove gaps in restricted positions, multiple domains and missing promoter sequences, there are 5258 TFs remaining, and we defined the critical residues based on three LacI family proteins that have structures bound to DNA: LacI (PDB codes 1efa, 1jwl, 2pe5); CcpA (PDB codes 1rzr, 1zvv); and PurR (PDB codes 1bdh,1 bdi, 1jfs, 1jft, 1jh9, 1pnr, 1qp0, 1qp4, 1qp7, 1qpz, 1qqa, 1qqb, 1vpw, 1wet, 1zay, 2pua, 2pub, 2puc, 2pud, 2pue, 2puf, 2pug). Based on those structures, we determine that there are 10 critical residues (positions 2,3,12,13,14,17,18,24,25,26) in the respective Pfam HMM domain (PF00356). Using those 10 positions to define the specificity classes, there are a total of 1827 classes. There are 23 119 TetR domains which, after the same data filtering as above, lead to 21 883 TFs. In TetR, we defined the critical residues based on three proteins that have structures bound to DNA in the PDB: TetR (PDB code 1qpi); QacR (PDB code 1jt0); CGL2612 (PDB code 2yvh). Based on those structures, we determine that there are seven critical residues (positions 20, 29, 30, 31, 32, 34, 35) from the respective Pfam HMM domain (PF00440). Using those seven positions to define specificity classes, there are a total of 6207 classes. The distribution of the sequences into these specificity clusters is shown in Figure 2.

Table 1.

Dataset sizes for LacI and TetR

Type	LacI (PF00356)	TetR (PF00440)
Domains	5989	23 119
TFs	5258 (1827)	21 883 (6207)
USP >= 10 sequences	1733 (32)	8124 (226)
Predicted motifs	1716 (31)	7923 (214)
Within 1HD of motif CR tag	1958 (95)	11 394 (1335)
Within 2HD of motif CR tag	2409 (293)	16 929 (3801)

The values shown are the number of sequences (with the exception of the first values that are the number of domains) and within the parentheses are the number of specificity clusters. Briefly, USPs are promoter sets that have been filtered to remove redundancy (see Section 2 for more detail). Hamming Distance (HD) is a measure of similarity, the number of substitutions required to change one string into another.

Fig. 2.

Log-scale plot showing size distribution of specificity clusters for LacI (inverted triangles) and TetR (squares).

The identity of the residues at the critical residue positions defines a sequence tag. For example, the cluster TetR-SPKGSYH refers to the set of all proteins that are classified as belonging to the TetR family of HTH proteins and have residues S, P, K, G, S, Y, H in HMM alignment positions 20, 29, 30, 31, 32, 34, 35, respectively. For motif finding, the promoter sequences with potential binding sites were inferred using the computationally derived operons, taking the promoter of the operon containing the TF, and the upstream and downstream operon promoters as well. These three promoters were concatenated into a ‘super-promoter’, which likely contained at least one binding site for the TF.

There are a large number of similar genomes that have been sequenced; many times these are simply different strains of model prokaryotic organisms. This introduces the issue of similar sequence due to a similar lineage which could be resolved using a phylogenetic tree. However, there is also the potential issue of horizontal gene transfer as well. In order to resolve the potential promoter redundancy issue, if the promoters were too similar, they were reduced to one exemplar sequence.

In order to ensure stability in motif finding, a minimum of 10 USPs was required for running MEME. With this threshold criteria, there were 32 (1733) and 226 (8124) classes (TFs) for LacI and TetR, respectively, and putative motifs were obtained for 31 and 214 of them. The majority of classes without motif prediction were simply due to a lack of sufficient USPs to reliably undertake motif finding (Table 1).

RegulonDB was used to validate the datasets where E.coli was excluded. These datasets comprise a subset of the full dataset and will be described in further detail; however, the predicted motifs and sequence datasets for all of the classes are available at http://ural.wustl.edu/∼gsahota/HTHmotif/. The external validation test using RegulonDB showed that in LacI, there were six true positives and one false negative, for an accuracy of 86% (Table 2 and Supplementary Fig. 1). For TetR, there were four true positives and one false negative, for an accuracy of 80% (Table 3 and Supplementary Fig. 2). Additionally, we included an analysis of whether the motif was present as part of the super-promoter of the excluded TF to test the hypothesis of local regulation (Tables 2 and 3). In most instances, it appears to be a valid assumption, but even in TetR-RAPTYSR where this assumption was not true, the protocol was still able to predict the correct motif, due to local regulation in other bacterial organisms in the same cluster.

Table 2.

Validation results for LacI using RegulonDB 6.7

Locus ID	Name	CR Tag	Sequences	USP	Matches in RegulonDB	Autoreg
b1658	purR	IKSTTSHRFV	168	60	Y	+
b2837	galR	IKSVASRPKA	140	45	Y	+
b3753	rbsR	MKSTSSHRFV	116	41	Y	+
b4241	treR	IKGKSSRSGV	97	15	Y	+
b0345	lacI	LYSYQSRSHV	37	14	Y	+
b2714	ascG	MLSKASRGYV	62	11	Y	+
b3934	cytR	MKSTASRDKV	85	12	N	+
b1320	ycjW	IYSKSSRTNI	61	20	−	+

The matches in RegulonDB are coded as follows: Y means a match to any site, N means no matches and – means no RegulonDB site. The autoreg column is a + if there is a match to the super-promoter and - if there is no match.

Table 3.

Validation results for TetR using RegulonDB 6.7

Locus ID	Name	CR Tag	Sequences	USP	Matches in RegulonDB	Autoreg
b3963	fabR	RAPTSYR	193	81	Y	−
b1649	nemR	SPKGSYH	141	49	Y	+
b0313	betI	ASTGISH	98	41	Y	+
b3264	envR	NTRGAYW	104	27	Y	+
b1013	rutR	ESKTNLY	95	18	N	+
b3641	slmA	ASEAAYR	282	148	−	+
b0846	ybjK	RPLGSTY	118	45	−	+
b4251	yjgJ	ANPPSYA	87	19	−	+
b0796	ybiH	RNIATTY	105	17	−	+
b1111	ycfQ	AKAPTYA	97	17	−	+

The matches in RegulonDB are coded as follows: Y means a match to any site, N means no matches and – means no RegulonDB site. The autoreg column is a + if there is a match to the super-promoter and - if there is no match.

4 DISCUSSION

Using primarily genomic sequence data augmented with structural priors, we are able to determine putative motifs for a number of bacterial TFs in two families. The method described is capable of working not only with fully sequenced genomes, but also with sufficiently long contigs, allowing for the use of assembled metagenomic reads. Using the MEME program, putative motifs were determined for 31 (LacI) and 214 (TetR) classes of TFs representing ∼1/3 of the sequences of each of these TF families. For validation, classes that had an excluded E.coli USPs were selected, 8 (LacI) and 10 (TetR). Of these selected classes, 7 (LacI) and 5 (TetR) had known regulatory sites in RegulonDB. The majority of these motifs, 6/7 for LacI and 4/5 for TetR, were consistent with the known regulatory sites defined based on RegulonDB, validating this approach. Even some of the motifs that did not match to known sites with scores exceeding our stringent threshold still had fairly high scores and are likely to be very similar to the true motifs for those classes.

While this approach has proven to be useful, there are several modifications to the method we describe in this article that should offer further improvements in our ability to determine binding motifs for bacterial TFs. The current protocol assumes a fixed-width gap between the half-sites of the motif. However, there is no guarantee that proteins with similar critical residues must have similar gaps in the spacer region between the half-sites, as the regions of the protein that determine these variable gaps are generally outside of the DNA binding domain (Laguri et al., 2003; Mao et al., 2005; Reece and Ptashne, 1993). Even within the test set, we can see evidence of multiple widths in TetR-SPKGSYH. In the first and third motif, there is a TAGACC half site, separated by a 4 or 0 base spacer from the complementary GGTCTA. For TetR-NPKGSYH, these spacers are 3 or 0 bases. An EM-based algorithm that allowed variable spacing between the two parts of E.coli promoters had been published previously (Cardon and Stormo, 1992) and a similar approach could increase the power of detecting some motifs that may be missed simply because they have multiple binding widths. Current gapped motif finders are not capable of dealing with sequence fragments, which is important in the context of the ‘super-promoters’.

We only applied MEME to classes with at least 10 USPs because motif finding is more reliable with larger datasets. However, many of the classes with less than 10 USPs are very similar to other classes with 10 or more, and we expect that TFs with very similar critical residues will bind to very similar motifs. This means that we could use the motifs from the larger classes as priors to aid in the discovery of the motifs for the smaller classes. As shown in Table 1, there are an additional 95 and 1335 classes that are at a Hamming distance of one (HD = 1) away from the larger classes for the LacI and TetR families, respectively. If we go to HD = 2, the number of classes increases to 293 (LacI) and 3801 (TetR). This could greatly increase the number of TF classes for which motifs could be determined and further expand the repertoire of TF-motif pairs. In the current implementation, a set of putative motifs is predicted for the TF cluster; however, the correct motif within the set is not specified. In conjunction with the above-described gapped motif finder, these HD classes could also be used to filter out inconsistent or incorrect motif predictions, under the assumption that similar CR tags lead to similar half-sites or motifs. This refined analysis would lead to a one-to-one mapping of a predicted motif to a TF cluster. Another benefit of having a large number of TF-motif pairs is the determination of the interacting residues. Our choice of the critical residues is based on crystal structures of DNA–protein complexes where we have used a distance cutoff between an amino acid and a base pair to identify those residues that may, in at least some members of the family, contribute to the specificity of binding. It has been shown before that interface residues are only partially conserved across DNA binding domains (Contreras-Moreira et al., 2010). In this article, the union of all such residues was used, leading to a potential overspecification of the critical residue set, in turn decreasing the size of certain classes. In addition, it may be that some residues, while close to the DNA, do not participate in binding specificity and could be eliminated from the critical residue set, which would increase the size of the classes. In general, correlations between the aligned protein sequences and alignments of the motifs can be useful in determining which protein residues interact with which base pairs (Mahony et al., 2007; Noyes et al., 2008). This could then be used to determine the critical residues even for TF families currently without crystal structures for DNA–protein complexes.

Finally, there are many more HTH families that can be addressed with this approach. HTH proteins are classified as the clan CL0123 in Pfam and there are 141 HTH subfamilies of which 22 are mainly bacterial domains and contain protein–DNA crystal structures where the domain interacts with DNA. When taking into account the variability in size of the families, this actually covers approximately 1/2 of the potential HTH TF proteins, so the method has significant potential to cover a large amount of the potential HTH TF proteins. In some of these families, we may have motifs with variable gaps in their spacer regions and differing configurations of the half-sites such as direct repeats instead of palindromic motifs, and sometimes even mixtures of the two modes. This will require a modification to the current protocol, but may provide for a much larger collection of binding motifs for specific bacterial TFs.