Abstract
In order to have confidence in model-based phylogenetic methods, such as maximum likelihood (ML) and Bayesian analyses, one must use an appropriate model of molecular evolution identified using statistically rigorous criteria. Although model selection methods such as the likelihood ratio test and Akaike information criterion are widely used in the phylogenetic literature, model selection methods lack the ability to reject all models if they provide an inadequate fit to the data. There are two methods, however, that assess absolute model adequacy, the frequentist Goldman–Cox (GC) test and Bayesian posterior predictive simulations (PPSs), which are commonly used in conjunction with the multinomial log likelihood test statistic. In this study, we use empirical and simulated data to evaluate the adequacy of common substitution models using both frequentist and Bayesian methods and compare the results with those obtained with model selection methods. In addition, we investigate the relationship between model adequacy and performance in ML and Bayesian analyses in terms of topology, branch lengths, and bipartition support. We show that tests of model adequacy based on the multinomial likelihood often fail to reject simple substitution models, especially when the models incorporate among-site rate variation (ASRV), and normally fail to reject less complex models than those chosen by model selection methods. In addition, we find that PPSs often fail to reject simpler models than the GC test. Use of the simplest substitution models not rejected based on fit normally results in similar but divergent estimates of tree topology and branch lengths. In addition, use of the simplest adequate substitution models can affect estimates of bipartition support, although these differences are often small with the largest differences confined to poorly supported nodes. We also find that alternative assumptions about ASRV can affect tree topology, tree length, and bipartition support. Our results suggest that using the simplest substitution models not rejected based on fit may be a valid alternative to implementing more complex models identified by model selection methods. However, all common substitution models may fail to recover the correct topology and assign appropriate bipartition support if the true tree shape is difficult to estimate regardless of model adequacy.
Keywords: Bayesian, Goldman–Cox, maximum likelihood, model adequacy, parametric bootstrap, posterior predictive simulation
Introduction
Statistical methods of phylogenetic inference, such as maximum likelihood (ML) and Bayesian estimation, utilize an explicit model of molecular evolution, normally selected from a group of nucleotide substitution models referred to as the general time reversible (GTR; Tavaré 1986) family. Model choice is critical because use of an underparameterized model can mislead an analysis by failing to account fully for multiple substitutions at the same site while inclusion of superfluous parameters can increase the variance in parameter estimates (e.g., Gaut and Lewis 1995; Sullivan and Swofford 1997, 2001; Lemmon and Moriarty 2004). Consequently, model selection methods such as the hierarchical implementation of the likelihood ratio test (hLRT; Frati et al. 1997; Sullivan et al. 1997; Posada and Crandall 1998), Akaike information criterion (AIC; Akaike 1973), Bayesian information criterion (BIC; Schwarz 1978), and decision theory (DT) approach (Minin et al. 2003; Abdo et al. 2004) identify substitution models that optimize the trade off between bias and variance according to their respective statistical criteria (see Posada and Buckley 2004 and Sullivan and Joyce 2005 for reviews of model selection methods). Although use of any model selection method is preferable to choosing a model arbitrarily (Ripplinger and Sullivan 2008), these are relative fit methods that lack the ability to reject all models if none provides an adequate fit to the data. That is, none of the typical model selection methods actually assess goodness of fit in an absolute sense.
There are two methods that assess the absolute fit between a substitution model and the data: the Goldman–Cox (GC) test (also known as the parametric bootstrap goodness-of-fit test; Reeves 1992; Goldman 1993; Whelan et al. 2001) and posterior predictive simulation (PPS; Rubin 1984; Gelman et al. 1996; Huelsenbeck et al. 2001; Bollback 2002, 2005). Both tests normally utilize the multinomial log likelihood test statistic, which is calculated as the weighted sum of site pattern log likelihoods. The GC test is a frequentist method used to evaluate the hypothesis of a perfect fit between the model and data using a null distribution generated with the parametric bootstrap. To conduct a GC test, one first performs a ML analysis and calculates the value of the realized test statistic
where the first component is the multinomial log likelihood and the second component is the log likelihood constrained to a particular substitution model. Data for the null distribution are simulated using maximum likelihood estimates (MLEs) of the tree topology, branch lengths, and substitution model parameters and subsequently analyzed in the same manner as the original data. Test statistics are then calculated for each replicate and used to form the null distribution; a P value is calculated by determining the rank of the realized test statistic in relation to the null distribution.
PPS (e.g., Bollback 2002) is a Bayesian method for assessing model adequacy that utilizes parameter estimates drawn from their respective posterior distributions rather than MLEs, which eliminates the reliance on point estimates associated with the GC test. In order to conduct PPSs, one first calculates the realized test statistic (the multinomial likelihood) and conducts a Bayesian analysis to produce posterior distributions for the tree topology, branch lengths, and substitution model parameters. Data for the null, or predictive, distribution are generated in a manner similar to the parametric bootstrap except simulation parameters are sampled from the posterior distribution independently for each replicate. A multinomial test statistic is subsequently calculated for each replicate and used to form the null distribution; the realized test statistic is evaluated against this distribution.
Because tests of model adequacy are computationally intensive, they are rarely used as model selection strategies and have instead been used to investigate the fit of particular substitution models. Goldman (1993) used the parametric bootstrap to evaluate the fit of three relatively simple GTR family models [Jukes–Cantor (JC; Jukes and Cantor 1969), Felsenstein 81 (F81; Felsenstein 1981), and Hasegawa–Kishino–Yano (HKY; Hasegawa et al. 1985)] to primate ψη-globin pseudogene and tree-of-life small subunit rRNA data sets and was able to reject both the JC and the F81 models, as well as the HKY model when applied to the rRNA data set. Similarly, Whelan et al. (2001) used the GC test to reject the GTR model (Tavaré 1986) for a primate mitochondrial data set. Conversely, Bollback (2002) used PPSs to evaluate the fit between the JC, HKY, and GTR models and the primate ψη-globin pseudogene data set analyzed by Goldman (1993) and was unable to reject any of the models. Furthermore, several authors have been unable to reject the adequacy of substitution models using the GC test when the models accounted for among-site rate variation (ASRV). For example, Carstens et al. (2005) were unable to reject the HKY + Γ model for a salamander cytochrome b (cyt b) data set, and Demboski and Sullivan (2003) were unable to reject the GTR + Γ model for chipmunk cyt b data.
Despite instances where model adequacy methods have failed to reject GTR family models, there has been speculation that this set of models is insufficient (e.g., Sanderson and Kim 2000; Revell et al. 2005; Kelchner and Thomas 2007) and, consequently, several authors have suggested a need for rigorous analysis of model adequacy using the GC test and PPSs (Sullivan and Joyce 2005; Gatesy 2007). However, Waddell et al. (2009) have shown that the GC test can lack power. They could not reject the GTR + I + Γ model as inadequate using the GC test for a single data set but demonstrated that sets of taxa exhibited data patterns that deviated significantly from those expected under the model using pairwise tests of symmetry.
Here, we extend the examination of the adequacy of the GTR family models on an array of data using both the GC test and the PPSs. We first evaluate the fit of 56 common substitution models on each of 25 empirical data sets and compare the results with those obtained with model selection methods. We then test whether or not use of the simplest models not rejected based on absolute goodness of fit produces significantly different estimates of topology, branch lengths, and bipartition support than models chosen by model selection. Last, we evaluate the adequacy of GTR family models on simulated data sets and investigate the performance of both adequate and insufficient models in recovering the true tree, estimating branch lengths, and assigning support to appropriate bipartitions.
Methods
Data Collection
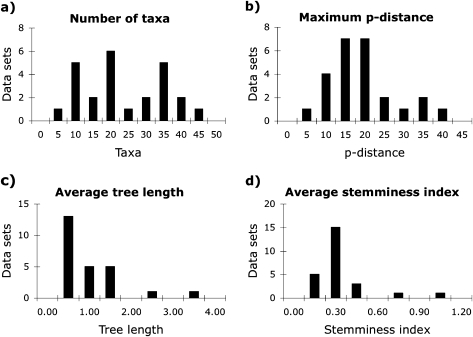
In order to assess the performance of model adequacy methods under a variety of conditions, we downloaded 25 diverse data sets from the phylogenetic database TreeBASE (http://www.treebase.org). The culled data included 2 arthropod, 1 sponge, 2 vertebrate, 7 flowering plant, 1 red algae, 4 club fungus, 6 sac fungus, 1 slime net, and 1 water mold data set, which comprised 2 mitochondrial, 3 chloroplast, and 20 nuclear gene sequence alignments. We first imported the data sets into PAUP*4.0b10 (Swofford 2002) and removed alignment regions the original authors had labeled as poor or ambiguous. We then removed redundant haplotypes using Collapse 1.2 (available from http://darwin.uvigo.es) while treating gaps as fifth character states. Because inclusion of gaps and ambiguous characters causes difficulty in calculating the multinomial likelihood, these characters were removed; nonetheless, the resulting pool of data sets exhibited a large amount of diversity (fig. 1). Citations for each data set, as well as data collected as part of this study, are provided in supplementary material, Supplementary Material online.
FIG. 1.
Summary statistics for the 25 empirical data sets analyzed as part of this study. The data sets contained (a) 5–44 haplotypes ( = 21) and 203–2,279 (
= 21) and 203–2,279 ( = 736) nucleotides, (b) a maximum p distance of 4.0–36.5% (
= 736) nucleotides, (b) a maximum p distance of 4.0–36.5% ( = 16.8%), (c) a weighted average tree length of 0.08–3.32 (
= 16.8%), (c) a weighted average tree length of 0.08–3.32 ( = 0.74%), and (d) a weighted average stemminess index of 0.02–0.93 (
= 0.74%), and (d) a weighted average stemminess index of 0.02–0.93 ( = 0.26%). Tree lengths and stemminess indices were calculated as BIC weighted averages across all ML trees constructed with the 56 nucleotide models implemented in Modeltest and DT-ModSel.
= 0.26%). Tree lengths and stemminess indices were calculated as BIC weighted averages across all ML trees constructed with the 56 nucleotide models implemented in Modeltest and DT-ModSel.
Frequentist Analysis
We began our analysis by identifying optimal models according to the hLRT, corrected AIC (AICc), BIC, and DT model selection methods; models were selected from among the 56 GTR family models implemented in Modeltest3.7 (Posada and Crandall 1998) and DT-ModSel (Minin et al. 2003). In order to identify best-fit models under the various relative criteria, we first used PAUP* to calculate ML scores for each candidate model and then used Modeltest to select optimal models according to the hLRT, AICc, and BIC. Similarly, we recalculated ML scores and used DT-ModSel to identify models with the lowest expected risk. Branch lengths were not included during model selection, and sequence length was used to approximate sample size in the AICc, BIC, and DT calculations (e.g., Posada and Buckley 2004; Ripplinger and Sullivan 2008).
After conducting model selection, we performed GC tests for all 56 substitution models to determine which models exhibited an adequate fit to the data. We first conducted ML analyses in PAUP* to obtain realized test statistics and estimates of the topology, branch lengths, and substitution model parameters. Model parameters were initially estimated from a neighbor joining (NJ) tree constructed with LogDet distance (Lockhart et al. 1994) and used as starting values for a heuristic ML search using ten random addition starting trees and tree-bisection-reconnection (TBR) branch swapping. We then generated 100 data replicates for the null distribution using Seq-Gen (Rambaut and Grassly 1997), which utilizes simulation to produce a sequence alignment given a tree, branch lengths, and substitution model parameters. Each replicate was subsequently analyzed in the same manner as the original data and the difference between the multinomial and constrained likelihoods was calculated to form the null distribution. Last, we calculated a P value by evaluating the test statistic against the null distribution and assessed the outcome at α = 0.05.
In order to assess the relative performance of statistically supported models, we performed additional ML analyses using substitution models chosen by model selection methods and the simplest models not rejected by the GC test. For each analysis, we estimated initial model parameters from a NJ starting tree constructed with LogDet distance, which were used as starting values for a ML heuristic search with ten random addition starting trees and TBR branch swapping. We subsequently reoptimized parameter estimates and performed additional search iterations until the tree topology stabilized (Sullivan et al. 2005). In order to quantify differences among models chosen with alternative methods, we calculated symmetric distance differences (SDDs; Robinson and Foulds 1981) and sum of branch lengths for ML trees constructed with models chosen by model selection methods as well as the simplest models not rejected by the GC test. Last, we conducted ML nonparametric bootstrap analyses for each supported model using 1,000 replicates, substitution model parameters optimized on the preceding ML analysis, ten random addition starting trees, and TBR branch swapping. In cases where the Γ-shape parameter exceeded the limit of 300, the parameter was optimized on the limit instead of the empirical value.
Bayesian Analysis
Because only 24 GTR family models can be implemented in MrBayes3.1.2 (Huelsenbeck et al. 2001; Ronquist and Huelsenbeck 2003), we repeated model selection according to the hLRT, AICc, and BIC using a version of MrModeltest (Nylander 2004) we adapted to include BIC scores. In addition, we identified substitution models with minimum posterior risk using a version of DT-ModSel we modified to select among pertinent models. We subsequently employed MrBayes to perform Bayesian Markov chain Monte Carlo analyses for each data set using all 24 applicable models. For each analysis, we performed two independent runs from random starting trees, each with three heated and one cold chain, for 5 × 106 generations; trees and substitution model parameters were sampled every 100 generations. We confirmed that the chains had converged upon the stationary distribution by analyzing both log likelihood plots and the standard deviation of split frequencies. We discarded the first 500,000 generations (10%) of each analysis as burn-in. We then conducted PPSs using MAPPS (Bollback 2002), which calculate the realized test statistic (multinomial likelihood) from the sequence alignment, produces data replicates by sampling 1,000 joint tree and model parameter posterior probabilities and constructs the null distribution by calculating test statistics for each data replicate. Finally, we calculated average posterior tree lengths using substitution models chosen by model selection methods as well as the simplest models not rejected by PPSs.
Simulation Analysis
Although use of empirical data allows us to investigate the effects of substitution model adequacy on a range of real world scenarios, it would also be useful to utilize simulated data to explore the relationship between the model adequacy and the accuracy of phylogenetic inference. Consequently, we performed simulations based on shrew mitochondrial DNA (Brandli et al. 2005) and water mold nuclear DNA (Mirabolfathy et al. 2001) data sets, both of which elicited unusual behavior from model adequacy methods. In order to obtain a tree topology for simulation, we conducted ML analyses for each data set using the GTR + I + Γ model. For each analysis, initial model parameters were estimated based on a NJ tree constructed with LogDet distance and used as starting values for a ML heuristic search with ten random addition starting trees and TBR branch swapping; the ML search was reiterated until the tree topologies converged. We partitioned the shrew data set into three parts consisting of the cyt b gene, control region, and cytochrome oxidase II (COXII) gene; the cyt b and COXII genes were further divided by codon position to produce a total of seven data partitions. Similarly, the water mold data set was divided into three subsets representing the internal transcribed spacer (ITS) 1 region, the 5.8S rRNA gene, and the ITS2 region. For each partition, we obtained MLEs of GTR + I + Γ model parameters from a ML analysis constrained to the true tree topology and used Seq-Gen to simulate ten replicates. We then concatenated the simulated data to form ten sets of partitioned replicates for each data set. We subsequently analyzed the replicates in the same manner as the empirical data except that phylogenetic analyses were conducted using all applicable models instead of limiting the analysis to models identified by model selection methods and the simplest models not rejected based on fit.
Results
Empirical Analysis
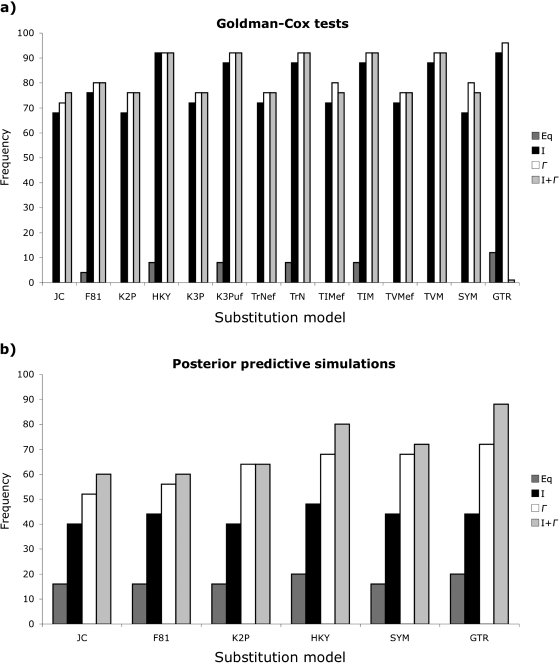
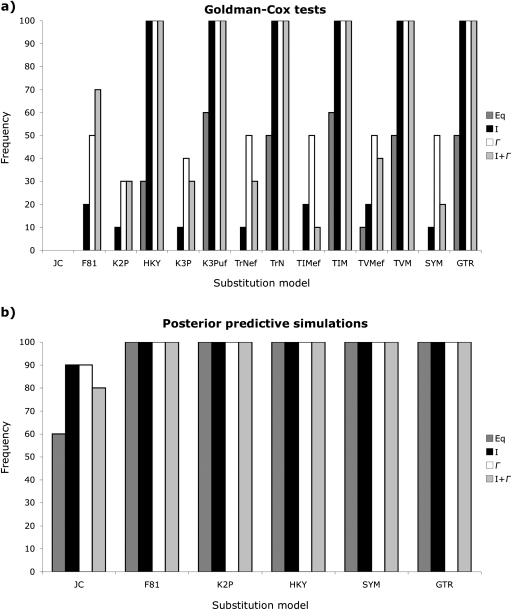
The GC test often failed to reject simple substitution models as long as they incorporated ASRV [invariable sites (I), Γ-distributed rates (Γ), or a combination of the two (I + Γ); fig. 2a]. Although the simple JC model, which assumes both equal base frequencies and substitution rates, was rejected for all data sets, JC + I could not be rejected for 68% of the data and both JC + Γ and JC + I + Γ could not be rejected for 72% of the data. The GC test identified the F81 model, which incorporates unequal base frequencies and equal substitution rates, as the simplest adequate model for one data set, whereas F81 + I and F81 + Γ were the simplest models not rejected for another data set. Similarly, the Kimura 2-parameter model (K2P; Kimura 1980) with Γ-distributed rate variation, which assumes equal base frequencies and unequal transition/transversion rates, was the simplest model not rejected for one data set, whereas HKY + I and HKY + Γ, which incorporate both unequal base frequencies and transition/transversion rates, were identified as the simplest nonrejectable models for an additional two data sets. Only two data sets required complex models; the transversional model (TVM) with invariable sites or Γ-distributed rates was needed to capture adequately the signal from a small geranium data set (p distance = 14.1%, BIC-weighted tree length = 0.19, and BIC-weighted stemminess index = 0.02), whereas the most complex GTR + I + Γ model, which assumes unequal base frequencies and independent substitution rates, was required to fit the 32 shrew sequences used for simulation (p distance = 13.8%, BIC-weighted tree length = 0.49, and BIC-weighted stemminess index = 0.22).
FIG. 2.
Frequency with which common substitution models are not rejected by (a) GC tests and (b) PPSs for 25 empirical data sets. Simple models such as JC, which assumes equal base frequencies and substitution rates, normally cannot be rejected as long as they incorporate a proportion of invariable sites (I), Γ-distributed rates (Γ), or a combination of the two (I + Γ). Assessed models include JC, F81, which assumes unequal base frequencies and equal substitution rates, K2P, which incorporates equal base frequencies and separate transition and transversion rates, HKY, which assumes unequal base frequencies and separate transition and transversion rates, K3P, which incorporates equal base frequencies, two transversion rates, and equal transition rates, K3Puf with unequal base frequencies, Tamura–Nei, which assumes unequal base frequencies, one transversion rate, and independent transition rates, TrNef with equal base frequencies, transitional (TIM), which incorporates unequal base frequencies, two transversion, and independent transition rates, TIMef with equal base frequencies, transversional (TVM), which incorporates unequal base frequencies, independent transversion rates, and one transition rate, TVMef with equal base frequencies, symmetrical (SYM), which assumes equal base frequencies and independent substitution rates, and GTR, which incorporates unequal base frequencies and independent substitution rates. Overall, PPSs failed to reject somewhat simpler models than the GC test.
Similarly, PPSs often failed to reject simple models, especially when those models incorporated ASRV (fig. 2b). The JC model without ASRV was the simplest nonrejectable model for 16% of the data sets, whereas JC + I, JC + Γ, and JC + I + Γ could not be rejected for 40%, 52%, and 60% of the data, respectively. PPSs identified F81 + I as the simplest adequate model for one data set, K2P + Γ as the simplest nonrejectable model for an additional data set, and K2P + I + Γ as the simplest adequate model for two data sets. All models were rejected for an additional two data sets, including the water mold data used for simulation (p distance = 17.8% and 15.6%, BIC-weighted tree length = 0.91 and 0.63, and BIC-weighted stemminess index = 0.21 for both data sets), but neither of these data sets were the ones that required complex models when evaluated with the GC test.
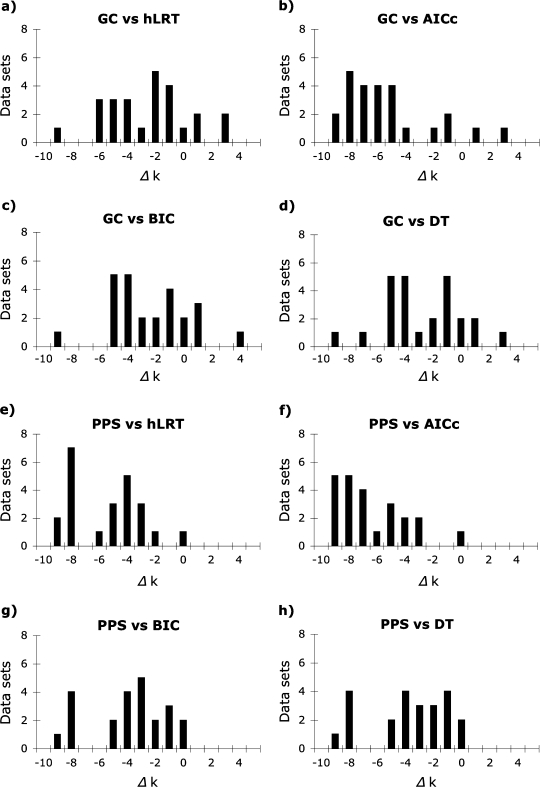
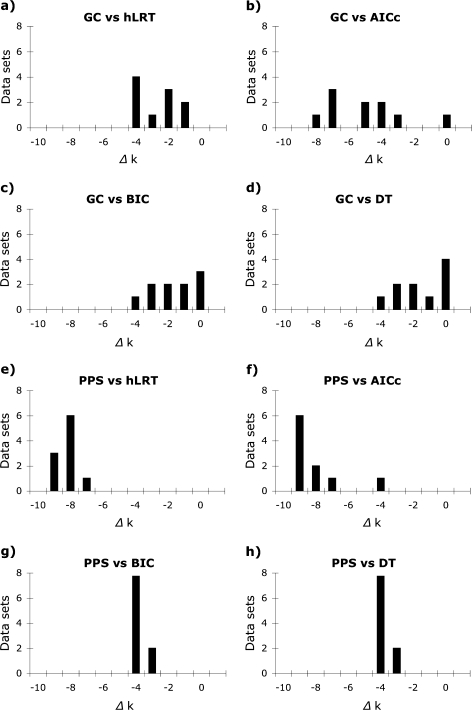
In most cases, both the GC test and the PPSs failed to reject models that were much less complex than those identified by model selection methods (fig. 3). There was a significant difference in complexity among substitution models chosen by model selection methods and the simplest models not rejected by the GC test [median (M) = 4.0 (hLRT), 8.0 (AICc), 5.0 (BIC), 5.0 (DT), and 1.0 (GC) parameters; Friedman rank sum test adjusted for ties, P < 0.01, df = 4] due to both the large number of parameters inferred by the AICc and relatively simple models not rejected by the GC test (evaluated using pairwise Wilcoxon signed rank tests adjusted for ties with the Bonferroni multiple-test correction). Consequently, optimal models identified by model selection methods were normally supported as adequate by the GC test (84%, 96%, 80%, and 84% of the models chosen by the hLRT, AICc, BIC, and DT methods, respectively). Similarly, there was a significant difference in the number of parameters incorporated by substitution models chosen by model selection methods from the reduced set of models implemented in MrBayes and the simplest models not rejected by PPSs [M = 6.0 (hLRT), 9.0 (AICc), 5.0 (BIC), 5.0 (DT), and 1.0 (PPS); Friedman test, P < 0.01, df = 4] due primarily to the complex models chosen by the AICc and the simple models not rejected by PPSs (evaluated with Wilcoxon signed rank tests). Substitution models selected by model selection methods were normally supported by PPSs but at a lower rate than the GC test (72% of models selected using the hLRT, AICc, and BIC and 68% of models selected by DT were supported by PPSs).
FIG. 3.
Difference in number of parameters between the simplest models not rejected by GC tests or PPSs and best-fit models identified using the hLRT, corrected AIC (AICc), BIC, and DT approach for 25 empirical data sets. Both tests of model adequacy often failed to reject models that were simpler than those chosen by model selection methods, especially the AICc.
The use of alternative substitution models chosen by model selection methods, as well as use of the simplest models not rejected by the GC test, resulted in similar but statistically significant differences in SDDs among ML tree topologies [M = 0.34 (hLRT), 0.34 (AICc), 0.31 (BIC), 0.31 (DT), and 0.31 (GC); Friedman test, P = 0.04, df = 4]. However, no significant differences among treatments could be detected using pairwise Wilcoxon signed rank tests with a multiple-test correction. Furthermore, although use of statistically supported models resulted in ML trees with similar length, there was a statistically significant difference in the sum of branch lengths [M = 0.49 (hLRT), 0.49 (AICc), 0.49 (BIC), 0.49 (DT), and 0.48 (GC); Friedman test, P < 0.01, df = 4] due to shorter trees inferred using the simplest models not rejected by the GC test (evaluated using Wilcoxon signed rank tests). Median bootstrap values calculated using models selected by model selection methods and the GC test tended to be fairly similar [M = 82% (hLRT), 80% (AICc), 79% (BIC), 79% (DT), and 81% (GC)]. However, Friedman’s test cannot be applied to this data because bootstrap values calculated for bipartitions on the same tree are not independent from one and other. Although the median difference in bootstrap support between models chosen by model selection methods and the simplest models not rejected by the GC test was only 2% (for all model selection methods), the maximum difference ranged from 34% (AICc vs. GC) to 47% (hLRT, BIC, and DT vs. GC), with the largest differences typically confined to more poorly supported bipartitions. Similarly, the use of substitution models chosen by model selection methods from the reduced set of models implemented in MrBayes, as well as use of the simplest models not rejected by PPSs, resulted in a significant difference in SDDs among average posterior tree lengths [M = 0.69 (hLRT), 0.66 (AICc), 0.58 (BIC), 0.58 (DT), and 0.95 (PPS); Friedman, P = 0.01, df = 4], although no significant pairwise differences could be identified using Wilcoxon signed rank tests with the Bonferroni correction. Median posterior probabilities were more similar than bootstrap values [M = 96% (hLRT), 96% (AICc), 96% (BIC), 96% (DT), and 97% (PPS)]. Although the median difference in bipartition posterior probabilities was small (M = 1% for hLRT and DT vs. PPS and 2% for AICc and BIC vs. PPS), the maximum difference in posterior probabilities was much larger than the maximum difference in bootstrap values, ranging from 72% (hLRT, BIC, and DT vs. PPS) to 74% (AICc vs. PPS).
Simulation Analysis
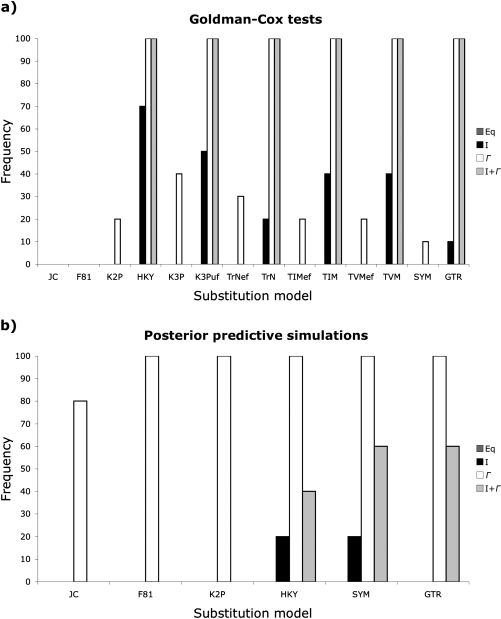
Although the GC test and PPSs both failed to reject relatively simple substitution models for replicates generated from the shrew data set, PPSs typically supported less complex models than the GC test (fig. 4). The GC test rejected the JC model with and without ASRV for all replicates. K2P + Γ was the simplest nonrejectable model for two replicates, whereas the GC test identified HKY + I and HKY + Γ as the simplest adequate models for two additional replicates and HKY + Γ alone as the simplest adequate model for three replicates. The more complex Kimura 3-parameter (K3P; Kimura 1981) model with Γ-distributed rate variation, which assumes unequal base frequencies and two transversion rates, was the simplest nonrejectable model for one replicate, whereas the equal base frequency Tamura–Nei model (TrNef; Tamura and Nei 1993) with Γ-distributed rates was the simplest nonrejectable model for an additional replicate. The GC test identified both K3P + Γ and TrNef + Γ as the simplest adequate models for the remaining replicate. Conversely, PPSs identified JC + Γ as the simplest nonrejectable model for eight replicates and K2P + Γ as the simplest substitution model for the remaining two replicates.
FIG. 4.
Rate with which substitution models are not rejected by (a) GC tests and (b) PPSs for ten replicates generated by simulating stochastic evolution using a partitioned GTR + I + Γ model constrained to the ML topology identified for a shrew mitochondrial data set. GC tests typically did not reject models that incorporated both unequal base frequencies and transition/transversion substitution rates, especially when the models also included Γ. Conversely, PPSs often failed to reject even the simplest models as long as they incorporated Γ.
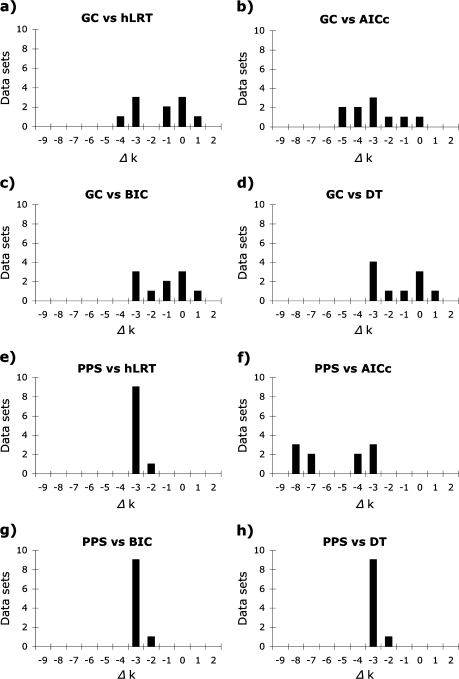
Both the GC test and the PPSs failed to reject less complex substitution models than those identified by model selection methods (fig. 5). There was a significant difference in model complexity among substitution models identified by model selection methods and the simplest models not rejected by the GC test [M = 6.5 (hLRT), 9.5 (AICc), 5.0 (BIC), 5.0 (DT), and 4.0 (GC) parameters; Friedman test, P > 0.01, df = 4] due primarily to the parameter-rich models chosen by the AICc and the simple models not rejected by the GC test (evaluated with pairwise Wilcoxon signed rank tests). Similarly, there was also a significant difference in complexity among models chosen by model selection methods from the reduced set of models implemented in MrBayes and the simplest models not rejected by PPSs [M = 9.0 (hLRT), 10.0 (AICc), 5.0 (BIC), 5.0 (DT), and 1.0 (PPS) parameters; Friedman test, P > 0.01, df = 4] due to differences among the complex models chosen by the hLRT and AICc, simpler models selected by the BIC and DT, and least complex models identified as adequate by PPSs (evaluated with Wilcoxon signed rank tests).
FIG. 5.
Disparity in number of parameters between the simplest model(s) not rejected by GC tests or the PPSs and optimal models identified by the hLRT, AICc, BIC, and DT methods for ten replicates from a shrew data set. Both tests of model adequacy often failed to reject models that were simpler than those chosen by model selection methods.
Use of all 56 substitution models lead to the recovery of an incorrect ML tree for all ten replicates, with standardized SDDs from the true tree ranging from 0.38 to 0.72. Although there was no significant difference in SDDs among ML tree topologies when using the substitution models identified by model selection methods or the simplest models not rejected by the GC test [M = 0.49 (hLRT), 0.50 (AICc), 0.49 (BIC), 0.49 (DT), and 0.50 (GC); Friedman test, P = 0.93, df = 4], there was a significant difference in SDDs among ML trees when using substitution models that made alternative assumptions about ASRV [M = 0.47 (equal rates, eq), 0.50 (I), 0.50 (Γ), and 0.50 (I + Γ); Friedman test, P > 0.01, df = 3]. The use alternative statistically supported models resulted in similar but statistically significantly different tree lengths [M = 0.45 (hLRT), 0.45 (AICc), 0.45 (BIC), 0.45 (DT), and 0.44 (GC); Friedman test, P < 0.01, df = 4], although no significant pairwise differences could be detected using Wilcoxon signed rank tests with the Bonferroni correction. Similarly, there was a significant difference in branch lengths among models that made different assumptions about ASRV [M = 0.34 (eq), 0.42 (I), 0.43 (Γ), and 0.44 (I + Γ); Friedman test, P < 0.01, df = 3] due to significant differences among all treatment pairs (evaluated with Wilcoxon signed rank tests). Although all models tended to underestimate the true tree length (0.49), equal rates models performed worse than those that incorporated ASRV. There was a significant difference in SDDs among average posterior tree lengths between substitution models chosen by model selection methods and the simplest models not rejected by PPSs [M = 0.50 (hLRT), 0.50 (AICc), 0.50 (BIC), 0.50 (DT), and 0.42 (GC); Friedman test, P < 0.01, df = 4] due to significantly shorter trees inferred using the simplest substitution models not rejected by PPS (evaluated with Wilcoxon signed rank tests). Furthermore, there was significant difference among models that made alternative assumptions about ASRV [M = 0.36 (eq), 0.45 (I), 0.47 (Γ), and 0.47 (I + Γ); Friedman test, P < 0.01, df = 3] due to models that assume equal substitution rates or a proportion of invariable sites. The results were similar to those obtained under ML; equal rates models underestimated tree length more than models that incorporated ASRV (especially, the Γ-distribution).
Concordant with previous results, tests of model adequacy failed to reject simple models for replicates generated from a water mold data set (fig. 6). The GC test again rejected JC with and without ASRV for all replicates. F81 + I, F81 + Γ, K2P + I + Γ, and K3P + Γ were the simplest nonrejectable models for one replicate apiece. The GC test identified K2P + I and K2P + Γ as the simplest adequate models for one replicate; HKY + I and HKY + Γ were the simplest models not rejected for an additional replicate. The equal rates HKY model and K2P + Γ model were identified as the simplest adequate models for two replicates apiece. Conversely, PPSs identified the equal rates JC model as the simplest adequate model for six replicates and JC + I, JC + Γ, and equal rates K2P as the simplest nonrejectable models for the remaining four replicates.
FIG. 6.
Frequency with which common substitution models are not rejected by (a) GC tests and (b) PPSs for ten replicates generated using a gene partitioned GTR + I + Γ model and ML topology for a water mold data set. Although both methods failed to reject relatively simple models, PPSs normally failed to reject less complex models (including JC without ASRV) than the GC test.
Both tests of model adequacy failed to reject simpler models than those selected by model selection methods (fig. 7), which is similar to results obtained from the empirical and shrew simulation data. There was a significant difference in the number of parameters incorporated by models chosen by model selection methods and the simplest models not rejected by the GC test [M = 4.5 (hLRT), 6.0 (AICc), 4.5 (BIC), 5.0 (DT), and 3.5 (GC); Friedman test, P < 0.01, df = 4] due to the difference between the complex models chosen by the AICc and the relatively simple models not rejected by the GC test (evaluated with Wilcoxon signed rank tests). Similarly, there was a significant difference in model complexity among models selected by model selection methods from the reduced set of models implemented in MrBayes and the least complex models not rejected by PPSs [M = 4.0 (hLRT), 7.0 (AICc), 4.0 (BIC), 4.0 (DT), and 0.0 (PPS) parameters; Friedman test, P < 0.01, df = 4] due to the simple models not rejected by PPSs (evaluated with pairwise Wilcoxon signed rank tests).
FIG. 7.
Difference in number of parameters between the simplest model(s) not rejected by GC tests or PPSs and best-fit models identified using hLRT, AICc, BIC, and DT for ten replicates generated from a water mold data set. Both tests of model adequacy normally failed to reject simpler models than those chosen by model selection methods, especially the AICc.
All 56 substitution models inferred the same ML topology for nine of the ten replicates despite the rejection of several simple models using the GC test. Use of all substitution models resulted in the recovery of the true tree for eight replicates and the recovery of the same incorrect tree for an additional replicate, whereas models that incorporated the least complex rate matrix outperformed parameter-rich models for the remaining replicate. Consequently, there was no significant difference in SDDs among ML tree topologies generated using substitution models identified by model selection methods and the least complex models not rejected by the GC test (M = 0 for all methods; Friedman test, P < 0.99, df = 4) or among models that made different assumptions about ASRV (M = 0 for all methods; Friedman test, P < 0.99, df = 3). Although use of alternative models chosen by model selection methods, as well as the simplest models deemed adequate by the GC test, did not result in statistically significant differences in SDDs [M = 0.13 (hLRT), 0.13 (AICc), 0.12 (BIC), 0.13 (DT), and 0.13 (GC); Friedman test, P = 0.25, df = 4], there was a significant difference in the sum of branch lengths among models that made alternative assumptions about ASRV [M = 0.12 (eq), 0.13 (I), 0.13 (Γ), and 0.13 (I + Γ); Friedman test, P < 0.01, df = 3] due to significantly shorter trees inferred using equal rates models (evaluated with Wilcoxon signed rank tests). Median bootstrap values calculated using models selected by model selection methods and the GC test were quite similar [M = 95% (hLRT), 94% (AICc), 95% (BIC), 94% (DT), and 94% (GC)]. Even though the median difference in bootstrap support between models chosen by model selection methods and the simplest models not rejected by the GC test was only 1% (for all methods), the maximum difference ranged from 8% (hLRT and BIC vs. GC) to 54% (DT vs. GC) with the largest difference (54%) due to a bipartition with low bootstrap support. Similarly, the median difference in bootstrap support between models that made alternative assumptions about ASRV was 1%, with the maximum difference in bipartition support ranging from 14% to 55%, with the largest differences confined to more poorly supported nodes. There was a significant difference in SDDs among average posterior tree lengths generated using substitution models chosen by model selection methods and PPSs [M = 0.14 (hLRT), 0.15 (AICc), 0.14 (BIC), 0.14 (DT), and 0.14 (PPS); Friedman test, P < 0.01, df = 4], although no significant differences could be detected among treatment pairs (evaluated with Wilcoxon signed rank tests). Similarly, there was a significant difference among models that made alternative assumptions about ASRV [M = 0.14 (eq), 0.15 (I), 0.14 (Γ), and 0.14 (I + Γ); Friedman test, P < 0.01, df = 3], with all models, especially those containing a proportion of invariable sites, overestimating the true tree length (0.13). Median posterior probabilities calculated using models selected by model selection methods and PPSs were quite similar (M = 100% for all methods). Even though the median difference in posterior probabilities between models chosen by model selection methods and the simplest models not rejected by PPSs was less than 1% (for all methods), the maximum difference ranged from 15% (hLRT vs. PPS) to 24% (AICc vs. PPS) with the larger differences due to poorly supported bipartitions. Similarly, the median difference in posterior probabilities between models that made alternative assumptions about ASRV was less than 1%, with the maximum difference in bipartition support ranging from 1% to 15%.
Discussion
Although model selection methods such as the hLRT and AIC are widely used in the phylogenetic literature, these methods choose the best substitution model from a set of possible alternatives based on relative fits and consequently cannot evaluate the adequacy of fit between the model and data. We have found that two methods that assess absolute model adequacy, the frequentist GC test and Bayesian PPSs, in conjunction with the multinomial log likelihood test statistic, normally fail to reject less complex substitution models than those chosen by model selection methods. Although the multinomial likelihood, which describes site pattern frequencies, is more general than substitution models implemented in phylogenetic analysis, it fulfills the requirement by both the GC test and PPSs for a test statistic that provides a perfect fit between the model and sequence data.
One interpretation of our results is that the current set of substitution models provides an adequate fit to the majority of phylogenetic data sets, a result that is surprising and in direct contradiction with speculation that the current set of substitution models is inadequate (e.g., Sanderson and Kim 2000). Our finding that ASRV, especially the Γ-shape parameter, is an important component of common substitution models has been reached in a number of other studies (e.g., Buckley et al. 2001; Lemmon and Moriarty 2004; Kelchner and Thomas 2007). We have also demonstrated that PPSs often fail to reject simpler models than the GC test, a result that is concordant with that obtained by Bollback (2001) for a primate ψη-globin pseudogene data set. This result can be explained by the fact that PPSs incorporate more uncertainty by sampling from relevant posterior distributions rather than relying on MLEs (Huelsenbeck et al. 2000).
An alternative explanation for our results is that data set wide tests that assess deviations from the expected multinomial likelihoods may only be sufficiently powerful to detect large deviations from the expectations of the GTR family of models (e.g., lack of ASRV or equal vs. unequal base frequencies). Interpreted in conjunction with recent work by Waddell et al. (2009), it may be the case that these tests essentially average deviations from the model across taxa and that marginalization to subsets of the character-by-taxon matrix will yield more powerful tests of absolute model fit.
In addition, we found that although using the simplest models not rejected based on fit often leads to divergent tree topologies and branch lengths, they were not significantly different from those estimated using more complex models. However, use of the simplest models not rejected by model adequacy methods affected bipartition support in some instances, although these differences were often confined to poorly supported bipartitions. Nevertheless, although use of substitution models that made alternative assumptions about ASRV did not affect tree topology, it did influence branch lengths and bipartition support. This result is similar to that obtained by Buckley et al. (2001).
As expected, we found no correlation between substitution model adequacy and phylogenetic performance; instead model performance depended strongly on the underlying tree shape. Although all substitution models tend to perform well when the true tree contains long internal branches (i.e., the tree has a high stemminess index; Fiala and Sokal 1985), use of an appropriate model becomes paramount when the tree contains long external branches separated by a short internal branch, a situation known as the Felsenstein zone (Felsenstein 1978; Sullivan and Swofford 2001; Swofford et al. 2001). Model selection is also important in the inverse-Felsenstein zone, where the misinterpretation of convergent evolution along two adjacent long external branches can favor underparameterized models (Sullivan and Swofford 2001; Swofford et al. 2001). Consequently, we would expect optimal trees inferred for data sets where all models recovered the same tree topology to have a higher stemminess index than trees calculated for data sets where models inferred different topologies (Sullivan and Joyce 2005). We calculated stemminess indexes for our data using the BioPerl module Bio::Phylo::Forest::Trees (available at http://www.cpan.org) and found that data sets for which all models recovered the same tree topology had a significantly higher stemminess index than other data sets (ML: Wilcoxon rank sum test, P < 0.01; Bayesian: Wilcoxon, P < 0.01).
Although simple substitution models (such as JC with ASRV) may perform adequately for many empirical data sets, even the most complex GTR + I +Γ model may fail to recover the correct tree when the underlying tree shape has a low stemminess index (i.e., contains many short internal branches), suggesting that one cannot always improve phylogenetic performance by further parameterizing the rate matrix of GTR family models.
Consequently, the use of alternative models, generated by partitioning the common set of substitution models, proposing gene-specific models, or adding novel parameters to these models, may be necessary to correctly infer difficult-to-estimate tree shapes. Data sets are often partitioned by gene or codon position, a strategy that may increase phylogenetic performance (e.g., Castoe et al. 2004; Brown and Lemmon 2007). Ribosomal RNA genes, often utilized in phylogenetic analysis, can be partitioned into stem and loop regions or one may use an explicit RNA model such as the doublet model implemented in MrBayes (Schoniger and von Haeseler 1994), which accounts for correlation among substitutions in stem regions. Similarly, one may use codon models that utilize the genetic code to account for synonymous/nonsynonymous substitution bias in protein-coding genes (Goldman and Yang 1994; Yang et al. 2000), even though codon-partitioned models that account for ASRV may perform as well as codon models without the computational burden (Ren et al. 2005). Although common substitution models assume the evolutionary process is homogeneous across the tree, this assumption is based more on computational tractability than biological realism. Nonstationary models have been developed that incorporate compositional heterogeneity (Foster 2004) as well as nonstationary substitution rates due to covarion-like evolution (Tuffley and Steel 1998; Huelsenbeck 2002). Because use of common substitution models does not necessarily lead to the recovery of the true tree, even if these models have an adequate fit to the data (using data set wide tests), it would be useful to expand current model selection methods and automated software to incorporate alternative sets of substitution models.
Supplementary Material
Supplementary Material is available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).
Acknowledgments
This research is part of the University of Idaho Initiative for Bioinformatics and Evolutionary Studies (IBEST); funding for the IBEST Bioinformatics Core is provided by the National Institute of Health/National Center for Research Resources grants P20RR16448 and P20RR016454. We would like to thank Celeste Brown, Jason Evans, Paul Joyce, David Posada, Jeff Thorne, Peter Waddell, Chris Williams, and an anonymous reviewer for their comments that helped improve this manuscript. We would also like to thank Celeste Brown and our systems administrators for their assistance in using the IBEST Beowulf clusters.
References
- Abdo Z, Minin VN, Joyce P, Sullivan J. Accounting for uncertainty in the tree topology has little effect on the decision-theoretic approach to model selection in phylogeny estimation. Mol Biol Evol. 2004;22:691–703. doi: 10.1093/molbev/msi050. [DOI] [PubMed] [Google Scholar]
- Akaike H. Information theory and an extension of the maximum likelihood principle. In: Petrov BN, Caski F, editors. Proceedings of the Second International Symposium on Information Theory. Budapest (Hungary): Akademiai Kiado; 1973. pp. 267–281. [Google Scholar]
- Bollback JP. Bayesian model adequacy and choice in phylogenetics. Mol Biol Evol. 2002;19:1171–1180. doi: 10.1093/oxfordjournals.molbev.a004175. [DOI] [PubMed] [Google Scholar]
- Bollback JP. Posterior mapping and predictive distributions. In: Nielsen R, editor. Statistical methods in molecular evolution. New York: Springer; 2005. pp. 1–25. [Google Scholar]
- Brandli L, Lawson Handley LJ, Vogel P, Perrin N. Evolutionary history of the greater white-toothed shrew (Crocidura russula) inferred from analysis of mtDNA, Y and X chromosome markers. Mol Phylogenet Evol. 2005;37:832–844. doi: 10.1016/j.ympev.2005.06.019. [DOI] [PubMed] [Google Scholar]
- Brown JM, Lemmon AR. The importance of data partitioning and the utility of Bayes factors in Bayesin phylogenetics. Syst Biol. 2007;56:643–655. doi: 10.1080/10635150701546249. [DOI] [PubMed] [Google Scholar]
- Buckley TR, Simon C, Chambers GK. Exploring among-site rate variation models in a maximum-likelihood framework using empirical data: Effects of model assumptions on estimates of topology, branch lengths, and bootstrap support. Syst Biol. 2001;50:67–86. [PubMed] [Google Scholar]
- Carstens BC, Degenhardt JD, Stevenson AS, Sullivan J. Accounting for coalescent stochasticity in testing phylogeographic hypotheses: testing models of Pleistocene population structure in the Idaho giant salamander Dicamptodon aterrimus. Mol Ecol. 2005;14:255–265. doi: 10.1111/j.1365-294X.2004.02404.x. [DOI] [PubMed] [Google Scholar]
- Castoe TA, Doan TM, Parkinson CL. Data partitions and complex models in Bayesian analysis: the phylogeny of Gymnophthalmid lizards. Syst Biol. 2004;53:448–469. doi: 10.1080/10635150490445797. [DOI] [PubMed] [Google Scholar]
- Demboski J, Sullivan J. Extensive mtDNA variation within the yellow-pine chipmunk, Tamias amoenus (Rodentia: Sciuridae), and phylogeographic inferences for northwest North America. Mol Phylogenet Evol. 2003;26:389–408. doi: 10.1016/s1055-7903(02)00363-9. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. Cases in which parsimony or compatibility methods will be positively misleading. Syst Zool. 1978;27:401–410. [Google Scholar]
- Felsenstein J. Evolutionary trees from DNA sequences: a maximum-likelihood approach. J Mol Evol. 1981;17:368–376. doi: 10.1007/BF01734359. [DOI] [PubMed] [Google Scholar]
- Fiala KL, Sokal RR. Factors determining the accuracy of cladogram estimation: evaluation using computer simulation. Evolution. 1985;39:609–622. doi: 10.1111/j.1558-5646.1985.tb00398.x. [DOI] [PubMed] [Google Scholar]
- Foster PG. Modeling compositional heterogeneity. Syst Biol. 2004;53:485–495. doi: 10.1080/10635150490445779. [DOI] [PubMed] [Google Scholar]
- Frati F, Simon C, Sullivan J, Swofford DL. Evolution of the mitochondrial cytochrome oxidase II gene in Collembola. J Mol Evol. 1997;44:145–158. doi: 10.1007/pl00006131. [DOI] [PubMed] [Google Scholar]
- Gatesy J. A tenth crucial question regarding model use in phylogenetics. Trends Ecol Evol. 2007;22:509–510. doi: 10.1016/j.tree.2007.08.002. [DOI] [PubMed] [Google Scholar]
- Gaut BS, Lewis PO. Success of maximum likelihood phylogeny inference in the four-taxon case. Mol Biol Evol. 1995;12:152–162. doi: 10.1093/oxfordjournals.molbev.a040183. [DOI] [PubMed] [Google Scholar]
- Gelman A, Meng X-L, Stern H. Posterior predictive assessment of model fitness via realized discrepancies. Stat Sin. 1996;6:733–807. [Google Scholar]
- Goldman N. Statistical tests of models of DNA substitution. J Mol Evol. 1993;36:182–198. doi: 10.1007/BF00166252. [DOI] [PubMed] [Google Scholar]
- Goldman N, Yang Z. A codon-based model of nucleotide substitution for protein-coding DNA sequences. Mol Biol Evol. 1994;11:725–736. doi: 10.1093/oxfordjournals.molbev.a040153. [DOI] [PubMed] [Google Scholar]
- Hasegawa M, Kishino K, Yano T. Dating the human-ape split by a molecular clock of mitochondrial DNA. J Mol Evol. 1985;22:160–174. doi: 10.1007/BF02101694. [DOI] [PubMed] [Google Scholar]
- Huelsenbeck JP. Testing a covariotide model of DNA substitution. Mol Biol Evol. 2002;19:698–707. doi: 10.1093/oxfordjournals.molbev.a004128. [DOI] [PubMed] [Google Scholar]
- Huelsenbeck JP, Rannala B, Masly JP. Accommodating phylogenetic uncertainty in evolutionary studies. Science. 2000;288:2349–2350. doi: 10.1126/science.288.5475.2349. [DOI] [PubMed] [Google Scholar]
- Huelsenbeck JP, Ronquist F, Nielson R, Bollback JP. Bayesian inference of phylogeny and its impact on evolutionary biology. Science. 2001;294:2310–2314. doi: 10.1126/science.1065889. [DOI] [PubMed] [Google Scholar]
- Jukes TH, Cantor CR. Evolution of protein molecules. In: Munro HN, editor. Mammalian protein metabolism. New York: Academic Press; 1969. pp. 21–132. [Google Scholar]
- Kelchner SA, Thomas MA. Model use in phylogenetics: nine key questions. Trends Ecol Evol. 2007;22:87–94. doi: 10.1016/j.tree.2006.10.004. [DOI] [PubMed] [Google Scholar]
- Kimura M. A simple method of estimating evolutionary rate of base substitutions through comparative studies of nucleotide sequences. J Mol Evol. 1980;16:111–120. doi: 10.1007/BF01731581. [DOI] [PubMed] [Google Scholar]
- Kimura M. Estimation of evolutionary distances between homologous nucleotide sequences. Proc Nattl Acad Sci U S A. 1981;78:454–458. doi: 10.1073/pnas.78.1.454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemmon AR, Moriarty EC. The importance of proper model assumptions in Bayesian phylogenetics. Syst Biol. 2004;53:265–277. doi: 10.1080/10635150490423520. [DOI] [PubMed] [Google Scholar]
- Lockhart PJ, Steel MA, Hendy MD, Penny D. Recovering evolutionary trees under a more realistic model of sequence evolution. Mol Biol Evol. 1994;11:605–612. doi: 10.1093/oxfordjournals.molbev.a040136. [DOI] [PubMed] [Google Scholar]
- Minin V, Abdo Z, Joyce P, Sullivan J. Performance-based selection of likelihood models for phylogeny estimation. Syst Biol. 2003;52:1–10. doi: 10.1080/10635150390235494. [DOI] [PubMed] [Google Scholar]
- Mirabolfathy M, Cooke DEL, Duncan JM, Williams NA, Ershad D, Rahimian H, Alizadeh A. Phytophthora pistaciae sp. nov. and Phytophthora melonis (Katsura): the principal causes of pistachio gummosis in Iran. Mycol Res. 2001;105:1166–1175. [Google Scholar]
- Nylander JAA. MrModeltest v2. Program distributed by the author. Uppsala (Sweden): Evolutionary Biology Centre, Uppsala University; 2004. [Google Scholar]
- Posada D, Buckley TR. Model selection and model averaging in phylogenetics: advantages of Akaike information criterion and Bayesian approaches over likelihood ratio tests. Syst Biol. 2004;53:793–808. doi: 10.1080/10635150490522304. [DOI] [PubMed] [Google Scholar]
- Posada D, Crandall KA. Modeltest: testing the model of DNA substitution. Bioinformatics. 1998;14:817–818. doi: 10.1093/bioinformatics/14.9.817. [DOI] [PubMed] [Google Scholar]
- Rambaut A, Grassly NC. Seq-Gen: an application for the Monte Carlo simulation of DNA sequence evolution along phylogenetic trees. Comput Appl Biosci. 1997;13:235–238. doi: 10.1093/bioinformatics/13.3.235. [DOI] [PubMed] [Google Scholar]
- Reeves JH. Heterogeneity in the substitution process of amino acid sites of proteins coded for by mitochondrial DNA. J Mol Evol. 1992;35:17–31. doi: 10.1007/BF00160257. [DOI] [PubMed] [Google Scholar]
- Ren F, Tanaka H, Yang Z. An empirical examination of the utility of codon-substitution models in phylogeny reconstruction. Syst Biol. 2005;54:808–818. doi: 10.1080/10635150500354688. [DOI] [PubMed] [Google Scholar]
- Revell LJ, Harmon LJ, Glor RE. Underparametrized model of sequence evolution leads to bias in the estimation of diversification rates from molecular phylogenies. Syst Biol. 2005;54:973–983. doi: 10.1080/10635150500354647. [DOI] [PubMed] [Google Scholar]
- Ripplinger J, Sullivan J. Does choice in model selection affect maximum likelihood analysis? Syst Biol. 2008;57:76–85. doi: 10.1080/10635150801898920. [DOI] [PubMed] [Google Scholar]
- Robinson DF, Foulds LR. Comparison of phylogenetic trees. Math Biosci. 1981;53:131–147. [Google Scholar]
- Ronquist F, Huelsenbeck JP. MrBayes 3: Bayesian phylogenetic inference under mixed models. Bioinformatics. 2003;19:1572–1574. doi: 10.1093/bioinformatics/btg180. [DOI] [PubMed] [Google Scholar]
- Rubin DB. Bayesianly justifiable and relevant frequency calculations for the applied statistician. Ann Stat. 1984;12:1151–1172. [Google Scholar]
- Sanderson MJ, Kim J. Parametric phylogenetics? Syst Biol. 2000;49:817–829. doi: 10.1080/106351500750049860. [DOI] [PubMed] [Google Scholar]
- Schoniger M, von Haeseler A. A stochastic model for the evolution of autocorrelated DNA sequences. Mol Phylogenet Evol. 1994;3:240–247. doi: 10.1006/mpev.1994.1026. [DOI] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimensions of a model. Ann Stat. 1978;6:461–464. [Google Scholar]
- Sullivan J, Abdo Z, Joyce P, Swofford DL. Evaluating the performance of a successive-approximations approach to parameter optimization in maximum-likelihood phylogeny estimation. Mol Biol Evol. 2005;22:1386–2392. doi: 10.1093/molbev/msi129. [DOI] [PubMed] [Google Scholar]
- Sullivan J, Joyce P. Model selection in phylogenetics. Ann Rev Ecol Evol Syst. 2005;36:445–466. [Google Scholar]
- Sullivan J, Markert JA, Kilpatrick CW. Phylogeography and molecular systematics of the Peromyscus aztecus species group (Rodentia: Muridae) inferred using parsimony and likelihood. Syst Biol. 1997;46:426–440. doi: 10.1093/sysbio/46.3.426. [DOI] [PubMed] [Google Scholar]
- Sullivan J, Swofford DL. Are guinea pigs rodents? The importance of adequate models in molecular phylogenetics. J Mammal Evol. 1997;4:77–86. [Google Scholar]
- Sullivan J, Swofford DL. Should we use model-based methods for phylogenetic inference when we know that assumptions about among-site rate variation and nucleotide substitution pattern are violated? Syst Biol. 2001;50:723–729. doi: 10.1080/106351501753328848. [DOI] [PubMed] [Google Scholar]
- Swofford DL. PAUP*: phylogenetic analysis using parsimony (*and other methods). Version 4.0b10. Sunderland (MA): Sinauer Associates; 2002. [Google Scholar]
- Swofford DL, Waddell PJ, Huelsenbeck JP, Foster PG, Lewis PO, Rogers JS. Bias in phylogenetic estimation and its relevance to the choice between parsimony and likelihood methods. Syst Biol. 2001;50:525–539. [PubMed] [Google Scholar]
- Tamura K, Nei M. Estimation of the number of nucleotide substitutions in the control region of mitochondrial DNA in humans and chimpanzees. Mol Biol Evol. 1993;10:512–526. doi: 10.1093/oxfordjournals.molbev.a040023. [DOI] [PubMed] [Google Scholar]
- Tavaré S. Some probabilistic and statistical problems in the analysis of DNA sequences. In: Miura RM, editor. Some mathematical questions in biology: DNA sequence analysis. Lectures on Mathematics in the Life Sciences. 1986. Vol. 17. New York American Mathematical Society. p. 57–86. [Google Scholar]
- Tuffley C, Steel M. Modeling the covarion hypothesis of nucleotide substitution. Math Biosci. 1998;147:63–91. doi: 10.1016/s0025-5564(97)00081-3. [DOI] [PubMed] [Google Scholar]
- Waddell PJ, Ota R, Penny D. Measuring fit of sequence data to phylogenetic model: gain of power using marginal tests. J Mol Evol. 2009;69:289–299. doi: 10.1007/s00239-009-9268-8. [DOI] [PubMed] [Google Scholar]
- Whelan S, Lio P, Goldman N. Molecular phylogenetics: state-of-the-art methods for looking into the past. Trends Genet. 2001;17:262–272. doi: 10.1016/s0168-9525(01)02272-7. [DOI] [PubMed] [Google Scholar]
- Yang Z, Nielsen R, Goldman N, Pedersen AMK. Codon-substitution models for heterogeneous selection pressure at amino acid sites. Genetics. 2000;155:431–449. doi: 10.1093/genetics/155.1.431. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.