Disentangling the Functional Roles of Morphology and Motion in the Swimming of Fish

Abstract

In fishes the shape of the body and the swimming mode generally are correlated. Slender-bodied fishes such as eels, lampreys, and many sharks tend to swim in the anguilliform mode, in which much of the body undulates at high amplitude. Fishes with broad tails and a narrow caudal peduncle, in contrast, tend to swim in the carangiform mode, in which the tail undulates at high amplitude. Such fishes also tend to have different wake structures. Carangiform swimmers generally produce two staggered vortices per tail beat and a strong downstream jet, while anguilliform swimmers produce a more complex wake, containing at least two pairs of vortices per tail beat and relatively little downstream flow. Are these differences a result of the different swimming modes or of the different body shapes, or both? Disentangling the functional roles requires a multipronged approach, using experiments on live fishes as well as computational simulations and physical models. We present experimental results from swimming eels (anguilliform), bluegill sunfish (carangiform), and rainbow trout (subcarangiform) that demonstrate differences in the wakes and in swimming performance. The swimming of mackerel and lamprey was also simulated computationally with realistic body shapes and both swimming modes: the normal carangiform mackerel and anguilliform lamprey, then an anguilliform mackerel and carangiform lamprey. The gross structure of simulated wakes (single versus double vortex row) depended strongly on Strouhal number, while body shape influenced the complexity of the vortex row, and the swimming mode had the weakest effect. Performance was affected even by small differences in the wakes: both experimental and computational results indicate that anguilliform swimmers are more efficient at lower swimming speeds, while carangiform swimmers are more efficient at high speed. At high Reynolds number, the lamprey-shaped swimmer produced a more complex wake than the mackerel-shaped swimmer, similar to the experimental results. Finally, we show results from a simple physical model of a flapping fin, using fins of different flexural stiffness. When actuated in the same way, fins of different stiffnesses propel themselves at different speeds with different kinematics. Future experimental and computational work will need to consider the mechanisms underlying production of the anguilliform and carangiform swimming modes, because anguilliform swimmers tend to be less stiff, in general, than are carangiform swimmers.

Introduction

More than 500-million years ago, the earliest vertebrates emerged, with an approximately cylindrical, elongate body similar in shape to modern lampreys or eels (Liem et al. 2001). Since then, fishes have evolved a huge diversity of body shapes. Basal vertebrate lineages, such as lampreys (Petromyzontiformes) and hagfishes (Myxiniformes), preserve the early elongate morphology (Fig. 1A). More derived species, such as tunas and mackerels (Scombridae), the lamnid sharks, and some cetaceans, have convergently evolved a streamlined, torpedo-shaped body and a broad, wing-like tail (Fig. 1C). Nevertheless, many vertebrate lineages have independently returned to the basal elongate form, including the true eels (Anguillidae), some catfish species, and needlefishes (Belonidae) (Liao 2002, Ward and Brainerd 2007).

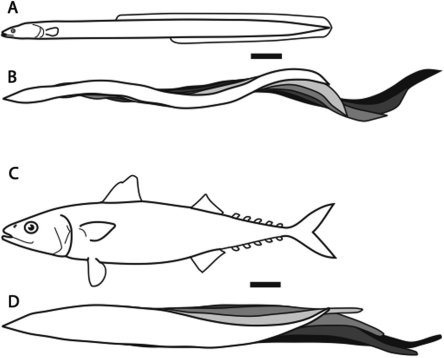
Fig. 1.

Differences in body shape and swimming mode. (A) Eel body shape from the side and (B) anguilliform swimming mode from the top. (C) Mackerel body shape and (D) carangiform swimming mode. Kinematics panels (B and D) show forward progression at equally spaced time intervals through a tail beat cycle during swimming at ∼1.8 l s⁻¹. Scale bars are 2 cm. After Lauder and Tytell (2006); data on mackerel modified from Donley and Dickson (2000).

These shifts in body shape are often correlated with differences in swimming kinematics. A variety of swimming modes have been recognized (Breder 1926), but the continuum from anguilliform (eel-like) to carangiform (mackerel-like) seems to apply to a large number of different fishes. Fishes that swim in the anguilliform mode, including the elongate lineages mentioned above, tend to have undulations along their entire body, particularly at high speeds, with a nearly complete bending wave (Fig. 1B) (e.g., Aleyev 1977; Gillis 1998; Liao 2002). Carangiform swimmers, in contrast, tend to have much less motion in their anterior body, and less than a full bending wave on their bodies (Fig. 1D; Lauder and Tytell 2006).

It seems likely that locomotory performance has been a key factor in the morphological and behavioral diversification in fishes. Nearly all fishes swim to escape predators, to feed, and to find mates. All of these behaviors are critical for an animal’s survival, and therefore high performance in these areas should be under strong selective pressure (e.g., see Langerhans 2009 for an example of predator-driven selection on locomotor performance). Intuitively, selection for different behaviors might push in different directions. For instance, escaping predators requires high accelerations, which might favor a body shape with large fins and a deep body (Webb 1984). Alternatively, foraging for food often requires swimming long distances, which might favor a body shape with small fins and a streamlined body with low drag (Webb 1984). Differences in swimming modes may also contribute to swimming performance. Lighthill’s elongate-body theory suggests that all thrust forces are produced at the tail tip; movement anterior to that point is just wasted effort (Lighthill 1971). Thus, the theory suggests that the carangiform mode may be more efficient, because that mode minimizes motion of the anterior part of the body. However, because anguilliform swimming has a complete body wave, the forces tend to fluctuate less (Lighthill 1970; Tytell 2007; Borazjani and Sotiropoulos 2009). Smaller fluctuations in the force output might result in less energy being wasted producing a wake, an important component of the total energy budget of swimming (Webb and Cotel 2010).

Thus, it is difficult to predict the functional consequences of different swimming modes and body shapes. Yet, because of the putatively strong selective pressures on locomotor performance, understanding these consequences would provide important insight into the morphological and behavioral diversity of fishes. In this review, we summarize some recent experimental and computational work from our groups that shed light on hydrodynamic performance of fishes of different shapes and swimming modes.

In all cases, it will be important to consider two key non-dimensional variables: the Reynolds number (Re) and the Strouhal number (St). Re characterizes the relative importance of viscosity and inertia, and is defined as follows:

(1)

where L is the length of the fish, U is the swimming speed, and ν is the kinematic viscosity of water. St describes the rate of the tail’s motion relative to forward motion:

(2)

where f and A are, respectively, the frequency and amplitude of the tail beat. Re for most swimming fishes is much greater than 1, indicating that viscosity is relatively unimportant. Most fishes swim with a St near 0.3 (Triantafyllou et al. 1993), although this can often increase at low swimming speeds (i.e., low Re) (Lauder and Tytell 2006; Borazjani and Sotiropoulos 2008, 2009).

Below, we first describe experimental measurements of patterns of flow in the wakes of fishes of differing body shapes and with different swimming modes. Then we consider some recent computational work that attempts to disentangle the functional consequences of swimming mode and body shape. Because of the complexity of the computations, simulations were performed in three orders of magnitude: Re = 300, comparable to the Re of juvenile fishes and some larvae; Re = 4000, an intermediate range; and Re = ∞, a simulation with zero viscosity that may be representative of the flows around large adult fishes. The computations were intended to examine the hydrodynamic processes involved in the swimming of fishes with different body shapes and swimming modes, not to replicate experimental results directly. Nevertheless, comparing experimental and computational results is informative, and we discuss the similarities and differences below. Finally, we propose that understanding the interaction between the fluid and the fish's body will be an important avenue for future study. Flexibility of the body and the partitioning of active muscular work and passive responses to fluid forces is another important difference among fishes, and likely has consequences for swimming performance.

Experimental hydrodynamics

Recent studies use a technique called digital particle image velocimetry (PIV; Willert and Gharib 1991) to observe the motion of fluid around the fish’s body. In these studies, a high-speed camera is generally used to film the fish as it swims in a flow tunnel. Small reflective particles are placed in the flow, and a single plane, usually horizontal, is illuminated using laser light, showing the motion of the particles. The PIV algorithm is used to track the particles, producing a field of vectors showing the motion of fluid in that plane over time. See Tytell (E. D. Tytell, submitted for publication) and Lauder and Tytell (2006) for more details of the methods.

The wakes of eels and mackerels differ

Experimental measurements of the fluid flow around swimming fishes indicate that carangiform swimmers, such as the mackerel (Scomber japonicus) and the bluegill sunfish (Lepomis macrochirus), produce a qualitatively different wake than does the American eel (Anguilla rostrata), an anguilliform swimmer. These differences are present even for fishes swimming at very similar Re and St.

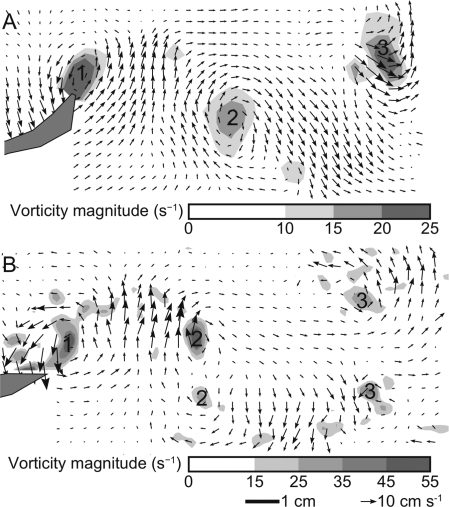
Studies of carangiform swimmers confirmed early observations (e.g., Aleyev 1977; Gray 1968) that the tail wake of these fishes contains a single vortex per half tail beat (i.e., each time the tail reaches its maximum lateral excursion) with a jet that angles laterally and away from the fish. Fig. 2A shows an example of such a wake from a bluegill sunfish. The Re in this example is 40 000 and the St is 0.42.

Fig. 2.

Example of wakes of swimming bluegill sunfish and eels. Panels show horizontal planes near the fishes’ tails. Speed and direction of flow are shown by arrows and magnitude of vorticity by shades of gray. The fishes’ tails are shown in gray on the left. Vortices are numbered by the half tail beat in which each was shed. (A) A carangiform swimmer, the bluegill sunfish, Lepomis macrochirus), swimming at 1.70 l s⁻¹. Only one vortex is shed per half tail beat. (B) An anguilliform swimmer, the American eel, A. rostrata, swimming at 1.34 l s⁻¹. Note that two vortices are shed per half tail beat. The scale bars and scale vectors are the same for both panels, but the vorticity scales are different.

This general pattern was confirmed for a variety of fishes, including mullet (Chelon labrosus; Müller et al. 1997), giant danio (Devario aequipinattus; Anderson 1996), bluegill sunfish (Drucker and Lauder 2001), and chub mackerel (S. japonicus; Nauen and Lauder 2002). A wake with this pattern is called a reverse von Kármán wake (von Kármán and Burgers 1934) or a 2S wake (referring to the two single vortices shed per cycle), and is indicative of thrust (Koochesfahani 1989).

The thrust wake of carangiform swimmers suggests that, for such fishes, the tail produces primarily thrust while the body produces primarily drag. Because the fishes are swimming at constant velocity, the net force, or the sum of thrust and drag, must be zero when averaged over the body and over a tail beat cycle (Tytell 2007). For carangiform swimmers, analysis of the wake close to the tail shows primarily the effect of the tail on the flow, and thus shows a thrust wake.

Careful study of the wake of swimming eels, which use the anguilliform mode, showed that they produce a qualitatively different wake (Müller et al. 2001; Tytell and Lauder 2004). Rather than a 2S wake structure with a jet indicating production of thrust, eels produce at least two pairs of vortices per tail beat (a ‘2P’ or higher-order wake structure) with a purely lateral jet (Tytell and Lauder 2004). Figure 2B shows an example at a Re of 65 000 and a St of 0.36. The wake structure suggests that swimming eels balance thrust and drag rather evenly over their bodies and over time. When thrust and drag are not so evenly balanced, for instance, during linear acceleration, the eel’s wake becomes closer to the 2S wake typical of carangiform swimmers (Tytell 2004).

Performance during steady swimming

For steadily swimming animals, it is not feasible to estimate propulsive efficiency from wake measurements of this sort (Tytell 2007). Two separate metrics may be informative: total power P_tot and propulsive efficiency η. Propulsive efficiency is the ratio of useful power (the thrust power required to overcome drag) to total power,

(3)

where T is the thrust force, U is again the swimming speed, and P_wake is power wasted producing a wake. It is notoriously difficult to measure the thrust T for self-propelled objects (Schultz and Webb 2002; Tytell 2007), but P_wake is the easily measurable kinetic energy passing through the wake per unit time. A perfectly efficient swimmer would put all of its energy into forward propulsion, and leave behind no wake. For streamlined objects, like fishes, in which the drag force D may be small and thus the thrust force is also small, then P_wake may represent a sizeable component of the total energy budget (Webb and Cotel 2010). Thus, if the thrust power is not dramatically different among different fishes, then the wake power may serve as a proxy measure for comparing their swimming efficiencies. To non-dimensionalize power to compare across fishes of different sizes and swimming speeds, we use power coefficients C_P,wake and C_P,tot:

(4)

where S is the wetted surface area of the fish.

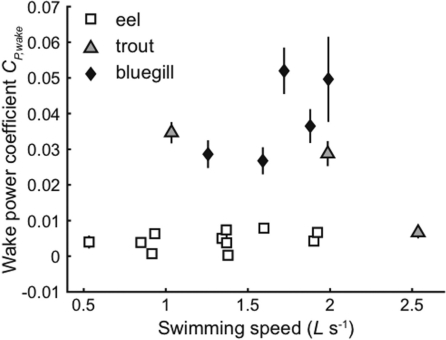
Figure 3 shows a comparison of the wake power coefficient across three fish species, the American eel A. rostrata, an anguilliform swimmer; the bluegill sunfish L. macrochirus, a carangiform swimmer; and the rainbow trout Oncorhyncus mykiss, a subcarangiform swimmer. Because these three fishes are evolutionarily quite distant from one another, the results may represent the different phylogenetic history of the species. However, the values show an intriguing correlation with the lifestyles of the fishes. Eels tend to migrate very long distances while swimming at relatively low speeds, roughly one body length per second or less (van Ginneken et al. 2005), and waste little power at this speeds. Interestingly, they also appear to waste relatively little energy at higher and lower speeds. Trout, by contrast, tend to swim in high flow streams, and waste little power at their highest speed, but not at lower speeds. Finally, bluegill waste the largest amount of power, but since they are a species commonly found in ponds and slow-moving steams, they may not be very well adapted to steady swimming. Instead, they may be adapted more for maneuverability.

Fig. 3.

Wake power coefficients for three different fishes swimming at a range of speeds. Relative to their body size, eels waste the smallest amount of energy producing a wake, while bluegill sunfish waste much more energy. Wakes of trout contain relatively little energy, but only at the highest swimming speed. Modified from Tytell (2007).

Why do these fishes differ in hydrodynamic performance? Is it because their bodies differ morphologically, or because they swim differently? Such questions are quite difficult to address experimentally, because behavior and morphology are strongly correlated. In this case, the best way to approach the problem is using computational fluid dynamics (CFD). Using a computational simulation, one can vary body shape and swimming mode independently and determine the functional consequences.

Computational studies

The three computational studies reviewed here, Borazjani and Sotiropoulos (2008, 2009, 2010), all use the same computational framework, with one important difference in the study from 2010. First, the body of the fish is specified as a set of K points r^k(t), each of which has a prescribed velocity U^k(t) that represent the swimming kinematics. At the same time, the three-dimensional (3D) Navier–Stokes equations for fluid motion are solved around this body. When non-dimensionalized by the average swimming speed U and the fish’s body length L, the equations read

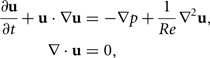(5)

where u is the fluid velocity vector and p is the fluid pressure divided by the density and velocity squared. The fish’s body serves as a boundary condition for the fluid solver, as follows:

(6)

meaning that the fluid velocity u must be equal to the body velocity U^k at the surface of the body defined by the r^k points at every point in time t. This boundary condition [Equation (6)] requires that the fluid does not penetrate the body (no-flux condition) and that it does not slip along the boundary. For inviscid flows, Re = ∞, only the normal component of the fluid velocity is prescribed at the boundary, enforcing the no-flux condition, but allowing it to slip along the surface.

Equation (5) with boundary conditions (6) are solved using a hybrid Cartesian/immersed-boundary method. Unlike traditional immersed boundary methods (Peskin 2002), this method allows the motion of the boundary to be specified exactly as a sharp interface between the fluid and solid. The method has been extensively validated for flows with complex moving boundaries, including problems with fluid-structure interaction. See Gilmanov and Sotiropoulos (2005), Ge and Sotiropoulos (2007), and Borazjani et al. (2008) for more details.

In the first two studies (Borazjani and Sotiropoulos 2008, 2009), the swimming speed U and the dynamic viscosity ν are prescribed to set Re [Equation (1)], then the tail beat frequency f is varied to examine the effect of St. For these simulations, the net force on the simulated fish may not be zero. The swimmer is effectively tethered, with an imaginary tether that moves at a constant speed U and takes up any excess axial or lateral force. One key parameter that the simulations estimated was the self-propelled swimming speed U₀, the speed of the tether such that the net force was zero, and the corresponding self-propelled St₀. These studies each examined a single body shape and swimming mode: first, a mackerel swimming in the carangiform mode (CM; Borazjani and Sotiropoulos 2008); and second, a lamprey swimming in the anguilliform mode (AL; Borazjani and Sotiropoulos 2009).

In the last study (Borazjani and Sotiropoulos 2010), although the kinematics are prescribed, the swimmers are self-propelled, because the fluid forces in the axial direction are coupled to the motion of the swimmer’s center of mass:

(7)

where m is the mass of the swimmer, U* is the normalized swimming speed, F_A is the force in the axial direction, and U₀ is the self-propelled swimming speed from the simulations in which the body was tethered (Borazjani and Sotiropoulos 2008). The normalized swimming speed U* is defined as U* = U/U₀. Equation (7) is coupled with the solution of the Navier–Stokes equations [Equation (5)] using the fluid–structure interaction approach described in detail by Borazjani et al. (2008). As described in detail by Borazjani and Sotiropoulos (2010), for efficient simulation of self-propelled swimmers, the Navier–Stokes equations are formulated and solved in a coordinate frame that moves with the fish’s center of mass.

In this study, because the actual swimming speed U is computed from the fluid-structure interaction, Re and St can only be set approximately based on the tethered simulations. In all cases, the data from the tethered mackerel are used as the baseline. First, to reach a given Re, the viscosity is set appropriately and the self-propelled swimming speed U₀ and St₀ are selected from the simulations in which the body was tethered. Frequency of tail beat is set based on St₀. Then the swimmer is allowed to move, solving the coupled equations. The actual swimming speed U that results from the computations is therefore not necessarily equal to U₀, and the actual St (St_act) may not be equal to St₀.

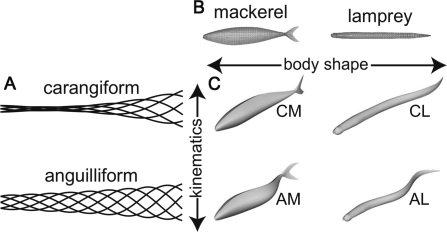
Using this computational framework, idealized approximations of anguilliform and carangiform kinematics (Fig. 4A) were combined with digitizations of the mackerel and lamprey body shapes (Fig. 4B). Anguilliform kinematics were based on data from a swimming lamprey (Ichthyomyzon unicuspis) from Hultmark et al. (2007) and carangiform kinematics were based on data from mackerel (Scomber scombrus) from Videler and Hess (1984). Note that lampreys swim with much more head motion than do true eels (Gillis 1998; Lauder and Tytell 2004). The geometry of the mackerel body was obtained by digitizing cross sections of a frozen mackerel (Gilmanov and Sotiropoulos 2005) and that of the lamprey body was based on a computed tomography scan provided by Dr Frank Fish. Thus, as shown in Fig. 4C, the simulations produced a mackerel swimming in the carangiform mode (CM), a lamprey swimming in the anguilliform mode (AL), as well as two artificial combinations: a mackerel swimming in the anguilliform mode (AM), and a lamprey swimming in the carangiform mode (CL). The abbreviations used here are different from those used by Borazjani and Sotiropoulos (2010).

Fig. 4.

Simulated swimming modes and body shapes. (A) Midline tracings of carangiform and anguilliform swimming motions, seen from above. Amplitudes are to scale. Carangiform kinematics from Videler and Hess (1984); anguilliform kinematics from Hultmark et al. (2007). Note that true eels often swim with less motion of the head than do lampreys. (B) Side views of the bodies of mackerel and lamprey. The bodies include only the caudal fins; other fins are neglected. (C) Plots of all combinations of shape and kinematics with the corresponding abbreviations.

For estimating power coefficients, we use the normalization from Tytell (2007), as stated above in Equation (4). This differs from the normalization in Borazjani and Sotiropoulos (2010), who used 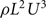. The wetted surface areas S for the simulated mackerel and lamprey bodies are 0.34L² and 0.15L², respectively.

In all of the simulations, the body motion is prescribed in advance. In contrast, for a real fish, the motion is a result of the balance between internal elasticity and muscular forces and external fluid forces. In the literature on fluid dynamics, such a balance is called ‘fluid–structure interaction’ or FSI. Simulating these interactions is currently very challenging. Thus, most current simulations use prescribed kinematics that have been measured from real fishes (e.g., Videler and Hess 1984; Tytell and Lauder 2004). Provided the measurements used as the basis for the computations are sufficiently accurate, such simulations will produce the same patterns of flow as that around a swimming fish with a flexible body that interacts with the fluid.

To simulate conditions for which no measurements exist, such as a mackerel swimming in the anguilliform mode, Borazjani and Sotiropoulos (2010) solved part of the fluid–structure interaction. They prescribed the motion of the swimmers relative to their centers of mass, but the center of mass moved as a consequence of the fluid forces. In these simulations, the inertia of the fish plays a role, but only on the movement of the center of mass; the computations prescribe the side-to-side motion of the simulated tail, and do not compute the effects of the tail’s inertia or flexibility. Nevertheless, because the side-to-side motion was digitized from a real fish that has a flexible tail, the computed fluid motion should accurately reflect the flow around a flexible tail. To investigate the effects of flexibility and inertia directly, future simulations will need to account for the complete fluid–structure interaction problem. Below, after we summarize the current computational results, we discuss some experimental results from a physical model and their implications for future computational work.

Wake structure differs according to St

The use of a simulated tether in the studies from 2008 and 2009 allowed St and Re to vary independently (Borazjani and Sotiropoulos 2008, 2009). Changing St alters the forces that the swimmer produces. To vary St while keeping Re constant means that the net force on the swimmer may not be zero. The simulated tether is thus required to keep the swimmer moving forward at a constant speed. The tether takes up any excess thrust or absorbs any excess drag. If it were removed, in most cases the swimmer would accelerate or decelerate. A special case is the ‘self-propelled speed’: the speed at which the net force on the tether is zero. At the self-propelled speed, the tether could be removed, and the swimmer would continue moving at the same speed.

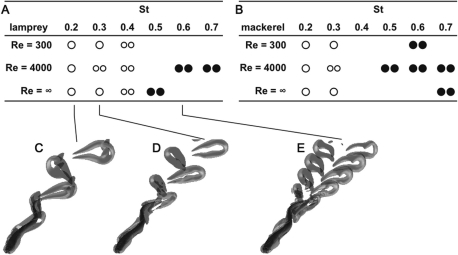
As St increases, the wake structure changes (Fig. 5). At low St, the wake generally consists of two single vortices shed per tailbeat (a 2S structure). For example, in Fig. 5C, the vortex loops are connected along the center line, making one wavy row. At high St, the wake splits into two pairs of vortices per tailbeat (a 2P structure). For example, in Fig. 5E, the vortex loops have disconnected in the middle and form two separate rows on the left and right. In the middle (St = 0.3), there are transitional wakes, in which a single vortex is initially shed as the tail reverses direction, but the spreading of the wake causes it to break apart into two vortices (Fig. 5D). St is the primary determinant of the overall structure of the wake. Re, body shape, and swimming mode have smaller effects on the gross wake structure (e.g., compare Fig. 5A and B).

Fig. 5.

Simulated wakes differ primarily as a function of St. Tables show the wake type after a steady swimming speed has been reached. (A) Lamprey body and anguilliform swimming mode; (B) Mackerel body and carangiform swimming mode. Types of wakes: open circle, single row; two filled circles, double row; two open circles, transition between single and double row. Transitional wakes start off as a single row, then, further downstream in the wake, transition to a double row. Example of wakes under steady-state conditions for the anguilliform lamprey at Re = 4000 and (C) St = 0.2, single row; (D) St = 0.3, transitional; and (E) St = 0.6, double row, are shown in the lower panels. Note that most of these cases are not self-propelled; the net force on the swimmer may be not equal to 0. Data from Borazjani and Sotiropoulos (2008, 2009).

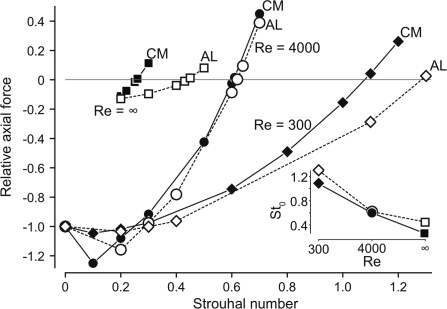
However, both Re and St are important functionally, particularly for force production (Fig. 6). In general, as St increases above some minimum value, the swimmer produces more thrust. With no motion (St = 0), the only force is the drag on the body (the ‘rigid-body drag’). Note that in the inviscid simulations (Re = ∞), the rigid-body drag is zero due to the absence of viscosity, which is why the St = 0 point is not plotted, but both (form) drag and thrust are non-zero for St ≠ 0 due to vortex shedding, which is present even in the absence of viscosity. For comparison, the Re = ∞ case is normalized by the same rigid-body drag as the Re = 4000 case (Fig. 6). For all simulations, as St begins to increase, the undulations initially increase the drag force, so that for St <0.2, the net force is actually greater (more negative) than the rigid-body drag. Above St = 0.2, the thrust force begins to increase and the net force climbs toward zero. At the critical St₀, the net force is zero. In this condition, the imaginary tether could be removed and the swimmer would continue to travel at a constant speed; the swimmer is thus self-propelled.

Fig. 6.

Relative axial force for the tethered swimmers as a function of St. Axial force is scaled by the rigid-body drag for each body shape for Re = 300 and 4000. For the Re = ∞ case, the rigid-body drag is zero; for comparison, the forces in this case are normalized by the rigid-body drag at Re = 4000. The carangiform mackerel (CM) is shown with filled symbols and solid lines for each Re (filled diamond, filled circle, and filled square, for Re = 300, 4000, and ∞, respectively), while the anguilliform lamprey (AL) is shown with open symbols and broken lines (open diamond, open circle, and open square, for Re = 300, 4000, and ∞, respectively). Inset shows St₀, the St at which the relative axial force is zero (i.e., the swimmer is self-propelled) for each Re.

This relationship between St and net force is strongly dependent on Re. St represents the importance of the undulatory motion; at low St, the undulations are small or slow relative to the forward motion, while at high St, the undulations are large or fast. In general, for a given St, drag is larger and thrust is smaller at low Re, but the effects of the undulations are non-linear. Drag, for example, consists of two components: skin friction, a viscous effect, and form drag, an effect due to pressure differences that is unrelated to viscosity. In both of the viscous regimes (Re = 300 and 4000), the largest component of the drag is skin friction, and its magnitude increases with increasing St. However, form drag behaves in a more complex way. Slow or small undulations cause the form drag to increase, with the result that the total drag is larger than that of the rigid body, but large or fast oscillations cause form drag to decrease by preventing separation of the fluid along the body (Borazjani and Sotiropoulos 2008). At Re = 4000, the increase in skin friction is sufficiently low that this reduction in form drag also serves to reduce the total drag below that of the rigid body, but no such drag-reducing effect is seen at Re = 300. Another important effect due to the Re is that the self-propelled St₀ decreases with increasing Re (Fig. 6, inset) (Borazjani and Sotiropoulos 2008; 2009). The St₀ values for the lamprey and mackerel both follow this pattern, but the values from lamprey are generally higher.

The dependence of wake structure and net force on the St and Re is not unexpected based on engineering work on flapping foils. Both high aspect ratio flaps (Koochesfahani 1989; Read et al. 2003) and low aspect ratio fins (Buchholz et al. 2008) shift from a 2S von Karman wake at low St to a 2P or higher order wake at high St. In such experiments, thrust also increases with increasing St (Read et al. 2003; Buchholz et al. 2008). Similar dependence of the wake structure on St has also been reported in experiments using a biomimetic fish-like robot (Epps et al. 2009).

Body shape influences wake structure, but swimming mode has only a small effect

In the study by Borazjani and Sotiropoulos (2010), the effects of body shape and swimming mode were examined directly by decoupling them (Fig. 4). In these simulations, the swimmer was allowed to move according to the net fluid force on the body. As before, three Re were examined. However, in this study, St could not vary independently of Re. Figure 6 shows that St₀, the Strouhal number at which net force is zero, decreases as Re increases. For steady motion, therefore, the low Re case is also a high St case, and the high Re case corresponds to low St. Since the two variables are so tightly linked, we will always refer to them together.

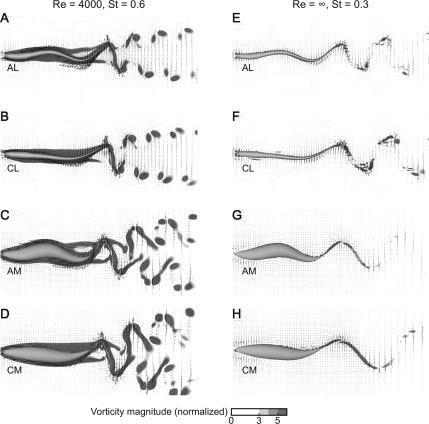
For each Re₀, St₀ case, the simulations of four combinations of body shape and swimming mode produced wakes that were broadly similar to each other. Figure 7 shows a comparison of the wakes for each swimmer in the Re₀ = 4000, St₀ = 0.6 case and in the Re₀ = ∞, St₀ = 0.3 case. The largest differences among the wakes are between the two columns in Fig. 7, corresponding to the Re, St differences. For a given Re₀ and St₀ case, the wakes differ among the swimmers, primarily across body shapes. The effect of differences in swimming mode is particularly small (for example, compare Fig. 7C and D).

Fig. 7.

Structure of the wake depends primarily on Re₀, St₀ and only secondarily on body shape or swimming mode. Panels show horizontal planes through the computational domain for all four combinations of body shape and swimming mode. Magnitude of vorticity is shown with shades of gray. Left column, Re₀ = 4000, St₀ = 0.6; right column, Re₀ = ∞, St₀ = 0.3. A, E, anguilliform lamprey; B, F, carangiform lamprey; C, G, anguilliform mackerel; and D, H, carangiform mackerel.

Both body shapes can produce both types of wakes. In particular, note that the mackerel body (AM and CM cases) can shed a 2P wake (Fig. 7C and D), although it is more complex than the wake shed by the lamprey body (Fig. 7A and B). The situation is reversed in the high Re₀, low St₀ case (Fig. 7E–H). The mackerel body produces a clear 2S wake, with two single, somewhat elongated vortices shed per tail beat (Fig. 7G and H). At the same Re₀, St₀, the lamprey body produces a transitional wake, initially producing elongate vortices that break apart. Experimental studies have shown that the eel wake develops in this transitional manner, at about the same St as in Fig. 7E (Tytell and Lauder 2004).

Body shape and swimming mode have substantial functional consequences

Despite the relatively modest differences among wakes for any Re₀, St₀ case, body shape and swimming mode have substantial effects on swimming performance. Table 1 summarizes these differences in performance. In general, anguilliform kinematics and the lamprey body shape seem to do better in the low and intermediate Re₀, St₀ cases, while the mackerel body and carangiform kinematics do better in the Re₀ = ∞, St₀ = 0.3.

Table 1.

Swimming performance from computational results as a function of body shape, swimming mode, and Re

	Re0 = 300, St0= 1.1 f0 = 5.5		Re = 4000, St0 = 0.6 f0 = 3		Re = ∞, St0 = 0.3 f0 = 1.5
	M	L	M	L	M	L
Stact
C	1.10 (2)	1.72 (4)	0.61 (2)	0.71 (4)	0.25 (1)	0.41 (3)
A	0.99 (1)	1.39 (3)	0.59 (1)	0.67 (3)	0.33 (2)	0.47 (4)
U*
C	1.00 (3)	0.64 (1)	0.98 (3)	0.84 (1)	1.20 (4)	0.74 (2)
A	1.11 (4)	0.79 (2)	1.01 (4)	0.90 (2)	0.92 (3)	0.64 (1)
URMS
C	1.4 × 10−2 (4)	0.5 × 10−2 (2)	6.8 × 10−3 (4)	1.7 × 10−3 (2)	3.8 × 10−3 (4)	0.6 × 10−3 (2)
A	1.3 × 10−2 (3)	0.2 × 10−2 (1)	4.4 × 10−3 (3)	0.6 × 10−3 (1)	2.2 × 10−3 (3)	0.4 × 10−3 (1)
CP,tot
C	0.95 (2)	3.61 (4)	0.10 (2)	0.14 (4)	3.7 × 10−3 (2)	4.2 × 10−3 (4)
A	0.73 (1)	2.26 (3)	0.08 (1)	0.11 (3)	3.5 × 10−3 (1)	3.9 × 10−3 (3)
CP,wake
C	0.77 (2)	3.15 (4)	0.076 (3)	0.103 (4)	2.0 × 10−3 (1)	3.3 × 10−3(4)
A	0.56 (1)	1.87 (3)	0.059 (1)	0.074 (2)	2.2 × 10−3 (2)	3.2 × 10−3 (3)
η
C	0.19 (3)	0.13 (1)	0.22 (1)	0.26 (3)	0.45 (4)	0.194 (2)
A	0.23 (4)	0.17 (2)	0.26 (2)	0.32 (4)	0.38 (3)	0.189 (1)

Values of each variable are shown as a 2 × 2 matrix of body shape and swimming mode. Numbers in parentheses indicate the rank of the value, from one (lowest) to four (highest). Lowest values are shown in italics; highest in bold. St_act, actual Strouhal number; U*, swimming speed; U_RMS, root-mean-square fluctuation in steady swimming speed; C_P,wake, wake power coefficient; C_P,tot, total propulsive power; η, Froude propulsive efficiency; M, mackerel body shape; L, lamprey body shape; C, carangiform swimming mode; A, anguilliform swimming mode. Modified from Borazjani and Sotiropoulos (2010); note that the power coefficients are normalized differently.

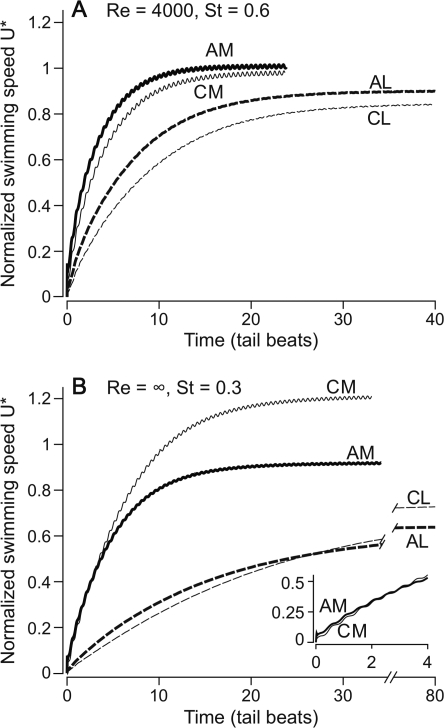
For all Re₀, St₀ cases, the mackerel body shape reached the highest swimming speeds. Figure 8 shows swimming speed plotted over time for the Re₀ = 4000, St₀ = 0.6 and Re₀ = ∞, St₀ = 0.3 cases. The Re₀ = 300, St₀ = 1.1 case is not shown because it has the same pattern as the intermediate Re₀, St₀ case. At low and intermediate Re₀, St₀, the difference among the body shapes is not substantial, but at Re₀ = ∞, St₀ = 0.3, the mackerel body swims nearly twice as fast as the lamprey body, regardless of swimming mode.

Fig. 8.

Simulated swimmers shaped like mackerel always swim fastest, while those with anguilliform kinematics swim faster at low Re, St and slower at high Re, St. Normalized swimming speed is plotted against time in tail beats. Mackerels’ body shapes are shown with solid lines, and lampreys' body shapes with broken lines. Anguilliform swimmers are shown with thick lines and carangiform swimmers with thin lines. Abbreviations: CM, carangiform mackerel; AM, anguilliform mackerel; AL, anguilliform lamprey; CL, carangiform lamprey. (A) Re = 4000, St = 0.6 case. (B) Re = ∞, St = 0.3 case. Note the break in the time axis to show the steady speeds for the lamprey-shaped swimmer. Inset shows early times for the AM and CM swimmers.

The influence of swimming mode is somewhat more subtle. In all cases, the anguilliform mode accelerates fastest. The inset in Fig. 8B shows that this is true for the mackerel body in the Re₀ = ∞, St₀ = 0.3 case. Additionally, in the first two Re₀, St₀ combinations, the anguilliform swimmers reach the highest speeds, when compared to carangiform swimmers of the same body shape. Thus, Fig. 8A shows that the anguilliform mackerel is the fastest overall at Re₀ = 4000, St₀ = 0.6. The situation reverses in the inviscid case. While the anguilliform swimmers accelerate fastest, the carangiform mode ultimately catches up and pulls out in front. The carangiform mackerel takes about three tail beats to pass the anguilliform mackerel, while the carangiform lamprey takes quite a bit longer, but ultimately passes the anguilliform lamprey after about 28 tail beats.

It is also clear from Fig. 8 that the mackerel body and the carangiform mode produce the largest fluctuations in velocity. Table 1 shows this pattern quantitatively (U_RMS). Experimentally, carangiform swimmers have been observed to have much larger velocity fluctuations in velocity than do swimming eels (Tytell 2007).

Energy consumption also shows striking differences among body shapes and swimming modes (Table 1). The anguilliform lamprey’s propulsive efficiency peaks at 0.32 in the intermediate case, with low efficiencies at both high and low Re₀, St₀, and a similar pattern is seen for the carangiform lamprey. In contrast, the mackerel’s efficiency increases with Re₀, St₀, reaching a maximum of 0.45 in the inviscid case. The difference between the efficiency of the two body shapes may reflect underlying differences in their mechanisms of thrust production, as well as their dependence on viscous effects. The mackerel-shaped swimmer produces thrust due to lift production around its wing-like caudal fin, an effect that does not depend on viscosity, and thus is most prominent at high Re. In contrast, the lamprey-shaped swimmer lacks a discrete tail fin, and instead produces thrust by using the undulatory wave to accelerate fluid along its body. Shear forces, which require viscosity, contribute to this effect, termed an ‘undulatory pump’ (Müller et al. 2001). Thus, thrust and efficiency decrease in the Re = ∞ case for the lamprey-shaped body.

As described above, Tytell (2007) suggested using wake power as a proxy for efficiency: if thrust power is comparable across fishes, then low C_P,wake should correlate with high η. In the low and high Re₀, St₀ cases, this correlation seems to hold (compare the ranks for C_P,wake and η in Table 1). However, in the intermediate case, the wake power seems to have very little relationship to efficiency.

Despite these differences in efficiency, the lamprey body always wastes the most power and requires the most total power (C_P,tot; Table 1). The mackerel’s body shape, long hypothesized to be tuned for low cost of transport (see e.g., Lighthill 1970), always includes the swimmer with the lowest total power. Surprisingly, however, the carangiform swimming mode uses more power than the anguilliform mode for a given body shape, so that the most profligate swimmer is the carangiform lamprey. The lowest power swimmer is usually the anguilliform mackerel, which might correspond to a fish like a needlefish (Liao 2002).

Conclusions

Our experimental and computational results show good agreement, both qualitatively and quantitatively. Because most experiments with swimming fish have been performed at Re >10 000, the best comparison between experimental and computational results is the inviscid case. Comparing wake structure, computations indicate that the mackerel-shaped swimmer produces a highly coherent wake with a single row of vortices (Fig. 7H), much as observed experimentally (Nauen and Lauder 2002; also see results from a bluegill shown in Fig. 2). In contrast, the lamprey-shaped swimmer sheds a more complex wake, which begins as a single row, then transitions to a bifurcated wake with many small vortical structures. Unlike the mackerel, the lamprey does not have a discrete tail that sheds well-defined vortices. Instead, vortices are shed along nearly the whole body. For a clearer example of this effect, see the 3D vortex structures shown in Figs. 16 and 17 in the Borazjani and Sotiropoulos (2009). Experimental data also indicate that eels shed a complex wake and produce an elongated shear layer during each half stroke that breaks up into two or more vortices (Tytell and Lauder 2004). As Re decreases, our computations indicate that the St increases. This effect has been observed in zebrafish larvae which swim with St as high as 2.0 at Re = 100 (Müller et al. 2008). At low Re and high St, both computations and experiments (Müller et al. 2008) indicate that the wake tends to bifurcate into two separate rows of vortices, regardless of body shape or swimming mode (Fig. 7A–D). Interestingly, zebrafish larvae swim using an anguilliform mode (Müller et al. 2008), which should result in higher swimming speeds, according to our computational results (similar to the AM swimmer in Fig. 8A).

Many more parameters can be estimated from the computations that can be measured directly. One parameter that can be compared quantitatively is the estimate of wasted power. For example, in Fig. 3, eels have a wasted power coefficient of 0.004 on average, and Table 1 shows that C_P,wake for the AL swimmer at high Re₀, St₀ is 0.003. Even though simulation does not include viscosity, the close correspondence in wasted power is striking.

Computational results indicate that both body shape and swimming mode have consequences for swimming performance. The mackerel body shape always swims faster than the lamprey body shape. At high Re, the carangiform swimming mode is also faster for steady swimming. However, in every case, the anguilliform swimmer accelerates faster. This observation matches experimental results on accelerating eels. As eels accelerate, they move their heads more, becoming, in a sense, more anguilliform (Tytell 2004).

Future directions

As we observed above, body shape and swimming mode are strongly correlated: elongate fishes tend to swim in an anguilliform mode, while other fishes tend to swim in a carangiform mode. However, our computations indicate that in several cases, it might be functionally useful to decouple swimming mode and body shape. For instance, the anguilliform mackerel swims the fastest at low and intermediate Re and uses the least total power in all cases (Table 1), while at high Re, the lamprey swims faster in the carangiform than in the anguilliform swimming mode. Do anguilliform mackerels or carangiform eels exist?

The diversity of fishes may provide examples of such swimmers. Needlefishes, for instance, might be akin to an anguilliform mackerel: they swim using an anguilliform mode, but have fins (Liao 2002). Their fins are not as pronounced as are those of mackerel, but are still quite different from those of true eels or lampreys. Many sharks, also, have well-defined fins but swim in an anguilliform pattern (Webb and Keyes 1982; Wilga and Lauder 2004). Computations indicate that such swimmers should accelerate well and have low cost of transport. Carangiform eels may also exist. For instance, we have noted the differences between the kinematics of true eels, which move their heads relatively little during steady swimming (Gillis 1998), and those of lampreys, particularly lamprey larvae, which have substantial side-to-side motion of the head (Ayers 1989; Ayali et al. 2009). True eels may be thus ‘more carangiform’ than lampreys. Within the diversity of fishes, it will be informative to compare performance of species that provide natural experiments akin to our computational manipulations.

The importance of flexibility of the body

The correlation between body shape and swimming mode is likely not an accident. Besides body shape and swimming mode, another difference between lampreys and mackerels is their internal body structure, particularly their flexural stiffness. Aleyev (1977) performed an extensive survey of the flexibility of fish bodies. Although the data provided are not enough to estimate a true Young’s modulus (Den Hartog 1961), his measurements indicate that eels are dramatically more flexible than mackerels, except in the posterior 20% of the body, in which mackerels are somewhat more flexible than eels (Aleyev 1977). Mackerels are likely not capable of bending their anterior bodies enough to produce an anguilliform motion.

Differences in stiffness thus mean that eels and mackerels probably differ in the relative proportion of passive and active control during swimming. Swimming kinematics result from a balance between internal muscular forces and external fluid forces. In very stiff-bodied fishes such as mackerels, that balance is probably shifted toward active control by muscles. Fluid forces may be relatively small compared to muscle forces. By contrast, lampreys and most elongate fishes (Aleyev 1977) have much floppier bodies, which likely means that their swimming kinematics are highly influenced by fluid forces, and the balance is shifted toward passive interaction with the fluid.

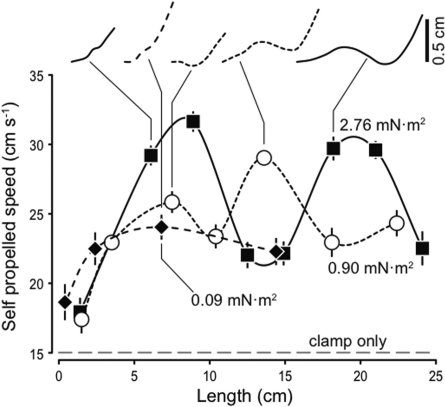
Recent experiments using a robotic flapping-foil device indicate that this balance may have substantial consequences. Given exactly the same driving parameters, steady swimming speed depends on foil length and flexural stiffness. For a given length, there may be one or more optima at different stiffnesses. Figure 9 shows the self-propelled speed of thin flapping plastic strips with different flexural stiffnesses. A flapping-foil device was constructed to drive rectangular plastic strips, 19 cm high by 6.8 cm in length, from side to side and to pitch them about their leading edge (Lauder et al. 2007). The device was mounted on low-friction air bearings, so that it could move forward or backward according to the forces the strip produced. Then the strip was placed in a flow tunnel that provided a constant flow. The self-propelled speed U₀ of a strip was the flow speed at which it moved neither forward nor back, on average, from an equilibrium position resulting from the small restoring forces of the device’s umbilical (Lauder et al. 2007). Sheets were made of homogeneous materials with stiffnesses of 2.76, 0.90, and 0.09 mN m², a height of 6.85 cm, and lengths from 0.4 to 24 cm. Each was tested with a driving heave amplitude of ±1 cm.

Fig. 9.

Flow speed at which the net force is zero (referred to as ‘self-propelled speed’; see text for details) for homogeneous flexible foils of different length and flexural stiffness. Traces show self-propelled speed plotted against foil length for flexural stiffness 2.76 mN m² (filled square), 0.90 mN m² (open circle), and 0.09 mN m² (filled diamond). Also shown is the self-propelled speed of the clamp that holds the foils on its own (dashed line). Foil height is 6.85 cm in all cases and they are all driven with a ± 1 cm heave motion at the leading edge. Top panel shows the maximum amplitude as a function of position along the foil from the leading edge to the trailing edge for several points, as examples.

Each sheet shows a complex behavior as the length is increased, with one or more optimal lengths to maximize self-propelled speed (Fig. 9). At a given length, there may also be an optimal stiffness (e.g., near 14 cm length in Fig. 9). Other computational studies also indicate that stiffness can have complex effects on propulsion. For example, Alben (2008) suggested that the total thrust and the propulsive efficiency depend in a complex way on the stiffness of a 2D flapping membrane. Other computational results suggest that flapping wings can benefit from a non-linear resonance that results from flexibility (Vanella et al. 2009), and that membranes reinforced by flexible rays can benefit from the bending of the rays (Shoele and Zhu 2009).

Extrapolating these results to fishes, for a given pattern of muscular activation, there is likely to be an optimum body stiffness for maximum steady swimming speed, which may change as a fish grows. Different lineages of fishes may have evolved that take advantage of different fluid-structure interactions. For example, fluid–structure interaction is important in producing the undulatory swimming motion in both sunfishes (Long et al. 1994) and lampreys (Bowtell and Williams 1991). Not only that, but fishes can dynamically alter their body stiffness by activating muscles on both sides of the body (Long and Nipper 1996; Long 1998), which may allow them to vary the degree of passive and active control.

The present computational framework cannot address these questions, because the kinematics are prescribed. In particular, the fully coupled problem linking the dynamics of an elastic body to the fluid motion around it is computationally quite challenging. However, as computational power increases and research progresses, such problems are becoming more tractable. An important avenue for future research will be examining the coupled dynamics of elastic bodies in fluids.

A combined approach will be important, using biological experiments in conjunction with computational and robotic techniques. The tails of fishes respond passively to fluid forces, advancing or delaying vortex shedding, which may have large effects (Fig. 9). However, such interactions may be subtle and difficult to measure experimentally. Because the present computational framework prescribes kinematics, it is only as good as our ability to measure the kinematics. Robotic approaches, by contrast, allow a high degree of control over both stiffness and driving parameters. These methods may be used to examine the effect of stiffness directly, as above (Fig. 9), or be used as inputs to future computational frameworks that are able to simulate passive interactions. In combination with comparative biological experiments examining differences across lineages of fishes, such approaches will be highly important for continuing work to understand the morphological and behavioral tradeoffs in the evolution of vertebrate locomotion.

Funding

This work was supported by the National Institutes of Health (FS32 NS054367 to E.D.T., R01 NS054274 to Avis H. Cohen); National Science Foundation (IBN0316675 and IBN0938043 to G.V.L); the National Center for Earth-surface Dynamics (EAR-0120914 to F.S.), the Minnesota Supercomputing Institute (to I.B. and F.S.); Grove City College Swezey Scientific Instrumentation and Research Fund (to T.V.B.).