Abstract
Temperature tolerance and sensitivity were examined for some North Atlantic marine species and linked to their energetics in terms of species-specific parameters described by dynamic energy budget (DEB) theory. There was a general lack of basic information on temperature tolerance and sensitivity for many species. Available data indicated that the ranges in tolerable temperatures were positively related to optimal growth temperatures. However, no clear relationships with temperature sensitivity were established and no clear differences between pelagic and demersal species were observed. The analysis was complicated by the fact that for pelagic species, experimental data were completely absent and even for well-studied species, information was incomplete and sometimes contradictory. Nevertheless, differences in life-history strategies were clearly reflected in parameter differences between related species. Two approaches were used in the estimation of DEB parameters: one based on the assumption that reserve hardly contributes to physical volume; the other does not make this assumption, but relies on body-size scaling relationships, using parameter values of a generalized animal as pseudo-data. Temperature tolerance and sensitivity seemed to be linked with the energetics of a species. In terms of growth, relatively high temperature optima, sensitivity and/or tolerance were related to lower relative assimilation rates as well as lower maintenance costs. Making the step from limited observations to underlying mechanisms is complicated and extrapolations should be carefully interpreted. Special attention should be devoted to the estimation of parameters using body-size scaling relationships predicted by the DEB theory.
Keywords: dynamic energy budget theory, dynamic energy budget parameters, temperature dependence, growth, energetics, marine species
1. Introduction
In general, life cycles of marine organisms comprise several distinct life-history stages (egg, larvae, juvenile, adult). Each of these successive stages often differs in their habitat requirements and, as a consequence, might depend on different and frequently spatially separated habitats (Rijnsdorp et al. 1995). For marine populations, it is a prerequisite that successive habitats are connected to allow survivors to mature and return to the spawning grounds for successful reproduction (the concept of life cycle closure; Sinclair 1988).
At each life-history stage and/or within each habitat, the spatio-temporal window of opportunity for development (somatic growth and reproduction) is set by both biotic factors (prey availability) and tolerance limits to abiotic factors whereby, for ectotherms, prevailing temperature conditions are a controlling factor (Fry 1947; Neill et al. 1994). The response to temperature conditions is frequently characterized in terms of temperature sensitivity and temperature tolerance range (Huey & Kingsolver 1989). Temperature tolerance range is the temperature zone where growth rates are positive. Within the range of tolerable temperatures, an optimal temperature, preferred temperatures and temperature sensitivity (reflecting the rate at which physiological reactions change with temperature) can be distinguished using different criteria. Besides an acute response to temperature, an individual can show acclimatization as a chronic response and adaptation, measured in timescales of generations, as an evolutionary response. The latter will ultimately allow a modification of the physiological performance and response of an organism over time. Furthermore, there is some evidence for ontogenetic changes in the range of tolerable temperatures (Irvin 1974; Rijnsdorp et al. 2009) and temperature sensitivity (Peck & Buckley 2007), indicating that optimal thermal habitats for growth may vary for different life stages. This has wide implications in terms of defining ‘ecologically relevant’ thermal tolerance of a species purely based on laboratory experiments conducted on specific life stages (Jobling 1994). In this respect, the lack of information regarding the physiology of late-larval/early-juvenile stages of many marine species is rather surprising, given that processes acting during these stages can create a bottleneck to successful life closure and have important consequences for recruitment strength (Bailey & Houde 1989; Sogard 1997).
Within the window for somatic growth and reproduction, any prediction of the physiological performance requires a general framework that describes the relationship between prevailing abiotic and biotic conditions and fish growth and reproduction rates. At the organismal level, the use of balanced energy budgets to predict various aspects (e.g. prey consumption and growth) has become common in the last five decades (Winberg 1956; Brett & Groves 1979; Hanson et al. 1997). However, the various allometric relationships are a purely statistical description of species-specific measurements and not physiologically based on first principles. These budgets are also unable to describe the energetics of an organism within variable environments.
Dynamic energy budgets (DEBs) are a framework describing the quantitative aspects of energy flows through an organism in a systematic and dynamic way (Kooijman 1988, 1993, 2000, 2010; Ross & Nisbet 1990). DEBs are based on first principles and can capture the energetics of species in a single model whereby interspecific differences are reflected by differences in parameter values. A second application of the DEB theory is the prediction of various body-size scaling relationships. Such relationships have been previously studied and debated for decades (see the pioneering work of Kleiber (1961) on the scaling of metabolic rate with body size) and, over time, numerous empirical relationships of biological rates as simple functions of body size and other variables have been established (for overview, see Peters (1983)). Although this descriptive ecology has proved to be valuable, it is criticized for seeking post hoc explanations of observed patterns without experimental tests of hypotheses (Blackburn & Gaston 1999). The DEB theory of Kooijman (1993, 2000, 2010), based on surface- and volume-related processes, is a clear response to this criticism but has not yet been recognized as such. Body-size scaling relationships provide basic information that can be applied to predict species characteristics in cases where basic information is lacking. In addition, the DEB theory can be used to analyse the discrepancy between modelled and observed growth rates based on energetic constraints, and to potentially identify important intrinsic and extrinsic (environmental) factors in species life-history strategies.
Finally, combining information on tolerance limits to environmental factors, particularly water temperature, and growth energetics by means of DEBs, can give considerable insight on the physiological plasticity of a species. Insight at the species level provides a sound foundation for analyses of ecosystem functioning and response to environmental variability such as climate change. Unfortunately, these bioenergetically-based analyses are largely unexplored.
In the present paper, we attempt to fill a critical gap in knowledge by examining interspecific differences in the temperature dependence of growth (reflected in species-specific differences in optimal temperatures, range in tolerable temperatures and thermal sensitivity), and relating these to differences in species bioenergetics as revealed by DEB parameters. For this purpose, information on the temperature tolerance and sensitivity was combined with estimates of the DEB parameters and with predictions of body-size scaling relationships based on DEB theory for fish and crustacean species of the northeast Atlantic, North Sea and coastal Wadden Sea ecosystems.
2. Material and methods
The main focus of this paper is on marine northeast Atlantic fish species. A set of species was selected that contained different, commercially important resources, ecosystem components (pelagic, demersal) and species with different positions in the food web (forage species, wasp-waist, apex predators). In addition, other abundant coastal species were added, including crustaceans. The initial list was reduced during the process of parameter estimation owing to a lack of basic data for some species. Furthermore, most information reported in the literature was only available for females. At the end, the following species remained: the flatfish species, plaice (Pleuronectes platessa), flounder (Platichthys flesus), dab (Limanda limanda) and sole (Solea solea), the common goby (Pomatoschistus microps) and the sand goby (Pomatoschistus minutus), the eelpout (Zoarces viviparous), bull-rout (Myoxocephalus scorpius), sea bass (Dicentrarchus labrax), Atlantic cod (Gadus morhua), Atlantic herring (Clupea harengus), sprat (Sprattus sprattus), European anchovy (Engraulis encrasicolus) and the crustacean species brown shrimp (Crangon crangon) and shore crab (Carcinus maenas).
(a). Temperature tolerance and sensitivity
(i). Temperature tolerance
Each species can only obtain positive rates of growth within a specific range of tolerable temperatures. This range is a reflection of both metabolism (showing a steady increase with temperature) and ingestion (increasing only until an abrupt decline occurs at high temperatures). As a result, growth is characterized by a steady increase with increasing temperature until a maximum, followed by a sharply defined upper boundary. Information on temperature tolerance is based on data on food intake or growth in relation to temperature.
(ii). Optimum temperature
The optimum temperature is defined as the temperature at which growth is maximal. Optimum temperature for growth has been shown to vary depending on food conditions and decline when food is limited (Brett 1979; Jobling 1994). In the present study, ad libitum (unrestricted) feeding was assumed.
(iii). Temperature sensitivity
Temperature sensitivity is an indication of the temperature dependence of physiological rates, i.e. the rates at which a reaction changes with temperature. Growth is an integrative process and an end product of the interaction among other physiological parameters affected by temperature. In the present study, temperature sensitivity was based on the exponential rate of increase in metabolism, preferably oxygen consumption rate, with increasing temperature commonly observed within a portion of the temperature tolerance range. In this paper, the Arrhenius relationship has been applied, usually providing a good explanation for the variation in the temperature dependence of metabolic rates across species (Gillooly et al. 2006). The species-specific Arrhenius temperature (TA, K) can be estimated as:
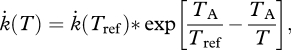 |
2.1 |
where 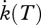 is a physiological rate at the ambient temperature T(K), and
is a physiological rate at the ambient temperature T(K), and 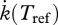 the physiological rate at the reference temperature Tref. TA can be determined from the slope of plots of
the physiological rate at the reference temperature Tref. TA can be determined from the slope of plots of 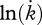 against 1/T. The procedure is illustrated in Freitas et al. (2007).
against 1/T. The procedure is illustrated in Freitas et al. (2007).
(b). Auxiliary theory for the standard DEB model
The state variables of the standard DEB model (reserve, structure, maturity; Sousa et al. 2010) can only be measured indirectly. This consequently applies to the parameter values and calls for auxiliary theory, which links quantities that can be measured to variables in the model. Progress has been made in recent years in developing auxiliary theory for the standard DEB model (e.g. Kooijman et al. 2008; Kooijman 2010).
The contribution of reserves to physical volume is no longer neglected, while physical length is still used as a proxy for structural volumetric length. This affects the way the shape coefficient δM (which converts physical length into volumetric length) is obtained from data. Previously, the volumetric structural length was identified with the volumetric length, but in the new approach it is obtained, together with the zoom factor z and other parameters simultaneously, from data on lengths, weights and other measurements (see next section).
Continued research also converted some compound parameters of the standard DEB model to primary ones and vice versa, to enhance the link with underlying processes (table 1); the electronic supplementary material gives a detailed account of the changes. These changes did not affect the standard DEB model as such.
Table 1.
Parameters of the standard DEB model in a time–length–energy frame with symbols and units used in this paper, together with other species-specific physiological parameters. Typical values for a generalized animal at 20°C are also indicated. The length measure in the specific searching rate refers to the environment, all other length measures to structure. Square brackets mean ‘per structural volume’, curly braces mean ‘per structural surface area’ and dots denote ‘per time’. Changes in the choice of primary parameters (P) and compound parameters (C) from DEB 2 (Kooijman 2000) to DEB 3 (Kooijman 2010) are indicated.
| symbol | units | interpretation | DEB 2 | DEB 3 | typical values |
|---|---|---|---|---|---|
| parameters | |||||
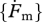 |
cm2 or 3 cm−2 d−1 | maximum surface-area-specific searching rate | — | P | 6.5 dm3 cm−2 d−1 |
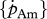 |
J cm–2 d−1 | maximum surface-area-specific assimilation rate | P | P | 22.5 J cm−2 d−1 |
| κX | — | assimilation efficiency | — | P | 0.8 |
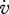 |
cm d−1 | energy conductance | C | P | 0.02 cm d−1 |
| κ | — | fraction of used energy spent on maintenance plus growth | P | P | 0.8 |
| κR | — | reproduction efficiency | P | P | 0.95 |
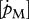 |
J cm−3 d−1 | volume-specific maintenance costs | P | P | 18 J cm−3 d−1 |
| [EG] | J cm−3 | volume-specific cost for structure | P | P | 2800 J cm−3 |
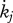 |
d−1 | maturity maintenance rate coefficient | — | P | 0.002 d−1 |
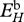 |
J | maturation at birth | — | P | 275 mJ |
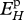 |
J | maturation at puberty | — | P | 166 J |
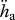 |
d−2 | Weibull ageing acceleration | P | P | |
| sG | — | Gompertz stress coefficient | — | P | |
| Lm | cm | maximum structural length: 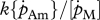
|
C | C | |
| K | J cm−2or –3 | half-saturation coefficient: 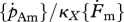
|
P | C | |
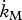 |
d−1 | maintenance rate coefficient: 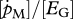
|
C | C | |
| g | — | energy investment ratio: 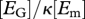
|
C | C | |
| [Em] | J cm−3 | maximum reserve density: 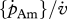
|
P | C | |
| scaling parameters | |||||
| z | — | zoom factor | |||
| δM | — | shape coefficient | |||
| conversion parameters | |||||
| µX | J mol−1 | energy–mass coupler for assimilation | |||
(c). Estimation procedure
Two approaches were used to determine the species-specific DEB parameters. The first was based on empirical derivation of individual parameters, from compilation of datasets for a species and checking the consistency of the individual parameter set with related species a posteriori. The second approach was based on body-size scaling relationships of the DEB theory and more oriented for an interspecies comparison. A direct comparison of the two approaches, however, is complicated, on one hand because the first approach does not allow estimating all the primary parameters that DEB 3 version now considers and, on the other hand, because they differ in the assumption of reserves contribution to body volume. Total body volume (Vw) includes not only structural volume (V) and reproduction volume (VR), but also a contribution from reserves (VE):
So far, previous parameter estimates for flatfish species (van der Veer et al. 2001) and bivalves (van der Veer et al. 2006) have neglected the contribution of reserves to volume, because differences in maximum size were small (bivalves) or because of the assumption that species replace energy reserves by water (flatfishes). However, the range in maximum sizes differs by more than a factor of 10 in the present study, and since reserve density scales with volumetric length, ignoring the contribution of reserves to total volume might introduce a more serious bias. To account for these differences, the two approaches are distinguished as:
— estimation of parameters based on datasets, i.e. in line with previous studies and assuming that the contribution of reserves to volume can be neglected (VE = 0);
— estimation of parameters based on DEB model predictions of body-size scaling relationships, and taking into account the contribution of reserves to body volume (VE ≠ 0).
(i). Parameter estimation assuming VE = 0
The methodology and required datasets followed those outlined by van der Veer et al. (2006, 2009). Parameter estimation could not be based on measurements made on a single individual owing to a general lack of complete datasets. Datasets were collected from the Web of Science and other sources. Information on maximum size (length) and wet mass was taken from Wheeler (1978), Fishbase (www.fishbase.org) and other data sources. Information on maximum observed length referred mostly to females. Maximum length of males was interpolated based on the ratio between the Von Bertalanffy L∞ parameter for males and females, whenever available. For flatfish, information published by van der Veer et al. (2001, 2009) was incorporated and for brown shrimp, the estimates were taken from Campos et al. (2009). The complete list of references used in the parameter estimation is given in electronic supplementary material.
The parameter set presented here differs slightly from previously published values (van der Veer et al. 2001, 2009) in the first place because we now assume that the energy conductance  is unlikely to vary substantially among species, and does not scale with body size, with the consequence that the maximum reserve capacity [Em] of a species is proportional to maximum (structural) length. Furthermore, the specific cost for structure [EG] and specific somatic maintenance costs
is unlikely to vary substantially among species, and does not scale with body size, with the consequence that the maximum reserve capacity [Em] of a species is proportional to maximum (structural) length. Furthermore, the specific cost for structure [EG] and specific somatic maintenance costs 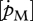 are related to cell complexity and, therefore, we assume that for related species, as well as for different sexes, their values will be similar (Kooijman 2000); sexes differ in maximum size because of their specific assimilation rate, and maybe because of κ, but not in specific somatic maintenance.
are related to cell complexity and, therefore, we assume that for related species, as well as for different sexes, their values will be similar (Kooijman 2000); sexes differ in maximum size because of their specific assimilation rate, and maybe because of κ, but not in specific somatic maintenance.
The resulting estimated parameter set was validated with data on maximum growth in relation to water temperature from different sources other than those used for parameter estimation. Observed discrepancies in predicted values on maximum growth were adjusted under the assumption that:
— differences between DEB simulations and growth observations indicated by different slopes in the simulated and observed growth relationships with temperature, imply an incorrect Arrhenius temperature;
— a systematic difference between DEB simulations and growth observations in absolute values indicate too high or too low values for
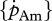 and
and 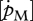 or [EG] and [Em].
or [EG] and [Em].
(ii). Parameter estimation assuming VE ≠ 0
For the parameter estimation based on body-size scaling relationships, the typical set of primary parameters of the standard DEB model for a generalized animal (theoretical reference for maximum structural length of 1 cm at 20°C) was used (table 1). The specific assimilation rate 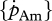 and the ageing acceleration
and the ageing acceleration 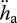 are primary parameters that are proportional to maximum length and the maturity thresholds proportional to maximum structural volume. All other primary parameters are intensive and do not depend on maximum length. This covariation is reflected in a scaling zoom factor z, i.e. the ratio of the maximum (structural) lengths of the two compared species. Structural length is obtained from an appropriately chosen actual (physical) length by multiplication with the shape coefficient δM.
are primary parameters that are proportional to maximum length and the maturity thresholds proportional to maximum structural volume. All other primary parameters are intensive and do not depend on maximum length. This covariation is reflected in a scaling zoom factor z, i.e. the ratio of the maximum (structural) lengths of the two compared species. Structural length is obtained from an appropriately chosen actual (physical) length by multiplication with the shape coefficient δM.
The zoom factor z, the shape coefficient δM and all primary parameters are estimated simultaneously from a (small) set of available data and the abovementioned parameter values for a generalized animal by minimization of a weighted sum of squared deviations between data and predictions. The parameter values of the generalized animal are thus treated as pseudo-data, and given small weight coefficients to ensure that if the real data have information about some primary parameter, it gets priority. The nature of the real data differs between species (depending on availability), and typically include maximum length and weight, length and age at birth and puberty and maximum reproduction rate. This one-step procedure is illustrated in electronic supplementary material. Scripts can be downloaded from the DEB laboratory (http://www.bio.vu.nl/thb/deb/) and are explained in the add_my_pet document (http://www.bio.vu.nl/thb/deb/deblab/add_my_pet/).
(c). Interspecies comparisons
Species-specific parameters were determined for different reference temperatures Tref and, hence, interspecies comparisons require a previous conversion of the DEB parameters that represent physiological rates (e.g. 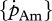 and
and 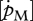 ) to a common temperature using formula (2.1). The new reference temperature was selected in such a way that it lies within the range of preferred temperatures, but below the optimal temperature.
) to a common temperature using formula (2.1). The new reference temperature was selected in such a way that it lies within the range of preferred temperatures, but below the optimal temperature.
Subsequently, the comparison of both sets of parameters (set I, based on the empirical procedure, and set II, based on the minimization procedure) was made, keeping in mind the different assumptions regarding reserves as previously stated. The comparison between the two parameter sets was done at reference temperatures of 10, 15 or 20°C, depending on the species.
3. Results
(a). Temperature
Estimates of temperature tolerance of the various species were based on experimental data on juveniles, except where otherwise stated. Information was taken from Freitas et al. (2007), except for dab (Fonds & Rijnsdorp 1988), sole (Lefrançois & Claireaux 2003), cod (Pörtner et al. 2001), eelpout and bull-rout (Fonds et al. 1989) and shore crab (McDonald et al. 2006). For herring, sprat and anchovy, either larval or juvenile data were used (Brawn 1960; M. Peck 2010, unpublished data). The latter species was assumed to have a similar tolerance as found for northern anchovy (Engraulis mordax) by Theilacker (1987). Species showed clear differences in optimal temperature and tolerance range (table 2). Most species could endure temperatures below 10°C, and interspecific differences were most pronounced at the upper temperature limit. The shore crab had the largest tolerance range of more than 30°C.
Table 2.
Temperature tolerance (range with positive reaction rate) and sensitivity parameters set for various North Atlantic marine species. For more information and references, see text. Interpolated values are in italic.
| TA (K) | Topt °C (K) | temperature tolerance range °C (K) | |
|---|---|---|---|
| P. platessa | 7000 | 20 (293) | 26 (273–299) |
| L. limanda | 4000 | 20 (293) | 26 (273–299) |
| P. flesus | 7000 | 20 (293) | 26 (273–299) |
| S. solea | 8500 | 20 (293) | 27 (276–303) |
| P. microps | 3500a | 20 (293) | 33 (273–306a) |
| P. minutus | 3500a | ||
| G. morhua | 7400 | 14 (287) | 24 (273–297) |
| M. scorpius | 4000 | 15 (288) | 23 (273–296) |
| Z. viviparous | 5000a | 13 (286) | 20 (273–293) |
| D. labrax | 5700 | 23 (296) | >33 (273–306) |
| C. harengus | 8000 | 18 (291) | >24 (273–297) |
| S. sprattus | 9300 | 19 (292) | >25 (275–300a) |
| E. encrasicolus | 9800 | 24 (297) | >27 (278–305) |
| C. crangon | 9000a | 23 (296) | 30 (273–303) |
| C. maenas | 6400 | 20 (293) | 35 (273–308a) |
aIn some cases, the DEB parameter validation procedure resulted in a correction of the estimates (see text for further explanations).
Information on temperature sensitivity TA (K) for cod, sea bass, common goby, sand goby, plaice, flounder, brown shrimp and shore crab was taken from Freitas et al. (2007); data for dab and sole were obtained from van der Veer et al. (2001) and for anchovy from Pecquerie (2008). For bull-rout and eelpout, TA(K) was calculated from data on oxygen consumption in relation to temperature published by Fonds et al. (1989). DEB parameter validation resulted in some cases in a correction of the Arrhenius temperature (table 2).
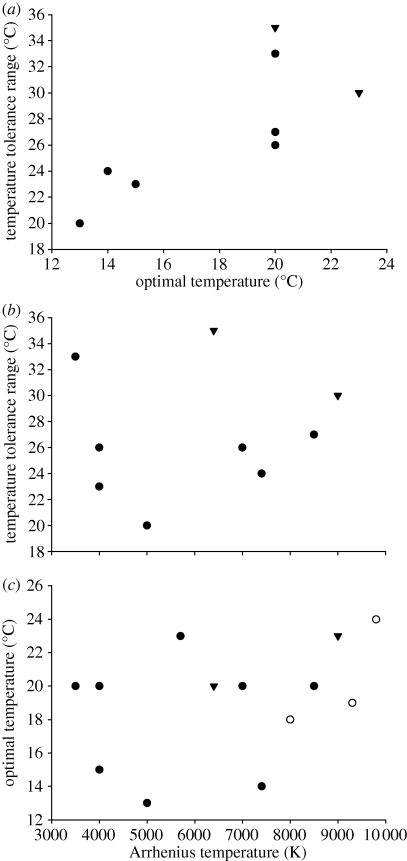
With respect to the various temperature parameters, there was a significantly positive relationship between temperature tolerance range and optimal temperature (figure 1a; Spearman rank correlation test: rs = 0.79, d.f. = 8, p < 0.025). A positive, but non-significant trend was present between temperature tolerance range and the Arrhenius temperature (figure 1b; rs = 0.12, d.f. = 8, p > 0.1), and between the optimal temperature and the Arrhenius temperature (figure 1c; rs = 0.26, d.f. = 12, p = 0.36).
Figure 1.
Relationships for a number of North Atlantic marine species between (a) temperature tolerance range (°C) and optimal temperature (°C); (b) temperature tolerance range and the Arrhenius temperature (K); and (c) optimal temperature (°C) and the Arrhenius temperature (K). Filled circles, demersal fish; open circles, pelagic fish; filled inverted triangles, crustaceans.
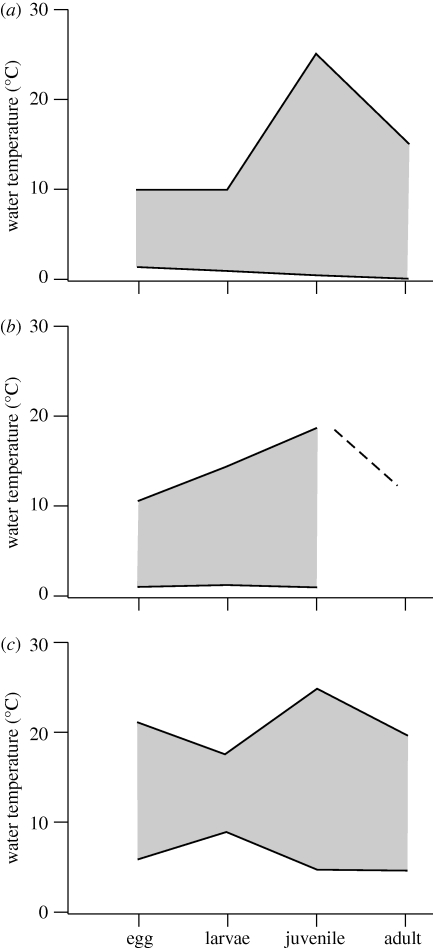
For a few species, information for different life stages was available. Information on plaice was based on Ryland et al. (1975), Talbot (1977) and Fonds et al. (1992); for cod it was based on a compilation made by Graham & Harrod (2009) and for brown shrimp it was based on Campos & van der Veer (2008). Temperature tolerance range varied during ontogeny, and the largest tolerance range occurred during the juvenile stage (figure 2).
Figure 2.
Temperature tolerance range (°C) of (a) plaice (Pleuronectes platessa), (b) cod (Gadus morhua) and (c) brown shrimp (Crangon crangon) in relation to life stages. For references, see text.
(b). Energetics
(i). Set I: parameter estimation assuming VE = 0
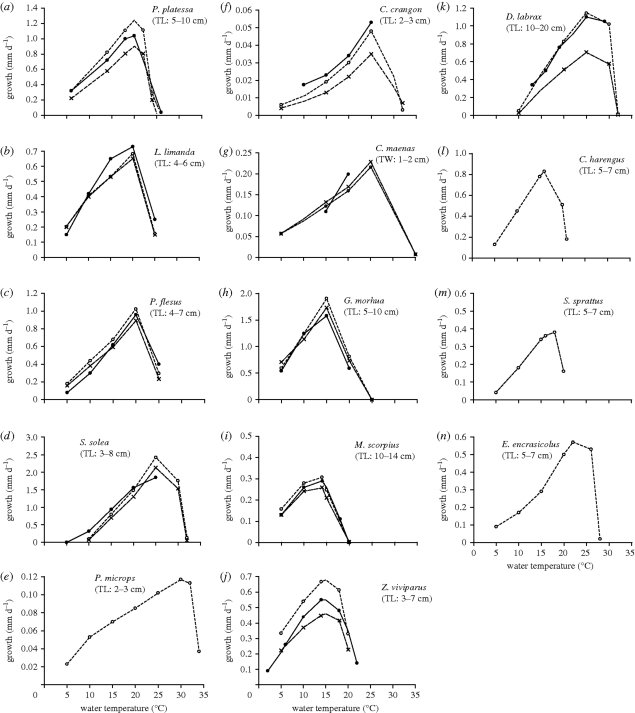
The estimated values for the various species based on empirical data, as well as the estimation procedures, are described in more detail in electronic supplementary material. This set was validated and adjusted based on a comparison with maximum growth data in relation to temperature (figure 3). Final estimates at the species-specific reference temperatures are shown in table 3.
Figure 3.
Comparison of observed maximum growth under laboratory conditions and DEB simulations for both females and males. For more information about the individual species and references, see text. Solid circles with solid lines, experimental data; open circles with dashed lines, DEB simulations female and crosses with dashed lines, DEB simulations male.
Table 3.
DEB parameter set for various North Atlantic marine species, for females and males (between brackets), based on experimental data after validation with maximum growth data in relation to water temperature. For more information, see electronic supplementary material and text.
| Tref (°C) | TA (K) | δM (–) | Lmax (cm) |
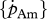 (J cm−2 d−1) (J cm−2 d−1) |
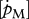 (J cm−3 d−1) (J cm−3 d−1) |
[Em] (J cm−3) | [EG] (J cm−3) | κ (–) | |
|---|---|---|---|---|---|---|---|---|---|
| P. platessa | 15 | 7000 | 0.219 | 78 (52) | 599 (358) | 29.8 | 2500 (1500) | 5600 | 0.85 (0.95) |
| L. limanda | 15 | 4000 | 0.216 | 51 (43) | 317 (240) | 29.8 | 1585 (1200) | 5600 | 0.85 (0.95) |
| P. flesus | 15 | 7000 | 0.224 | 56 (47) | 576 (335) | 29.8 | 2400 (1400) | 5600 | 0.65 (0.95) |
| S. solea | 20 | 8500 | 0.192 | 75 (64) | 864 (697) | 54.1 | 1986 (1600) | 5600 | 0.90 (0.95) |
| P. microps | 20 | 3500 | 0.190 | 6.5 | 65 | 33.6 | 272 | 5600 | 0.65 |
| P. minutus | 20 | 3500 | 0.190 | 9.5 | 93 | 33.6 | 390 | 5600 | 0.65 |
| G. morhua | 10 | 7400 | 0.209 | 190 | 1144 (1024) | 24.5 | 7330 (6565) | 5600 | 0.85 (0.95) |
| M. scorpius | 10 | 4000 | 0.230 | 60 (51) | 385 (293) | 23.8 | 5000 (3800) | 5600 | 0.85 (0.95) |
| Z. viviparous | 10 | 5000 | 0.157 | 50 (42) | 355 (170) | 39.5 (24.5) | 2275 (1090) | 5600 | 0.85 (0.95) |
| D. labrax | 20 | 5700 | 0.217 | 103 (87) | 1194 (864) | 41 | 3850 (2790) | 5600 | 0.85 (0.90) |
| C. harengus | 15 | 8000 | 0.190 | 43 | 468 | 46 | 1840 | 5600 | 0.80 |
| S. sprattus | 15 | 9300 | 0.180 | 16.5 | 180 | 46 | 652 | 5600 | 0.90 |
| E. encrasicolus | 20 | 9800 | 0.172 | 20 (17) | 329 | 62 | 645 | 5600 | 0.65 |
| C. crangon | 20 | 9000 | 0.213 | 9.5 (7.5) | 112 (75) | 47.1 | 850 (565) | 2500 | 0.80 (0.95) |
| C. maenas | 20 | 6400 | 0.581 | 8.5 (10) | 212 (210) | 34.4 | 2211 (2191) | 2500 | 0.80 (0.95) |
(ii). Set II: parameter estimation assuming VE ≠ 0
Estimated values based on body-size scaling relationships, using typical parameter values of a generalized animal as pseudo-data, are presented in table 4. The estimates for the primary parameters [EG] and 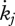 were for all species very close to the values of the generalized animal, i.e. [EG] = 2800 J cm−3 and
were for all species very close to the values of the generalized animal, i.e. [EG] = 2800 J cm−3 and 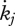 =0.002 d−1. The rest of the primary parameters were not estimated because data on feeding, maturation, reproduction and lifespan were not available for all species. Values for assimilation and maximum storage density varied for the different species by a factor of about 22 in line with differences in the zoom factor z. Table 4 also presents the fraction of maximum body weight that is structure, δV, for individuals with an empty reproduction buffer. This fraction is a function of parameter values (Kooijman 2010), and illustrates that the contribution of reserves in total body volume should not be neglected.
=0.002 d−1. The rest of the primary parameters were not estimated because data on feeding, maturation, reproduction and lifespan were not available for all species. Values for assimilation and maximum storage density varied for the different species by a factor of about 22 in line with differences in the zoom factor z. Table 4 also presents the fraction of maximum body weight that is structure, δV, for individuals with an empty reproduction buffer. This fraction is a function of parameter values (Kooijman 2010), and illustrates that the contribution of reserves in total body volume should not be neglected.
Table 4.
DEB parameter set based on body-size scaling relationships, using the typical parameter values of a generalized animal as pseudo-data. Temperature-dependent DEB parameters were converted to a species-specific reference temperature Tref for comparison with the estimates in table 3, using the species-specific Arrhenius temperature TA from table 2. δV is the fraction of body weight that is structure.
| Tref (°C) | δM (–) | z (–) |
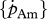 (J cm−2 d−1) (J cm−2 d−1) |
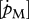 (J cm−3 d−1) (J cm−3 d−1) |
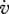 (cm d−1) (cm d−1) |
[Em] (J cm−3) | κ (−) | δV (−) | |
|---|---|---|---|---|---|---|---|---|---|
| standard DEB (generalized animal) | 20 | 1 | 22.5 | 18.0 | 0.0200 | 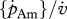 |
0.80 | ||
| P. platessa | 15 | 0.121 | 9.4 | 148 | 12.2 | 0.0129 | 11 473 | 0.78 | 0.143 |
| L. limanda | 15 | 0.130 | 6.6 | 125 | 14.9 | 0.0151 | 8278 | 0.79 | 0.187 |
| P. flesus | 15 | 0.131 | 7.4 | 115 | 12.4 | 0.0126 | 9127 | 0.79 | 0.173 |
| S. solea | 20 | 0.109 | 8.2 | 200 | 18.9 | 0.0196 | 10 204 | 0.77 | 0.157 |
| P. microps | 20 | 0.169 | 1.1 | 24 | 18.0 | 0.0203 | 1182 | 0.82 | 0.616 |
| P. minutus | 20 | 0.158 | 1.5 | 35 | 18.4 | 0.0197 | 1777 | 0.78 | 0.516 |
| G. morhua | 10 | 0.097 | 18.5 | 218 | 10.0 | 0.0082 | 26 585 | 0.85 | 0.067 |
| M. scorpius | 10 | 0.136 | 8.2 | 110 | 11.2 | 0.0123 | 8943 | 0.83 | 0.176 |
| Z. viviparous | 10 | 0.102 | 5.1 | 66 | 10.0 | 0.0106 | 6226 | 0.77 | 0.236 |
| D. labrax | 20 | 0.110 | 11.3 | 286 | 19.7 | 0.0184 | 15 543 | 0.78 | 0.109 |
| C. harengus | 15 | 0.122 | 5.3 | 77 | 11.4 | 0.0123 | 6260 | 0.78 | 0.233 |
| S. sprattus | 15 | 0.142 | 2.3 | 30 | 10.4 | 0.0127 | 2362 | 0.81 | 0.447 |
| E. encrasicolus | 20 | 0.130 | 2.6 | 60 | 18.2 | 0.0199 | 3015 | 0.79 | 0.387 |
| C. crangon | 20 | 0.175 | 1.7 | 36 | 17.7 | 0.0207 | 1739 | 0.82 | 0.526 |
| C. maenas | 20 | 0.565 | 4.8 | 95 | 15.9 | 0.0200 | 4750 | 0.80 | 0.286 |
(iii). Parameter set I versus parameter set II
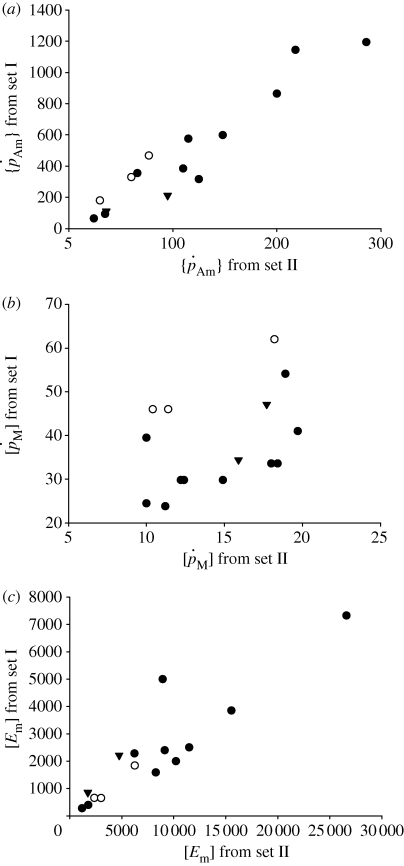
The order of magnitude of set II parameter values was lower than that of set I. For instance, for flatfishes, the volume-specific maintenance costs 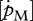 at 15°C obtained with the minimization procedure varied from 12 to 15 J cm−3 d−1, while the value empirically derived amounted to about 29.8 J cm−3 d−1. The same was true for assimilation rate
at 15°C obtained with the minimization procedure varied from 12 to 15 J cm−3 d−1, while the value empirically derived amounted to about 29.8 J cm−3 d−1. The same was true for assimilation rate 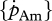 . The low energy conductance assumed in the minimization approach resulted in high predictions of the maximum storage density [Em]. For both assimilation rate and maximum storage density, set II (table 4) and set I (table 3) values were strongly correlated (figure 4a; set II
. The low energy conductance assumed in the minimization approach resulted in high predictions of the maximum storage density [Em]. For both assimilation rate and maximum storage density, set II (table 4) and set I (table 3) values were strongly correlated (figure 4a; set II 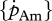 versus set I
versus set I 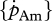 : rs = 0.90, d.f. = 13, p < 0.001; figure 4c; set II [Em] versus set I [Em]: rs = 0.86, d.f. = 13, p < 0.001). However, estimated values were on average approximately four times higher for assimilation rate and approximately 3.5 times lower for the maximum storage density. No significant correlation was found between the values of the volume-specific somatic maintenance rate
: rs = 0.90, d.f. = 13, p < 0.001; figure 4c; set II [Em] versus set I [Em]: rs = 0.86, d.f. = 13, p < 0.001). However, estimated values were on average approximately four times higher for assimilation rate and approximately 3.5 times lower for the maximum storage density. No significant correlation was found between the values of the volume-specific somatic maintenance rate 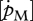 from the two sets (figure 4b).
from the two sets (figure 4b).
Figure 4.
Relationship between DEB parameters empirically derived (set I; table 3) and DEB parameters estimated by minimization procedures (set II; table 4). (a) maximum surface-area-specific assimilation rate 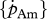 ; (b) maximum volume-specific somatic maintenance rate
; (b) maximum volume-specific somatic maintenance rate 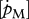 ; and (c) maximum storage density [Em]. Filled circles, demersal fish; open circles, pelagic fish; filled inverted triangles, crustaceans.
; and (c) maximum storage density [Em]. Filled circles, demersal fish; open circles, pelagic fish; filled inverted triangles, crustaceans.
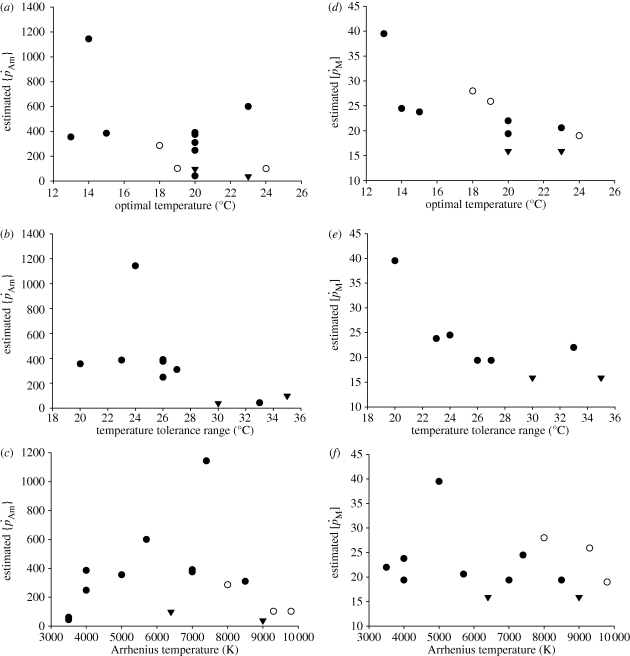
(c). Link between temperature parameters and energetics
For comparison of the various species, the surface-area-specific assimilation rate 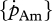 and the volume-specific maintenance rate
and the volume-specific maintenance rate 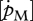 empirically derived were related with the optimal temperature, the Arrhenius temperature and temperature tolerance range, respectively, after conversion to 10°C using equation (2.1) (figure 5).
empirically derived were related with the optimal temperature, the Arrhenius temperature and temperature tolerance range, respectively, after conversion to 10°C using equation (2.1) (figure 5).
Figure 5.
Relationships between, respectively, maximum surface-area-specific assimilation rate 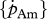 (a–c) and maximum volume-specific somatic maintenance rate
(a–c) and maximum volume-specific somatic maintenance rate 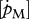 (d–f), at 10°C, with optimal temperature (°C) (a,d), temperature tolerance range (°C) (b,e) and Arrhenius temperature (K) (c,f). DEB parameter values from set I. Filled circles, demersal fish; open circles, pelagic fish; filled inverted triangles, crustaceans.
(d–f), at 10°C, with optimal temperature (°C) (a,d), temperature tolerance range (°C) (b,e) and Arrhenius temperature (K) (c,f). DEB parameter values from set I. Filled circles, demersal fish; open circles, pelagic fish; filled inverted triangles, crustaceans.
Surface-area-specific assimilation rate 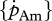 showed a significantly negative relationship with temperature tolerance range (figure 5b; rs = −0.58, d.f. = 8, p < 0.05), and negative but non-significant trends with the optimal temperature (figure 5a; rs = −0.39, d.f. = 12, p = 0.17) and the Arrhenius temperature (figure 5c; rs = −0.007, d.f. = 13, p = 0.98).
showed a significantly negative relationship with temperature tolerance range (figure 5b; rs = −0.58, d.f. = 8, p < 0.05), and negative but non-significant trends with the optimal temperature (figure 5a; rs = −0.39, d.f. = 12, p = 0.17) and the Arrhenius temperature (figure 5c; rs = −0.007, d.f. = 13, p = 0.98).
Volume-specific maintenance rate 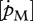 showed a strong negative correlation with the optimal temperature (figure 5d; rs = −0.80, d.f. = 12, p = 0.001) and a significant negative trend with tolerance range (figure 5e; rs = −0.69, d.f. = 8, p < 0.025). With respect to the Arrhenius temperature, no relationship with
showed a strong negative correlation with the optimal temperature (figure 5d; rs = −0.80, d.f. = 12, p = 0.001) and a significant negative trend with tolerance range (figure 5e; rs = −0.69, d.f. = 8, p < 0.025). With respect to the Arrhenius temperature, no relationship with 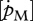 was found.
was found.
4. Discussion
The idea behind this paper is to compare the physiological performance of species by combining species-specific differences in temperature tolerance and sensitivity with their energetics reflected in the DEB parameters. The availability of reliable datasets is an important requirement but, unfortunately, basic information on temperature tolerance and sensitivity for many species is lacking. The absence of data on pelagic, schooling species, such as herring, sprat and anchovy, is somewhat understandable as laboratory rearing can be technically more challenging, but the lack of information on one of the most abundant, widely distributed and easy to handle species, the shore crab C. maenas, is more striking. An additional complication is that tolerance and temperature sensitivity appear to be flexible, causing plasticity of a species' physiology in response to short- and long-term environmental conditions (adaptation, etc.). Furthermore, nonlinear changes in sensitivity and tolerance during ontogeny may occur as has been found for C. crangon (Campos & van der Veer 2008). Finally, it is currently unknown whether there are differences between males and females. Therefore, although the present limited set of information should be interpreted with caution, it can, nevertheless, be seen as a step forward, advancing in our understanding of how organismal-level energetics are related to interspecific differences in thermal biology and, consequently, the impact of climate change on species interactions and community structure.
(a). Temperature
Based on tolerance range and optimal temperature, cold/temperate water (eelpout, bull-rout, herring, cod, sprat, various flatfishes) and warm water (gobiidae, shrimp, crab, sea bass, anchovy) species could be identified. This classification fits generally with the one based on biogeographic affinities (Boreal, Lusitanian) proposed by Yang (1982) and that has been followed in more recent studies (Tulp et al. 2008; Rijnsdorp et al. 2009). However, some discrepancies still occur, namely for sprat, a species occurring over a relatively large geographical (latitudinal) range, which has been considered both as a warm-water or cold-water species depending on the author. Species such as sprat challenge rigid classification schemes that separate groups based on thermal preference/tolerance, attributes that are more likely continuous (and not categorical) in nature. More importantly, species with wide geographical (latitudinal) ranges may show specific population adaptations to local environmental conditions, which also need to be considered.
With respect to temperature tolerance range, the high-temperature limit is more variable than the low-temperature limit. The lower limit was down to 10°C in almost all the species examined in this study, and approached 0°C in more than half of them. The high temperature limit was more variable, from 20°C to even 35°C, indicating that increasing temperatures, owing to either seasonal or longer term climate-driven changes, will modify the species composition of fish and crustacean assemblages. For instance, the nursery function of the Wadden Sea for plaice and herring (Zijlstra 1972) is restricted to maximum temperatures in the low 20s. At higher temperatures, not only shrimps but also crabs and gobiidae will become the dominant species, as has already been recently observed in intertidal areas during warm periods (H. W. van der Veer & J. IJ. Witte 2009, unpublished data). The fact that young (small) juvenile fishes seem to exploit a larger range in temperatures than either earlier or later life stages (e.g. Pörtner & Farrell 2008; Rijnsdorp et al. 2009) and that juvenile fishes select higher temperatures than do older (larger) conspecifics (McCauley & Huggins 1979; Lafrance et al. 2005) points to a differential vulnerability to changes in temperature, which should be accounted for when trying to predict individual responses to climate change. In coastal ecosystems, typically with larger variation in thermal regimes, these differential individual responses to increasing temperatures may result in a decrease in fish size or mass with consequences in the ecosystem structure and local production.
As expected, temperature tolerance range and optimal temperature are positively related. In this respect, mobile species do not deviate from sessile bivalves (van der Veer et al. 2006). The slightly positive trend of the Arrhenius temperature with temperature tolerance range diverges from the suggestion by Kooijman (2010): species with a large tolerance range that typically inhabit more variable temperature environments are expected to have lower temperature sensitivity (lower Arrhenius). However, in this respect, the dataset exhibits a large variation and thus no clear conclusions can be drawn. Moreover, the variability also masked any potential differences between pelagic and demersal species.
(b). Energetics
An energetic-based comparison of species with DEBs seems to be a promising route as only a few parameters are necessary to characterize a species. However, the token of the DEB model is energy, which requires a conversion for comparison of model simulations with observations. An issue is the general lack of reliable datasets preventing the use of standard protocols (Kooijman et al. 2008). For the pelagic species analysed, experimental data are completely absent and even for more well-studied species, information is often incomplete and/or contradictory. Moreover, some parameters are difficult to determine. Therefore, part of the analysis was based on the assumption that both [EG] and 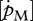 are related to cell complexity, and hence similar in related species as well as among sexes (Kooijman 2010). In a number of species, predicted maximum growth corresponded well with observations. However, in other cases discrepancies could not be reconciled or there was a lack of growth observations in relation to temperature. Information on growth of juvenile stages was particularly difficult to find, highlighting the fact that there is still lack of knowledge on the ecology of specific life stages for important species. This indicates that parameter estimates can only be considered exploratory, a rough approximation of the real values, requiring further experimental support and data for fine-tuning. The estimates for the pelagic species are particularly questionable.
are related to cell complexity, and hence similar in related species as well as among sexes (Kooijman 2010). In a number of species, predicted maximum growth corresponded well with observations. However, in other cases discrepancies could not be reconciled or there was a lack of growth observations in relation to temperature. Information on growth of juvenile stages was particularly difficult to find, highlighting the fact that there is still lack of knowledge on the ecology of specific life stages for important species. This indicates that parameter estimates can only be considered exploratory, a rough approximation of the real values, requiring further experimental support and data for fine-tuning. The estimates for the pelagic species are particularly questionable.
Some parameters, such as the volume-specific maintenance costs, represent different components depending on the type of species examined. In more active schooling species, higher maintenance costs reflect the higher cost of swimming compared with less active demersal species such as flatfishes with reduced swimming activity (Fonds et al. 1992). Therefore, differences in volume-specific maintenance costs between other fish species such as cod, sea bass and pelagic species reflect differences in activity patterns rather than differences in cell complexity. Differences in cell complexity are visible when comparing bivalves (12 J cm−3 d−1 at 10°C; van der Veer et al. 2006) with shrimps and shore crabs (16 J cm−3 d−1). Differences in life-history strategies (cf. Stearns 1992) are clearly reflected in the parameter values of the various flatfish species. Although being characterized by a similar blueprint (maintenance costs and costs for growth) the various species showed a large variability in energy uptake (310–490 J cm−2 d−1 at 10°C) and in energy allocation (κ in females varies from 0.65 to 0.90).
In DEB models, differences in energy budgets between sexes are reflected in different parameter values as in the case of different species (Kooijman 2010). Since DEB parameters are coupled to each other, dimorphism in ultimate size is related to differences in energy allocation (reflected in κ) and/or energy acquisition (ingestion, assimilation). In male fish, including flatfishes, reproductive investment in terms of energy used for gonadal production is typically lower than in females (Rijnsdorp & Ibelings 1989). However, males can also have additional ‘reproduction-related’ costs, namely territorial behaviour or parental care, which should be accounted. Differences in energy acquisition and assimilation seem to be the underlying cause for sexual differences in some flatfishes like dab L. limanda (Lozán 1992) and in percids (Rennie et al. 2008).
Our second approach to estimate parameters, based on body-size scaling relationships, is motivated by the observation that essential data are lacking for most species. Since maximum reserve capacity [Em] is expected to increase with maximum length, the assumption that reserve hardly contributes to physical volume is hard to substantiate for large-bodied species; wet-weight/dry-weight ratios do not vary that much with maximum length, so reserve is probably not replaced by water in small-bodied species. Deviations from predictions within this framework can be useful to detect species-specific adaptations in an evolutionary context (Kooijman et al. 2008).
We observed differences in results between both approaches. With the present dataset, it is unclear whether this indicates that for marine species the parameter values are different from those of other groups or whether the estimates are biased. The fact that predicted parameter values for plaice did not result in a good correspondence with observed growth patterns (not shown) might suggest that for marine species, typical values deviate from those presented by Kooijman (2010) for a generalized animal. However, more data are required to resolve this aspect.
(c). Are temperature tolerance and sensitivity linked with energetics?
Any discussion concerning a link between temperature tolerance and sensitivity with the energetics of a species should be considered as preliminary owing to the relatively small dataset and to uncertainties in some DEB parameter estimates for various species. From the DEB parameters, the surface-area-specific assimilation rate 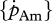 and the volume-specific somatic maintenance costs
and the volume-specific somatic maintenance costs 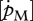 are, in this respect, the key parameters. First of all, they are temperature dependent and second, they reflect important energy fluxes.
are, in this respect, the key parameters. First of all, they are temperature dependent and second, they reflect important energy fluxes. 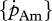 is the link with the environment that integrates feeding mode and prey species in one parameter.
is the link with the environment that integrates feeding mode and prey species in one parameter. 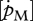 , on the other hand, is linked to turnover/activity processes reflecting the building design of the species and its complexity, and is a major factor in determining allocation to growth and reproduction. Differences in life-history strategies are therefore expected to act on (and to be reflected in) these parameters (Stearns 1992).
, on the other hand, is linked to turnover/activity processes reflecting the building design of the species and its complexity, and is a major factor in determining allocation to growth and reproduction. Differences in life-history strategies are therefore expected to act on (and to be reflected in) these parameters (Stearns 1992).
Both surface-area-specific assimilation rate and volume-specific maintenance rate appeared to decrease with increasing optimal temperature, temperature sensitivity and range of temperature tolerance. This might suggest that species with high optimal temperatures, living in fluctuating temperature environments, or those having greater metabolic sensitivity are compensated by having relatively lower assimilation rates and, surprisingly, lower maintenance costs. Generalizing these tendencies, species living under low and constant temperatures can afford a relatively high assimilation. On the other hand, species living in warm-water conditions may pay the price of a relatively low assimilation rate. Making the step from limited observations into underlying mechanisms is complicated especially because of the intimate coupling of processes of energy uptake and utilization. However, the preliminary work presented here is a promising approach to understand the response of species to temperature changes and is worth expanding in the near future. As noted by Rijnsdorp et al. (2009), responses at the population, community and ecosystem levels to climate change are ultimately the outcome of differences in individual physiological responses that affect trophic interactions. Integrating thermal tolerance and sensitivity information seems thus fundamental to understanding and predicting biological responses to global change.
The present study also highlights the need for additional, basic physiological data collected during controlled, multifactorial experiments quantifying rates of growth and metabolism (i.e. at different temperatures and feeding rates; cf. Peck et al. 2003). Parametrizations that embrace observed ontogenetic changes in metabolic scaling, which account for variability in prey energy densities within species with different feeding habitats, and which mechanistically couple resource allocation to other key environmental regulators (e.g. photothermal cues for the seasonal allocation of reserves), should also be pursued.
Acknowledgements
Thanks are due to our colleagues of the AquaDEB group for the fruitful discussions and to Henk Hobbelink for preparing some of the figures. Funding was provided by the FP6 project RECLAIM (contract no. 044133—FISH REG/A3(2006)D/14751). V.F. and J.F.M.F.C. were supported by grants from Fundação para a Ciência e Tecnologia (Portugal). J.C. was supported by a grant from the EEA Financial Mechanism and the Norwegian Financial Mechanism.
Footnotes
One contribution of 14 to a Theme Issue ‘Developments in dynamic energy budget theory and its applications’.
References
- Bailey K. M., Houde E. D.1989Predation on eggs and larvae of marine fishes and the recruitment problem. Adv. Mar. Biol. 25, 1–83 (doi:10.1016/S0065-2881(08)60187-X) [Google Scholar]
- Blackburn T. M., Gaston K. J.1999The relationship between animal abundance and body size: a review of the mechanisms. Adv. Ecol. Res. 28, 181–210 (doi:10.1016/S0065-2504(08)60033-1) [Google Scholar]
- Brawn V. M.1960Temperature tolerance of unacclimated herring (Clupea harengus L.). J. Fish. Res. Board Can. 17, 721–723 [Google Scholar]
- Brett J. R.1979Environmental factors and growth. In Fish physiology. Bioenergetics and growth, vol. 8 (eds Hoar W. S., Randall D. J., Brett J. R.), pp. 599–675 New York, NY: Academic Press [Google Scholar]
- Brett J. R., Groves T. D. D.1979Physiological energetics. In Fish physiology. Bioenergetics and growth, vol. 8 (eds Hoar W. S., Randall D. J., Brett J. R.), pp. 279–352 New York, NY: Academic Press [Google Scholar]
- Campos J., van der Veer H. W.2008Autecology of Crangon crangon (L.) with an emphasis on latitudinal trends. Oceanogr. Mar. Biol. Ann. Rev. 46, 65–104 [Google Scholar]
- Campos J., van der Veer H. W., Kooijman S. A. L. M.2009Contribution of different generations of the brown shrimp Crangon crangon (L.) in the Dutch Wadden Sea to commercial fisheries: a dynamic energy budget approach. J. Sea Res. 62, 106–113 (doi:10.1016/j.seares.2009.07.007) [Google Scholar]
- Fonds M., Rijnsdorp A. D.1988Eten and groeien. In Als een Vis in the Water (eds Osse J. W. M., Zijlstra J. J., Van Emden H. M.), pp. 120–138 Wageningen, The Netherlands: Pudoc [Google Scholar]
- Fonds M., Jaworski A., Iedema A., Van der Puyl P.1989Metabolism, food consumption and food conversion of the shorthorn sculpin (Myoxocephalus scorpius) and eelpout (Zoarces viviparus). ICES C.M. G-31, 1–10 [Google Scholar]
- Fonds M., Cronie R., Vethaak A. D., Van der Puyl P.1992Metabolism, food consumption and growth of plaice (Pleuronectes platessa) and flounder (Platichthys flesus) in relation to fish size and temperature. Neth. J. Sea Res. 29, 127–143 (doi:10.1016/0077-7579(92)90014-6) [Google Scholar]
- Freitas V., Campos J., Fonds M., van der Veer H. W.2007Potential impact of climate change on epibenthic predator–bivalve prey interactions in temperate estuaries. J. Therm. Biol. 32, 328–340 (doi:10.1016/j.jtherbio.2007.04.004) [Google Scholar]
- Fry F. E. J.1947Effects of the environment on animal activity. Univ. Toronto Stud. Boil. Ser. 55, 1–62 [Google Scholar]
- Gillooly J. F., Allen A. P., Savage V. M., Charnov E. L., West G. B., Brown J. H.2006Response to Clarke and Fraser: effects of temperature on metabolic rate. Funct. Ecol. 20, 400–404 (doi:10.1111/j.1365-2435.2006.01110.x) [Google Scholar]
- Graham C. T., Harrod C.2009Implications of climate change for the fishes of the British Isles. J. Fish Biol 74, 1143–1205 (doi:10.1111/j.1095-8649.2009.02180.x) [DOI] [PubMed] [Google Scholar]
- Hanson P., Johnson T., Kitchell J., Schindler D. E.1997Fish bioenergetics 3.0. Report WISCU-T-97-001,University of Wisconsin Sea Grant Institute, Madison, WI [Google Scholar]
- Huey R. B., Kingsolver J. G.1989Evolution of the thermal sensitivity of ectotherm performance. Trends Ecol. Evol. 4, 131–135 [DOI] [PubMed] [Google Scholar]
- Irvin D. N.1974. Temperature tolerance of early development stages of Dover sole, Solea solea (L.). In Proc. Int. Symp. on the Early Life History of Fish, Dunstaffnage Marine Research Laboratory, 17–23 May 1973, Oban, Scotland (ed. Blaxter J. H. S.), pp. 449–463 New York, NY: Springer [Google Scholar]
- Jobling M.1994Fish bioenergetics. London, UK: Chapman & Hall [Google Scholar]
- Kleiber M.1961The fire of life. An introduction to animal energetics. New York, NY: John Wiley and Sons [Google Scholar]
- Kooijman S. A. L. M.1988The Von Bertalanffy growth rate as a function of physiological parameters: a comparative analysis. In Mathematical ecology (eds Hallem T. G., Gross L. J., Levin S. A.), pp. 3–45 Singapore, Singapore: World Scientific [Google Scholar]
- Kooijman S. A. L. M.1993Dynamic energy budgets in biological systems. Theory and applications in ecotoxicology. Cambridge, UK: Cambridge University Press [Google Scholar]
- Kooijman S. A. L. M.2000Dynamic energy and mass budgets in biological systems. Cambridge, UK: Cambridge University Press [Google Scholar]
- Kooijman S. A. L. M.2010Dynamic energy budget theory for metabolic organization. Cambridge, UK: Cambridge University Press [Google Scholar]
- Kooijman S. A. L. M., Sousa T., Pecquerie L., van der Meer J., Jager T.2008From food-dependent statistics to metabolic parameters, a practical guide to the use of dynamic energy budget theory. Biol. Rev. 83, 533–552 [DOI] [PubMed] [Google Scholar]
- Lafrance P., Castonguay M., Chabot D., Audet C.2005Ontogenetic changes in temperature preference of Atlantic cod. J. Fish Biol. 66, 553–567 (doi:10.1111/j.0022-1112.2005.00623.x) [Google Scholar]
- Lefrançois C., Claireaux G.2003Influence of ambient oxygenation and temperature on metabolic scope and scope for heart rate in the common sole, Solea solea. Mar. Ecol. Prog. Ser. 259, 273–284 (doi:10.3354/meps259273) [Google Scholar]
- Lozán J. L.1992Sexual differences in food intake, digestive tract size, and growth performance of the dab Limanda limanda L. Neth. J. Sea Res. 29, 223–227 (doi:10.1016/0077-7579(92)90022-7) [Google Scholar]
- McCauley R. W., Huggins N.1979Ontogenetic and nonthermal seasonal effects on thermal preferenda of fish. Am. Zool 19, 267–271 [Google Scholar]
- McDonald P. S., Holsman K. K., Beauchamp D. A., Dumbauld B. R., Armstrong D. A.2006Bioenergetics modeling to investigate habitat use by the nonindigenous crab, Carcinus maenas, in Willapa Bay, Washington. Estua. Coasts 29, 1132–1149 [Google Scholar]
- Neill W. H., Miller J. M., van der Veer H. W., Winemiller K. O.1994Ecophysiology of marine fish recruitment: a conceptual framework for understanding interannual variability. Neth. J. Sea Res. 32, 135–152 (doi:10.1016/0077-7579(94)90037-X) [Google Scholar]
- Peck M. A., Buckley L. J.2007Measurements of larval Atlantic cod (Gadus morhua) routine metabolism and individual-based modeling. J. Appl. Ichthy. 24, 1–6 [Google Scholar]
- Peck M. A., Buckley L. J., Bengtson D. A.2003Effects of food consumption and temperature on growth rate and biochemical-based indicators of growth in early juvenile Atlantic cod (Gadus morhua) and haddock (Melanogrammus aeglefinus). Mar. Ecol. Prog. Ser. 251, 233–243 (doi:10.3354/meps251233) [Google Scholar]
- Pecquerie L.2008Bioenergetic modelling of the growth, development and reproduction of a small pelagic fish: the Bay of Biscay anchovy. PhD thesis,Agrocampus Rennes & Vrije Universiteit, Amsterdam [Google Scholar]
- Peters R. H.1983The ecological implications of body size. Cambridge, UK: Cambridge University Press [Google Scholar]
- Pörtner H. O., Farrell A. P.2008Physiology and climate change. Science 322, 690–692 (doi:10.1126/science.1163156) [DOI] [PubMed] [Google Scholar]
- Pörtner H. O., et al. 2001Climate induced temperature effects on growth performance fecundity and recruitment in marine fish: developing a hypothesis for cause and effect relationships in Atlantic cod (Gadus morhua) and common eelpout (Zoarces viviparus). Cont. Shelf Res. 21, 1975–1997 (doi:10.1016/S0278-4343(01)00038-3) [Google Scholar]
- Rennie M. D., Purchase C. F., Lester N., Collins N. C., Shuter B. J., Abrams P. A.2008Lazy males? Bioenergetic differences in energy acquisition and metabolism help to explain sexual size dimorphism in percids. J. Anim. Ecol. 77, 916–926 (doi:10.1111/j.1365-2656.2008.01412.x) [DOI] [PubMed] [Google Scholar]
- Rijnsdorp A. D., Ibelings B.1989Sexual dimorphism in the energetics of reproduction and growth of North Sea plaice, Pleuronectes platessa L. J. Fish Biol. 35, 401–415 (doi:10.1111/j.1095-8649.1989.tb02992.x) [Google Scholar]
- Rijnsdorp A. D., Berghahn R., Miller J. M., van der Veer H. W.1995Recruitment mechanisms in flatfish: what did we learn and where do we go? Neth. J. Sea Res. 34, 237–242 (doi:10.1016/0077-7579(95)90031-4) [Google Scholar]
- Rijnsdorp A. D., Peck M. A., Engelhard G. H., Möllmann C., Pinnegar J. K.2009Resolving the effect of climate change on fish populations. ICES J. Mar Sci. 66, 1570–1583 (doi:10.1093/icesjms/fsp056) [Google Scholar]
- Ross A. H., Nisbet R. M.1990Dynamic models of growth and reproduction of the mussel Mytilus edulis L. Func. Ecol. 4, 777–787 (doi:10.2307/2389444) [Google Scholar]
- Ryland J. S., Nichols J. H., Sykes A. M.1975Effect of temperature on the embryonic development of the plaice, Pleuronectes platessa L. (Teleostei). J. Exp. Mar. Biol. Ecol. 18, 121–137 (doi:10.1016/0022-0981(75)90069-6) [Google Scholar]
- Sinclair M.1988Marine populations: an essay on population regulation and speciation. Seattle, WA: University of Washington Press [Google Scholar]
- Sogard S. M.1997Size-selective mortality in the juvenile stage of teleost fishes: a review. Bull. Mar. Sci. 60, 1129–1157 [Google Scholar]
- Sousa T., Domingos T., Poggiale J.-C., Kooijman S. A. L. M.2010Dynamic energy budget theory restores coherence in biology. Phil. Trans. R. Soc. B 365, 3413–3428 (doi:10.1098/rstb.2010.0166) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stearns S. C.1992The evolution of life histories. Oxford, UK: Oxford University Press [Google Scholar]
- Talbot J. W.1977Dispersal of plaice eggs and larvae in Southern Bight of the North Sea. J. du Cons. 37, 221–248 [Google Scholar]
- Theilacker G. H.1987Feeding ecology and growth energetics of larval northern anchovy, Engraulis mordax. Fish. Bull. 85, 213–228 [Google Scholar]
- Tulp I., Bolle L. J., Rijnsdorp A. D.2008Signals from the shallows: in search of common patterns in long-term trends in Dutch estuarine and coastal fish. J. Sea Res. 60, 54–73 (doi:10.1016/j.seares.2008.04.004) [Google Scholar]
- van der Veer H. W., Kooijman S. A. L. M., van der Meer J.2001Intra- and interspecies comparison of energy flow in North Atlantic flatfish species by means of dynamic energy budgets. J. Sea Res. 45, 303–320 (doi:10.1016/S1385-1101(01)00061-2) [Google Scholar]
- van der Veer H. W., Cardoso J. F. M. F., van der Meer J.2006The estimation of DEB parameters for various northeast Atlantic bivalve species. J. Sea Res. 56, 107–124 [Google Scholar]
- van der Veer H. W., Cardoso J. F. M. F., Peck M. A., Kooijman S. A. L. M.2009Physiological performance of plaice Pleuronectes platessa (L.): a comparison of static and dynamic energy budgets. J. Sea Res. 62, 83–92 (doi:10.1016/j.seares.2009.02.001) [Google Scholar]
- Wheeler A.1978Key to the fishes of Northern Europe. London, UK: Frederick Warne Ltd [Google Scholar]
- Winberg G. G.1956Rate of metabolism and food requirements of fishes. Fish. Res. Board. Can. Transl. Ser. 194, 1–202 [Google Scholar]
- Yang J.1982The dominant fish fauna in the North Sea and its determination. J. Fish Biol. 20, 635–643 [Google Scholar]
- Zijlstra J. J.1972On the importance of the Wadden Sea as a nursery area in relation to the conservation of the southern North Sea fishery resources. Symp. Zool. Soc. Lond. 29, 233–258 [Google Scholar]