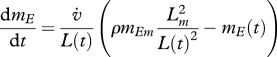Dynamic energy budget approaches for modelling organismal ageing

Abstract

Ageing is a complex multifactorial process involving a progressive physiological decline that, ultimately, leads to the death of an organism. It involves multiple changes in many components that play fundamental roles under healthy and pathological conditions. Simultaneously, every organism undergoes accumulative ‘wear and tear’ during its lifespan, which confounds the effects of the ageing process. The scenario is complicated even further by the presence of both age-dependent and age-independent competing causes of death. Various manipulations have been shown to interfere with the ageing process. Calorie restriction, for example, has been reported to increase the lifespan of a wide range of organisms, which suggests a strong relation between energy metabolism and ageing. Such a link is also supported within the main theories for ageing: the free radical hypothesis, for instance, links oxidative damage production directly to energy metabolism. The Dynamic Energy Budgets (DEB) theory, which characterizes the uptake and use of energy by living organisms, therefore constitutes a useful tool for gaining insight into the ageing process. Here we compare the existing DEB-based modelling approaches and, then, discuss how new biological evidence could be incorporated within a DEB framework.

1. Introduction

Few biological phenomena are as omnipresent in our society as the ageing process. Every day we see its effects on the human beings that surround us, and—possibly even more painfully—on ourselves when we look in the mirror. It is often said that life and death are inseparable, and that ageing is the path that brings us to our inevitable fate. From a more abstract and generic point of view, the ageing process has been defined as a ‘universal, irreversible, continuous, intrinsic, deleterious process that manifests itself in the form of a gradual physiological decline with age that causes an increase in the mortality rate’. This definition corresponds to the so-called biological ageing, a process that affects all individuals of the same species, although not necessarily at the same rate. It excludes diseases whose incidence increases with age, such as cardiovascular failure, various kinds of cancer and degenerative arthritis.

For most species, the population mortality rate results from a combination of age-dependent and age-independent factors (Gavrilov & Gavrilova 1991). In the wild, the age-independent component, which is associated with adverse environmental and ecological conditions, plays a major role in defining the life expectancy of most species (e.g. a zebra in the African savannah is more likely to die as the result of predation than of old age). The distinction between both types of factors is not clear-cut, however, as ageing-induced changes can, for instance, make individuals more fragile and, thus, more accident-prone and vulnerable to predation. In contrast, if the external hazards were removed, life expectancy would be mainly determined by age-associated factors. The study of animal models (e.g. mice, fruitflies and turquoise killifish) under controlled laboratory conditions is therefore regarded as a key approach for enhancing our understanding of the ageing process (Orr & Sohal 1994; Liang et al. 2003; Terzibasi et al. 2007). Remarkably, for a wide range of species, when the age-independent component is negligible, the population mortality follows the Gompertz law, proposed by the actuary Benjamin Gompertz, according to which the hazard rate increases exponentially with age (Gompertz 1825; Finch & Pike 1996). In mathematical terms, this can be expressed as:

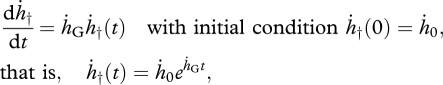1.1

1.2

where ḣ_† and S_† are the hazard rate (or mortality rate) and the survival function, respectively, and ḣ_G the Gompertz coefficient. The equation for S_†(t) above can be directly obtained from equation (1.1) and the general definition of hazard rate:

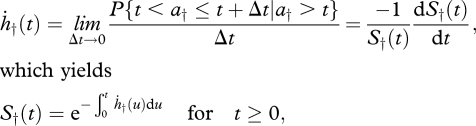1.3

with a_† the random variable age at the time of death (i.e. S_†(t) = P{a_† > t}). Besides the Gompertz law, there is another classic, widely used survival distribution (Ricklefs & Scheuerlein 2002): the Weibull model, which has the form:

1.4

that is, ḣ_†(t) = nḣ_Wⁿtⁿ⁻¹. The symbols ḣ_W and n represent the Weibull ageing rate and shape parameter, respectively (Weibull 1951).

Since Gompertz's and Weibull's efforts, several research groups have used mathematical modelling techniques to study ageing. Gavrilov & Gavrilova (1991) considered ageing as a systemic phenomenon and, therefore, viewed the mortality rate as a systemic failure rate and applied ideas from reliability theory to gain new insight. In contrast, Kirkwood & Kowald (1997) adopted a bottom-up approach and formulated a network theory for ageing, describing the dynamics of a population of mitochondria subjected to damage to their genetic material. Failure of the system as a whole was caused by the joint effects of defective mitochondria and cytoplasmic reactions. Bonsall & Mangel (2004) explored the impact of evolutionary ecology on species-specific longevity. Van Leeuwen et al. (2002) proposed a model to describe the food consumption, body growth and survival of laboratory rodents, which predicted well the observed differences in body weight and longevity in function of the food intake rate. De Magalhães & Toussaint (2004) developed a proteomic network map of human ageing, suggesting a relationship between the genetics of development and ageing. Furthermore, Xue and co-workers have recently derived a modular network of protein–protein interactions in fruitflies and humans, and then identified those modules that are responsible for the progression of ageing (Xue et al. 2007). Alternatively, other modelling efforts focused on particular molecular processes that have been implicated in ageing, such as telomere shortening (Shachar et al. 2008) or mTOR signalling (Blagosklonny 2007). Throughout this paper, however, we will concentrate our discussion on models for ageing based on the Dynamic Energy Budgets (DEB) theory.

The remainder of this paper is organized as follows. First, from an evolutionary gerontology point of view, we address the issue of why ageing occurs (§2). Thereafter, we succinctly discuss key molecular and cellular mechanisms responsible for how ageing manifests itself. Then, in §4, we present and compare existing DEB approaches to modelling ageing and mortality. Finally, in §5, we discuss exciting potential future applications of the DEB theory in gerontology and, in particular, we suggest how the existing approaches could be extended or modified to accommodate the latest advances in ageing research.

2. Evolutionary perspective on ageing

Intuitively, it might be tempting to view ageing as the result of natural wear and tear over time. This hypothesis, however, fails to explain that the ways in which different species age can differ substantially and that many exceptions exist that do not satisfy the definition of ageing provided in §1. Unicellular organisms that reproduce by cell division, for example, are perishable but do not undergo ageing as such. There are also multicellular organisms that are subjected to negligible ageing, as illustrated by naked mole-rats (Buffenstein 2005) and coelenterates like Hydra (Martinez 1998), where age-specific mortality rates remain constant. The mortality rates of several species of coral have even been shown to decrease with age and colony size (Babcook 1991). Extreme intraspecies variations in ageing also take place in nature: in a beehive, workers have a life expectancy of two to eight months, whereas their queen can live on for 5 years (Amdam & Page 2005). Furthermore, ageing is not always a gradual phenomenon: individuals from semelparous species die shortly after mating as a consequence of a massive production of corticoids. Examples include salmon (McQuillan et al. 2003) and males of the marsupial mouse Antechinus (McAllan 1998).

In Darwinian evolution, natural selection favours the propagation of mutations that, directly or indirectly, enhance reproductive success. As expressed by Charlesworth (2000), ‘at first sight, the nearly universal existence of senescence in species of multicellular organisms is paradoxical, given that natural selection supposedly causes the evolution of increased, not decreased, fitness’. However, the intra- and interspecies diversity in manifestations of ageing can only be understood within an evolutionary context. There are four key concepts in modern evolutionary gerontology:

• — late-acting deleterious mutations can remain in the population simply because natural selection does not act against them. This constitutes the basis for the Mutation Accumulation Theory for ageing (Medawar 1946);

• — mutations providing a reproductive advantage early in life can be actively favoured by natural selection even if they have adverse effects later in life. This is the basis for the Antagonistic Pleiotropy Theory for ageing (Williams 1957);

• — natural selection promotes the propagation of traits that enable a higher energy investment in reproduction (i.e. higher offspring production), which comes at the expense of a lower energy investment in maintenance processes. This concept, which is the basis for the Disposable Soma Theory (Kirkwood 1977, 2005), can be seen as a special case of antagonistic pleiotropy; and

• — natural selection forces can be effective in post-reproductive individuals when intergenerational transfers take place. This is a cornerstone for the Negative Senescence Theory (Lee 2003; Vaupel et al. 2004).

It is possible that the first two events take place simultaneously, and their relative impact on the evolution of ageing remains to be elucidated. They both rely on the hypothesis that mutations that adversely affect an organism prior or during its reproductive stage are very likely to be eliminated by natural selection, as such mutations strongly hamper the organism's ability to transfer its genetic material to next generations. The evolutionary implications of natural selection forces that decline in strength with age have been formalized by Hamilton (1966).

While here we have discussed the life history of ageing, in the next sections we will focus on the molecular and physiological mechanisms underlying the manifestations of the process.

3. Molecular, cellular and organismal ageing

Primary mammalian cells grown in culture have a finite replicative capacity. Once cells reach their maximum number of divisions, or Hayflick limit, they undergo growth arrest and become senescent (Hayflick 1974). This cellular phenotype is characterized by the presence of a number of biomarkers, including senescence-associated β-galactosidase activity, elevated p16 levels, formation of senescence-associated heterochromatin foci, changes in cell morphology (i.e. enlarged, flat cells) and lipofuscin accumulation (Campisi 2005). The Telomere Shortening Theory suggests that the end-replication problem, and the resulting loss in telomere length with every cell division, could be the cause of cellular senescence (for a review, see McCord & Broccoli (2008)). Oxidative stress is also believed to be a major mediator, since cellular senescence can be prematurely triggered by various stressful stimuli such as DNA damage and aberrant oncogene activity (Campisi 2005).

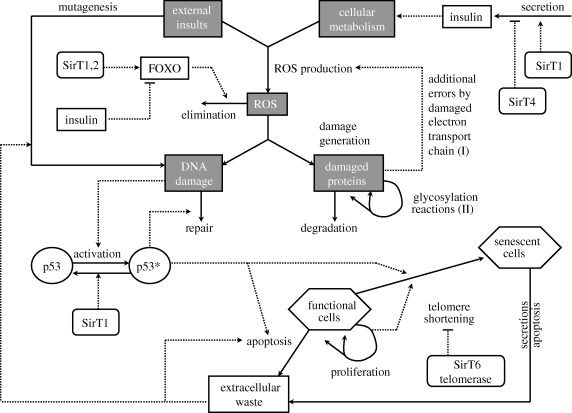
Telomere loss and DNA damage are known to induce activation of the p53 tumour suppressor. Its task is to judge the seriousness of the damage and decide whether the cell should be rehabilitated (DNA repair), growth arrested (cellular senescence) or sentenced to death (apoptosis). Lack of p53 function causes a substantial increase in tumour incidence in mice, whereas reintroduction of functional p53 in cancer cells induces growth inhibition and/or cell death. p53 might, however, be a double-edged sword: it has been suggested that high levels of p53 can accelerate the ageing process in mice (Tyner et al. 2002). However, García-Cao et al. (2002) have recently generated mice carrying supernumerary copies of the p53 gene that show cancer resistance and normal ageing. Furthermore, telomerase reverse transcriptase (TERT) overexpression in these mice produces ‘a systemic delay in ageing accompanied by extension of median lifespan’ (Tomás-Loba et al. 2008). In contrast to Tyner et al. (2002), these data indicate that it is possible to enhance p53's anti-cancer activity safely as a strategy for cancer treatment. Interestingly, a regulator of p53's activity, SirT1 (a member of the sirtuin family; Van Leeuwen & Laín 2009), and a downstream target of p53, p66^shc (Migliaccio et al. 1999), have themselves been implicated in organismal ageing. Figure 1 provides an overview of key molecular components and interactions involved in cellular senescence.

Figure 1.

Schematic illustrating the complexity of the molecular networks responsible for cellular ageing. Please note that the components and processes shown here only represent a small selection, which is inevitably biased by the authors' own research interests. Epigenetic changes and damage to mitochondrial DNA, for instance, could also play a major role. The grey boxes correspond to concepts that will be modelled in the next sections.

As cells constitute the vital building blocks of multicellular organisms, it is often assumed that cellular decline contributes to organismal ageing as well as to the onset of age-dependent diseases. Most of the proposed mechanisms for p53's ageing-promoting action, for instance, rely on the hypothesis that organismal ageing is the consequence of additive cellular ageing. With every stem-cell division comes a chance of DNA modification and, in some cell types, telomere shortening. Consequently, as genetic alterations accumulate gradually during the organism's lifespan, cells are at increasing risk of undergoing p53-mediated senescence or apoptosis. It has been hypothesized that an age-related decrease in stem-cell number and function causes a decline in tissue renewal and repair, inexorably leading to organ atrophy, age-related diseases and, eventually, death (Donehower 2002). In addition, it has been suggested that senescent cells might contribute actively to age-related diseases, including cancer, by producing secreted proteins that alter and destroy the surrounding tissue (Campisi 2005). These hypotheses can be viewed as a special case of the Antagonistic Pleiotropy Theory (§2), where cellular senescence pathways have a beneficial, tumour-suppressing function early in life but cause adverse, lifespan-reducing effects later on.

The inter-relationships between cellular senescence and organismal ageing are, however, far from trivial, as demonstrated by the fact that post-mitotic organisms, such as Caernorhabditis elegans and Drosophila melanogaster, can undergo gradual ageing. In particular, this observation makes a universal role of telomere shortening in organismal ageing highly disputable. Even in organisms where tissue renewal does occur in adult life, the Hayflick limit is possibly never reached during the organism's lifespan, as stem cells are known to maintain telomere length by expressing telomerase (Rubin 2002). Moreover, the fact that Tomás-Loba et al. (2008) observed increased life expectancy, but no changes in maximum lifespan, in super-p53 mice overexpressing TERT, in our view suggests that telomerase might provide protection against age-related diseases rather than interfere with the ageing process per se.

4. Body size, energetics, longevity and the DEB theory

Calorie restriction studies have revealed that, in a wide range of organisms, reduced energy intake without malnutrition correlates with extended life expectancies and fewer age-associated diseases. These observations reflect the fact that the molecular pathways involved in energy dynamics and ageing are intertwined and, in particular, many mechanisms regulating energy metabolism also influence the ageing process. The Rate of Living Theory for ageing (Pearl 1928) was the first quantitative law linking the species-specific maximum lifespan, ℒ, to the metabolic rate, ℛ. It states that the ‘amount of living’ (i.e. ℒ × ℛ/𝒲, with 𝒲 the species-specific body mass) is constant, and implies that organisms that ‘live fast’ wear out more quickly and, consequently, have shorter lifespans. This relation emerges naturally from the empirical observation that both ℛ and ℒ can be written as a function of body weight:

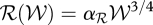
and

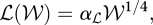
with α_ℛ and α_ℒ constants (Pearl 1928; Kleiber 1932). The relation between energy dynamics and ageing is also integrated within the disposable soma theory (§2), which postulates that the ageing evolutionary process balancing the energy invested in maintenance and reproduction. In its context, those species that have a low life expectancy in the wild, such as mice, are anticipated to have both high reproduction and ageing rates. Furthermore, the Free Radical Theory, which proposes that ageing is the result of the accumulation of oxidative damage, provided a first potential molecular mechanism underpinning the concept of rate of living. Free radicals are highly reactive species that are generated as a natural by-product of normal metabolic processes (Finkel & Holbrook 2000): it has been estimated that 1–2% of the oxygen consumed by the mitochondria is transformed into reactive oxygen species (ROS), which can cause oxidative damage to proteins, lipids and DNA. In this context, calorie restriction prolongs lifespan by reducing the production of ROS.

Organisms exposed to calorie restriction invariably show low insulin levels in conjunction with normal glucose levels in blood. Moreover, mutations in various components of the insulin signalling pathway, which is responsible for regulating glucose homeostasis, have been shown to affect lifespan dramatically (Russell & Kahn 2007). It is known that the insulin signal downregulates the activity of transcription factors of the forkhead-box (FOXO) family that regulate the expression of pro-longevity genes coding for proteins involved in the anti-ROS machinery (figure 1). Thus, according to the Endocrine Theory for ageing, the beneficial effects of calorie restriction are due to an enhanced elimination of oxidative stress (Russell & Kahn 2007). It is worth noting here that the sirtuins, which were mentioned above as regulators of p53, modulate both FOXO activity and insulin production (Van Leeuwen & Laín 2009).

The relationship between ageing and energy dynamics has puzzled biologists for many years and remains subject to debate (Speakman 2005; Hulbert et al. 2007), as many inter- and intraspecies variations in longevity cannot be explained on the basis of differences in metabolic rate alone. Moderate physical activity, for instance, is known to extend lifespan, despite the associated increase in metabolic rate. Moreover, while mammals and birds of comparable size have similar metabolic rates, the latter can live substantially longer. We believe that the DEB theory, which characterizes the uptake and use of energy by living organisms (Kooijman 1986, 2009; Sousa et al. 2008, 2010), constitutes a useful tool for enhancing our understanding of the complex inter-relations between body mass, energy dynamics and life expectancy. Below we illustrate the potential of the DEB theory in ageing research by revisiting various successful applications.

The basic concepts of the DEB theory are introduced in Sousa et al. (2010), while the equations for a sample organism are provided in table 1. In the context of the standard DEB theory, any living organism is built of two types of materials, namely structure and reserves. The chemical composition of each component is assumed to remain constant in time (strong homeostasis) but, as their relative amounts can change, the stoichiometry of the body as a whole is variable. The theory characterizes the dynamics of structure and reserves in terms of two state variables: the volumetric structural length, L, and the reserve density per structural volume, m_E (table 1). Total body weight can then be calculated as a weighted sum of L³ and m_E × L³.

Table 1.

Standard DEB model for an organism that has not allocated part of its reserves to reproduction (i.e. E_R = 0 in (Kooijman 2009)). For further information on the DEB theory, see Kooijman (2009) and Sousa et al. (2010). d_V, density of structural biomass; f(X), scaled functional response under ad libitum conditions, f ≡ 1); g, energy investment ratio; L(t), volumetric structural length; L_m, maximum length when f ≡ 1(or ρ = 1) and L_T ≡ 0; L_T, reduction in length owing to surface maintenance costs; m_E(t), reserve density; m_Em, maximum reserve density when f ≡ 1 (or ρ = 1); μ̄_E, specific chemical potential of the reserves; M_V(t), structural biomass in moles; [M_V], number of C atoms per unit of structural volume; ṗ_C(t), energy mobilization rate; ρ, food supply coefficient(e.g. under 25% calorie restriction, ρ = 0.75); ṙ(t), specific growth rate; v̇, energy conductance; w_E, molecular weight of the reserves; W(t), total body weight in grams; X, food density.

4.1
if the food intake rate depends on body size,
4.2
alternatively, if the food intake rate is constant,
4.3
4.4
4.5
4.6
4.7

Organisms go through various stages during their life cycle, including embryo, juvenile and adult. It is important to note that the initiation of an ‘ageing phenotype’ cannot be linked to a ‘maturity threshold’ because in some instances (e.g. low food availability) such a threshold would never be reached. Therefore, within the DEB framework, it is an accumulation of oxidative damage that is responsible for ageing-related physiological decline. Hence, the ageing-related hazard rate is assumed to be proportional to the amount of oxidative damage per structural mass, that is ḣ_† ∝ M_D/M_V, or, equivalently,

4.8

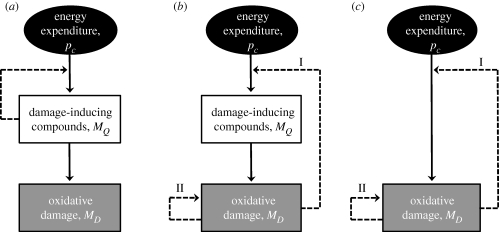
where m_D is the ‘damage density’ per structural biomass and β̇_† a damage-specific killing rate. As the behaviour of the structural biomass, which is defined as M_V(t) = [M_V]L(t)³ with [M_V] a constant parameter, is given by the general DEB framework (table 1 and Sousa et al. 2010), building a DEB-based model for ageing requires only the characterization of the dynamics of M_D. Below, we discuss three existing DEB applications in detail (figure 2): the first was developed to characterize the growth and mortality rates of laboratory rodents exposed to calorie restriction, the second to quantify the effect of toxicants and the third to model the growth and mortality rates of ectotherms. All include a link, direct or indirect, between the rate at which the energy in the reserves is being consumed, i.e. the energy mobilization rate ṗ_C, and the rate of generation of oxidative damage.

Figure 2.

Alternative DEB-based modelling approaches aimed at characterizing the amount of, M_D. Broken lines represent positive feedbacks loops. The biological interpretation of ‘damage-inducing compounds’, Q, and ‘damaged compounds’, D, can vary. (a) Approach developed by Kooijman (2009). Q = aberrant nuclear and mitochondrial DNA; and D = defective proteins. The dashed arrow indicates that damage-inducing compounds promote their own production. (b) Approach used by Jager et al. (2004) and Van Leeuwen et al. (2002). For the mechanisms underpinning feedbacks I and II, see figure 1. Q = reactive oxygen species (ROS); and D = defective proteins and DNA mutations. Under the assumption that the half-life of ROS is negligibly short, (b) reduces to (c).

(a). Application I: predicting the effects of calorie restriction

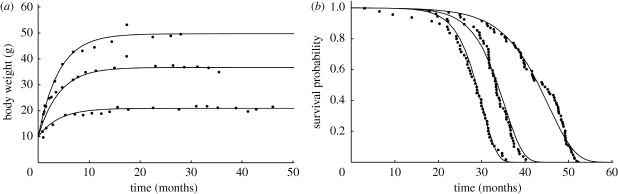
Van Leeuwen et al. (2002) proposed a DEB-based mathematical model coupling food intake, body growth and survival. As can be seen from figure 3, the model succeeded in predicting the body weight and life expectancy of laboratory rodents exposed to different levels of calorie restriction. The approach characterizes the intracellular dynamics of ROS and the associated oxidative stress. The coupling between oxidative damage and survival is given by equation (4.8). In short, the model was built on the basis of the following key assumptions: (i) the generation rate of ROS is proportional to the energy mobilization rate, ṗ_C; (ii) free radicals have a negligibly short half-life (i.e. the ROS generation rate translates immediately into a damage production rate), and consequently, in figure 2, model (b) reduces to (c); (iii) a fixed fraction of the newly produced damaged molecules are either repaired or degraded; (iv) existing oxidative damage causes an increase in the ROS production rate because components of the electron transport system are themselves targets for oxidation, rendering the system less accurate (figure 1 and feedback loop I in figure 2; model (b)); and (v) amplification of oxidative damage occurs due to chain glycosylation reactions (figure 1 and feedback loop II in figure 2c).

Figure 3.

Growth and survival of mice subject to 0, 25 and 56% calorie restriction. Images adapted from Van Leeuwen et al. (2002), with kind permission of Springer Science and Business Media. To account for the observation that ad libitum laboratory rodents consumed a constant amount of food independently of their size, Van Leeuwen et al. (2002) modified the expression for the reserve density (equation (4.2)), arriving at equation (4.3). Bullet points are data from Weindruch et al. (1986), while curves are simultaneous model fits. The curves only differ in the value of the food supply coefficient, ρ. Time is expressed in months. (a) Body weight (g); (b) survival probability.

Under the assumptions above, the changes in the amount of oxidative damage can be described by the following ordinary differential equation (ODE):

4.9

with initial condition M_D(0) = M_D0. The parameter ϕ_DC links the generation of oxidative damage to the energy mobilization rate, ν̇_a accounts for the amplification of damage (i.e. feedback loop II in figure 2) and γ_a quantifies the increase in ROS production resulting from defects in the electron transport chain. Notably, for fully grown organisms satisfying ϕ_DC ≡ 0, the expression for the hazard rate ((4.8) together with equation (4.9)) reduces to the Gompertz law for mortality, equation (1.1). Indeed, when growth ceases, M_V and ṗ_C reach their steady-state values, M_V^★ and ṗ_C^★, and, as a result, equation (4.9) can be easily solved analytically. Substitution of the solution into equation (4.8) yields

with initial value for the hazard rate, ḣ₀ = β̇_†M_D0/M_V^★, and Gompertz coefficient, ḣ_G = ν̇_a + γ_aṗ_C^★. Moreover, if the organism's food intake rate is kept constant (equation (4.3)), that is İ(t) ≡ ρİ_m with 0 ≤ ρ ≤ 1 a food supply coefficient, it can be shown that the value of the Gompertz coefficient is an increasing linear function of ρ (Van Leeuwen et al. 2002). The food supply coefficient ρ adopts its maximum value, i.e. ρ = 1, under ad libitum feeding conditions.

(b). Application II: assessing multiple life-cycle endpoints in toxicity tests

In the previous section, equations (4.8) and (4.9) described mortality as the result of toxic effects exerted by compounds produced inside the body. In addition, living organisms are exposed to a myriad of external factors that can interfere with the ageing process either directly, by affecting the values of ageing-related parameters, or indirectly, by affecting the values of other physiological parameters and phenomena. Motivated by these ideas, Jager et al. (2004) exploited the DEB theory to model the impact of toxicants, which enabled them to predict their effects on growth, survival and reproduction simultaneously.

Chemicals can affect the DEB framework in at least five possible ways (Kooijman 2009): (i) by decreasing the energy assimilation from food, (ii) by increasing the costs of somatic maintenance, (iii) by increasing the costs of body growth, (iv) by increasing the costs of reproduction, and (v) by having direct deleterious effects on embryos. Small changes in such physiological parameters can have dramatic effects on one or more life-cycle endpoints. The true functional relationship between the dose and the change in a particular DEB parameter can generally not been established. Therefore, for simplicity, the target parameter was taken to be proportional to the internal concentration minus an internal no-effect concentration, with the constraint that the parameter value has to remain non-negative. It was further assumed that the internal concentration is proportional to the external dose.

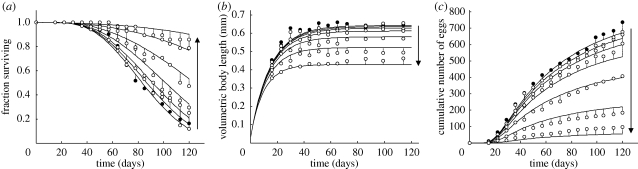
Jager et al. (2004) considered experimental data on the growth, survival and reproduction of groups of springtails (Folsomia candida), under the exposure of different levels of either cadmium or triphenyltin. The authors used the standard DEB model (table 1) to describe body growth and egg production, equations (4.8) and (4.9), to predict ageing-mediated deaths and a continuous form of the Euler-Lotka equation to characterize the population growth rate (for the technical details, the reader is referred to the original paper). For each of the five possible modes of action considered above, the data were fitted simultaneously (Jager et al. 2004). The best fits were obtained for hypotheses (i) and (ii) for cadmium and triphenyltin, respectively. The results for the latter are shown in figure 4.

Figure 4.

Growth, survival and egg production of springtails (F. candida) under exposure to triphenyltin (CAS 668-34-8). Bullet points are experimental data, whereas curves are simultaneous model fits. (a) Volumetric body length (mm); (b) survival probability; (c) cumulative number of eggs. Image reprinted with permission from Jager et al. (2004). Copyright ©American Chemical Society.

(c). Application III: bringing the Gompertz and Weibull laws together

In 2009, Kooijman proposed a slightly different approach to organismal ageing. The motivation for this was the observation that the model in §4a often fails to describe the survival curves of ectotherms (Kooijman 2009), even though it works exceptionally well for endotherms. The structure of the new model, which is depicted in figure 2a, relies upon the following key assumptions: (i) damage-inducing compounds are generated at a rate that is proportional to the mobilization rate per structural mass, with proportionality constant η_QC, (ii) damage-inducing compounds promote their own production (i.e. feedback loop in figure 2a), with proportionality constant ρ_a, (iii) damage-inducing compounds cause damage at a constant rate δ̇_DQ, and (iv) the resulting damaged compounds accumulate in the body. Hence, the system can be described by the ODEs:

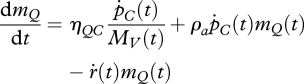4.10

and

4.11

where ṙ is the organism's specific growth rate, ṙ(t) = d ln M_V/dt. Because the organism's size changes over time and the model is expressed in damage densities, rather than absolute amounts, the state variables are subject to dilution by growth. Therefore, the equations have been adjusted by adding a sink term, −ṙ(t)m_*(t), for * = Q, D.

Let us now define a new variable, the ageing acceleration q¨, as q¨(t)= (β_†/M_V(t)) (dM_D/dt). From equation (4.11) and the definition of the damage density, m_D, we obtain that q¨(t) = ˙δ_DQβ_†m_Q(t). The model can thus be expressed in terms of q¨ and ḣ_† as follows:

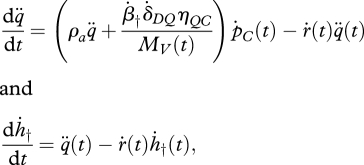4.11

with initial values, q¨(0) = 0 and ḣ_†(0) = ḣ₀. Substitution of the expression for ṗ_C (table 1; equation (4.4)) into the equations above leads to

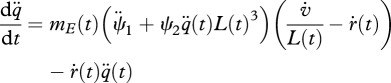4.12

and

4.13

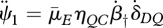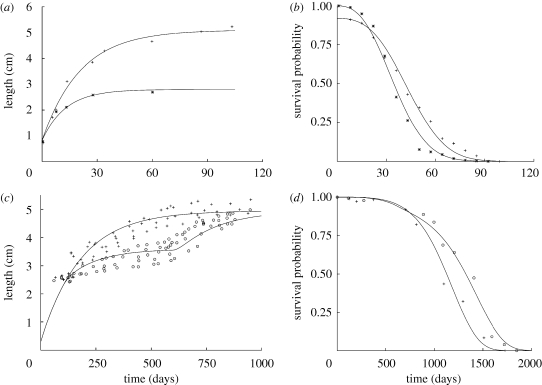
which has only two ageing-related parameters, and 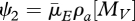, besides two initial conditions. Two applications of the model are depicted in figure 5. Figure 5a,b shows the growth and mortality of a species of water flea, Daphnia magna. Food availability remains constant during the experiment and, in addition, it can be assumed that the energy reserves are at steady state at birth. Under these conditions, the DEB expressions for the change in body size (table 1) reduce to the Von Bertalanffy growth law. Hence, the solid lines in figure 5a are Von Bertalanffy curves produced with the best-fit parameter values for males and females, respectively. Unlike the growth data, the associated survival data (figure 5b) were fitted simultaneously (the initial female mortality is assumed to be accidental). The fact that the ageing model performs well means that the differences in survival can be explained by gender-related differences in energetics alone. Figure 5c,d shows the growth and mortality of two cohorts of guppies, Poecilia reticulata. The first was fed ad libitum for the full duration of the experiment, whereas the second was exposed to transient calorie restriction. As in figure 5a,b, the two growth curves were fitted independently, whereas the associated survival curves were fitted simultaneously, and, once again, the model succeeds in predicting the observed differences in mortality. These examples illustrate the importance of accounting for energy metabolism and other physiological parameters in theoretical survival studies. Furthermore, such approaches can help pinpoint those physiological features responsible for changes in survival. Hence, comparison of the two sets of DEB parameter values estimated from figure 5b suggests that the gender-related differences in survival could be due to differences in energy allocation.

Figure 5.

Fits of the model shown in figure 2a against experimental data. Figures reprinted from Kooijman (2009) with permission from Cambridge University Press. (a,b) Growth curves and survival probabilities of male (asterisk) and female (plus symbol) water fleas (D. magna) at 18°C. Genders differ in their specific assimilation parameter alone. For further information, see fig. 6.1 in Kooijman (2009). (c,d) Body length and survival probability of two cohorts of guppies (P. reticulata). One group, plus symbol, was fed ad libitum throughout the experiment, whereas the other, open circles, was exposed to calorie restriction between days 100 and 600. For further information, see fig. 6.3 in Kooijman (2009).

(i). Model reduction for short growth periods at constant food density

If food availability remains constant and the growth period is short compared with lifespan, ṙ ≈ 0 and L(t) ≈ fL_m − L_T hold, with f the constant scaled functional response (table 1). Under these conditions, we can then solve equations (4.12) and (4.13) to obtain

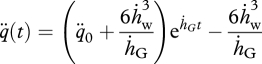4.14

and

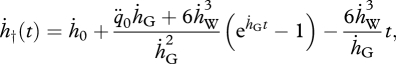4.15

where 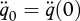and 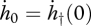. The Gompertz coefficient and Weibull ageing rate are defined as

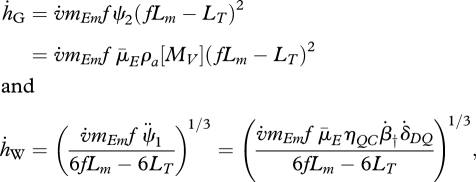respectively (Kooijman 2009). The motivation for these definitions will become clear below.

(ii). Weibull model for small Gompertz rates

If the effects of the ageing process are negligible during the embryo stage (i.e. 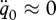and 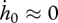), the equations above reduce to

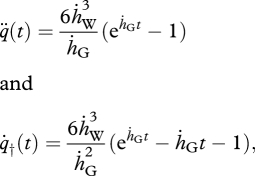which, when the Gompertz coefficient tends to zero (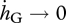), converge to

and

This constitutes a special case of the Weibull law, 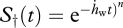, with shape parameter n = 3 (equation (1.4)).

(iii). Gompertz model for small Weibull rates

If ḣ ≈ 0, the initial ageing acceleration is non-zero (q¨ ≩ 0), and the value of the Weibull ageing rate tends to zero (ḣ_W³ → 0), and equations (4.14) and (4.15) can be approximated by

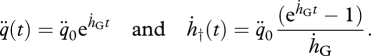If t_★ is such that ln(ḣ_Gt_★ ≫ 0, then the hazard rate reduces to the Gompertz law (equation (1.1)) for t ≥ t_★.

5. Discussion

Recent experimental findings have led to the identification of numerous endogenous and exogenous factors influencing ageing-related processes. The strong relationship between energy metabolism and ageing suggests that the DEB theory could constitute a tool naturally suited for ageing-related studies. With this in mind, in this paper we have critically examined and compared three DEB-based approaches to ageing, and below discuss some new, promising DEB-based avenues.

The main feature that distinguishes DEB-based models from other theoretical approaches to ageing is the strong coupling with energetics. That is, ageing is not modelled as an independent phenomenon, but as part of a framework describing the physiology of the organism. The strength of this approach can be seen in figures 3–5, where the observed differences in survival can be explained on the basis of differences in energetics alone. Thanks to their design, DEB models can be used to investigate the role of intrinsic, physiological parameters on the ageing process (e.g. gender differences in survival, figure 5b), and to assess the impact of exogenous factors (e.g. mortality rates under exposure to different doses of toxicants, figure 4) and experimental manipulations (e.g. increased lifespan in calorie-restricted animals, figures 3 and 5d).

Another important feature of the DEB-based models discussed above is their relationship with two widely used classic survival laws, namely the Gompertz and Weibull models. Hence, we have seen that a model with a structure according to figure 2b or 2c can reduce to the Gompertz model when body growth ceases. Alternatively, for models constructed according to figure 2a, both the Gompertz model and a Weibull model with shape parameter equal to three can be obtained as special cases. That is, the DEB theory brings the Gompertz and Weibull survival laws together and provides a plausible biological interpretation of their parameters.

Finally, the DEB framework characterizes fundamental processes that are non-species specific. Thanks to this universality, DEB-based models can be parameterized and/or adapted to describe physiological characteristics, such as growth and mortality rates, for any species of interest. Moreover, the DEB body size–scaling relationships and quantitative structure–activity relationships, which emerge naturally from the theory and have already proved to be predictive for intra- and interspecies differences (Kooijman 2009), open the door to DEB applications in evolutionary gerontology. In particular, as the theory provides quantitative expressions for both reproduction and maintenance costs, using DEB to formalize the disposable soma theory (§2) appears as a promising new line of research that could lead to novel experimentally testable predictions. Moreover, the DEB theory could constitute a useful tool to explore and compare the implications of the two main evolutionary explanations of ageing (Partridge & Barton 1993), involving passive and active natural selection of ageing-inducing traits, respectively.

Concerning the specific DEB applications presented here, although they predict survival data well, we can think of three obvious directions for future work: (i) develop alternative model structures to those shown in figure 2 and/or pursue new applications, (ii) refine and/or extend the model(s) to include additional features, and (iii) thereafter, perform new experiments to parameterize and validate these new, more complex models.

While the non-species-specific nature of the underlying DEB framework opens the door to a myriad of applications of DEB-based models, here we would like to highlight the following. Firstly, it would be an interesting exercise to vary the values of DEB parameters in a systematic manner and assess the impact on survival, as this could help identify new potential targets for interventions aimed at interfering with the ageing process or ageing-related diseases. Naturally, this work will become even more biologically and clinically relevant once the models have been extended to account for detailed molecular information. Secondly, the models in this paper could be combined with systems biology approaches to develop multiscale models for ageing. In such an approach, the DEB theory, which is built upon strict mass and energy conservation principles, would impose constraints on the subcellular level of organization. The feasibility of working bottom-up and top-down simultaneously in this way is explored for the first time in Vinga et al. (2010).

Efforts to refine and extend DEB models for ageing are currently concentrated on strengthening the coupling between ageing and energetics and on incorporating a higher level of detail at the molecular level. Concerning the former, while the models above include a strong dependence of ageing rates on metabolism, they neglect the potential impact of ageing-mediated physiological deterioration on energetics. An age-dependent reduction in the efficiency of the gastrointestinal epithelium could, for instance, cause a decrease in the energy assimilation rate from food. Moreover, while the costs of repairing ageing-related damage are likely to increase with age, at least till the repair systems become saturated, this energy burden has not yet been taken into account. Importantly, such feedback loops might be able to explain why many species are subject to body weight loss at old age.

The incorporation of molecular information requires that a compromise is reached between the levels of complexity of the model and the biological system that matches the data available for parameterizing the model. The complexity of the models reviewed above, for instance, was kept very low, as only growth and survival data were available at the time. More detailed models will require the integration of data from different levels of organization for their full parameterization. In addition to parameterization issues, incorporating further molecular information into DEB models for ageing implies at least two more challenges, which would need to be tackled a priori. Firstly, the DEB-model formulations in this paper are expressed in terms of an abstract quantity, namely the damage density. This implies that an organism that bears oxidative damage homogeneously distributed throughout its body has the same life expectancy as another, equally sized organism that has the same amount of oxidative damage but concentrated in, say, cardiac tissue, which seems highly unlikely. To model ageing based on non-homogeneous damage-density patterns is, however, a non-trivial task: tissues can vary in their susceptibility to different kinds of oxidative damage and, to complicate matters further, the impact of tissue dysfunction on the hazard rate depends on the organ(s) affected. A main difficulty in developing multicompartment models is that organ-specific parameters are largely unknown. Secondly, the DEB approaches described here are built upon the characterization of a general quantity, namely oxidative damage. Incorporating further biological information at the molecular level into such models inevitably requires a decision upon what kind of damage (e.g. DNA damage or ‘wrong proteins’) should be monitored. However, the kind of damage that is relevant for organismal ageing, as well as for the onset of age-dependent diseases, might vary among different tissues and species. In mammals, for instance, where stem-cell dynamics and the associated tissue renewal processes are key for maintaining a healthy phenotype, DNA damage has probably more impact on ageing than oxidative damage to proteins, as the latter have a very short lifespan owing to the rapid protein turnover rate occurring in growing cells. In contrast, we believe that in post-mitotic organisms, damage to long-lived proteins is likely to play a more important role in determining longevity than DNA damage.