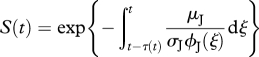Dynamic energy budget theory and population ecology: lessons from Daphnia

Abstract

Dynamic energy budget (DEB) theory offers a perspective on population ecology whose starting point is energy utilization by, and homeostasis within, individual organisms. It is natural to ask what it adds to the existing large body of individual-based ecological theory. We approach this question pragmatically—through detailed study of the individual physiology and population dynamics of the zooplankter Daphnia and its algal food. Standard DEB theory uses several state variables to characterize the state of an individual organism, thereby making the transition to population dynamics technically challenging, while ecologists demand maximally simple models that can be used in multi-scale modelling. We demonstrate that simpler representations of individual bioenergetics with a single state variable (size), and two life stages (juveniles and adults), contain sufficient detail on mass and energy budgets to yield good fits to data on growth, maturation and reproduction of individual Daphnia in response to food availability. The same simple representations of bioenergetics describe some features of Daphnia mortality, including enhanced mortality at low food that is not explicitly incorporated in the standard DEB model. Size-structured, population models incorporating this additional mortality component resolve some long-standing questions on stability and population cycles in Daphnia. We conclude that a bioenergetic model serving solely as a ‘regression’ connecting organismal performance to the history of its environment can rest on simpler representations than those of standard DEB. But there are associated costs with such pragmatism, notably loss of connection to theory describing interspecific variation in physiological rates. The latter is an important issue, as the type of detailed study reported here can only be performed for a handful of species.

1. Introduction

Many fundamental challenges in ecology require understanding how environmental change impacts the dynamics of interacting populations. The problems involved are of urgent societal importance, and it is clear that pure empiricism does not offer a practical way forward as there are too many different populations/environment combinations. Also, population change can be slow, and there are many contexts where experimentation would be impractical, prohibitively expensive or unethical. Consequently, theory must have a central role. Dynamic energy budget (DEB) offers a systematic way to relate processes at different organizational levels: molecules, cells, organisms, populations and ecosystems (Kooijman 2000; Nisbet et al. 2000; Sousa et al. 2008). DEB theory focuses on metabolic processes that are common to large groups of organisms, thereby offering some hope for generality, a key requirement for ecologists.

The core component of DEB theory is a dynamic model of physiological processes in the individual organism, and there is a well-established theoretical methodology for relating individual physiology and behaviour to population dynamics (Tuljapurkar & Caswell 1997). In a closed system, populations change through individual births and deaths, so a deterministic population model has the following components:

• — identification of a set of ‘i-state’ variables that fully determine reproductive performance for individuals in an arbitrary environment, Φ, and definition of a ‘p-state’ that describes the distribution of i-states within a population;

• — assumptions on i-state and Φ-dependence of mortality risk for individuals;

• — assumptions on feedbacks from the population to the environment.

The mathematical form taken by the population dynamic equations depends on the assumptions on individuals; commonly used choices are matrices (Caswell 2001), partial differential equations (de Roos 1997), delay-differential equations (Nisbet 1997) and integro-differential equations, which involve a distributed delay (Diekmann & Metz 2010).

In the canonical version of Kooijman's DEB model (Sousa et al. 2010), hereafter referred to as ‘standard DEB’, there are five i-state variables: structural biovolume, reserves, maturity, reproductive buffer and level of damage-inducing compounds. In certain circumstances, maturity can be left out of explicit consideration, and simplified treatments of mortality are defensible in many ecological applications (Kooijman 2010). Nevertheless, a population model based on standard DEB would, in principle, demand multiple i-state variables, leading in one approach to a partial differential equation with a correspondingly large number of independent variables (the i-states and time). Implementation of such complex models is a daunting, though feasible, task, but there are strong, pragmatic reasons for seeking simpler representations. Many pressing environmental concerns involve the processes that are central to DEB. Thus, at least for the short term, we require ways of exploiting the insights from DEB theory with simpler, perhaps less general, representations than are offered by Kooijman's approach.

A less utilitarian reason for looking for simplified representations for i-state dynamics is that in all but the most contrived laboratory situations, ecological processes occur at multiple time and spatial scales. In addition, many factors other than mass and energy budgets may contribute to population dynamics. Multi-scale problems require consistently formulated approximations that allow simplifications of descriptions at any one level. Indeed, the complexity of a DEB-based model may obscure insights at the population level that can be illuminated using simpler representations. In this paper, we emphasize representations in which organisms are represented by size and life stage (juvenile or adult). A large body of literature has established the ecological value of such models (Nisbet et al. 1989a,b; McCauley et al. 1996, 2008; de Roos & Persson 2003; Murdoch et al. 2003; de Roos et al. 2007; Nelson et al. 2007). But there are many other situations where simplification is desirable, a good example in this volume being the study of Poggiale et al. (2010). Each simplification of course needs careful evaluation to determine the sensitivity of population dynamics to details of the i-state dynamics.

A final, compelling, motive for seeking simplified representations of i-state dynamics is to enhance the likelihood of starting from the physiology of individuals and ending up with population-level explanations of population phenomena. A simple, well-understood example is the ‘prey-escape’ mechanism that generates large-amplitude consumer–resource cycles (de Roos et al. 1990). That mechanism is most easily understood by analysing a pair of population-level equations, which describe the delayed response of a consumer population to a deviation from equilibrium of the density of its resource; the resource population initially grows (‘escapes’), but the consumer eventually ‘catches up’ and then over-exploits the resource. These population-level equations can be derived from special assumptions on the dynamic biomass budgets of individuals (Nisbet et al. 1997). A recent example, relevant to the work in this paper, is the attempt by de Roos and collaborators to relate demographic change during population cycles in consumer–resource systems to population-level energy turnover in juveniles versus adults (de Roos & Persson 2003; de Roos et al. 2007).

Our broad aim in this paper is to better define the strengths and limitations of size- and stage-structured population models, and to evaluate the models of i-state dynamics that underpin them. Our approach is to base our models on general DEB-based mechanisms, but to focus much ‘testing’ effort on laboratory data on individuals and populations of a single, well-studied genus, Daphnia, with which we have extensive experience. Models that survive such detailed scrutiny and rigorous testing have some credibility when used in field situations where testing is much more difficult.

2. Daphnia as a model organism

Daphnia is an appropriate choice of model organism for many reasons. Daphnia have an important ecological function, as they represent a major component of the zooplankton in many temperate lakes and ponds. They commonly control the density of phytoplankton, and can generate ‘clear water’. There are data available at many levels of ecological organization (genome, individual, laboratory population, natural population). And Daphnia serves as a model organism for much ‘applied’ research, notably in its use in standardized toxicity tests.

(a). Individual growth, reproduction and mortality

Many investigators have studied how food availability affects growth and reproduction in the more common Daphnia species. Key literature prior to 1989 was reviewed by McCauley et al. (1990b); later publications with new data include McCauley et al. (1990a) and Nisbet et al. (2004). Some more recent literature has focused on food quality, characterized by the stoichiometry of key elements (Sterner & Elser 2002), with Urabe & Sterner (2001) demonstrating the importance for Daphnia growth and reproduction of C : N and C : P ratios in the algal food. In this paper, we restrict our discussion to effects of food quantity (represented as carbon content), but we have work in progress evaluating our approach to situations where stoichiometry is important.

There is a smaller body of literature with studies of mortality that span a broad range of ecologically relevant food ranges and cover a complete lifetime. Nisbet et al. (1989b) surveyed literature on Daphnia magna and Daphnia galeata together with subsequently published data from our own experiments (McCauley et al. 1990a). New experimental data for Daphnia pulex are discussed below.

(b). Population dynamics

There is a similarly large body of literature on laboratory populations of Daphnia with non-growing food. Success in quantitative modelling of these simple experiments has confirmed the central role of bioenergetic considerations for Daphnia population dynamics. McCauley et al. (1996) identified studies by Goulden and collaborators as being particularly well suited for modelling (Goulden & Hornig 1980; Goulden et al. 1982). One of us (Edward McCauley) has in addition performed many such experimental studies (Nisbet et al. 1997; Nelson et al. 2005; McCauley et al. 2008). In many cases, the population eventually fluctuates around a mean level that may be interpreted as an equilibrium. The ‘equilibrium’ population biomass and stage structure can be predicted to good accuracy using independently measured data on the feeding rate, assimilation efficiency, mortality and respiration rates of individuals.

Of much greater ecological interest is the population dynamics of Daphnia interacting with dynamic food. An analysis by Murdoch & McCauley (1985) demonstrated the occurrence of common dynamic patterns in a large number of Daphnia populations interacting with algal food in laboratory, microcosm and field systems. They noted the absence of large-amplitude prey-escape cycles, as predicted by simple theory for highly enriched systems (Rosenzweig 1971; de Roos et al. 1990; Gurney & Nisbet 1998; Murdoch et al. 2003). In a subsequent paper (McCauley & Murdoch 1987), they noted that for both stable and cycling populations, fecundities were very low. McCauley & Murdoch (1990) subsequently confirmed the absence of large-amplitude population cycles in some enriched mesocosms, work that motivated a theoretical study of five hypothesized mechanisms that might be responsible for the observed stability of most Daphnia populations, and rejection of four of these (Murdoch et al. 1998). However, further work by McCauley et al. (1999) established that these cycles may occur in carefully prepared microcosms with accelerated nutrient recycling, and also found compelling evidence of multiple periodic attractors. Two types of cycles were noted: large-amplitude cycles resembling those caused by the prey-escape mechanism and a distinctive type of small-amplitude cycle. The best metrics distinguishing the two types of cycles related to changes in Daphnia demography (Nelson et al. 2007; McCauley et al. 2008).

(c). Individuals in populations

For researchers interested in relating individual physiology to population dynamics, one obvious approach would appear to be to follow the ‘marked’ individual Daphnia in a population. Unfortunately, no non-intrusive technique has been developed that can be applied to Daphnia individuals that moult every 2–3 days. We have confronted this problem with two types of experiments: artificial assemblage of a population (AAP) and replication of the environment (RE). Data from both types of experiments are discussed later in this paper. Each experiment aims at measurement of the growth rate of individual Daphnia experiencing an environment similar to that achieved by individuals in populations.

AAP yields information on the performance of readily identifiable cohorts of individuals in a population near equilibrium—for details, see electronic supplementary material—corresponding to neonates, immatures (or ‘adolescents’), ‘small adults’ and ‘large adults’. Individuals from these cohorts are used to create a population with the same mix of size classes as was achieved in laboratory populations with non-growing food—see above. The evolution of these multimodal equilibrium size distributions can be used to estimate fecundity and rates of growth and mortality in populations near equilibrium. In addition, we have recently used data from AAP experiments to estimate variability in growth rates (Ananthasubramaniam et al. in press).

The artificial cohort approach sheds only limited insight on the performance of individuals in non-equilibrium situations—including cycling populations. For such situations, RE is appropriate. We perform bioassays that involve studying the growth over several days of individual animals living in water withdrawn from populations. We refer the reader to McCauley et al. (2008) for details.

In summary, we have a large body of information on growth and reproduction of individual Daphnia, some limited data on Daphnia mortality rates and population dynamic information in different laboratory environments and in the field. We have two indirect approaches to estimation of the performance of individual organisms experiencing the food environment experienced by individuals in populations. Both of these approaches generate key information used in subsequent validation of population models.

3. Simplified models of daphnia physiology

(a). Models for growth and reproduction

Growth and reproduction in individual Daphnia varies with food supply, and many authors have developed dynamic models describing this phenomenon. The level of complexity of these models varies from detailed moult-by-moult descriptions (e.g. Gurney et al. 1990) to parameter-sparse, continuous-time, representations (Kooijman 1986, 2000; Nisbet et al. 2004). The models differ in their assumptions regarding priority for energy allocation; however, all models recognize in some manner increased ‘priority’ for reproduction versus growth as an animal ages.

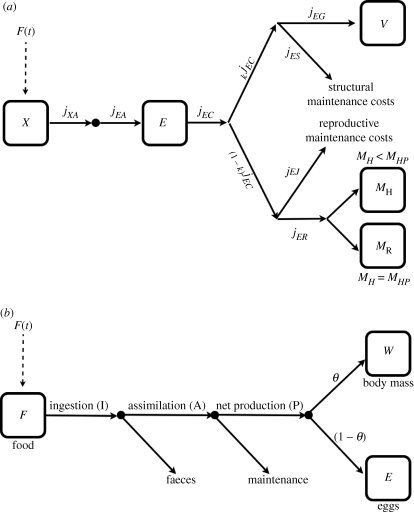
The simplest, and historically the first, energetically based models for Daphnia growth assumed size-dependent resource allocation (e.g. Sinko & Streifer 1969; Paloheimo et al. 1982). Size was represented in the model by dry weight or carbon mass, which is related to a measure of length by an allometric relationship. Size-dependent resource allocation was modelled by assuming that the proportion of ‘net production’ (assimilation rate less maintenance rate) assigned to growth decreases with size (Paloheimo et al. 1982; Andersen 1997; Lika & Nisbet 2000; Nisbet et al. 2004). The implied energy flows are shown schematically in figure 1, along with the flows recognized in the standard DEB model. The key attraction of the less sophisticated net-production-based representations is that the i-state is one-dimensional.

Figure 1.

State variables and fluxes in the (a) standard DEB and (b) net production models. Details of the DEB model are in the electronic supplementary material. Equations for the net production model are in table 1.

Many key features of Kooijman's DEB theory, notably the κ-rule for energy partitioning, were inspired by his early research on Daphnia (Kooijman 1986). For isomorphs growing in a constant food environment, Kooijman's standard DEB model predicts that the proportion of net production assigned to growth decreases with the animal's size; however, with standard DEB, this is a property that is derived from more fundamental assumptions, whereas it is an assumption in the net production models. Thus, by using the net production representation, we are abandoning the rigorous conceptual foundations of standard DEB, but retaining a connection to some of the observations that motivated it.

We previously fitted and tested a net production model, using a dataset on growth and reproduction of individual D. pulex, grown in transfer cultures at four food levels (Nisbet et al. 2004). Equations are in table 1. That study, along with previous work (Gurney et al. 1990), demonstrated the importance of keeping track of the daily variations in food concentration, and not assuming ‘constant’ food levels as is common in fitting DEB models to data (Kooijman et al. 2008). A second key requirement in obtaining a good match of model to data was size dependence of the proportion of net production allocated to growth.

Table 1.

The net production models of individual growth and reproduction. An animal assimilates carbon from food and uses it for basal maintenance. Net production, assimilation minus maintenance, represents surplus carbon that can be assigned to growth (i.e. production of new somatic tissue) or egg production. The ‘full’ model is that of Nisbet et al. (2004), the stage-structured model is a simplified version in which assimilation rates are assumed identical for the two life stages: juvenile and adult.

state variables	W = carbon content of animal (mgC)
	E = cumulative egg production (fecundity = dE/dt)
	X = density of food in the environment (mgC l−1)
rates	I = ingestion rate (mgC d−1)
	A = assimilation rate (mgC d−1)
	M = maintenance rate (mgC d−1)
	P = A − M = net production rate (mgC d−1)
balance equations		somatic growth (mgC d−1)
		egg production (number of eggs per day)
		food depletion (mgC d−1)
	X is reset to XR if t = nTR, where n is an integer	transfer culture conditions
model functions	W = ξLq	allometric (carbon) weight–length relation
	M = mW	maintenance rate proportional to weight (full net production model)
	M = 0	maintenance included in assimilation efficiency (stage-structured model)
	A = Am(W) f(X)	assimilation rate depends multiplicatively on size (carbon content) and food density
	with: Am(W) to be fitted	full net production model
	Θ(W) to be fitted	stage-structured model size-dependent allocation to growth
		Holling type 2 functional response
	parameters	ξ	parameter in carbon-length relation (mgC mm−q)
q		exponent in carbon-length relation (dimensionless)
Xh		half-saturation constant (mgC l−1)
we		carbon required for an egg (mgC)
m		specific maintenance rate (d−1)
AJ, AA		assimilation rates for juveniles and adults in the stage-structured model (mgC d−1)
ɛa		assimilation efficiency (dimensionless)
TR		interval between transfers to fresh food (day)
v		system volume (l)

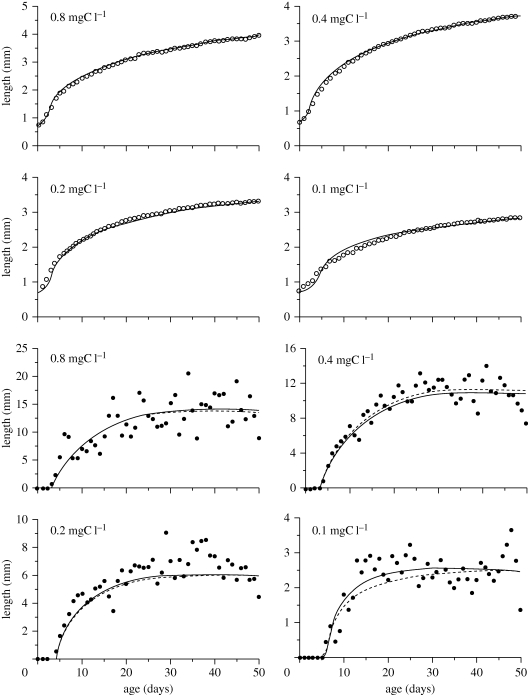
The fits of the net production model are shown in figure 2. Subsequent (R. M. Nisbet & E. McCauley 2004, unpublished data) analysis showed a similarly good fit to a variant of the standard DEB model where the allocation parameter, κ, was allowed to vary with length, an assumption consistent with Kooijman's rationale for the κ-rule (Kooijman 2010, ch. 2). This similarity in quality of fits suggests that the conceptual differences between standard DEB and net-production-based representations are not critical for the pragmatic purpose of adequately describing the performance of individuals.

Figure 2.

Fits (solid line) of the net production model in table 1 to data on growth (open circles) and reproduction (filled circles) for individual Daphnia pulex grown in 100 ml containers at 20°C and at four food levels (indicated on panels). The dashed lines are fits with an alternative form of functional response involving Kooijman's ‘synthesizing unit’. Data from Nisbet et al. (2004).

Having established that patterns of growth and reproduction can be described by a low-dimensional model, we now demonstrate that further simplification is possible. Key to this simplification is the observation by McCauley & Murdoch (1987) noted above that fecundities in Daphnia populations are typically low. Thus, we now report fits to the ‘standard’ DEB model and a simple model, but restrict our analysis to the lowest two food levels for the data in figure 2.

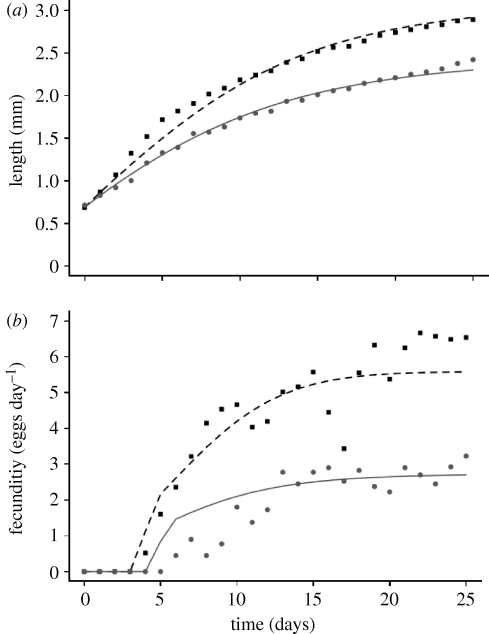
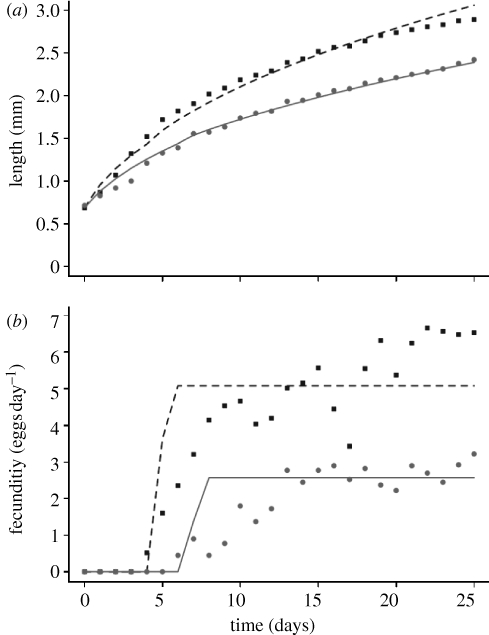
We first consider the standard DEB model, i.e. we insist on a constant (size-independent) value for κ; for details, see electronic supplementary material, A. Since the daily variations in food are known to strongly impact the observed dynamics, it was not possible to use approaches that assume constancy of food density, such as those of Kooijman et al. (2008). Instead, we used a similar methodology to Nisbet et al. (2004)—for details, see the electronic supplementary material. Results, shown in figure 3, show a good visual match of the model to data.

Figure 3.

(a) Growth and (b) reproduction of individual D. pulex in transfer cultures fitted by the standard DEB model. Experimental details in Nisbet et al. (2004). Nominal food levels: 0.2 mgC l⁻¹ (squares and dashed line); 0.1 mgC l⁻¹ (circles and solid line). For details of the fitting method, see electronic supplementary material, A.

A further, major simplification is to make precisely those assumptions on individuals that lead to simple continuous-time, stage-structured, population models with dynamically varying time delays (Nisbet & Gurney 1983; Nisbet 1997; Murdoch et al. 2003). Individuals are characterized solely as ‘juveniles’ or ‘adults’ with all juveniles and all adults having the same physiological rates at any given instant. Lengths are calculated from carbon using an empirical weight–length relationship (Paloheimo et al. 1982; Nisbet et al. 1989b, 2004; McCauley et al. 1990b). Equations are in table 1. The fits from this ‘stage-structured’ individual model are shown in figure 4. This model can only give a single value for the fecundity, so we could never capture the rising fecundity through ontogeny. Yet, it is striking how well the growth curves match the data, given the naivety of the model.

Figure 4.

(a) Growth and (b) reproduction of individual D. pulex in transfer cultures fitted by an individual model with same assumptions as stage-structured population model. Experimental details in Nisbet et al. (2004). Nominal food levels: 0.2 mgC l⁻¹ (squares and dashed line); 0.1 mgC l⁻¹ (circles and solid line).

(b). Models for mortality

As noted earlier, previous information on the determinants of Daphnia mortality was obtained for Daphnia species other than our focal species, D. pulex. We therefore followed the daily growth, reproduction and moulting of a large number of individual D. pulex reared in isolation in different food environments from birth until death. Experimental and analytical details are in the electronic supplementary material, B.

We performed a standard analysis of age-specific survival rates, obtaining estimates of daily hazard rate. Key findings were:

1. Juvenile mortality is food dependent, being high at the lowest and the highest food treatments.

2. For each food level, mortality is lowest in the first 20 days of adult life.

3. Within the low mortality phase, increasing food density decreases the death rate.

4. In later life, the rate of increase of mortality increases with food level.

Findings (ii), (iii) and (iv) are consistent with Kooijman's (2000, 2010) interpretation of an age-dependent hazard rate caused by accumulation of damage-inducing compounds—see also van Leeuwen et al. (2010). The standard DEB representation does not include a mechanism (other than starvation) to quantify high juvenile mortality when food densities are low (finding (i)), but such a mechanism could be easily developed.

We then performed an analysis that aimed to characterize mortality within our stage-structured representation—electronic supplementary material, B. We found significantly different relationships between net production and probability of dying for juveniles and adults, with a much stronger relationship occurring with juveniles.

4. Population dynamics

The previous section discussed a sequence of increasingly simple models of growth and reproduction in individual Daphnia. The simplest of these, the stage-structured model, might appear absurdly over-simple; we included it because it opens the way to using a particularly convenient presentation of population dynamics involving delay-differential equations with state-dependent time delays (Nisbet & Gurney 1983; Nisbet 1997). Table 2 contains the equations for a size-structured model constructed according to this recipe, with individual dynamics given by the stage-structured model (McCauley et al. 2008).

Table 2.

Stage-structured Daphnia population model. For further details, see the electronic supplementary material to McCauley et al. (2008).

state variables
X(t)	food abundance (mgC l−1) at time t
J(t)	number of juvenile Daphnia at time t
A(t)	number of adult Daphnia at time t
τ (t)	juvenile stage duration for individual maturing at time t
balance equations
additional relationships
	juvenile through stage survivorship
	juvenile development condition (determines τ (t))
functions
	resource growth function
	juvenile ingestion function
	adult ingestion function
parameters
q	maximum per capita resource growth rate (d−1)
K	resource-carrying capacity (mgC l−1)
IJ	maximum ingestion rate of juveniles (mgC d−1)
IA	maximum ingestion rate of adults (mgC d−1)
Xh	half-saturation constant in the functional response (mgC l−1)
χ	proportion of available carbon partitioned to reproduction (dimensionless)
γ	conversion of available carbon into number of new offspring (dimensionless)
σJ	conversion of ingestion into available carbon for juveniles (dimensionless)
σA	conversion of ingestion into available carbon for adults (dimensionless)
μJ	parameter characterizing juvenile mortality (d−2 mgC−1)
μA	adult mortality rate (d−1)
w	carbon gain required for a juvenile to mature into an adult (mgC)

One immediate calculation is possible with this model: the demography of a population at equilibrium (Gurney et al. 1996). With parameters taken from the fits of our stage-structured representation of individual growth and reproduction (figure 4), and an estimated strength of the food dependence of juvenile and adult mortality from the electronic supplementary material, we estimate the juvenile stage duration to be around 37 days. We compared this with a previous independent estimate that used data from the ‘artificial cohort’ experiments with non-dynamic food described above; for this size range, the calculated stage duration was 35–40 days (McCauley et al. 2008, fig. 4).

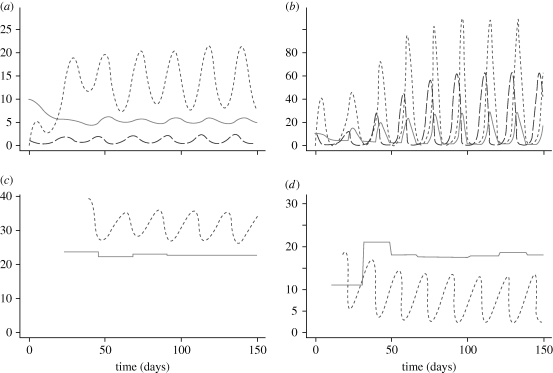
We then considered dynamic food with logistic dynamics as in table 2. The model has a range of levels of prey enrichment (characterized by the carrying capacity, K) over which multiple periodic attractors are found (Nelson et al. 2007; McCauley et al. 2008; Ananthasubramaniam et al. in press). Examples of small- and large-amplitude cycles are shown in figure 5. A striking, and testable, property of the two attractors is the relationship of the cycle period to the juvenile development time—also illustrated in figure 5. Individuals in populations executing the small-amplitude cycles grow slowly, with the juvenile stage duration being longer than the cycle period. There is more variation in the stage duration for individuals executing the large amplitude (prey escape), but, with our parameter values, it is typically shorter than the cycle period.

Figure 5.

(a,c) Small-amplitude cycles and (b,d) large-amplitude cycles in the Daphnia population model of table 2. Populations are in (a,b). (c,d) The relationship between instantaneous juvenile stage duration and an estimate of the cycle period for each type of cycle. (a,b) Long-dash line, F×100; short-dash line, juvenile; solid line, adult. (c,d) Dashed line, stage duration; solid line, cycle period.

In summary, a population model based on our simplified, stage-structured representation of the energetics of growth, reproduction and mortality captures key features of the qualitative dynamics, and some quantitative aspects of the observed dynamics of interacting Daphnia and algal populations.

5. Discussion

The immediate ‘take-home’ message from our research on Daphnia is that population models with a single i-state (size) and two life stages (juvenile and adult) are consistent in many respects with the physiological performance of individuals, and are adequate to describe even rather complex population dynamics. Thus, our research offers empirical support for the growing use of stage-structured models in population ecology. This is particularly important for research on multi-species interactions that demands minimal representations of any one species. For example, de Roos, Persson and collaborators have made fundamental contributions to our understanding of marine fisheries with the aid of such models (Persson et al. 2007; de Roos et al. 2008; Van Leeuwen et al. 2008). Size- and stage-structured consumer–resource models also represent a possible focus for some general ecological theory. They neglect many aspects of metabolic organization within organisms, but have a well-defined mathematical structure that allows some very general mathematical analyses that unify much previous theory based on specific models. Diekmann et al. (2010) make a major contribution to this unification through work that is in part motivated by previous efforts to model Daphnia dynamics.

There is also growing evidence that size-structured models will lead to new fundamental insights in community ecology. Again, we highlight one example, the work of K. Andersen and collaborators on size-structured communities (e.g. Andersen & Beyer 2006). By characterizing species by their asymptotic size, an approach also used by Kooijman in the theory of body-size scaling relations (Kooijman 2000, 2010), they developed a new theory on marine size spectra whose origins have been a long debated theme in marine macroecology.

In short, if we regard a DEB or bioenergetic model as primarily a ‘regression’ model connecting organismal performance to the history of its environment, our work suggests that there are many circumstances where the regression relation can be rather simple, with the unobservable variables that feature in standard DEB theory being unnecessary. We still achieve considerable generality with this approach as size-structured models invoke the most basic physiological features at the heart of DEB theory (feeding, respiration, strong homeostasis). Our Daphnia models and the fish models of de Roos and collaborators described above differ primarily in parameter values—again a key principle of DEB-based theory.

There are of course ecological situations where the simplifications that lead to the simplest stage- or size-structured population models are inappropriate. The most common missing ingredient is some explicit representation of reserve dynamics, a central feature of DEB theory. Many populations experience strong seasonal fluctuations in temperature and/or food availability, and for such situations, standard DEB and its extensions (e.g. Pecquerie et al. 2009) are appropriate. Likewise, standard DEB theory seems the natural approach to describing systems with internal symbionts (e.g. Muller et al. 2009) or population dynamics involving parasites that subsist on reserves (Hall et al. 2009).

In addition, phenomenologically based DEB models have two serious, ecological inadequacies when compared with Kooijman's DEB theory. The most striking is that only Kooijman's model leads to a theory of body-size scaling relations, thereby offering not only a compact representation of individual physiology, but the potential to predict parameters for one species from measurements on others. This is a critical issue, as the type of detailed study reported here for Daphnia can only be performed for a handful of species. For example, one of us recently studied a phenomenological model of bioenergetics and toxicant accumulation in the Northern Right Whale (Klanjscek et al. 2007). Generalizing the findings of this paper to other marine mammal species required a DEB-based analysis (Noonburg et al. 2010). The second serious limitation of more empirically based DEB models is the lack of an obvious way to connect properties of dissimilar life stages, in particular embryos versus feeding stages; that is, we cannot construct empirically based, complete life cycle, phenomenologically based DEB models.

Evaluating these two aspects of simpler DEB models should be a high priority for theoretical ecologists interested in using DEB theory. Each relates to core assumptions of Kooijman's DEB theory that can only be indirectly tested. The body-size scaling relations require very strict adherence to the assumptions (defined clearly by Sousa et al. 2008) regarding partitioning of biomass into structure and reserves, assumptions that are sometimes relaxed, at least implicitly, by DEB modellers. Complete life-cycle models rely on the concept of maturity and on conservation of parameter values among life stages. Figuring out ways of experimentally challenging these assumptions must be a high priority. If they survive, then Kooijman's DEB model will have greatly enhanced credibility as being far more than a regression.