Influence of weather conditions on the flight of migrating black storks

Abstract

This study tested the potential influence of meteorological parameters (temperature, humidity, wind direction, thermal convection) on different migration characteristics (namely flight speed, altitude and direction and daily distance) in 16 black storks (Ciconia nigra). The birds were tracked by satellite during their entire autumnal and spring migration, from 1998 to 2006. Our data reveal that during their 27-day-long migration between Europe and Africa (mean distance of 4100 km), the periods of maximum flight activity corresponded to periods of maximum thermal energy, underlining the importance of atmospheric thermal convection in the migratory flight of the black stork. In some cases, tailwind was recorded at the same altitude and position as the birds, and was associated with a significant rise in flight speed, but wind often produced a side azimuth along the birds' migratory route. Whatever the season, the distance travelled daily was on average shorter in Europe than in Africa, with values of 200 and 270 km d⁻¹, respectively. The fastest instantaneous flight speeds of up to 112 km h⁻¹ were also observed above Africa. This observation confirms the hypothesis of thermal-dependant flight behaviour, and also reveals differences in flight costs between Europe and Africa. Furthermore, differences in food availability, a crucial factor for black storks during their flight between Europe and Africa, may also contribute to the above-mentioned shift in daily flight speeds.

1. Introduction

The evaluation of factors influencing migratory routes and patterns is a great challenge in animal migration research. A recent movement ecology model (MEM) now gives us the possibility to evaluate the roles played by different factors, both external (turbulence, horizontal winds and topography), and internal ones (heart rate), as well as the influence of present state (altitude, speed) and past behaviour in determining the navigation and movement of soaring migrants (Mandel et al. 2008; Nathan et al. 2008). The mechanisms of soaring flight (including phases of glide and flapping) influence the energy budget of birds (Welham & Ydenberg 1993; Hedenström & Alerstam 1995). The efficiency of this specific type of flight (Norberg 1996), where movement is achieved by the use of air currents, is obviously linked to a lower use of the flight muscles and a minimization of mechanical work. Energy expenditure may be as much as 23 times the basal metabolic rate in birds using intensive flapping (Tatner & Bryant 1986) compared with 1.8 times in birds that only use gliding (Utter & Lefebvre 1970; Adams et al. 1986). Moreover, flight energetic models estimate energetic costs to be low in soaring birds when taking advantage of wind conditions (Pennycuick 1989; Weimerskirch et al. 2000). Similarly, studies on bird migration dealing with meteorological influences on migratory direction, flight speed and departure date have identified wind as an important weather component (Richardson 1978; Meyer et al. 2000; Barriocanal et al. 2002; Weimerskirch et al. 2002; Liechti 2006; Åkesson & Hedenström 2007). Tailwinds can minimize both the time and energy birds allocate to migration (Houston 1998). For example, it has been suggested (Åkesson & Hedenström 2007; Weber & Houston 1997) that tailwind is a prerequisite for successful migratory travel in several species. Flight speeds recorded in small passerine birds and soaring birds flying without favourable wind conditions range from 25 to 40 km h⁻¹, and between 60 and 70 km h⁻¹ for Anseriformes (Pennycuick 1972, 1975, 1989; Alerstam 1976; Porter et al. 1983; Tsovel & Allon 1991; Spaar & Bruderer 1996; Bruderer et al. 1999; Shamoun-Baranes et al. 2003a). With the help of strong tailwinds, flight speeds can reach up to 180 km h⁻¹ in Ciconiiformes (mainly Ardeidae) (Liechti & Schaller 1999). This information, however, pertains to migratory characteristics recorded at a few points along the migratory path. It would be of greater interest to evaluate how far such meteorological parameters have an impact on the entire migration pattern as shown by Shamoun-Baranes et al. (2010) in red knots (Calidris canutus canutus). Satellite tracking allows the collection of detailed information on complete migration routes, travel time, stopovers and wintering sites (Fuller et al. 1998; Meyburg & Meyburg 1999; Berthold et al. 2001; Hake et al. 2001; Alerstam et al. 2006; Nathan et al. 2008). Once these data have been combined with ambient temperature, wind, plant phenology or latitude, they can be used to build models for forecasting migratory characteristics (Klaassen et al. 2004; Marra et al. 2005; Bauer et al. 2008), such as flight speed (Shamoun-Baranes et al. 2003b) or flight altitudes (Shamoun-Baranes et al. 2003c) in soaring birds.

The utilization of the MEM in a migration study on turkey vultures (Cathartes aura) supports the hypothesis that proximate route choices are influenced by external meteorological and topographic factors (rugged terrain) (Mandel et al. 2008). Thermal convection (upward movement of a parcel of air to a higher altitude) can be a second possible factor influencing flight speed (per hour) and direction, altitude and daily distance, especially in the larger soaring migrants (some Accipitriformes and the Ciconiiformes). These birds generally prefer days with strong updrafts for migration (Shannon et al. 2002; Shamoun-Baranes et al. 2003a,c). Several studies have already described the use of thermals and other emerging air drafts by medium- and large-sized birds to save energy, followed by gliding in the desired direction after reaching an optimal altitude (Pennycuick 1972; Hopkins et al. 1975; Leshem & YomTov 1996; Shannon et al. 2002; Shamoun-Baranes et al. 2003a).

In order to evaluate how birds can take advantage of both wind and thermal convection over the totality of migration travel, it is first necessary to understand the flight characteristics and predict the migration departure, the altitude reached and so on. Two large soaring species, the white stork (Ciconia ciconia) and the black stork (Ciconia nigra), are both suitable models for this scientific problem. Their migratory route is situated between western Europe (breeding area) and West Africa (wintering ground) (Hagemeijer & Blair 1997; Ferrero & Pizarro 2003), migrating via either the Gibraltar or Bosporus straits, as shown by direct observation, tag recovery and more recently by satellite telemetry (Hancock et al. 1992; Elphick 1995; Peske et al. 1998; Bobek et al. 2003, 2008; Jadoul et al. 2003). To estimate how the flight characteristics of the black stork can be modulated by meteorological parameters, we analysed the influence of wind azimuth and/or thermal energy on three migratory flight characteristics: daily distance, flight speed and altitude. We compared results for autumn and spring migration and for migration over Europe and Africa. We formulated the two following hypotheses: (i) speed and direction of wind has a strong influence on the flight speed of storks; (ii) thermal convection mainly influences the altitude of birds and also affects their flight speed, although to a lesser degree.

2. Material and methods

Our study was conducted on 16 black storks (10 adults or potential breeders and six sub-adults/juveniles or non-breeders) captured using gin traps and cage traps placed on streams where storks were feeding (Chevallier et al. 2008) in Europe (France, n = 13 and Belgium, n = 2) and in Africa (Burkina Faso, n = 1) between 1998 and 2006. The potential breeder is an individual reaching sexual maturity, but we do not know if this bird bred during the study period. The effective breeder is an individual we are sure has bred during the study period. The total of 16 birds produced 21 one-way migration journeys (16 in autumn and five in spring). Five birds were tracked for both autumn and spring journeys (table 1).

Table 1.

Movement of 16 black storks observed in 21 migratory paths. PB, potential breeder; N-B, non-breeder (subadult and juvenile). Migration period, departure and arrival of migration. Days of migration correspond to the number of days spent travelling and on stopovers.

storks	migration period	departure	arrival	A; total travel distance (km)	B; migration days	D; travel days	E; mean travel speed (km d−1)
Carole (PB)	18 Sep 1999–7 Oct 1999	France	Mauritania	3930	20	17	231
Claude (PB)	20 Sep 2005–28 Sep 2005	France	Spain	1715	9	5	343
Dany (PB)	18 Sep 2005–4 Oct 2005	France	Mauritania-Mali	4782	17	15	319
Dany (PB)	9 Mar 2005–26 Mar 2005	Mali	France	4882	18	18	271
Elisabeth (PB)	11 Sep–28 Sep 2000	France	Burkina Faso	4932	18	18	274
Jean-Paul (PB)	9 Sep–28 Sep 1999	France	Mali	4480	20	16	280
Joséphine (PB)	25 Sep–15 Oct 2005	France	Sénégal-Mauritania	4189	21	12	349
Joséphine (PB)	14 Mar–26 Mar 2005	Sénégal-Mauritania	France	4115	13	11	374
Joséphine (PB)	14 Mar–26 Mar 2005	Sénégal-Mauritania	France	4115	13	11	374
Guelayé (PBa)	25 Sep–28 Sep 2000	France	Spain	829	4	4	207
Marie (PBa)	21 Sep–16 Oct 1998	Belgium	Sénégal-Mauritania	5535	26	20	277
Marie (PBa)	12 Feb–13 Mar 1999	Sénégal-Mauritania	France	4900	30	24	204
Oasis (PBa)	4 Sep–26 Sep 2000	France	Mauritania	3934	23	23	171
Astérix (PBa)	21 Sep–1 Oct 2000	France	Mali	3795	11	11	345
Aurélia (N-B)	1 Apr–8 June 2004	Burkina Faso	Germany	7305	69	31	236
Aurélia (N-B)	25 July–28 Sep 2004	Germany	Algeria	3572	66	12	298
Camille (N-B)	8 Sep–26 Nov 2005	France	Mali	4619	82	21	220
Daniel (N-B)	4 Sep–9 Oct 1999	France	Burkina Faso	4890	36	20	245
Esco-libure (N-B)	8 Sep–19 Sep 1999	Belgium	Mauritania	3634	12	12	303
Gérard (N-B)	1 Oct–24 Oct 1998	France	Mali	4636	24	23	202
Gérard (N-B)	2 Apr–8 May 1999	Mali	France	4190	37	22	190
Vincent (N-B)	2 Oct–12 Oct 2006	France	Spain	1240	13	7	177
total mean				4100 ± 314	27.1 ± 4.5	16.3 ± 1.5	262.6 ± 13.4
mean excluding five birds without stopovers				4273 ± 357

^aEffective breeder.

(a). Satellite platform deployments

The birds were equipped with a satellite platform transmitter PTT (North Star Science and Technology, King George, USA, unit; weight ranging from 75 to 110 g for ARGOS PTT, n = 13 individuals; from 45 to 70 g for Solar-GPS PTT, Microwave Telemetry, Columbia, USA, n = 3 individuals). All PTTs were encased in a backpack and attached as high as possible on the stork's back with a Teflon ribbon harness in order to avoid feathers covering solar panels. The Solar-GPS and ARGOS PTTs were programmed to collect data every hour during daylight (from 05.00 to 21.00 h, local time) and upload the data every 72 h via Telnet. The number of locations recorded with Solar-GPS PTTs was higher than with ARGOS PTTs. A total of 1524 ARGOS locations including 70 ± 17 ARGOS locations/bird and 204 ± 70 Solar-GPS locations/bird were recorded during 384 cumulated days for all birds (24 ± 4 days per bird). The accuracy for the Solar-GPS location was ±10 m (as verified in the field in Burkina Faso and Ghana by means of a manual GPS Garmin Etrex Venture). The ARGOS system classified the location accuracy into several categories. Standard location classes (LC) are defined from highest to lowest quality location estimate codes as follows: LC 3 (estimated accuracy of 150 m), LC 2 (between 150 and 350 m) and LC 1 (between 350 and 1000 m), LC 0 (1000 m). LC A, B and Z location estimates have failed specified quality assurance tests and therefore provide no location accuracy estimation (CLS/Argos 1996). When the location estimates from LC 3 were not available for a period of more than 24 h, the estimates from LC 2-1-0 were used. The accuracy for the ARGOS PTT was ±150 m for the best ARGOS location (LC 3, CLS/Argos 1996). Location estimates from LC A, B and Z were not used for analysis. The individual locations were mapped using Geographical Information Systems, Mapinfo Professional v. 8.0 (2005) and Arcview GIS v. 3.1 (1998).

(b). Flight parameters

The daily distance travelled (km d⁻¹) was defined as the distance travelled between two successive night locations. For birds tagged with ARGOS PTT showing few locations during daily flight, we used a linear interpolation (with Matlab) in order to obtain hourly locations. This allowed us to combine the hourly ARGOS locations with weather data.

The distance travelled is established using the hourly step time (km h⁻¹), i.e. a straight line is computed linking two locations (plan projection) for each hourly location. The distance of this straight line is then corrected by taking into account the deformation (Earth rotundity) of this projection to obtain a ‘spherical distance’ (SIGOGNETRACK of Mapinfo Professional v. 8.0 (2005)). Night locations were calculated as the mean of all locations obtained between 18.00 and 4.00 h GMT. When no location was obtained during this period, we extended the period to 2 h before 18.00 h and after 4.00 h. The daily distance was defined as the sum of distances travelled over 24 successive hours. We used the software SIGOGNETRACK (Géo-Hyd (c) Société 2005) for tracing and calculating daily courses during the migration.

Flight altitude can only be obtained by the use of GPS PTT. This concerns three birds. Flight altitude was calculated by subtracting the local relief altitude from the absolute altitude above sea level using a field numerical model of Europe and Africa with Vertical Mapper 3.1 (spatial analysis and display software, Mapinfo Professional v. 8.0 (2005)), hence obtaining relative altitude with cell spatial resolution of 600 m.

Hourly headings, relative to track direction (relative to ground), were calculated using hourly segments in Matlab software (Matlab 5.3 2008) for a period of 9 h (assuming that the duration of active flight was between 10 and 18 h).

To compare the speed and distance of migration above Europe and West Africa, two groups of data were constituted: Europe, with data from breeding sites in France and Germany to Gibraltar (36.00° N/5.61077° W); and West Africa, with data from Tanger (35°78 N, 5°8 W) southward up to known wintering sites in Burkina Faso (11.00° N/1.1° W).

(c). Meteorological data

Several meteorological variables were extracted from the European Center for Medium-Range Weather Forecasts (ECMWF) reanalysis data archives. These data were provided by METEO FRANCE, Paris, France (DIR/Nord-Est, France). The datasets were based on quantities analysed or computed within the ERA-40 data assimilation scheme or from forecasts based on these analyses. These data were given for every 6 h (00.00, 06.00, 12.00 and 18.00 h UTC) with a spatial resolution of 2.5° latitude by 2.5° longitude global grid. They were processed in Matlab before being compared with track data. The average distance between two grid locations was approximately 100 km. We built a linear extrapolation from the four nearest model grid points. The program made a spatial and hourly linear interpolation to determine the weather parameter at each GPS or Argos point. For U and V in particular, we made a vectorial interpolation allowing us to find the azimuth and amplitude of winds at the location and time of each recorded bird position.

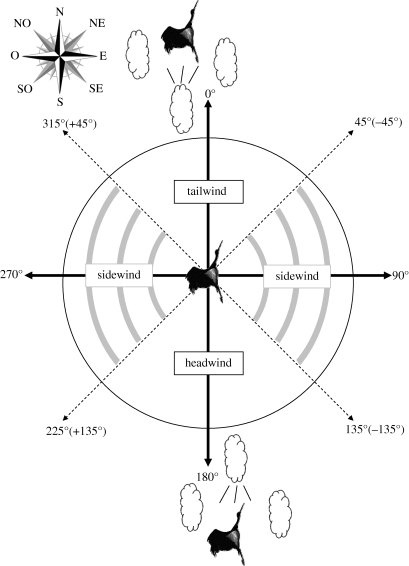
The 850 mb U and V wind variables (wind speed along the X- and Y-axes, respectively) were used to calculate a head/tailwind component and a sidewind component. For the analyses of wind influence on bird flight, the tail and headwind component as well as the sidewind component were calculated in relation to the mean flight directions between two points. Tailwinds were considered as positive values and headwinds as negative values. Wind directions +/− (45–135°) relative to the flight direction were considered as sidewinds (figure 1). Wind direction (°) and wind speed (m s⁻¹) were measured at different altitudes (10, 110, 988, 1500 and 3000 m) and were selected at the same time and position as the satellite-tracked birds to test the influence of wind on bird flight. To obtain thermal energy values, we calculated temperature differences between the modelled data at given pressure levels of 1000, 925, 850 and 700 mb, corresponding to standard atmospheric condition values of 110, 988, 1500 and 3000 m, respectively. A temperature gradient (°C/100 m) was then calculated for these three pressure levels. The mean of these three values gave an estimate of the temperature gradient for the position of each bird, their values ranging from 0 to almost 1. These values were then grouped into four thermal energy classes, from the lowest class 1 (less than 0.5°C/100 m), through class 2 (0.5–0.6°C/100 m) and class 3 (0.6–0.8°C/100 m) to the highest class 4 (greater than 0.8°C/100 m). For example, if T at 1000 mb = 10°C and at 850 mb = 8°C, the gradient is then (8–10)/(988–110 m)*100). A difference of 0.8°C between two altitudes (100 m) corresponds to the threshold of high thermal energy.

Figure 1.

Schematic view of wind azimuth in the following example: a black stork flying in a south–north direction.

(d). Statistical analyses

Analyses of variance (denoted F) were followed by post hoc Bonferroni tests (two-tailed). To take into account the fact that five birds were followed in both autumn and spring, mixed linear models (denoted mixed F) were performed to test the monthly and continent variations in different parameters. Firstly, statistical models incorporated distance and duration of migration (travel days) as dependent variables (table 1), and seasons (spring/autumn) or continent (Europe/Africa) were included as independent variables. Secondly, flight characteristics (hourly flight speed and altitude) and occurrence of thermal energy were included as dependent variables and hours (24 h) were included as independent variables. Wind directions at an angle of +45° to +135° or −45° to −135° in relation to flight direction were considered to be sidewinds (figure 1). Angles range between +45° to −45° for tailwinds, and +135° to −135° for headwinds. To test the influence of atmospheric conditions on the flight characteristics of birds, we carried out regression analysis with the determination coefficient (r²). All statistical analyses were performed with SPSS, v. 16. Data values are presented as means ± s.e.

3. Results

(a). Departures, arrivals and flight direction

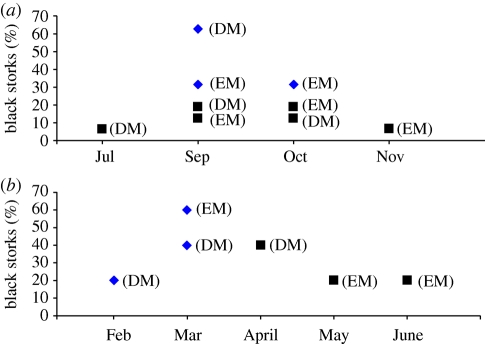
Autumn migrations from Europe to Africa began in September for potential breeders and in September and October for non-breeders (table 1 and figure 2). The majority of birds from both groups (94%) arrived in Africa between September and October. They were recorded in Mauritania (457/1524 locations, or 30%), Mali (381), Burkina Faso (229), Spain (229), Senegal (152) and Ghana (76). Departures for spring migration from Africa occurred from February to April and birds arrived in Europe from March to June. Departure and arrival dates were seen to be earlier for breeding than for non-breeding birds.

Figure 2.

Departure and end of migration (Europe–Africa–Europe). (a) Autumnal migration; (b) spring migration. DM, departure of migration; EM, end of migration. Filled diamonds, potential breeders; filled squares, non-breeders.

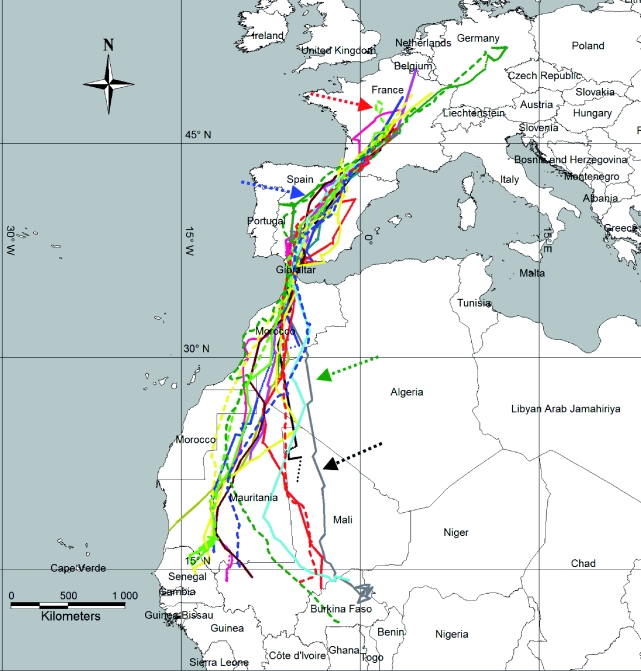
During autumn migration, storks in Europe maintained a direct SSW course that was initiated before crossing the Eastern Massif Central in France. In Africa, the storks first flew south across the Moroccan Atlas (figure 3), i.e. through the Ouanoukrim and Toubkal mountains. At the western edge of Algeria, the storks separated and continued in different directions (SSE and SSW) depending on their wintering destination (Senegal, Mauritania, Mali, Burkina Faso, Niger). During spring migration, each stork in Africa followed a NW flight path. Black storks reached the Strait of Gibraltar, flew NNE or NE to attain the mid-west of Spain, then continued either northward or NNE up to Germany.

Figure 3.

Autumn (September–November, solid line) and spring (February–June, dashed line) migration routes of the 16 black storks between Europe and Africa (autumn, solid line; spring, dashed line). Average wind azimuths (dashed line) are added on the map. Red dotted line, wind azimuth in spring (Europe); blue dotted line, wind azimuth in autumn (Europe); green dotted line, wind azimuth in autumn (Africa); black dotted line, wind azimuth in spring (Africa).

(b). Distance and duration of migration

The distances travelled by storks per day were not significantly different between autumn and spring, whether all individuals were considered together (265 ± 15 versus 258 ± 33 km d⁻¹, n = 16 versus 5, mixed F_1,19 = 0.05, p > 0.05) or in an intra-individual comparison (289 ± 25 versus 258 ± 33 km d⁻¹, respectively, mixed F_1,8 = 0.59, n = 5, p > 0.05). Similar results were found for the travel days (excluding stopover) in Europe and Africa; no significant difference was found between seasons for both global analysis of all birds (14.7 ± 1.5 versus 21.2 ± 3.3 days, mixed F_1,19 = 3.14, p > 0.05) and intra-individual comparison (16.4 ± 2.2 versus 21.2 ± 3.3 days, mixed F_1,8 = 1.458, p > 0.05). We therefore pooled autumn and spring data for the following analyses.

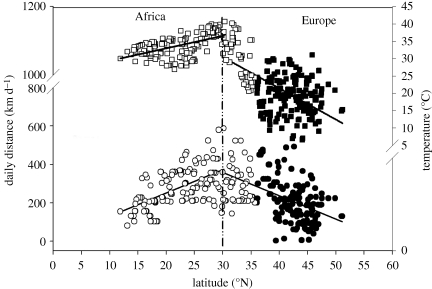
During their migration, the 16 birds travelled a mean total distance of 4100 ± 314 km (n = 21 tracks) for a mean effective migration time of 27.1 ± 4.5 days, corresponding to a mean daily travelled distance of 264 ± 13 km d⁻¹ (table 1 and figure 3). The distance flown above Europe was significantly shorter than above Africa (1699 ± 163 versus 2791 ± 172 km, mixed F_1,34 = 21.31, p < 0.001), while the time spent in flight above Europe tended to be shorter than above Africa (8.7 ± 0.7 versus 10.9 ± 0.8 days, mixed F_1,34 = 4.07, p = 0.052). In addition, the storks had shorter daily travel distances in Europe compared with Africa (200 ± 15 versus 270 ± 16 km d⁻¹, mixed F_1,34 = 10.38, p < 0.001). Interestingly, daily travelled distance and latitude were negatively related while travelling in Europe but positively related in Africa (figure 4). Consequently, the maximum daily travelled distances occurred around the Strait of Gibraltar, with a value of 588 km d⁻¹ on the African side and 493 km d⁻¹ on the European side.

Figure 4.

Relationship between latitude and daily travelled distance or temperature above Africa (respectively, slope = 12.12, r² = 0.31, p < 0.001; slope = 0.36, r² = 0.29, p < 0.001) and Europe (respectively, slope = −12.10, r² = 0.28, p < 0.001; slope = −0.90, r² = 0.35, p < 0.001). Filled and open circles, daily distance; filled and open squares, temperature.

(c). Flight characteristics and atmospheric conditions

Mean flight altitude and flight speed values for the entire migration of the three birds tracked with GPS PTT were found to be 495 ± 50 m above surface level and 33.0 ± 1.7 km h⁻¹, respectively. Assuming a similar flight altitude for the remaining birds tracked with ARGOS PTT, we selected wind speed and direction at an altitude of 110 m (the closest to 495 m of the altitudinal meteorological measurements available) and related those to flight speed and azimuth for all birds. We found no relationship between flight speed and wind speed, whatever the wind direction (r² = 0.001, p > 0.05, n = 1801 hourly points cumulated for the 16 birds) during the entire migration. Black storks flew most of the journey with sidewinds (67.3% of flight time), regardless of migratory season or continent and no relationship was found between bird flight and sidewind (r² = 0.008, p > 0.05, n = 1212 hourly points; figure 3). In the same way, during the rare times birds encountered tailwinds (9%), wind speed did not influence bird flight (r² = 0.09, p > 0.05, n = 163 hourly points). A negative and significant linear relationship was obtained when headwinds were selected (23.6%, r² = 0.10, p = 0.034, n = 426 hourly points).

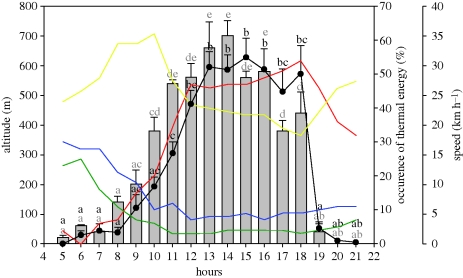
We analysed flight speed per hour and found that the lowest and highest values occurred, respectively, between 6.00 and 9.00 h and between 11.00 and 16.00 h (F_17,683 = 43.477, p < 0.001; figure 5). For each bird, the maximum flight speed (range 47–112 km h⁻¹) occurred above Africa. Similarly, the hourly analysis showed that low flight altitudes occurred between 6.00 and 8.00 h and high flight altitudes between 12.00 and 18.00 h (F_14,537 = 19.776, p < 0.001; figure 5). Flight altitude followed a time pattern similar to that of flight speeds and was, moreover, positively related to flight speed (r² = 0.92, p < 0.001).

Figure 5.

Hourly variations of two flight parameters (means of speed and altitude) for the three black storks tagged with GPS PTT. The statistical analysis is processed independently for migration speed and flight speed. Different letters indicate that the hourly data of migration speed are significantly different after ANOVA (same presentation for data of flight altitude). Four classes of thermal energy, numbered from the lowest (1) to the highest (4), are shown by coloured solid lines. Red line, 4; yellow line, 3; blue line, 2; green line, 1. Grey bars, speed; black line with filled circles, altitude.

The per cent of occurrence of the highest thermal energy varied throughout the day (F_3,1598 = 16.259, p < 0.001), being at its maximum usually between 12.00 and 18.00 h (figure 5). Importantly, hourly flight speed was significantly correlated with the highest thermal energy value (r² = 0.38, p < 0.001; figure 5). Therefore, of all the meteorological parameters investigated here, thermal energy had the highest impact on the daily flight activity of the black stork throughout migration.

4. Discussion

The variability recorded in flight speed during migration has been explained in the white stork by the combination of three factors: prevalence of tailwinds, thermal convection and food availability (Liechti et al. 1996; Shamoun-Baranes et al. 2003a; Klaassen et al. 2008). For the black stork, we will first consider the influence of wind azimuth. Previous studies on other birds have revealed a strong influence of wind azimuth on the direction of migratory flight (Richardson 1990) and speed, when birds follow the wind azimuth (Spaar & Bruderer 1996). It has also been shown that many species tend to select periods of favourable wind azimuth (Richardson 1990). The red-tailed hawk (Buteo jamaicensis) waits for the best time to move over long distances, i.e. when winds are strong (20 km h⁻¹ and more) and blow in the same direction as the route taken by this species. This has a positive impact on the arrival date at wintering areas (Maransky et al. 1997). Alerstam & Hedenström (1998) suggest that wind azimuth could force birds to change their course, even if this means reducing their daily distance. Our data show that headwind reduced the flight speed of black storks but the sidewind, the most frequent wind direction, had no influence on the flight speed of birds. Wind does not therefore seem to be a decisive factor in the daily distance covered by the black stork. Moreover, neither the overall duration, nor mean daily distance seem to differ between the two seasons of migration. However, the small sample size of birds during the spring migration means that we should be cautious about the certainty of this conclusion. This result contrasts with observations in the white stork, where seasonal variations in daily distance have been reported (Berthold et al. 1997, 2001; Van den Bossche et al. 1999). In this species, Shamoun-Baranes et al. (2003b) reported longer daily distances in autumn compared with spring owing to dominant autumnal tailwinds.

The second factor known to affect the characteristics of migration of soaring birds is the prevalence of thermal convection (Leshem & YomTov 1996; Liechti et al. 1996; Shamoun-Baranes et al. 2003a,c). Because wind azimuths were similar in Europe and Africa, the daily distance covered by birds may be altered in a similar manner when flying across these two continents. However, black storks covered a higher daily mean distance in Africa (270 km d⁻¹) than in Europe (200 km d⁻¹). Accordingly, the time thus spent flying over both continents was comparable, despite a much longer distance travelled over Africa than in Europe. In the same way, maximum flight speeds (km h⁻¹) for all individuals were accomplished on the African continent, and there was a net decrease in the mean daily distance of black storks north of latitude 35° N. A higher migration speed in Africa compared with Europe has also been reported for white storks using the eastern migration route (Shamoun-Baranes et al. 2003b). Moreover, we found a coincidence of pattern in black storks, on a daily time scale, between the distribution of thermal convection and the windows of migratory activities. Higher migration efficiency at high altitudes has also been observed for several species of gliders in Africa, including the white stork (Pennycuick 1972; Berthold et al. 1997, 2001; Bruderer et al. 1999). Indeed, the birds can glide for a fairly long period of time at high altitude and therefore be more selective in the use of high thermals (Bruderer et al. 1999). We suggest that thermals (linked to temperature), which are much more numerous and powerful in latitudes south of 35° N, are probably the best explanation for the fact that the highest daily distance (km d⁻¹) and flight speed (km d⁻¹) were recorded in the African zone.

Food availability may also play a role in the distances travelled by migrating birds (Klaassen et al. 2008). The scarcity of suitable feeding places for the black stork, a fish-eating species (Chevallier et al. in press), could further explain the longer distances travelled daily when crossing the desert areas of West Africa. A sharp decrease has been observed in food sources in West Africa over recent decades because of climate changes and desertification (Dallinga & Schoenmakers 1987).

The use of satellite tracking has greatly improved our knowledge of how meteorological parameters influence the migratory performances of storks. It has provided new insights on behavioural flapping flight performed by birds in different environmental conditions. We have demonstrated the role of temperature on flight altitudes chosen by black storks, but information on the consequences of energy expenditure on birds flying at these altitudes is not yet available. Future studies may be able to provide this information through the use of a combination of satellite tracking and measurements of energetic costs of locomotion (e.g. by accelerometry).