Excavated substrate modulates growth instability during nest building in ants

Abstract

In social insects, the nests of the same species can show a large difference in size and shape. Despite these large variations, the nests share the same substructures, some appearing during nest growth. In ants, the interplay between nest size and digging activity leads to two successive morphological transitions from circular to branched shapes (budding along the perimeter of the circular cavity and tunnelling of the galleries). Like several other self-organized collective behaviours, this phenomenon, as well as the entire nest-digging process, is thought to be modulated by environmental properties. The present study investigates the effect of excavated substrate on the nest morphogenesis and the morphological transitions by using two materials with different cohesions. Here, we show that the two morphological transitions occur more frequently with a cohesive substrate than with a granular one: 96 per cent of cohesive experiments showed both transitions, whereas only 50 per cent did in granular experiments. We found that transitions and excavation cessation follow area–response thresholds: the shape transitions take place and the digging activity stops when the dug area reaches the corresponding threshold values. The shape transition thresholds are lower with the cohesive substrate and that of stopping digging is independent of nest shape and material. According to simulations, the experimental frequencies of transitions found their origin in the competition between transitions and activity cessation and in the difference between the transition threshold values of each substrate. Our results demonstrate how the substrate properties modulate the collective response and lead to various patterns. Considering the non-specific mechanisms at work, such effects of substrate coarseness have their counterparts in various collective behaviours, generating alternative patterns to colonize and exploit the environment.

1. Introduction

Social insects are among the most impressive builders in nature considering the difference in scale between the nest and the insects, and the long lifetime of the construction compared with that of their inhabitants (Grassé 1984; Hansell 2005). These nests are composed of basic building modules and have reached a high degree of complexity in animal architecture (Theraulaz et al. 2003). The different patterns are intimately linked to various functions (Turner 2000; Hansell 2005) such as thermoregulation (Seeley & Heinrich 1981; Jones & Oldroyd 2007), nest ventilation (Lüscher 1961; Kleineidam et al. 2001), regulation of nest volume according to the colony size (Collins 1981; Tschinkel 2005; Josens & Soki in press), defence mechanisms (Deligne & Pasteels 1982), or even modulation of social interactions (Buhl et al. 2004a,b).

The coordination required to accurately build such complex structures is achieved by efficient mechanisms, such as stigmergy (Grassé 1959; Deneubourg 1977; Theraulaz & Bonabeau 1995; Camazine et al. 2001) or the use of templates (Franks et al. 1992; Bonabeau et al. 1997).

The subterranean nests of ants show a wide diversity of patterns ranging from highly stereotyped structures (Tschinkel 2003, 2004, 2005) to apparently highly disorganized ones (Cassill et al. 2002). However, we have recently shown (Toffin et al. 2009) that a characteristic sequence of events occurs during nest excavation in ants. Two extreme morphologies successively appear through a morphological transition process: an initially rounded and smooth chamber is initially dug before it becomes more irregular as buds appear on the nest walls. Thereafter, some of these buds may develop into lateral galleries. This phenomenon can account for the building of the most basic nest modules and is merely a by-product of digging dynamics and nest growth that does not require any behavioural complexity to occur.

Several studies have highlighted the effect of environment on such self-organized behaviours (Deneubourg et al. 1989; Franks et al. 1991; Bonabeau et al. 1998; Nicolis & Deneubourg 1999; Detrain & Deneubourg 2002; Jeanson et al. 2003; Challet et al. 2005; Colasurdo et al. 2007; Jost et al. 2007; Dussutour et al. 2008). The surrounding characteristics modify the collective pattern by triggering changes in individual responses or even by simply mediating the interaction between workers. Moreover, it is well known that individual behaviours, digging dynamics and therefore nest morphology can be controlled and regulated by various factors that can act as a physical template or feedback over the phenomenon. These factors may be of social (Franks et al. 1992; Franks & Deneubourg 1997; Rasse & Deneubourg 2001; Tschinkel 2004; Buhl et al. 2004a,b, 2005; Toffin et al. 2009), or of environmental origin (Tohmé 1972; Bollazzi et al. 2008).

In this paper, we focus on the effect of the building materials on nest morphogenesis by performing two-dimensional digging experiments using two substrates of different cohesions. We show that substrate cohesion affects the sequence of nest-shape transition and the frequency at which each pattern occurs.

2. Material and methods

(a). Ants

The experiments were performed using the Lasius niger ant, a common monogynous and monomorphic Palaearctic ant species whose collective behaviour, such as foraging and aggregation, have been well described. Typical colony size may vary from thousands to tens of thousands of individuals. Workers are characterized by an age polyethism (Lenoir & Ataya 1983) in which younger ants are brood tenders and may become foragers as they grow older. This is an opportunistic species that can feed on insects (Pontin 1961), but its main food consists of aphids and honeydew (Pontin 1958).

Some nests may be found under plate rocks, but most of them are dug in the soil and can be easily located by the soil crater(s) or mound(s) surrounding their entrance(s). The nest structure mainly consists of two fundamental building blocks (i.e. chambers and tunnels), while the volume of the nest is correlated with colony size (Rasse & Deneubourg 2001).

We used 11 queenless colonies of L. niger species (1500–2500 individuals) collected on the Université libre de Bruxelles campus in Brussels. They were reared under laboratory conditions (20 ± 1°C under a 08.00–20.00 daylight cycle) for at least two months before the experiments, and fed ad libitum with water–sugar solution (1 M) and freshly killed mealworms (Tenebrio molitor).

(b). Digging set-up

The two-dimensional digging set-up consisted of a horizontal closed digging area made of two glass plates (42 × 42 cm) that contained a thin layer of excavated substrate (h = 0.2 cm). The upper face of the digging area contained a central hole, which communicated by means of a vertical tunnel, with a circular arena (ø_tunnel = 1.1 cm; ø_arena = 10 cm).

Two different substrates were used during the experiments: the granular substrate was made up of Brusselean sand (a yellow sand of very fine and homogeneous granularity) and the cohesive substrate was made up of a mix of clay powder and Brusselean sand (respective dry weight proportions of 25 and 75%). Each substrate was moistened with 15 per cent of dry substrate weight in water.

The granular substrate has no to little cohesive strength when wet, cannot be moulded and easily crumbles when dry. On the contrary, the cohesive substrate is plastic when moist and does not crumble, owing to its cohesive strength. During the experiments, no structural collapse in the granular substrate was observed. The digging method of ants is known to change according to the nature of the substrate: in granular soil (sandy soil) workers remove single large grains or clusters of grains by successive grabs with the mandibles (Sudd 1969), whereas in cohesive soil (clay or rain-dampened soil), the shape of the extracted pellets suggests an extraction method with the mandibles more similar to ice cream scooping (Cassill et al. 2002). We characterized both substrates at a microscopic level by estimating pellet size (electronic supplementary material, table S1).

(c). Experimental procedure

Groups of 50 workers were randomly selected from 11 mother colonies 24 h before the experiment began and supplied with food ad libitum during this lapse of time. They were not fed during the whole experiment to prevent them from being engaged in tasks other than nest excavation. Ants were dropped into the circular arena at the beginning of the experiment. Experiments were conducted over a 90 h period and 24 experiments were undertaken using the granular substrate and 25 with the cohesive one. The death rate never exceeded 10 per cent of the group size. After each experiment, the 50 workers were not returned to their mother colony to prevent picking the same ants for different replicates.

(d). Shape characterization

Snapshots of the excavated nest were taken from below under red light (Depickère et al. 2004) every 10 min. Automatic image analysis C++ software was used to compute the nest area (A), perimeter (P) and the circumscribed circle area of the nest (AC) for each snapshot.

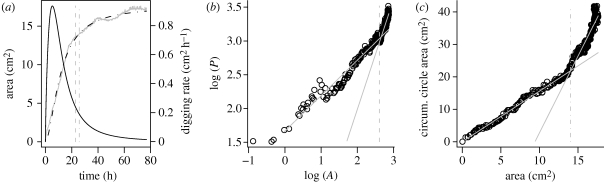
The nest morphogenesis showed morphological transitions that separated the excavation into distinct and successive growth stages (figure 2b,c and electronic supplementary material, figure S1b,c). By different stages, we mean periods of collective growth that qualitatively and quantitatively differed, despite the fact that no environmental change had occurred. The nest shape evolution was described using the relationship between A, P and AC (Pons et al. 1999). The equation A = P^ω describes the transition from a circular and regular nest (ω ≈ 0.5) to a rough and wrinkled shape (ω > 0.5), whereas AC = δ+ γA illustrates the shape transition from a rounded and compact cavity (γ ≈ 1) to a ramified and tunnelled nest (γ ≫ 1).

Figure 2.

Dynamics of excavation and shape transitions in granular substrate (experiment 6). (a) Dynamics of nest excavation, showing evolution of both nest area A (and its fit by equation (3.1), parameters value: α = 1.71, β = 11.59 h, A_M = 17.62 cm²) and rate of digging against time. The two morphological transitions are represented by vertical dashed lines. (b) Characterization of first transition point with the relationship between P and A (ω₁ = 0.52; ω₂ = 1.63; A₁ = 13.54 cm²). (c) Determination of second transition time using scatterplot of A versus AC (γ₁ = 1.56; γ₂ = 4.73; A₂ = 14.03 cm²). (a) Solid grey line, area; dashed-dotted line, fitting equation (3.1); solid black line, digging rate.

Shape transition points were characterized using a linear regression method (Draper & Smith 1981) that splits a global set of values (of size N) into two subsets (of sizes n₁ and n₂ = N−n₁), computes their linear regression parameters and a common standard deviation, according to the following equation:

where a₀ and b₀ are the linear regression line parameters of the first subset (before transition) and a₀ + a₁ = a₂ and b₀ + b₁ = b₂ are those of the second subset (after transition). For the first transition a₀ = 0, b₀ = ω and y = log(P) and x = log(A), for the second transition a₀ = δ, b₀ = γ, y = AC and x = A. Stage is a binary variable whose value is 0 and one for points of the first and second subsets, respectively.

The first standard deviation value is calculated with n₁ = 1. For each subsequent calculation step (as long as n₁ < N − 1), the size of n₁ is increased by adding the next point (in chronological order), this value being removed from the n₂ subset. The optimal nest area at which transition between two morphologically distinct growths occurs is the value of A that minimizes the global standard deviation. Statistical significance of the transition was also tested using an F-test comparing the two alternative hypothesis (i.e. one global set versus two distinct sets of points).

(e). Statistical analysis

The difference between granular and cohesive substrates in linear regression slopes was tested using a previous method (Wonnacott & Wonnacott 1990) with the Substrate as the binary variable according to the experimental group (cohesive: Substrate = 0; granular: Substrate = 1).

All the statistical analyses, including Mann–Whitney, log rank and χ² tests, were conducted using R software (Ihaka & Gentleman 1996) (v. 2.8.1). The significance of the statistical tests was fixed at α = 0.05.

3. Results

(a). Morphological growth

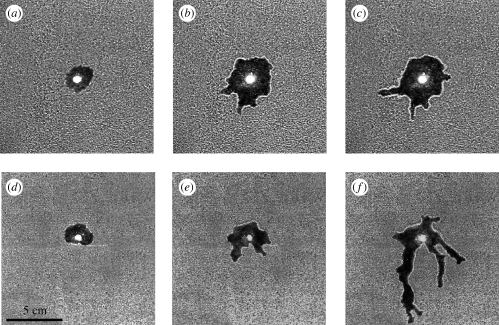
On the basics of the methodology used in our previous work (Toffin et al. 2009), we observed two morphological transitions that separated the excavation into three distinct and successive growth stages (figure 1, see electronic supplementary material video S1V). The first stage was characterized by the excavation of a regular and almost circular main chamber (ω₁ ≈ 0.5 for both materials, figure 1a,d and table 1). When the nest area (A, cm²) reached a value A₁ (first transition), the nest wall abruptly became rougher as ‘buds’ appeared on it, corresponding to the second stage (ω increases and reaches values of ω₂ > 1.0, figures 1b,e, 2b, table 1 and electronic supplementary material, figure S1c). Finally, when the nest area reached a second critical value A₂ (second transition), the main central chamber growth ceased and some of the buds extended, becoming lateral galleries (figure 1c,f). This third and final stage was characterized by the steep increase in γ value corresponding to the extension of lateral tunnels (figure 2c, table 1 and electronic supplementary material, figure S1c).

Figure 1.

Sequences of experimental nest excavation in (a–c) granular (experiment 6) and (d–f) cohesive substrates (experiment 18). Snapshots have been taken during (a,d) first, (b,e) second and (c,f) third stage.

Table 1.

Digging dynamics and nest geometry values for experiments showing the two morphological transitions (granular n = 12, cohesive n = 24).

	mean ± s.d.		Mann–Whitney
	granular	cohesive	U	p
geometry
ω1	0.52 ± 0.09	0.58 ± 0.06	78	0.026
ω2	1.61 ± 0.52	1.14 ± 0.45	216	0.015
γ1	1.76 ± 0.26	2.03 ± 0.55	104	0.188
γ2	7.58 ± 6.45	4.62 ± 3.30	194	0.097
dynamics
A1	11.94 ± 6.13	5.99 ± 2.55	245	<0.001
A2	15.38 ± 6.46	9.47 ± 4.51	236	0.001
R1	0.547 ± 0.535	0.484 ± 0.290	162	0.562
R2	0.222 ± 0.304	0.246 ± 0.205	171	0.379
ρ1	0.063 ± 0.079	0.096 ± 0.065	101	0.156
ρ2	0.016 ± 0.022	0.033 ± 0.037	92	0.084

These transitions occurred in both substrates but the material affected their frequency of occurrence: 96 per cent of cohesive experiments showed both transitions (table 2), whereas only 50 per cent did in granular experiments (table 2). In this last substrate, 21 per cent of the experiments showed only the first transition, the remaining 29 per cent showed no transition at all. χ² analysis assessed that the occurrence of both transitions was not independent of the substrate (χ² = 11.038, d.f. = 1, p = 0.00089, table 2c). Moreover, areas of the first (A₁) and second transition (A₂) were statistically smaller in the cohesive substrate than in the granular substrate (table 1). These results show the higher instability of the isotropic growth in the cohesive material, which leads to sooner and more frequent selection of punctual digging sites and their subsequent development into lateral galleries.

Table 2.

Occurrence of transitions according to substrate (number in parenthesis stands for the percentage of each case). (a,b) Tables showing the number of experiments showing no, one or both morphological transitions. (a) Table for granular substrate (n = 24). (b) Table for cohesive substrate (n = 25). (c) Tables (a,b) have been merged into one 2 × 2 contingency table (n = 49) to remove sampling zeroes and test with χ² analysis, the independence of presenting both transitions against the substrate (χ² = 11.038, d.f. = 1, p = 0.00089, occurrence of both transitions is not independent of substrate).

(a) granular
second transition	first transition
	yes	no
yes	12 (50%)	0 (0%)
no	5 (21%)	7 (29%)
(b) cohesive
	first transition
second transition	yes	no
yes	24 (96%)	0 (0%)
no	1 (4%)	0 (0%)
(c)
	transitions
substrate	both	else
sand	12 (50%)	12 (50%)
clay	24 (96%)	1 (4%)

When the only experiments that showed both transitions were considered, it was found that the final nest sizes (A_M) were not statistically different between granular and cohesive groups (granular: A_M = 20.32 ± 7.82, n = 12; cohesive: A_M = 15.49 ± 6.19, n = 24; Mann–Whitney: U = 195, p = 0.090).

(b). Excavation dynamics

Whatever the excavated substrate, the nest dynamics of excavation were similar to what has been previously described (Rasse & Deneubourg 2001; Buhl et al. 2005; Toffin et al. 2009) (figure 2a and electronic supplementary material, figure S1a). Excavations began with a fast and amplified increase in nest area (A), during which the digging rate (R = dA/dt, cm² h⁻¹) reached its maximal value (R_M). The excavation rate then decreased until the digging ceased when the nest area had reached its maximal value (A_M). The nest area was described at any given time by the following equation:

3.1

where A_Max is the plateau value of the nest area (the value A_M = 0.95A_Max and its corresponding value t_M was used for this analysis), t (hours) is the experimental time, α stands for the cooperation level between workers (cooperativity, i.e. positive feedback, increases with α) and β (hours) is the half-digging time (A = 0.5A_Max). Fitted values of α (granular: 1.30 ± 0.36, n = 24; cohesive: 1.24 ± 0.23, n = 25; Mann–Whitney, U = 308, p = 0.882) and A_M (granular: 16.63 ± 7.45, n = 24; cohesive: 15.52 ± 6.06, n = 25; Mann–Whitney, U = 317, p = 0.744) were not statistically different between substrates. However, the cohesive condition showed higher values of β (granular: 11.07 ± 5.53, n = 24; cohesive: 14.50 ± 4.86, n = 25; Mann–Whitney, U = 179, p = 0.015) which highlighted a slower digging rate in this substrate. Whatever the substrate, the distribution of A_M was independent of time, with no (or weak) correlation being found between A_M and β or t_M.

(c). State change model

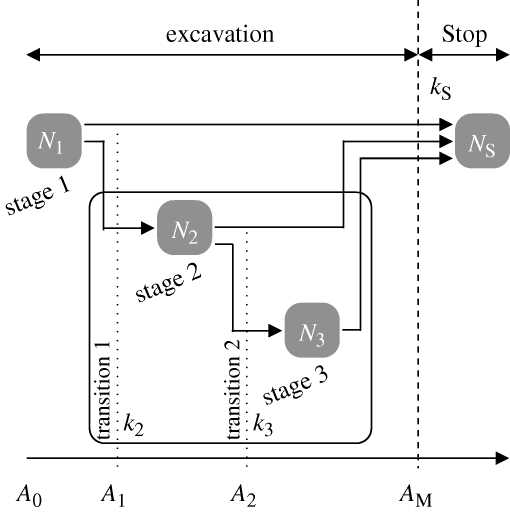
On the basis of our results and previous works, a model was developed to describe the dynamics of building and the coupling between state transition and nest-size regulation. Each experiment was in one of the four possible states (figure 3):

• — still digging and in the first growth stage (state 1, N₁), initial state of every experiment;

• — still digging and in the second growth stage (state 2, N₂), first transition has occurred;

• — still digging and in the third growth stage (state 3, N₃), second transition has occurred; or

• — digging activity has ceased (state Stop, N_S), ultimate state of every experiment.

Figure 3.

Decision diagram of the states model. Only the state N_S is mandatory, Stop being the final achievement of each experiment, the other ones (N₁ and N₂) are optional.

The corresponding fractions of the total number of experiments in each state were f₁, f₂, f₃ and f_S. According to the results, passing through states 2 and 3 is not mandatory to reach the state Stop: experiments may stop whether or not morphological transition has occurred. It can thus be supposed that these two events (shape transition and activity stopping) are independent. However, the second transition occurs after the first one. Three sequences may thus be described, only one of them generating the third state (figure 3).

The value of f_i decreases at a rate proportional to the probabilities k_S to stop digging and for i = 1 and 2 to the probability k_i+1 to shift from state i to state i + 1 (from state 1 to state 2 and from state 2 to state 3). As regulation of nest volume during excavation has been previously shown (Franks et al. 1992; Franks & Deneubourg 1997; Rasse & Deneubourg 2001; Buhl et al. 2004a,b, 2005) and according to our results, the probability k_S to stop digging depends on the nest size but remains independent of the state. Similarly, k_i (with i = 1 and 2) also depends on the nest size.

At any given area, the change of the different fraction of experiments is governed by the following system of differential equations:

3.2a

3.2b

3.2c

The fraction f of still active experiments decreases as follows:

3.2d

with

and

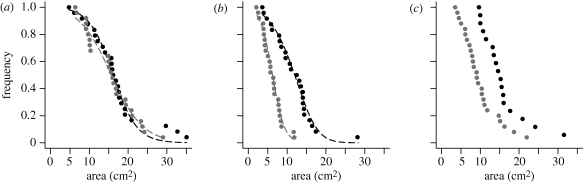
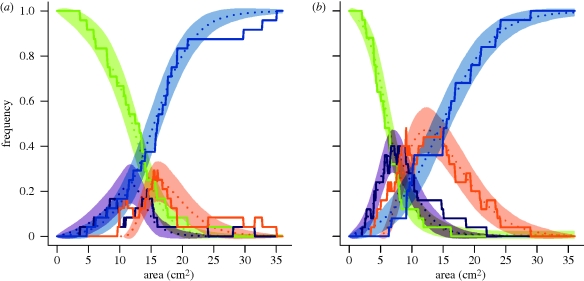
Survival curves of still active experiments in both substrates followed a sigmoidal curve (figure 4a) and were not statistically different (log-rank test: χ² = 0.3, d.f. = 1, n = 49, p = 0.575):

Figure 4.

Survival curve of experiment state in each substrate. (a–c) Points correspond to the experimental values and dashed lines to their nonlinear fitting of the survival curve. (a) Survival curve of still digging experiments (in state 1, 2 or 3). The equation (3.4) fits well the experimental survival in both substrates (granular: η_S = 0.313, c_S = 15.46 cm², n = 24, F_1,22 = 1057.3, p < 0.001, r² = 0.980; cohesive: η_S = 0.239, c_S = 14.61 cm², n = 25, F_1,23 = 753.62, p < 0.001, r² = 0.970). (b) Survival curve of still rounded nests (in first stage, state 1). The equation (3.5) fits well the experimental distributions (granular: η₂ = 0.237, c₂ = 12.74 cm², n = 24, F_1,22 = 1081.5, p < 0.0001, r² = 0.980; cohesive: η₂ = 0.639, c₂ = 5.97 cm², n = 25, F_1,23 = 1745, p < 0.0001, r² = 0.987). (c) Survival curve of experiments still in second stage (state 2). The experimental distributions could not be fitted by equation (3.5). The c₃ and η₃ parameters have been determined by using Monte–Carlo simulations (electronic supplementary material). Black filled circles, granular; grey filled circles, cohesive.

3.3

Replacing f in equation (3.2d) by equation (3.3), it was shown that the probability k_S to stop digging is a threshold function (Mailleux et al. 2000; Sumpter 2006):

3.4

where the parameter c_S corresponds to the threshold area value and η_S stands for the sensitivity to difference between the dug area A and the threshold c_S (η_s is the steepness of the curve).

No statistical difference was observed for η_S (granular: η_S = 0.313; cohesive: η_S = 0.239; t-test: t₄₅ = 1.098, p = 0.278) and the difference between the c_S (granular: c_S = 15.456 cm²; cohesive: c_S = 14.614 cm²; t-test: t₄₅ = 12.504, p < 0.0001) is to be taken cautiously as the distributions of A_M were not statistically different.

Assuming that the probability of transition between state 1 and state 2 is also a threshold function, the integration of equation (3.2a) gives the survival curve of the fraction in state 1:

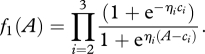3.5

The survival curves for the first stage were different between the two substrates (figure 4b,c; log-rank test: χ² = 22.1, d.f. = 1, n = 49, p < 0.0001) and so were their fitting parameters (granular: c₂ = 12.743 cm², cohesive: c₂ = 5.969 cm², t-test: t₄₅ = 124.03, p < 0.0001; granular: η₂ = 0.237, cohesive: η₂ = 0.639, t-test: t₄₅ = 7.359, p < 0.0001). The survival curves for the second transition were also different between conditions (log-rank test: χ² = 8, d.f. = 1, n = 42, p = 0.005). However, the fitting could not be done for the second transition using the same procedure based on the integration of equation (3.2b). Therefore, the values of η₃ and c₃ were determined with simulations.

(d). Simulations

Simulations were performed based on the equation S1 in the electronic supplementary material. For each substrate, a set of simulations contained a number of replicates equal to the experimental group size (granular: n = 24; cohesive: n = 25).

Simulations were first used to determine the values of η₃ and c₃ (electronic supplementary material). The resulting landscapes showed that for each substrate, the optimal parameter values were c₃ = c₂ and η₃ = 0.95. These indicate that the difference between substrates in the proportion of nests in stage 3 (table 2) was not owing to differences in second transition properties. It was rather a consequence of the area at which the first transition occurred (A₁).

Then, 1000 sets of simulations were launched for each substrate and simulated and experimental distributions of each state were compared. Despite a numerical difference, the proportions of simulated nests showing both transitions reproduced well the experimental disparity between substrates (proportion of nests with both transitions; granular: experimental = 50%, simulated = 43%; cohesive: experimental = 96%, simulated = 71%). The generated dynamics of each state fraction f_i were in good agreement with the experimental results (figure 5). Moreover, the mean values of area for each state change (A₁, A₂, A_M) were quite similar for simulations and experiments, whatever the substrate (table 3). The simulations were thus able to qualitatively and quantitatively reproduce the experimental results.

Figure 5.

Simulations reproduced well the dynamics according to area of each state fraction f_i in each substrate. (a,b) Dot lines figure the mean fraction f_i of experiments in state i, s.d. being figured in shades. Experimental dynamics are figured in full lines. (a) Simulations for granular substrate (24 replicates for each of 1000 simulations; η₂ = 0.237, c₂ = c₃ = 12.74, η₃ = 0.95, η_S = 0.313, c_S = 15.46). (b) Simulations for cohesive substrate (25 replicates for each of 1000 simulations; η₂ = 0.639, c₂ = c₃ = 5.97, η₃ = 0.95, η_S = 0.239, c_S = 14.61). Green, f₁; purple, f₂; orange, f₃; blue, f_S.

Table 3.

Areas of morphological transition of experiments (exp., granular n = 12, cohesive n = 24) and simulations (sim., granular N = 10 257, cohesive N = 17 679) showing the two transitions. (Simulations parameters (granular: η₂ = 0.237, c₂ = c₃ = 12.74, η₃ = 0.95, η_S = 0.313, c_S = 15.46; cohesive: η₂ = 0.639, c₂ = c₃ = 5.969, η₃ = 0.95, η_S = 0.239, c_S = 14.614).)

	mean ± s.d.
	granular (exp.)	granular (sim.)	cohesive (exp.)	cohesive (sim.)
AM	20.32 ± 7.82	19.55 ± 4.09	15.49 ± 6.19	17.57 ± 5.46
A1	11.94 ± 6.13	10.54 ± 4.68	5.99 ± 2.55	5.91 ± 2.52
A2	15.38 ± 6.46	14.81 ± 2.38	9.47 ± 4.51	9.69 ± 2.92

(e). Effect of density

Despite a faster excavation in granular than in cohesive substrate before the first transition, the digging rates at the first transition (R₁) were not statistically different between conditions (table 1). For a given material (sand, granular substrate) and whatever the population size, the first transition is known to occur at a characteristically low value of density of activity defined as ρ = R/A (Toffin et al. 2009). Here, for both materials, the ρ values remained close, suggesting that this ratio was still a good predictor of the first morphological transition. However, owing to the low value of the first transition area in the cohesive material, the corresponding ρ value in this substrate was greater (1.5×). The same trends were observed for the second transition (table 1).

4. Discussion

The effect of the digging material was quantified and its properties linked to the emergence of the different shapes observed. We show here two successive morphological transitions leading to the branching of originally rounded nests, whose dynamics and frequency were strongly affected by the excavated material: cohesive substrate promoted earlier and more frequent branching of the nest. The rounded shape and the branched pattern are two extreme and opposite nest morphologies that are in competition during the nest digging. At the first transition, small buds appear on the nest wall. Later on, the main chamber expansion will stop and some buds will be enlarged, becoming lateral galleries, until the excavation completely ceases.

The transitions and the cessation of excavation are described with threshold functions that depend on nest area. The differences between the two substrates lie only in the first transition parameters (η₂ and c₂), which lead to earlier first transition in cohesive material. The second transition is highly deterministic (η₃ large) and occurs as soon as the second stage is reached: its occurrence thus highly depends on the value of the first transition area (A₁). The second stage can, therefore, be considered as a transitory stage, during which tiny perturbations of the system (small digging heterogeneities or small buds) can make the system evolve towards the branched pattern. When the threshold value of the first transition c₂ (and thus of the second transition c₃) is close to that of the stopping threshold (c_S), excavation cessation before transitions have occurred is more likely to occur, which illustrates our experimental results in the granular substrate. The existence of thresholds at a collective level explains qualitatively and quantitatively different responses in each of the substrates.

Environmental properties have already been shown to influence collective processes by modulating individual responses (Challet et al. 2005; Dussutour et al. 2008), which may imply individual thresholds. On the other hand, several works have suggested that the environment may also mediate the interaction between individual behaviours (Detrain & Deneubourg 2002; Jeanson et al. 2003; Bernadou & Fourcassie 2008; Toffin et al. 2009), hence altering the amplification processes and leading to various collective patterns without implying behavioural modifications. The thresholds are consequences of dynamics instabilities (Camazine et al. 2001; Colasurdo et al. 2007).

We have previously highlighted the fundamental mechanisms of the morphological transitions during nest building (Toffin et al. 2009). For a given material (sand) and whatever the population size, the density of activity ρ = R/A is a predictor of the morphological transition. For a given nest size (A), it quantifies the minimal excavating ‘pressure’ (collective digging effort, i.e. the digging rate R) that is required to maintain an isotropic growth. As long as the ρ value is high enough, the collective work can ‘dampen’ the appearance of heterogeneities and the ants dig isotropically (stage 1). As a consequence of the nest growth, the excavating pressure is continuously diluted, and when ρ reaches a critical low value of density, the heterogeneities cannot be dampened anymore. Hence, buds appear along the main cavity (stage 2) and may finally turn into long lateral galleries (stage 3). As ρ is adimensional, it should help to understand our results and compare the two substrates despite their structural differences. Similar to our previous findings (Toffin et al. 2009), ρ can be considered as a good predictor of the morphological transitions. Nevertheless, the value of ratio ρ at the first transition seems partly dependent on the substrate characteristics.

According to this scenario, a substrate that modifies the digging rate (R) and/or the importance of the heterogeneities resulting from excavation should have an impact on the nest morphogenesis. We measured that the pellets were larger in the cohesive substrate (30% and see the electronic supplementary material), hence their removal, hence created bigger heterogeneities than in the granular material. Maintaining isotropy in nests of similar areas, therefore, requires a higher digging activity in the cohesive than in the granular substrate. However, the mean excavation rate (R) is lower in the cohesive material, which amplifies the appearance of heterogeneities along the nest wall. This last result also suggests a more difficult excavation and higher digging costs in a cohesive medium than in a granular one, which could also favour digging where excavation has been initiated, as suggested by previous works (Aleksiev et al. 2007). Therefore, the isotropy is broken sooner in cohesive substrates, which explains the higher instability of stage 1 and the higher frequency of both morphological transitions observed in this material.

The second transition is no more than a collective choice. This selection process is at work throughout the entire excavation, but it is concealed as long as the digging activity is important, with the main chamber expanding isotropically. When the decreasing density of activity is too low, the opportunity to discriminate and focus on particular sites increases and the excavation enters the second stage. The selection process can then quickly override the collective isotropic work and the nest growth shifts to a localized digging, which leads to the development of lateral galleries. This collective choice is similar to those described in various situations where different amplification processes are in competition (Nicolis & Deneubourg 1999; Detrain & Deneubourg 2002), and may hence fulfil the same requirements to occur (Bonabeau et al. 1997; Camazine et al. 2001) among which are a sufficient number of involved workers (Deneubourg 1977; Buhl et al. 2005).

Concerning the general topic of collective building, our scenario offers a convenient explanation, even in homogeneous environments, for the wide diversity of nest shapes that has already been described in many species. However, while substrate homogeneity is convenient to apprehend the effect of material on nest morphogenesis, it remains somewhat theoretical as a natural soil contains heterogeneities at scales intermediate to the sizes of pellets and nests (e.g. granulometry). Moreover, the digging material itself may be altered, for instance by humidity, which might change its cohesion on a global scale. Therefore, both of these variations in substrate quality change the impact on nest morphogenesis. Shape variability between species (Grassé 1984; O'Donnell & Jeanne 2002; Tschinkel 2003) may lie within specific preferences in nesting mediums, and intra-specific diversity (Grassé 1984; Tschinkel 2004, 2005) may, on the contrary, find its origin in a high acceptance in nesting conditions.

More generally, depending on the environmental characteristics, the shape transition mechanism may lead to an exclusive and specific pattern of environment exploitation or, on the contrary, to coexisting strategies of dissemination. Our findings may be applied to a wide variety of dynamical systems, such as those showing growth phenomena, collective displacements and collective choice (Franks et al. 1991; Detrain & Deneubourg 2002).