Abstract
Recent empirical studies indicate that grandparents favour some categories of grandchildren over others. Here, we expand the previous theoretical foundation for this finding and show that grandchild-harming phenotypes are predicted to evolve by ‘sexually antagonistic zygotic drive (SA-zygotic drive) of the sex chromosomes’. We use the logic of Hamilton's rule to develop a new ‘no-cost-to-self nepotism rule’ that greatly simplifies the determination of the invasion criteria for mutations that cause grandparents to harm grandchildren. We use this theory to generate predictions that distinguish SA-zygotic drive from theory based solely on paternity assurance. The major diagnostic prediction is that grandmothers, and to a lesser degree grandfathers, will evolve grandson-harming phenotypes that reduce the level of sib competition experienced by their more closely related granddaughters, especially in their sons' families. This prediction is supported by data from recent studies showing (i) grandmothers invest more in granddaughters than grandsons, and counterintuitively, (ii) paternal grandmothers reduce the survival of their grandsons. We conclude that SA-zygotic drive is plausibly operating in humans via sexually antagonistic grandparental care.
Keywords: grandparental care, Hamilton's rule, sexually antagonistic zygotic drive, sex chromosomes
1. Introduction
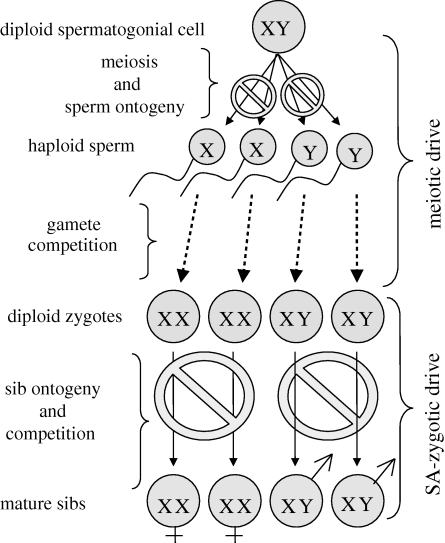
When males are the heterogametic sex, a father transmits his Y chromosome to his sons and his X chromosome to his daughters. This simple transmission asymmetry has profound evolutionary consequences in the context of intragenomic conflict when there is competition among siblings. In this case, there is natural selection for selfish genetic elements, that are X- or Y-linked, that harm the sex of offspring that does not carry them—thereby increasing the competitive ability (for shared resources) of the sex of offspring that does carry them (Miller et al. 2006; Rice et al. 2008, 2009). The phenotypes produced by these sex-linked selfish elements are called ‘sexually antagonistic zygotic drive (hereafter SA-zygotic drive) of the sex chromosomes’. SA-zygotic drive evolves under far less evolutionary constraint than offspring-harming selfish elements on the autosomes (such as Medea elements in Tribolium; Beeman et al. 1992) because the sex-specific transmission of a father's X and Y chromosomes greatly facilitates the evolution of sexually antagonistic green-beard effects (as described in Rice et al. 2008). In figure 1, we illustrate how SA-zygotic drive extends the logic of the well-known process of sex-linked meiotic drive (evolving in response to competition among haploid X- and Y-bearing sperm) into the diploid stage of the life cycle (evolving in response to competition among diploid brothers and sisters carrying their father's Y or X chromosome, respectively). Our previous theoretical work (Miller et al. 2006; Rice et al. 2008, 2009) has shown that the phenotypes that are predicted to mediate SA-zygotic drive in nuclear families include sexually antagonistic: (i) maternal or paternal effects (especially in the context of trans-generational epigenetic influences on gene expression), (ii) sib–sib interactions, and (iii) parental investment. Here we expand this logic to the context of an extended family in which grandparents can differentially ‘care’ for grandchildren (we use the term care here to include all phenotypes of grandparents that influence the survival or vigour of grandchildren) based on both their gender and their lineage (i.e. grandsons and granddaughters derived from sons (patriline) or daughters (matriline)). This theory is used to generate empirical predictions that are unique to SA-zygotic drive operating through asymmetrical grandparental care, as opposed to asymmetries in relatedness that arise owing to extra-pair infidelity alone. We then compare the predictions of SA-zygotic drive to the patterns of human grandparental care that have recently been described in empirical studies (Chrastil et al. 2006; Fox et al. 2010). We conclude that there is surprisingly strong evidence that SA-zygotic drive is operating in humans via sexually antagonistic grandparental care. This conclusion is in sharp contrast to previous work concluding that paternity assurance, and not the asymmetrical transmission of sex-linked genes to grandsons and granddaughters, is the predominant selective factor influencing evolved patterns of grandparental care (Chrastil et al. 2006).
Figure 1.
Meiotic versus SA-zygotic drive. Sperm competition provides the selective environment for the evolution of meiotic drive of the sex chromosomes. In this context, each sex chromosome is selected to disrupt (circular stop symbols) the post-meiotic ontogeny of the type of gamete (X- or Y-bearing) that does not carry it. Sib competition provides the selective environment for the evolution of SA-zygotic drive. In this context, each sex chromosome is selected to disrupt (circular stop symbols) the post-zygotic ontogeny of the type of offspring (male or female) that does not carry it. This disruption can be mediated by sex-specific (i) epigenetic paternal effects, (ii) sib–sib interactions, (iii) paternal investment, and as shown here, (iv) grandparental investment. The strong functional similarity with meiotic drive, but operating during diploid rather than haploid ontogeny, motivates the term ‘SA-zygotic drive’.
2. Grandparent/grandchild relatedness
Chrastil et al. (2006) were the first to quantify the idea that care by grandparents might be influenced by the asymmetrical relatedness of sex chromosomes between grandchildren and their matrilineal and patrilineal grandparents. They considered the joint effects of (i) paternity assurance (Pa = the average probability that an offspring is sired by the social mate, 0 ≤ Pa ≤1) and (ii) average levels of X and Y relatedness to grandchildren (assuming no infidelity by social mates) on selection for differential investment by grandparents in the eight types of grandparent–grandchild relationships (i.e. the maternal grandmother's (MGM) and grandfather's (MGF) investment in their male and female grandchildren and the paternal grandmother's (PGM) and grandfather's (PGF) investment in their male and female grandchildren). Relatedness for the X, Y and autosomes are summarized in table 1. Chrastil et al. (2006) reported that the observed patterns of grandparental care (based on questionnaires completed by adult grandchildren asking them to recall how much care each of their grandparents provided to them while they were young) were far more tightly correlated with autosomal relatedness (varying only by the level of paternity assurance) compared with relatedness of the sex chromosomes (varying by both paternity assurance and the asymmetrical transmission of the X and Y).
Table 1.
Relatedness (R) between grandparents and grandchildren for the X, Y and autosomes (A). The first term in each cell (fraction or zero) is the level of relatedness assuming no extra-pair paternity and the second term is the level of paternity assurance (Pa = the average probability that no extra-pair paternity occurs in each generation of a line of descent, 0 ≤ Pa ≤1). Figures in bold are explained in the text.
| MGM | MGF | PGM | PGF | ||
|---|---|---|---|---|---|
| grandson | A | 1/4 * 1 | 1/4 * Pa | 1/4 * Pa | 1/4 * Pa2 |
| X | 1/4 * 1 | 1/2 * Pa | 0 * Pa | 0 * Pa2 | |
| Y | 0 * 1 | 0 * Pa | 0 * Pa | 1 * Pa2 | |
| granddaughter | A | 1/4 * 1 | 1/4 * Pa | 1/4 * Pa | 1/4 * Pa2 |
| X | 1/4 * 1 | 1/2 * Pa | 1/2 * Pa | 0 * Pa2 | |
| Y | 0 * 1 | 0 * Pa | 0 * Pa | 0 * Pa2 | |
| average over the | A | 1/4 | 1/4 * Pa | 1/4 * Pa | 1/4 * Pa2 |
| sex of grandchild | X | 1/4 | 1/2 * Pa | 1/4 * Pa | 0 |
| Y | 0 | 0 | 0 | 1/2 * Pa2 | |
| average over the | A | 1/8 * (1 + Pa) |
1/8 * (1 + Pa)*Pa |
||
| sex of grandchild | X | 1/8 * (1 + 2Pa) |
1/8 * Pa |
||
| and grandparents | Y |
0 |
1/4 * Pa2 |
||
Here we integrate the work of Chrastil et al. (2006) into the more general theory of SA-zygotic drive. This is done to make predictions about the fate of selfish sex-linked mutations that cause grandparents to harm the sex of grandchildren that does not carry them. We begin by replacing Chrastil et al.'s (2006) population genetic invasion analysis with a far simpler alternative that leads to an extension of Hamilton's rule of altruism. This simpler, more intuitive approach makes the theory far more accessible to empiricists without loss of accuracy, and it permits the influence of the level of dominance of mutations to be easily incorporated. We specifically focus on the invasion criteria for mutations, on the X or autosomes, that (i) indirectly harm one sex of grandchildren by redirecting grandparental investment towards the sex of grandchildren that carry them, or the mathematical equivalent and (ii) directly harm the sex of grandchild that is less closely related and thereby increase the survival of the other sex owing to reduced sib competition. We also re-evaluate the large body of empirical data that has been used to conclude that paternity assurance, rather than selfish sex-linked genes, is the major selective agent leading to biased grandparental care. We conclude that these data, especially those from a more recent study (Fox et al. 2010), indicate that asymmetrical grandparental care is strongly influenced by the kinds of selfish, sex-linked genes that fuel SA-zygotic drive: the opposite conclusion of Chrastil et al. (2006).
Fox et al. (2010) further quantified the logic of Chrastil et al. (2006), focusing on grandmothers, to include the estimated degree of relatedness for the entire genome. They concluded that because the human X constitutes about 4.4 per cent of the genomic DNA, with nearly double the density of genes compared with the autosomes, the relatedness of grandmothers to grandchildren will differ: the MGM shares an average of 25 per cent of her genes with both grandsons and granddaughters while the PGM shares an average of about 23 per cent of her genes with grandsons and 27 per cent with granddaughters. These calculations assume perfect paternity assurance. We can, however, easily add paternity assurance to Fox et al.'s (2010) calculations: relatedness of grandmother to grandchild is 0.25, 0.25, 0.27Pa and 0.23Pa for the dyads MGM–GD, MGM–GS, PGM–GD and PGM–GS, respectively (GD, granddaughter; GS, grandson). This genome-wide perspective illustrates that paternal grandsons are least related to their grandmothers, but unless paternity uncertainty is substantial, all grandchildren have substantial and similar genome-wide relatedness to their grandmothers. We will use the theory of SA-zygotic drive to explain why grandparents should evolve to harm some categories of grandchildren, while helping others, despite high genome-wide relatedness to all categories.
3. Invasion of selfish grandparental investment mutations
In principle, both the X and Y sex chromosomes (and autosomes) can potentially carry mutations influencing parental and grandparental care. Our previous modelling work, on antagonistic coevolution between the X and Y in the context of SA-zygotic drive, indicated that when the Y was highly degenerated, the X chromosome's influence (on reducing the competitive ability of the sex of sibling that does not carry it) will overwhelm the effect of the Y owing to its higher mutation potential (Rice et al. 2008). This is not to imply that the Y has no influence. For example, recent microarray data on polymorphic Y chromosomes of the fruitfly Drosophila melanogaster demonstrated that this chromosome influences the level of expression of over a thousand genes located on the X and autosomes (Lemos et al. 2008). The Y has also been shown in mammals (Lahn & Page 1997) and flies (Koerich et al. 2008) to accumulate new structural genes over time. Nonetheless, there are many-fold more functional genes on the human X compared with the Y (Lahn & Page 1997), and for this reason its mutational potential should far surpass that of the Y, causing it to predominate over the Y in its influence on grandparental care. For this reason, we focus here on X-linked influences on grandparental care.
A father's X chromosome is transmitted intact to his daughters and never to his sons. This simple asymmetry favours selfish X-linked mutations that cause fathers to divert their limited supply of parental investment from sons to daughters, i.e. helping their daughters at the expense of their sons, or to directly harm sons to reduce sib competition with their sisters (Miller et al. 2006; Rice et al. 2008, 2009). Since a father's X chromosome is inherited exclusively from his mother, the PGM's X chromosomes are selected to help or harm her patrilineal grandchildren in the same way as her son's X is selected to influence his children (Rice et al. 2008). Unlike her son's X, however, no Y is present in the grandmother to counterbalance any biased investment tendency that may evolve by which grandmothers favour their son's daughters over his sons.
We begin with the null model of uniform (or random) grandparental investment in all types of grandchildren. We then focus on mutations that preferentially help one sex of grandchild at the expense of the other. Because more investment in one category of grandchildren necessarily depletes limited resources that could have been provided to another category, differential grandparental investment will generally entail both helping and hurting interactions.
Consider an individual (actor) that helps a second individual (recipientHelped) at the expense of a third individual (recipientHarmed). Further assume that this help/harm phenotype of the actor does not incur a cost with respect to its individual fitness (as would be the case for post-reproductive grandparents). Next consider Hamilton's rule of altruism: C < R * B, where C is the cost to an altruist, B is the benefit to the recipient of the altruism and R is the level of relatedness. We extend this logic to the context of an individual (actor) influencing others (at no fitness cost to oneself) by helping one member of a dyad at the expense of the other member. A rare mutation producing this phenotype will invade a gene pool when
| 3.1 |
where CHarmed is the cost to the harmed individual, BHelped is the benefit to the helped individual, RHelped is the relatedness to the helped individual and RHarmed is the relatedness to the harmed individual.
We will refer to this as the ‘no-cost-to-self nepotism rule’ (NCTS-nepotism rule, see derivation below). If the helping phenotype harmed the actor, and the dyad consisted of oneself and another individual, RHarmed = 1 and the NCTS-nepotism rule becomes Hamilton's rule of altruism. Assuming that grandparents are post-reproductive, or asymptotically so, we can use a weighted average extension of this simple relationship to evaluate selection on new mutations that influence differential (i.e. non-uniform) grandparental investment. We will specifically contrast the invasion criteria for these mutations when they are autosomal (relatedness determined exclusively by paternity assurance) or X-linked (relatedness determined by both paternity assurance and the asymmetrical transmission of a father's X to his sons and daughters).
(a). Invasion criteria
Consider a rare allele that causes its bearer to help one individual at the expense of another, e.g. helping a granddaughter at the expense of a grandson. Specifically, let the relative viability of the helped individual increase from 1 to 1 + B while that of the harmed individual decreases from 1 to 1 − C. We assume that the allele has no direct effects on the viability of its bearer and that effects B and C are small. Then the inclusive fitness of the allele is proportional to RHelped * (1 + B) + RHarmed * (1 − C), where RHelped and RHarmed are the relatedness of the focal individual to the helped and harmed individuals, respectively (by relatedness, we mean the probability of identity by descent). Then the allele under consideration invades when rare if,
which is the foundation for the NCTS-nepotism rule (equation (3.1)).
Next, we allow for the effects of the allele on viability of the affected individuals to be dependent both on the sex of its bearer (e.g. on whether the allele is present in a male or female) and on the genetic relationship between the focal individual and both individuals of the dyad. Then, the inclusive fitness is proportional to a weighted sum of terms in the form
The sum is taken over all relevant types of genetic relationships between the actor and the recipients, and the weight for each term equals the probabilities that the allele finds itself in the corresponding actor/recipients interaction. This weighted sum can be expressed as
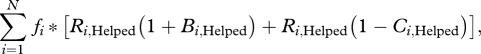 |
where i denotes a specific actor/recipients combination (e.g. one of the eight entries in table 1), N is the number of possible actor helped/harmed interactions and fi is the relative frequency, or probability, of the ith category of interaction. The allele invades if its inclusive fitness is higher than that of the resident allele for which Bi = Ci = 0. In this case,
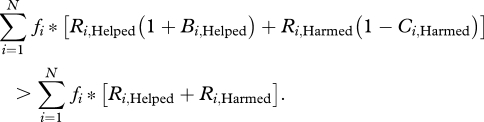 |
Rearrangement yields
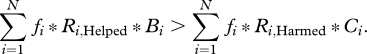 |
3.2 |
Comparing inequalities (3.1) and (3.2) demonstrates that the invasion criteria represent a weighted average of the NCTS-nepotism rule, with weights being the relative frequencies of the possible actor/recipients categories. Note that our derivation of the weighted form of Hamilton's rule given by inequality (3.2) explicitly used the assumptions standard in derivations of this type (i.e. additive genetics, additive fitnesses and weak selection; McElreath & Boyd 2007). A comparison of our approach with the population genetic model of Chrastil et al. (2006) (after correcting a minor error in the published model) shows that both methods lead to the same results (electronic supplementary material).
In the case of grandparental care, n = 8 (see the eight entries in table 1), and assuming equal access to all types of grandchildren, fi is determined by the proportion of X or autosomes residing in each of the four types of grandparents, and the relatedness values (Ri's that are adjusted for paternity assurance) for each of the eight grandparent/grandchild categories are shown in table 1. To determine the invasion capability of a mutation causing a particular helped/harmed grandparental care phenotype, we calculate a weighted average of the NCTS-nepotism rule. Below we illustrate our approach in several examples of increasing complexity.
(b). More investment to matrilineal grandchildren
When paternity assurance is high (Pa close to 1), only genes on the X are strongly selected to invest more in matrilineal compared with patrilineal grandchildren (see bottom of table 1 and figure 2). Molecular data on modern humans indicate that paternity assurance is generally high (median estimate = 96.3%; Bellis et al. 2005), although a value of 90 per cent is commonly cited without supporting data). Nonetheless, both imperfect paternity assurance and X-linkage make grandchildren more closely related to matrilineal compared with patrilineal grandparents, although this effect is far larger for the X unless paternity assurance is very low (see bottom of table 1 and figure 2). Therefore, data showing that grandparents invest more in matrilineal grandchildren provide little diagnostic evidence for the operation of SA-zygotic drive in humans, since paternity assurance alone on the X and autosomes makes this same qualitative prediction. For this reason, we do not consider here the invasion criteria for mutations on the X and autosomes that bias grandparental care towards matrilineal grandchildren.
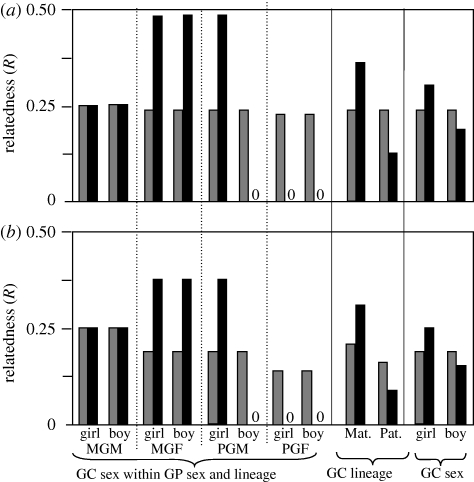
Figure 2.
Variation in relatedness (R) between grandparents and grandchildren is substantially larger for the X (black bars) compared with the autosomes (grey bars) at multiple levels. Panel (a) assumes paternity assurance is near the norm estimated for modern humans (Pa = 0.96; Bellis et al. 2005), while panel (b) assumes a much lower level of paternity assurance (Pa = 0.75). GC, grandchild; GP, grandparent; Pat, patrilineal; Mat, matrilineal; MGM(F), matrilineal grandmother (grandfather); PGM(F), patrilineal grandmother (grandfather).
Imperfect paternity assurance and the asymmetrical transmission of the paternal X create a different rank-ordering of relatedness between types of grandparents and their grandchildren (grandsons and granddaughters combined). We first consider the combined sexes of grandchildren here because most empirical studies report pooled data across the two sexes of grandchildren. On the autosomes, the ordering of relatedness of grandparents to their grandchildren is MGM > MGF = PGM > PGF, while on the X it is MGF > MGM > PGM > PGF, given that Pa is substantial. i.e. >0.5 (Euler & Weitzel 1996; Chrastil et al. 2006) (table 1). These rankings, however, have limited application to the expected rank-ordering of grandparental care because: (i) human females tend to provide far more care to young children compared with males (Coon 1971; Lockard et al. 1979) and (ii) the behaviour of married grandparents is likely to be statistically correlated (e.g. if they tend to travel and live together) and married couples may strongly influence each other's behaviour (e.g. if the head of household determined the pair's agenda). Grandfathers may be particularly strongly selected to influence the level of care given by grandmothers to different categories of grandchildren owing to strong differences in a grandfather's relatedness to them (table 1 and figure 2). For these reasons, we think that the four categories of grandparental investment cannot be treated as independent entities for comparison and that the only meaningful predictions for grandparental care are: MGM > PGM and MGF > PGF, i.e. the same non-diagnostic prediction, compared with paternity assurance alone, as described in the previous paragraph.
(c). More investment in granddaughters
A final asymmetry concerns the sex of grandchildren. For the autosomes, the relatedness between grandparents and grandchildren is independent of a grandchild's sex. On the X, however, relatedness, and hence optimal allocation of grandparental care, is expected to sometimes depend on the grandchild's sex. The Xs in PGMs have zero relatedness to their grandsons while in granddaughters they have double the level of relatedness found for the autosomes (table 1 and figure 2). This striking asymmetry strongly selects for X-linked mutations that divert PGMs' investment from grandsons to granddaughters, or that cause the PGM to directly (although not necessarily consciously) harm grandsons and thereby reduce the sib competition experienced by granddaughters (Fox et al. 2010). This predicted asymmetry in the sex-specific care of the PGM is the major qualitative difference between the SA-zygotic drive of the sex chromosomes and the theory of asymmetrical grandparental care that is based on paternity assurance alone.
Diversion of the PGM's investment from grandsons to granddaughters, or harming grandsons to reduce sib competition with granddaughters, can be achieved by three kinds of selfish mutations. The simplest mutation is one that is expressed in both male and female grandparents, and that produces the same phenotype in each sex. Consider a dominant X-linked mutation that caused all grandparents to divert investment from grandsons to granddaughters. Applying a weighted average of the NCTS-nepotism rule (recall that two-thirds of X chromosomes reside in females and one-third in males),
 |
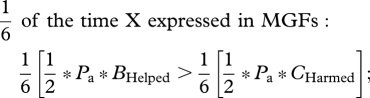 |
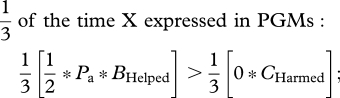 |
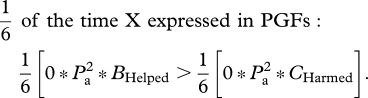 |
Summing all weighted inequalities,
or
and
Using this same weighted-average NCTS-nepotism rule, it can be shown that as dominance declines, it becomes more difficult for the selfish mutation to accumulate (table 2, mutant phenotype 1). So a dominant X-linked mutation that caused both sexes of grandparents to help granddaughters at the expense of grandsons would spread in a population so long as the cost to grandsons was no more than about twice of the benefit to granddaughters. With additive gene expression, the cost–benefit ratio must be less that about 1.5. On the autosomes, preferential grandparental investment in granddaughters will only evolve when care diverted from grandsons towards granddaughters somehow helps the granddaughters more than it harms the grandsons (CHelped/BHarmed < 1; table 2, mutant phenotype 1). We see no a priori reason why this would generally be the case, and when sexual selection is stronger in males, the opposite pattern may commonly be the case.
Table 2.
Constraints for the invasion of mutations influencing grandparental investment. The inequalities were calculated using a weighted average NCTS-nepotism rule (inequality (3.2)), and assuming dosage compensation of the X in males, so that additive mutations are expressed more strongly in males.
| mutant phenotype | constraint for accumulation |
|---|---|
| 1. all GPs invest more in granddaughters | |
| autosomes (dom. or add.) | CHarmed/BHelped < 1 |
| X (dom.) | CHarmed/BHelped < [1+3Pa]/[1+Pa] |
| 3X (add.) | CHarmed/BHelped < [1+3Pa]/[1+2Pa] |
| 2. GMs invest more in granddaughters | |
| autosomes (dom. or add.) | CHarmed/BHelped < 1 |
| X (dom. or add.) | CHarmed/BHelped < (1 + 2Pa) |
| 3. PGMs invest more in daughters | |
| autosomes (dom. or add.) | CHarmed/BHelped < 1 |
| X (dom. or add.) | CHarmed/BHelped < ∞ |
Next consider a more complex mutation that has a sex-limited effect, i.e. a mutation that was silent in grandfathers but that caused both MGMs and PGMs to help granddaughters at the expense of grandsons (mutant phenotype 2 in table 2). On the X, using a weighted-average NCTS-nepotism rule, the constraints for the accumulation of such a dominant mutation are CHarmed/BHelped <(1 + 2Pa). Reducing the level of dominance (additive mutation) has no effect on this constraint. Carrying out the same calculations for a dominant or an additive autosomal gene, the constraint on the cost/benefit ratio is CHarmed/BHelped < 1. So an X-linked mutation that caused both MGMs and PGMs to invest more in granddaughters at the expense of grandsons would spread in a population so long as the cost to grandsons was no more than about three times the cost to grandsons. For an autosomal mutation, this phenotype (diverting care from grandsons to granddaughters) will only evolve when extra care to granddaughters is more helpful to them than reduced care harms grandsons (BHelped > CHarmed).
Finally, consider a sex-limited/X-linked mutation that causes only PGMs to favour granddaughters. PGMs have a striking X-linked asymmetry in their relatedness to granddaughters versus grandsons: PGMs are related by 1/2 to granddaughters and by zero to grandsons, while MGMs are equally related to grandsons and granddaughters (table 1 and figure 2). Applying the weighted-average NCTS-nepotism rule, the mutation will spread when CHarmed/BHelped < ∞ (mutant phenotype 3, table 2). For an autosomal mutation, the cost/benefit ratio constraints are CHarm/BHelp < 1. So an X-linked mutation that caused only patrilineal grandmothers to help granddaughters at the expense of grandsons would spread in a population so long as there is any net benefit to granddaughters (BHelped > 0), irrespective of the cost to grandsons. For an autosomal mutation, this phenotype (PGMs diverting care from grandsons to granddaughters) will only evolve when CHarmed/BHelped < 1. Figure 3 illustrates the differences in the constraints for invasion of mutations with progressively more sex- and lineage-specific expression.
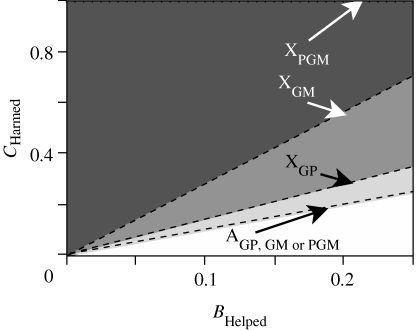
Figure 3.
The parameter space (area below dashed lines) supporting the invasion of additive mutations that helps granddaughters (with benefit BHelped) at the expense of their grandsons (with cost CHarmed). XGP depicts mutations on the X that affect all grandparents; XGM depicts mutations on the X that affect only grandmothers; XPGM depicts mutations on the X that affect only patrilineal grandmothers; AGP, GM or PGM depicts mutations on the autosomes and affects all grandparents, only grandmothers or only patrilineal grandmothers, respectively.
4. Predictions
There is one major prediction of SA-zygotic drive concerning patterns of grandparental care that is qualitatively different from predictions based on paternity assurance alone: mutations can accumulate on the X that cause granddaughters to be favoured at the expense of grandsons by all grandparents, all grandmothers or only PGMs. There are successively weaker constraints for the invasion of mutations favouring granddaughters as the mutation becomes more restricted in the type of grandparent in which it is expressed, with no constraint (CHarmed/BHelped < ∞) in the case of a mutation causing only the PGM to have this phenotype (figure 3). This harmful grandparental behaviour with respect to grandsons need not be overt or conscious, but may simply be greater attentiveness or more stringent restrictions on dangerous behaviour of granddaughters compared with grandsons.
If the effect size of such a grandson-harming/granddaughter-helping mutation were large, the population sex ratio would become biased and Fisherian sex-ratio evolution and counterevolution by the autosomes (or to a lesser degree, the highly degenerated Y) would be expected to rapidly silence these mutations—so they would have only a short, transient effect. When the effect size is small, however, Fisherian sex-ratio evolution is slow and counterevolution by the autosomes will be slow or absent altogether (when the harm to one sex is less than or equal to the benefit to the other; Rice et al. 2008), so a longer lasting phenotype of PGMs helping granddaughters at the expense of grandsons is expected to be observed in humans.
5. Compliance with recently published data
Published studies on grandparental care fall into two major categories. Those that measure the survival of offspring when a grandparent of a particular type is present compared with when they are absent (hereafter ‘survival studies’). These studies have been done in pre-industrialized historic or contemporary populations. The reported data are the odds ratio of the probability of young grandchildren surviving when the grandparent is present divided by this same probability when the grandparent is absent. Logistic regression is used to adjust for other uncontrolled variables, such as number of other siblings, etc.
The second type of study is based on questionnaires, usually given to grown grandchildren, asking them to recall how much care the MGM, MGF, PGM and PGF provided while they were young (hereafter ‘questionnaire studies’). Most questionnaire studies do not report the gender of grandchildren. These studies show a fairly consistent consensus pattern:
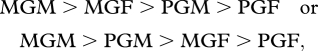 |
with the two patterns sometimes reversing for different measures of grandparental care within the same study (for a succinct review of these studies, see Bishop et al. 2009). The fact that MGFs are commonly reported to provide more care than PGMs, despite the norm of human females providing much more care to young children compared with males, provides at least weak support for the operation of SA-zygotic drive (selfish X elements) in humans since this pattern is not predicted under paternity assurance alone (because PGMs and MGFs each have equal autosomal relatedness, assuming no cuckoldry, and one opportunity for cuckoldry in their pedigree linking them to the grandchild, table 1) except, perhaps, when a PGM also is an MGM (i.e. she has grandchildren both through her sons and daughters). In this case, it has been suggested that the grandmother should preferentially invest in her daughters' children (owing to paternity assurance) and, as a result, therefore will reduce her investment in grandchildren to which she is the PGM (Laham et al. 2005). Some support has been found for this hypothesis (Laham et al. 2005), but see Bishop et al. (2009). However, these results are not in conflict with what is predicted under SA-zygotic drive.
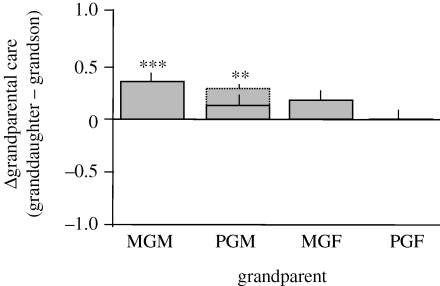
We found only one questionnaire study that reported data for grandsons and granddaughters separately (reported in two instalments, Chrastil et al. (2006) and Euler & Weitzel (1996)). We summarize their results in figure 4. As predicted by SA-zygotic drive, but not paternity assurance, there was evidence that both PGM and MGM provided more care for their granddaughters compared with their grandsons. The study by Chrastil et al. (2006) also analysed another questionnaire survey, taken from an unpublished PhD dissertation, measuring how much grandchildren enjoyed, or preferred, being with each of the four grandparent types. We have not analysed these data here because it is not clear to us how to interpret the results relative to levels of grandparental care, e.g. it may be less enjoyable to a grandchild to interact with strict grandparents, but they may nonetheless provide better care.
Figure 4.
Summary of the data from Chrastil et al. (2006) concerning sex-specific grandparental care as measured by the difference (Δ) in the amount of grandparental care that granddaughters (n = 889) recalled receiving minus the amounted recalled by grandsons (n = 455). Seven was the highest possible care score for each sex of grandchild and the period of care was up until the age of 7 years. Data depicted by solid bars are from a restricted sample (n = 1344) in which grandchildren had all four grandparents alive at age seven. The dashed bar depicts the MGM's larger difference in care between grandsons and granddaughters that was observed when the entire sample (n = 2968) was analysed. Standard errors are shown as vertical lines, ***p < 0.001 for the restricted sample and **p < 0.01 for the entire sample.
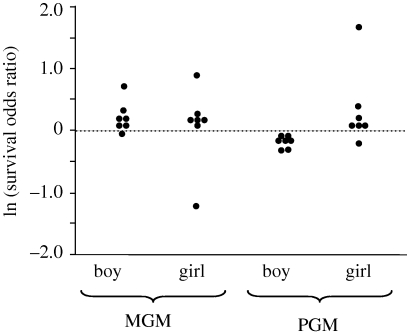
Most of the survival studies were carried out to test the ‘grandmother’ hypothesis for the evolution of menopause, i.e. that menopause evolved because older females are selected to invest in their grandchildren rather than their own children. Fox et al. (2010) recently carried out a meta-analysis of the seven extant survival studies. These studies all tested the hypothesis that the presence of grandmothers influenced the survival of their grandchildren. When pooling the studies and ignoring the sex of the grandchildren, the studies were in poor agreement. But when male and female grandchildren were grouped separately by Fox et al. (2010), a clear consensus pattern was observed. The presence of an MGM generally increased the survival of both her grandsons and granddaughters, whereas the presence of a PGM increased the survival of her granddaughters while it decreased the survival of her grandsons (figure 5). This stunning result is unexplainable by paternity uncertainty, but in full accord with the predictions of SA-zygotic drive. Moreover, when grandmothers were present, paired analysis of each of the seven studies indicated that the presence of an MGM was just as likely to be more helpful (increased by more than the survival odds ratio) for granddaughters as for grandsons (figure 5). PGMs, however, typically augmented the survival of granddaughters more than grandsons.
Figure 5.
Summary of the data from Fox et al. (2010) concerning sex-specific influence of grandmothers on the survival of grandchildren. The influence of a grandmother's presence on a grandchild's survival is expressed as the log of the odds ratio of the probability of grandchildren surviving when a grandmother was present divided by this same probability when a grandmother was absent. Dotted horizontal line depicts the value corresponding to no survival effect. The presence of MGMs increased grandchild survival of both sexes combined (p = 0.0129, binomial test) with no difference between the sexes (Fisher's exact test, p = 1.0) and no tendency to favour granddaughters over grandsons (matched pair Wilcoxon signed-rank test, p = 0.58). In contrast, the presence of the PGM had no net effect on both sexes of grandchildren combined (p = 0.79, binomial test), but her effect differed between the sexes (Fisher's exact test, p = 0.005), favouring granddaughters over grandsons (matched pair Wilcoxon signed-rank test, p = 0.031) and having the harmful effect on grandsons (p = 0.019, Wilcoxon signed-rank test), which is predicted by SA-zygotic drive.
6. Discussion
The idea that the asymmetrical transmission of sex chromosomes leads to conflicts of interest within families was developed independently by Miller et al. (2006), in the context of nuclear families (SA-zygotic drive), and Euler & Weitzel (1996) and Chrastil et al. (2006) in the context of grandparental care. Our purpose here was to show that the invasion analysis of Chrastil et al. (2006) can be expressed as an extension of the more general theory of SA-zygotic drive and in a simpler context (Hamilton's rule of altruism) that is well understood by a wide diversity of biologists. We also set out to show why we consider the main conclusion of Chrastil et al. (2006)—that paternity uncertainty, and not sex chromosomal inheritance, is the major determinant of asymmetrical grandparental care—is not supported by the empirical data presently available.
Humans provide an unusually high opportunity for SA-zygotic drive to operate because their substantial amount of paternal investment in offspring sets them apart from most other mammals, and many other types of animals. The care given by post-reproductive grandparents to their grandchildren expands the capacity for SA-zygotic drive to operate in extended families. One of the major phenotypes predicted to evolve in grandparents in response to SA-zygotic drive is qualitatively the same as the prediction based on paternity assurance alone, i.e. investing more in matrilineal grandchildren. However, only SA-zygotic drive also uniquely predicts that mutations will accumulate that cause grandparents to help granddaughters at the expense of grandsons. Selection for this phenotype occurs only in PGMs, but our modelling analysis indicates that it can evolve in other types of grandparents as a correlated effect.
The pioneering invasion analysis by Chrastil et al. (2006) made the pivotal prediction that the asymmetrical inheritance of X chromosomes will make some categories of grandchildren more closely related to grandparents than others, and hence grandparental care should be asymmetrical. As pointed out by Fox et al. (2010), however, when both the X and autosomes are considered together, all grandparents are predicted to invest in all types of grandchildren (since genome-wide relatedness is high for all categories unless paternity uncertainty is very low), although more investment should accrue to grandchildren with higher X-linked relatedness to their grandparents. Our SA-zygotic drive approach makes the unique prediction that the evolution of selfish elements on the X will cause grandparents to directly harm grandsons (in order to reduce sib competition and increase the survival of granddaughters), despite the high levels of genome-wide relatedness to all categories of grandchildren. Just as the maternally transmitted endosymbiont Wobachia is selected to evolve a son-killer phenotype that reduces sib competition from male offspring that do not propagate it (despite the harm to the nuclear genome), so too is the X chromosome selected to harm the sex of a grandchild that does not carry it, despite the harm to the autosomes.
The single survey study that we found that separated grandparental care by the sex of the grandchild (reported successively in Euler & Weitzel (1996) and Chrastil et al. (2006)), found that both MGMs and PGMs tended to provide more care to granddaughters compared with grandsons. This pattern fits the prediction that X chromosome relatedness influences grandparental care, and it is consistent with the operation of the more general phenomenon of SA-zygotic drive operating through grandmothers. Despite this finding, however, Chrastil et al. (2006) concluded that the asymmetrical inheritance of the sex chromosomes had little influence on the pattern of grandparental care, and that paternity uncertainty was predominantly responsible for the observed patterns. This conclusion was based on measures of the relative amount of care provided by the MGM, MGF, PGM and PGF. The major limitation of these studies is that they are based on recollections of long-past grandchild–grandparent interactions, and it is not clear to us how well these recollections, and the survey questions used, truly represent total grandparental care.
The survival studies, in our view, should capture a more complete assessment of the impact of grandparental care on the fitness of grandchildren. The meta-analysis of the seven extant studies of grandmaternal care (Fox et al. 2010) indicates that the presence of grandmothers generally increased the survival of grandchildren except for the PGM/grandson category, where grandson survival decreased when the PGM was present. Fox et al. (2010) concluded that ‘Whether the grandmother effect is dependent on proportion of shared genes or only X-relatedness is difficult to discern at this point, as the two would seem to be so closely correlated’. We do not agree with this conclusion. The observed harming phenotype of PGMs seems poorly explained by the small differences in genome-wide relatedness to patrilineal grandchildren (0.23Pa versus 0.27Pa), but is readily explained by the invasion of selfish X-linked mutations that code for the sexually antagonistic phenotype (grandson-harming) predicted by SA-zygotic drive. Despite this interpretational disagreement, the grandson-harming results of Fox et al. (2010) provide strong support for the pivotal, and counterintuitive, prediction of SA-zygotic drive: PGMs harm grandsons that have zero X-linked relatedness to them. This finding also provides compelling evidence that SA-zygotic drive is plausibly operating in humans via grandparental care.
Care by grandmothers is common in many animals. For example, in species like elephants and deer, long-lasting matriarchic groups including a mother, her young offspring, her mature daughters and her daughters' offspring are common (Vaughan et al. 2000). These matriarchic groups, however, provide little opportunity for the operation of SA-zygotic drive via grandparental care because the X-linked asymmetries in relatedness are absent outside the patriline. If similar matriarchic groups were studied in female-heterogametic groups, like birds, then the selfish genetic elements that fuel SA-zygotic drive would be predicted to evolve in the context of matrilineal grandmaternal care.
The next step in testing for the operation of SA-zygotic drive in humans should focus on fathers. The paternal X is strongly selected to accumulate mutations that bias paternal investment in daughters and their Y is similarly selected to influence them to invest more in sons. Because of the strong degeneration of the human's Y, the X should prevail in an X–Y arms race and mutations should accumulate that cause fathers (and possibly mothers as a correlated effect) to favour their daughters over their sons (Rice et al. 2008). The recent finding that grandparental investment favours granddaughters at the expense of grandsons (Fox et al. 2010) suggests that a similar phenomenon should have evolved at the level of fathers within nuclear families—a prediction that would apply to all species with male parental investment and heterogamety. Then why has not a daughter-harming phenotype of fathers been widely reported, as predicted by SA-zygotic drive? Given that grandmother effects were initially obscured by pooling grandsons and granddaughters, we suspect that this same factor may have interfered with the detection of a sexually antagonistic father effect. Human males also (i) provide less child care than females and (ii) have a counterbalancing influence of the Y chromosome, which collectively weakens an X-effect in fathers, and therefore makes it harder to detect. Hopefully, our study will stimulate a search for SA-zygotic drive via a father's asymmetrical influence on the fitness of his sons and daughters.
Acknowledgements
This work was supported by grants to W.R.R. (National Science Foundation (DEB-0128780 and DEB-0111613) and National Institutes of Health (1R01HD057974-01)), S.G. (National Science Foundation (DEB-0111613) and National Institutes of Health (GM56693)) and to U.F. (The Wenner-Gren Foundations). We thank Kathryn Schoenrock for copyediting assistance.
References
- Beeman R. W., Friesen K. S., Denell R. E.1992Maternal-effect selfish genes in flour beetles. Science 256, 89–92 (doi:10.1126/science.1566060) [DOI] [PubMed] [Google Scholar]
- Bellis M. A., Hughes K., Hughes S., Ashton J. R.2005Measuring paternal discrepancy and its public health consequences. J. Epidemiol. Commun. Health 59, 749–754 (doi:10.1136/jech.2005.036517) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop D. I., Meyer B. C., Schmidt T. M., Gray B. R.2009Differential investment behavior between grandparents and grandchildren: the role of paternity uncertainty. Evol. Psychol. 7, 66–77 [Google Scholar]
- Chrastil E. R., Getz W. M., Euler H. A., Starks P. T.2006Paternity uncertainty overrides sex chromosome selection for preferential grandparenting. Evol. Hum. Behav. 27, 206–223 (doi:10.1016/j.evolhumbehav.2005.09.002) [Google Scholar]
- Coon C. S.1971The hunting peoples. Boston, MA: Little [Google Scholar]
- Euler H. A., Weitzel B.1996Discriminative grandparental solicitude as reproductive strategy. Hum. Nat. 7, 39–59 [DOI] [PubMed] [Google Scholar]
- Fox M., Sear R., Beise J., Ragsdale G., Voland E., Knapp L. A.2010Grandma plays favourites: X-chromosome relatedness and sex-specific childhood mortality. Proc. R. Soc. B 277, 567–573 (doi:10.1098/rspb.2009.1660) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koerich L. B., Wang X., Clark A. G., Carvalho A. B.2008Low conservation of gene content in the Drosophila Y chromosome. Nature 456, 949–951 (doi:10.1038/nature07463) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laham S. M., Gonsalkorale K., von Hippel W.2005Darwinian grandparenting: preferential investment in more certain kin. Pers. Soc. Psychol. Bull. 31, 63–72 (doi:10.1177/0146167204271318) [DOI] [PubMed] [Google Scholar]
- Lahn B. T., Page D. C.1997Functional coherence of the human Y chromosome. Science 278, 675–680 (doi:10.1126/science.278.5338.675) [DOI] [PubMed] [Google Scholar]
- Lemos B., Araripe L. O., Hartl D. L.2008Polymorphic Y chromosomes harbor cryptic variation with manifold functional consequences. Science 319, 91–93 (doi:10.1126/science.1148861) [DOI] [PubMed] [Google Scholar]
- Lockard J. S., Daley P. C., Gunderson V. M.1979Maternal and paternal differences in infant carry—United-States and African Data. Am. Nat. 113, 235–246 [Google Scholar]
- McElreath R., Boyd R.2007Mathematical models of social evolution: a guide for the perplexed. Chicago, IL: University of Chicago Press [Google Scholar]
- Miller P. M., Gavrilets S., Rice W. R.2006Sexual conflict via maternal-effect genes in ZW species. Science 312, 73–73 (doi:10.1126/science.1123727) [DOI] [PubMed] [Google Scholar]
- Rice W. R., Gavrilets S., Friberg U.2008Sexually antagonistic ‘zygotic drive’ of the sex chromosomes. PLoS Genet. 4, e1000313 (doi:10.1371/journal.pgen.1000313) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice W. R., Gavrilets S., Friberg U.2009Sexually antagonistic chromosomal cuckoos. Biol. Lett. 5, 686–688 (doi:10.1098/rsbl.2009.0061) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaughan T. A., Ryan J. M., Czaplewski N. J.2000Mammalogy. Fort Worth, TX: Saunders College Pub [Google Scholar]