The evolution of migration in a seasonal environment

Abstract

Despite the fact that migration occurs in a wide variety of taxa worldwide, little is known about the conditions under which migration is expected to evolve from an ancestral resident population. We develop a model that focuses on ecological factors affecting the evolution of migration in a seasonal environment within a genetically explicit framework. We model the evolution of migration for two common types of migration: ‘shared breeding’ where migrants share a breeding ground with residents and migrate to a separate non-breeding area, versus ‘shared non-breeding’, where migrants share a non-breeding ground with residents and migrate to a separate breeding area. Ecologically, migration is more easily established in the shared-breeding case versus the shared-non-breeding case. Genetically, the additive effect of a migratory allele affects its establishment more in the shared-non-breeding case versus the shared-breeding case, whereas the dominance effect of the allele affects its establishment more in the shared-breeding case versus the shared-non-breeding case. Generally, migratory alleles can invade even when residents are competitively superior to migrants during the shared season. Partial migration occurs when the population is polymorphic for migratory and non-migratory alleles, and is dependent upon which season is shared and the additive and dominance behaviour of the migratory allele.

1. Introduction

Migration is one of the most fascinating behaviours found in nature, but how it evolved in such a wide variety of taxonomic groups and geographical locations has largely remained a mystery. There have been several hypotheses that propose the steps involved in the transition from a sedentary to a migratory species over an evolutionary time scale (Cox 1968, 1985; Levy & Stiles 1992; Rappole & Jones 2002), but these are often specific to a particular taxon or geographical region and are difficult to test in contemporary populations. Perhaps more informative for understanding why migration is so common are models that produce quantitative predictions for the demographic conditions under which migration is expected to evolve from a resident (sedentary) ancestral population. Lundberg (1987) derived conditions for the evolution of partial migration (i.e. some individuals in a population are migratory while others are resident) under the scenario in which migratory individuals shared a breeding site with the residents but migrated to a separate non-breeding site (what we term here as the ‘shared-breeding’ case). Kaitala et al. (1993) extended this shared-breeding model to include age-structure and a stochastic environment, and earlier work by Cohen (1967) also assumed a shared-breeding case. Bell (2000) studies and Taylor & Norris (2007) derived conditions for both partial and complete migration in a ‘shared-non-breeding’ case, whereby migrants establish a new breeding site and return to the ‘resident’ site during the non-breeding period. Although it is well documented that partially migratory populations may be composed of migrant and resident individuals that either share a breeding site (e.g. Smith & Nilson 1987; Andriaensen & Dhondt 1990; Boyle 2008) or share a non-breeding site (e.g. Klein & Brown 1994; Alonso et al. 2000; Morrissey 2004), no genetically explicit model has been developed to compare the conditions under which migration is expected to evolve under these two different cases.

Kokko & Lundberg (2001) and Holt & Fryxell (in press) examined conditions for migration using a two-habitat model that allowed for populations to be resident at both the ‘breeding’ or ‘non-breeding’ site. Kokko & Lundberg (2001) found that migration evolves when breeding sites are a limiting resource. Holt & Fryxell (in press) demonstrated that a species capable of persisting as residents in two separate sites is vulnerable to the invasion of a migratory genotype if there is a difference in geometric mean fitness between habitats. While both models are useful under assumptions of weak seasonality, it is likely that migratory behaviour in many species arose from the ability of individuals to take advantage of seasonal variation in resources (e.g. Boyle & Conway 2007).

Thus, we still lack a general model for the evolution of migration in a seasonal environment that incorporates genetic, ecological and demographic information. In this paper, we use a simple two-season population model with a single genetic locus determining migratory behaviour to derive the conditions under which (i) a migratory allele can invade a resident population and (ii) a resident allele can counter-invade a migratory population and create a stable genetic polymorphism (i.e. partial migration).

Our analysis uses a standard technique in theoretical evolutionary genetics to understand the evolution of migration, namely evolutionary invasion analysis (e.g. Otto & Day 2007). An evolutionary invasion analysis calculates whether a new mutation will spread in a population. An evolutionary invasion analysis is particularly applicable to our study of migration because we focus on the initial evolutionary transition to migration. During this initial transition, the ancestral population is not migratory and the migratory behaviour must arise by rare new mutations. The single locus two-allele model will give insight into how the additive and dominance effects of a migratory allele affect the establishment of migration.

2. Overview of model and analysis

We start with a resident (non-migratory) ancestral population in which non-migratory juveniles may exhibit one-way dispersal from the natal site to the migratory site. Dispersal is distinguished from migration in that dispersal occurs only once and is unidirectional, whereas migration is the bidirectional movement of an individual throughout its lifetime (Dingle 1996). Furthermore, our model assumes that migration is a life strategy, such that if an individual is migratory when it is born, then it is migratory throughout its life.

We consider two cases whereby migration may evolve. In the shared-breeding case, migratory individuals breed randomly with resident individuals, they migrate to a different site for the non-breeding season and, prior to the subsequent breeding season, return to the resident ancestral breeding grounds (figure 1a). In the shared-non-breeding case, migratory individuals breed separately from residents, but migratory offspring may be born on either the resident or migrant breeding grounds provided that both migratory and resident alleles are segregating (figure 1b).

Figure 1.

Two cases under which migration may evolve from a resident ancestor. (a) In the shared-breeding case, migrants initially share a breeding site with residents and migrate to a new site during the non-breeding period. (b) In the shared-non-breeding case, migrants initially share a non-breeding site with residents and migrate to a different site during the breeding period. Under either case, if a migratory allele invades a resident population, it may remain partially migratory (both residents and migrants) or may evolve to be completely migratory (loss of residents). Grey region, resident site; black ring, migrant site.

For migratory behaviour, we model a single locus in which the wild-type allele (a) is resident and the alternate allele (A) is migratory. Individuals that are homozygous for the migratory allele take on the migratory life strategy with probability x, and individuals that are heterozygous for the migratory allele take on the migratory life strategy with probability hx, where 0 < h < 1. Accordingly, the additive effect of the migratory allele is x/2 and the dominance effect is h. When migratory individuals breed separately from residents, there is still gene flow between the migratory and resident lineages provided that either hx or x are less than one. We assume that migratory individuals follow environmental clues such that they time migration correctly. For instance, in the shared-non-breeding case, migrants wait until just prior to the breeding season to migrate. This assumption coincides with the finding that in blackcaps (Sylvia atricapilla), the probability of migrating and migratory activity is genetically correlated (Pulido et al. 1996).

We assume strong seasonality such that, in the shared-breeding case, migratory individuals over-winter but cannot stay and breed at the migratory site (birth rate is zero) and that, in the shared-non-breeding case, migratory individuals breed but cannot ‘over-winter’ at the migratory site (survival is zero). Allowing for juvenile dispersal in the shared-non-breeding model has important consequences because an individual with a resident genotype born from heterozygote parents on the migratory breeding grounds would otherwise die if it stayed there for the non-breeding season. In the shared-breeding model, the migratory non-breeding site acts as a black-hole sink (sensu Gomulkiewicz et al. 1999) for individuals with a resident genotype that happen to disperse there.

The fitness of a genotype is defined by its density-dependent birth rate, its density-dependent survival during the non-breeding season, its probability of surviving migration if it is migratory and its probability of surviving dispersal if it is dispersive. It is assumed that all adults survive the breeding season.

Discrete-time recursion models are derived for both the shared-breeding and shared-non-breeding models (see appendix A). Table 1 is provided as a guide to the parameters that are presented in the recursion models and will aid in the interpretation of stability conditions presented in §3. We analyse the situations under which a migratory allele that arises by mutation can invade an ancestral resident population that is at demographic equilibrium. Upon the introduction of a migratory allele, a local stability analysis is performed to determine whether the resident equilibrium is stable. If stable, then the overall growth rate of migratory genotypes is less than 1 and it, therefore, does not invade the resident population. If unstable, then the migratory allele can invade the population. In addition, we also derive conditions for the stability of the migratory equilibrium upon introduction of a resident allele. Together, these conditions are informative about when a population is expected to be resident, partially migratory and completely migratory with respect to the alleles that are present in the population.

Table 1.

Definitions of parameter values used in the models. (HF, high fecundity; LS, low survivorship.)

parameter	description	value
general
Q	type of generation time	0 = non-overlapping, 1 = overlapping
x, h	probabilities that an individual will be migratory. An individual with an AA genotype is migratory with probability x. An individual with an Aa genotype is migratory with a probability hx	x varies from 0.5 to 1, h equals 0.5
sM	migratory survival	0.95
sD	dispersal survival	0.95
m12	dispersal probability of non-migratory juvenile from resident site to migratory site	0.05
m21	dispersal probability of non-migratory juvenile from migratory site to resident site	0–1.0
bR	density-independent birth rate for residents	{0.5 for LF–HS, 1.0 for HF–LS} (assuming overlapping generations)
bM	density-independent birth rate for migrants	varies
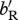
	density-dependent effect on birth for residents	{7.02 × 10−6, 7.02 × 10−5, 2.63 × 10−6, 2.63 × 10−5}
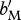
	density-dependent effect on birth for migrants	varies
dR	density-independent survival for residents	{0.95 for LF–HS, 0.7125 for HF–LS}
dM	density-independent survival for migrants	varies
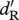
	density-dependent effect on survival for residents	5 × 10−6
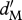
	density-dependent effect on survival for migrants	varies
equilibrium parameters
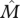
	migrant population size	depends on model and equilibrium; generally a complicated function
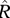
	resident population size	depends on model and equilibrium; generally a complicated function
stability of residents to migratory invasion at equilibrium
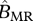
	birth rate of a migrant–resident mating
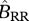
	birth rate of a resident–resident mating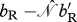
ΔM	survival of migrants (shared breeding)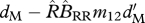
ΔR	survival of residents (shared breeding)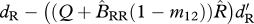
ΞM	survival of migrants (shared non-breeding)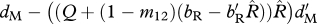
ΞR	survival of residents (shared non-breeding)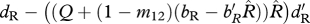
stability of migrants to resident invasion at equilibrium
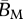
	average birth rate of a migrant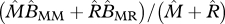
	average birth rate of a resident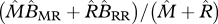
	overall average birth rate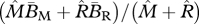
ΩM	survival of migrants (shared breeding)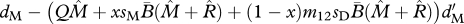
ΩR	survival of residents (shared breeding)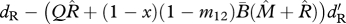
ΨM	survival of migrants (shared non-breeding)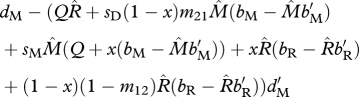
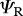
	survival of residents (shared non-breeding)

Finally, we explore the effects of the following parameters on the stability of the resident and migratory equilibrium: density-dependent and independent components of birth and survival, and the probability of a genotype migrating or dispersing. We also examine the consequence of overlapping versus non-overlapping generations. Overlapping generations may be important with respect to the evolution of migration because in the shared-breeding case, with overlapping generations, allele frequencies do not attain Hardy–Weinberg proportions after random mating.

3. Results

(a). Conditions for invasion of the migratory allele

In the shared-breeding model, the resident equilibrium is unstable (migratory allele can invade) when the following condition holds (see table 1 for complete list of terms and the appendix for the derivation of this equation):

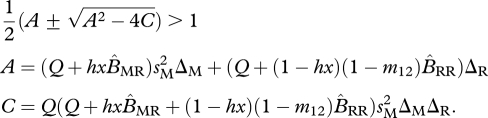3.1

When generations are non-overlapping (Q = 0), condition (3.1) simplifies to 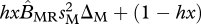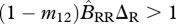, which is easily interpretable as the sum of the growth rates of migratory Aa individuals and non-migratory Aa individuals must be greater than 1. The C term adjusts the growth rate to account for overlapping generations (Q = 1).

In the shared-non-breeding model, the resident equilibrium is unstable when at least one of the following two conditions hold:

3.2a

or

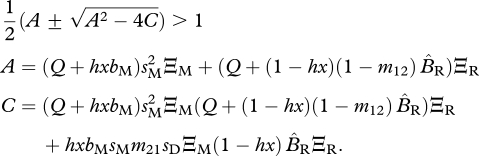3.2b

Condition (3.2a) defines the stability of the resident equilibrium unless m₂₁ (probability of dispersal from the migratory site to the resident site) is large and x is small, otherwise condition (3.2b) defines stability.

When condition (3.2a) dominates, destabilization of the resident equilibrium in the shared-non-breeding case is driven by the success of homozygous (AA) migrants. This is in contrast to the shared-breeding case, where destabilization is driven by heterozygous (Aa) individuals. The reason is that, in the shared-non-breeding case, there is a degree of inbreeding occurring owing to assortative mating. In the shared-non-breeding case only AA and Aa migrants mate with each other, whereas in the shared-breeding case, AA, Aa and aa individuals (both migrants and residents) randomly mate.

When x is small and m₂₁ is large, resident Aa individuals contribute to destabilizing the resident equilibrium. The requirement that m₂₁ needs to be large indicates that dispersal of resident Aa individuals to the ancestral grounds is an important factor destabilizing the resident equilibrium.

(b). Equivalence between shared-breeding and shared-non-breeding models

Here, we determine the demographic conditions under which the shared-breeding and shared-non-breeding models are equivalent with respect to the invasion of the migratory allele. Although Taylor & Norris (2007) stated that the conditions would be the same for the shared-breeding and shared-non-breeding cases, we show that is actually not correct. The shared-breeding and shared-non-breeding models are demographically equivalent when the growth rates of the migratory allele are the same. To determine these conditions, we set x = 1, h = 1 and Q = 0, which follow the assumptions of the Taylor & Norris (2007) ecological model.

Under these assumptions, in the shared-breeding case, the growth rate is 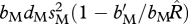, and, in the shared-non-breeding case, the growth rate is 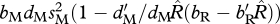. Equating these growth rates leads to the equivalence condition:

3.3

Condition (3.3) says that the shared-breeding case (left side of equation) is equivalent to the shared-non-breeding case (right side) if the scaled effect density dependence on migratory birth rates in the shared-breeding case is times greater than the scaled effect of density dependence on migratory survival rate in the shared-non-breeding case. In other words, if the scaled effects of density dependence on birth and survival are equal, then a migratory allele will have an easier time invading the shared-breeding case versus the shared-non-breeding case.

When generations are overlapping (Q = 1), the equivalence condition is

3.4

The equivalence condition (3.4) demonstrates that the shared-breeding case is even more strongly favoured when generations are overlapping compared with when generations are non-overlapping because the term 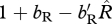is multiplied by 1 + 1/b_M, which is greater than one. Overall, our analysis demonstrates that the shared-breeding and shared-non-breeding cases are not ecologically equivalent with respect to the invasion of the migratory allele.

(c). Numerical analysis for the invasion of the migratory allele: the effects of life history and probability of migration

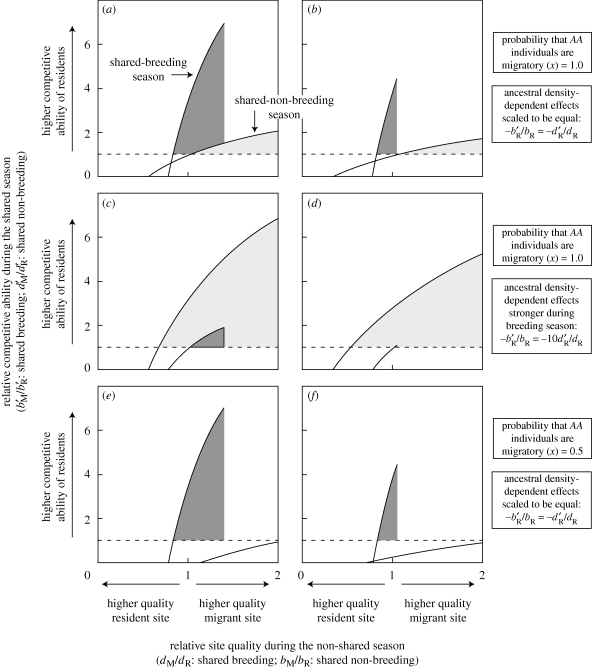
Two common life histories in animals are species that have high fecundity and low survivorship (HF–LS) and species that have low fecundity and high survivorship (LF–HS). Figure 2a,b shows that when the scaled density-dependent effects on birth are equal to the scaled density-dependent effects on survival in the ancestor, a migratory allele can invade more easily in the shared-breeding versus shared-non-breeding case for both the HF–LS and LF–HS life histories, in agreement with the analysis in §3b. The migratory allele invades more easily because it can invade when (i) the migratory site is of poorer quality and (ii) migrants are poorer competitors relative to residents.

Figure 2.

Conditions under which a migratory allele is able to invade a resident population in relation to competition (y-axis) and relative site quality (x-axis). In the ancestor, scaled density-dependent effects on birth in the shared-breeding case and on survival in the shared-non-breeding case are equal for the (a) high-fecundity and low-survival (HF–LS) life history and for the (b) low-fecundity and high-survival (LF–HS) life history, respectively with x = 1.0 and h = 0.5. Parts (a,b) support the prediction from condition (3.4) that the migrant allele will invade more easily in the shared-breeding case for both life histories when density-dependent effects on birth and survival are scaled to be equal. In the ancestor, scaled density-dependent effects on birth in the shared-breeding case are 10 times greater than the scaled density-dependent effects on survival in the shared-non-breeding case for the (c) HF–LS life history and for the (d) LF–HS life history, respectively, with x = 1.0 and h = 0.5. Parts (c,d) support the prediction from condition (3.4) that the migrant allele can invade more easily in the shared-non-breeding case for both life histories when density-dependent effects on birth are stronger than effects on survival. In (e,f), the demographic parameters are the same as in (a,b), except the migration probability is lowered to x = 0.5. Parts (e,f) suggest that the invasion of the migratory allele is not affected strongly by x in the shared-breeding case, but is affected strongly in the shared-non-breeding case. In the shared-breeding scenario, the sharp threshold along the x-axis occurs because the probability of survival cannot be greater than 1.0. Thus, if the resident ancestors' survivorship is 0.7125, the maximum value of d_M/d_R is 1.4. For (a,c,e), d_R = 0.7125 and b_R = 1.0, and for (b,d,f), d_R = 0.95 and b_R = 0.5. For (a–f), 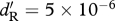, for (a,e) 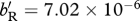, for (b,f) 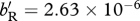, whereas for (c) 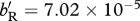and for (d) . All other parameter values are fixed across panels: Q = 1, m₁₂ = 0.05, m₂₁ = 0.05, s_M = 0.95 and s_D = 0.95.

When the scaled density-dependent effects on birth are greater than times the scaled density-dependent effects on survival, the analysis in §3b predicts a migrant allele will invade more easily in the shared-non-breeding case. Figure 2c,d illustrates this point by showing a large reduction in the parameter space, allowing for migration in the shared-breeding case and an increase in parameter space in the shared-non-breeding case.

Lastly, when the migration rate is reduced from x = 1.0 to x = 0.5, the stability conditions do not change for the shared-breeding case but dramatically changed for the shared-non-breeding case (compare figure 2a with 2e, and figure 2b with 2f). This difference occurs in both types of life histories.

(d). Conditions for counter-invasion of the resident allele

For the shared-breeding model, a population that is fixed for the migratory allele has an unstable demographic equilibrium in the presence of a rare resident allele (i.e. the resident allele is able to invade a fully migratory population potentially resulting in a partially migratory population) when:

3.5

The form of condition (3.5) is the same as condition (3.1), although they will differ quantitatively because the equilibrium structure of a population fixed for the migratory allele is different from that of a population fixed for the resident allele. In particular, provided that x < 1, both migratory and resident individuals will be present when a population is fixed for the migratory allele A.

In the shared-non-breeding model, the instability conditions for the migratory equilibrium are similar in form to condition (3.2). If either of the following conditions hold,

3.6a

or

3.6b

then the fully migratory equilibrium is unstable to the invasion of the resident allele. Condition (3.6a) defines the stability condition when resident AA individuals are absent. This occurs when x is large.

(e). Numerical analysis for counter-invasion of the resident allele

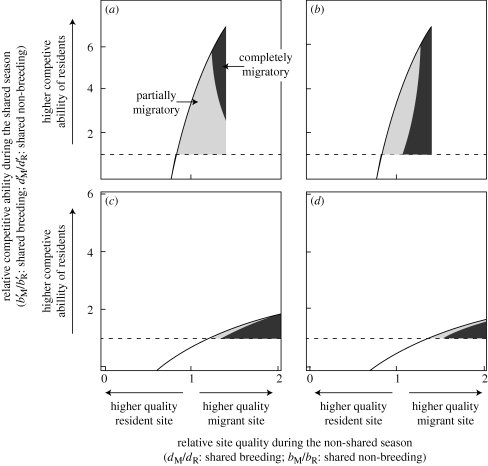
The season that is shared between migrants and residents influence the stability of the equilibrium when the population is fixed for the migratory allele (figure 3). In the shared-breeding case and for HF–LS species, migrants can often be much weaker competitors (figure 2a,e), which tends to allow the resident allele to counter-invade the migratory population, resulting in a stable polymorphism (partial migration) that occurs under a range of x values (figure 3a,b). For an LF–HS species in the shared-breeding case, a stable polymorphism is typical over a broad range of x (data not shown). In the shared-non-breeding case, the results for both life histories are similar (figure 3c,d shows conditions for HF–LS species only). Opposite to the shared-breeding case, as x → 1, the conditions for a stable polymorphism decline (figure 3c,d). When x = 1, the resident allele never invades (always complete migration) and when x = 0.5, the resident allele always invades (always partial migration).

Figure 3.

Counter-invasion of resident alleles in migratory populations and conditions for partial migration in relation to competition (y-axis) and relative site quality (x-axis). (a,b) The shared-breeding case and (c,d) the shared-non-breeding case with different values of x for each panel. For all panels, the partial migration (grey) region represent the conditions in which the growth rate of the resident allele is greater than 1 in a population otherwise fixed for the migratory allele (i.e. a stable polymorphism will occur). The dark region represents conditions in which the growth rate of the resident allele is less than or equal to 1 (counter-invasion is not successful and population remains migratory). For the shared-non-breeding case, x = 1 is not shown because the resident allele never invades (population always completely migratory) and x = 0.5 is not shown because the resident allele always invades (population always partially migratory). All panels represent the case for HF–LS species and all parameters, except x, correspond to figure 2a,b. (a) x = 1; (b) x = 0.5; (c) x = 0.85; (d) x = 0.7.

(f). Resident reservoir for migratory invasion

If the probability of the migratory strategy is low, conditions favouring the evolution of migration are very restrictive or non-existent in the shared-non-breeding case, but remain identical or nearly identical in the shared-breeding case (see figure 2, comparing top versus bottom). The reason for the difference is that, in the shared-breeding case, resident individuals persist on the ancestral grounds. By contrast, in the shared-non-breeding case, resident individuals typically die on the migratory breeding grounds when dispersal rates are low. In the shared-non-breeding model, if the dispersal rate between the migratory and resident breeding grounds is increased, the conditions for the evolution of migration become more favourable and fully recover as m₂₁ → 1.

4. Discussion

We provide a model that combines genetic and demographic information to predict the conditions under which (i) a migratory allele will invade a resident population and (ii) a population will be partially migratory. Our analysis shows that the shared-breeding and shared-non-breeding cases are not equivalent. The properties of heterozygotes determine whether a migratory allele invades in the shared-breeding case, whereas, in the shared-non-breeding case, the properties of homozygotes determine the invasion conditions of the migratory allele (provided the probability of migration is relatively high and dispersal rates are low). Furthermore, there are also purely demographic (non-genetic) reasons for the differences between the shared-breeding and shared-non-breeding cases. In the shared-non-breeding case, migrants experience increased density-dependent effects because they must over-winter with residents after the population has undergone a period of growth through birth. In the shared-breeding case, migrants over-winter separately from residents and, thus, do not experience strong density-dependent effects during survival because the migratory non-breeding population is initially not as large as the resident non-breeding population.

It is important to note that while ecologically the shared-breeding case is favoured, genetically the shared-breeding case is more sensitive to the dominance effect of a migratory allele. If a migratory allele is strongly recessive (h ≪ 0.5), then the benefit of the shared-breeding case as a result of ecology may be counterbalanced by the recessivity of migration. Although the shared-breeding case is sensitive to the dominance effect of a migratory allele, the shared-non-breeding case is sensitive to the additive effect of the migratory allele. In the shared-breeding case, a reduction in x from 1.0 to 0.5 did not affect the establishment of the migratory allele, but in the shared-non-breeding case, its establishment was strongly affected.

Ecologically, our results suggest that a comparison between the scaled effects of density dependence on birth and the scaled density-dependent effects on survival will differentiate whether migration is more likely to evolve through shared breeding versus shared non-breeding. When generations are overlapping, the condition for the shared-breeding case to be preferred over the shared-non-breeding case is that the scaled density-dependent effect on birth is less than 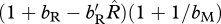times the scaled density-dependent effects on survival. When generations are non-overlapping, the condition is that the scaled density-dependent effect on birth is less than 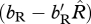times the scaled density-dependent effects on survival.

We assume strong seasonality such that non-migratory individuals born on the migratory breeding grounds die during the non-breeding season (shared-non-breeding case). Likewise, non-migratory individuals that disperse to the non-breeding grounds also die during the breeding season (shared-breeding case). Further analysis is required when weaker seasonality is assumed, allowing for survival on migratory sites throughout the year. Holt & Fryxell's (in press) model assumes weak seasonality, and a promising approach may be to integrate explicit genetic information in their model.

The threshold of invasion by the migratory allele is characterized by a positive relationship between the quality of the migrant site during the non-shared season and the competitive ability of residents during the shared season (figure 2). How high these competitive asymmetries and site-quality ratios can reach before the migratory allele is unable to invade depends on the interaction between life history and whether it is a shared-breeding or shared-non-breeding case.

Our results support the empirical work of Berthold & Querner (1981) that partial migration in a species can be genetically determined as opposed to environmentally determined. More broadly, our results suggest that partial migration occurs under the shared-non-breeding case when there is a migratory site of high quality and migrants are poor competitors relative to residents, or when the migratory site is of lower quality and migrants are relatively better (but not superior) competitors relative to residents (figure 3c,d). Partial migration occurs in the shared-breeding case when migratory-site quality is not too high and the relative competitive ability of migrants is not too low (figure 3a,b). It is fairly easy to infer why stronger relative density dependence on migrants promotes the evolution of partial migration in the shared-non-breeding case. When migrants are strong competitors, complete migration evolves and cannot be invaded by the resident allele. It is more difficult to infer why weaker density dependence on migrants favours partial migration in the shared-breeding case. Insight into why weaker density dependence favours partial migration is that the resident allele initially invades primarily through offspring of Aa × AA matings. On average, an Aa × AA mating involves individuals that have the migratory life strategy. If the birth rate of migratory parents is restricted by density dependence, then growth rate of the resident allele will also be restricted. A result consistent with this inference is that as the probability of migration declines, the resident allele will not invade when the quality of the migratory site is high. With a high-quality migratory site and a lower probability of migration, the resident site has a higher equilibrium number of AA individuals upon the introduction of a non-migratory allele (a). There is, accordingly, stronger density dependence.

Our results are consistent with the general results of Kokko & Lundberg (2001) (eqns (12a,b)) and Holt & Fryxell (in press) and indicate that important insight into differences between the shared-breeding and shared-non-breeding models of migration is gained by explicitly modelling underlying density-dependent effects. Evolutionary stable strategy models that subsume density-dependent birth and survival into a single reproductive term (often modelled as r) can overlook demographic processes that differentiate types of migration, such as shared breeding versus shared non-breeding.

The genetic model used in this paper follows the standard approach in evolutionary invasion analysis that assumes a single allele arises by mutation that causes migratory behaviour (Otto & Day 2007). During the initial evolutionary transition to migration in an otherwise non-migratory species, alleles must first arise through mutation, which occurs at a low rate. Even if there are several loci that may affect migration, there may be a low probability that more than one locus is segregating an allele that causes migration. In species that are migratory, genetic studies have found supporting evidence that the behaviour is polygenetic (Berthold 1988; Pulido & Berthold 2003; Pulido 2007), but it is important to note that the present-day polygenetic nature of migration is probably the result of thousands to millions of years of history as a migratory species. During this period, there has been time for alleles at different loci that affect migration to arise by mutation and establish themselves in a population. A polygenic model of migratory behaviour is probably necessary to understand present-day evolutionary processes in species that have a long history of migratory behaviour, particularly with respect to understanding evolutionary response to environmental change (Pulido et al. 2001).

Our model did not allow for the possibility that residency and migratory behaviour may depend on an individual's sex, age or both (e.g. Newton 2008, ch. 15). At the individual level, a mixed-strategy involving both residency and migration may be an evolutionary stable strategy when generations are overlapping (Kaitala et al. 1993).

Our work should be viewed as a foundation in which specific evolutionary and ecological circumstances can be overlaid and for which specific parameters such as habitat quality, density dependence and the genetic control of migration can be relatively easily adjusted to derive predictions about specific taxa or geographical regions.

APPENDIX A. THE EVOLUTION OF MIGRATION IN A SEASONAL ENVIRONMENT

Individuals are diploid. The number of resident individuals is R_i and migrant individuals is M_i for i ∈ {AA, Aa, aa}. The order of events during the life cycle is birth → migration or dispersal → survival → migration. An indicator variable Q denotes overlapping Q = 1 versus non-overlapping (Q = 0) generations.

(a). Shared-breeding model

During reproduction, three types of matings can occur at the level of resident and migratory individuals. A resident can mate with a resident, a resident can mate with a migrant or a migrant can mate with a migrant. The number of viable offspring when a resident mates with a resident is B_RR, when a resident mates with a migrant the number of offspring is B_MR and when a migrant mates with a migrant the number of offspring is B_MM. For simplicity, we assume B_MR = B_MM. Birth is density dependent and following Taylor & Norris (2007) is modelled as 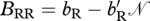and 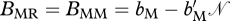, where b_i (i ∈{R,M}) is the density-independent birth rate and (i ∈ {R, M}) is the effect of density-dependence on birth rate multiplied by 𝒩, the total population size (𝒩 = R_AA + R_Aa + R_aa + M_AA + M_Aa + M_aa). A linear assumption in density dependence results in population dynamics that tend to be non-oscillatory and non-chaotic. It is important to emphasize that our model of birth gives the number of viable offspring that survive up to the non-breeding season. Accordingly, it incorporates both birth and offspring survivorship during the breeding season. Residents survive during the non-breeding season with probability 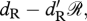where ℛ is the number of resident individuals. Migrants survive with probability 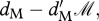where ℳ is the number of migrant individuals. During migration, the probability of survival is s_M.

For N ∈ {R,M}, after reproduction, the numbers of offspring for each genotype are

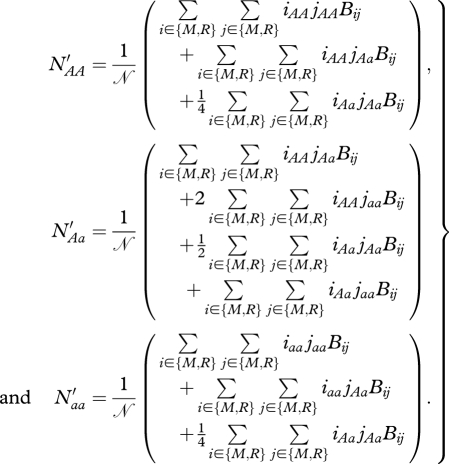A1

Following survival and immediately before the next breeding season, resident numbers are

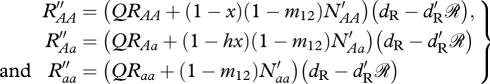A2

where

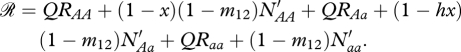The parameter m₁₂ is the dispersal rate of non-migratory offspring from the ancestral breeding grounds to the migratory grounds. Migrants that survive to breed are required to survive migration and survive the non-breeding season resulting in the following recursive step:

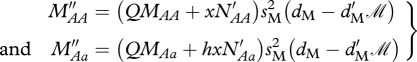A3

where

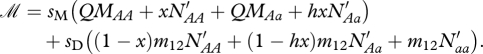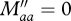because aa individuals are resident. s_M is the survival of migrants during migration and s_D is the survival probability of disperses during dispersal.

(b). Shared-non-breeding model

Birth occurs separately, but for N ∈ {R,M} offspring numbers for both migrants and residents can be expressed as:

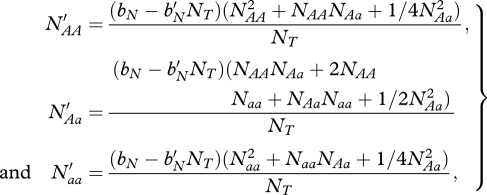A4

where N_T = N_AA + N_Aa + N_aa.

Density-dependent survival occurs together on the ancestral grounds. For individuals that were on the migratory grounds during the breeding season, they need to disperse or migrate to the ancestral grounds in order to survive. Genotype numbers following survival and migration are

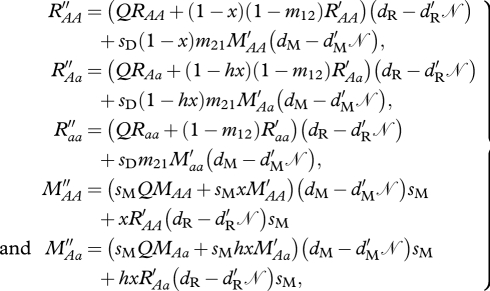A5

where the size of the population prior to survival is

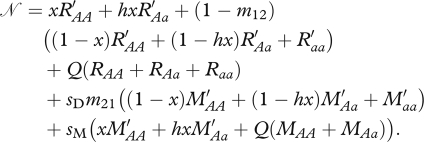A6

m₁₂ is the dispersal rate of non-migratory offspring from the natal grounds to the migratory grounds. m₂₁ is the dispersal rate of non-migratory offspring from the migratory natal grounds to the non-breeding grounds.

(c). Local stability analysis

There are six types of individuals in the two models: resident AA, Aa and aa individuals and migratory AA, Aa, aa individuals. At demographic equilibrium, a Jacobian matrix can be written given the changes in size of the six types of individuals. Ordering the derivatives properly results in a Jacobian matrix with block-diagonal structure in which one block consists of aa individuals and the second block consists of AA and Aa individuals when analysing the stability of the resident equilibrium. Eigenvalues of the block consisting of AA and Aa individuals gives the overall growth rates for these individuals near the demographic equilibrium when that equilibrium is subject to a small perturbation, such that an A allele is introduced by mutation. The eigenvectors of the block give the directions of growth. The stability of the fully migratory equilibrium follows the same approach, except that the growth rate of the block consisting of aa and Aa individuals is calculated. In §3, the instability conditions of the demographic equilibria are given. Inspection of the eigenvectors associated with the eigenvalues indicates that when an instability condition is met, the population moves away from an equilibrium point.