Folding and Finding RNA Secondary Structure

SUMMARY

Optimal exploitation of the expanding database of sequences requires rapid finding and folding of RNAs. Methods are reviewed that automate folding and discovery of RNAs with algorithms that couple thermodynamics with chemical mapping, NMR, and/or sequence comparison. New functional noncoding RNAs in genome sequences can be found by combining sequence comparison with the assumption that functional noncoding RNAs will have more favorable folding free energies than other RNAs. When a new RNA is discovered, experiments and sequence comparison can restrict folding space so that secondary structure can be rapidly determined with the help of predicted free energies. In turn, secondary structure restricts folding in three dimensions, which allows modeling of three-dimensional structure. An example from a domain of a retrotransposon is described. Discovery of new RNAs and their structures will provide insights into evolution, biology, and design of therapeutics. Applications to studies of evolution are also reviewed.

Combining sequence comparison and thermodynamic considerations with experimental approaches such as chemical mapping and NMR allows rapid modeling of RNA secondary structure.

Cellular RNA was considered merely an intermediate between DNA and protein for much of the history of molecular biology (except in RNA viruses). The discovery of catalytic RNA showed that this schema had to be revised. The finding that RNA could possess functionality once believed to be the sole domain of protein enzymes, led to the hypothesis that RNA could have preceded protein and DNA in an “RNA World.” Echoes of the RNA world remain in that RNA continues to perform functions developed early in evolution, e.g., as the catalyst for protein synthesis (Moore and Steitz 2010). There is recent evidence that an unexpectedly large fraction of DNA in higher eukaryotes, perhaps 90%, is transcribed into RNA (Birney et al. 2007). A positive correlation between an increased proportion of noncoding versus coding RNA and an organism’s developmental complexity has been observed (Taft and Mattick 2003). This trend has been suggested to mean that noncoding RNA represents a “new genetics” and may very well be the engine of eukaryotic complexity (Mattick 2004). RNA may have evolved and may continue to evolve many yet unknown functions. Evolution may be slow to eliminate nonfunctional RNAs. RNAs without current function, however, may constitute a pool of molecules that might be adapted to fill novel roles, such as gene regulatory elements or defenses against transposons and viruses. One of the themes of this article is to describe methods for finding functional RNAs and their structures, which in turn can reveal structure-function and evolutionary relationships.

Evolution is restrained by fundamental chemical and physical principles of which thermodynamics is one. Although much of the sequence dependence of RNA thermodynamics is unknown, for RNA sequences of fewer than 700 nucleotides it is possible to correctly predict roughly 70% of secondary structure from thermodynamics alone (Mathews et al. 2004). This success suggests that thermodynamics is a major determinant of secondary structure and thus of evolution of structured RNAs. Perhaps thermodynamics was particularly important in the early stages of evolution when RNA molecules had a high degree of structural plasticity. Once a functional structure was generated in an evolving population of RNAs, there would be a driving force for stabilizing that particular structure over alternative folds in the population. Thus, structures developed early in evolution may be determined more by free energy minimization of the RNA than structures developed later. For example, later structures may depend more on the kinetics of folding and on interaction with proteins. Our understanding of evolution and structure at the molecular level is still evolving and currently somewhat primitive.

A second theme of this article is overcoming current limitations through the combined application of thermodynamics, sequence comparison, and experiment to rapidly model RNA secondary structures. The methods facilitate finding RNA sequences with functions that rely on secondary structure.

1. FOLDING RNA INTO SECONDARY STRUCTURES

1.1. Free Energy Minimization

If folding was determined by thermodynamics alone and if the sequence dependence of thermodynamics was completely understood, then it would be possible to predict secondary structure from sequence alone. For a unimolecular reaction such as the folding of an RNA molecule:

$$\mathrm{U}\leftrightarrow \mathrm{F}\mathrm{K}=[\mathrm{F}]/[\mathrm{U}]={\mathrm{e}}^{-\mathrm{\Delta }{\mathrm{G}}^{\mathrm{o}}\mathrm{/}\mathrm{RT}}.$$

Here, K is the equilibrium constant giving the ratio of concentrations for folded, F, and unfolded, U, species at equilibrium; ΔG° is the standard free energy difference between F and U; R is the gas constant; and T is the temperature in kelvins. The challenge of predicting secondary structure from thermodynamics is to find the base-pairing that gives the lowest free energy change in going from the unfolded to folded state, and therefore the highest concentration of folded species. Generally this search is accomplished with a dynamic programming algorithm, a type of recursive algorithm that is commonly used to solve optimization problems in biology (e.g., sequence alignment) and elsewhere. Dynamic programming can implicitly search the entire set of possible RNA secondary structures to find the lowest free energy structure without the necessity of generating all structures explicitly. The free energy change is typically approximated with a nearest neighbor model in which the ΔG° is the sum of free energy increments for the various nearest neighbor motifs (e.g., stacked base pairs in an RNA helix) that occur in a structure (Turner 2000; Mathews et al. 2005). Parameters for the nearest neighbor increments have been experimentally determined by optical melting studies (Xia et al. 1998; Turner 2000; Mathews et al. 2004), by relating parameters to the number of occurrences of various motifs in known secondary structures (Do et al. 2006), by optimizing parameters to predict known secondary structures (Ninio 1979; Papanicolaou et al. 1984), or by some combination of the previous (Jaeger et al. 1989; Mathews et al. 1999; Andronescu et al. 2007).

1.2. Partition Functions and Probabilities

Because the accuracy of secondary structure prediction is limited in part by an incomplete knowledge of the folding rules, there is significant interest in determining the quality of predictions. One approach to estimating the quality of prediction is to assign a probability to the prediction using a partition function.

The partition function, Q, contains a description of the ensemble thermodynamic properties of a system and is defined as the sum of the equilibrium constants for all possible secondary structures of a given sequence. The fraction of strands that will fold into a particular structure is the equilibrium constant for that structure, divided by Q. Counter-intuitively, the lowest free energy structure often occurs with a vanishingly small probability. For example, given the calculated partition function for the Tetrahymena group I intron (1.8 × 10¹⁰⁷), the probability that a strand folds into its predicted minimum free energy structure is 1 in 760 million. Many base pairs, however, are common to a large number of the low free energy structures. These common pairs are well represented in the structural ensemble and thus can have high pairing probability. In fact, 80 base pairs out of 144 predicted for the Tetrahymena group I intron have 90% or higher pairing probability.

Using probabilistic methods, three approaches are taken to enhance the information provided by structure prediction. The first is to predict the lowest free energy structure and then color annotate the structure with base pairing probabilities (Mathews 2004). Pairs of higher probability are more likely to be correctly predicted pairs (Mathews 2004). Therefore, the user can have greater confidence in the highly probable pairs (>90%) being truly informative of native secondary structure.

A second approach is to simply assemble structures of highly probable pairs (Mathews 2004). For example, structures can be assembled of pairs that exceed a given pairing probability threshold. These are valid structures, i.e., a nucleotide will only pair with up to one other nucleotide, if the threshold is set at 50% pairing probability or higher. The quality of the predicted pairs is high, but these structures are generally not saturated with pairs (Mathews 2004). Alternatively, structures can be assembled using the most probable pairs using a dynamic programming algorithm (Do et al. 2006; Hamada et al. 2009; Lu et al. 2009). These structures are called maximum expected accuracy structures.

A third approach is to sample structures from the folding ensemble according to their probability of occurring, using stochastic sampling (Ding and Lawrence 2003). The sampled structures can be analyzed to determine base pairing probabilities. Additionally, predicted structures can be clustered. A representative structure, called a centroid, of the most populated cluster can be a more accurate prediction of the native structure than the predicted lowest free energy structure (Ding et al. 2005). Stochastic sampling and clustering are especially useful for analyzing an RNA that natively populates more than one structure, e.g., a riboswitch sequence, because each structure should appear as a distinct cluster.

1.3. Available Programs

Table 1 summarizes some of the available computer programs for RNA secondary structure prediction and their features. This list is confined to those that predict structure based on thermodynamics, although alternative approaches based on reproducing structural features in the database of known structures also show promise (Dowell and Eddy 2004; Do et al. 2006).

Table 1.

Secondary structure prediction programs. This table provides a list of software packages that predict secondary structures using thermodynamics

Program:	URL:	Features:
RNAstructure	http://rna.urmc.rochester.edu/RNAstructure.html	JAVA/Windows Graphical User Interface; Command Line Interface; C++ Class Library
Sfold	http://sfold.wadsworth.org/	Web server
UNAFold/mfold	http://mfold.bioinfo.rpi.edu/	Web server; Command Line Interface
Vienna RNA Package	http://www.tbi.univie.ac.at/RNA/	Web server; Command Line Interface; C Function Library

2. RESTRAINING FOLDING SPACE

Free energy minimization alone typically predicts correctly only about 70% of secondary structure. There are several reasons for the limited accuracy. For example, folding may not be determined only by thermodynamics, the sequence dependence of free energy changes is far from completely known, and the folding space for RNA is enormous; an RNA of n nucleotides has 1.8ⁿ possible secondary structures (Zuker and Sankoff 1984). Finding the correct secondary structure can be compared to the difficulty of using random keystrokes to type correctly a sentence with 28 letters and spaces. This would take 27²⁸, or about 10⁴⁰, keystrokes. If, however, a letter is fixed whenever it is typed correctly, then it would only take a few thousand keystrokes (Dawkins 1987; Zwanzig et al. 1992). There are only 4 letters in the RNA alphabet and the “words” are helixes and loops. In an analogous way, knowing that a given nucleotide is in a base pair or a loop greatly reduces the remaining folding space. Thus, the folding problem becomes tractable if there are ways to deduce when a base pair or loop is correct. Several approaches for this are described below.

2.1. Experiments

Experiments can provide constraints and restraints to reduce folding space. The methods most commonly used employ chemical modification of bases (Inoue and Cech 1985; Moazed et al. 1986; Ehresmann et al. 1987; Mathews et al. 2004) or ribose sugars (Merino et al. 2005; Deigan et al. 2009) to identify nucleotides that are unpaired or in loosely structured regions. Modified sites can be rapidly read out by primer extension using reverse transcriptase, which will stop at the base 3′ of the modified site. By using multiple primers, any length RNA can be interrogated. Chemical agents are useful for restraining unpaired or loosely paired bases. Nuclear magnetic resonance (NMR) spectra can be used to constrain base paired nucleotides (Hart et al. 2008).

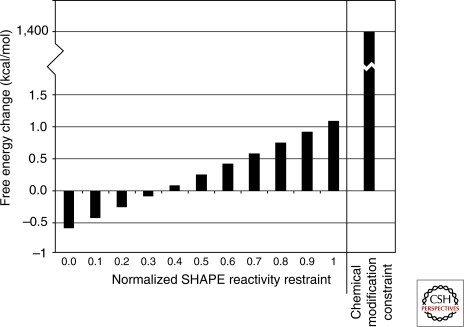
Dimethyl sulfate (DMS), 1-cyclohexyl-3-(2-morpholinoethyl)carbodiimide metho-p-toluenesulfanate (CMCT), and kethoxal react with the Watson-Crick faces of A and C, U, and G, respectively. DMS is of special use as it can be applied in living cells for in vivo mapping of truly native RNA structures (Harris et al. 1995; Zaug and Cech 1995). Chemical reactivity has been applied as a constraint in the RNAstructure folding program (Mathews et al. 2004). The constraint applied is that a base that reacts cannot be in a Watson-Crick pair flanked by Watson-Crick pairs (Fig. 1). The same constraint can be applied for reactivity that cleaves the backbone in loops: such as with Pb²⁺ (Lindell et al. 2002) or with hydrolysis (Li and Breaker 1999; Soukup and Breaker 1999).

Figure 1.

Folding constraints and restraints. Traditional chemical agents that act on bases are applied as folding constraints, i.e., a base accessible to chemical modification cannot be in a base pair flanked by Watson-Crick pairs on each side. In RNAstructure, this is implemented by assigning a large positive free energy to any conformation that violates the constraint. SHAPE reactivity is applied as a folding restraint, i.e., a free energy change bonus or penalty for pairing of a nucleotide. For nucleotides with low SHAPE reactivity, a pairing stabilization is provided and for high reactivity, a pairing penalty is provided. The SHAPE restraint is provided per nucleotide in a base pair stack. Therefore, the free energy change is applied twice per nucleotide buried in a helix and once per nucleotide in a pair at the end of a helix (Deigan et al. 2009).

N-methylisotoic anhydride (NMIA) and related molecules react with flexible ribose groups (Merino et al. 2005; Mortimer and Weeks 2007). Thus, reactive nucleotides are presumably not in strong Watson-Crick pairs or rigid tertiary interactions. Reactivity is less sensitive to local environment than that of DMS, CMCT, and kethoxal (Wilkinson et al. 2009), presumably because the electrostatic environment of the sugars is more uniform than that of the bases. Because this “SHAPE” chemistry interrogates the ribose of every nucleotide, relative reactivity can be assigned to every nucleotide. Readout by capillary gel electrophoresis has provided quantification that allows relative reactivity to be used as restraints. That is, relative reactivity provides a measure of the likelihood of a nucleotide being unpaired or paired, rather than an absolute constraint (Fig. 1). This allows lack of reactivity to be interpreted as a favorable likelihood for Watson-Crick base pairing (Deigan et al. 2009). Although lack of reactivity may also reflect strong tertiary interactions, runs of consecutive Watson-Crick base pairs in helixes are usually longer than consecutive tertiary interactions so that helixes are favored more by the enhancement in the probability increment for Watson-Crick base pairing.

NMR interrogates the chemical environment of nuclei. The chemical shifts of an imino hydrogen proton and the attached nitrogen nucleus provide a signature that identifies whether the imino proton is in a Watson-Crick GC, AU, or wobble GU pair. Because the imino protons are close to each other in the middle of a helix, they can exchange energy, which is measurable using two-dimensional NMR spectroscopy. Thus, it is possible to determine that helixes with certain sequences of base pairs must be present in the secondary structure. This provides information complementary to chemical modification, which identifies unpaired nucleotides most definitively. An algorithm for NMR assisted prediction of secondary structure (NAPSS) is available (Hart et al. 2008). Because the method identifies double helixes, it is especially effective for revealing pseudoknots. It also provides a few initial assignments of resonances, which can facilitate determination of three-dimensional structure. It is limited, however, to RNAs that are labeled with ¹⁵N and that can be studied by NMR. The latter limitation probably restricts the maximum length of the RNA to somewhere between 100 and 300 nucleotides. Another disadvantage of NMR is that relatively large amounts of RNA are required compared to chemical methods.

2.2. Structure Comparison

RNAs whose biological function depends on their structure (e.g., tRNA, rRNA, etc.) should show structural conservation when comparisons are made between RNAs of related species (Woese and Pace 1993). Thus, another approach for identifying correct base pairs and loops is their occurrence in the same or similar locations in homologous (i.e., evolutionarily related) RNAs. The structure comparison approach has the advantages that it gives the structure in the cell, should work for sequences not governed by thermodynamics, can identify pseudoknots, non-Watson-Crick base pairs and elements of the tertiary structure; it also leverages the exploding database of sequences. Structure comparison may not be applicable to all RNAs, however. To determine secondary structure de novo from sequence analysis, multiple, homologous sequences are required, as are high quality alignments of the sequences. These requirements may be hard to meet for rare RNAs or RNAs with high levels of variability.

The manual determination of a conserved structure from a set of sequences is called comparative sequence analysis and involves aligning available sequences to identify covariant sites: sites that show correlated mutations. Synchronized mutation between sites is interpreted as the manifestation of functional (structural) constraints on the molecular evolution of the RNA. Double point mutations in aligned sites that preserve base pairing (e.g., G-C mutating to A-U, C-G, etc.) are the simplest covariations to identify and interpret. Simply, to model base pairing one searches an alignment of RNA sequences for “structurally silent” mutations. Comparative sequence analysis is phenomenally accurate at predicting a structure (>95% of predicted pairs correct) when significant human effort and skill are applied (Gutell et al. 2002).

2.3. Combined Methods for Determining Secondary Structure: An Example from the 5′ Regions of R2 Retrotransposon RNA

An illustrative example for determining RNA secondary structure comes from the region that occurs toward the 5′ terminus of silk moth R2 retroelements. This roughly 350 nucleotide structured region was discovered as a persistent “contaminant” in preparations of the silk moth, Bombyx mori, R2 encoded protein. This RNA is strongly bound by R2 protein and this binding is an essential part of R2 element insertion into the host genome (Christensen et al. 2006). An initial structural model was proposed using free energy minimization with a single sequence, constrained by chemical modification and oligonucleotide binding data (Kierzek et al. 2008). Unusual structural features of this model inspired further probing of a 74 nucleotide fragment using NMR, which revealed a pseudoknot structure for this fragment (Hart et al. 2008).

As additional R2 sequences became available, it was possible to use comparative sequence analysis to interrogate the structure of this RNA (Kierzek et al. 2009). Each of four additional R2 sequences was subjected to the same battery of chemical reagents (i.e., DMS, CMCT, and NMIA) and oligonucleotide binding experiments as B. mori. These data were used in constrained free energy minimization and combined with the B. mori NAPSS results to provide initial structural hypotheses for manual alignment and comparative analysis. The reasonability of the structural hypotheses was gauged with a partition function calculation and annotation of the base pairing probabilities. The alignment and secondary structures were altered to maximize the conservation of structure and the formation of compensatory base changes.

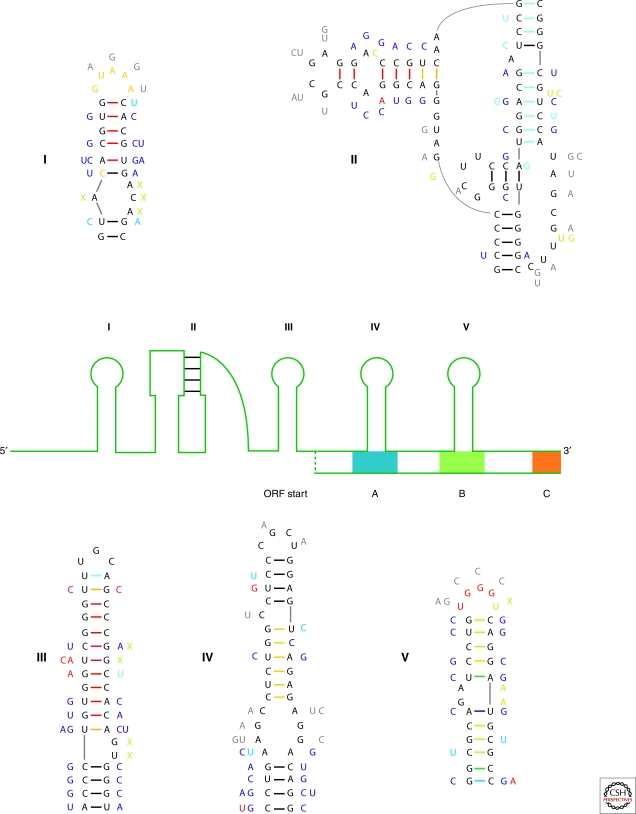
The results of this modeling are summarized in Figure 2. There are five regions in this RNA that are structurally conserved. These are organized into four hairpin loop structures and a pseudoknot. One of the interesting features revealed by structure alignment was that two of the conserved hairpins, falling within the coding region of this RNA, correspond to conserved protein coding regions. Evidently, evolution acted on two levels: mutations that preserved RNA base pairing could also be synonymous substitutions with respect to amino acid coding. The secondary structures shown in Figure 2 are consistent with chemical mapping and NMR results; they are well supported by consistent and compensatory mutations (single and double point mutations that preserve base pairing). Moreover, for each single sequence fold, these conserved structures are composed of high probability base pairs as determined from partition function calculations. This wealth of data is summarized in Figure 2.

Figure 2.

Determination of Structured Regions of an RNA. A cartoon of the 5′ region of the silk moth R2 retrotransposon is shown. The conserved structure is organized into four hairpin loops (labeled I and III–V) and a pseudoknot (labeled II). Also shown are three conserved coding regions (A–C) and a putative open reading frame (ORF) start site. The five conserved structures are detailed with data that went into the structural modeling. The sequences shown are for B. mori whereas mutations are those that occur in four other moth species. Mutational data appear next to the main sequence and is color annotated: dark blue are double mutations that maintain base pairing (compensatory), light blue are single point mutations that maintain pairing (consistent), gray are mutations in loops, red disrupt canonical base pairs (inconsistent), green are insertions (green X represents a deletion). Experimental mapping is color annotated on the backbone sequence: red are NMIA only modifications and orange are modifications by both traditional mapping agents (DMS or CMCT) and NMIA. Base pairs are indicated with dashes between nucleotides and are color annotated for probability from partition function calculation: Red, probability (P) ≥99%; Orange, 99% > P ≥ 95%; Yellow, 95% > P ≥ 90%; Dark Green, 90% > P ≥ 80%; Light Green, 80% > P ≥ 70%; Light Blue, 70% > P ≥ 60%; Dark Blue, 60% > P ≥ 50%; Black <50%. Many base pairs in the pseudoknot have low probability because the RNAstructure program does not allow pseudoknots and thus, under-counts them in the partition function.

3. AUTOMATING COMPARATIVE SEQUENCE ANALYSIS

The example of comparative analysis given above represents a significant investment in time and a certain degree of artisanal craftsmanship. To date, no completely accurate computational approach exists for automating comparative analysis, but a number of distinct approaches have been applied to the problem. Overall, these methods are helpful at generating hypotheses that can be tested with manual comparison or experiments.

3.1. Three General Approaches to Predicting Conserved Secondary Structures

It would be most efficient to deduce correctly secondary structure from sequence alone, and programs are available for attempting this when multiple sequences are available. The problem of predicting the lowest free energy structure common to multiple sequences has been approached from three directions. The first approach is to simultaneously find both the lowest free energy structure and the optimum alignment of sequences. The second approach is to start with the sequences aligned by nucleotide identity and then find the conserved pairs in the given alignment. The final approach is to predict low free energy structures for each sequence separately and then to sort through the predicted structures to find the structures common to all sequences.

3.2. Approach 1: Fold and Align

The concept of using a dynamic programming algorithm to simultaneously fold and align a set of sequences was introduced by Sankoff (Sankoff 1985). This idea was implemented in practical computer programs such as Dynalign and Foldalign to find lowest free energy common structures (Mathews and Turner 2002; Havgaard et al. 2005). To make calculations feasible for long sequences (currently up to about 2000 nucleotides), other data are used to restrict the possible structures or alignments. The current approach in Dynalign, for example, is to rule out base pairs that can only exist in structures with high folding free energies (Uzilov et al. 2006) and to rule out alignments that are extremely unlikely (<10⁻³) based on statistical analysis of aligned sequences (Harmanci et al. 2007). Additional algorithms have been developed to use scoring schemes based on producing structures similar to secondary structures present in databases of known structures (Holmes 2005; Dowell and Eddy 2006; Do et al. 2008).

To determine confidence estimates for predictions of base pairs common to two sequences, a partition function algorithm for common structures was developed, called PARTS (Harmanci et al. 2008). This algorithm calculates equilibrium constants for common structures with a pseudo free energy score derived from base pair probabilities determined for each sequence and sequence alignment probabilities. The shortcut of using base pairing probabilities for scoring saves significant computation time and had been previously proposed (Hofacker et al. 2004; Hofacker and Stadler 2004) and used in the structure prediction programs LocARNA (Will et al. 2007) and Murlet (Kiryu et al. 2007). As with single sequences, base pairs that form with greater probability in common structures are more likely to be correctly predicted than those of low probability (Harmanci et al. 2008). Additionally, the partition function allows for stochastic sampling and clustering of structures conserved between the two sequences (Harmanci et al. 2009). As expected, the additional information contained in two sequences improves the fidelity of structure prediction as evidenced by the fact that the individual clusters contain structures that are much more similar to each other than for single sequence structure sampling (Harmanci et al. 2009).

Because of the computational cost, practical calculations are only performed with two sequences. To determine a structure common to more than two sequences, methods have been developed that use greedy heuristics to find the common structure using multiple pairwise calculations (Bellamy-Royds and Turcotte 2007; Kiryu et al. 2007; Torarinsson et al. 2007; Will et al. 2007). The drawback to this approach is that any calculations performed early in the set that have poor prediction accuracy will make the subsequent predictions poor as well.

3.3. Approach 2: Align then Fold

In the second approach, a multiple sequence alignment is constructed based on sequence information alone and then the lowest free energy structure is predicted that is common to all or most sequences (Lück et al. 1996; Hofacker et al. 2002; Bernhart et al. 2008). Calculations are improved by also providing free energy change bonuses for base pair formation at sites of covariation, where structure is conserved, but sequence is not.

The advantage to this approach is speed. It can be applied to almost any number of sequences and takes roughly the same calculation time as structure prediction for a single sequence of the same length as the alignment length. The drawback is that the quality of the structure prediction depends on the quality of the alignment. Alignments based on sequence alone may not properly reflect the structural homology that relates the set of sequences, and it is possible to miss compensating base pair changes that are key to evaluating the quality of the structure prediction. In a Catch 22, without a structurally informed alignment, it is difficult to develop a structural model to refine the alignment. The program ConStruct, however, addresses this limitation by providing a graphical user interface by which the user can manually adjust the alignment to facilitate the testing of structural models and iteratively refine the alignment and structure (Lück et al. 1999).

3.4. Approach 3: Fold then Align

In the third approach, a set of low free energy secondary structures is determined for each of multiple sequences and then the predicted structures are analyzed to find the lowest free energy structure common to all sequences (Reeder and Giegerich 2005). The direct implementation of this would be nearly computationally intractable because the number of low free energy structures for a given sequence is enormous (Wuchty et al. 1999). It is also known that the number of structures for a sequence with a folding free energy change below a threshold increases exponentially as the threshold is raised higher. Therefore, if the structures were explicitly analyzed, then it would be hard or impossible to sort through enough low free energy structures to make this approach feasible.

Instead of directly using this approach on structures, Giegerich and coworkers apply the algorithm on folding topologies, called abstract shapes (Giegerich et al. 2004). For example, one level of shape abstraction is to examine just the branching topology of the structure, without considering the internal or bulge loops. With increasing threshold above the lowest free energy structure, the number of abstract shapes increases much more slowly than the increase in number of structures (Voss et al. 2006).

The Fold then Align approach has the advantages of being faster than Fold and Align and also not being subject to the limited accuracy of sequence alignment as in Align then Fold. It has the drawback that the common abstract shape is found, which does not exactly predict which pairs are homologous, although an estimate can be generated by postprocessing (Höchsmann et al. 2004).

3.5. Available Programs

Table 2 shows a list of the available programs for predicting conserved secondary structures. This table is restricted to those programs that work using thermodynamics as a basis, although these approaches have been explored using alternative scoring methods.

Table 2.

Programs for the prediction of a conserved RNA secondary structure. This table provides a list of programs that predict conserved secondary structures using thermodynamics

Program:	URL:	Type:
ConStruct	http://www.biophys.uni-duesseldorf.de/local/ConStruct/ConStruct.html	Align then Fold
Dynalign	http://rna.urmc.rochester.edu/dynalign.html	Fold and Align
FOLDALIGN	http://foldalign.ku.dk/	Fold and Align
LocARNA	http://www.bioinf.uni-freiburg.de/Software/LocARNA/	Fold and Align
Murlet	http://murlet.ncrna.org/	Fold and Align
PARTS	http://rna.urmc.rochester.edu/parts.html	Fold and Align
RNAalifold	http://rna.tbi.univie.ac.at/	Align then Fold
RNAcast	http://bibiserv.techfak.uni-bielefeld.de/rnacast/	Fold then Align

4. FINDING FUNCTIONAL RNA

Given the number of sequenced whole genomes and the fact that much of these genomes are transcribed, there is significant interest in finding genes for noncoding RNA (ncRNA) sequences, i.e., genes that encode RNA sequences that function without being translated to a protein. This work fits into two categories, in which the first is the discovery of RNA sequences of a specific, known type and the second is the discovery of new types of RNA. Predictions of thermodynamic stability play important roles in both types of searches.

Because RNA structure is more highly conserved than sequence, methods to scan for specific ncRNAs test for the formation of a specific secondary structure. The earliest successful methods required training to a specific type of RNA either by automated training to a sequence alignment (Eddy and Durbin 1994) or by development of scores based on specific knowledge (Fichant and Burks 1991; Lowe and Eddy 1997; Lowe and Eddy 1999). A different program, called RNAmotif, was developed to scan for a user-specified secondary structure or class of structures, in which the user provides a descriptor of the structure (Macke et al. 2001). The drawback to this search method is that it is prone to predicting false positives. For example, a large number of potential cloverleaf structures encoded in genome sequences are not tRNA sequences (Tsui et al. 2003). Fortunately, predicted folding free energy change is an excellent criterion for separating the true positives from false positives (Tsui et al. 2003). In other words, the sequences with the potential to fold as cloverleafs, but are not tRNA sequences, nearly always had less favorable folding free energy change compared to true tRNA sequences folded as cloverleafs.

The problem of finding novel ncRNAs also can rely on predicted folding free energy change. It was hypothesized early that ncRNA sequences have lower folding free energy changes than random sequences (Le et al. 1988; Chen et al. 1990). This hypothesis proved controversial and one reason for the controversy is whether the correct controls for testing this hypothesis are random sequences with the same nucleotide content or dinucleotide content; this is because the stacking nearest neighbor parameters depend on dinucleotides (Seffens and Digby 1999; Workman and Krogh 1999). It is now generally accepted that there is a statistical trend for ncRNAs to have lower folding free energy change than matched control sequences with identical dinucleotide content (Clote et al. 2005; Uzilov et al. 2006). This trend, however, is not large enough to find with high sensitivity and specificity ncRNA sequences in genomes because of a large overlap in the distributions of folding free energy changes for ncRNAs and controls (Rivas and Eddy 2000; Uzilov et al. 2006).

The discovery of conserved ncRNA genes by scanning genome alignments, however, is achievable by evaluating thermodynamic stability. The programs that perform these scans have, as their basis, algorithms that predict conserved secondary structures using either “align then fold” or “fold and align” approaches as described earlier. For example, RNAz uses the align then fold algorithm RNAalifold to identify stable RNA structures in multiple genome alignments (Washietl et al. 2005). The fold and align algorithm, Dynalign, adjusts the original genome alignment to reflect an alignment based on RNA structure and therefore is capable of finding ncRNAs that have diverged farther in sequence than RNAz (Uzilov et al. 2006). The drawback is that it is slower. Foldalign, another fold and align algorithm, has also been used to find conserved, structured RNA in genomes (Torarinsson et al. 2006). It has been applied to compare genome sequences in regions that are not alignable based on sequence alone and it found numerous conserved putative ncRNA genes.

5. FUTURE DIRECTIONS

The progress in rapid determination of secondary structure lays the foundation for accelerating determination of three dimensional structure. There are NMR fingerprints for various loop motifs (Varani et al. 1996; Moore 2001) and there will likely also be chemical mapping fingerprints. Models of three-dimensional (3D) structures can be tested for consistency with chemical mapping and NMR data. Computers are constantly becoming more powerful so that it is possible to envision methods based on physics (e.g., molecular mechanics) or homology or a combination of the two for correctly predicting secondary and even 3D structure (Westhof et al. 2010) quickly on the basis of sequence alone. Physics based methods, however, will require a more fundamental understanding of molecular interactions determining thermodynamics and structure (Yildirim and Turner 2005). Understanding the physics of the molecular interactions should also lead to improved predictions of RNA dynamics, which are likely to be important for many functions.

A hindrance to homology modeling of RNA 3D structure is that, in comparison to protein structures, the collection of high resolution RNA 3D structures is relatively impoverished. The list of high resolution RNA structures has been growing steadily, however, and “information-based” approaches to 3D structure determination show promise. For example, the MC-Sym algorithm (Parisien and Major 2008) decomposes elements of RNA 3D structure into graphical representations, called “cyclic motifs,” which can facilitate homology modeling. Resulting 3D models can be constrained by complementary data, such as NMR and chemical mapping to weed out poor models.

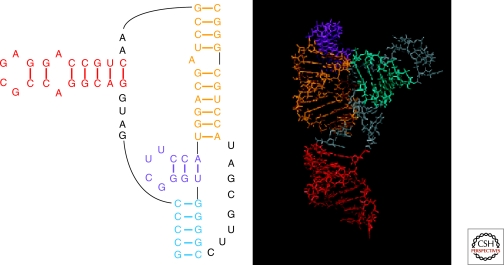
The B. mori R2 RNA 5′ region again provides an illustrative example of the process of moving from primary to secondary to 3D structure. As indicated in Figure 2, energy minimization guided by chemical mapping, oligonucleotide binding, NMR and comparative analysis was able to determine the base pairing of the R2 pseudoknot. Knowledge of the correct base pairing is a strong restraint on possible 3D folding, and this was used to constrain MC-Sym modeling of the R2 pseudoknot. The resulting 3D models were further screened by searching for helix–helix stacking that was consistent with NMR results: namely the NMR signature that connected the minor hairpin and the longer of the two pseudoknot helices (Hart et al. 2008). The final 3D model for this pseudoknot (Fig. 3) was selected based on consistency with chemical mapping data (mainly used to rule out possible tertiary interactions) and similarity to models of the four other silk moth pseudoknots.

Figure 3.

Experiment and Sequence Comparison are Used to Model 3D Structure. Homology with known structures was used to propose 3D folds for the B. mori R2 element pseudoknot from MC-Sym (Parisien and Major 2008) which were then screened with respect to experimental data (e.g. solvent accessibility to chemical reagents [Kierzek 2009] and helix stacking from NMR [Hart et al. 2008]). Helical motifs in the 3D model are color coded to match the secondary structural model.

The ability to rapidly model RNA structure may facilitate discovery of therapeutics that target RNA. Structure in the target mRNA is an important consideration in designing siRNAs (Lu and Mathews 2007; Shao et al. 2007; Tafer et al. 2008) and determining microRNA targets (Rehmsmeier et al. 2004; Long et al. 2007). Additionally, the Disney group is using small-molecule microarray methods to deduce the basis for matching potential drugs with RNA motifs that bind them strongly (Childs-Disney et al. 2007; Disney and Childs-Disney 2007). Microarray methods based on short, chemically modified oligonucleotides (Kierzek et al. 2008; Kierzek et al. 2009) are also providing insight into the rules that govern oligonucleotide binding to structured RNAs, which should facilitate design of nucleic acid based therapeutics.

6. APPLICATION TO THE STUDY OF EVOLUTION

Structural comparisons may allow discovery of new fundamental principles of evolution and biology. For example, studies of systems biology are revealing intricate regulatory networks in cells and providing hypotheses of their evolution (Feschotte 2008). It is likely that RNA/RNA interactions are important in at least some networks. In turn, new biological principles discovered on the basis of RNA/RNA interactions can then be applied to accelerating discovery of new functional RNAs and of their structures.

The identification of microRNAs (miRNAs) and miRNA targets is an excellent example of how methods for folding and finding RNA have contributed to our knowledge of biology. MicroRNAs are one type of RNA important for regulatory networks. MicroRNAs are involved in a number of important cellular processes, such as development, apoptosis, and cell differentiation/proliferation (Bartel 2004). As well, miRNAs may have roles in the progression of at least 70 human diseases (Lu et al. 2008), including cancer and cardiovascular disease. Identification of putative miRNAs can be accomplished using algorithms based on RNA folding thermodynamics (Lim et al. 2003a; Lim et al. 2003b). Additionally, thermodynamics lay at the heart of many miRNA target prediction software (Kiriakidou et al. 2004; Rehmsmeier et al. 2004; Krek et al. 2005). Applications of such software have revealed complex miRNA networks where single miRNAs have multiple binding sites in target mRNAs.

The evolutionary origins of miRNAs are still being unraveled, but interesting results suggest at least some arise from transposable elements. Fifty five miRNAs, representing 12% of experimentally characterized human miRNAs, apparently originated from transposons (Piriyapongsa et al. 2007). Indeed, certain families of transposable elements appear to be natural fodder for the evolution of miRNAs: miniature inverted-repeat transposable elements (MITES) possess complementary palindromic termini separated by short linkers (Feschotte et al. 2002). When transcribed, these MITES have the ability to fold into hairpins that are structurally similar to precursor miRNA hairpins.

In addition to being able to generate new miRNAs, transposons may be responsible for evolving miRNA networks (Feschotte 2008). In their replication in host genomes, transposons may replicate miRNA genes, or insert new miRNA target sites into host genes. This process is evidenced by the finding that multiple genes may be regulated by the same miRNA. RNA structural constraints act on the evolution of miRNA biogenesis and targeting. RNA thermodynamics are crucial to many miRNA target site prediction programs (Berezikov et al. 2006; Kruger and Rehmsmeier 2006) and have played an important role in predicting and classifying families of miRNAs (Kaczkowski et al. 2009) and miRNA regulatory networks (Rehmsmeier et al. 2004).

Another key conserved regulatory pathway is RNA mediated transcriptional gene silencing. In one mode of action, small RNAs regulate DNA methylation, an important epigenetic mechanism of gene control (Hawkins and Morris 2008). This mode of action silences repetitive “junk” elements: a process vital for maintaining genome health. Again, tandem repeat sequences (associated with repetitive elements) appear to be important for the production of the small double-stranded RNAs needed to stimulate DNA methylation (Chan et al. 2006).

6.1. RNA Structure and Phylogenetic Reconstruction

Prediction and analyses of structured RNAs play fundamentally important roles in elucidating the evolutionary connections that link all organisms. It was the analysis of ribosomal RNA sequences that led Woese to propose the Archaea as a distinct major branch on the “Tree of Life” (Woese et al. 1990).

In addition to resolving these deep phylogenetic relationships, structured RNAs are commonly used markers for phylogenetic reconstruction at higher taxonomical levels. Internally transcribed spacer (ITS) regions of ribosomal RNAs are popular targets for phylogenetic analysis (Alvarez and Wendel 2003). These particular RNAs are not under the strict functional constraints of ribosomal RNA, and thus have enough variation to make them appropriate for higher level classifications. Though evolving under less stringent evolutionary constraints, the ITS2 RNA shows a conserved core secondary structure common throughout eukaryotes (Schultz et al. 2005). Presence of secondary structure in phylogenetic markers has important implications for phylogeny reconstruction. Sequence alignments, the basis for phylogenetic comparison, that do not account for structural homology may not reflect true evolutionary relationships. Compensatory mutations can confound phylogenetic analysis, as the nucleotides that constitute the alignments are not independently evolving characters, but are rather linked by higher order constraints, e.g., base pairing (Alvarez and Wendel 2003).

With the ability to generate good structural models for these phylogenetic markers RNA structure can facilitate, rather than confound, phylogeny reconstruction. Knowledge of RNA secondary structure can improve alignment quality (Goertzen et al. 2003). With accurate knowledge of paired sites, patterns of compensatory mutations between aligned species can be used to infer phylogeny (Wolf et al. 2005). Phylogenetic reconstruction methods that rely on models of sequence evolution, such as likelihood-based methods, also benefit from structural knowledge: paired and loop regions of structured RNAs are better accounted for using evolutionary models that account for different mutational rates for changes in paired or unpaired nucleotides (Telford et al. 2005). To facilitate such studies, an ITS2 secondary structure database (>100,000 entries) has been created using structural models based on free energy minimization and guided by comparative analysis (Selig et al. 2008).

Elements of RNA secondary structure themselves can be treated as evolving characters and phylogenetic connections may be traced by changes in structural character states (Knudsen and Caetano-Anolles 2008). Deconstructing RNA secondary structure into evolving characters and subjecting them to cladistic analysis allows for the study of the origin of particular substructures, e.g., hairpin loops. Such cladistic analysis of RNA secondary structure has led to insights into the molecular evolution of the tRNA cloverleaf structure (Sun and Caetano-Anolles 2008). This method of using structure as a character has also been applied to the classification of species using rRNA (Caetano-Anolles 2002), ITS RNA (Tippery and Les 2008) and tRNA (Sun and Caetano-Anolles 2008) and to investigate evolutionary trends in the structures of SINE elements (Sun et al. 2007).

6.2. Investigating Evolution: The RNA Model

The prediction of RNA structure is useful for understanding evolution from both in silico and in vitro studies. A number of fundamental evolutionary concepts can be explored using RNA. In RNA, genotype may be considered as the sequence of nucleotides, whereas the phenotype is the structure that may be formed by that sequence. Genetic variation may be simply modeled with mutations in the sequence (e.g., mutations introduced in silico). Selection may be introduced as a constraint on structure or thermodynamic stability in computer modeling. The concept of phenotypic plasticity applies to RNA: a single sequence may have multiple accessible secondary structures; as does the concept of neutrality: A single structure may be accessible to a number of sequences (Fontana 2002).

For computational modeling of evolutionary principles, RNA has a number of qualities that can be exploited to draw generalized conclusions. The thermodynamic model of RNA folding is physically grounded and results in a straight forward mapping of genotype (sequence) to phenotype (secondary structure). From a given sequence, it is possible to explore the entire phenotypic space (the set of accessible structures). Studies of genotype-phenotype mappings have revealed neutral networks connecting phenotypes (common structures) with sequence space (sequences that have the given phenotype). Such neutral networks explain the evolvability of nucleic acids by linking neutral drift and selection (Schuster and Stadler 2003). Neutral drift, the accumulation of structurally silent mutations, allows an evolving RNA to sample sequences with different plastic repertoires (available phenotypes); this is the basis of structural innovation. Such an evolutionary path was simulated for evolving a tRNA structure: long phases of phenotypic stasis were punctuated by structural (evolutionary) innovations along the path to the optimal tRNA structure (Schuster 2001). Neutral network theory found practical application in the discovery of an in vitro evolved RNA sequence at the intersection of two neutral networks that simultaneously performed catalytic activities of two different ribozymes (cleavage ribozyme and RNA ligase) (Schultes and Bartel 2000). Similarly, structure calculations were used to engineer a neutral path between two aptamer variants, whose intermediates were capable of binding to two substrates (FAD and GMP) (Held et al. 2003).

The availability of tools for folding and finding RNA made possible the studies discussed earlier, and many more. These tools will improve with advances in computer science, our understanding of the forces that govern RNA folding, and our understanding of fundamental biology. If even a tiny fraction of the noncoding portions of eukaryotic genomes represents functional RNA, then there is a colossal task to identify and understand these molecules. What other fascinating RNAs and complex RNA-based networks remain to be discovered?

With new RNAs come new opportunities to study evolution. Newly revealed RNAs may provide important markers for refining the phylogenetic relations that map the tree of life. We may also better understand the trajectories of and the evolutionary forces acting on structured RNAs: a critical component to understanding the RNA World.