A Novel Approach to Prediction of Mild Obstructive Sleep Disordered Breathing in a Population-Based Sample: The Sleep Heart Health Study

Abstract

This manuscript considers a data-mining approach for the prediction of mild obstructive sleep disordered breathing, defined as an elevated respiratory disturbance index (RDI), in 5,530 participants in a community-based study, the Sleep Heart Health Study. The prediction algorithm was built using modern ensemble learning algorithms, boosting in specific, which allowed for assessing potential high-dimensional interactions between predictor variables or classifiers. To evaluate the performance of the algorithm, the data were split into training and validation sets for varying thresholds for predicting the probability of a high RDI (≥ 7 events per hour in the given results). Based on a moderate classification threshold from the boosting algorithm, the estimated post-test odds of a high RDI were 2.20 times higher than the pre-test odds given a positive test, while the corresponding post-test odds were decreased by 52% given a negative test (sensitivity and specificity of 0.66 and 0.70, respectively). In rank order, the following variables had the largest impact on prediction performance: neck circumference, body mass index, age, snoring frequency, waist circumference, and snoring loudness.

Citation:

Caffo B; Diener-West M; Punjabi NM; Samet J. A novel approach to prediction of mild obstructive sleep disordered breathing in a population-based sample: the Sleep Heart Health Study. SLEEP 2010;33(12):1641-1648.

IN THE ROUTINE CLINICAL EVALUATION OF PATIENTS FOR POSSIBLE SLEEP DISORDERED BREATHING, PHYSICIANS MAKE JUDGMENTS AS TO THE LIKELIHOOD that a particular person is affected and decide whether polysomnography is warranted based on this likelihood. Their judgments draw on elements of the patient's history, such as reports of snoring or excessive daytime somnolence, demographic factors, and weight or body mass index (BMI). If the estimated likelihood is sufficiently high, then the physician may consider ordering a polysomnogram (PSG). Similarly, media outlets and medical societies put forward recommendations to the public for self-referral to a primary care or sleep physician for the evaluation of possible sleep disordered breathing. For example, in response to the recent publication of the authors' manuscript on sleep and mortality,¹ CBS news recommended that patients discuss with their physicians the need for polysomnography in the presence of severe snoring, restless sleep, frequent waking up at night, and excessive daytime exhaustion.² Faced with continued patient concern about having sleep disordered breathing, clinicians need tools to identify those individuals most likely to have sleep disordered breathing so as to avoid unneeded referral for a PSG.

At the core of this discussion are two questions related to the prediction of the eventual result of a PSG in the general population: first, how predictable is the result of a PSG, and second, what easily collected variables are most influential for predicting the result of a PSG?

A number of previous studies have considered whether the respiratory disturbance index (RDI) or the apnea-hypopnea index (AHI) can be predicted with sufficient certainty using such clinical information; these findings reviewed below generally indicate limited predictive power.

In this manuscript, we consider the prediction of RDI in participants in the Sleep Heart Health Study (SHHS)³ using modern ensemble learning algorithms to make predictions based on classifications of predictor variables.⁴ Ensemble learning algorithms base their predictions on a collection (ensemble) of simpler prediction equations. We focus on the prediction of mildly elevated RDI values, because patients with severe disease are presumably easier to diagnose without the aid of screening prediction algorithms. The goals of this manuscript are 3-fold: The first is to investigate the cross-sectional prediction of RDI in a population-based sample using these modern ensemble learning algorithms, which sort the data based on patterns of clustering of classifiers.⁴ A related second goal is to investigate the overall predictability of RDI in this population. A third goal is to demonstrate the utility of ensemble learning algorithms to sleep researchers, as these methods are potentially useful for reducing large amounts of data, such as polysomnographic data, to their most informative elements.

This study differs from other previous analyses that focused on individual predictors of RDI or change in RDI.^5–8 However, there has been related work on the prediction of sleep disordered breathing and RDI. For example, a recent review of prediction formulas for severe sleep disordered breathing (RDI ≥ 20/h) reported sensitivities varying between 76% and 96% and specificities varying between 13% and 54%.⁹ Similarly, neural networks have been applied to polysomnographic data for prediction of RDI in a retrospectively sampled series of patients.¹⁰ In this obese population (average BMI of 31 kg/m²), the prediction accuracy for obstructive sleep apnea (OSA, defined as RDI ≥ 10/h) was estimated to be 91%, with 99% sensitivity and 80% specificity. Rowley et al. tested 4 prediction algorithms and concluded that prediction algorithms may not be able to accurately discriminate OSA, yet may be useful for identifying people with severe disease (RDI ≥ 20/h) for split-night protocols.¹¹ Zerah-Lancer et al. evaluated the predictive value of pulmonary function parameters for moderate sleep apnea (defined as an RDI ≥ 15/h) using a logistic regression analysis of a population of obese snorers,¹² finding a sensitivity of 98% and specificity of 86%. Further work in clinical obese populations focusing on the prediction of sleep apnea from body habitus measurements has been published.^13,14 Prediction of OSA has also been considered in children.¹⁵ A logistic regression analysis of data from a retrospective sample was performed by Santaolalla et al.¹⁶; the authors found a sensitivity of 75% and a specificity of 66%. Logistic regression models also were used to evaluate the accuracy of the Berlin Questionnaire for predicting mild sleep apnea (RDI ≥ 5/h).¹⁵ A sensitivity of 86% and a specificity of 77% were found. Finally, in related work, snoring has been shown to predict daytime sleepiness independently of sleep disordered breathing.¹⁸

Our investigation differed from these previous analyses in several important aspects. First, by using ensemble statistical learning algorithms, we were able to explore potentially high-dimensional interactions among multiple predictors, which may convey useful aggregate information. Moreover, instead of considering the statistical significance of individual predictors in a typical model-based approach, we considered the overall predictability of RDI based on the algorithm classifications. Secondly, our data sample was different from the typical obese, clinically referred populations used in much of the previous research on RDI prediction. Many of these studies focused on moderate or severe sleep apnea. Instead, we considered community-based screening for mild sleep apnea.

METHODS

Data

The data are from the SHHS, a multicenter set of cohort studies with participants recruited from the Atherosclerosis Risk in Communities Study (ARIC), the Cardiovascular Health Study (CHS), the Framingham Heart Study, the Strong Heart Study, and the Tucson Health and Environment cohorts. The full details of the study design have been reported.³ Participants in the SHHS initially completed a questionnaire about their sleep habits and an in-home overnight PSG as described previously.¹⁹ Approval for the study protocol was obtained from the institutional review boards of the participating institution and informed consent was obtained for all subjects.

Extensive covariate data are available from the parent cohorts and from the additional data collection that was part of the SHHS. For this analysis, we focused on those predictors that would routinely be collected during a clinical evaluation or by simple questioning along with body habitus data. The predictors considered included body mass index (BMI), age, gender, race (white, black, or other), blood pressure (systolic BP and diastolic BP), waist-to-hip ratio (“waist”), neck circumference, and whether the participant was on anti-hypertensive medications. Each of these variables has been found to be a key correlate of RDI.^7,8,19–25 In addition, several questions from the Sleep Habits Questionnaire were used to reflect questions typically asked by clinicians. These included inquiries on snoring habits^25,26 and the component questions of the Epworth Sleepiness Scale. Table 1 provides a complete list of the variables considered in the algorithms.

Table 1.

Predictor variables considered in the ensemble learning algorithms for the prediction of RDI

Body mass index

Gender

Age (years)

Race (white/black/other)

Systolic blood pressure (mm Hg)

Diastolic blood pressure (mm Hg)

Waist diameter (cm)

Hip diameter (cm)

Neck circumference (cm)

Taking anti-hypertensive medications

Angina (yes/no)

Heart attack (yes/no)

CABG (yes/no)

Coronary angioplasty (yes/no)

Other cardiac (yes/no)

Fall asleep at the dinner table (4)

Awakened by coughing (events/month)

Awakened by chest pain (events/month)

Doze off while driving (4)

Feel unrested (events/month)

Awakened by heartburn (events/month)

Hours of sleep on weekday (number)

Doze off in car (4)

Awakened by leg cramps (events/month)

Doze off while lying down (4)

House members near when (4)

Minutes to fall asleep (number)

Have you ever snored (Y/N/Don't Know)

How often do you snore (4)

How loud is your snoring (4)

Snoring increasing or decreasing (4)

Nap 5 minutes or more (events/week)

Awakened for bathroom (events/month)

Not get enough sleep (events/month)

Awakened by noise (events/month)

Awakened by joint pain (events/month)

Doze off as a passenger (4)

Doze off while sitting (4)

Doze off while sitting in public (4)

Doze off while reading (4)

Doze off while sitting and talking (4)

Feel sleepy during the day (events/month)

Awakened by shortness of breath (events/month)

Awakened by sweats (events/month)

Trouble falling asleep (events/month)

Time falling asleep, weekday (AM/PM)

Time falling asleep, weekend (AM/PM)

Take sleeping medication (events/month)

Time wake up, weekday (AM/PM)

Time wake up, weekend (AM/PM)

Doze off watching TV (4)

Unable to resume sleep morning (events/month)

Unable to resume sleep night (events/month)

(events/month) represents the number of events per month

(4) represents a four point scale: no chance, slight chance, moderate chance, high chance.

We emphasize that the variables included in the prediction model can be easily obtained in the course of a standard clinical visit. In addition, because the focus was on prediction, causal directions are not relevant. For example, blood pressure measurements and anti-hypertensive medication use (probable causal outcomes of sleep disordered breathing^24,27,28) were included as a predictors.

Analysis

Ensemble learning algorithms, algorithms based on aggregating information from “a committee” of prediction equations, were used to predict probabilities of RDI for various thresholds. Specifically, these algorithms iteratively implement a predictor or classifier and the resulting prediction equation is a weighted combination (ensemble) of classifiers. We investigated the random forests²⁹ and boosting³⁰ algorithms, though focus on boosting for simplicity, as it consistently (though only slightly) outperformed random forests on our data in terms of prediction error and areas under estimated ROC curves. Boosting algorithms are well known to be easily implementable and, in the terms of size of estimated prediction error, performed the best among the other prediction algorithms used.³¹ Here we give an overview of boosting and its inputs.

In boosting, a collection of weak classifiers, i.e., ones whose error rate is slightly better than guessing,⁴ are used to produce a single strong one. In general, boosting proceeds iteratively, adding classifiers to the prediction algorithm in such a way that the next classifier focuses on the residuals of the previous classifiers. The implementation of boosting used herein performed the following: it took the current prediction algorithm and used regression to find a decision tree that minimized the errors in the most current fit; a so-called shrinkage parameter weakened the impact of the individual classifiers, preventing over-fitting for the individual classifiers while yielding influence to the resulting ensemble of classifiers. The important inputs were: the number of trees, the size of each tree (referred to as the interaction-depth), the shrinkage parameter, and how large of a subset of the data is used to create each tree (referred to as the bag fraction).

A key benefit of boosting is its insensitivity to over-fitting when including multiple extraneous or collinear predictors. Hence our strategy was to use a complete battery of predictors that could easily be collected in a routine clinical exam. To obtain a simpler prediction model, we then explored subset models including only the most influential variables that approximated this full model.

The maximum percentage of missing data for the variables considered was 4% of the original 6,441 subjects. However, discordant missingness across the variables considered reduced the number of subjects to 5,530. The observations with complete data on all of the predictors were split randomly into training (4,147 participants) and validation sets (1,383 participants). The outcome of interest was a binary variable representing whether RDI was larger or smaller than a specified cut-off; we considered 5, 7, and 9 events per hour.

With regard to sleep measurement, unattended nocturnal polysomnography was conducted in each participant's home containing: C3-A2 and C4-A1 electroencephalograms, right and left electroculograms, a single bipolar electrocardiogram, and a chin electromyogram, pulse oximetry (oxyhemoglobin saturation), and inductance plethysmography (for measuring chest and abdominal excursions). Details on equipment, protocol, failure rates, scoring, and quality assurance and control have been previously published.³² An apnea was identified if airflow was absent or nearly absent for ≥ 10 sec. A hypopnea was identified if discernible, discrete reductions in airflow or thoracoabdominal movement (≥ 30% below baseline values) occurred for ≥ 10 sec. The respiratory disturbance index (RDI) was defined as the number of apneas or hypopneas with a 4% decrease in oxygen saturation per hour slept.

We note that the RDI is a count, i.e., events per hour, and hence an alternate statistical approach might not categorize RDI, but instead treat the apnea and hypopnea events comprising RDI as Poisson or overdispersed Poisson counts, weighted by the total time asleep. This approach was explored; however, it was abandoned for the more easily interpreted prediction of exceeding a clinical cut-point or threshold for elevated RDI. In addition, we note that, the primary goal is to assist a physician in predicting individuals at risk for sleep disordered breathing, for which a PSG may be needed and treatment recommended. In contrast, approaches for modeling RDI as a Poisson random variable would focus on modeling the majority of the subjects having low counts.

The algorithms were developed and “trained” using 10-fold cross-validation.⁴. In this approach, groups of 10 participants were repeatedly eliminated from the training set, such that the algorithm was built on the remaining (4,147 – 10) subjects. The prediction error was estimated by comparing the actual outcomes on the subjects not used in building the prediction equation with the predicted outcomes. The boosting algorithm was run with 10,000 trees, a training fraction of 90%. Otherwise, the default values were employed, including setting the interaction depth to one, implying that simple regression stumps were used to create the ensemble, the shrinkage rate to 0.0001, which protects against over-fitting, and the out of bag fraction to 0.5, which forced 50% of the data to be used in the creation of the weak classifiers included in the prediction algorithm. Each of the remaining tuning parameters were varied and cross-validation prediction errors checked (results not shown) to evaluate the robustness of results to these assumptions.

The separate validation set was not involved in the training of the algorithms. The results presented in the following section are based on implementing the trained prediction algorithms on the validation set. In the running of the prediction algorithm, the questionnaire data with 4 ordered outcomes (see Table 1) were treated as factors, while the events-per-unit-time data were treated as continuous.

Analyses were performed using the R statistical software package (version 2.5.0)³³ and specifically using the gbm library listed at the Comprehensive R Archive Network (www.cran.r-project.org).

RESULTS

Table 2 shows the basic characteristics of the sample. The average age for both men and women was approximately 65 years; weight-related measurements demonstrate that the sample was, on average, moderately overweight. Table 3 highlights that the majority of participants had very low RDI values, although over 1,400 (26%) had evidence of mild disease, with an RDI > 11 events per hour.

Table 2.

Baseline characteristics of the total sample stratified by RDI status (< 7 vs. ≥ 7 events per hour) and gender

	Males		Females
	RDI < 7 Mean (SD)	RDI ≥ 7 Mean (SD)	RDI < 7 Mean (SD)	RDI ≥ 7 Mean (SD)
Age (years)	63.50 (10.61)	65.88 (9.98)	63.37 (10.58)	67.15 (10.29)
BMI (kg/m2)	27.10 (3.87)	29.55 (4.66)	27.09 (4.97)	31.26 (6.57)
Neck (cm)	40.15 (2.96)	41.76 (3.38)	34.92 (2.93)	37.01 (3.31)
Weight (kg)	82.50 (13.17)	89.62 (15.86)	69.98 (13.93)	79.97 (17.77)
SBP (mm)	130.32 (18.61)	132.75 (18.29)	129.29 (18.91)	133.78 (19.31)
DBP (mm)	75.54 (11.03)	75.75 (11.45)	72.73 (11.03)	72.66 (10.71)
ESS	11.61 (3.19)	12.27 (3.38)	11.12 (2.98)	11.50 (3.18)
N	1,336	1,278	2,103	813

ESS, Epworth Sleepiness Scale

Table 3.

Distribution of RDI by gender in the total sample

RDI (events/hour)	Males No. (%)	Females No. (%)	Total No. (%)
(0.0, 5.0)	1,090 (0.42)	1,828 (0.63)	2,918 (0.53)
(5.0, 7.0)	246 (0.09)	275 (0.09)	521 (0.09)
(7.0, 9.0)	191 (0.07)	178 (0.06)	369 (0.07)
(9.0, 11.0)	165 (0.06)	121 (0.04)	286 (0.05)
> 11.0	922 (0.35)	514 (0.18)	1,436 (0.26)

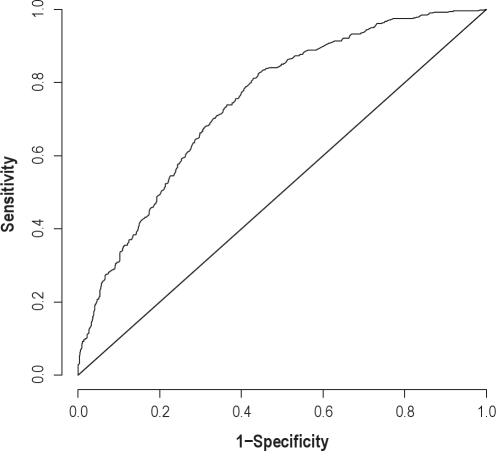
Figure 1 depicts the estimated receiver operating characteristic (ROC)^34,35 for the boosting prediction algorithm. This curve displays the trade-off between the true positive and false positive rates for predicting an RDI ≥ 7 events/h, with an ideal algorithm corresponding to sensitivity and specificity each equaling to one, depicted in the upper left hand corner of the plot, and random guessing corresponding to the identity line. The estimated ROC curve for the boosting algorithm was similar to, but slightly above that of the random forest algorithm. The area under the curve (AUC) for each ROC curve was calculated, with more desirable AUCs being closer to 1. A crude comparison suggests that they are similar for the 2 algorithms, estimated as 0.73 and 0.74 for random forests and boosting, respectively. A 95% nonparametric percentile bootstrap confidence interval estimate of the ratio of the boosting AUC versus the random forests AUC yielded [0.996, 1.028], suggesting no statistically significant difference in prediction between the 2 methods.

Figure 1.

Estimated ROC curve for the boosting algorithm from the validation data for predicting an RDI ≥ 7 events per h.

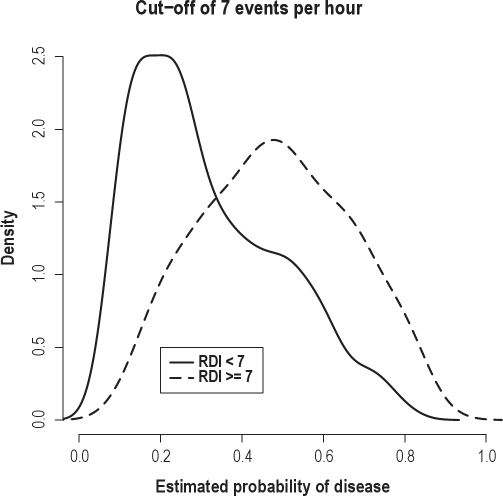
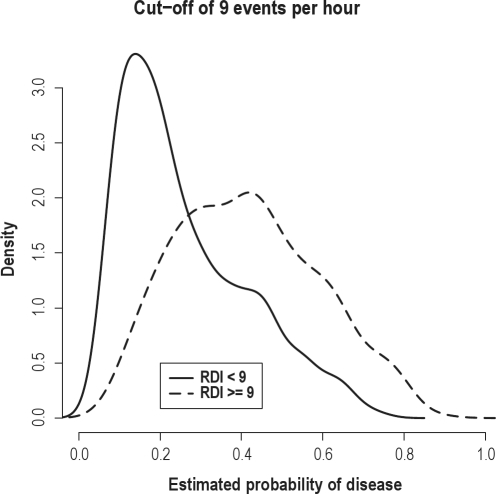
Because the performance of the boosting and random forests algorithms was consistent across all analyses, we focus on the results of the boosting algorithm. Figure 2 displays the estimated densities for the predicted probability of disease for the diseased and non-diseased groups under the boosting algorithm for predicting an RDI ≥ 7 events/h. There was considerable separation in the 2 curves, indicating satisfactory performance of the algorithms with an RDI cut-point large enough to be clinically relevant. For comparison, Figure 3 displays the same density plot employing a cut-point of 9 events/h. While the prediction improves in the right tail of the distribution, there is greater overlap of the 2 densities overall. The performance of the prediction algorithm did not change substantially for the lower RDI cut-off of 5 events/h. For this reason, the remaining results are provided for the RDI cutoff ≥ 7 events.

Figure 2.

Plots displaying the distributions of the predicted probability of disease from the boosting algorithm for subjects with an actual RDI > 7 events/h (dashed) and < 7 events/h (solid). The distributions were estimated from the validation set.

Figure 3.

Plots displaying the distributions of the predicted probability of disease from the boosting algorithm for subjects with an actual RDI > 9 events/h (dashed) and < 9 events/h (solid). The distributions were estimated from the validation set.

For a cut-off of 7 events/h, the area under the ROC curve was 0.74. Table 4 shows the estimated sensitivity, specificity, positive and negative diagnostic likelihood ratios (DLR+ and DLR−), and positive and negative predictive values (PPV and NPV) for 5 thresholds for the predicted probability of an RDI ≥ 7 events/h from the validation data set. The results suggested a difficulty in obtaining appropriate specificity, similar to the generally low specificity observed in related literature. For example, consider the rule of surmising that a subject has an actual RDI > 7 if their estimated probability from the boosting algorithm is larger than 30%. Using the validation set, the resulting sensitivity of this procedure is estimated to be 53%, while the specificity is 84%. Thus, at each of the considered thresholds, the algorithm appears to rule out disease much better than it detects it.

Table 4.

Estimated sensitivity, specificity, diagnostic likelihood ratios, and positive and negative predictive values for various thresholds for the predicted probability of an RDI ≥ 7 events per hour using the validation data set

Threshold for predicted probability	Sens.	Spec.	DLR+	DLR−	PPV	NPV
0.1	1.00	0.07	1.07	0.56	0.39	0.97
0.2	0.93	0.32	1.37	0.21	0.45	0.89
0.3	0.82	0.56	1.86	0.33	0.53	0.84
0.4	0.66	0.70	2.20	0.48	0.57	0.77
0.5	0.46	0.81	2.50	0.66	0.60	0.72

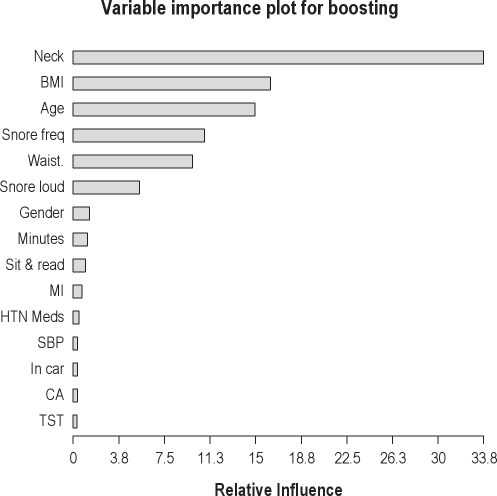
By appropriately permuting inputs to the iterations of the algorithm, ad hoc measures of relative variable importance can be quantified. With regard to relative variable importance, a participant's neck circumference, BMI, age, snoring frequency, and waist circumference had the most influence on prediction (listed from greatest to least influence in Figure 4). These listed variables were followed by how loudly the participant snored, gender, sleep latency, and whether or not he or she fell asleep while sitting and reading.

Figure 4.

Variable importance plot for boosting predictions for the top 15 most influential predictors based on the validation data set. Variable names (compare with Table 1) are neck = neck circumference; BMI = body mass index; age = age in years; Snore frequency = response to the question “How often do your snore?”; Waist = waist circumference; Snore loud = response to “How loud is your snoring?”; Gender = gender of participant; Minutes = minutes to fall asleep; Sit & read = response to the question “What is the chance that you would doze off or fall asleep while sitting and reading?”; MI = MD said patient had a heart attack; HTN Meds = whether or not the participant is taking anti-hypertensive medications; SBP = systolic blood pressure; In car = response to the question “What is chance that you would doze off or fall asleep while in a car while stopped for a few minutes in traffic?”; CA = MD said patient had coronary angioplasty; TST = total sleep time.

Finally, we applied the algorithm using only those variables that were deemed most influential from the boosting algorithm as predictors. In addition to those listed above, these also included presence or absence of a previous heart attack. Table 5 lists the AUC values under the ROC curves for various prediction methods using either all predictors or the subset of most influential predictors. The AUC results for the boosting algorithm are the same for both predictor sets. For the predictor subset, we also show predictions obtained using neural networks and logistic regression, treating continuous variables as linear and incorporating no interactions. These represent the most frequently used techniques for RDI prediction. The logistic regression model had a higher AUC than random forests and neural networks on this predictor space. The boosting algorithm had the highest AUC, though it must be emphasized that the boosting algorithm was used to identify the influential predictors.

Table 5.

Areas under the ROC curve for prediction of RDI ≥ 7 events per hour using the validation data set

Method	AUC
Using all predictors
Boosting	0.747
Random Forests	0.734
Using subset*
Boosting	0.747
Random Forests	0.708
Neural Networks	0.711
Logistic regression	0.716

^*Neck circumference, BMI, age, snoring frequency, waist circumfer-ence, snoring loudness, gender, minutes to falling asleep, response to “What is the chance that you would doze off or fall asleep while sitting and reading?”, and presence or absence of a heart attack.

DISCUSSION

We employed novel methods for predicting mild obstructive sleep apnea in a community-based sample. The main strengths of the approach are the comprehensiveness of the data set and the prediction algorithms used. Using learning ensemble methods, we found that, among the predictor variables considered (see Table 1), a participant's neck circumference, BMI, age, frequency of snoring, and waist circumference are the most informative variables for predicting RDI. In practice, because the prediction algorithm is based on easily collected data, the boosting algorithm and training data from the SHHS could inform early clinical diagnoses of mild obstructive sleep apnea and might be used to identify who should have monitoring of sleep habits or referral for PSG.

For the boosting prediction algorithm, a threshold of 0.4 for the predicted probability of having an RDI of 7 or more events per hour resulted in a diagnostic likelihood ratio plus (DLR+) of 2.20 and a DLR− of 0.48. That is, the estimated post-test odds of an RDI over 7 are 2.20 times that of the pre-test odds in the light of a positive classification by the algorithm, and 0.48 times lower in the presence of a negative classification. This somewhat modest increase in odds of a high RDI may seem contradictory to the perceived amount of information contained in the variables used for prediction. However, we stress the important distinction that our prediction results apply to a community-based sample, and could be used as a component of a referral process or in public health campaigns.

Our results contrast with the better sensitivity for the prediction of mild or moderate obstructive sleep apnea seen in populations with existing referrals to sleep clinics. In these studies, useful information in the referral process is embedded in the sample that is not present in the SHHS. Hence, the high number of PSG-confirmed cases generally results in algorithms with a high sensitivity on the population in question.

In the terms of the prediction algorithm employed, the most similar paper is the work by Kirby et al.,¹⁰ who used neural networks to predict obstructive sleep apnea in a retrospective study of chart-reviewed patients referred to sleep clinic. Their reported high sensitivity (98.9%) is to be expected, while the reported confidence interval for the specificity (70% to 90%) contains our estimate (71%, see Table 5). However, the results are not directly comparable, as their clinical cut-off (10 events/h) and definition of an obstructive hypopnea differed from ours. A similarly high sensitivity (92.2%) was seen in another clinically referred population in Pillar et al.,³⁶ though their specificity was quite low (18.2%, again, using a different gold standard definition with a cut-off of 10 events/h). When the authors repeated the prediction on a non-referred population, their sensitivity dropped dramatically (32%), and the specificity increased in turn (94%).

Prediction performance from referral populations is perhaps more interesting for distinguishing between moderate and severe cases. In the study by Rowley et al.,¹¹ a prediction algorithm was developed to screen patients for split night protocols. The authors reported success with classifying severe and moderate cases, but less success with screening for the disease itself. Again, the issue was one of specificity, with reported values between 13% and 54%.

Clinical subjects deemed at risk for sleep apnea were considered in Zerah-Lancner et al.¹² They found a high sensitivity (98%) and a high specificity (86%) in prospective validation of a prediction algorithm obtained using stepwise logistic regression. Their procedure was suggested as a screening tool to prevent polysomnograms for low-risk subjects refereed to sleep clinics. In contrast, our prediction methods would be more useful in the referral process.

Similar to the prediction algorithms developed on referral subjects, notable work has appeared on obese populations. Sharma et al.¹³ considered obese subjects presenting to the hospital for non–sleep-related symptoms. Their subjects presented no overt obstructive sleep apnea symptoms. As would be expected, they saw a decrease in the sensitivity over studies employing referral subjects, and an increase in specificity (89.2 and 88.5, respectively). Similarly, Dixon and colleagues¹⁴ reported similar results in obese subjects who were considered for laparoscopic adjustable gastric band surgery.

We do not discuss the related methodology of finding significant predictors of obstructive sleep apnea,^5–8 as our focus was on prediction of OSA, regardless of the significance or causal foundation of the inputs. However, measures of variable importance, a concept related to finding significant predictors, were explored. Across nearly all methods, neck circumference produced the greatest reduction in prediction error and had the largest measure of variable importance. Perhaps more novel is the decomposition of the various components of snoring and the suggestion that snoring frequency and vigor (loudness) have the largest impact among the snoring-related questions on the prediction of RDI.

Measurement error in RDI may degrade prediction performance. Use of a more stable gold standard measure of sleep disturbance, such as those based on multiple night studies may allow for better prediction and more accurate validation of prediction equations. However, night-to-night RDI measurements have shown good stability.³⁷

Also, we note the important role of the available variation in the collection of predictors. For example, race, which played no role in the prediction algorithm, may have a large impact that was not detectable given the mostly white (75%) sample. We reiterate that the community-based sample from the Sleep Heart Health is a main strength of this study. As such, the prediction performance found in this study represents a useful baseline for assessing the value of the RDI-related information contained in these measurements in the population.

However, further work remains warranted to validate prediction algorithms for this area. Specifically, the data splitting methods used to evaluate prediction error only investigate so-called internal validity; that is, evaluating the performance of the prediction algorithms using data from the same study used to create them. Evaluating external validity, using data from alternative studies, would give much better evidence regarding the robustness of the algorithms in the terms of generalizing to other populations. In addition, application of the algorithms to sleep clinic samples would yield important information on the role and accuracy of the referral process.

It is important to stress that the sample used in development largely informs the potential utility of the prediction algorithm. Our predictions from the community-based SHHS are potentially relevant for public health campaigns on awareness of sleep disordered breathing or other broad referral processes. In contrast, clinical samples from primary care physicians would be relevant for the development of checklisting rules for referrals. Hence we emphasize the need a comprehensive study of multiple populations to fully understand the translational utility of algorithmic prediction of RDI.

DISCLOSURE STATEMENT

This was not an industry supported study. Dr. Punjabi has received research support from ResMed and has participated in speaking engagements for Respironics and ResMed. The other authors have indicated no financial conflicts of interest.