Abstract
Study Objectives:
Sleep continuity is commonly assessed with polysomnographic measures such as sleep efficiency, sleep stage percentages, and the arousal index. The aim of this study was to examine whether the transition rate between different sleep stages could be used as an index of sleep continuity to predict self-reported sleep quality independent of other commonly used metrics.
Design and Setting:
Analysis of the Sleep Heart Health Study polysomnographic data.
Participants:
A community cohort.
Measurements and Results:
Sleep recordings on 5,684 participants were deemed to be of sufficient quality to allow visual scoring of NREM and REM sleep. For each participant, we tabulated the frequency of transitions between wake, NREM sleep, and REM sleep. An overall transition rate was determined as the number of all transitions per hour sleep. Stage-specific transition rates between wake, NREM sleep, and REM sleep were also determined. A 5-point Likert scale was used to assess the subjective experience of restless and light sleep the morning after the sleep study. Multivariable regression models showed that a high overall sleep stage transition rate was associated with restless and light sleep independent of several covariates including total sleep time, percentages of sleep stages, wake time after sleep onset, and the arousal index. Compared to the lowest quartile of the overall transition rate (< 7.76 events/h), the odds ratios for restless sleep were 1.27, 1.42, and 1.38, for the second (7.77–10.10 events/h), third (10.11–13.34 events/h), and fourth (≥ 13.35 events/h) quartiles, respectively. Analysis of stage-specific transition rates showed that transitions between wake and NREM sleep were also independently associated with restless and light sleep.
Conclusions:
Assessing overall and stage-specific transition rates provides a complementary approach for assessing sleep continuity. Incorporating such measures, along with conventional metrics, could yield useful insights into the significance of sleep continuity for clinical outcomes.
Citation:
Laffan A; Caffo B; Swihart BJ; Punjabi NM. Utility of sleep stage transitions in assessing sleep continuity. SLEEP 2010;33(12):1681-1686.
Keywords: Sleep fragmentation, sleep continuity, sleep-stage transitions, sleep quality
IT IS BECOMING INCREASING EVIDENT THAT, IN ADDITION TO SLEEP DURATION, CONTINUITY OF SLEEP IS ESSENTIAL FOR ITS RESTORATIVE VALUE.1,2 Empirical evidence garnered over the last decade suggests that sleep disruption and poor sleep quality, even in the absence of sleep loss, can increase daytime sleep tendency, decrease psychomotor performance, cause deficits in attention and memory, and impair glucose homeostasis.3–7 In fact, fragmented sleep is a cardinal feature of several sleep related disorders such as obstructive sleep apnea and may independently contribute to the pathogenesis of associated adverse sequelae.
In clinical practice and research, continuity of sleep is commonly assessed with polysomnographic measures such as the arousal index, sleep efficiency, sleep stage percentages, and wake time after sleep onset. While these metrics can provide useful insights on sleep architecture, each has its inherent limitations. For example, sleep stage percentages, while useful as global measures, provide little information on sleep micro-architecture and account for only a fraction of the total variance in clinical outcomes.8 Seminal work conducted over three decades ago by Baekeland et al.9 showed that the frequency of nocturnal awakenings and the duration of wakefulness are, in fact, better predictors of feeling rested upon awakening than the amount of slow wave or REM sleep. These findings have been subsequently confirmed in studies of experimental sleep disruption which have also shown that sleep stage summaries are not well correlated with impairments in performance or the degree of daytime sleepiness.10
Assessing the frequency of electroencephalographic (EEG) arousals, which does provide information on sleep micro-architecture has become common practice but is not without significant challenges. Scoring of EEG arousals is a tedious process and without rigorous training is fraught with considerable inter- and intra-rater variability.8 Moreover, a number of studies have found that the arousal index is modestly correlated with impairments in daytime function.11 Several complementary and potentially more sensitive approaches for characterizing sleep continuity have been proposed including quantifying autonomic events, assessing cyclic alternating pattern in the EEG, and using cardiopulmonary coupling as an index of sleep state instability.12,13 Although research on the utility of these measures in predicting health consequences is steadily growing, empirical evidence on their validity is currently limited.
In addition to some of the polysomnographic measures highlighted above, the number14 and the rate15,16 of transitions between various sleep stages has also been proposed as a metric of sleep quality. Although still somewhat crude, sleep stage transition data can be readily derived from the conventional hypnogram. To date, a number of studies have examined the utility of the sleep stage transitions in the clinical and research arena using the number,14 rate,15,16 or the time between transitions17–23 as a metric of sleep quality. A consistent observation across these studies has been the significant correlation with other measures of sleep discontinuity such as the frequency of EEG arousals. Thus, it remains to be determined whether sleep stage transition rates, independent of the conventional measures of sleep architecture, can predict daytime outcomes. The primary aim of this study was to determine whether stage-specific and overall transition rates derived from the sleep hypnogram can offer additional information regarding daytime measures beyond that provided by conventional metrics. To achieve this goal, data from the community-based Sleep Heart Health Study were utilized to determine the utility of various stage-specific transition rates in predicting the subjective experience of sleep quality the morning after the sleep study. It was hypothesized that, independent of the measures such as sleep stage percentages, the arousal index, and wake time after sleep onset, sleep stage transition rates would predict the subjective experience of poor sleep quality.
METHODS
Study Sample
The sample for the current study consisted of the baseline cohort of the Sleep Heart Health Study, a multi-center longitudinal study on the cardiovascular consequences of obstructive sleep apnea. Participants for the study were drawn from existing epidemiologic cohorts including The Framingham Offspring and Omni Cohort Studies, The Atherosclerosis Risk in Communities Study, The Cardiovascular Health Study, The Strong Heart Study, The Tucson Epidemiologic Study of Respiratory Disease, and The New York city studies on hypertension which included the New York Hospital cohort, the Harlem cohort, and the Work Site cohort. Details regarding the design and methodology for recruiting and characterizing the sample have been previously described.24 Eligible participants were ≥ 40 years of age and were not being treated for obstructive sleep apnea with positive pressure therapy, oral appliance, oxygen, or tracheostomy. A total of 6,441 participants completed the baseline examination and constitute the study cohort. All participants were required to provide written consent and the protocol was approved by the institutional review board of each of the investigative sites.
Polysomnography and Assessment of Subjective Sleep Quality
In-home sleep studies were conducted on the cohort by trained technicians using a portable monitor (Compumedics P-series, Compumedics Ltd., Abbotsville, Australia). The recording montage consisted of continuous recordings of the following physiologic channels: C3-A2 and C4-A1 electro-encephalogram (EEG), right and left electro-oculogram (EOG), a single bipolar electrocardiogram (ECG), chin electromyogram (EMG), oxyhemoglobin saturation by pulse oximetry, chest and abdominal excursion by inductance plethysmography, airflow by an oronasal thermocouple, and body position by a mercury gauge.25 Recordings were stored in real time and were then shipped to a central reading center for review and scoring.
Sleep recordings were reviewed for study quality by the central reading center and only those studies of sufficient quality25 that allowed for visual scoring of sleep stages (wake, stage 1, stage 2, slow wave, and REM sleep) were included in the current analysis (N = 5,684). Sleep stage scoring was performed by trained technicians according to standard criteria.26 EEG arousals were identified as abrupt shifts ≥ 3-sec duration in EEG frequency. In REM sleep, scoring of arousals also required concurrent increases in EMG amplitude. The arousal index was defined as the average number of arousals per hour of sleep. An overall transition rate, defined as the number of sleep stage transitions per hour of sleep between wake, NREM sleep, and REM sleep, was derived for each participant and used as a measure of sleep continuity. The overall transition rate was divided into stage-specific rates for each of the 6 possible transitions. These included wake-to-NREM (WN), NREM-to-wake (NW), NREM-to-REM (NR), REM-to-NREM (RN), REM-to-wake (RW), and wake-to-REM (WR) transitions.
The morning after the sleep study, each participant completed a questionnaire which included the assessments on subjective sleep quality using two 5-point Likert scales in response to the following question: “My sleep last night was?” On the first scale, responses ranged from “1” light to “5” deep. On the second scale, responses ranged from “1” restless to “5” restful. These two variables constituted the dependent variables for the current study as outlined below.
Statistical Analysis
The Pearson product moment correlation was used to assess the correlation between different stage-specific transitions. Analysis of variance and χ2 statistics were used to assess differences in demographic and sleep parameters by quartile of overall transition rate. Because the two dependent variables were ordinal with a score range from 1 to 5, generalized linear models for categorical data27 were used to model the odds for self-reported restless and light sleep as a function of the overall transition rate while accounting for other measures of sleep architecture (e.g., sleep stage percentages, arousal index) and covariates such as age, sex, race, and body mass index. Initially, analyses were conducted for each of the two categorical variables using the polytomous logistic regression model to characterize the association between transition rates and the ordinal score for restless and light sleep. For a dependent variable with 5 levels, the polytomous model gives 4 equations with 4 corresponding coefficients for each category and covariate combination. Although the polytomous model offers the advantage of simultaneously examining the effect of transition rates on all response categories, the technique generates a cumbersome set of parameter estimates. Thus, to simplify exposition, the scale for each response was collapsed to create a dichotomous variable (1 versus 0) as follows. Responses of “1” or “2” on each scale were coded as a 1 to indicate restless and light sleep, whereas responses of “3,” “4,” or “5” were coded as a 0 to indicate restful and deep sleep. Binary logistic regression was then used to model the association between transition rates and the 2 dichotomized scales. Because the findings were materially indifferent whether the subjective scores were modeled as polytomous or dichotomous variables, results from the dichotomous analysis are presented for ease of interpretation. Nonetheless, the odds ratios from the polytomous model are provided for the stage-specific transition rates (see appendix, available online only at www.journalsleep.org). Transition rates between wake, NREM sleep, and REM sleep were categorized into quartiles, and the odds ratios for restless and light sleep were determined comparing the 4th quartile to the other 3 quartiles. To assess nonlinear dose-response associations between transition rates and reports of restless and light sleep, flexible multivariable regression splines were used.28 Finally, sensitivity analyses were conducted based on a randomly selected subset of the study sample using 50% of the observations to confirm that the observed associations were unbiased and provided results similar to the entire study sample. All analyses were conducted using the SAS 9.0 software package.
RESULTS
The study sample included 5,684 participants with 3,002 women (52.8%) and 2,682 men (47.2%). Combining all 6 types of sleep stage transitions, the median overall transition rate for the sample was 10.11 events/h (interquartile range [IQR]: 7.76–13.35). Transitions between NREM sleep and wake (i.e., NW and WN transitions) were the most common, accounting for approximately 70% of all sleep stage transitions. The least common transition was from wake to REM sleep (WR), with a median rate of 0.21 events/h. A high degree of correlation was noted between reciprocal transitions (e.g., WN and NW) with weak or no correlations between non-reciprocal transitions (Table 1).
Table 1.
Pearson correlations [95% confidence intervals] between different stage-specific transition rates
| Transition Type | WN | NW | NR | RN | RW |
|---|---|---|---|---|---|
| WN | 1.00 | – | – | – | – |
| NW | 0.988 [0.987, 0.989] | 1.00 | – | – | – |
| NR | 0.011 [−0.015, 0.037] | −0.076 [−0.101, −0.050] | 1.00 | – | – |
| RN | −0.175 [−0.200, −0.149] | −0.154 [−0.179, −0.128] | 0.717 [0.704, 0.730] | 1.00 | – |
| RW | 0.282 [0.257, 0.306] | 0.182 [0.157, 0.207] | 0.347 [0.324, 0.370] | −0.171 [−0.196, −0.146] | 1.00 |
| WR | 0.222 [0.197, 0.247] | 0.191 [0.165, 0.215] | 0.068 [0.042, 0.094] | −0.118 [−0.143, −0.092] | 0.861 [0.854, 0.868] |
WN refers to wake-to-NREM; NW, NREM-to-wake; NR, NREM-to-REM; RN, REM-to-NREM; RW, REM-to-wake; WR, wake-to-REM.
Demographic correlates of a high overall sleep stage transition rate included age, male sex, and race (Table 2). In addition, the arousal index, percentages of NREM and REM sleep, and total sleep time were also associated with a high overall transition rate (Table 2). Restless and light sleep were reported by 1,894 (33.3%) and 1,493 (26.3%) of the study participants, respectively, and were also more prevalent in those with a high overall transition rate. Compared to participants without restless sleep, those with restless sleep had higher rates for WN (4.18 vs. 4.70 events/h; P < 0.0001) and NW (3.75 vs. 4.27 events/h; P < 0.0001) transitions. Similarly, compared to participants without light sleep, those with light sleep had had higher rates for WN (4.16 vs. 4.90 events/h; P < 0.0001) and NW (3.72 vs. 4.47 events/h; P < 0.0001) transitions. Additional bivariate analyses between the categorical responses for restless and light sleep and various parameters of sleep architecture showed that the rate of transitioning between wake and NREM sleep, the arousal index, and wake time after sleep onset were the only three parameters that were correlated with the subjective experience of restless and light sleep (data not shown). Finally, because EEG arousals are often associated with sleep stage shifts, the overall transition index was correlated with the arousal index (r = 0.50; 95% CI: 0.48 to 0.52) and wake time after sleep onset (r = 0.49; 95% CI: 0.47 to 0.51).
Table 2.
Study sample characteristics by quartile of overall sleep stage transition rate
| Variable | Quartile of overall transition rate (events/h) |
|||
|---|---|---|---|---|
| < 7.76 | 7.77–10.10 | 10.11–13.34 | ≥ 13.35 | |
| Age, years | 61.5 (11.1) | 61.3 (10.8) | 62.6 (10.5) | 65.5 (10.3) |
| Body mass index, kg/m2 | 28.6 (5.6) | 28.3 (5.4) | 28.4 (5.3) | 28.5 (4.9) |
| Sex, % | ||||
| Women | 31.9 | 27.9 | 24.6 | 15.7 |
| Men | 17.3 | 21.8 | 25.5 | 35.5 |
| Race,% | ||||
| White | 24.9 | 24.6 | 25.7 | 24.8 |
| African American | 24.1 | 23.8 | 23.6 | 28.6 |
| Native American | 24.7 | 25.9 | 21.6 | 27.8 |
| Hispanic | 31.4 | 30.0 | 23.8 | 14.8 |
| Other | 23.8 | 31.3 | 20.0 | 25.0 |
| Apnea-hypopnea index, events/h | 6.9 (10.7) | 7.2 (11.2) | 8.2 (11.2) | 12.2 (14.3) |
| Arousal index, events/h | 13.5 (7.7) | 17.0 (8.6) | 19.7 (9.1) | 26.2 (11.7) |
| Total sleep time, minutes | 378.0 (63.0) | 372.3 (60.0) | 361.4 (56.4) | 327.9 (66.8) |
| Wake after sleep onset, minutes | 38.5 (33.7) | 51.0 (36.7) | 64.4 (39.2) | 92.8 (49.7) |
| Sleep efficiency, % | 86.2 (8.7) | 84.0 (8.7) | 81.1 (8.7) | 74.6 (11.2) |
| Sleep architecture | ||||
| Stage 1 sleep, % | 3.5 (2.4) | 4.5 (2.8) | 5.7 (3.4) | 8.4 (5.2) |
| Stage 2 sleep, % | 54.4 (12.1) | 56.3 (11.3) | 57.1 (11.4) | 60.2 (11.4) |
| Slow wave sleep, % | 21.2 (12.3) | 18.7 (11.4) | 17.1 (11.5) | 13.5 (10.9) |
| REM sleep, % | 20.9 (6.0) | 20.5 (5.9) | 20.1 (5.8) | 17.6 (6.6) |
| Restless sleep, % | 18.7 | 23.8 | 27.5 | 30.0 |
| Light sleep, % | 17.8 | 21.8 | 27.5 | 32.9 |
P < 0.0001 for comparisons of age, sex, apnea-hypopnea index, arousal index, total sleep time, wake after sleep onset, sleep efficiency, stage 1 sleep, stage 2 sleep, slow wave sleep, and REM sleep across quartiles of overall transition rate using χ2 and analysis of variance to compare categorical and continuous variables, respectively. Values reported are means (standard deviations) or percentages.
Logistic regression models were then developed to examine the independent correlates of restless and light sleep. Three nested models were used to assess incremental effects of different covariates on the association between stage-specific transition rates and reports of restless and light sleep (Table 3). The base model included age, sex, race, and body mass index as covariates. The second model added total sleep time and percentage of sleep stages to the base model. The third model added the arousal index and wake time after sleep onset in addition to the covariates of the second model. Sleep efficiency was not added as a covariate given the high correlation (r = −0.83; 95% CI: −0.82 to −0.84) with wake time after sleep onset, which was included in all multivariable models. In each of the final models presented, the highest quartile of stage-specific transition index was compared to the lower 3 quartiles. These analyses showed that despite adjustments for several covariates, including multiple collinear variables of sleep quality (i.e., the arousal index, wake after sleep onset, and percentage of various sleep stages), the WN and NW transition rates were independently associated with higher odds for restless and light sleep. Interestingly, the WR transition rate was inversely associated with restless sleep and reached borderline statistical significance with light sleep. In contrast, none of the other stage-specific transitions (i.e., NR, RN, and RW) were associated with either restless or light sleep in unadjusted or adjusted analyses.
Table 3.
Odds ratios [95% confidence intervals] for the association between sleep stage transition rates and self-reported restless and light sleep
| Transition | Q4 vs.Q1-3 Cutoff point | Restless Sleep |
Light Sleep |
||||
|---|---|---|---|---|---|---|---|
| Model 1a | Model 2b | Model 3c | Model 1a | Model 2b | Model 3c | ||
| WN | 5.23 events/h | 1.90 [1.67, 2.17] | 1.43 [1.24, 1.66] | 1.21 [1.03, 1.41] | 1.97 [1.72, 2.26] | 1.46 [1.25, 1.70] | 1.20 [1.02, 1.42] |
| NW | 4.74 events/h | 1.89 [1.66, 2.15] | 1.40 [1.21, 1.63] | 1.18 [1.01, 1.38] | 1.98 [1.73, 2.27] | 1.44 [1.24, 1.68] | 1.19 [1.01, 1.40] |
| NR | 1.32 events/h | 0.97 [0.85, 1.10] | 0.98 [0.86, 1.12] | 0.97 [0.85, 1.11] | 0.94 [0.81, 1.08] | 0.95 [0.83, 1.10] | 0.94 [0.81, 1.08] |
| RN | 0.69 events/h | 0.97 [0.85, 1.10] | 1.04 [0.91, 1.19] | 1.05 [0.92, 1.20] | 0.91 [0.79, 1.05] | 0.98 [0.85, 1.14] | 0.98 [0.85, 1.14] |
| RW | 1.29 events/h | 1.01 [0.89, 1.15] | 0.96 [0.83, 1.10] | 0.89 [0.77, 1.02] | 1.04 [0.90, 1.19] | 1.02 [0.88, 1.18] | 0.93 [0.81, 1.08] |
| WR | 0.58 events/h | 0.87 [0.76, 0.99] | 0.86 [0.75, 0.98] | 0.79 [0.69, 0.91] | 0.92 [0.80, 1.05] | 0.93 [0.80, 1.08] | 0.85 [0.74, 0.99] |
Model 1: Adjusted for age, sex, race, and body mass index.
Model 2: Adjusted for age, sex, race, body mass index, total sleep time, and sleep stage percentages.
Model 3: Adjusted for age, sex, race, body mass index, total sleep time, sleep stage percentages, wake time after sleep onset, and the arousal index.
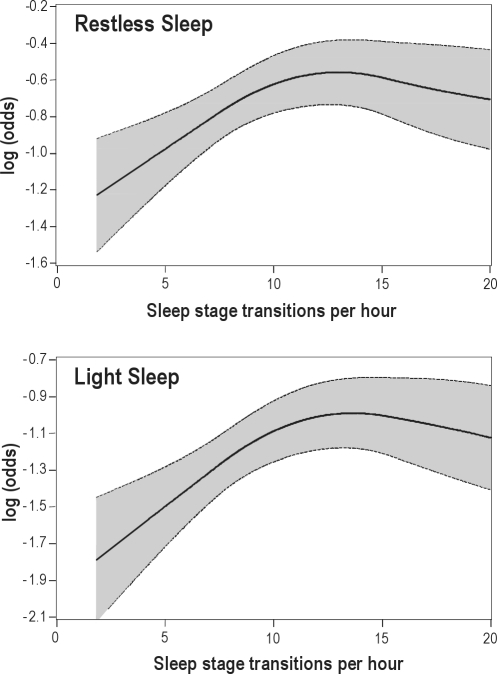
To assess whether the overall transition rate, which combines all 6 stage-specific transitions, was associated with restless and light sleep, several multivariable models were developed. Table 4 shows the adjusted odds ratios for quartiles of the overall transition rate from multivariable models that also included concurrent adjustments for total sleep time, sleep stage percentages, wake time after sleep onset, and the arousal index. As noted in the analyses of stage-specific transitions, the overall transition rate was independently correlated with the experience of restless and light sleep. Polynomial regression splines (Figure 1) that flexibly depict the association between the overall transition rate and restless and light sleep showed that the propensity (i.e., log odds) for restless and light sleep increased linearly with the overall transition rate but then reached a plateau as the sleep stage transition rate exceeded approximately 12 events/h.
Table 4.
Multivariable odds ratios* [95% confidence intervals] for the association between overall sleep stage transition rate and self-reported restless and light sleep
| Variable | Quartile (events/h) | Restless Sleep | Light Sleep |
|---|---|---|---|
| Overall Transition Rate | < 7.76 | 1.00 [Reference] | 1.00 [Reference] |
| 7.77–10.10 | 1.27 [1.07, 1.50] | 1.16 [0.96, 1.40] | |
| 10.11–13.34 | 1.42 [1.20, 1.70] | 1.41 [1.17, 1.71] | |
| ≥ 13.35 | 1.38 [1.12, 1.69] | 1.44 [1.16, 1.79] |
Adjusted for age, sex, race, body mass index, total sleep time, sleep stage percentages, wake time after sleep onset, and the arousal index.
Figure 1.
Multivariable adjusted log (odds) of restless (upper panel) and light sleep (lower panel) as a function of overall sleep stage transition index.
DISCUSSION
The primary objective of this study was to assess the extent to which sleep stage transitions could be used to characterize the degree of sleep disruption above and beyond conventional polysomnographic measures of sleep. Using data from a large community-based cohort study with overnight polysomnography, our results demonstrate that sleep stage transitions are predictive of the subjective experience of impaired sleep quality. Specifically, overall and stage-specific transition rates were associated with self-reported restless and light sleep independent of factors including age, sex, race, body mass index, and a wide repertoire of conventional sleep related metrics. Collectively, the results of this study indicate that sleep stage transition rates are useful in predicting specific outcomes and thus provide additional information about sleep continuity.
A number of studies have previously shown that information on transitions from one sleep stage to another, including wakefulness, may offer a convenient approach for assessing sleep continuity.15–23 Data from the sleep hypnogram can be partitioned in two components: (1) the duration of a sleep stage prior to a transition, and (2) the number of different sleep stage transitions. Previous studies on adult20–22 and pediatric samples23 have shown that modeling the duration of contiguous sleeps stages, as a measure of sleep continuity, can reveal substantial differences that are not evident when comparing classical measures of sleep architecture, such as the sleep stage percentages and the arousal index between those with and without obstructive sleep apnea. Moreover, studies that have examined sleep stage transition rates have similarly concluded that these rates are useful in differentiating patient subgroups and in predicting clinical outcomes.15,16,29 The current study advances the existing literature by presenting a critical analysis of the potential role of sleep stage transitions on subjective sleep quality independent of the effects explained by commonly used metrics. Collectively, the available body of empirical evidence indicates that an accurate appraisal of sleep architecture should utilize complementary measures that depict micro and macro level information regarding sleep continuity. A major implication of the findings reported here is that the subjective experience of feeling rested in the morning is likely determined by several core components including sleep duration, transient EEG arousals that not associated with a sleep stage shift, and the rate of sleep stage transitions. Our findings also raise the issue of whether arousals, as indexed by the presence or absence of a concurrent stage shift, can have differential effects on clinical outcomes. Additional research is certainly needed to better define the full spectrum of arousals and how physiological characteristics of an arousal (e.g., absence or presence of a stage shift) can influence the recuperative and restorative value of sleep.
Evaluating whether a metric of sleep stage transitions provides a valid measure of sleep continuity requires the consideration of whether it actually measures what it purports. Certainly, the data herein show that stage transition rates have criterion validity, as they were able to independently predict the subjective experience of sleep quality on the following morning. The replication of the association between sleep stage transition rates and other clinical outcomes such as incident hypertension, cardiovascular disease, and possibly mortality will further validate their utility and represents a logical extension of this line of research. It is interesting to note that, of the six stage-specific transition types, the reciprocal WN-NW transition pair had the strongest association with poor self-reported sleep quality followed by the WR-RN pair. In contrast no significant effect of the NR-RN transition pair on sleep quality was observed. These results are not surprising given that alternation of NREM sleep with REM sleep across the night is a fundamental characteristic of normal sleep in all homeothermic species. Although remarkable progress has been made in our understanding of the neural circuitry that regulates NREM and REM sleep,30,31 the functional significance of the NREM-REM oscillation remains a mystery. Nonetheless, it is important to recognize that while cycling between NREM-REM sleep is part of normal sleep and may have an essential role, excessive oscillations between NREM and REM sleep, as in severe obstructive sleep apnea, may have untoward effects on daytime function. Given that the reciprocal NR and RN transitions were infrequent in our study sample, isolating the implications of these transitions was not possible.
There are several important limitations of this study that merit discussion. First, sleep was classified as NREM and REM and not further subdivided into distinct stages of NREM sleep. Thus, transitions between individual NREM stages were not included. Our decision to collapse all of NREM sleep into one state was driven by the greater reliability of scoring NREM sleep32 than its individual components and by the need to initially assess the utility of a limited number of transitions. Incorporating all of the NREM sleep stages (i.e., 1, 2, and slow wave sleep) along with REM sleep and wake would have generated a total of 20 different transitions types and substantially increased the complexity of our results. Second, criterion validity for sleep stage transition rates was assessed using self-reported sleep quality, which is certainly predisposed to measurement error due to recall bias. However, because sleep quality was assessed immediately after the sleep study, the potential of such bias is limited. Third, the determination of overall transition index, which collapses all of the stage-specific transitions, is based on the premise that each type of transition contributes equally to overall sleep quality. Analyses by stage-specific transitions show that transitions between NREM sleep and wake are most common and predict poor sleep quality, whereas the WR transition predicts better sleep quality. Thus, while it is certainly useful to examine stage-specific transitions, using the overall transition rate provides a simple and single measure for characterizing sleep-state instability. Finally, it is important to recognize that, despite rigorous training and centralized scoring of the polysomnograms in the Sleep Heart Health Study, differences in the reliability of scoring EEG arousals and sleep stages may have contributed to the findings reported herein.32 Because EEG arousals had more inter-scorer variability (intraclass correlation coefficient 0.54) than scoring NREM or REM sleep (κ statistics: 0.87–0.90), it is certainly possible that the independent association between sleep stage transition rates and subjective sleep quality is attributable to this difference in reliability. These limitations notwithstanding, the current study also has several strengths. These include the use of a large community cohort that was systematically characterized with overnight polysomnography and the inclusion of several covariates to account for potential confounding. Perhaps the most important strength of this study is the examination of the association between sleep stage transition rates and self-reported sleep quality independent of commonly used measures of sleep quality including, sleep stage percentages, frequency of EEG arousals, total sleep time, and wake time after sleep onset.
In summary, the results of this study demonstrate that sleep stage transition rates provide a useful measure which can predict the subjective experience of sleep quality independent of conventional measures of sleep architecture. Fragmented sleep is less restorative than consolidated sleep and may also have long-term clinical effects. Our ability to identify the health effects of disrupted sleep will require that we employ a repertoire of metrics to fully capture the micro and macro-level information on sleep architecture. Because sleep stages are readily available, assessing transition rates will only enhance our ability to define the role of sleep continuity in health and disease.
DISCLOSURE STATEMENT
This was not an industry supported study. Dr. Punjabi has participated in a clinical trial supported by ResMed. He received no income for the study. The other authors have indicated no financial conflicts of interest.
ACKNOWLEDGMENTS
This study was supported by the following National Institutes of Health Grants: HL086862 and HL075078.
Appendix
The Multinomial Approach to Modeling Sleep Stage Transitions
The polytomous logistic regression model is an extension of the binomial logistic regression model which accommodates multinomial responses. The polytomous model does not impose any restrictions on the ordinality of the response variable. The model is represented as follows:
where αk = 0 and βk = 0. The vector β = (β1, β2,…βk)' corresponds to the regression coefficients for the log-odds of (Y = yj) relative to the reference category (Y = yk), and there are (k-1) intercept parameters αj. Exponentiating the regression coefficient bl, for the lth covariate xl will results in the odds ratio comparing (Y = yj) versus (Y = yk) for a unit increase in xl. The two response scales were as follows:
Using “5” as the reference category, the polytomous model yields four odds ratios corresponding to each of the other response categories (1, 2, 3, and 4) as compared to the reference category for a particular covariate (e.g., transition rate). For the association between WN transition rates and self-reported sleep quality, these odds ratios estimate the effect of a high (4th quartile) versus low (quartiles 1–3) transition rate on the probability of a “1,” “2,” “3,” or “4,” response versus a “5” response. Table S1 describes the odds ratios for each of the 6 stage-specific transition rates derived from the multivariable adjusted polytomous logistic model for the restless and light sleep variables. As noted with the analyses of the dichotomous scales, WN and NW transitions were strongly predictive of restless and light sleep quality. However, to simplify exposition, the effect of each stage-specific transition rate is expressed by a single odds ratio in our reported analysis from the dichotomized outcome instead of 4 odds ratios from the polytomous model.
Table S1.
Odds ratios [95% confidence intervals] for the association between sleep stage transition rates, self-reported restless and light sleep using the polytomous multivariable* logistic regression model
| Transition | Q4 vs.Q1-3 Cutoff point | Restless Sleep |
Light Sleep |
||
|---|---|---|---|---|---|
| Response | Odds Ratio | Response | Odds Ratio | ||
| (Restful) | (Deep) | ||||
| WN | 5.23 events/h | 5 | Reference | 5 | Reference |
| 4 | 1.09 [0.94, 1.25] | 4 | 1.13 [0.97, 1.32] | ||
| 3 | 1.15 [1.00, 1.31] | 3 | 1.22 [1.05, 1.41] | ||
| 2 | 1.19 [1.04, 1.38] | 2 | 1.23 [1.05, 1.44] | ||
| 1 | 1.26 [1.07, 1.47] | 1 | 1.40 [1.17, 1.67] | ||
| (Restless) | (Light) | ||||
| NW | 4.74 events/h | 5 | Reference | 5 | Reference |
| 4 | 1.05 [0.92, 1.21] | 4 | 1.13 [0.97, 1.32] | ||
| 3 | 1.11 [0.97, 1.27] | 3 | 1.23 [1.06, 1.42] | ||
| 2 | 1.16 [1.01, 1.33] | 2 | 1.23 [1.05, 1.44] | ||
| 1 | 1.20 [1.03, 1.41] | 1 | 1.60 [1.17, 1.67] | ||
| NR | 1.32 events/h | 5 | Reference | 5 | Reference |
| 4 | 0.96 [0.86, 1.07] | 4 | 0.95 [0.85, 1.07] | ||
| 3 | 0.99 [0.90, 1.10] | 3 | 0.94 [0.84, 1.04] | ||
| 2 | 0.95 [0.85, 1.06] | 2 | 0.90 [0.80, 1.02] | ||
| 1 | 1.00 [0.88, 1.14] | 1 | 0.96 [0.83, 1.11] | ||
| RN | 0.69 events/h | 5 | Reference | 5 | Reference |
| 4 | 0.97 [0.87, 1.07] | 4 | 0.94 [0.84, 1.05] | ||
| 3 | 0.92 [0.83, 1.02] | 3 | 0.90 [0.81, 1.00] | ||
| 2 | 0.96 [0.86, 1.07] | 2 | 0.91 [0.80, 1.02] | ||
| 1 | 1.00 [0.88, 1.14] | 1 | 0.94 [0.82, 1.09] | ||
| RW | 1.29 events/h | 5 | Reference | 5 | Reference |
| 4 | 0.99 [0.88, 1.12] | 4 | 1.03 [0.91, 1.17] | ||
| 3 | 1.03 [0.92, 1.16] | 3 | 1.04 [0.93, 1.18] | ||
| 2 | 0.94 [0.83, 1.06] | 2 | 1.02 [0.90, 1.17] | ||
| 1 | 0.99 [0.87, 1.14] | 1 | 0.96 [0.82, 1.12] | ||
| WR | 0.58 events/h | 5 | Reference | 5 | Reference |
| 4 | 1.06 [0.94, 1.18] | 4 | 1.03 [0.91, 1.16] | ||
| 3 | 1.03 [0.93, 1.16] | 3 | 1.03 [0.92, 1.15] | ||
| 2 | 0.93 [0.83, 1.05] | 2 | 0.96 [0.84, 1.09] | ||
| 1 | 0.91 [0.79, 1.05] | 1 | 0.92 [0.79, 1.08] | ||
Adjusted for age, sex, race, body mass index, total sleep time, sleep stage percentages, wake time after sleep onset, and the arousal index.
REFERENCES
- 1.Wesensten NJ, Balkin TJ, Belenky G. Does sleep fragmentation impact recuperation? A review and reanalysis. J Sleep Res. 1999;8:237–45. doi: 10.1046/j.1365-2869.1999.00161.x. [DOI] [PubMed] [Google Scholar]
- 2.Bonnet MH, Arand DL. Clinical effects of sleep fragmentation versus sleep deprivation. Sleep Med Rev. 2003;7:297–310. doi: 10.1053/smrv.2001.0245. [DOI] [PubMed] [Google Scholar]
- 3.Stepanski E, Lamphere J, Roehrs T, Zorick F, Roth T. Experimental sleep fragmentation in normal subjects. Int J Neurosci. 1987;33:207–14. doi: 10.3109/00207458708987405. [DOI] [PubMed] [Google Scholar]
- 4.Jones K, Harrison Y. Frontal lobe function, sleep loss and fragmented sleep. Sleep Med Rev. 2001;5:463–75. doi: 10.1053/smrv.2001.0203. [DOI] [PubMed] [Google Scholar]
- 5.Kingshott RN, Cosway RJ, Deary IJ, Douglas NJ. The effect of sleep fragmentation on cognitive processing using computerized topographic brain mapping. J Sleep Res. 2000;9:353–7. doi: 10.1046/j.1365-2869.2000.00223.x. [DOI] [PubMed] [Google Scholar]
- 6.Tasali E, Leproult R, Ehrmann DA, Van Cauter E. Slow-wave sleep and the risk of type 2 diabetes in humans. Proc Natl Acad Sci U S A. 2008;105:1044–9. doi: 10.1073/pnas.0706446105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Stamatakis KA, Punjabi NM. Effects of sleep fragmentation on glucose metabolism in normal subjects. Chest. 2010;137:95–101. doi: 10.1378/chest.09-0791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bonnet MH, Doghramji K, Roehrs T, et al. The scoring of arousal in sleep: reliability, validity, and alternatives. J Clin Sleep Med. 2007;3:133–45. [PubMed] [Google Scholar]
- 9.Baekeland F, Hoy P. Reported vs recorded sleep characteristics. Arch Gen Psychiatry. 1971;24:548–51. doi: 10.1001/archpsyc.1971.01750120064011. [DOI] [PubMed] [Google Scholar]
- 10.Bonnet MH. Sleep restoration as a function of periodic awakening, movement, or electroencephalographic change. Sleep. 1987;10:364–73. doi: 10.1093/sleep/10.4.364. [DOI] [PubMed] [Google Scholar]
- 11.Stepanski EJ. The effect of sleep fragmentation on daytime function. Sleep. 2002;25:268–76. doi: 10.1093/sleep/25.3.268. [DOI] [PubMed] [Google Scholar]
- 12.Halasz P, Terzano M, Parrino L, Bodizs R. The nature of arousal in sleep. J Sleep Res. 2004;13:1–23. doi: 10.1111/j.1365-2869.2004.00388.x. [DOI] [PubMed] [Google Scholar]
- 13.Thomas RJ, Mietus JE, Peng CK, Goldberger AL. An electrocardiogram-based technique to assess cardiopulmonary coupling during sleep. Sleep. 2005;28:1151–61. doi: 10.1093/sleep/28.9.1151. [DOI] [PubMed] [Google Scholar]
- 14.Stepanski E, Lamphere J, Badia P, Zorick F, Roth T. Sleep fragmentation and daytime sleepiness. Sleep. 1984;7:18–26. doi: 10.1093/sleep/7.1.18. [DOI] [PubMed] [Google Scholar]
- 15.Haba-Rubio J, Ibanez V, Sforza E. An alternative measure of sleep fragmentation in clinical practice: the sleep fragmentation index. Sleep Med. 2004;5:577–81. doi: 10.1016/j.sleep.2004.06.007. [DOI] [PubMed] [Google Scholar]
- 16.Swarnkar V, Abeyratne UR, Hukins C, Duce B. A state transition-based method for quantifying EEG sleep fragmentation. Med Biol Eng Comput. 2009 doi: 10.1007/s11517-009-0524-2. [DOI] [PubMed] [Google Scholar]
- 17.Yassouridis A, Steiger A, Klinger A, Fahrmeir L. Modelling and exploring human sleep with event history analysis. J Sleep Res. 1999;8:25–36. doi: 10.1046/j.1365-2869.1999.00133.x. [DOI] [PubMed] [Google Scholar]
- 18.Lo CC, Amaral LAN, Havlin S, et al. Dynamics of sleep-wake transitions during sleep. Europhysics Letters. 2002;57:625–31. [Google Scholar]
- 19.Lo CC, Chou T, Penzel T, et al. Common scale-invariant patterns of sleep-wake transitions across mammalian species. Proceedings of the Natl Acad Sci U S A. 2004;101:17545–8. doi: 10.1073/pnas.0408242101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Penzel T, Lo CC, Ivanov P, Kesper K, Becker H, Vogelmeier C. Analysis of sleep fragmentation and sleep structure in patients with sleep apnea and normal volunteers. Conf Proc IEEE Eng Med Biol Soc. 2005;3:2591–4. doi: 10.1109/IEMBS.2005.1616999. [DOI] [PubMed] [Google Scholar]
- 21.Norman RG, Scott MA, Ayappa I, Walsleben JA, Rapoport DM. Sleep continuity measured by survival curve analysis. Sleep. 2006;29:1625–31. doi: 10.1093/sleep/29.12.1625. [DOI] [PubMed] [Google Scholar]
- 22.Swihart BJ, Caffo B, Bandeen-Roche K, Punjabi NM. Characterizing sleep structure using the hypnogram. J Clin Sleep Med. 2008;4:349–55. [PMC free article] [PubMed] [Google Scholar]
- 23.Chervin RD, Fetterolf JL, Ruzicka RL, Thelen BJ, Burns JW. Sleep stage dynamics differ between children with and without obstructive sleep apnea. Sleep. 2009;32:1325–32. doi: 10.1093/sleep/32.10.1325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Quan SF, Howard BV, Iber C, et al. The Sleep Heart Health Study: design, rationale, and methods. Sleep. 1997;20:1077–85. [PubMed] [Google Scholar]
- 25.Redline S, Sanders MH, Lind BK, et al. Methods for obtaining and analyzing unattended polysomnography data for a multicenter study. Sleep Heart Health Research Group. Sleep. 1998;21:759–67. [PubMed] [Google Scholar]
- 26.Rechtschaffen A, Kales A. Washington, DC: US Government Printing Office; 1968. Manual of standardized terminology, techniques and scoring system for sleep stages of human subjects. [Google Scholar]
- 27.Hosmer DW, Lemeshow S. John Wiley & Sons, Inc.; 1989. Applied logistic regression. [Google Scholar]
- 28.Greenland S. Dose-response and trend analysis in epidemiology: alternatives to categorical analysis. Epidemiology. 1995;6:356–65. doi: 10.1097/00001648-199507000-00005. [DOI] [PubMed] [Google Scholar]
- 29.Morrell MJ, Finn L, Kim H, Peppard PE, Badr MS, Young T. Sleep fragmentation, awake blood pressure, and sleep-disordered breathing in a population-based study. Am J Respir Crit Care Med. 2000;162:2091–6. doi: 10.1164/ajrccm.162.6.9904008. [DOI] [PubMed] [Google Scholar]
- 30.Saper CB, Scammell TE, Lu J. Hypothalamic regulation of sleep and circadian rhythms. Nature. 2005;437:1257–63. doi: 10.1038/nature04284. [DOI] [PubMed] [Google Scholar]
- 31.Lu J, Sherman D, Devor M, Saper CB. A putative flip-flop switch for control of REM sleep. Nature. 2006;441:589–94. doi: 10.1038/nature04767. [DOI] [PubMed] [Google Scholar]
- 32.Whitney CW, Gottlieb DJ, Redline S, et al. Reliability of scoring respiratory disturbance indices and sleep staging. Sleep. 1998;21:749–57. doi: 10.1093/sleep/21.7.749. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1.
Odds ratios [95% confidence intervals] for the association between sleep stage transition rates, self-reported restless and light sleep using the polytomous multivariable* logistic regression model
| Transition | Q4 vs.Q1-3 Cutoff point | Restless Sleep |
Light Sleep |
||
|---|---|---|---|---|---|
| Response | Odds Ratio | Response | Odds Ratio | ||
| (Restful) | (Deep) | ||||
| WN | 5.23 events/h | 5 | Reference | 5 | Reference |
| 4 | 1.09 [0.94, 1.25] | 4 | 1.13 [0.97, 1.32] | ||
| 3 | 1.15 [1.00, 1.31] | 3 | 1.22 [1.05, 1.41] | ||
| 2 | 1.19 [1.04, 1.38] | 2 | 1.23 [1.05, 1.44] | ||
| 1 | 1.26 [1.07, 1.47] | 1 | 1.40 [1.17, 1.67] | ||
| (Restless) | (Light) | ||||
| NW | 4.74 events/h | 5 | Reference | 5 | Reference |
| 4 | 1.05 [0.92, 1.21] | 4 | 1.13 [0.97, 1.32] | ||
| 3 | 1.11 [0.97, 1.27] | 3 | 1.23 [1.06, 1.42] | ||
| 2 | 1.16 [1.01, 1.33] | 2 | 1.23 [1.05, 1.44] | ||
| 1 | 1.20 [1.03, 1.41] | 1 | 1.60 [1.17, 1.67] | ||
| NR | 1.32 events/h | 5 | Reference | 5 | Reference |
| 4 | 0.96 [0.86, 1.07] | 4 | 0.95 [0.85, 1.07] | ||
| 3 | 0.99 [0.90, 1.10] | 3 | 0.94 [0.84, 1.04] | ||
| 2 | 0.95 [0.85, 1.06] | 2 | 0.90 [0.80, 1.02] | ||
| 1 | 1.00 [0.88, 1.14] | 1 | 0.96 [0.83, 1.11] | ||
| RN | 0.69 events/h | 5 | Reference | 5 | Reference |
| 4 | 0.97 [0.87, 1.07] | 4 | 0.94 [0.84, 1.05] | ||
| 3 | 0.92 [0.83, 1.02] | 3 | 0.90 [0.81, 1.00] | ||
| 2 | 0.96 [0.86, 1.07] | 2 | 0.91 [0.80, 1.02] | ||
| 1 | 1.00 [0.88, 1.14] | 1 | 0.94 [0.82, 1.09] | ||
| RW | 1.29 events/h | 5 | Reference | 5 | Reference |
| 4 | 0.99 [0.88, 1.12] | 4 | 1.03 [0.91, 1.17] | ||
| 3 | 1.03 [0.92, 1.16] | 3 | 1.04 [0.93, 1.18] | ||
| 2 | 0.94 [0.83, 1.06] | 2 | 1.02 [0.90, 1.17] | ||
| 1 | 0.99 [0.87, 1.14] | 1 | 0.96 [0.82, 1.12] | ||
| WR | 0.58 events/h | 5 | Reference | 5 | Reference |
| 4 | 1.06 [0.94, 1.18] | 4 | 1.03 [0.91, 1.16] | ||
| 3 | 1.03 [0.93, 1.16] | 3 | 1.03 [0.92, 1.15] | ||
| 2 | 0.93 [0.83, 1.05] | 2 | 0.96 [0.84, 1.09] | ||
| 1 | 0.91 [0.79, 1.05] | 1 | 0.92 [0.79, 1.08] | ||
Adjusted for age, sex, race, body mass index, total sleep time, sleep stage percentages, wake time after sleep onset, and the arousal index.