Properties of small molecular drug loading and diffusion in a fluorinated PEG hydrogel studied by ¹H molecular diffusion NMR and ¹⁹F spin diffusion NMR

Abstract

R_f-PEG (fluoroalkyl double-ended poly(ethylene glycol)) hydrogel is potentially useful as a drug delivery depot due to its advanced properties of sol–gel two-phase coexistence and low surface erosion. In this study, ¹H molecular diffusion nuclear magnetic resonance (NMR) and ¹⁹F spin diffusion NMR were used to probe the drug loading and diffusion properties of the R_f-PEG hydrogel for small anticancer drugs, 5-fluorouracil (FU) and its hydrophobic analog, 1,3-dimethyl-5-fluorouracil (DMFU). It was found that FU has a larger apparent diffusion coefficient than that of DMFU, and the diffusion of the latter was more hindered. The result of ¹⁹F spin diffusion NMR for the corresponding freeze-dried samples indicates that a larger portion of DMFU resided in the R_f core/IPDU intermediate-layer region (where IPDU refers to isophorone diurethane, as a linker to interconnect the R_f group and the PEG chain) than that of FU while the opposite is true in the PEG–water phase. To understand the experimental data, a diffusion model was proposed to include: (1) hindered diffusion of the drug molecules in the R_f core/IPDU-intermediate-layer region; (2) relatively free diffusion of the drug molecules in the PEG-water phase (or region); and (3) diffusive exchange of the probe molecules between the above two regions. This study also shows that molecular diffusion NMR combined with spin diffusion NMR is useful in studying the drug loading and diffusion properties in hydrogels for the purpose of drug delivery applications.

Introduction

R_f-PEGs (fluoroalkyl double-ended poly(ethylene glycol)) belong to a class of biocompatible and biodegradable fluorinated polymers [1–4]. Micelles formed by R_f-PEGs in water consist of a hydrophobic fluorocarbon core (R_f core) shielded by a large hydrophilic poly(ethylene glycol) shell (PEG shell). Certain combinations of the PEG chain length and fluorocarbon size lead to sol–gel two-phase coexistence and low surface erosion in water due to the high degree of cross linking of the R_f-PEG chains between the micelles [5]. These properties make the R_f-PEG potentially useful as a drug delivery depot for controlled and sustained drug delivery [5, 6]. Previously, we have used ¹⁹F T ₁ relaxation nuclear magnetic resonance (NMR) [7] and variable temperature-dependent EPR [4] to study the R_f-PEG’s property to encapsulate hydrophobic drugs by employing a probe molecule made of free radical labeled anticancer drug, chlorambucil-tempol adduct [4, 7, 8]. Further insight into the structure of the drug-micelle assembly was obtained through molecular dynamics simulations [7] From these studies, we also learned that the IPDU (isophorone diurethane) units which were used to link the fluoroalcohol to the PEG chain form the hydrophobic intermediate layer (IPDU intermediate layer) under aqueous conditions in addition to the already known R_f core and PEG shell. The IPDU intermediate layer is lipophilic in nature, and is able to hold lipophilic/hydrophobic drugs [7]. In this study, we have used molecular diffusion NMR and ¹⁹F spin diffusion NMR to study the drug loading and diffusion properties of the R_f-PEG hydrogel for a small hydrophilic anticancer drug and its hydrophobic analog.

Diffusion NMR is a noninvasive technique to study molecular diffusion in solutions [9]. Pulsed field gradient spin echo (PFGSE) NMR employs a spin echo pulse sequence together with pulsed field gradients to analyze the diffusion and other translational motion of molecules in a wide variety of media [9–12]. The diffusion coefficient and model of diffusion can be obtained. One of the first studies to focus on the diffusion of molecules in colloidal systems dates back to 1968, and was conducted by Tanner and Stejskal [13]. In their study, one artificial system of thin liquid layers (mica stack), three different kinds of plant cells (yeast, apple, and tobacco pith), and one octanol-in-water emulsion was studied. Useful information regarding the model of diffusion was obtained through analyses of equations for restricted diffusion. Many groups have since carried out more diffusion experiments for the studies of hydrogels [14, 15], protein binding [16] polymer chain motion in gels [17], surfactants [18, 19], oil–water emulsions [20–22], and separations [23]. To circumvent the short T ₂ time in viscous solutions, the pulsed field gradient stimulated echo (PFGSTE) pulse sequence was developed [9, 24, 25]. Compared with the PFGSE, PFGSTE pulse sequence makes use of the possibly longer T ₁ time to observe the NMR signal in viscous media for a longer time [26]. Another pulse sequence referred to as CONVEX (CONVection compensation/EXcitation sculpting) has been used to study the diffusion of solute molecules in PVA hydrogels [15]. This pulse sequence includes a water suppression step to avoid the interruption by the water signal during the diffusion measurement. Many other variations of NMR diffusion techniques [9, 20, 22, 27] and theoretical models have also been developed to treat hindered diffusion and restricted diffusion including diffusion in a sphere and a cylinder [22, 28, 29]. For instance, Garasanin et al. [22] examined the diffusion of the poly(dimethylsiloxane) (PDMS) fluid, its restricted diffusion inside the emulsion droplets and the Brownian diffusion of the droplets. Time-dependent diffusion NMR techniques were also developed to study the inhomogeneous diffusion of probe molecules in cross linked polymer gels [30]. The theory of solute particles undergoing restricted diffusion and the corresponding mathematical approximations useful in treating such systems have well been compiled in the review by Price [9]. A theoretical model to treat diffusion coupled with chemical exchanges was reviewed by Momot and Kuchel [31]. This model is useful for the study of drug delivery systems. A study of NMR line shapes due to diffusive exchange and relaxation process was also reported [32].

To compliment the information obtained from molecular diffusion NMR, we also performed ¹⁹F spin diffusion NMR which utilizes the dipolar interactions of abundant nuclear spins to probe spin dipolar coupled networks. Thus, molecular miscibility and domain size of spin coupled networks can be probed [33, 34].

We have used 5-fluorouracil (FU), and its hydrophobic analog, 1,3-dimethyl-5-fluorouracil (DMFU), as examples of small molecules to study the property of the R_f-PEG hydrogel as a drug delivery depot. FU belongs to a group of anticancer drugs known as antimetabolites [35, 36]. It is used for the treatment of colon cancer, rectal cancer, breast cancer, stomach cancer, and pancreatic cancer. DMFU is a hydrophobic analog of FU with both the ring amino groups being methylated [37]. FU and DMFU contain both proton and fluorine groups which make it convenient to use both the ¹H and the ¹⁹F NMR signals to study their drug loading and diffusion characters in the R_f-PEG hydrogel.

Experimental

6KC6 R_f-PEG (C₆F₁₃-CH₂CH₂O-IPDU-O-(CH₂CH₂O-)n-IPDU-OCH₂CH₂-F₁₃C₆) was synthesized as described in previous methods [5]. The term 6KC6 refers to the PEG with MW 6,000 Daltons (6 K) and the fluoroalcohol group with six fluorinated carbon atoms (C6). IPDU refers to isophorone diurethane. In the R_f-PEG, either side of the PEG chain is linked to an R_f group through the linker IPDU. FU and DMFU with purity greater than 99% were purchased from Sigma Aldrich (USA), and their chemical structures are given in Scheme 1. All solvents used were of analytical reagent grade purchased from Fischer Scientific (USA). To prepare the gel samples, 100 mg of 6KC6 R_f-PEG and 5 mg of FU or DMFU were dissolved in 1 ml methylene chloride. The homogenous mixture was allowed to air dry completely. Then, 0.9 ml D₂O was added to the mixture to make the 10% 6KC6 R_f-PEG hydrogel samples. The hydrogels were then homogenized using a Branson sonicator. The gel samples were stabilized at room temperature for more than 24 h before the NMR study. To study the drug loading properties using solid state ¹⁹F spin diffusion NMR, the FU and DMFU loaded hydrogel samples were freeze-dried with a Labconco Inc. lyophilizer.

Scheme 1.

Chemical structures of FU and DMFU

The diffusion NMR experiments were carried out with a Bruker Avance™ 600 MHz system equipped with a 5-mm Diff30 water-cooled diffusion probe and a gradient amplifier capable of achieving gradient strength up to 1,200 G/cm. ¹H PFGSTE NMR [26] and PFGSE NMR sequences [11, 12] were used. The PFGSE experiments were carried out with Δ = 20 ms and δ = 1 ms, where δ denotes the gradient duration time and Δ the distance between the two front edges of the gradient pulses. The echo intensity for each experiment was attenuated by varying the gradient strength g from 0 to 1,200 G/cm. All the signal intensities relative to the corresponding g = 0 ones were used to remove the T ₂ effects on the NMR signal intensities. Molecular diffusions of FU and DMFU in the 6KC6 R_f-PEG hydrogel were observed through acquiring ¹H NMR signal, and the diffusions of the R_f-PEG chains were observed through acquiring ¹H and ¹⁹F NMR signals. All NMR experiments including those described below were carried out at 25°C.

Another kind of diffusion NMR experiment using the PFGSTE pulse sequence was also carried out in which the echo intensity was measured by varying Δ while keeping all the other parameters including δ and g constant. The advantage of this technique arises from the ability to monitor the diffusion of the probe molecule for a much longer time by using a lower gradient strength. In this manner, we could see the hindrance effect of the probe molecule due to translational barriers. For short Δ values, a probe molecule may not diffuse too far to show the hindrance effect. However, when Δ is increased, this effect on the NMR signal intensity can show up by approaching nonzero echo intensity while zero echo intensity is approached for free diffusion besides the variation of the diffusion curves according to the model of diffusion. In the experiment, Δ was varied from 0 to 200 ms while the gradient strength was fixed at 75 G/cm and δ at 1 ms. To eliminate the T ₁ and T ₂ effects on the echoed NMR signal intensities, the signal intensity for each experiment was measured by alternating the pulse sequences with and without the gradient pulses and the ratio of the signal intensities with and without the gradients for each Δ value was then plotted against the corresponding (Δ−δ/3) values. Samples used for this experiment include FU in D₂O, FU in 6K PEG D₂O, FU in the 6KC6 R_f-PEG hydrogel and DMFU in the 6KC6 R_f-PEG hydrogel.

In order to evaluate the locations of FU and DMFU in the R_f-PEG hydrogel, we carried out a ¹⁹F solid state spin diffusion NMR experiment for the freeze-dried FU and DMFU hydrogel samples. The drug molecules enclosed in the R_f core/IPDU intermediate-layer region may show ¹⁹F cross peaks with the peaks of the R_f group in the two-dimensional spectrum. To avoid averaging out the ¹⁹F–¹⁹F dipolar coupling, the samples were run in a static condition. A Doty XC4 ¹H/¹⁹F/X triple resonance 600 MHz solid state NMR probe was used. The two-dimensional spin diffusion pulse sequence [38] with a mixing time of 100 ms and a recycling delay of 3 s was employed.

Results

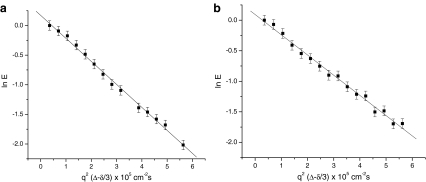
Results for the PFGSE experiments of FU and DMFU in the R_f-PEG hydrogel are shown in Fig. 1a and b, respectively. The data are shown by plotting the natural logarithms of the normalized echo intensities E = I _g/I ₀ (where I _g is the attenuated NMR signal intensity by the pulsed field gradient and I ₀ is the intensity without the attenuation) against q ²(Δ−δ/3), where q = γgδ. Only the experiments for g = 0−200 G/cm were run because the NMR signal intensities decayed to lower than 10% of the original signals with gradient strengths larger than 200 G/cm. The solution for a particle’s free diffusion relating the relative echo intensity E and the diffusion coefficient D is given by [9]:

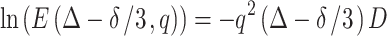1

where γ is the nuclear gyromagnetic ratio, D is the diffusion coefficient, and q = γgδ (δ, g, and Δ have been defined in the Experimental section) [11, 12]. All the experimental points in Fig. 1 fit Eq. 1 approximately. This was, of course, done without giving a clear model of diffusion but just used as a convenient way to show the data. The calculated apparent diffusion coefficients are 6.76 ± 0.09 × 10⁻⁶ and 3.31 ± 0.08 × 10⁻⁶ (cm²/s) for FU and DMFU, respectively. The apparent diffusion coefficient of FU is larger than that of DMFU in the 6KC6 R_f-PEG hydrogel. They may show the mixed effect of the diffusion coefficients for the drug molecules in the R_f core/IPDU intermediate-layer region and in the PEG–water phase (or region). The diffusive exchange of the drug molecules between the two regions may also contribute to the apparent diffusion coefficients.

Fig. 1.

Semilog plots of the relative NMR signal attenuations for the diffusions of a FU in the R_f-PEG hydrogel and b DMFU in the R_f-PEG hydrogel, and their corresponding theoretical fits to Eq. 1

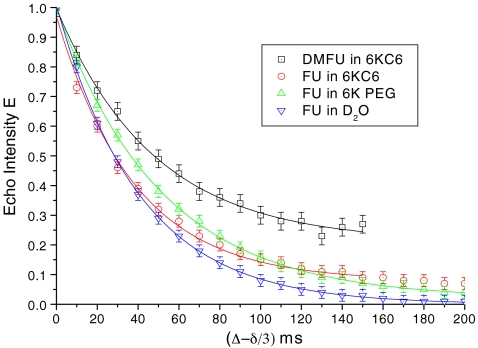
To gather more experimental data in order to find the boundary effect and the exchange effect between the probe molecules in the R_f core/IPDU intermediate-layer region and in the PEG–water phase, PFGSTE diffusion experiments where Δ was varied from 0 to 200 ms while the gradient was fixed at g = 75 G/cm and δ = 1 ms were carried out. The results are shown in Fig. 2, where (∆−δ/3) is used as the unit of the horizontal axis. Besides the samples of FU in 6KC6 hydrogel and DMFU in 6KC6 hydrogel, experiments for FU in 6K PEG solution and FU in D₂O were also carried out for the purpose of comparison. All these sets of experimental data fit the following exponential decays well:

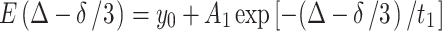2

Fig. 2.

Experimental NMR signal attenuations with diffusion time (∆−δ/3) for DMFU in 6KC6 (squares), FU in 6KC6 (diamonds), FU in 6K PEG (upright triangle), and FU in D₂O (inverted triangles). The corresponding lines show the data fitting with the first-order exponential decays as shown in Eq. 2

The corresponding parameters of y ₀, A ₁, and t ₁ are listed in Table 1. Further discussions for the meanings of these parameters will be conducted in the Discussion section.

Table 1.

Parameters calculated using Eq. 2 for the experimental curves in Fig. 2

	FU in D2O	FU in PEG solution	FU in Rf-PEG hydrogel	DMFU in Rf-PEG hydrogel
y 0	0.000 ± 0.002	0.019 ± 0.003	0.078 ± 0.006	0.21 ± 0.01
A 1	1.007 ± 0.004	0.976 ± 0.004	0.92 ± 0.01	0.79 ± 0.01
t 1 (ms−1)	40.5 ± 0.4	51.4 ± 0.6	38 ± 1	48 ± 2

In order to evaluate the diffusion of the polymeric chains of the R_f-PEG itself, and thus their effects on the observed diffusions of FU and DMFU in the R_f-PEG hydrogels, we carried out ¹H and ¹⁹F molecular diffusion NMR experiments on a sample of the R_f-PEG hydrogel (6KC6) without any probe molecules loaded in it. We found that even by using the maximum possible gradient (1,200 G/cm), it was hard to get any significant signal attenuations to estimate the diffusion coefficients for the R_f group and the PEG chains. This indicates that the hydrogel networks are quite inflexible arising from the formation of the cross linked network through the R_f-PEG chains. Therefore, we can consider the polymeric chains as being fixed in the hydrogel while only the drug molecules did the translational motions in the hydrogel.

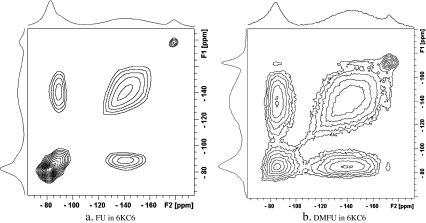
To probe the locations of FU and DMFU in the R_f-PEG hydrogel, we carried out a two-dimensional (2D) solid state ¹⁹F spin diffusion NMR experiments for the freeze-dried FU and DMFU 6KC6 R_f-PEG hydrogel samples, respectively. In the 2D NMR spectrum, cross-peaks appear if two nuclei are in proximity (within some angstroms) to each other. Thus if FU or DMFU was encapsulated into the R_f core/IPDU intermediate-layer region, we may see cross peaks between the peaks of the drug fluorine groups and the R_f groups. Otherwise, no cross peak would be observed. Of course, the appearance and the intensities of the cross peaks depend on the length of the mixing time, the closeness of the atoms and the motion of the molecules. The experimental results are shown in Fig. 3, where Fig. 3a is for FU in R_f-PEG and Fig. 3b is for DMFU in R_f-PEG. The terminal CF₃ groups of the R_f core appear at −81 ppm and those of the CF₂ chains range from −122 to −168 ppm. The chemical shifts of the ¹⁹F in FU and DMFU appear at −178 and −172 ppm, respectively. The peaks in the 2D spectra are intrinsically broad due to the static condition of the samples which does not allow the dipolar interaction to be averaged out in order to detect the spin diffusions. In Fig. 3a, cross peaks only appear between the CF₂ and CF₃ ¹⁹F diagonal peaks, but no noticeable cross peak between the FU ¹⁹F peak and those of the R_f groups was observed. When turned to the case of DMFU (Fig. 3b), in addition to the cross peaks between R_f CF₂ and R_f CF₃, the ¹⁹F nucleus of DMFU also shows cross peaks with the CF₂ and CF₃ ¹⁹F peaks. These spectra indicate that there was a significant portion of DMFU molecules in close contact with the R_f core unit, while the amount of FU molecules in close contact with the R_f core units might be much lower.

Fig. 3.

2D ¹⁹F spin diffusion spectra of the freeze-dried a FU in R_f-PEG hydrogel and b DMFU in R_f-PEG hydrogel

Discussion

Figure 1 showed that the apparent diffusion coefficient of FU is larger than that of DMFU in the R_f-PEG hydrogel. The diffusion coefficient for a dilute suspension of spherical particles is given by the Stokes–Einstein equation

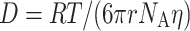3

where R _g denotes the gas constant, T is the temperature, r is the hydrodynamic radius of a spherical particle, N _A is Avogadro’s constant, and η is the viscosity of the solution. The ratio of the apparent diffusion coefficients of FU to DMFU is 2.04. This number should not represent the ratio of the hydrodynamic radii of FU to DMFU because, as shown in Scheme 1, the molecular size difference between FU and DMFU cannot be so large even though they were not spherical and the effect of hydrations to the ratio were not considered. Thus, the different diffusion coefficients suggest that FU and DMFU diffused with different kinetic parameters and/or models in the R_f-PEG hydrogel. This hypothesis is also supported by the different curves shown in Fig. 2 and their corresponding parameters in Table 1. The larger y ₀ of DMFU could indicate that the diffusion of DMFU was more hindered than FU. The more hindered effect for the DMFU could have attenuated the NMR signal less. The spin diffusion results in Fig. 3 have actually shown that more DMFU resided in or was in close contact with the R_f core unit than FU. In order to evaluate the hindrance effect on the drug’s diffusions in the R_f-PEG micelle, we have first reviewed the theoretical models of restricted diffusion [9, 10, 13, 20, 22, 29]. Starting to get some understanding into the possible model of diffusion, we first employed the simplest model used to treat diffusion in a reflecting sphere [9, 20, 22]. In this model, when the solute is in contact with a reflecting sphere or boundary, the spin is neither transported through the boundary, nor is it relaxed by the boundary. The most common approximations for this kind of diffusion include the short gradient pulse (SGP) and Gaussian phase distribution (GPD) [9, 13, 39]. Under the GPD approximation, the signal attenuation is given as an expression including the summation of the mth root of Bessel equation [9, 22]. In the condition of diffusion for a long period (DΔ>>R ²), this equation is reduced to the following form:

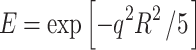4

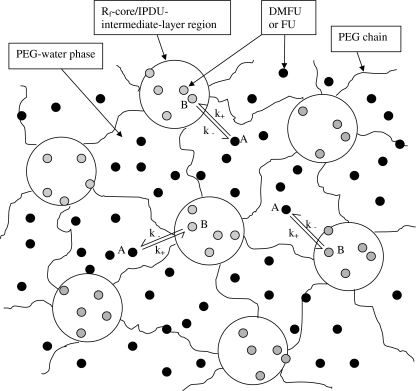
where R denotes the maximum distance that a molecule can diffuse. The NMR signal attenuation is independent on Δ but decreases significantly with the increase of R. Using Eq. 4 and the y ₀ values in Table 1, we could obtain that the maximum distances for that FU and DMFU diffused in the R_f-PEG hydrogel were 17.8 and 13.9 μm, respectively. Of course, these results are by no means right because the boundary condition between the R_f core/IPDU intermediate-layer region and the PEG–water phase does not satisfy that defined for the restricted diffusion. From our previous study, we have learned that the diameter of the IPDU intermediate layer is about 25 Å in an anhydrous condition. If the diffusion of DMFU was heavily restricted within the R_f core/IPDU intermediate layer, we would have seen a much severer restriction according to Eq. 4. Thus, besides diffusion within the R_f core/IPDU intermediate-layer region, DMFU should also have undergone longer range diffusion in the PEG–water phase. Because DMFU is much more hydrophobic than FU, more DMFU molecules could have resided in the R_f core/IPDU intermediate-layer region than the FU. (This idea has experimentally been proven by the ¹⁹F spin diffusion spectra in Fig. 3.) FU should also have behaved more or less like DMFU, but with a lesser population in the R_f core/IPDU intermediate-layer region due its higher hydrophilicity. The boundary condition between the two regions could not isolate the drug molecules in each of the regions. Thus, besides the diffusion in each of the regions, there should also be diffusive exchanges for the DMFU and the FU between the R_f core/IPDU intermediate-layer region and the PEG–water phase. In synopsis, the model of diffusion is given by the diagram of Fig. 4. Part of the FU and DMFU shown as “B” slowly diffuse (the diffusion is more hindered) in the R_f core/IPDU intermediate-layer region (seen as a smaller compartment) and part of them shown as “A” diffuse in the PEG–water phase (seen as a larger compartment) with more rapid diffusion rates. The two parts also diffusively exchange to each other. The reason for the more hindered diffusion of B is attributed to the relative immobility of the R_f chains and the IPDU units.

Fig. 4.

Model of diffusion of DMFU and FU in the R_f-PEG hydrogel where the relative size of the PEG–water phase (or region) has been scaled down significantly relative to the R_f core/IPDU intermediate-layer region. A (black dot) represents FU or DMFU in the PEG–water phase and B (gray dot) represents FU or DMFU in the R_f core/IPDU intermediate-layer region. The diffusive exchange rate constants are given as k ₊ and k ₋ for A to B and B to A, respectively

To theoretically describe our model of diffusion, the diffusion equation should include (1) the hindered/slow diffusion of the drug molecules in the R_f core/IPDU intermediate-layer region; (2) the relatively free/fast diffusion of the drug molecules in the PEG–water phase (although strictly to say, the PEG–water phase is not an ideally free phase); and (3) the diffusive exchange between the two regions on the boundary (or the interface) of the two regions. Bloch equations for the motions of the macroscopic nuclear magnetizations including the effect of diffusion and diffusive exchange under the time dependent pulsed field gradient can be written as [9, 31, 40, 41]:

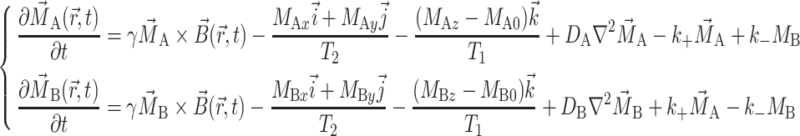5

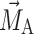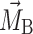where and denote the magnetization of the probe molecules (DMFU or FU) in the PEG–water phase and in the R_f core/IPDU intermediate-layer region, respectively, k ₊ and k _– denotes the forward and reverse exchange rate constants for A to B, and 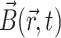denotes the magnetic field including the static magnetic field and the time dependent pulsed field gradient field. The NMR line shapes resulting from the Bloch equations where no time-dependent pulsed field gradient is included have been treated by Belton and Hills [32]. Their theoretical treatment considers how the line shape is changed due to the relaxation effect on the boundary and the diffusive exchange between the two compartments of their model system. Their treatment relies on the distinguished chemical shifts of the probe molecules in the two compartments. The distinguished chemical shifts, however, rarely exist for systems without selectively adding a paramagnetic relaxation reagent [42]. Here, we use the pulsed field gradient technique to attenuate the NMR signal intensities in order to probe the properties of diffusion for our system. The chemical shift distinction of the NMR signals of the two components is not necessary using this method. The ¹⁹F molecular diffusion experiment has shown that the R_f core was quite immobile in space. Thus, after the drug molecules entered the R_f core/IPDU intermediate-layer region, their translational freedom can be treated solely as the diffusion of the drug molecules in this region. In addition, the drug’s diffusion in this region was hindered due to the relative immobility of the R_f chains and the IPDU units. In contrast to the much smaller size of the R_f core/IPDU intermediate-layer region, as a suitable approximation, the probe molecules in the PEG–water phase can diffuse in a much longer range and the diffusion is much less hindered. It would be complicated to find the theoretical solution (more accurately to say approximation) to Eq. 5. Thus, we will discuss a few approximations specifically pertaining to the R_f-PEG hydrogel system. Furthermore, all the relaxation effects in these approximations will not be included as they have been removed in the signal intensities as shown in Figs. 1 and 2.

Assuming that the diffusions of both A and B were free in each of the regions without any diffusive exchange, then Eq. 5 will be reduced to two independent Bloch equations for A and B, respectively. The solution of each of them is an exponential decay function [9]. Because the NMR signals of A and B are indistinguishable, the solution for Eq. 5 would be described by the sum of their two double exponential decays:

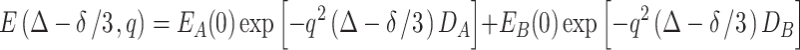6

This, of course, does not represent the empirical result as shown in Eq. 2, where only one exponential decay appears.

If all of the drug molecules were dissolved in the PEG–water phase, Eq. 6 will be reduced to a single exponential decay (the first term). If all of the drug molecules were restricted in the R_f core/IPDU intermediate-layer region, at a long diffusion duration (DΔ>>R ²), the GPD approximation would result in the solution as shown in Eq. 4. The equation to describe the diffusions of the combination of the two cases without any diffusive exchange between the two regions would be:

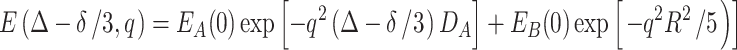7

where E _A(0) and E _B(0) represent the normalized signal intensities (i.e., E _A(0) + E _B(0) = 1) corresponding to the drug’s populations in the two regions. Since R is very small for the R_f core/IPDU intermediate-layer region, the second term is approximately equal to be E _B(0). Thus, Eq. 7 becomes

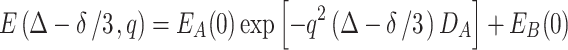8

This could also represent the approximation, if the diffusion in the R_f core/IPDU intermediate-layer region is very slow. This equation represents the empirical solution of Eq. 2. Bear in mind that until this point, we have assumed that the diffusive exchange would not have existed. However, for diffusion limited exchange, if the diffusion coefficient D _B is much smaller than D _A and thus the exchange is very slow, this solution is a fair approximation for Eq. 5.

It has been known that for the case of free diffusions of A and B in one phase with the existence of molecular exchange between them, the solution for Eq. 5 is [31]:

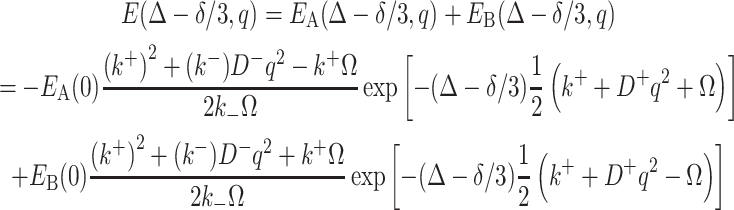9

where k ⁺ = k ₊ + k ₋, k ^- = k ₊−k _-, q = γδg, D ⁺ = D _A + D _B, D ⁻ = D _A−D _B and Ω = [(k ⁻ + q ² D ⁻)² + 4k ₊ k ₋]^1/2. Plot of E(Δ − δ/3,q) versus (Δ − δ/3) would show the mixed double exponential decays at a short diffusion time. With a longer diffusion time, the curve would tend to show the single exponential decay for the component with slow diffusion. This case can be related to our system by making the following conditions: (1) B is carried by the R_f core/IPDU intermediate-layer region in the PEG–water phase; (2) the diffusion of the R_f core/IPDU intermediate-layer region is zero (which has been shown by the ¹⁹F diffusion experiment); (3) the diffusion of B in the R_f core/IPDU intermediate-layer region is slow due to the relative immobility of the R_f chains and the IPDU units; (4) the diffusive exchange between A and B exists. These conditions lead to D _B = 0. Thus, Eq. (9) becomes

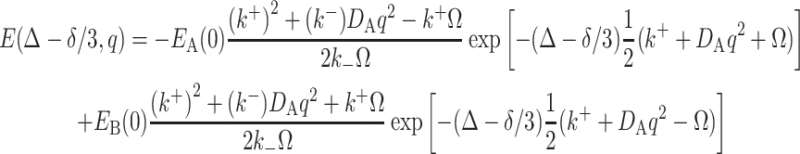10

where Ω = [(k ⁻ + q ² D _A)² + 4k ₊ k _-]^1/2. If 4k ₊ k ₋ in Ω is small and thus can be ignored, then Eq. 10 becomes

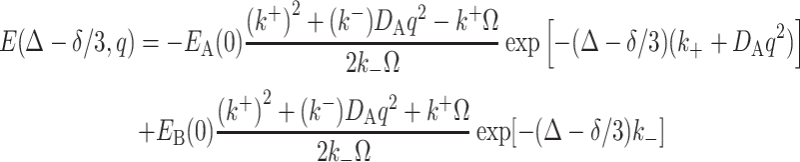11

The second term decays much slower than the first term due to the vanished D _B. When k ₋ (and also k ₊ due to the exchangeable equilibrium) approaches zero, Eq. (11) becomes

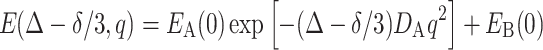12

It is reasonable that the diffusion of the drug molecules in the R_f core/IPDU intermediate-layer region is slow due to the relative immobility of the R_f chains and the IPDU units. Thus, if the diffusive exchange is diffusion limited for the drug molecules in the R_f core/IPDU intermediate-layer region, the exchange rate constants are small. Based on these arguments, Eq. (12) could be a reasonable approximation to the solution of Eq. 5. This approach leads to the same solution as shown in Eq. 8.

For the exact case of the molecular diffusion in the R_f-PEG hydrogel, the diffusion coefficient of B may not be zero, although it should be small and also the rate constants of the diffusive exchange is not zero although they should be small as well. If the diffusive exchange rates were very rapid, the curve in Fig. 2 for the DMFU’s diffusion should approach to zero but not to a nonzero value. We would expect that the attenuation of the NMR signal intensity for drug’s diffusion in the R_f-PEG hydrogel can be more accurately represented by the hybridization of Eqs. 7 and 9. For the current study, we are not going to pursue the more accurate solution further.

Comparing Eq. 8 or Eq. 12 with Eq. 2, we obtain E _B(0) ≈ y ₀ = 0.21 for DMFU (Table 1). This indicates that about 21% of the DMFU molecules were populated in the R_f core/IPDU intermediate-layer region, while 79% of the DMFU molecules were populated in the PEG–water phase assuming. Similarly, 7.8% of the FU molecules were populated in the R_f core/IPDU intermediate-layer region, while 82% of the molecules were populated in the PEG–water phase. FU is more hydrophilic than DMFU, and thus it is reasonable that more DMFU could have resided in the R_f core/IPDU intermediate-layer region than FU. Although Fig. 3b did not show the cross peaks of FU with the R_f groups, it does not necessarily mean that there were not FU in the R_f core/IPDU intermediate-layer region. Most of the 7.8% FU could reside in the IPDU intermediate layer. Although the R_f core/IPDU intermediate-layer region and the PEG chains could also hinder the diffusions of the drug molecules in the PEG–water phase, the effect could be much smaller than the hindrance to the diffusion of the probe molecules in the R_f core/IPDU intermediate-layer region. The y₀ values of FU’s diffusion in the PEG solution (y ₀ = 0.019) and in water (y ₀ = 0.000) show that the hindrance effects of PEG and water are quite small.

For the current approximation, Eq. 8 or Eq. 12 could be used to estimate the diffusion coefficients of DMFU and FU in the PEG–water phase. Using this equation, they were found to be 5.18 × 10⁻⁶ and 6.54 × 10⁻⁶ cm²/s, respectively. The corresponding apparent diffusion coefficients calculated using the data of Fig. 1 are 3.31 × 10⁻⁶ and 6.76 × 10⁻⁶ cm²/s, respectively. Because the Δ value was kept small (20 ms) for the experiments done for Fig. 1, which may not allow too much time for considerable diffusive exchange, the apparent diffusion coefficients calculated from Fig. 1 should be closer to the true values than those calculated from Fig. 2 using Eq. 8 or Eq. 12.

Conclusion

In summary, based on the results of molecular diffusion and solid state spin diffusion experiments, we have proposed the model of diffusion of small molecules in the R_f-PEG hydrogel. We have seen that a greater percentage of DMFU molecules resided in the R_f core/IPDU intermediate-layer region than that of FU. This is well correlated to the degrees of the drug’s hydrophobicities. The drug’s diffusion occurred in the PEG–water phase through the diffusive exchange process between the R_f core/IPDU intermediate-layer region and the PEG–water phase. This provides a piece of useful information for drug delivery applications regarding the drug loading and diffusion properties of the R_f-PEG hydrogel. We would expect that small hydrophobic drugs can be held by the R_f core/IPDU intermediate-layer region to a much greater extent than hydrophilic drugs and hydrophobic drugs may tend to degrade more from the gel surface to the body together with the R_f-PEG micelles. In contrast to hydrophobic drugs, small hydrophilic drugs tend to diffuse from the PEG–water phase to the body more quickly. Our previous studies on a larger hydrophobic drug, chlorambucil-tempol adduct, shows that the drug was encapsulated in the IPDU intermediate layer [4, 7]. Besides the drug loading capacity of the IPDU intermediate layer, the R_f core may also play a role to host the DMFU molecules as can be seen from the spin diffusion spectrum in Fig. 3b. The smaller molecular size, the hydrophobicity, and the presence of the fluorine atom in the molecule may have helped to do so. We have learned that the drug loading property in the R_f-PEG hydrogel is dependent on the compatibility of the hydrophobic core-layer region of the R_f-PEG hydrogel with the size, chemical composition, and hydrophobicity of the drugs. This opens the door to design particular polymer units to form the intermediate layer between the R_f core and the PEG shell for customized drug delivery. This study also demonstrates that the NMR techniques used in this research are useful to probe the loading and diffusion properties of drugs in polymeric micelles.