Boundary crossing in epithelial wound healing

Abstract

The processes of wound healing and collective cell migration have been studied for decades. Intensive research has been devoted to understanding the mechanisms involved in wound healing, but the role of cell-substrate interactions is still not thoroughly understood. Here we probe the role of cell-substrate interactions by examining in vitro the healing of monolayers of human corneal epithelial (HCE) cells cultured on artificial extracellular matrix (aECM) proteins. We find that the rate of wound healing is dependent on the concentration of fibronectin-derived (RGD) cell-adhesion ligands in the aECM substrate. The wound closure rate varies nearly sixfold on the substrates examined, despite the fact that the rates of migration and proliferation of individual cells show little sensitivity to the RGD concentration (which varies 40-fold). To explain this apparent contradiction, we study collective migration by means of a dynamic Monte Carlo simulation. The cells in the simulation spread, retract, and proliferate with probabilities obtained from a simple phenomenological model. The results indicate that the overall wound closure rate is determined primarily by the rate at which cells cross the boundary between the aECM protein and the matrix deposited under the cell sheet.

The collective migration of cells is fundamental to wound healing, morphogenesis, and many bioengineering applications. Wound healing in particular involves the migration of cell sheets over adhesive surfaces. Two mechanisms of migration have been identified in wound healing (1). First is the “purse string” mechanism in which a marginal actomyosin cable develops along the wound edge, and wound closure proceeds with contraction of the actin belt (2). The second mechanism involves active spreading and migration of cells at the wound edge, known commonly as “lamellipodial crawling.” The latter mechanism is more frequently observed in vitro and has been characterized by using scratch-wound models. In these models, cells experience an injury, which triggers cell migration through various biochemical signaling events (3). It has also been argued that the availability of free space is sufficient to initiate cell migration in the absence of mechanical injury (4–6). Upon wounding, proliferation is up-regulated (7).

Adhesive cell-substratum interactions are required for sustained migration into the wound area (8, 9). The rates of migration of individual cells are governed by surface adhesivity in a biphasic fashion, at least under certain conditions (10). Surfaces modified with adhesion ligands such as fibronectin (FN) (11–13) and Arg-Gly-Asp (RGD) peptides have been shown to facilitate wound healing, and it is reasonable to infer that the observed increases in healing rates arise primarily from faster migration of individual cells. We show here that other factors can be more important.

The substrates used in this work were prepared from artificial extracellular matrix (aECM) proteins that combine domains derived from fibronectin and elastin (Fig. S1). We and others have shown that such aECM proteins can be cross-linked to yield materials with elastic moduli similar to those of natural elastins (14, 15) and that presentation of the fibronectin-derived RGD sequence promotes cell spreading and adhesion (16–18).

Wound healing was examined in monolayers of human corneal epithelial cells (HCE) cultured on aECM protein substrates that present controlled, varying densities of the RGD sequence. HCE cells undergo rapid reepithelization in vivo (19). Both the α₅β₁ and α_vβ₃ integrins, which bind RGD, are up-regulated by wounding (20). Cross-linked films with estimated RGD surface densities varying from 7.7 × 10³ to 3.1 × 10⁵ per μm² were prepared by mixing aECM proteins containing RGD and “scrambled” (RDG) domains (see SI Text). Substrates are identified by specifying the percentage of the RGD protein in the film (e.g., 100% RGD).

Results and Discussion

Cell Spreading.

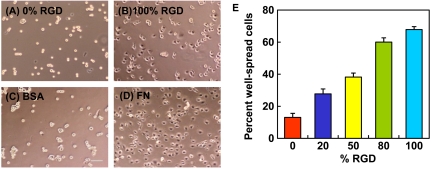
HCE cells were allowed to spread on spin-coated aECM films containing varying RGD densities. After 4 h, HCE cells were well-spread on cross-linked 100% RGD and on adsorbed FN but remained rounded on the scrambled control (0% RGD) and on adsorbed BSA surfaces (Fig. 1 A–D). To quantify these differences, projected areas of 250 cells were measured at each of several time points over a 4-h period. Cells with projected areas larger than 300 μm² were considered well-spread. The percentage of well-spread cells on aECM films increased with RGD density (Fig. 1E). Although some cells eventually spread on the scrambled control substrate, spreading on the control surface was likely a consequence of cellular secretion of ECM proteins (21, 22).

Fig. 1.

HCE cell spreading behavior. Phase contrast images of HCE cells after 4 h on cross-linked spin-coated aECM films prepared from 0% RGD (A) or 100% RGD (B), adsorbed bovine serum albumin (BSA) (C) and adsorbed fibronectin (FN) (D). Scale bar, 100 μm. (E) Percent well-spread cells after 4 h on spin-coated aECM films with varying RGD densities. Error bars represent SEM.

Wound Healing.

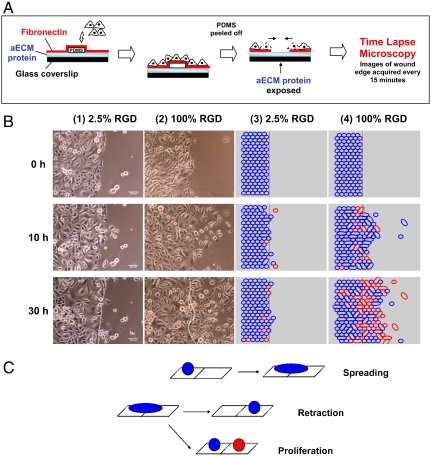
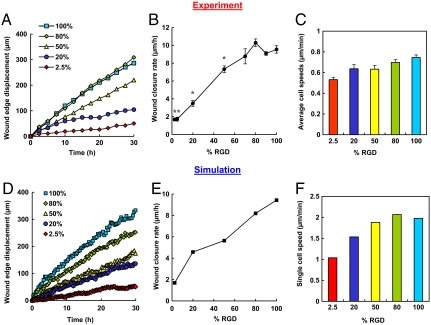
Conventional scratch-wound assays are of limited use in studies of cell-substrate interactions because of interference from proteins deposited by cells removed from the wound. Nikolić et al. (6) and others (4) have shown that removal of a PDMS barrier triggers cell responses similar to those observed in scratch-wound assays. Using a similar approach, we precoated glass coverslips with the protein of interest and laid down a short PDMS slab to provide a temporary platform for cell attachment. To facilitate cell attachment, fibronectin was incubated in each well overnight prior to plating of HCE cells (Fig. 2A). Removal of the PDMS slab placed the edge of the wounded cell sheet in contact with the test surface. HCE cells migrated collectively in the direction of the wound by lamellipodial crawling on 100% RGD, consistent with previous reports (5, 23). On 2.5% RGD, however, minimal advance of the cell sheet was observed, even though cells at the wound edge were constantly extending protrusions (Fig. 2B and Movies S1–S6). Fig. 3A shows the average displacement of the cell sheet on various surfaces as a function of time. The overall wound closure rate increases approximately 5.6-fold as the RGD density increases (Fig. 3B and Table S1). Individual cells within the cell sheet were also tracked for the last 10 h of each video (Fig. 3C). Cells were selected at random and only cells on the test surface were included in the analysis. Surprisingly, cells migrated just 40% faster on 100% RGD than on 2.5% RGD.

Fig. 2.

(A) Schematic of wound-healing experiment. aECM proteins were spin-coated and cross-linked on glass coverslips and mounted in multiwell tissue culture plates. A slab of PDMS was laid on top of the protein film and fibronectin solution was allowed to adsorb overnight at 4 ºC to aid cell attachment. HCE cells were grown to confluence and the PDMS was peeled off. The protein film was rinsed twice with serum-free medium and the wounded cell sheet was allowed to migrate over the aECM protein. This process was monitored by time-lapse microscopy. (B) Time course of wound healing on 2.5% RGD and 100% RGD substrates. (Panels 1 and 2) Experimental images showing the progression of the wound edge on 2.5% and 100% RGD, respectively, at various time intervals. (Panels 3 and 4) Snapshots of simulated wound edges for 2.5% RGD and 100% RGD substrates. “Daughter cells” are shown in red. The initial positions of the wound edge are indicated by white lines in the images at 30 h. (C) Schematic of the Monte Carlo simulation. In the model, cells can spread with probability W_s to take up two lattice sites, retract to either one of the sites with probability W_r, or undergo proliferation with probability W_p. Following each proliferation event, the daughter cell is colored red; thus the number of red cells corresponds to the contribution of proliferation to cell number. The decision regarding which cell is the daughter and which cell is the “mother” was made by generating a random number.

Fig. 3.

Wound-healing behavior observed in experiments (A–C) and simulations (D –F). (A) Displacement of the wound edge for various surfaces over time. (B) Wound closure rate for substrates with varying RGD densities. *, significant difference from 100% RGD (P < 0.05). (C) Average speeds for individual cells migrating on the test surface for the last 10 h. (D) Displacement of simulated wound edges as a function of time. (E) Wound-closure rate as a function of RGD percentage. The wound-closure rate is fivefold faster on 100% RGD than on 2.5% RGD, consistent with experimental observations. (F) Single cell speed as a function of RGD concentration. Only cells on the test surface were included. Error bars represent SEM.

This result was puzzling—we expected the increase in wound closure rate with RGD concentration to be a consequence of an increase in cell speed. But a 1.4-fold increase in cell speed cannot explain the observed 5.6-fold increase in wound closure rate. We considered the possibility that differences in proliferation rates might provide an explanation, so we determined the fraction of cells in the wound area that arose through cell division. We found that even on the most highly adhesive surfaces, proliferation provided no more than 15% of the cells in the wound area (Fig. S7B and Table S2). Variation in proliferation rates therefore cannot account for large differences in the rates of wound closure. Finally, we imagined that a critical event might be the “decision” made by each cell as it comes into contact with the test surface. Does the cell cross to the test surface or retreat to the matrix deposited beneath the confluent cell monolayer? If the rate of crossing increases with the adhesivity of the test surface, wound healing should occur more rapidly on surfaces bearing higher RGD densities. By counting cells in the wound area after 30 h and subtracting proliferation events, we estimated that boundary crossing contributes approximately 4.3-fold more cells to wound healing on 100% RGD than on 2.5% RGD (Fig. S7D and Table S2). In order to gain additional insight into the various factors that determine the wound-healing rate, we performed computer simulations of the healing process.

Dynamic Monte Carlo simulation.

The surface was modeled as a 2D hexagonal lattice in which each lattice site was either occupied by a cell or empty. Cell migration in the simulation proceeds via a two-step mechanism: First, the cell spreads onto an adjacent lattice site, and then it retracts to a single lattice site (Fig. 2C). If retraction vacates the site occupied by the cell before it spread, migration has occurred.

We define the x-axis as the axis perpendicular to the wound edge, and the initial position of the wound edge (the boundary) as x = 0. Thus, in the initial configuration of the simulation, cells occupy all the lattice sites whose x positions are smaller than zero, and the rest of the sites are empty. As the simulation progresses, cells cross the boundary into the wound area, and the value of x at the wound edge position increases. We denote the transition probabilities for spreading, retraction, and proliferation by W_s, W_r, and W_p, respectively. We use a simple model for spreading and retraction behavior to estimate the values of W_s and W_r for the different surfaces, based on experimental data. Because FN is a major component of the matrix deposited beneath the confluent monolayer, the probabilities for spreading and retraction for lattice sites with x < 0 were taken to be those for FN. We estimated the proliferation rate (W_p) by constructing rate equations according to the simulation rules and solving them in the low cell concentration limit. The doubling time was then compared to experimental data.

The cells in the simulation behaved similarly to those observed experimentally, in the dynamic nature of their bonds and in the difference in cell behaviors observed on surfaces that present different densities of RGD ligands. Fig. 2B compares snapshots taken from the simulation and from experiments for the 100% and 2.5% RGD surfaces. The wound closure rates derived from the simulation are shown in Fig. 3E. The wound closure rate is defined as the average distance traveled by the wound edge per unit time (Fig. 3D). As observed experimentally, there is a 5.6-fold difference between the wound closure rates on the 100% and on 2.5% RGD surfaces. Fig. 3F shows the single cell speeds calculated from the simulation for surfaces bearing various RGD densities. At each time point, only cells on the test surface were included in the analysis. The difference between the single cell speeds on 100% RGD and 2.5% RGD is only 1.9-fold. These observations are consistent with the experimental results and confirm that the increase in overall wound closure rate does not require faster cell migration.

The Variation in Wound-Closure Rate Is Determined Primarily by the Rate of Boundary Crossing.

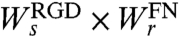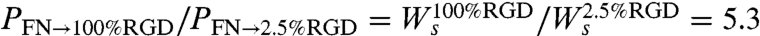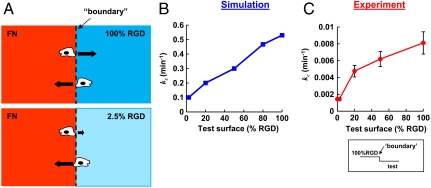
The probability that a cell crosses the matrix boundary is given by its probability to spread onto the RGD test surface multiplied by its probability to retract from the FN surface, i.e., . Hence, the ratio of the probabilities for crossing to the 100% RGD and 2.5% RGD test surfaces is: . The second equality was obtained from the spreading rates used in the simulation. We used the cell spreading assay data (Fig. 1E) to determine these rates (see additional details in SI Text). Hence, the 5.3-fold difference in crossing probability arises from the 5.3-fold difference in the rate of cell spreading. Following the same logic, we can also explain the small differences in cell speed observed in the simulation for surfaces with different RGD concentrations. The ratio between single cell migration rates on 100% and 2.5% RGD is 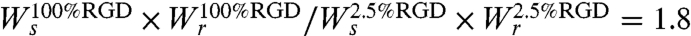. The simulation results suggest that the 5.6-fold variation in wound-closure rates observed experimentally arises primarily from variation in boundary-crossing rates (Fig. 4B and Fig. S6B).

Fig. 4.

(A) Schematic representation of boundary crossing. Black arrows represent relative crossing rates for each condition. B and C show the rate constants of crossing, k_c (from 100% RGD to the test surfaces), for simulation and experimental data, respectively. In both curves, the crossing rates from 100% RGD to 100% RGD and from 100% RGD to 2.5% RGD differ by a factor of five. Error bars in C are experimental errors (see SI Text).

To measure boundary-crossing rates directly, we prepared substrates by spin-coating one layer of aECM protein on top of another (Fig. S2). Single HCE cells were seeded on these surfaces, and cells at the boundary were followed by time-lapse microscopy (see Movies S1–S6). The total time in contact with the boundary and the subsequent decision (i.e., to cross the boundary or not) were recorded for each cell. The crossing rate was calculated by dividing the number of crossings by the total time in contact with the boundary. The results confirm that the crossing rate increases 5.7-fold as the adhesivity of the substrate increases (Fig. 4C), consistent with the hypothesis that the variation in wound-closure rate is determined primarily by variation in the rate of boundary crossing.

Concluding Remarks

In summary, we find that the rate of healing of epithelial cell monolayers cultured on aECM proteins increases with increasing density of adhesion ligands presented at the substrate surface. As shown both experimentally and through simulation of the healing process, the variation in healing rate arises primarily from variation in the rate at which cells cross the boundary between the matrix deposited by the cell monolayer and the aECM protein; variation in the rates of migration and proliferation play comparatively minor roles. The simulation method described here can be applied to many cell types, and—through variation in the cell–cell interaction energy (see SI Text)—captures a broad range of wound-healing behavior, from diffusion-like behavior in which cell–cell contacts break and reform (as observed for corneal epithelial cells) to behavior that resembles that of an elastic sheet in which cell–cell contacts remain unchanged during wound healing (as observed in monolayers of MDCK cells) (24).

Materials and Methods

Protein Expression and Purification.

Standard methods for cloning, bacterial growth, protein expression, sodium dodecyl sulfate-polyacrylamide gel electrophoresis (SDS/PAGE), and Western blotting were used to prepare and characterize aECM proteins containing RGD and RDG domains (17). Typical yields of protein obtained from 10 L fermentation cultures were approximately 500 mg. The molar mass of each aECM protein was 34.8 kDa.

Preparation of Spin-Coated aECM Films.

Round glass coverslips (12 mm diameter; No. 1, Deckgläser) were sonicated in a mixture of ethanol and KOH for 15 min and rinsed several times with distilled H₂O. aECM protein solutions were prepared by dissolving mixtures of aECM-RGD and aECM-RDG (100 mg/ml in ddH₂O) for 3–4 h at 4 °C. Protein solutions containing 2.5%, 5%, 20%, 35%, 50%, 70%, 75%, 80%, 90%, and 100% aECM-RGD were prepared. Bis[sulfosuccinimidyl]suberate (BS³) was used to cross-link the aECM protein substrates. BS³ (2.0 mg; Pierce) was dissolved in 17 μl of sterile distilled H₂O and added to 150 μl of protein solution, mixed and centrifuged to remove bubbles. The stoichiometric ratio of activated esters in BS³ to primary amines in the aECM proteins was roughly 1∶1. A 17 μl volume of BS³-protein solution was then spin-coated on a 12 mm diameter round glass cover slip at 7,000 rpm for 30 sec at 4 °C. Each protein film was stored overnight at 4 °C before use.

Generation of aECM Films Containing Boundaries.

We prepared 100 μl of aECM protein solutions (25 mg/ml in distilled H₂O) containing 0%, 2.5%, 20%, 50%, and 100% aECM-RGD and BS³ (0.29 mg in 2.5 μl ddH₂O) as previously described. The protein solution (17 μl) was spin-coated onto a 12 mm diameter round glass coverslip at 5,000 rpm 30 sec at 4 °C. Protein films were allowed to dry overnight at 4 °C. Subsequently, 600 μl of a second aECM protein solution (15 mg/ml) was mixed with 1.725 mg of BS³ dissolved in 12.75 μl distilled H₂O. A small volume (2 μl) of the second aECM protein solution was pipetted across the middle of the film and spin-coated at 5,000 rpm for 30 sec at 4 °C. Under these conditions, a boundary was generated between two distinct aECM surfaces.

Wound-Healing Assay.

The experimental set up was adapted from Nikolic et al. with modifications (6). Slabs of polydimethylsiloxane (PDMS; Sylgard 184, Dow Corning) were cast to 0.3 mm thickness according to the manufacturer’s instructions. Briefly, PDMS was mixed at 10∶1 PDMS base/curing agent ratio, poured into a 100 mm Petri dish to a height of 0.3 mm, degassed in a desiccator for at least 1 h and baked for at least 2 h at 65 °C. Slabs of PDMS with lateral dimensions roughly 2 mmx2 mm were cut with a sterile scalpel, sterilized with ethanol and air-dried. Use of thin (0.3 mm) blocks of PDMS allowed cells to maintain confluence across the edge of the slab and prevented contact between cells and the underlying substrate surface. The PDMS slabs were placed at the center of the coverslips containing spin-coated aECM films. These coverslips were then mounted in 24-well tissue culture plates by using sterile vacuum grease (Dow Corning). To all wells, 500 μl of FN was added overnight at 4 °C to cover the entire surface to aid cell-adhesion. The next day, 2 × 10⁵ primary HCE cells were seeded into each well and allowed to grow to confluence over 3–5 d. The medium was changed every 2 d. Once a confluent monolayer formed, the PDMS slabs were lifted with sterile tweezers to create a wounded cell sheet. A schematic drawing of the experimental set up is shown in Fig. 2A. Each well was rinsed twice with fresh medium before the start of each experiment to remove any cell debris. Meanwhile, a chamber was set up around the microscope to maintain the microscope stage and chamber interior at 37 °C with 5% CO₂/95% air to sustain cells. A hole was opened in the cover of one of the empty wells in the 24-well plate and an air supply was attached to ensure that cells were maintained under the CO₂/air mixture. Water was also added to surrounding empty wells to prevent excessive evaporation of the medium. Wound closure was followed for 30 h by time-lapse phase contrast microscopy on a Nikon Eclipse TE300 microscope at 10 × magnification. Digital images of at least 5 different spots of the wound edge for each substrate were acquired every 15 min using MetaMorph v6.3.2 (Molecular Devices). The wound areas immediately after wounding (t = 0 h) and after 30 h (t = 30 h) were traced manually using ImageJ v1.37 (NIH, http://rsb.info.nih.gov/ij/). The difference in the two areas was then divided by the length of the wound edge to yield the distance traveled by the cell sheet. This distance was then divided by the total time (30 h) to give the wound-closure rate. The reported wound-closure rates were obtained by averaging the rates calculated from videos recorded in at least three independent experiments. Individual cells within the sheet were also tracked manually using ImageJ, with MTrackJ, a plug-in created by Meijering and colleagues at the University Medical Center Rotterdam, Netherlands (http://www.bigr.nl/). Trajectories of individual cells were tracked frame by frame for the last 10 h for each video and the average speeds of individual cells were averaged for all cells migrating on the test surface. The extent to which proliferation on the test surface contributed to wound closure was quantified by counting the number of proliferation events on the test surface and comparing that number to the total number of cells on the test surface at the end of the experiment. The number of cells that crossed the boundary was calculated by counting the number of cells on the test surface at the end of the experiment and subtracting the number of cells that result of proliferation (subtracting the number of proliferation events on the test surface).

Modeling Spreading, Retraction, and Proliferation.

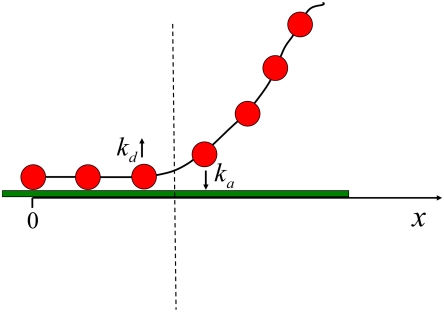
We use a simple phenomenological model to estimate numerical values for the rates of cell spreading, retraction, and proliferation. As shown in Fig. 5, the cell membrane is modeled as a chain of beads that represent integrin receptors or clusters, and spreading and retraction involve adsorption and desorption of receptor clusters at the ligand-bearing surface. Only the receptor clusters adjacent to the cell edge (which is represented by the dashed line in Fig. 5) can adsorb or desorb. The rate constants for adsorption and desorption are k_a and k_d, respectively. During spreading and retraction, the cell edge performs a random walk where each adsorption event results in an increase in its x position while each desorption event results in a decrease in its x position.

Fig. 5.

Schematic illustration of the cell spreading and retraction model. The beads represent integrin receptor clusters, while the chain represents the cell membrane. The cell edge is represented by the dashed line. Receptor clusters adjacent to the cell edge can adsorb or desorb with rate constants k_a and k_d, respectively.

The master equation that describes the processes discussed above is of the form

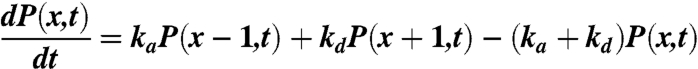[1]

where P(x,t) is the probability of the cell edge to be at position x at time t, and x is measured in units equal to the average distance between receptor clusters. The solution for the average cell edge displacement is

[2]

An increase in 〈x〉 corresponds to an increase in the cell area in contact with the surface. Therefore, we define the spreading rate, W_s, as the change in the average value of x with time

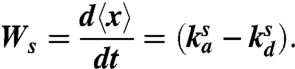[3]

Similarly, the retraction rate, W_r, is defined as

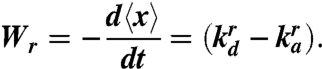[4]

The forces exerted by the cell influence the effective rate of receptor adsorption and desorption events (k_a and k_d). Because the forces exerted by the cell differ depending on whether the cell is spreading or retracting, the rate constants for adsorption and desorption in these two cases will be different. Consequently, we add a superscript in Eqs. 3 and 4 (s or r) to denote the cell state (spreading or retraction).

In a cell-free system with receptors incorporated into a rigid planar membrane, the binding of the receptors to surface ligands can be described as a second order reaction. Denoting the rate constant for binding by k and the rate constant for unbinding by k_-1, the ratio of these rate constants is k_-1/k = exp(-ε/k_BT) where ε > 0 is the binding energy (the difference in energy between the unbound and bound states).

For the case of a flexible cell membrane, the spreading process is associated with a change in membrane shape. The shape deformation results in an energy barrier that we denote by ε_el. Spreading and retraction processes are not spontaneous and require forces to be generated by the cell (25). In the case of spreading, a protrusive force is exerted on the cell membrane and reduces the energy barrier associated with membrane deformation by an amount fγ where f is the force applied by the cell and γ is the distance over which the force is applied (10, 26). In this case the rate constants for adsorption and desorption in our model are

[5]

When retracting, the cell pulls on the receptor–ligand bond, thereby reducing the energy barrier associated with bond breakage by an amount f^′γ^′ (25–26).

In this case, the rate constants take the form

[6]

Following Eqs. 3–6, the rates for spreading and retraction can be expressed as

[7]

[8]

Using Eqs. 7 and 8, we can connect the spreading and retraction rates on surfaces with the same RGD fraction, φ_RGD:

[9]

In Eq. 9, W_s(FN) denotes the spreading rate on fibronectin, 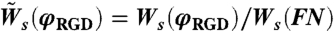and 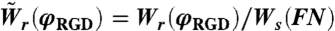are the spreading and retraction rates relative to the spreading rate on fibronectin and A ≡ k exp(-ε_el/k_BT + fγ/k_BT)/W_s(FN). We can use the results from the spreading assay (Fig. 1E) in order to get a numerical value for the constant A (see SI Text for details).

The rest of the model parameters were estimated on the basis of experimental results described in the literature:

1. γ is the characteristic distance between bonds that link the cell and the substrate (the distance between beads in our model) and is estimated to be 100 nm (27).

2. The characteristic traction force is assumed in the literature to be on the order of 1 nN/μm² (10, 28, 29) and the protrusion has a typical diameter of 0.1 μm (29), comparable to the average distance between bonds (27). These estimates lead to a traction force, f^′, on the order of 8 pN. The RGD–integrin bond length, γ^′, is on the order of 1 nm (10, 26).

3. Recent estimates suggest that the thermal deformation of the membrane is on the order of 5–10 nm (29, 30) implying that the energy required for deformation on the scale of the distance between bonds (∼100 nm) cannot be provided by thermal fluctuations. Consequently, we assume that the term exp(-ε_el/k_BT) in Eq. 9 is negligible.

The rates of spreading and retraction in the simulation are normalized by the rate of spreading on FN, i.e., the values used in the simulation are 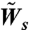and 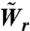, respectively. When a cell retracts, it either has to break the bonds with its neighbors or “pull” its neighbors along. Thus, the final expression for the retraction rate depends on the cell–cell interaction energy (see SI Text for details). For each RGD concentration, φ_RGD, the spreading rate, 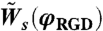, was taken from the experimental data presented in Fig. S3. The value for the retraction rate on the same surface, 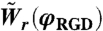was calculated using Eq. 9.

The proliferation rate was calculated using

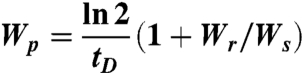[10]

where t_D is the doubling time for human corneal epithelial (HCE) cells (for derivation of Eq. 10, see SI Text). Using the values for W_r and W_s on FN and t_D = 25 h (31), we get W_p = 0.05 h^-1. We assume that W_p is identical on all surfaces.

Dynamic Monte Carlo Simulation.

We use a dynamic Monte Carlo scheme (32–33) to simulate the dynamics of collective cell migration. The surface is modeled as a 100 × 100 hexagonal lattice with a lattice constant of d = 50 μm, which is on the order of a cell diameter. At time t = 0, the first 10 columns of the lattice are occupied by cells (total number of cells, N = 1,000), while the rest of the lattice sites are empty. Because proliferation is enabled, N increases with time. In every Monte Carlo step, N cells are chosen randomly and an attempt is made to change their state according to the appropriate rates for spreading, retraction, and proliferation (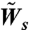, , 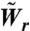and W_p, respectively). All the rates in the simulation are scaled to ensure that the time steps are small enough so that in any Monte Carlo (MC) step only one event can occur. The interaction energy between nearest neighbor cells in the simulation is ε_cell-cell/k_BT_eff = 0.7 (for details see SI Text). The conversion between simulation time and experimental time was done by a one-time calibration, equating the wound-closure rates obtained from simulation and experiment for the 2.5% RGD substrate. By using this approach, we find that 1 MC step corresponds to 0.15 min and W_s(FN) = 0.54 min^-1.

Boundary-Crossing Experiments.

aECM surfaces containing substrate boundaries were mounted into the wells of a 24-well tissue culture plate. HCE cells (1 × 10⁴) were added to each well and allowed to attach for 2 h at 37 °C under 5% CO₂/95% air. Images of the boundary at several positions on the aECM film were acquired every 15 min for 24 h, by using phase contrast microscopy at 37 °C under 5% CO₂/95% air. Time-lapse videos were analyzed using ImageJ. We tracked cells that contacted the boundary and recorded the time spent at the boundary before a “decision” was made (i.e., the cell crossed the boundary or moved away). We considered each encounter a separate “event” (i.e., once the cell leaves the boundary and recontacts the boundary again, the timing restarts). The total amount of time spent at the boundary, t_total, the total number of events, N, and the total number of cells that subsequently decide to cross the boundary, N_c, were recorded for at least 150 events for each condition. The rate constant of boundary crossing, k_c, was calculated using

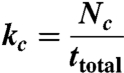[11]

(see SI Text for a derivation of Eq. 11).

The uncertainty in the rate constant for boundary crossing is k_cΔt/〈t〉 where 〈t〉 = t_total/N is the average waiting time at the boundary and Δt is the 15-min time interval between two consecutive time-lapse images.

Statistical Analysis.

For all experimental data, the statistical significance of differences was estimated by analysis of variance followed by the Tukey test. Differences were taken to be significant at P ≤ 0.05.