External Validity of Risk Models: Use of Benchmark Values to Disentangle a Case-Mix Effect From Incorrect Coefficients

Yvonne Vergouwe; Karel G M Moons; Ewout W Steyerberg

doi:10.1093/aje/kwq223

. 2010 Aug 31;172(8):971–980. doi: 10.1093/aje/kwq223

External Validity of Risk Models: Use of Benchmark Values to Disentangle a Case-Mix Effect From Incorrect Coefficients

Yvonne Vergouwe ^*, Karel G M Moons, Ewout W Steyerberg

PMCID: PMC2984249 PMID: 20807737

Abstract

Various performance measures related to calibration and discrimination are available for the assessment of risk models. When the validity of a risk model is assessed in a new population, estimates of the model's performance can be influenced in several ways. The regression coefficients can be incorrect, which indeed results in an invalid model. However, the distribution of patient characteristics (case mix) may also influence the performance of the model. Here the authors consider a number of typical situations that can be encountered in external validation studies. Theoretical relations between differences in development and validation samples and performance measures are studied by simulation. Benchmark values for the performance measures are proposed to disentangle a case-mix effect from incorrect regression coefficients, when interpreting the model's estimated performance in validation samples. The authors demonstrate the use of the benchmark values using data on traumatic brain injury obtained from the International Tirilazad Trial and the North American Tirilazad Trial (1991–1994).

Keywords: epidemiologic methods; models, statistical; reproducibility of results; risk assessment; risk model

Modeling the absolute risk of disease is a major focus of research in cancer and cardiovascular disease, as well as in other diseases. Well-known examples are the Gail model for risk prediction of invasive breast cancer (1) and the Framingham Heart Study risk scores (2). Such models are developed for several purposes, including counseling and designing intervention studies. A vital aspect of risk models is adequate performance in other populations (3–5), also referred to as external validity, generalizability, or transportability.

To assess model performance, risks for the subjects in the validation sample are calculated with the risk model and compared with the actual outcomes in the validation sample. It is often assumed that the validity of a model is determined by the closeness of the performance estimated in the validation sample, with measures such as the concordance (c) statistic and R², to the performance estimated in the development data sample (6).

As an example, external validity may be assessed in other ethnic groups. The Framingham Heart Study risk score was developed in a US white, middle-class population (2) and validated in Native Americans (7). The discriminative ability of the model expressed with the c statistic was 0.83 among women in the development sample and 0.75 in the validation sample. Indeed, some predictor effects were different for the Native Americans compared with the development population, which indicates that the fit of the model was suboptimal. However, the distributions of women's characteristics (case mix) also differed between the development and validation populations. White persons more often had high blood pressure than the Native Americans. As a result, the validation sample was more homogeneous, which makes discrimination more difficult. The latter is a population aspect and is not related to model fit.

Clearly, differences in case mix and in predictor effects between development and validation populations must both be considered for proper interpretation of model performance estimates in external validation studies. In the current analysis, we aimed to examine the relations of differences in case mix and predictor effects with model performance. We therefore performed some simulation studies. We also aimed to develop benchmark values for performance measures, to improve the interpretation of validation results. We illustrate the usefulness of these benchmark values in a case study of traumatic brain injury patients, where the model's performance upon external validation was better than expected from the development sample.

DIFFERENCES BETWEEN DEVELOPMENT AND VALIDATION SAMPLES

We distinguish 2 types of differences between development and validation samples: Either the case mix is different or the predictor effects, expressed as regression coefficients, are different (Table 1).

Table 1.

Differences Between Development and Validation Samples That Determine the External Validity of Risk Models

Type of Difference and Scenario	Difference Between Samples	Characteristic of Validation Situation	Example
Case mix
1	Distribution of predictors included in the model	Different selection of patients based on predictors considered in the model	Validation in different setting
2	Distribution of predictors omitted from the model	Different selection of patients based on predictors not considered in the model	Validation in different setting
Regression coefficients
3	Effects of the included predictors	Sample from different population compared with development situation	Validation in different setting
4	Effect of the linear predictor	Overfitted model is validated	Validation of model from small development sample

Open in a new tab

Differences in case mix

Case mix refers to predictors included in the model (“included predictors”), but it may also refer to variables that are related to the outcome and not included in the developed model (“omitted predictors”). A difference in case mix between development and validation samples may occur when more severely ill subjects are included in the validation sample. For instance, the Framingham risk model was developed in the general population and may be validated in patients at lower risk of cardiovascular disease. Furthermore, less heterogeneity may exist in subjects from the validation sample. The Gail model, for instance, was developed among women participating in a screening program (1) and was validated in patients from a randomized trial, with stricter inclusion criteria (8). Differences in severity of disease affect mainly the mean predictor values; differences in heterogeneity affect mainly the variances of the predictor values.

Differences in regression coefficients

Predictor effects, and hence the regression coefficients of the predictors included in the model, can be different in the development and validation samples, as a result of differences in the methods used for data collection or in the definitions of the predictors or the outcome variable (9). The predictor effects can also be truly different in the development and validation populations, even when the same variable definitions have been applied. An example is the predictive effect of diabetes on the risk of cardiovascular disease, which was stronger in Native Americans than in whites (7).

Another reason for different regression coefficients is statistical overfitting. An overfitted model may fit the development data well but gives predictions that are too extreme for new patients. Overfitting leads to a smaller predictive effect of the linear predictor (lp) upon external validation. The lp is the sum product of regression coefficients of the risk model and predictor values (lp = α + β₁ × x₁ + … + β_i × x_i, in which α is the intercept and β₁–β_i are the regression coefficients of the predictors x₁–x_i). The reduced predictive effect of the lp due to overfitting might have already been detected at internal validation—for instance, using bootstrap resampling (10, 11). Overfitting is most likely for models developed in small samples with a relatively large number of (candidate) predictors (12, 13). Shrinkage of coefficients at model development might be applied to prevent overestimation of regression coefficients for predictive purposes (14, 15). Unfortunately, coefficients are not shrunken for many currently developed models (16, 17).

SIMULATION STUDIES

We conducted simulation studies to assess the influences of differences in case mix and regression coefficients between development and validation samples on model performance. We simulated large samples (n = 500,000) to validate logistic regression models that predict a binary outcome y (y = 1 if the outcome (e.g., mortality) occurred and y = 0 if the outcome did not occur). Validation samples were simulated for several risk models. For each model, lp could be calculated per patient in the simulated validation sample. The risk of y (p(y)) equals 1/(1 + exp(−lp)). The outcome value y (1 or 0) was then generated by comparing p(y) with an independently generated variable u having a uniform distribution from 0 to 1. We used the rule y = 1 if p(y) ≥ u, and y = 0 otherwise (see the Web Appendix, which is posted on the Journal’s Web site (http://aje.oxfordjournals.org/), for the simulation code used in the study).

The validity of predicted risks was assessed graphically by plotting predictions on the x axis and the observed outcome on the y axis. Calibration, that is, the agreement between predicted risks and observed outcome proportions, can be visualized as the distance between a LOESS smoothed curve of observed outcomes and the 45-degree line (perfect agreement or calibration) (12, 18). Note that the observed outcome proportion by decile of prediction in such a plot is a graphical illustration of the Hosmer-Lemeshow goodness-of-fit test (19).

Performance measures for calibration were based on a recalibration model with logit(y) = a + b × lp. Calibration-in-the-large was assessed with the intercept a, given that slope b is set to 1 (a|b = 1) (20–22). The Hosmer-Lemeshow test statistic was also estimated (19).

Discriminative ability refers to the ability to distinguish subjects with the outcome from subjects without the outcome, and it was measured with the c statistic (23). This statistic is equal to the area under the receiver operating characteristic curve, if the outcome variable is binary, as in our study (24). Furthermore, we estimated single overall performance measures to combine discrimination and calibration aspects, that is, R² and the Brier score (25). A number of R² statistics are available (26). We estimated Nagelkerke's R² (27), since this statistic is based on the model likelihood, which is also used to fit generalized linear regression models such as logistic models and survival models. In general, Nagelkerke's R² is slightly larger than R² measures that use the squared correlation of the observed outcome and predicted risk (26). Indeed, R² and the Brier score mainly capture discrimination, if the parameters are estimated for recalibrated predictions.

Simulation of a different case mix

To study the influence of differences in case mix between the development and validation samples, we started with a simple model in which the outcome y in the validation sample had a single predictor x (model 1). The predictor was normally distributed with mean equal to 0 and a standard deviation (SD) of 1 (x ∼ N(0,1)). The intercept α was set to 0, and the logistic regression coefficient β was 1.5. Hence, lp = 1.5 × x.

More (or less) severely ill subjects in the validation sample (scenario 1A) were simulated by including subjects with higher x values more (or less) frequently. To do so, we compared the x values with values randomly drawn from a normal distribution with N(0,0.8) (see the Web Appendix for the R code used). As a result, the mean value of x was higher, that is, 0.6 (or lower, i.e., −0.6). We simulated a more (or less) heterogeneous case-mix (scenario 1B) by including subjects with extreme values of x more (or less) frequently (see Web Appendix for R code). As a result, the variance of x was higher, that is, 2.0 (or lower, i.e., 0.5).

Further, we simulated scenarios in which the outcome y in the validation sample was determined not only by the included predictor x but also by a second, though omitted, predictor z (z ∼ N(0,1)), with lp = 1.5 × x + 1.5 × z, with α = 0 and x and z being moderately correlated (scenario 2). Moderate correlation between x and z (Pearson correlation coefficient: r = 0.33) resulted in a regression coefficient for x that was 1.5, both in the unadjusted analysis (a model with x only) and in the adjusted analysis (a model with z included).

Differences in the distribution of the omitted predictor z were similarly generated as for the included predictor x, described above for scenario 1, to again introduce more or less severity of illness (scenario 2A) or more or less heterogeneity (scenario 2B) in case mix.

Simulation of different regression coefficients

To study the effect of different regression coefficients on model performance, we simulated another risk model (model 2) which contained 10 uncorrelated predictors. The predictors were normally distributed with mean 0 and decreasing SDs, with x₁ ∼ N(0,1), x₂ ∼ N(0,0.9), …, x₁₀ ∼ N(1,0.1). The model was lp = α + β₁ × x₁ + β₂ × x₂ + … + β₁₀ × x₁₀, where α is the intercept (set to 0) and β_i are the regression coefficients of predictors x_i (each set to 1). As a result, lp = x₁ + x₂ + x₃ + x₄ + x₅ + x₆ + x₇ + x₈ + x₉ + x₁₀.

We used an arbitrary example of differences in predictor effects in the validation sample, with half of the predictors having 0.5 times the effect of the development sample and half having 1.5 times the effect. We validated predictions from the model with regression coefficients equal to 1 in samples where lp_val = 0.5 × x₁ + 1.5 × x₂ + 0.5 × x₃ + 1.5 × x₄ + 0.5 × x₅ + 1.5 × x₆ + 0.5 × x₇ + 1.5 × x₈ + 0.5 × x₉ + 1.5 × x₁₀ was in fact the correct or true linear predictor (scenario 3). The x values were distributed as in the development sample. Next, we developed a model with 10 predictors on a development sample that contained only 100 subjects to obtain a model that was severely overfitted. This model, lp_dev = 0.1 + 1.3 × x₁ + 2.1 × x₂ + 1.1 × x₃ + 0.7 × x₄ + 1.3 × x₅ + 1.5 × x₆ + 1.7 × x₇ + 2.5 × x₈ + 2.1 × x₉ + 0.9 × x₁₀, was validated in validation samples with lp_val = x₁ + x₂ + x₃ + x₄ + x₅ + x₆ + x₇ + x₈ + x₉ + x₁₀ (scenario 4).

SIMULATION RESULTS

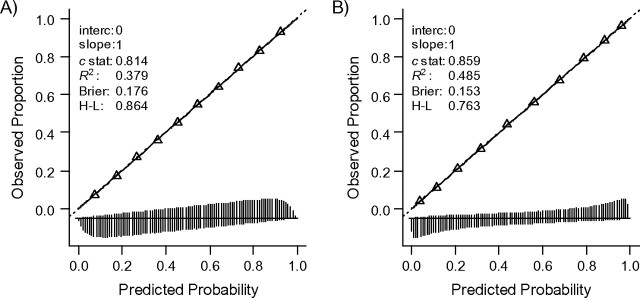
The simulated risk models with 1 and 10 predictors were, by definition, well-calibrated in the development sample (Figure 1, panels A and B) with good discriminative ability (c = 0.814 and c = 0.859, respectively). When the model was applied in another sample of the same underlying development population, the performance was by definition identical.

Differences in case mix

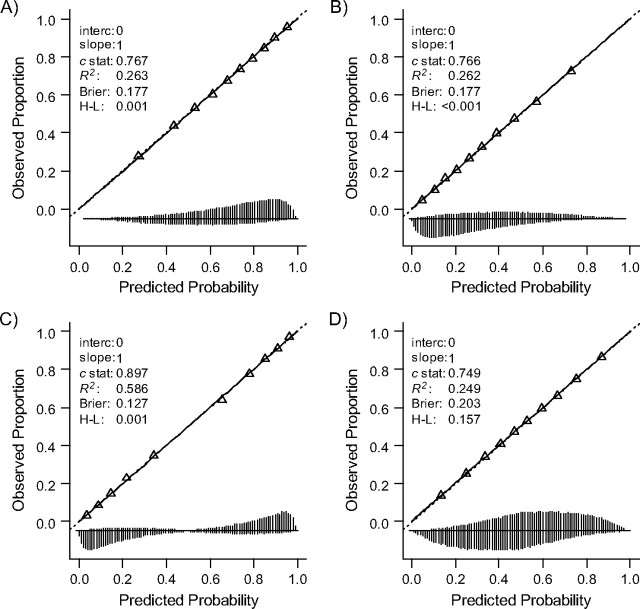
Changes in the distribution of the included predictor caused by differences in either disease severity (scenario 1A) or the homogeneity of the sample (scenario 1B) did not affect calibration of the risk model with 1 predictor (Figure 2). Calibration-in-the-large (a|b = 1) was equal to 0; the calibration slope b was very close to 1. Nevertheless, the Hosmer-Lemeshow test indicated misfit in Figure 2, panels A–C (P < 0.001). Apparently, the Hosmer-Lemeshow test is extremely sensitive for random variation in large simulation samples (here, n = 500,000). A more severe (Figure 2, panel A) or less severe (Figure 2, panel B) case mix was associated with somewhat less spread in predictions (SD of lp = SD(lp) = 1.2) as compared with the development sample (SD(lp) = 1.5) in both subjects with the outcome and subjects without the outcome (see also vertical lines at the bottom), and hence a lower c statistic (0.766 instead of 0.814).

Figure 2. — Influence on the performance of model 1 (1 predictor included), when more or less severe cases are selected (panels A and B) and more or less heterogeneous cases are selected (panels C and D) according to observed predictor values (“x”). Panels A and B: 50% of the subjects were selected, with higher or lower likelihood of selection with higher x values. Panels C and D: approximately 35% of the subjects were selected, with higher or lower likelihood of selection with more extreme x values. See the legend of Figure 1 for explanation of lines and symbols.

A more heterogeneous sample according to the included predictor (scenario 1B, SD(lp) = 2.1) was related to a higher discriminative ability. The model could distinguish more subjects with very low or very high predictions (c = 0.898 instead of c = 0.814; Figure 2, panel C). The reverse was found for validation in a sample with less heterogeneity (SD(lp) = 1.1, c = 0.747; Figure 2, panel D).

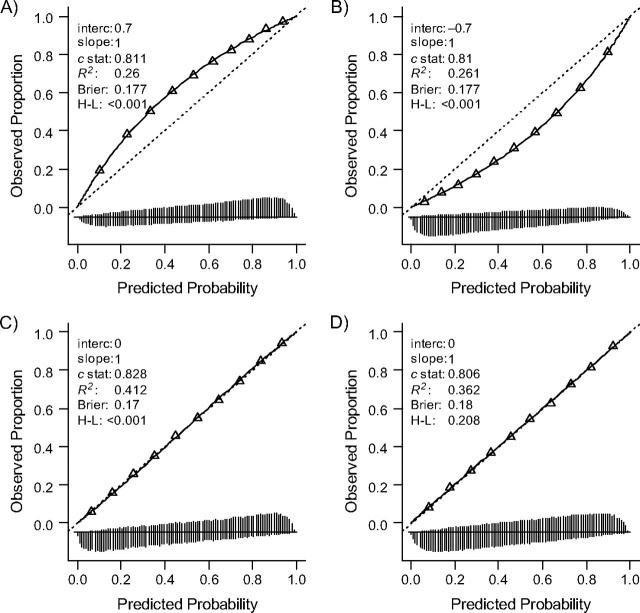
A more severe case mix according to the missed predictor z (scenario 2A) caused a systematic miscalibration of predictions (Figure 3, panel A); predictions were on average too low. The calibration-in-the-large (a|b = 1) value was 0.7, which reflects the fact that more cases were found than predicted (67% vs. 55%). The calibration slope was 1 on the logit scale. Discrimination was similar to that in the development sample (c = 0.810), with similar spread in lp (SD(lp) = 1.5). The reverse calibration problem was noted when the focus of selection was on less severely ill subjects according to the omitted predictor (Figure 3, panel B). A more or less heterogeneous distribution of the omitted predictor showed good calibration. The distribution of the lp was slightly different (SD(lp) = 1.6 for more heterogeneity in the omitted predictor; SD(lp) = 1.4 for less heterogeneity). As a consequence, discrimination was also slightly different (Figure 3, panels C and D).

Differences in regression coefficients

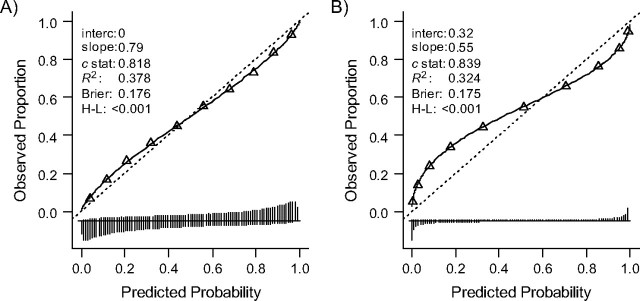
Different predictor effects in the validation sample as compared with the development sample for the model with 10 predictors (scenario 3) resulted here in a calibration slope smaller than 1 (0.79) and less discriminative ability (c = 0.818 instead of c = 0.859; Figure 4, panel A), when applied in the validation samples. The lower discrimination was a result of differences in regression coefficients, since the spread in lp was slightly higher in the validation sample (SD(lp) = 2.1 as compared with SD(lp) = 2.0 in the development sample). Note that we have introduced only 1 type of difference in the regression coefficients. Other introduced differences in regression coefficients might have given different results. The overfitted model (scenario 4) clearly showed a smaller calibration slope of 0.55 (Figure 4, panel B). Predicted risks were too low in the lower range and too high in the upper range. When we developed 20 new models on 100 subjects drawn at random from the development sample, all 20 models were highly overfitted, with a median slope of 0.48 in the validation sample.

Figure 4. — Influence on the performance of model 2 (10 predictors included) when regression coefficients are different. Predictor effects were different in the validation sample, that is, 0.5 or 1.5 times as large (panel A), or the model was overfitted in the development phase (panel B). See the legend of Figure 1 for explanation of lines and symbols.

BENCHMARK VALUES FOR MODEL PERFORMANCE MEASURES

The results of our simulation studies indicate that the interpretation of model performance estimates in external validation samples is not straightforward. Differences between the development and validation samples in case mix and regression coefficients can both influence the model's performance. Benchmark values for model performance measures may be helpful, to disentangle the case-mix effect from the effect of the coefficients. We consider 2 types of benchmark values that can be calculated in the validation phase for better interpretation of model performance.

The first type of benchmark value is the case-mix-corrected value. This is the performance under the condition that the model predictions are statistically correct in the validation sample. For a regression model, this means that the regression coefficients for the predictors in the model and the model intercept are fully correct for the validation population. A practical approach to estimate the case-mix-corrected values is to simulate the outcome y with the case mix of the validation sample, given that the risk model is correct. This is simply obtained by first calculating the predicted risks for each subject in the validation sample and subsequently generating the outcome value based on this prediction. With at least 100 repetitions for each subject, stable estimates of the benchmark values are obtained.

A second type of benchmark value is the performance that can be obtained by refitting the model in the validation sample. The regression coefficients are then optimal for the validation sample and hence provide an upper bound for the performance, which would be obtained if the coefficients from the development population were exactly equal to those in the validation population. The validation of the Framingham Heart Study risk score included such refitted benchmark values (7). The c statistic estimated in the development sample (0.83 for women) was compared with that estimated in the validation sample (0.75). The refitted model in the validation sample corresponded to a c statistic of 0.86. The refitted benchmark value indicates that the regression coefficients were different for the validation population, if the case mix was similar. To estimate the relative importance of the case mix, the case-mix-corrected benchmark value is needed.

We note that the benchmark values are useful for discriminative and overall performance measures. Since the risk model is considered correct (case-mix-corrected value) or the regression coefficients are refitted (refitted value), the benchmark values for calibration correspond in both situations to perfect calibration with calibration-in-the-large equal to 0 and the calibration slope equal to 1.

EXAMPLE OF BENCHMARK VALUES IN A CASE STUDY

We illustrate the use of the benchmark values in a case study on the prediction of 6-month outcome in subjects with traumatic brain injury. We developed a model to predict an unfavorable outcome (i.e., death, a vegetative state, or severe disability) with data on 1,118 subjects (456 (41%) had an unfavorable outcome) from the International Tirilazad Trial (28). The validity of the risk model was studied in 1,041 subjects (395 (38%) had an unfavorable outcome) who were enrolled in the North American Tirilazad Trial (29). Both trials included subjects with severe or moderate traumatic brain injury. We considered 3 predictors in a logistic regression model: age, motor score, and pupillary reactivity (30).

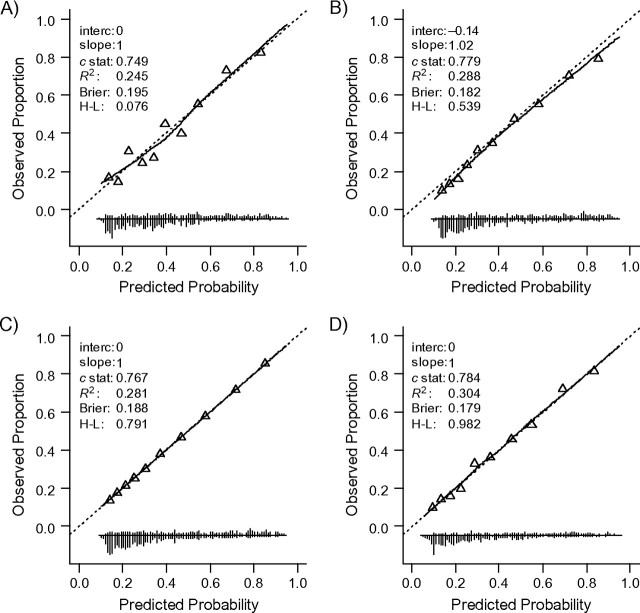
The model showed perfect calibration and reasonable discrimination (c = 0.749) and overall performance (R² = 24.5%, Brier score = 0.195; Figure 5, panel A and Table 2) in the development sample. Internal validation by bootstrapping showed minor optimism (c decreased to 0.740, R² decreased to 22.3%, and Brier score increased to 0.199). Surprisingly, discrimination was higher in the external validation sample (i.e., c = 0.779; Figure 5, panel B). The case-mix-corrected benchmark value for c was 0.767 (Figure 5, panel C), indicating that a large part of the higher performance should be attributed to a more heterogeneous case mix. Indeed, the linear predictor had a larger variability in the validation sample than in the development sample (SD(lp) = 1.1 and SD(lp) = 1.0, respectively). When the model was refitted in the validation sample, the performance was similar to the performance of the previously developed model when externally validated (c = 0.784; Figure 5, panel D), reflecting similar regression coefficients. A similar pattern was noted for R² and the Brier score. The predictor effects were overall slightly stronger in the validation population, as indicated by the calibration slope of 1.02 (Figure 5, panel B).

Table 2.

Performance of a Risk Model for Traumatic Brain Injury^a

Measure	International Tirilazad Trial (n = 1,118)		North American Tirilazad Trial (n = 1,041)
Measure	Apparent	Optimism-Corrected	Externally Validated	Case-Mix-Corrected	Refitted
c statistic	0.749	0.740	0.779	0.767	0.784
R², %	24.5	22.3	28.8	28.1	30.4
Brier score	0.195	0.199	0.182	0.188	0.179

Open in a new tab

The model was developed in the International Tirilazad Trial and validated in the North American Tirilazad Trial, 1991–1994.

DISCUSSION

Testing the validity of a risk model in new subjects is an important step in studying the model's generalizability to other populations. We showed that a model's performance depends not only on the correctness of the fitted regression coefficients but also on the case mix of the validation sample. Lower discriminative ability in the validation sample as compared with the development sample can be the result of a more homogeneous validation case mix; regression coefficients from the model can still be correct. Hence, the results of validation studies may not be directly interpretable. In order to disentangle case-mix effects from the effect of regression coefficients, we introduced a new benchmark value for model performance measures.

Calibration was assessed with the recalibration parameters (intercept and calibration slope) proposed by Cox (20) and with the Hosmer-Lemeshow test (19). Although it is widely used, the Hosmer-Lemeshow test has a number of drawbacks. The grouping of patients by predicted risks, though common, is arbitrary and imprecise. The test has limited power to detect misfit in small samples, as also addressed by Hosmer and Lemeshow themselves (31), and minor, irrelevant misfit is identified in large samples. The latter was also shown in our simulations. Further, the Hosmer-Lemeshow test has poor interpretability (12). The recalibration parameters are more informative (20, 32). The values of the parameters should not be statistically different from 0 (intercept) and 1 (slope).

Recently, benchmark values were proposed in a systematic review on model performance measures for the interpretation of validation results (33). The proposed benchmarks included theoretical minimum and maximum values for performance measures, estimates based on the overall outcome incidence (no-information value), the apparent performance of the model, the performance estimate corrected for optimism after internal validation, and the performance of a model for which the predictors are uncorrelated with the outcome. These benchmarks are useful but do not distinguish case-mix influences from incorrectness of the regression coefficients. Therefore, we introduce a new benchmark value that considers the distribution of the observed predictor values in the validation sample. We label this benchmark the case-mix-corrected performance, similar to Harrell's optimism-corrected performance for internally validated performance using bootstrap resampling (12). The second benchmark is the refitted performance, which is obtained by reestimating the regression coefficients of the included predictors in the validation sample, and it has often been used before. Note that if the validation sample is small, the reestimated regression coefficients will be too optimistic. The optimism-corrected performance of the refitted model should then be estimated for a proper comparison between the performance of the original model and that of the refitted model.

The benchmark approach (case-mix-corrected performance) focuses on the expected discrimination, given correct model fit. Another approach would be to test the model fit. A simple test for misfit in the validation sample is a likelihood ratio test for a model with the linear predictor included as an offset variable (34). This is an overall test for differences in estimated regression coefficients in the validation samples, taking the estimates from the development sample as a reference. If the test indicates adequate fit, the estimated discrimination indicates the heterogeneity in the new patients. Comparison of discriminative ability between the development and validation samples as an indication of model performance has become irrelevant. Correct model fit is also assumed if R² and Brier score are estimated after recalibration of the predictions. Comparison of such estimates between the development and validation samples only indicates differences in heterogeneity. A validation plot can be used to visualize the model (mis)fit and discrimination combined in 1 figure.

Our study had several limitations. We focused on the point estimates of the performance measures rather than statistical inferences. Interpretation of point estimates without statistical testing requires reasonable sample sizes. We previously showed that validation samples should have at least 100 events for reasonable power to detect differences in model performance and hence provide precise point estimates (35). Small samples will give imprecise point estimates, which require careful interpretation of the validation results.

Further, we focused only on dichotomous outcome values that were analyzed with logistic regression analysis. Our findings translate easily to the survival context with time-to-event data. Such data can be modeled with Cox proportional hazards regression analysis, for instance. The baseline hazard can be considered a group of time-dependent intercepts, and the regression coefficients can be used to calculate the linear predictor. High variance of the linear predictor in the validation sample indicates large heterogeneity, provided that the fit of the survival model is adequate. The same performance measures that are used for the dichotomous situation, such as R² and the c statistic, can be estimated for time-to-event outcomes. A typical complexity with time-to-event outcomes, though, is that observations may be censored. Consensus is lacking on the appropriate way to account for censoring in estimation of the c statistic. Several estimators have been proposed that can accommodate censored data (36, 37). Once the performance measures have been chosen, benchmark values for the performance measures can be estimated by simulating the outcome given perfect calibration. In case of time-to-event outcomes, survival times and censoring times are simulated, rather than dichotomous values.

In conclusion, comparison of estimates of model performance in the development and validation populations solely can result in wrong inferences about model validity. The performance of risk models can be influenced by differences in regression coefficients between the development and validation samples, but also by differences in case mix. These differences should be disentangled for a better interpretation of validation results. Estimation of 2 types of benchmark values, the case-mix-corrected performance and the refitted performance, can be helpful for this purpose.

Acknowledgments

Author affiliations: Julius Center for Health Sciences and Primary Care, University Medical Center Utrecht, Utrecht, the Netherlands (Yvonne Vergouwe, Karel G. M. Moons); and Center for Medical Decision Sciences, Department of Public Health, Erasmus Medical Center, Rotterdam, the Netherlands (Yvonne Vergouwe, Ewout W. Steyerberg).

This research was supported by the Netherlands Organization for Scientific Research (grants 016.046.360, 9120.8004, 17099.25039, and 981.10.65) and the US National Institutes of Health (grant NS 42691).

Conflict of interest: none declared.

Glossary

Abbreviation

SD: standard deviation

References

1.Gail MH, Brinton LA, Byar DP, et al. Projecting individualized probabilities of developing breast cancer for white females who are being examined annually. J Natl Cancer Inst. 1989;81(24):1879–1886. doi: 10.1093/jnci/81.24.1879. [DOI] [PubMed] [Google Scholar]
2.Wilson PW, D'Agostino RB, Levy D, et al. Prediction of coronary heart disease using risk factor categories. Circulation. 1998;97(18):1837–1847. doi: 10.1161/01.cir.97.18.1837. [DOI] [PubMed] [Google Scholar]
3.Justice AC, Covinsky KE, Berlin JA. Assessing the generalizability of prognostic information. Ann Intern Med. 1999;130(6):515–524. doi: 10.7326/0003-4819-130-6-199903160-00016. [DOI] [PubMed] [Google Scholar]
4.Altman DG, Royston P. What do we mean by validating a prognostic model? Stat Med. 2000;19(4):453–473. doi: 10.1002/(sici)1097-0258(20000229)19:4<453::aid-sim350>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
5.Bleeker SE, Moll HA, Steyerberg EW, et al. External validation is necessary in prediction research: a clinical example. J Clin Epidemiol. 2003;56(9):826–832. doi: 10.1016/s0895-4356(03)00207-5. [DOI] [PubMed] [Google Scholar]
6.Taylor JM, Ankerst DP, Andridge RR. Validation of biomarker-based risk prediction models. Clin Cancer Res. 2008;14(19):5977–5983. doi: 10.1158/1078-0432.CCR-07-4534. [DOI] [PMC free article] [PubMed] [Google Scholar]
7.D'Agostino RB, Sr, Grundy S, Sullivan LM, et al. Validation of the Framingham coronary heart disease prediction scores: results of a multiple ethnic groups investigation. JAMA. 2001;286(2):180–187. doi: 10.1001/jama.286.2.180. [DOI] [PubMed] [Google Scholar]
8.Boyle P, Mezzetti M, La Vecchia C, et al. Contribution of three components to individual cancer risk predicting breast cancer risk in Italy. Eur J Cancer Prev. 2004;13(3):183–191. doi: 10.1097/01.cej.0000130014.83901.53. [DOI] [PubMed] [Google Scholar]
9.Simon R, Altman DG. Statistical aspects of prognostic factor studies in oncology. Br J Cancer. 1994;69(6):979–985. doi: 10.1038/bjc.1994.192. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Harrell FE, Jr, Lee KL, Matchar DB, et al. Regression models for prognostic prediction: advantages, problems, and suggested solutions. Cancer Treat Rep. 1985;69(10):1071–1077. [PubMed] [Google Scholar]
11.Steyerberg EW, Harrell FE, Jr, Borsboom GJ, et al. Internal validation of predictive models: efficiency of some procedures for logistic regression analysis. J Clin Epidemiol. 2001;54(8):774–781. doi: 10.1016/s0895-4356(01)00341-9. [DOI] [PubMed] [Google Scholar]
12.Harrell FE., Jr . Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis. New York, NY: Springer-Verlag New York; 2001. [Google Scholar]
13.Steyerberg EW, Eijkemans MJ, Harrell FE, Jr, et al. Prognostic modelling with logistic regression analysis: a comparison of selection and estimation methods in small data sets. Stat Med. 2000;19(8):1059–1079. doi: 10.1002/(sici)1097-0258(20000430)19:8<1059::aid-sim412>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]
14.Copas JB. Regression, prediction and shrinkage. J R Stat Soc Series B. 1983;45(3):311–354. [Google Scholar]
15.van Houwelingen JC, le Cessie S. Predictive value of statistical models. Stat Med. 1990;9(11):1303–1325. doi: 10.1002/sim.4780091109. [DOI] [PubMed] [Google Scholar]
16.Mushkudiani NA, Hukkelhoven CW, Hernández AV, et al. A systematic review finds methodological improvements necessary for prognostic models in determining traumatic brain injury outcomes. J Clin Epidemiol. 2008;61(4):331–343. doi: 10.1016/j.jclinepi.2007.06.011. [DOI] [PubMed] [Google Scholar]
17.Counsell C, Dennis M. Systematic review of prognostic models in patients with acute stroke. Cerebrovasc Dis. 2001;12(3):159–170. doi: 10.1159/000047699. [DOI] [PubMed] [Google Scholar]
18.Steyerberg EW. Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating. New York, NY: Springer Publishing Company; 2009. [Google Scholar]
19.Lemeshow S, Hosmer DW. Applied Logistic Regression. New York, NY: John Wiley & Sons, Inc; 1989. [Google Scholar]
20.Cox DR. Two further applications of a model for binary regression. Biometrika. 1958;45(3-4):562–565. [Google Scholar]
21.Miller ME, Hui SL, Tierney WM. Validation techniques for logistic regression models. Stat Med. 1991;10(8):1213–1226. doi: 10.1002/sim.4780100805. [DOI] [PubMed] [Google Scholar]
22.Van Houwelingen HC, Thorogood J. Construction, validation and updating of a prognostic model for kidney graft survival. Stat Med. 1995;14(18):1999–2008. doi: 10.1002/sim.4780141806. [DOI] [PubMed] [Google Scholar]
23.Harrell FE, Jr, Califf RM, Pryor DB, et al. Evaluating the yield of medical tests. JAMA. 1982;247(18):2543–2546. [PubMed] [Google Scholar]
24.Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143(1):29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]
25.Brier GW. Verification of forecasts expressed in terms of probability. Mon Weather Rev. 1950;78(1):1–3. [Google Scholar]
26.Mittlböck M, Schemper M. Explained variation for logistic regression. Stat Med. 1996;15(19):1987–1997. doi: 10.1002/(SICI)1097-0258(19961015)15:19<1987::AID-SIM318>3.0.CO;2-9. [DOI] [PubMed] [Google Scholar]
27.Nagelkerke NJD. A note on a general definition of the coefficient of determination. Biometrika. 1991;78(3):691–692. [Google Scholar]
28.Hukkelhoven CW, Steyerberg EW, Farace E, et al. Regional differences in patient characteristics, case management, and outcomes in traumatic brain injury: experience from the tirilazad trials. J Neurosurg. 2002;97(3):549–557. doi: 10.3171/jns.2002.97.3.0549. [DOI] [PubMed] [Google Scholar]
29.Marshall LF, Maas AI, Marshall SB, et al. A multicenter trial on the efficacy of using tirilazad mesylate in cases of head injury. J Neurosurg. 1998;89(4):519–525. doi: 10.3171/jns.1998.89.4.0519. [DOI] [PubMed] [Google Scholar]
30.Steyerberg EW, Mushkudiani N, Perel P, et al. Predicting outcome after traumatic brain injury: development and international validation of prognostic scores based on admission characteristics. PLoS Med. 2008;5(8):1251–1260. doi: 10.1371/journal.pmed.0050165. [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Hosmer DW, Hosmer T, le Cessie S, et al. A comparison of goodness-of-fit tests for the logistic regression model. Stat Med. 1997;16(9):965–980. doi: 10.1002/(sici)1097-0258(19970515)16:9<965::aid-sim509>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
32.Steyerberg EW, Vickers AJ, Cook NR, et al. Assessing the performance of prediction models: a framework for traditional and novel measures. Epidemiology. 2010;21(1):128–138. doi: 10.1097/EDE.0b013e3181c30fb2. [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Gerds TA, Cai T, Schumacher M. The performance of risk prediction models. Biom J. 2008;50(4):457–479. doi: 10.1002/bimj.200810443. [DOI] [PubMed] [Google Scholar]
34.Steyerberg EW, Borsboom GJ, van Houwelingen HC, et al. Validation and updating of predictive logistic regression models: a study on sample size and shrinkage. Stat Med. 2004;23(16):2567–2586. doi: 10.1002/sim.1844. [DOI] [PubMed] [Google Scholar]
35.Vergouwe Y, Steyerberg EW, Eijkemans MJ, et al. Substantial effective sample sizes were required for external validation studies of predictive logistic regression models. J Clin Epidemiol. 2005;58(5):475–483. doi: 10.1016/j.jclinepi.2004.06.017. [DOI] [PubMed] [Google Scholar]
36.Heagerty PJ, Lumley T, Pepe MS. Time-dependent ROC curves for censored survival data and a diagnostic marker. Biometrics. 2000;56(2):337–344. doi: 10.1111/j.0006-341x.2000.00337.x. [DOI] [PubMed] [Google Scholar]
37.Heagerty PJ, Zheng Y. Survival model predictive accuracy and ROC curves. Biometrics. 2005;61(1):92–105. doi: 10.1111/j.0006-341X.2005.030814.x. [DOI] [PubMed] [Google Scholar]

[bib1] 1.Gail MH, Brinton LA, Byar DP, et al. Projecting individualized probabilities of developing breast cancer for white females who are being examined annually. J Natl Cancer Inst. 1989;81(24):1879–1886. doi: 10.1093/jnci/81.24.1879. [DOI] [PubMed] [Google Scholar]

[bib2] 2.Wilson PW, D'Agostino RB, Levy D, et al. Prediction of coronary heart disease using risk factor categories. Circulation. 1998;97(18):1837–1847. doi: 10.1161/01.cir.97.18.1837. [DOI] [PubMed] [Google Scholar]

[bib3] 3.Justice AC, Covinsky KE, Berlin JA. Assessing the generalizability of prognostic information. Ann Intern Med. 1999;130(6):515–524. doi: 10.7326/0003-4819-130-6-199903160-00016. [DOI] [PubMed] [Google Scholar]

[bib4] 4.Altman DG, Royston P. What do we mean by validating a prognostic model? Stat Med. 2000;19(4):453–473. doi: 10.1002/(sici)1097-0258(20000229)19:4<453::aid-sim350>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]

[bib5] 5.Bleeker SE, Moll HA, Steyerberg EW, et al. External validation is necessary in prediction research: a clinical example. J Clin Epidemiol. 2003;56(9):826–832. doi: 10.1016/s0895-4356(03)00207-5. [DOI] [PubMed] [Google Scholar]

[bib6] 6.Taylor JM, Ankerst DP, Andridge RR. Validation of biomarker-based risk prediction models. Clin Cancer Res. 2008;14(19):5977–5983. doi: 10.1158/1078-0432.CCR-07-4534. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib7] 7.D'Agostino RB, Sr, Grundy S, Sullivan LM, et al. Validation of the Framingham coronary heart disease prediction scores: results of a multiple ethnic groups investigation. JAMA. 2001;286(2):180–187. doi: 10.1001/jama.286.2.180. [DOI] [PubMed] [Google Scholar]

[bib8] 8.Boyle P, Mezzetti M, La Vecchia C, et al. Contribution of three components to individual cancer risk predicting breast cancer risk in Italy. Eur J Cancer Prev. 2004;13(3):183–191. doi: 10.1097/01.cej.0000130014.83901.53. [DOI] [PubMed] [Google Scholar]

[bib9] 9.Simon R, Altman DG. Statistical aspects of prognostic factor studies in oncology. Br J Cancer. 1994;69(6):979–985. doi: 10.1038/bjc.1994.192. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib10] 10.Harrell FE, Jr, Lee KL, Matchar DB, et al. Regression models for prognostic prediction: advantages, problems, and suggested solutions. Cancer Treat Rep. 1985;69(10):1071–1077. [PubMed] [Google Scholar]

[bib11] 11.Steyerberg EW, Harrell FE, Jr, Borsboom GJ, et al. Internal validation of predictive models: efficiency of some procedures for logistic regression analysis. J Clin Epidemiol. 2001;54(8):774–781. doi: 10.1016/s0895-4356(01)00341-9. [DOI] [PubMed] [Google Scholar]

[bib12] 12.Harrell FE., Jr . Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis. New York, NY: Springer-Verlag New York; 2001. [Google Scholar]

[bib13] 13.Steyerberg EW, Eijkemans MJ, Harrell FE, Jr, et al. Prognostic modelling with logistic regression analysis: a comparison of selection and estimation methods in small data sets. Stat Med. 2000;19(8):1059–1079. doi: 10.1002/(sici)1097-0258(20000430)19:8<1059::aid-sim412>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]

[bib14] 14.Copas JB. Regression, prediction and shrinkage. J R Stat Soc Series B. 1983;45(3):311–354. [Google Scholar]

[bib15] 15.van Houwelingen JC, le Cessie S. Predictive value of statistical models. Stat Med. 1990;9(11):1303–1325. doi: 10.1002/sim.4780091109. [DOI] [PubMed] [Google Scholar]

[bib16] 16.Mushkudiani NA, Hukkelhoven CW, Hernández AV, et al. A systematic review finds methodological improvements necessary for prognostic models in determining traumatic brain injury outcomes. J Clin Epidemiol. 2008;61(4):331–343. doi: 10.1016/j.jclinepi.2007.06.011. [DOI] [PubMed] [Google Scholar]

[bib17] 17.Counsell C, Dennis M. Systematic review of prognostic models in patients with acute stroke. Cerebrovasc Dis. 2001;12(3):159–170. doi: 10.1159/000047699. [DOI] [PubMed] [Google Scholar]

[bib18] 18.Steyerberg EW. Clinical Prediction Models: A Practical Approach to Development, Validation, and Updating. New York, NY: Springer Publishing Company; 2009. [Google Scholar]

[bib19] 19.Lemeshow S, Hosmer DW. Applied Logistic Regression. New York, NY: John Wiley & Sons, Inc; 1989. [Google Scholar]

[bib20] 20.Cox DR. Two further applications of a model for binary regression. Biometrika. 1958;45(3-4):562–565. [Google Scholar]

[bib21] 21.Miller ME, Hui SL, Tierney WM. Validation techniques for logistic regression models. Stat Med. 1991;10(8):1213–1226. doi: 10.1002/sim.4780100805. [DOI] [PubMed] [Google Scholar]

[bib22] 22.Van Houwelingen HC, Thorogood J. Construction, validation and updating of a prognostic model for kidney graft survival. Stat Med. 1995;14(18):1999–2008. doi: 10.1002/sim.4780141806. [DOI] [PubMed] [Google Scholar]

[bib23] 23.Harrell FE, Jr, Califf RM, Pryor DB, et al. Evaluating the yield of medical tests. JAMA. 1982;247(18):2543–2546. [PubMed] [Google Scholar]

[bib24] 24.Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143(1):29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]

[bib25] 25.Brier GW. Verification of forecasts expressed in terms of probability. Mon Weather Rev. 1950;78(1):1–3. [Google Scholar]

[bib26] 26.Mittlböck M, Schemper M. Explained variation for logistic regression. Stat Med. 1996;15(19):1987–1997. doi: 10.1002/(SICI)1097-0258(19961015)15:19<1987::AID-SIM318>3.0.CO;2-9. [DOI] [PubMed] [Google Scholar]

[bib27] 27.Nagelkerke NJD. A note on a general definition of the coefficient of determination. Biometrika. 1991;78(3):691–692. [Google Scholar]

[bib28] 28.Hukkelhoven CW, Steyerberg EW, Farace E, et al. Regional differences in patient characteristics, case management, and outcomes in traumatic brain injury: experience from the tirilazad trials. J Neurosurg. 2002;97(3):549–557. doi: 10.3171/jns.2002.97.3.0549. [DOI] [PubMed] [Google Scholar]

[bib29] 29.Marshall LF, Maas AI, Marshall SB, et al. A multicenter trial on the efficacy of using tirilazad mesylate in cases of head injury. J Neurosurg. 1998;89(4):519–525. doi: 10.3171/jns.1998.89.4.0519. [DOI] [PubMed] [Google Scholar]

[bib30] 30.Steyerberg EW, Mushkudiani N, Perel P, et al. Predicting outcome after traumatic brain injury: development and international validation of prognostic scores based on admission characteristics. PLoS Med. 2008;5(8):1251–1260. doi: 10.1371/journal.pmed.0050165. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib31] 31.Hosmer DW, Hosmer T, le Cessie S, et al. A comparison of goodness-of-fit tests for the logistic regression model. Stat Med. 1997;16(9):965–980. doi: 10.1002/(sici)1097-0258(19970515)16:9<965::aid-sim509>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]

[bib32] 32.Steyerberg EW, Vickers AJ, Cook NR, et al. Assessing the performance of prediction models: a framework for traditional and novel measures. Epidemiology. 2010;21(1):128–138. doi: 10.1097/EDE.0b013e3181c30fb2. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib33] 33.Gerds TA, Cai T, Schumacher M. The performance of risk prediction models. Biom J. 2008;50(4):457–479. doi: 10.1002/bimj.200810443. [DOI] [PubMed] [Google Scholar]

[bib34] 34.Steyerberg EW, Borsboom GJ, van Houwelingen HC, et al. Validation and updating of predictive logistic regression models: a study on sample size and shrinkage. Stat Med. 2004;23(16):2567–2586. doi: 10.1002/sim.1844. [DOI] [PubMed] [Google Scholar]

[bib35] 35.Vergouwe Y, Steyerberg EW, Eijkemans MJ, et al. Substantial effective sample sizes were required for external validation studies of predictive logistic regression models. J Clin Epidemiol. 2005;58(5):475–483. doi: 10.1016/j.jclinepi.2004.06.017. [DOI] [PubMed] [Google Scholar]

[bib36] 36.Heagerty PJ, Lumley T, Pepe MS. Time-dependent ROC curves for censored survival data and a diagnostic marker. Biometrics. 2000;56(2):337–344. doi: 10.1111/j.0006-341x.2000.00337.x. [DOI] [PubMed] [Google Scholar]

[bib37] 37.Heagerty PJ, Zheng Y. Survival model predictive accuracy and ROC curves. Biometrics. 2005;61(1):92–105. doi: 10.1111/j.0006-341X.2005.030814.x. [DOI] [PubMed] [Google Scholar]

PERMALINK

External Validity of Risk Models: Use of Benchmark Values to Disentangle a Case-Mix Effect From Incorrect Coefficients

Yvonne Vergouwe

Karel G M Moons

Ewout W Steyerberg

Abstract