Mapping Health Data: Improved Privacy Protection With Donut Method Geomasking

Abstract

A major challenge in mapping health data is protecting patient privacy while maintaining the spatial resolution necessary for spatial surveillance and outbreak identification. A new adaptive geomasking technique, referred to as the donut method, extends current methods of random displacement by ensuring a user-defined minimum level of geoprivacy. In donut method geomasking, each geocoded address is relocated in a random direction by at least a minimum distance, but less than a maximum distance. The authors compared the donut method with current methods of random perturbation and aggregation regarding measures of privacy protection and cluster detection performance by masking multiple disease field simulations under a range of parameters. Both the donut method and random perturbation performed better than aggregation in cluster detection measures. The performance of the donut method in geoprivacy measures was at least 42.7% higher and in cluster detection measures was less than 4.8% lower than that of random perturbation. Results show that the donut method provides a consistently higher level of privacy protection with a minimal decrease in cluster detection performance, especially in areas where the risk to individual geoprivacy is greatest.

Advances in geostatistical computing have enabled epidemiologists to examine the spatial and spatio-temporal distribution of diseases by mapping patient location information. Disease maps have a wide range of applications, from hypothesis generation to public health surveillance. Assessment of the spatial heterogeneity of a disease within a specified time frame allows investigators to highlight areas with unusually high or low rates, identify spatial patterns that may indicate clusters or “hot spots” of disease, or obtain clues as to disease etiology and community-level risk factors through ecologic regression studies (1–3). In addition, spatial patterns of disease may change over time, possibly serving as a geographic early warning disease surveillance system when case data are mapped in real time (4, 5). At the policy level, disease maps may aid decisions regarding intervention or prevention programs, allocation of health care resources, and assessment of inequalities or provide context for further epidemiologic studies (2, 6).

In the United States, a number of laws and guidelines, such as the Public Health Service Act (1946), the Privacy Act of 1974, and the Health Insurance Portability and Accountability Act (1996), place restrictions on the collection and dissemination of data in order to protect patient confidentiality and prevent identification of individuals (7, 8). In disease mapping, publishing maps that use exact patient location information jeopardizes patients' privacy because of “reverse geocoding” techniques. Reverse geocoding can generate an approximate address based on a latitude and longitude (9, 10). Consequently, geographic location is considered a personal identifier that could breach patient or study subject confidentiality if known, so it presents an ethical hurdle requiring justification for inclusion in data sets and analyses. A major challenge in working with geographic health data then becomes protecting patient confidentiality while maintaining the spatial resolution necessary for small-area analyses such as outbreak and cluster detection. This problem also extends to the sharing of data with researchers and analysts. Many governmental agencies have access to sensitive information combined with address data. Sharing these data directly with researchers may compromise individuals' privacy. Thus, patients' geoprivacy must be protected so that individuals cannot be identified through locational information (7, 11).

In response, a variety of methods have been proposed that modify the geographic coordinates of the original data set to mask patients' locational information. The aim of these geomasks is to protect patient geoprivacy while allowing for valid geographic analyses of the data (12). However, when geomasks are used, a trade-off exists between privacy protection and accuracy of analytical results (7, 8, 13). For example, the most common geomasking practice is to aggregate individual-level information to preexisting administrative or political boundaries, such as census tracts or zip codes. Although patient geoprivacy protection improves, aggregation causes a loss in data resolution. If the disease process operates at a finer resolution than the aggregated data, aggregation decreases the power, sensitivity, and specificity of detecting an excess risk (4, 7, 12, 14, 15). For example, if addresses are analyzed as center points of zip code or census tracts, spatial cluster detection algorithms perform worse than when addresses are analyzed at exact locations, particularly when case locations of a single cluster cross administrative boundaries (8). Similarly, the farther a point is moved from its original location, the greater the introduced error. This error increases the magnitude of anonymization but decreases spatial detection performance (13).

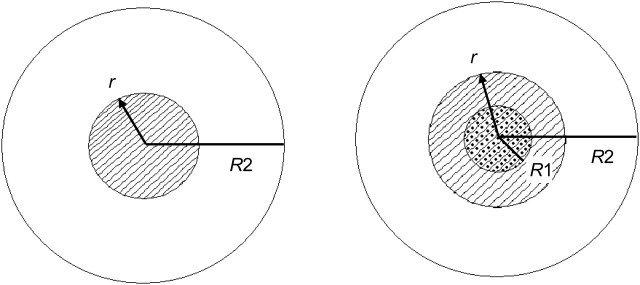
Other geomasks, such as random perturbation, have been proposed that reduce the amount of introduced error in the data set, which improves cluster detection performance but also increases the risk to patient privacy. For example, in random perturbation masking, each individual point is moved a random distance in a random direction from its original location. However, as shown in Figure 1, the randomly generated masked point may be located on or near the original coordinates. This is a problem because, while the number of individuals geomasked to their original locations may constitute only a small proportion of the overall data set, an adversary intent on reidentification may reverse geocode all points with the assumption that a few individuals will be correctly identified. Furthermore, researchers analyzing surveillance data from government agencies, such as departments of public health, may be restricted from accessing any individually identifiable health information, in which case anonymity of all individuals must be ensured before data access is granted (16). Methods are needed that protect geoprivacy without significantly affecting the accuracy of analytical results.

Figure 1.

Comparison of random perturbation (left) and donut method (right) geomasks. For a given Max k geoprivacy level, the Euclidean distance R2 is calculated for each point from the underlying population density. The population within a circular region of radius R2 around a point is equal to Max k, with R2 being the maximum distance the point may be displaced from its original location. For the donut method (right), a Min k (dotted) is also given that defines the minimum displacement R1. The actual distance displaced, r, ranges in value from 0 to R2 for random perturbation (left) and from R1 to R2 for the donut method (right). The population within the circular region of radius r (striped) is the actual k achieved by the geomask.

In this simulation, we examine a new adaptive geomasking technique, referred to as the donut method, which extends current methods of random displacement by ensuring that an address is not randomly assigned on or too near its original location. Although versions of the donut method have been proposed for use with mobile systems and environmental exposure data (16, 17), we examine the donut method here as it applies to disease mapping. In donut method geomasking, each geocoded address is relocated in a random direction by at least a minimum distance, but less than a maximum distance (10). In addition, each point is moved a distance inversely proportional to the underlying population density, which provides privacy protection while minimizing the introduced spatial error (10, 12, 13). For example, persons in high-density urban areas do not need to be moved as far as persons in low-density rural areas to achieve the same magnitude of anonymization. The donut method is an adaptive geomask because the dimensions of the mask around each point vary to meet specified anonymity constraints based on the underlying population density (16, 17). Accounting for population density variation also optimizes the donut method by minimizing the distances required for privacy protection while maximizing analytical validity.

In this implementation of the donut method, we retained each geomasked location within the administrative boundaries of the original point. Since the population at risk is often derived from areal demographics, it is important to keep geomasked points within their original administrative boundaries to maintain each case with its associated population at risk. Doing so also allows researchers to derive accurate aggregated data without accessing the original data set since aggregation of the geomasked points matches that of the original locations. However, the donut method may be implemented without the administrative boundary restriction, depending on the research environment. We compared the donut method with simple random perturbation and aggregation to assess its effectiveness in terms of both cluster detection and protection of patient geoprivacy.

MATERIALS AND METHODS

We constructed 3 disease field simulations over a 4-county region of varying population density to assess how a health data set is affected by geomasking (Web Figure 1, the first of 2 supplementary figures posted on the Journal's Web site (http://aje.oupjournals.org/)). Each disease field consisted of endemic background cases spatially distributed across the study area and 3 injected case clusters. The background cases were generated by assigning a random incidence rate, between 0 and 500 infections per 100,000 people, to each census block group. The endemic incidence rate was then combined with the 2000 US Census population to determine the number of background cases per block group, which were placed a random distance from the areal centroid but within census block group boundaries (18). We then injected 3 circular clusters into the disease field.

Cluster center points were identified in one region each of low, medium, and high population density. Cluster cases were then distributed a random distance and direction from each center point using a uniformly distributed pseudo-random number generator in the MATLAB programming environment (19). Cluster cases were also allowed to cross administrative boundaries, resulting in clusters that spanned multiple census block groups. To reflect the observed local spatial structure of an infectious disease such as gonorrhea (20, 21), the radius of each cluster was proportionate to the underlying population density. Therefore, cluster cases in the high-density area were spatially more compact than cluster cases in the low-density area. However, between disease fields, in addition to having different endemic incidence rates, the maximum cluster radius was varied manually to ensure 3 distinct data sets.

Geomask definitions

Aggregation sets the benchmark for privacy protection when comparing current geomasking methods, while random perturbation has been demonstrated to provide superior cluster detection performance. Each of the baseline disease fields was therefore masked using the donut method (Figure 1), random perturbation, and aggregation to the centroid of the census block group.

In random perturbation geomasking, points are displaced randomly within a circular region around their original locations. In donut method geomasking, points are moved at least a minimum distance and are therefore displaced in a torus, or donut-shaped region, around their original locations. With both random perturbation and the donut method, the maximum distance a point can be displaced from its original location corresponds to the outer radius R2 of the geomask around that point (Figure 1).

To determine R2, we used the k-anonymity metric, where k refers to the number of people among whom a specific de-identified cluster case cannot be reversely identified (13, 22). For example, if an individual case is moved a distance R2 from its original location, the k-anonymity achieved by the displacement is the population within a circular region of radius R2 around the original point. Conversely, given a desired k-anonymity level, R2 may be calculated from the underlying population density. The R2 radius of a particular point is the same for both random perturbation and donut method geomasks, but it will vary from point to point since cases in low-density areas need to be moved farther distances than those in high-density areas in order to achieve the same magnitude of k-anonymity. We used predefined maximum k-anonymity, or Max K, levels to calculate sets of R2 radii for each disease field. For the donut method, a minimum k-anonymity, or Min K, was also defined to determine the inner radius R1 of the torus, or the minimum distance each point was to be moved. Each disease field was geomasked at multiple Max K and Min K values to examine how changing the size of the random perturbation and donut method geomasks affected results.

To determine the actual distance and angle to move each point in random perturbation and donut method geomasking, a uniformly distributed pseudo-random number generator in MATLAB (19) was used, bounded by the condition that the new coordinates fall within the specified geomask region. Another condition was that points not be displaced out of their original administrative boundaries. Therefore, for a point located near the edge of its census block group, the geomask regions would be dissected by the block group boundaries, resembling a rough “slice of pie” for random perturbation and an “eaten donut” for the donut method. For aggregation geomasking, points were displaced to the centroid of their respective census block groups.

Since the aggregation geomask is based on administrative boundaries, it does not vary from point to point because of anonymity constraints and is therefore a “fixed” mask. In contrast, the donut method is an adaptive mask because the range of the mask at each point is determined by the underlying population density and user-specified minimum and maximum k-anonymity. Random perturbation may be considered “semiadaptive” because, while its outer radii may vary, it is not bounded by any minimum anonymity constraint.

Privacy protection

The k-anonymity metric was also used to measure privacy protection performance. As shown in Figure 1, if an individual case is moved an actual distance r from its original location, the actual k achieved by the displacement is the population within a circular region of radius r around the original point. Higher actual k values correspond to higher magnitudes of anonymization. Therefore, how well each geomask performed with respect to privacy protection was assessed by recording the actual distance that points were displaced from their original location and then calculating the actual k achieved with each method.

Cluster detection

Geomasking introduces error into the data set, which affects the performance of cluster detection algorithms such as the spatial scan statistic test implemented by the SaTScan program (8). The ideal outcome would be for geographic analysis of the geomasked data to match that of the original data set. Therefore, we compared the sensitivity and specificity of the donut method masked, random perturbation masked, and aggregated disease fields with those of the baseline (unmasked) data to assess how geomasking affected cluster detection performance.

Cluster detection performance was analyzed for each disease field iteration with the SaTScan Spatial Bernouilli Model scanning algorithm (23, 24). We used a circular scanning window to identify the most likely clusters and assign them a P value. We assumed spatial clustering when the P value of SaTScan-identified clusters was less than 0.05 on the basis of 999 Monte Carlo simulations.

Cluster detection sensitivity and specificity were calculated for each masking technique. Sensitivity was defined as the number of simulated cluster cases identified by SaTScan divided by the total number of cluster cases injected into each disease field. Specificity was defined as the number of endemic background cases not belonging to SaTScan clusters divided by the total number of endemic cases.

RESULTS

We examined how the donut method compared with current methods of random perturbation and aggregation in protecting patient privacy while maintaining cluster detection performance by masking multiple disease field simulations under a range of parameters. Each of the 3 disease fields consisted of approximately 2,500 endemic background cases and 150 cluster cases (3 clusters × 50 cases). We examined how the size of the random perturbation and donut method geomasks affected the results by geomasking each disease field for 10 different Max K levels with 20 iterations per level. Thus, a total of 600 iterations were generated for random perturbation and donut method geomasking (3 disease fields × 10 Max K levels × 20 iterations/level). For the donut method, Min K was defined as 10% of the Max K level.

Distance displaced and k-anonymity

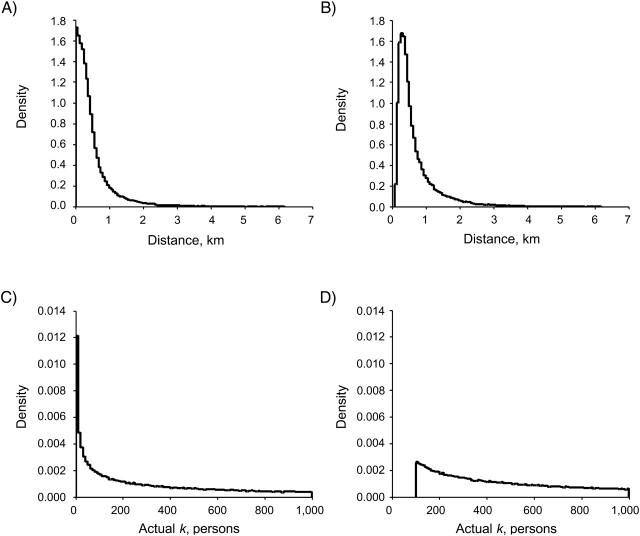
Random perturbation and donut method geomasks protect patient privacy by displacing cases random distances from their original location within a defined region. In random perturbation geomasking, the distance that points are displaced range in value from 0 to the upper limit of R2, as determined by the Max K level and underlying population density. In donut method geomasking, distance values range from the lower limit of R1, as determined by the Min K level, to the upper limit of R2. We plotted density scaled histograms of the Euclidean distance moved (Figure 2a and b) and actual k achieved (Figure 2c and d) for all points masked using random perturbation and the donut method at a Max K level of 1,000 people to examine how far points in our simulation were displaced from their original locations. As shown in Figure 2a, the majority of random perturbation masked points were displaced very small distances, with the highest likelihood being a value at or near zero. Correspondingly, most random perturbation masked points had an actual k value of zero (Figure 2c), placing them at high risk of reidentification.

Figure 2.

For a given geoprivacy level (Max k = 1,000), shown are density-scaled histograms of the A) distance displaced with random perturbation, B) distance displaced with the donut method, C) actual k achieved with random perturbation, and D) actual k achieved with the donut method (all iterations). With the donut method, points were perturbed at least a minimum distance from their original locations. Correspondingly, the donut method maintained a minimum level of k-anonymity with more points achieving higher actual k values.

In comparison, the distance distribution of donut method masked points (Figure 2b), while also skewed toward the lower bound, had all positive values. With a Min K level of 100 people, all lower-bound values of R1 were greater than zero (Figure 2b), and donut method masked points were displaced far enough from their original locations to ensure an actual k value of at least the Min K level. As shown in Figure 2d, the minimum actual k value achieved with the donut method was 100 people. Compared with random perturbation, the donut method reduces risk to patient privacy by ensuring that all points achieve at least the user-defined Min K value.

Privacy protection performance

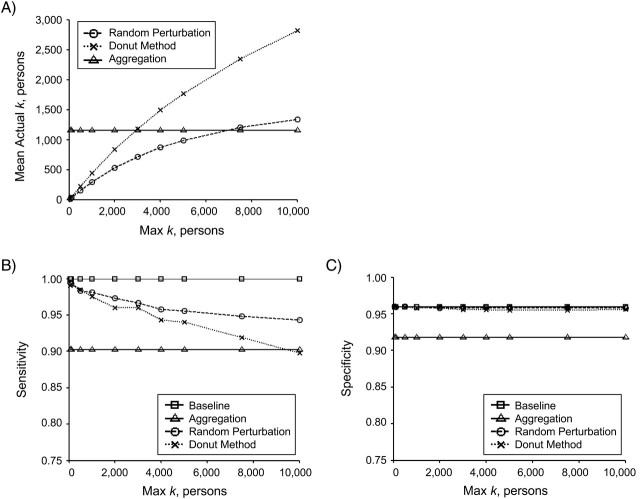
We examined random perturbation and donut method geomasking at 10 different Max K levels. As the Max K level increased, so did the outer radius R2, and thus the size, of the random perturbation and donut method geomasks around each point. Increasing geomask size increased the amount of error introduced into the data set, thereby raising the level of privacy protection. Figure 3a shows the mean actual k achieved by random perturbation, donut method, and aggregation geomasking, averaged across all disease field simulations, as a function of the Max K level. Because the distance displacements from aggregation are independent of the Max K level, the aggregation mean actual k value remains constant through the plot and serves as a benchmark against which to compare random perturbation and the donut method.

Figure 3.

Average A) actual k, B) sensitivity, and C) specificity for random perturbation and the donut method as a function of Max k. At all levels, the donut method, compared with random perturbation, achieved higher average k-anonymity. Regarding sensitivity, both random perturbation and the donut method performed worse than baseline (no geomasking) and better than aggregation, with no significant difference in specificity.

At all levels, the donut method mean actual k was greater than that of random perturbation, with the difference increasing as the Max K level increased. For Max K levels of less than 3,000 people, aggregation yielded a higher value than the donut method and random perturbation. However, for higher levels of Max K, the mean actual k of the donut method surpassed that of aggregation. In other words, the donut method provided a consistently higher level of patient privacy when compared with random perturbation. Compared with aggregation, the donut method performed worse at low levels of Max K, but, as Max K and the size of the geomask increased, the donut method provided increasingly higher levels of privacy protection that quickly outperformed the level achieved by aggregation.

Cluster detection performance

Increasing the amount of error introduced with greater privacy protection decreases cluster detection performance (13). Figure 3 also displays the average sensitivity (Figure 3b) and specificity (Figure 3c) from SaTScan analyses of the baseline, random perturbation masked, donut method masked, and aggregated disease fields as a function of the Max K level. Since the spatial distributions of points in the baseline and aggregated disease fields are independent of the Max K level, their sensitivity and specificity values are also independent of Max K and therefore are constant through the plots. Analyses of the baseline disease fields yielded the highest average values and serve as a benchmark against which to compare the geomasked data.

With respect to sensitivity (Figure 3b), random perturbation geomasking yielded values closest to the baseline results. Donut method sensitivity values were similar to random perturbation values at low levels of Max K, but they diverged as Max K increased, particularly at levels greater than 5,000 persons. However, at all but the greatest Max K level, both the donut method and random perturbation performed better than aggregation. Similarly, in terms of specificity (Figure 3c), both the donut method and random perturbation yielded values that were higher than aggregation at all levels and that closely matched the baseline results. As shown in Figure 3b, the sensitivity of the donut method and random perturbation were comparable and outperformed aggregation at Max K levels below 5,000 persons. At higher Max K levels, donut method cluster detection sensitivity declined at a faster rate and performed worse than that of random perturbation.

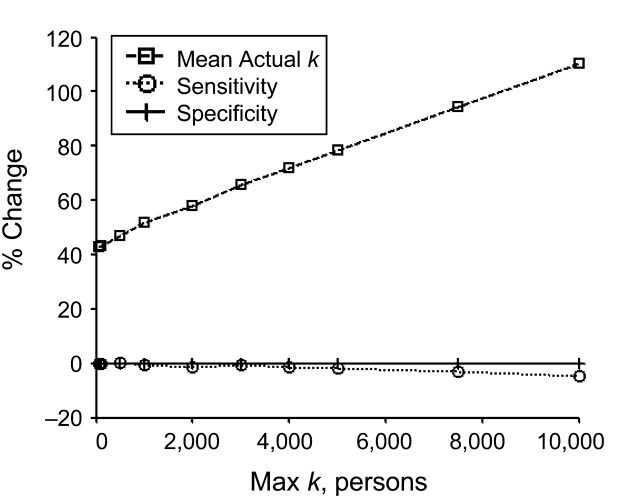
Although Figure 3 shows the relative performance of the geomasking methods, the magnitude of the difference between geomasks is difficult to assess because of differing units between plots. To further examine the relative trade-off between the donut method and random perturbation regarding measures of privacy protection and cluster detection, we plotted the percent change in mean actual k, sensitivity, and specificity values when using the donut method over random perturbation as a function of the Max K level (Figure 4). The percent change in mean actual k ranged from 42.7% to 110.5%. The percent change in sensitivity ranged from 0% to −4.8%; the percent change in specificity hovered around zero. These results show that, compared with random perturbation, the minimum percent increase in privacy protection with the donut method is approximately 9 times greater than the maximum decrease in cluster detection measures.

Figure 4.

Average percent change between random perturbation and donut method values as a function of Max k. The percent change in mean actual k was significantly higher and increased at a faster rate than that of sensitivity and specificity.

DISCUSSION

Aggregation is a commonly used geomasking method because of the magnitude of anonymization it provides. However, particularly for local phenomena that cross administrative boundaries, aggregation obscures spatial details needed for in-depth geographic analyses. In contrast, random perturbation masking allows access to health data at the geopoint level but may not sufficiently protect patient privacy. Suggested ways to improve random perturbation include using a normal random number generator to spread out the distance distribution, but these methods do not eliminate the possibility in random perturbation that a point may be placed on or near its original location. Other proposed methods, such as linear programming (25), require specific information, such as the locations of all possible patients, that is unavailable for most study areas.

In this simulation study, the donut method, a straightforward extension of current geomasking methods, provided a consistently higher level of privacy protection with a generally minimal decrease in cluster detection performance. The donut method was particularly valuable at low levels of k-anonymity where the risk to individual geoprivacy is greatest. As shown in Figures 1 and 2, the donut method relocated each case in the data set far enough from its original location to ensure at least a minimum level of anonymization. Furthermore, the donut method provides this minimum level of privacy protection without sacrificing analytical validity. Examination of actual k values below the 50th percentile shows that the donut method provided a clear advantage in privacy protection at lower percentiles while maintaining the same cluster detection sensitivity as random perturbation (Web Figure 2).

Another major advantage of the donut method is the ability to solicit user input in determining the minimum and maximum levels of privacy protection. Factors such as population density, endemic disease frequency, cluster size, and social stigma associated with the disease may influence the optimal level of anonymization. In addition, the donut method is able to incorporate suggested improvements for other point geomasks, such as using demographic characteristics of the underlying population to determine the privacy protection level. For example, in addition to population density, gender- and age-based adjustments may be used to determine the inner and outer radii of the donut to account for spatial variation in population distribution patterns (13). Additional research is needed to examine the optimal parameters of the donut method geomask in real-world settings.

We used simulated data to model the spatial pattern of real-world disease fields that may not completely reflect performance with actual data. For example, while the size and shape of real-world disease clusters are often irregular, we injected circular clusters into the simulated baseline disease fields. In these analyses, we used a circular SaTScan window, which maximized the likelihood that the unmasked cluster cases would be identified. Additional research will be required to investigate the performance of geomasks when applied to real-world data sets and examined with a variety of outbreak detection tools.

With increased use of geographic information systems, geocoded addresses offer new insights and opportunities for epidemiologic research and public health planning. However, unmodified geocoded addresses threaten the privacy and confidentiality of patients and research participants. As implemented for other forms of private health and personal identifying information, obscuring individuals' locational information is critical, yet often overlooked. The donut method presented here provides researchers and public health practitioners with a flexible technique that maximizes privacy protection with minimal loss of geographic resolution to accurately detect disease clusters.

To facilitate dissemination of the donut method, source code written for the MATLAB program (19) detailing our application of this method is available on the University of North Carolina (UNC)–BMElab Web page by accessing http://www.unc.edu/depts/case/BMElab/ and clicking on the “donutGeomask” link in the left-hand menu. Readers interested in other versions should contact the corresponding author.