Factor analysis model evaluation through likelihood cross-validation

Abstract

Medical research studies utilize survey instruments consisting of responses to multiple items combined into one or more scales. These studies can benefit from methods for evaluating those scales. Such an approach is presented for evaluating exploratory and confirmatory factor analysis models with decisions about covariance structure, including the number of factors, the factor extraction procedure, the allocation of survey items to summated scales and the extent of inter-scale dependence, made objectively using a likelihood-based form of cross-validation. This approach is demonstrated through example analyses using baseline data for three survey instruments from a clinical trial involving adolescents with type 1 diabetes.

1 Introduction

Medical research studies utilize survey instruments consisting of responses to multiple items combined into one or more scales. Such scales can be identified using exploratory factor analysis (EFA) or, when prior information on expected factor/scale structure is available, they can be validated using confirmatory factor analysis (CFA). The scales may be the factor scores, computed by summing appropriately weighted and possibly standardized items, or they may be summated scales, computed by summing unweighted and appropriately reverse coded marker items for the factors. These scales are used as measures of their underlying constructs, often in different contexts from those in which they were developed. An objective approach, based on likelihood cross-validation (LCV), is presented for evaluating how well scales perform with available data. This approach may also be applied in scale development, but is demonstrated in the context of assessing results for established scales.

2 Conducting factor analysis

In EFA, a choice is required for the number of factors. This is sometimes based on conventions like eigenvalues greater than 1 or eigenvalues accounting for over 5% or 10% individually, or over 70% or 80% jointly, of the total.¹ Scree plots with factors plotted in decreasing eigenvalue order are also sometimes used, selecting the number of factors appearing to separate factors with large versus small eigenvalues. It can also be based on penalized likelihood criteria like the Akaike information criterion (AIC) and the Schwarz Bayesian information criterion (BIC).²

Given a choice for the number of factors and for the factor extraction procedure, the associated loadings are usually rotated using one of several possible rotation schemes to assist in the identification of marker items associated with each factor, that is, those with strong loadings on one factor and weak loadings on the others. Conventional approaches are based on changing strong factor loadings, for example, in excess of 0.3 or 0.35³ or 0.4,¹ to unit loadings and others to zero loadings. If an item loads strongly on more than one factor, the usual convention is to discard it.¹ Discussions of this process do not always address the issue of strong, but negative, loadings. Items can be reverse coded prior to analysis based on theoretical considerations, as recommended by Hatcher¹ and discussed by DeVellis,⁴ but this only reduces the chance of strong, negative loadings. In general, the strength of a loading needs to be measured by its absolute value with the possibility that preconceptions about appropriate reverse coding might need modification based on the signs of factor loadings. In any case, however marker items are identified, they produce summated scales as alternatives to associated factor scores, computed by summing unweighted and possibly reverse coded marker items associated in disjoint sets with each of the factors.

While such comparisons of different factor loading adjustments are related to the EFA issue of interpretation of rotated factors, they are also similar to comparisons that can be addressed through CFA. The basic difference is that in EFA the comparison is between choices determined through data analytic methods, whereas in CFA the comparison is between choices determined through theoretical considerations based on prior research. Of course, when considering modifications of theory-based models with unacceptable fit, CFA becomes data-driven as well. EFA and CFA are not mutually exclusive. Any data set that is reasonably subjected to CFA can also be subjected to EFA with the resulting scales possibly included in confirmatory assessments.

For example, one possible scenario is that scales are available based on prior analysis of data collected in one context, and CFA is to be conducted to assess whether these existing scales also apply to a new set of data collected in some other context. The purpose is to confirm that the existing scales may be reasonably used within the new context, but if the opposite conclusion is reached, EFA can provide alternative data-based scales to apply to the new data as measures of the underlying constructs of the existing scales (or appropriately adjusted versions of those constructs). Moreover, EFA-generated scales provide a suitable benchmark on which to base the confirmation of existing scales. In other words, CFA can be conducted to assess how well the new data can be modeled using existing scales, not by themselves alone but compared to scales determined directly from those data by EFA. Users of established scales ought to address this applicability issue as a matter of standard procedure prior to using those scales in analyses addressing the specific aims of their studies. In any case, it seems prudent to supplement a CFA with an EFA applied to the same data and include EFA-generated scales along with theory-based scales in CFA comparisons.

One advantage of CFA over EFA is that it supports specification of the covariance structure for scales. EFA, on the other hand, supports independent factors in unrotated or orthogonally rotated form, or oblique rotated factors with unstructured covariance but no intermediate specifiable forms. CFA comparisons can be conducted using covariance structure models based on EFA-generated scales with adjustment to have specific inter-scale covariance structures. Such adjustments are similar to adjustments to factor loadings since both are just ways to perturb underlying covariance structure models within the factor analytic class. More general covariance structure models, for example, those based on path models between sets of latent and manifest variables, can also be subjected to such comparisons. These assessments can be conducted objectively using LCV.

3 Likelihood cross-validation

This section provides background information and formulation for a likelihood-based cross-validation approach for evaluating factor analysis models. This approach is used in the reported analyses of Section 5.

3.1 Background

Cross-validation is based on systematically deleting subsets of the data, called folds. Splitting or holdout is the simple case with the data split into two disjoint subsets, the training set used for parameter estimation and the holdout set, comprising a single fold, for prediction purposes. This approach has been used in the structural equation modeling (SEM) context.⁵ Only a portion of the data, the holdout set, is used for model evaluation. The training set needs to be large enough to obtain reliable parameter estimates, whereas the holdout set needs to be large enough to provide a dependable test of the model. The k-fold cross-validation approach,^6,7 on the other hand, uses k disjoint folds partitioning the data on some equitable basis. All observations are used in the model evaluation. The complements of each of the folds need to be large enough to obtain reliable parameter estimates. The folds, on the other hand, do not need to be large since they are all combined to generate an evaluation of the model. Splitting is an incomplete version of two-fold cross-validation. Leave-one-out (LOO) cross-validation is the most commonly used special case with each observation in its own fold.

Deletion of observations for reported cross-validation computations will be subject-wise, deleting complete vectors of item responses for subjects in folds. This approach has been used in multivariate contexts by Lee⁸ and Smyth.⁹ A more general item-within-subject deletion approach seems potentially beneficial, partitioning the set of all item values for all subjects into folds rather than just the set of subjects, but requires support for missing item values for subjects, a feature not provided by the factor analysis software used in example analyses. Krzanowski¹⁰ uses an intermediate deletion scheme in the principal components analysis context. This modified LOO cross-validation scheme deletes, for each subject–item pair, responses to all items for that subject and responses for all subjects to that item.

A cross-validation scheme also depends on how observations are allocated to folds. Random assignment of some kind is commonly used (except in the LOO case), but systematic approaches that depend on observed data values are feasible. The approach used for reported analyses assigns observations to a fold when uniform random-fold assignment variables take on values within the same one of k equal-sized subintervals of (0, 1).

Least squares cross-validation (LSCV) is a frequently used scoring approach, summing scores equal to squared (deleted) errors between observed values and their predictions computed from deleted parameter estimates. Likelihood cross-validation, on the other hand, scores observations by their likelihoods evaluated at deleted parameter estimates. LCV for the case of regression with univariate normal response and known constant variance is equivalent to LSCV, and so LCV generalizes LSCV to arbitrary distributions. LSCV is used in contexts other than regression. For example, Krzanowski¹⁰ uses a form of LSCV, adjusting for degrees of freedom, to choose the number of principal components. However, in the factor analysis setting, factor extraction via maximum-likelihood is a commonly used alternative to approaches based on principal components, treating observations as normally distributed with factor analytic covariance structure. LCV utilizes the full specification of this assumed covariance structure, whereas LSCV is based implicitly on a distinctly different context (univariate response with known constant variance).

Cross-validation is used in comparisons of multiple models to determine which is most compatible with the data and which other models have competitive scores. Whereas the model with the best LCV score within some family of models is a natural choice, models from that family with competitive scores may be attractive alternatives, especially if they have less complex structure. As an example, consider the issue of identifying an appropriate number of factors for a fixed set of observed item responses using a fixed factor extraction procedure like maximum-likelihood. Models corresponding to different choices for the number of factors can be evaluated by comparing their LCV scores to the best (maximum) LCV score over all such choices. The observed item responses are reasonably modeled using any number of factors for which the associated LCV score is not too much worse than (e.g., within 1% of) the best score. When smaller numbers of factors than the one with the best score generate scores close to the best score, they represent parsimonious, nearly optimal alternatives to the optimal choice.

3.2 Formulation

Let y_i denote the vector of d item responses for the ith subject out of n total subjects. Assume that these are realizations of a random vector y with mean vector μ and covariance matrix Σ sampled independently from the same population. The mean vector will be treated as an unknown constant as is common for factor analysis, but more general models with μ a function of explanatory variables are readily handled. Let S = {1, …, n} be the set of subject indexes, and denote the maximum-likelihood estimate of μ and Σ under a multivariate normal distribution with unstructured covariance matrix by μ̂(S) and Σ̂(S; UN), respectively. In other words, μ̂(S) is the average over the indexes in S of the n observed response vectors y_i and Σ̂(S; UN) is the average of the cross product matrices (y_i − μ̂(S)) · (y_i − μ̂(S))^T. For any other covariance structure model M, denote the corresponding maximum-likelihood estimate of Σ by Σ̂(S; M).

Denote by L(y; μ, Σ) the likelihood for y when it is treated as multivariate, normally distributed with mean vector μ and covariance matrix Σ. For any nonempty set S′ of indexes in S and any covariance structure model M, denote by μ̂(S′) the average of the response vectors y_i over the indexes i in S′ and by Σ̂(S′; M) the associated maximum likelihood estimates of Σ. Let S_h for 1 ≤ h ≤ k denote k folds that partition S into nonempty subsets with nonempty complements $S_h^{\text{c}}=S\backslash S_h$. Denote by S_h(i) the unique fold containing the index i. The contribution to the LCV score for the ith observation is given by

$${\text{LCV}}_i=L({\mathit{\text{y}}}_i;\widehat{\mathit{\text{μ}}}(S_{h(i)}^{\text{c}}),\widehat{\mathit{\text{∑}}}(S_{h(i)}^{\text{c}};M))$$ (1)

and so taking the log of Equation (1) gives the associated deleted log-likelihood term satisfying

$$log({\text{LCV}}_i)=-{({\mathit{\text{y}}}_i-\widehat{\mathit{\text{μ}}}(S_{h(i)}^{\text{c}}))}^{\text{T}}\cdot {\widehat{\mathit{\text{∑}}}}^{-1}(S_{h(i)}^{\text{c}};M)\cdot \frac{({\mathit{\text{y}}}_i-\widehat{\mathit{\text{μ}}}(S_{h(i)}^{\text{c}}))}{2}-\frac{log({(2\cdot \pi )}^d\cdot |\widehat{\mathit{\text{∑}}}(S_{h(i)}^{\text{c}};M)|)}{2}$$ (2)

Moreover, the terms (2) for the n_h observations of fold S_h sum to

$$log(\text{LCV}(S_h))=-n_h\cdot \frac{tr({\widehat{\mathit{\text{∑}}}}^{-1}(S_h^{\text{c}};M)\cdot (\widehat{\mathit{\text{∑}}}(S_h;\text{UN})+\mathit{\text{D}}(S_h)))}{2}-n_h\cdot \frac{log({(2\cdot \pi )}^d\cdot |\widehat{\mathit{\text{∑}}}(S_h^{\text{c}};M)|)}{2}$$ (3)

where

$$\mathit{\text{D}}(S_h)=(\widehat{\mathit{\text{μ}}}\text{(}{S}_h\text{)}-\widehat{\mathit{\text{μ}}}\text{(}{S}_h^{\text{c}}))\cdot {(\widehat{\mathit{\text{μ}}}\text{(}{S}_h)-\widehat{\mathit{\text{μ}}}\text{(}{S}_h^{\text{c}}))}^{\text{T}}$$

is the matrix of cross-products of differences between average item responses for fold S_h and its complement. Note that LCV(S_h) as defined by Equation (3) utilizes the sufficient statistics μ̂(S_h) and Σ̂(S_h; UN) for estimating the parameters of the multivariate normal distribution over fold S_h, providing a measure of how close the estimates $\widehat{\mathit{\text{μ}}}\text{(}{S}_h^{\text{c}})$ and $\widehat{\mathit{\text{∑}}}(S_h^{\text{c}};M)$ of those parameters determined by model M applied to the complement of the fold are to these sufficient statistics for the fold. The LCV score

$$\text{LCV}={\Pi }_{\{1\le h\le k\}}\text{LCV}{(S_h)}^{1/m}$$ (4)

is then obtained by combining these individual-fold closeness scores over all folds, where m = d · n is the total number of item responses for all subjects. It is sufficient just to multiply the individual-fold scores, but mth roots are taken in Equation (4) so that the LCV score is the geometric average deleted likelihood and its log is the average deleted log-likelihood over all item responses for all subjects. Models with larger LCV scores are better models with better predictive capability and more compatible with the available data as measured using deleted predictions determined by the fold assignment.

Any covariance matrix estimation procedure P, not just maximum-likelihood estimation, can be used to generate LCV scores by replacing the maximum-likelihood estimates Σ̂(S′; M) for subsets S′ of S by their corresponding estimates Σ̂(S′; M, P). This allows for assessment of the effect of using other factor extraction methods than maximum-likelihood. Non-normal multivariate distributions can also be used to compute LCV scores, for example, extensions to the multivariate normal distribution accounting for skew¹¹ or for kurtosis.¹²

In the case of EFA applied to the correlation matrix, the covariance matrix has the form Σ = V^1/2 · (Λ · Λ^T + Ψ) · V^1/2. V is the diagonal matrix of coordinate variances v_r for 1 ≤ r ≤ d. Λ is the d × f matrix of loadings λ_rs of the d standardized coordinate variables $z_r=(y_r-{\mu }_r)/v_r^{1/2}$ on the f > 0 latent common factors. These common factors are assumed to be independent with zero means and unit variances. Ψ is the diagonal matrix of variances for the unique factors, that is, the errors u_r for the standardized coordinate variables after accounting for their dependence on the common factors. The unique factors are independent of the common factors and of each other. Since R = Λ · Λ^T + Ψ is a correlation matrix, it has unit diagonal elements. The associated maximum-likelihood estimate Σ̂(S; FA(f)) for this model (with M = FA(f) for fixed f = 1, 2, …) is the analogous function of the maximum-likelihood estimators V̂(S; UN) (with the same diagonal elements as Σ̂(S; UN)), Λ̂(S; FA(f)) and Ψ̂(S; FA(f)) for V, Λ and Ψ, respectively. The special case with f = 0 common factors corresponds to independent items, that is, Σ = V.

The software tool we use for EFA is PROC FACTOR.¹³ The default option is to factor the correlation matrix. When factoring a covariance matrix, PROC FACTOR treats the problem like factoring a weighted correlation matrix. In any case, PROC FACTOR using factor extraction procedure P generates estimates Λ̂(S; FA(f), P) and Ψ̂(S; FA(f), P) for Λ and Ψ, respectively, which combine to produce an estimate of the correlation matrix given by

$$\widehat{\mathit{\text{R}}}(S;\text{FA}(f),\text{P})=\widehat{\mathit{\text{Λ}}}(S;\text{FA}(f),\text{P})\cdot \widehat{\mathit{\text{Λ}}}{(S;\text{FA}(f),P)}^{\text{T}}+\widehat{\mathit{\text{Ψ}}}(S;\text{FA}(f),P).$$

We then convert this to an estimate Σ̂(S; FA(f), P) of the covariance matrix by pre- and post-multiplying it by V̂^1/2 (S; UN). PROC FACTOR, though, uses the associated unbiased variance estimate 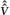(S; UN) of V.

The software tool we use for CFA is PROC CALIS.¹³ Since PROC CALIS and PROC FACTOR use different search algorithms, they can produce slightly different solutions for the same model which can then have slightly different LCV scores. PROC CALIS generates the maximum-likelihood estimate R̂(S; M) of the correlation matrix for a given model M along with an associated unbiased estimate 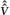(S; M) of the diagonal variance matrix V. We then compute the maximum-likelihood estimate Σ̂(S; M) of the covariance matrix by pre- and post-multiplying R̂(S; M) by V̂^1/2 (S; M), using the maximum-likelihood estimate V̂(S; M) = 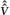(S; M) · (n − 1)/n.

4 Example data

Factor analysis model evaluation using LCV is demonstrated in Section 5 through analyses of baseline data froma clinical trial, the adolescents benefit from control (ABCs) of diabetes study.¹⁴ Three different survey instruments, completed by the adolescents in this study, are considered in reported analyses. All produce summated scales computed by adding up appropriately reverse coded item responses.

The children's depression inventory (CDI)¹⁵ was developed to measure depressive symptoms in children and adolescents. It has 27 items with range 0–2 and five sub-scales measuring different aspects of depression, that is, negative mood, interpretation problems, ineffectiveness, anhedonia and negative self-esteem. However, the total scale summing all 27 items, after reverse coding 13 of them, is commonly used by itself. Higher total CDI scores indicate higher levels of depressive symptoms.

The family adaptability and cohesion evaluation scale (FACES) II¹⁶ assesses family functioning through two scales measuring perception of levels of family adaptability and cohesion. Adaptability refers to the family's ability to alter its role relationships and power structure in response to situational and developmental stress, whereas cohesion describes the emotional bonding within a family. FACES has 30 items with range 1–5; 14 of these are summed, after reverse coding two of them, to obtain adaptability whereas the remaining 16 are summed, after reverse coding six of them, to obtain cohesion. Higher scores indicate higher levels of family adaptability and cohesion, respectively.

The diabetes quality of life for youth instrument (DQOLY)¹⁷ provides an assessment of children's and adolescents' perceptions of the impact of intensified diabetes regimens on their general satisfaction with life and on concerns over social, school and peer relationships related to having type 1 diabetes. It has 51 items with range 1–5 used to produce three scales measuring perception of three aspects of the quality of life. The impact of diabetes scale is based on 23 items, the worry scale on 11 other items, and the satisfaction scale on the remaining 17 items. Higher quality of life corresponds to lower impact and worry scores and higher satisfaction scores. One item from the impact scale is reverse coded and none from the other scales, but satisfaction has the reverse orientation to the other scales.

Baseline data for 103 ABC subjects without any missing values for any items of the three instruments are analyzed in Section 5, without prior reverse coding of any items. These analyses are conducted using SAS macros that have been developed to provide general support for factor analysis model evaluation using LCV (Section 5.9).

5 Example analyses

Example analyses are presented in this section using the data described in Section 4. LCV scoring as defined in Section 3.2 is used to evaluate factor analysis models for these data. Sections 5.1–5.4 address issues related to conducting an EFA and generating associated summated scales. Sections 5.5–5.7 address issues related to confirming the appropriateness of recommended scales for the ABC data. Section 5.8 addresses item residual analyses for assessing the normality assumption, and Section 5.9 provides an overview of the SAS macros developed for evaluating EFA and CFA models through LCV.

5.1 LCV with maximum-likelihood factor extraction

Table 1 reports numbers of factors chosen for the three sets of ABC item responses through maximizing LCV scores using various choices for the number of folds. In each case, a simple grid search was performed over the choices of 0–10 factors, with factors extracted using maximum-likelihood. The recommended number of factors (1 for CDI, 2 for FACES, 3 for DQOLY) is chosen in all cases except one (DQOLY with five folds). This indicates that recommended numbers of scales for these instruments are reasonable choices for the ABC data, providing evidence of the applicability of the associated scales to those data. This also suggests that there is unlikely to be an impact to the choice for the number of folds as long as it is not too small.

Table 1.

Numbers of factors chosen through LCV for varying numbers of folds

No. of foldsa	No. of factorsb			% reduction in LCVc
	CDI	FACES	DQOLY	CDI	FACES	DQOLY
5	1	2	2	1.57	0.67	1.93
10	1	2	3	0.00	0.25	0.74
15	1	2	3	0.45	0.30	0.30
20	1	2	3	0.46	0.28	0.34
25	1	2	3	0.87	0.25	0.28
30	1	2	3	0.59	0.19	0.26
35	1	2	3	1.02	0.41	0.06
50	1	2	3	0.84	0.15	0.33
75	1	2	3	0.89	0.19	0.07
100	1	2	3	0.69	0.12	0.15
LOOd	1	2	3	0.82	0.00	0.00

^aWith observations assigned to one of the k folds when the associated random numbers fall within each of the k equal sized subintervals of (0, 1) except for the LOO case.

^bThe choice with the best LCV score for a fixed number of folds considering 0–10 factors chosen through maximum-likelihood factor extraction.

^cThe percent reduction relative to the best LCV score over all choices for the number of folds, that is, 0.52092 for CDI with 10 folds, 0.24306 for FACES with LOO and 0.25393 for DQOLY with LOO.

^dLOO = leave-one-out, with each observation in a separate fold.

Table 1 also reports, for each set of items, percent reductions in LCV scores from the best score. The choice of 10 folds (as recommended in a different context by Kohavi⁷) provides a competitive score within 1% of the best overall score for all the three sets of items. However, increasingly larger numbers of folds will likely be needed to obtain competitive scores for increasingly larger sample sizes and/or numbers of items. One possibility suggested by the results presented in Table 1 is to use the first local maximum. For each of the three sets of items, the first local maximum generates a highly competitive score within 0.5% of the associated overall maximum. The subsequent local maxima can generate better scores, but the increase is unlikely to be substantial enough to justify the extra computational effort. Following this guideline, subsequent analyses use 10 folds for CDI and FACES and 15 folds for DQOLY.

Using these specific numbers of folds, the independent items model generates percent reductions of 6.28%, 10.80% and 10.24% for CDI, FACES and DQOLY, respectively, compared to 22.48%, 13.16% and 39.76% for the unstructured covariance model. Independence appears to be too simple, whereas unstructured covariance appears to be consistently worse and often much worse. Factor analysis models with a few factors seem to provide a nice balance between the simplicity of independence and the complexity of unstructured covariance.

5.2 Alternate criteria and factor extraction procedures

A variety of informal conventions and penalized likelihood criteria have been recommended for choosing the number of factors. Those factors may be extracted using a variety of procedures. Johnson and Wichern¹⁸ consider maximum-likelihood and principal component extraction as the procedures having the ‘most to recommend them’ (p. 411). They also discuss the principal factor procedure. PROC FACTOR supports a one-step version of this procedure as well as an iterated version, also called principal axis factoring, which may be the most frequently used in practice.¹⁹ These three procedures seem the most fundamental for use in choosing the number of factors.

Table 2 contains numbers of factors chosen for the three sets of ABC items through a variety of criteria and extracted using these three fundamental procedures (using the one-step version of the principal factor procedure). The recommended number of scales provides a benchmark for assessing the performance of these different ways to choose the number of factors. Only the LCV approach generates the same number of factors as recommended for each of the three sets of items. One other approach, minimizing BIC, generates results somewhat consistent with these recommended numbers, suggesting that it might provide in practice a competitive choice for the number of factors. All other approaches, including the popular eigenvalue greater than 1 convention and minimizing AIC, are ineffective, usually producing larger numbers of factors than recommended, and often much larger. The results presented in Table 2 also indicate that the same informal convention applied with a different factor extraction procedure can produce quite different choices for the number of factors.

Table 2.

Numbers of factors chosen through various selection criteria

Criterion	Number of factors
	CDI	FACES	DQOLY
Recommended no.	1	2	3
Maximum-likelihood extraction
Smallest no. with P-value > 0.05 for test that no. of factors is sufficient	5	8	13
Minimum AIC	5	9	9
Minimum BIC	1	2	2
Maximum LCVa	1	2	3
Principal component extractionb
Largest no. with eigenvalue > 1	10	8	15
Largest no. with % of total eigenvalue > 5%	5	4	3
Largest no. with % of total eigenvalue > 10%	1	1	2
Smallest no. with cumulative % of total eigenvalue > 70%	10	10	14
Smallest no. with cumulative % of total eigenvalue > 80%	14	14	8
One-step principal factor extractionb
Largest no. with eigenvalue > 1	4	4	11
Largest no. with % of total eigenvalue > 5%	6	6	4
Largest no. with % of total eigenvalue > 10%	4	2	2
Smallest no. with cumulative % of total eigenvalue > 70%	4	4	8
Smallest no. with cumulative % of total eigenvalue > 80%	5	5	11

^aUsing 10 folds for CDI and FACES and 15 folds for DQOLY.

^bApplied to the correlation matrix.

PROC FACTOR also supports other factor extraction procedures including the alpha factor, Harris component, image component and unweighted least squares procedures.¹³ Iterated principal factor extraction can be started from either principal component (the default) or one-step principal factor extraction; we start with the default, but this has little effect on the final solution. Factor analysis is ordinarily applied to the correlation matrix¹⁸ and this is the default option for PROC FACTOR, but is also sometimes applied to the covariance matrix instead. This has no effect on maximum-likelihood extraction due to the invariance property of maximum-likelihood estimation but can have an effect on other extraction procedures. Alpha factor and Harris component extraction, though, can only be applied to the correlation matrix. LCV can be used to compare all these extraction procedures applied to either type of matrix, although its formulation favors maximum-likelihood extraction.

Table 3 contains numbers of factors chosen for the three sets of ABC items through maximizing LCV under alternative factor extraction procedures. The alpha factor extraction procedure is the one procedure supported by PROC FACTOR not included in Table 3 since it does not always converge (e.g., for 1–3 factors, LCV scores can only be computed for 3 factors with CDI items, 2–3 factors with FACES items and 3 factors with DQOLY items). In contrast, all other extraction procedures converge for 1–10 factors with all the three sets of items. All these procedures generate nearly the same LCV scores, all within 1% of the best overall score for each instrument. Moreover, recommended choices for the number of factors are selected in all cases. These results indicate that there is little difference between factor extraction procedures for these three sets of item responses and suggest that this may also hold in general. The uniformity in the choice of the number of factors across all procedures is a consequence of adapting the number of folds to the items under analysis. If 10 folds are used for DQOLY, half of the procedures choose 2 factors and the rest 3 factors, but scores for 3 factors are always within 1% of the best overall score. Note further that, even though the LCV formulation favors maximum-likelihood extraction, other extraction procedures can have competitive LCV scores and even slightly better scores (as for unweighted least squares and iterated principal factor extraction with CDI items).

Table 3.

Number of factors with maximal LCV^a under various factor extraction procedures

Factor extraction procedure	Number of factors (% reduction in LCVb)
	CDI	FACES	DQOLY
Maximum-likelihood	1 (0.12)	2 (0.00)	3 (0.00)
Harris component	1 (0.28)	2 (0.21)	3 (0.36)
Applied to correlation matrix
Principal component	1 (0.26)	2 (0.71)	3 (0.66)
One-step principal factor	1 (0.12)	2 (0.25)	3 (0.38)
Iterated principal factor	1 (0.03)	2 (0.14)	3 (0.06)
Image component	1 (0.40)	2 (0.76)	3 (0.68)
Unweighted least squares	1 (0.03)	2 (0.14)	3 (0.06)
Applied to covariance matrix
Principal component	1 (0.17)	2 (0.72)	3 (0.57)
One-step principal factor	1 (0.04)	2 (0.25)	3 (0.28)
Iterated principal factor	1 (0.00)	2 (0.16)	3 (0.05)
Image component	1 (0.31)	2 (0.75)	3 (0.61)
Unweighted least squares	1 (0.00)	2 (0.24)	3 (0.14)

^aUsing 10 folds for CDI and FACES and 15 folds for DQOLY.

^bThe best LCV scores are 0.52152 for CDI under unweighted least squares or iterated principal factor, both applied to the covariance matrix, 0.24245 for FACES under maximum-likelihood and 0.25317 for DQOLY under maximum likelihood.

5.3 Reverse coding

CDI consists of a single scale with 13 of its items reverse coded. These are exactly the items with negative factor loadings when one factor is extracted (using maximum-likelihood throughout this section) from the CDI item responses of the ABC data.

FACES consists of two scales with eight of its 30 items reverse coded. When two factors are extracted, only three items have maximum unrotated absolute loadings generated by negative loadings including only two of the eight items that are supposed to be reverse coded and another, item 12, that is not supposed to be reverse coded. When these factors are varimax rotated, the maximum absolute loading is generated by a negative loading in only one case, item 12 again (Table 4 and the associated discussion in Section 5.4). On the other hand, if only one factor is extracted, all eight of the items that are supposed to be reverse coded have negative loadings plus one more, item 12 again.

Table 4.

Varimax rotated factor loadings and item–scale allocations for FACES items

Item	Factor loadings		Item–scale allocationsa
	1	2	Standard	>0.30	>0.35	>0.40	>0
1	0.64503	−0.27421	Cohesion	1	1	1	1
2	0.47538	−0.35285	Adaptability	–	–	1	1
3	−0.01366	0.59069	Cohesionb	2	2	2	2
4	0.33462	−0.23034	Adaptability	1	–	–	1
5	0.43355	−0.27192	Cohesion	1	1	1	1
6	0.39248	0.01834	Adaptability	1	1	–	1
7	0.55661	−0.32226	Cohesion	–	1	1	1
8	0.64686	−0.41541	Adaptability	–	–	–	1
9	−0.14408	0.36423	Cohesionb	2	2	–	2
10	0.51768	0.23001	Adaptability	1	1	1	1
11	0.34744	−0.11259	Cohesion	1	–	–	1
12	−0.24736	0.19594	Adaptability	–	–	–	1c
13	0.32858	−0.00391	Cohesion	1	–	–	1
14	0.25503	0.12260	Adaptability	–	–	–	1
15	0.04067	0.47832	Cohesionb	2	2	2	2
16	0.66894	−0.09130	Adaptability	1	1	1	1
17	0.49873	−0.39283	Cohesion	–	–	1	1
18	0.74188	−0.09633	Adaptability	1	1	1	1
19	−0.14649	0.67138	Cohesionb	2	2	2	2
20	0.55461	−0.12604	Adaptability	1	1	1	1
21	0.53772	−0.15560	Cohesion	1	1	1	1
22	0.62272	−0.22104	Adaptability	1	1	1	1
23	0.51443	−0.43999	Cohesion	–	–	–	1
24	−0.12205	0.36283	Adaptabilityb	2	2	–	2
25	−0.13417	0.79168	Cohesionb	2	2	2	2
26	0.68833	−0.25879	Adaptability	1	1	1	1
27	0.47736	−0.15510	Cohesion	1	1	1	1
28	−0.02356	0.36986	Adaptabilityb	2	2	–	2
29	−0.22977	0.53643	Cohesionb	2	2	2	2
30	0.66117	−0.14169	Cohesion	1	1	1	1

^aFor all but the standard allocation, allocate items to scales depending on which factor has the maximum absolute loading, dropping items (indicated by a dash ‘–’) if the maximum absolute loading does not exceed the cutoff or if both absolute loadings exceed the cutoff. The loading for the factor with the highest maximum absolute value is in boldface.

^bItems reverse coded in standard FACES scale computations.

^cMaximum absolute loading occurs for a negative loading.

These results for the FACES items indicate that the signs of loadings for multiple factors, whether unrotated or rotated, are unlikely to provide satisfactory evidence about appropriate reverse coding (although the examples of Section 5.4 suggest that rotation seems to separate items that require reverse coding from those that do not). However, they also suggest that signs for loadings on a single factor (for which rotation is a moot issue) can be used to determine reverse coding, even when more than one factor is appropriate for the data. This situation also holds for DQOLY. It has three recommended scales with only one item reverse coded but the satisfaction scale has the reverse orientation to the other two scales. When only one factor is extracted, the DQOLY items with negative loadings include all 17 of the satisfaction items plus the one other item (7) that is supposed to be reverse coded.

These results suggest that a reasonable way to decide which items need reverse coding (besides any such adjustments performed prior to factor analysis) is to choose the ones with negative loadings for the single factor case. Furthermore, the close consistency of the results of such an analysis for the ABC data and the recommended reverse coding adds to the evidence of the applicability of these three sets of scales to those data. The only exception, FACES item 12, is stated as ‘it is hard to know what the rules are in our family’ and is used in computing family adaptability. In the standard FACES formulation, families are considered to become more adaptable as their rules become more vaguely defined. The results for the ABC data suggest the alternate possibility that families having an adolescent with diabetes might be more adaptable when they have more precisely defined rules, which could provide flexibility to adapt in ways that do not violate those rules. However, such a conclusion needs confirmation through analyses of data for other families of this kind.

5.4 Item–scale allocation

Informal conventions are commonly used to identify marker items for summated scales, usually after rotation. PROC FACTOR supports a variety of orthogonal rotation schemes, for example, equamax, parsimax, quartimax and varimax rotation, as well as oblique rotation schemes, for example, Harris–Kaiser rotation and promax rotation starting from any of the orthogonal rotations or from a Harris–Kaiser rotation.¹³ Varimax rotation is recognized as the most commonly used type of orthogonal rotation scheme.^1,19 The actual choice though is up to the scale developer's personal preference, and so it is of interest to assess the effect, if any, of the rotation scheme on item–scale allocation. The above 10 example rotation schemes are considered in reported analyses. Only maximum-likelihood extraction is used, but the results presented in Table 3 suggest that the conclusions would not be affected much by consideration of other factor extraction procedures. CDI has only 1 factor with all its items allocated to 1 scale, and so item–scale allocation is only an issue for FACES and DQOLY.

Varimax rotated factor loadings for FACES items are displayed in Table 4 to examine the impact of conventions for assigning items to summated scales. Only one item, item 12, has its maximum absolute loading generated by a negative loading but this maximum absolute loading is less than 0.3, the smallest commonly recommended cutoff for discarding an item. This item and item 14 are the only ones with maximum absolute loading below this cutoff, indicating that some FACES items may contribute negligible information about underlying factors for the ABC data. Furthermore, there are five more items with both absolute loadings higher than 0.3, which by another convention indicates they should also be discarded and not used in generated summated scales. If a cutoff of 0.4 is used instead, only two items (8 and 23) load more strongly than this on both factors, but nine other items have maximum absolute loadings less than the cutoff and should be discarded as well. Intermediate results are produced by a cutoff of 0.35. Similar results hold for the varimax rotated loadings of DQOLY (Table 5), except that no maximum absolute loading corresponds to a negative loading.

Table 5.

Varimax rotated factor loadings and item–scale allocations for DQOLY items

Item	Factor loadings			Item–scale allocationsa
	1	2	3	Standard	>0.30	>0.35	>0.40	>0
1	−0.07342	0.48473	0.20552	Impact	2	2	2	2
2	0.01073	0.51509	0.28943	Impact	2	2	2	2
3	−0.11955	0.53906	0.15484	Impact	2	2	2	2
4	0.05436	0.58053	0.03494	Impact	2	2	2	2
5	−0.02367	0.49108	0.05617	Impact	2	2	2	2
6	−0.04404	0.58213	0.18326	Impact	2	2	2	2
7	0.28137	−0.17069	−0.27210	Impactb	–	–	–	1
8	−0.04298	0.37755	0.08818	Impact	2	2	–	2
9	−0.13659	0.36454	0.11906	Impact	2	2	–	2
10	−0.17217	0.52483	0.02458	Impact	2	2	2	2
11	−0.09942	0.41191	−0.02948	Impact	2	2	2	2
12	0.10994	0.30868	0.13813	Impact	2	–	–	2
13	−0.15365	0.51997	0.18643	Impact	2	2	2	2
14	−0.05307	0.32793	0.02442	Impact	2	–	–	2
15	−0.11588	0.28625	0.25836	Impact	–	–	–	2
16	−0.13469	0.25410	0.21982	Impact	–	–	–	2
17	−0.18990	0.34076	0.28553	Impact	2	–	–	2
18	−0.13467	0.44469	0.06114	Impact	2	2	2	2
19	−0.17097	0.36199	0.00503	Impact	2	2	–	2
20	−0.16068	0.47077	0.11254	Impact	2	2	2	2
21	0.03129	0.47531	0.24921	Impact	2	2	2	2
22	0.05933	0.43363	0.27344	Impact	2	2	2	2
23	0.13291	0.43252	0.13551	Impact	2	2	2	2
24	−0.00969	0.04656	0.92476	Worry	3	3	3	3
25	−0.02317	0.03855	0.80693	Worry	3	3	3	3
26	−0.09245	0.21553	0.45821	Worry	3	3	3	3
27	−0.01265	0.28615	0.46838	Worry	3	3	3	3
28	0.04957	0.09158	0.44242	Worry	3	3	3	3
29	−0.17572	0.21024	0.53897	Worry	3	3	3	3
30	−0.02069	0.25439	0.54210	Worry	3	3	3	3
31	−0.24682	0.32205	0.14868	Worry	2	–	–	2
32	−0.10480	0.49604	−0.05264	Worry	2	2	2	2
33	−0.03324	0.47697	0.23190	Worry	2	2	2	2
34	−0.17260	0.57946	0.35469	Worry	–	–	2	2
35	0.54794	−0.28430	0.00232	Satisfaction	1	1	1	1
36	0.39953	−0.22385	−0.07395	Satisfaction	1	1	–	1
37	0.62011	−0.12980	0.04812	Satisfaction	1	1	1	1
38	0.66689	−0.07818	0.07689	Satisfaction	1	1	1	1
39	0.47624	−0.14221	0.00355	Satisfaction	1	1	1	1
40	0.47266	−0.33544	−0.04736	Satisfaction	–	1	1	1
41	0.63984	0.18462	0.15136	Satisfaction	1	1	1	1
42	0.67354	−0.15478	−0.08360	Satisfaction	1	1	1	1
43	0.78270	0.01059	−0.03968	Satisfaction	1	1	1	1
44	0.69324	−0.00247	−0.08781	Satisfaction	1	1	1	1
45	0.64731	−0.17999	−0.29907	Satisfaction	1	1	1	1
46	0.61370	−0.01280	−0.14619	Satisfaction	1	1	1	1
47	0.69647	−0.13853	−0.07435	Satisfaction	1	1	1	1
48	0.81646	0.01330	−0.08607	Satisfaction	1	1	1	1
49	0.61162	0.08599	0.07538	Satisfaction	1	1	1	1
50	0.71589	−0.06499	−0.10234	Satisfaction	1	1	1	1
51	0.59565	−0.13019	−0.09928	Satisfaction	1	1	1	1

^aFor all but the standard allocation, allocate items to scales depending on which factor has the maximum absolute loading, dropping items (indicated by a dash ‘–’) if the maximum absolute loading does not exceed the cutoff or if two of more absolute loadings exceed the cutoff. The loading for the factor with the highest maximum absolute value is in boldface.

^bItem reverse coded in standard DQOLY scale computations.

These item reduction conventions seem to indicate that substantial numbers of FACES and DQOLY items could be discarded from the ABC data. These are established scales, though, and so it does not seem appropriate to discard their items; item reduction has already taken place as a part of scale development. However, if the item reduction process can discount substantial numbers of items from established scales, it is quite possible that it can also discount valuable items when used as a part of scale development. An objective assessment of the impact of removing items during scale development seems important to guarantee that a substantial amount of information is not lost (Section 5.7).

For evaluation of established scales, approaches that use all items seem more appropriate. So consider the item–scale allocation that associates each item with the factor for which it has the highest absolute loading (assuming the highly likely situation that there is only one such factor for each item). Then assign it a unit loading with the same sign as its original loading on that factor and zero loadings on all other factors. This produces the allocation in the last column of Table 4 with 22 FACES items assigned to scale 1 and the remaining eight items to scale 2. Varimax allocation assigns all recommended reverse coded items to scale 2 and no others (and so there is no need to reverse code them) as well as all the other items, with item 12 reverse coded, to scale 1. Varimax rotation thus comes close to separating the items into two subsets with reverse orientations. The results would be equivalent if the items had been reverse coded before factor analyzing them since this would only change the signs of the loadings in Table 4. All other rotation schemes (Table 6) produce the same allocation as varimax rotation. Only unrotated factor loadings produce a different allocation, a much different one with three items (9, 24, 29) shifted from scale 2 to scale 1 and reverse coded and two items (10, 14) shifted from scale 1 to scale 2 with unchanged orientation.

Table 6.

Item–scale allocations

Allocation basis	Scale
	1	2	3
FACES
Recommendeda
+1	1,5,7,11,13,17,21,23,27,30	2,4,6,8,10,12,14,16,18,20,22,26
−1	3,9,15,19,25,29	24,28
Varimaxb
+1	1,2,4–8,10,11,13,14,16–18,20–23,26,27,30	3,9,15,19,24,25,28,29
−1	12
Unrotated
+1	1,2,4–8,11,13,16–18,20–23,26,27,30	3,10,14,15,19,25,28
−1	9,12,24,29
DQOLY
Recommendedc
+1	1–6,8–23	24–34	35–51
−1	7
Varimaxd
+1	1–6,8–23,31–34	24–30	7,35–51
−1
Equamaxe
+1	1–6,8–14,18–23,31–34	15–17,24–30	35–51
−1		7
Quartimax
+1	1–6,8–23,27,31–34	24–26,28–30	7,35–51
−1
Promax started from equamax
+1	1–6,8–14,16–23,31–34	15,24–30	7,35–51
−1
Unrotated
+1	4–6,8,10,11,14,23,32	12,21,22,24,25,27,28,30,41,49	1–3,9,13,15–20,26,29,31,33,34
−1			7,35–40,42–48,50,51

^aScales 1–2 are the cohesion and adaptability scales, respectively.

^bAlso generated by equamax, parsimax, quartimax, Harris–Kaiser and promax starting from equamax, parsimax, quartimax, varimax or Harris–Kaiser.

^cScales 1–3 are the disease impact, worry, and satisfaction scales respectively.

^dAlso generated by Harris–Kaiser and promax starting from quartimax, varimax, or Harris–Kaiser.

^eAlso generated by parsimax and promax starting from parsimax.

Table 5 contains item–scale allocations based on varimax rotation for the DQOLY item responses from the ABC data. The last column contains allocations without deletion. Scale 3 is assigned all 17 satisfaction items plus the one item, item 7 from the impact scale, usually recommended for reverse coding. Thus, scale 3 is essentially a satisfaction scale but also consists of all the DQOLY items with recommended reverse orientation. Scale 2 consists of the first seven of the 11 worry scale items and so is a partial worry scale. Scale 1 consists of all the impact items except item 7 plus the remaining four worry items and so is primarily an impact scale augmented with aspects of the original worry scale. The other rotation schemes (Table 6) generate three other distinct allocations, but with small adjustments, shifting the allocation of items 7 and 15–17 in one case, only item 27 in another and only item 15 in the third. Items usually reverse coded are either assigned together or else are given negative unit loadings when combined with items usually not reverse coded. Unrotated factor loadings on the other hand produce a much different allocation.

Rotation results (except for no rotation) provide subjective evidence of reasonable applicability of recommended DQOLY scales to the ABC data since only small adjustments from recommended allocations are produced. On the other hand, results for these rotations applied to FACES, while the same for all rotations, are quite different from the recommended allocation. However, these alternate allocations might not result in substantial predictive differences. To address this issue requires objective assessment of rotation results, but rotations do not change the underlying covariance structure and so cannot be compared directly using LCV. However, rotations suggest changes in factor loadings to values of 0 and ±1 which produce changes to the covariance structure, and so these adjustments can be evaluated by LCV. In this way, rotations can be evaluated using LCV scores for models based on the item–scale allocations they suggest. This issue is addressed using CFA in Section 5.5.

These rotation results also indicate that the choice of rotation scheme may have at most a small impact on generated scales. For the 2 factor case (using FACES items), all rotations generate exactly the same item–scale allocations. For the 3 factor case (using DQOLY items), four different allocations are generated by the 10 different rotation schemes, but these are not too different from each other. In both cases, though, there are distinct differences between using and not using a rotation with no rotation producing allocations much different from recommended allocations. This suggests a likely advantage to basing summated scales on rotated, instead of unrotated, factor loadings. On the other hand, rotations tend to separate items into groups with the same orientation (in which case reverse coding is irrelevant).

5.5 Factor loading adjustments

To compare alternative factor loading adjustments for the three sets of ABC items (Table 7), associated CFA models will be generated with all their unique factors independent of each other and independent of all common factors. The impact of estimating covariances for the unique factors could be addressed with LCV but will not be for brevity. Alternative covariance structures for the common factors will be considered, though.

Table 7.

Assessment of alternate scales

Scales	% reduction in LCV from best
CDI (one scale)a
EFA, estimated loadings	0.00
Recommended, usual unit loadings	0.80
FACES (two scales)b
EFA, independent scales, estimated loadings	0.21
EFA, dependent scales, estimated loadings	0.21
Varimax rotated, independent scales, unit loadings	1.75
Varimax rotated, dependent scales, unit loadings	1.18
Varimax rotated, dependent scales, estimated loadings	0.00
Unrotated, independent scales, unit loadings	2.90
Unrotated, dependent scales, unit loadings	2.43
Unrotated, dependent scales, estimated loadings	0.64
Recommended, independent scales, usual unit loadings	5.61
Recommended, dependent scales
Usual unit loadings	3.52
Item 12 also reverse coded	2.75
Estimated loadings	1.20
DQOLY (three scales)c
EFA, independent scales, estimated loadings	0.93
EFA, dependent scales, estimated loadings	0.93
Varimax rotated, independent scales, unit loadings	0.94
Varimax rotated, dependent scales, unit loadings
One estimated correlation
Factors 1–2 dependent	0.56
Factors 1–3 dependent	0.75
Factors 2–3 dependent	0.94
Two estimated correlations
Factors 1–2 independent	0.77
Factors 1–3 independent	0.58
Factors 2–3 independent	0.68
Three estimated correlations	0.40
Varimax rotated, dependent scales, estimated loadings	0.00
Equamax rotated, independent scales, unit loadings	1.15
Equamax rotated, dependent scales, unit loadings	0.45
Equamax rotated, dependent scales, estimated loadings	0.13
Quarimax rotated, independent scales, unit loadings	1.05
Quarimax rotated, dependent scales, unit loadings	0.54
Quartimax rotated, dependent scales, estimated loadings	0.10
Promax rotated from equamax, independent scales, unit loadings	1.06
Promax rotated from equamax, dependent scales	0.49
Unit loadings
Estimated loadings	0.04
Unrotated, independent scales, unit loadings	5.63
Unrotated, dependent scales, unit loadings	4.68
Unrotated, dependent scales, estimated loadings	3.89
Recommended, independent scales, usual unit loadings	1.94
Recommended, dependent scales, usual unit loadings	1.03
Recommended, dependent scales, estimated loadings	0.83

^aThe best LCV score using 10 folds is 0.52092 for EFA.

^bThe best LCV score using 10 folds is 0.24297 for varimax rotation with loadings and interfactor correlation estimated.

^cThe best LCV score using 15 folds is 0.25556 for varimax rotation with loadings and all inter-factor correlations estimated.

The use of a single scale is the appropriate choice for CDI. The summated scale with recommended reverse coding (same as that suggested by the EFA factor loadings) is a nearly optimal choice (within 1% of the best overall score) for the CDI items of the ABC data, whereas the factor analysis model has the better score.

For FACES, the best overall model is generated by the scales based on a varimax rotation of the 2 factor EFA model but with estimated rather than unit loadings together with estimated inter-scale correlation. Thus, EFA models with all items loading on all factors can be improved by assigning items to factors in disjoint sets, as long as dependence between the factors is also accounted for. However, the EFA model is nearly optimal and outperforms the varimax-based summated scales (with unit loadings instead of estimated loadings). The scales based on unrotated factors are distinctly noncompetitive, unless loadings and the inter-scale correlation are estimated. Treating scales as correlated is a consistently better alternative to treating them as independent, except for EFA models for which there is no difference. Consideration of dependent factors adds nothing to an EFA model since item dependence is accounted for by treating all items as loading on all factors. On the other hand, since summated scale scores measure related aspects for the same subject, they are likely to be correlated, and so it seems more appropriate to treat them as dependent rather than as independent.

The recommended FACES summated scales are not competitive, even when treated as dependent. Reverse coding item 12 as well provides a beneficial effect, but the recommended scales are still tangibly worse than the best model (with more than a 2% decrease). Alternately, recommended scales can be improved to a competitive level (within 2% of best) by estimating loadings and the inter-scale correlation. However, the varimax-based summated scales are nearly optimal when their inter-scale correlation is estimated, and so seem preferable to the recommended scales for the ABC data. On the other hand, they represent latent constructs that are only related to, but not the same as, family adaptability and cohesion as represented by the recommended summated scales. Thus, scores for the varimax-based summated scales should not be directly compared to family adaptability and cohesion scores from other studies. Also, it seems prudent to repeat any analyses conducted using the varimax-based summated scales, replacing them by the recommended summated scales to assess the impact of that choice on the results.

For DQOLY, the best overall model is once again generated by the scales based on a varimax rotation of the EFA model with loadings and inter-scale correlations estimated. If any or all of the inter-scale correlations are set to zero, these scales still provide a nearly optimal alternative. The EFA model is also nearly optimal. Other rotation schemes can suggest alternate summated scales, but these all provide nearly optimal choices as long as scales are treated as dependent. On the other hand, scales based on unrotated factors are not competitive even with estimated loadings and inter-scale correlations. The recommended summated scales are competitive alternatives, improve with estimated inter-scale correlations, and become nearly optimal with loadings estimated as well.

5.6 Realignment of items to scales

The results presented in Table 7 indicate that varimax-based scales have the potential for providing a nearly optimal item–scale allocation as long as loadings and inter-scale correlations are estimated. This may be further assessed by searching for an improved item–scale allocation, realigning each item one at a time from its currently allocated scale to each of the other scales. The use of estimated versus unit loadings for this search has the advantage of not needing to decide appropriate reverse coding for realigned items. This search would continue as long as the score improves and when it stops, summated scales can be determined from signs of loadings for the final allocation generated by the search.

This item realignment process applied to the FACES items produces no improvements to the two varimax-based scales. Percent reductions in LCV scores range from 0.02% for the least important item (14) to 1.44% for the most important item (18). For DQOLY, only one realignment of the varimax-based scales generates an improvement. A negligible 0.01% improvement is produced by switching item 7 from scale 3 to scale 1, making its allocation more consistent with its recommended allocation. After making this switch, no further realignments produce improvements. These results suggest that varimax item–scale allocations are likely in general to provide a nearly optimal, if not optimal, choice, indicating that it may be a reasonable strategy not to consider such intensive item realignment computations.

5.7 Item removal

As a part of scale development, it is necessary to consider removing items and not using them in any of the scales. If all responses to an item are removed from the data, the resulting LCV score will be affected as a consequence of reduced dimensionality (from d to d − 1 items) and not just because the item was no longer allocated to any of the scales. For this reason, it is more appropriate to assess the impact of item removal using models based on all available items, but with selected items having zero loadings on all factors. Limited decreases in LCV scores can be allowed to obtain parsimonious sets of items to allocate to scales. Removal of a single item can have a small, tolerable impact, but the combined impact of multiple removals would eventually reach the point at which it would be prohibitive to remove more items (e.g., when the joint removal penalty first exceeds 1% or 2%). Such an item removal process could be applied to summated scales with unit loadings but it could be applied instead to scales with estimated loadings for consistency with item realignment (which is the approach used in results reported below for ABC items).

For scales based on established instruments, it seems more appropriate not to remove an item unless this produces a tangible improvement (e.g., more than a 2% increase in the LCV score). Furthermore, an indication that all items of the instrument are of some value is obtained when removal of each individual item produces a reduction in the LCV score. For CDI, removal of each of the five items (9, 18, 23, 25, 26) produces a negligible percent increase in LCV (at most 0.04%). All other items are of some value with the most valuable item (11) generating a percent reduction in LCV of 1.42%. For FACES, all items are of distinct value with percent reductions ranging from 1.17% for the least important item (12) to 3.10% for the most important item (8). For DQOLY, all items of the realigned scale (Section 5.6) are of small individual value with percent reductions ranging from 0.01% for the least important item (7) to 0.84% for the most important item (48). These results indicate that removal of individual items from the three instruments does not produce a tangible improvement, adding to the evidence of the applicability of these instruments to the ABC data, but there are several CDI items whose removal would produce very small improvements.

5.8 Item residual analyses

For d item responses observed for each of n subjects, the n × 1 vector r_j of residuals for the jth item satisfies r_j = (I − H) · w_j where w_j is the vector of all n observed values for that item (formed from the jth entries of the vectors y_i of Section 3.2), I is the n × n identity matrix, H = J/n is the hat matrix (for the simple intercept only regression model) and J is the n × n matrix with all unit entries. The covariance for an arbitrary pair of item residual vectors r_j and r_j′ is

$$(I-H)\cdot ({\sum }_{j{j}^{\prime }}\cdot I)\cdot {(I-H)}^{\text{T}}={\sum }_{j{j}^{\prime }}\cdot (I-H)\cdot {(I-H)}^{\text{T}}$$

since items for different subjects are independent, where Σ = (Σ_jj′) is the covariance matrix between all pairs of items. Thus, the d · n × 1 vector r formed by combining the vectors r_j over all d items has covariance matrix Σ_r = Σ ⊗ (I − H) · (I − H)^T, that is, it is the Kronecker product of the matrices Σ and (I − H) · (I − H)^T with d · n × d · n entries. Let (Σ_r)⁻¹ = U^T · U, where U is upper triangular; then s = U · r is the associated composite standardized residual vector with independent entries and unit variances across all items and all subjects. These standardized residuals can be used to assess the assumption of normality as in a univariate regression setting. However, the size of the matrix Σ_r can be prohibitively large for typical data sets [for the example data it contains from (27 · 103)² to (51 · 103)² entries]. To reduce the effort needed to compute standardized residuals, we standardize residuals for each fold S_h separately using the common estimate of Σ based on all the data and the individual estimates μ(S_h) of the means for each fold and then combine these for all folds to conduct residual analyses. To conduct example residual analyses, we used scales for the three ABC instruments with the best LCV scores in Table 7.

The standardized residuals for CDI (Figure 1) include an outlier with extreme value of about −7. This is generated by a response to item 25 with scores of 0–2 corresponding respectively to responses that ‘nobody really loves me,’ ‘I am not sure if anybody loves me,’ and ‘I am sure that somebody loves me.’ One subject scored item 25 as a 0, another as a 1, and the remaining 101 subjects scored it as a 2 so that it almost constant. The outlier corresponds to the subject responding with a 0. Furthermore, the spread in the residuals tends to increase as the item mean gets closer to the extreme values of 0 and 2, generating more extreme values than would be expected for truly standardized residuals (up to ±5 and sometimes even beyond that). The associated normal probability plot (Figure 2) generated by these residuals is distinctly curved. The assumption of multivariate normality appears suspect for the CDI item scores. Note also that subjects provided primarily low or primarily high scores for each item so that item means never take on intermediate values near 1.

Figure 1.

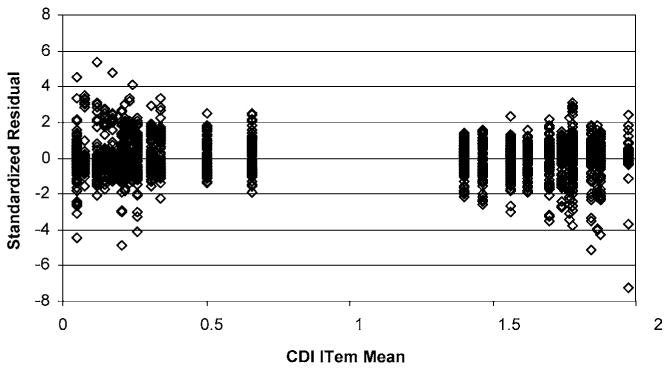
Standardized residual plot for the CDI items.

Figure 2.

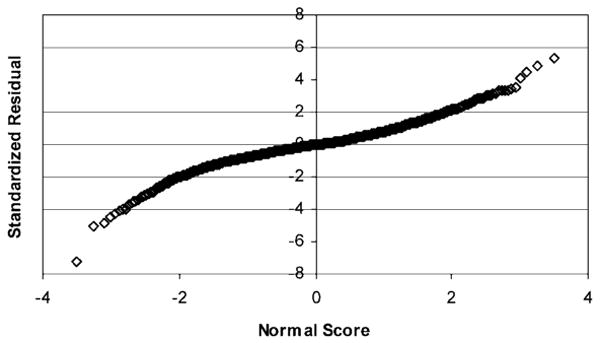
Normal probability plot for the CDI items.

The standardized residuals for FACES (Figure 3), on the other hand, have a reasonable appearance with values within ±4 and most of the time between ±3. The normal probability plot (Figure 4) for these residuals is also reasonably linear. There does not appear to be any reason to question the assumption of multivariate normality for the FACES item scores. Furthermore, item means do not come very close to the extremes of 1 and 5, taking on values between about 2.0 and 4.5.

Figure 3.

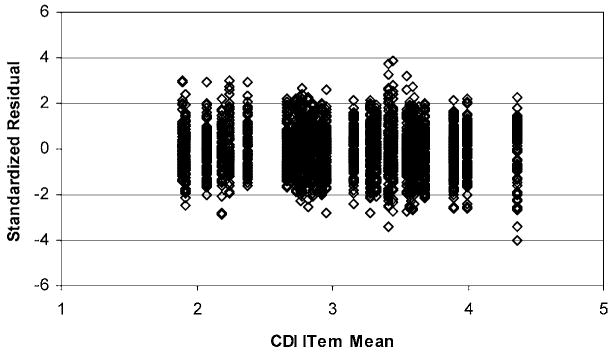
Standardized residual plot for the FACES items.

Figure 4.

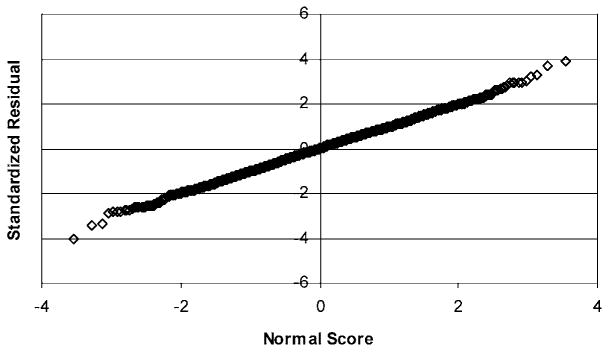
Normal probability plot for the FACES items.

The standardized residuals for DQOLY (Figure 5) have a somewhat intermediate appearance. The spread tends to increase as item means approach the boundaries, but the values are primarily within ±4 and not too much further than that in the few exceptional cases. The normal probability plot (Figure 6) for these residuals wiggles somewhat, but with a distinctly linear trend. The assumption of multivariate normality may not be distinctly problematic for the DQOLY item scores. Furthermore, item means do not come very close to the extremes of 1 and 5, taking on values between about 1.5 and 4.5. Not having item means too close to the extremes seems a necessary condition for the appropriateness of the assumption of multivariate normality.

Figure 5.

Standardized residual plot for the DQOLY items.

Figure 6.

Normal probability plot for the DQOLY items.

5.9 Computational support

Results reported in Sections 5.1–5.8 were computed using specialized SAS macros providing general support for factor analysis model evaluation using LCV. These macros along with the data, driver programs and documentation for reported analyses can be obtained at http://www.ohsu.edu/son/faculty/knafl/factoranalysis.html (accessed 22 June 2006). An overview of these macros is provided in this section. Detailed documentation on macro parameters is provided in header comments within the macro code.

The LCVEFA macro provides support for EFA. It iteratively invokes PROC FACTOR to obtain estimates for complements of folds and then combines these to generate the LCV score. For example, the following invocation

$$\%\text{LCVEFA}(\text{datain}=\text{datalib.ABCitems},\text{yprefix}=\text{FACES},\text{yfirst}=1,\text{ylast}=30,\text{nfactors}=2,\text{kfold}=10,\text{rotatlst}=\text{VARIMAX},\text{scalegen}=\text{Y},\text{scalescr}=\text{Y});$$

requests computation of the 10-fold LCV score for the 2-factor solution for the 30 FACES items. The parameter datain specifies that the source SAS data set is called ABCitems and resides in the library called datalib, previously specified as a pseudonym for the appropriate physical folder (using the SAS libname command). The variables containing the items have names FACES1–FACES30, with the common prefix FACES specified by the parameter yprefix and with indexes ranging from 1 to 30 specified by the parameters yfirst and ylast. If the names do not have this form, they can be specified as a list of names using the parameter yvars.

The number of folds is specified using the parameter kfold. The number of factors to extract is specified with the parameter nfactors. When nfactors =. (rather than setting it to a specific number), LCV scores are computed for nfactors starting at 0 up to the value of the parameter maxnfact with a default of 10 factors. This latter feature was used to generate the results presented in Table 1.

The parameter methlist specifies a list of possible factor extraction procedures (or methods) to use. The default maximum-likelihood procedure (methlist = ml) is used in the above invocation. When more than one entry is included in the list, the macro runs all the requested procedures. Results are generated in the output by default only for methlist/nfactors combinations with scores within 1% of the best score (with this cutoff percent controlled by the parameter keeptol). A complete list can be outputted as well if desired. In any case, all the results are stored in a data set for possible later reference.

The parameter rotatlst specifies a list of possible rotation schemes to apply to the methlist/nfactors combination with the best LCV score. Only varimax rotation is requested in the example. Since the parameter scalegen is set to Y (for yes), the associated summated scale is generated with marker items determined by the approach of the last columns of Tables 4 and 5. The associated LCV score for this summated scale is generated as well because the parameter scalescr is also set to Y. This score is computed by invoking the LCVCFA macro.

The LCVCFA macro provides support for CFA. It iteratively invokes PROC CALIS to obtain estimates for complements of folds and then combines these to generate the LCV score. For example, the following invocation

$$\%\text{LCVCFA}(\text{datain}=\text{datalib.ABCitems},\text{yprefix}=\text{DQOLY},\text{yfirst}=1,\text{ylast}=51,\text{nfactors}=3,\text{kfold}=15,\text{loadings}=1–68–23<100:7<-100:24–34<010:35–51<001);$$

requests computation of the 15-fold LCV score for the three recommended summated scales for the 51 DQOLY items. The parameter loadings contains a list, separated by colons (:), designating assignments of items by indexes to scales (or factors). Each of these assignments begins with a sublist of item indexes followed by common loadings on each of the three scales for all those indexes, separated by a less than sign (<). For example, items 1–6 and 8–23 are all assigned loadings of 1 on the first scale and loadings of 0 on the other two scales, thus designating them as marker items for scale 1. Item 7 is also assigned to the first scale but with a loading of −1, so it is effectively reverse coded. Thus, the first scale is the standard DQOLY impact scale. Scales 2 and 3 are also the standard DQOLY worry and satisfaction scales, respectively assigned items 24–34 and 35–51 without reverse coding.

By default, LCVCFA treats all the scales as dependent with estimated covariances. The parameter ffcovs (for factor-to-factor covariances) can be used to set covariances of pairs of factors to user-specified values. For example,

$$\text{ffcovs}=12.:13.:230$$

means estimate the covariances between scales 1 and 2 as well as between scales 1 and 3 (the value ‘.’ means to estimate the actual value) while setting the covariance between scales 2 and 3 to a value of 0, thereby treating this latter pair of scales as independent, but not the other two pairs.

The recommended scales with estimated loadings can be requested by changing the parameter loadings setting to

$$\text{loadings}=1–23<.00:24–34<0.0:35–51<00.$$

while leaving the other parameter settings unchanged. Note that item 7 no longer requires separate treatment from the other impact items since the signs of estimated loadings determine the orientation of items. An item can be removed (as in Section 5.7) by assigning it all 0 loadings.

The syntax used by LCVCFA to specify loadings and covariances requires that all variable names have a fixed format, consisting of a prefix followed by an index. This imposes a mild restriction on the structure of the input data set while providing the advantage of flexible specification of the CFA model compared to the standard PROC CALIS syntax.¹³ The parameter LCVCFA settings are translated into standard PROC CALIS linear structural equation syntax, which can be displayed by setting the prntcode parameter to Y. That syntax requires the user to specify names for estimated parameter values that can require substantial changes for even small adjustments to the model. These adjustments are more readily specified through the macro parameters.

6 Conclusions

Likelihood cross-validation provides an objective basis for assessing factor analysis models, for both exploratory as well as confirmatory purposes. It can be used to assess the impact of different numbers of factors, alternative factor extraction procedures, factor loading adjustments based on rotation schemes, comparison of possible summated scales, specifications of inter-scale correlation, realignment of item–scale allocation and item removal. It can be used for these purposes when assessing the applicability of established scales to specific data, by comparing alternative scales based on EFA factor scores or scales determined from possibly rotated versions of these factor scores to scales based on recommended item–scale allocations or on other theoretical considerations. Assessments of these kinds have been demonstrated through analyses of data for three established instruments utilizing small numbers of scales, and so further evaluation is needed using a wider variety of factor analysis data sets. Likelihood cross-validation can also be used in scale development for similar purposes, but further investigation is needed to evaluate its use in that context.