Skip to main content
PMC home page
European Journal of Human Genetics logoLink to European Journal of Human Genetics
. 2009 Mar 11;17(10):1231–1240. doi: 10.1038/ejhg.2009.15

Using biological networks to search for interacting loci in genome-wide association studies

Mathieu Emily 1,2,*, Thomas Mailund 1, Jotun Hein 3, Leif Schauser 1, Mikkel Heide Schierup 1
PMCID: PMC2986645  PMID: 19277065

Abstract

Genome-wide association studies have identified a large number of single-nucleotide polymorphisms (SNPs) that individually predispose to diseases. However, many genetic risk factors remain unaccounted for. Proteins coded by genes interact in the cell, and it is most likely that certain variants mainly affect the phenotype in combination with other variants, termed epistasis. An exhaustive search for epistatic effects is computationally demanding, as several billions of SNP pairs exist for typical genotyping chips. In this study, the experimental knowledge on biological networks is used to narrow the search for two-locus epistasis. We provide evidence that this approach is computationally feasible and statistically powerful. By applying this method to the Wellcome Trust Case–Control Consortium data sets, we report four significant cases of epistasis between unlinked loci, in susceptibility to Crohn's disease, bipolar disorder, hypertension and rheumatoid arthritis.

Keywords: association studies, genome-wide scan, epistasis, biological network

Introduction

The past years have witnessed remarkable success in the identification of low-penetrance, high-frequency susceptibility variants in common, complex diseases.1, 2, 3, 4, 5, 6, 7, 8, 9, 10 These show the efficiency of case–control association mapping, when sample sizes are sufficiently large (in thousands) and when the set of single-nucleotide polymorphism (SNP) marker is sufficiently dense (hundred of thousands of markers). Enthusiasm has replaced a long discussion of the feasibility of association mapping studies for two main reasons. On the one hand, replication in a second cohort (or population) of genome-wide significant findings allows weeding out of the false-positive findings that the field previously has suffered from. On the other hand, the major breakthrough was technological rather than methodological. The completion of the human genome,1 followed by the HapMap project,2 has led to the design of efficient genotyping chips that can be run on thousands of cases and controls. A prominent example is the typing of 17 000 individuals for 500 000 SNPs in seven common diseases (bipolar disorder (BD), coronary artery disease (CAD), Crohn's disease (CD), hypertension (HT), rheumatoid arthritis (RA), type 1 diabetes (T1D) and type 2 diabetes (T2D)), by the Wellcome Trust Case–Control Consortium (WTCCC).3 These data have been released for scientific investigation and are used in this study.

However, a large part of the genetic variance in many of these diseases is still unaccounted for. It can be explained by several reasons: first, genes are assumed to interact with their environment; second, the coverage of the SNP chips is not perfect; third, there may be many rare, highly penetrant variants that association mapping is not designed for; fourth, the detection of variants with low genotypic risk might require sample sizes larger than what is currently available; and fifth, susceptibility might be caused by the interaction of genetic variants. Many efforts have been made to identify gene–environment interaction in susceptibility to complex diseases. The next generation of chips will improve coverage, alleviating the second problem. The third issue, low-frequency variants, will be dealt with by using resequencing data. Replicating high ranking SNPs with larger sample sizes, as well as combining data sets in meta-analysis, will provide insight into very low odds ratio variants, avoiding the fourth problem. In this study, we focused our attention on the detection of interaction, also known as epistasis, referring to the fourth item.

Detecting epistasis is a challenge, as it requires improvements in analysis methods rather than genotyping technology. To our knowledge, only one study dealing with SNP–SNP interaction at the genome scale has been published, and it reports only negative findings.4 Searching exhaustively for two-locus epistasis using a 500-k chip requires testing of 125 billion SNP pairs. Such a large number of tests is a challenge both statistically and computationally. Statistically, it implies that significant tests after correction for multiple testing should have P-values lower than 10−13. Extrapolating from single variant findings, such low P-values should be very rare for the sample sizes of existing studies, even though it has been shown that searching for all SNP pairs may be a powerful approach.5 Although it is computationally possible to perform 125 billion tests, these tests have to be very simple to be run in a reasonable time even on large CPU clusters.

Alternatively, the search for interacting SNPs can be prioritized. As many epistatic models result in some marginal effect, an obvious approach is to restrict the search to marker pairs where at least one of the markers shows a single association. Simulations have proved that this approach can be powerful,6 but so far its use on genome-wide real data sets has not been reported. A complement approach is to restrict the search to marker sets that a priori are expected to interact on the basis of our biological knowledge.7

Such an approach has been very recently proposed.8 In this review article, Pattin and Moore have suggested that the use of expert knowledge extracted from protein interaction databases may allow for a more efficient analysis of genome-wide studies. Here, we propose a similar approach by combining the biological and statistical perspective of epistasis. We postulate that two genes that biologically interact are good candidates to a statistical analysis of epistasis in susceptibility to complex diseases. We present the first approach coupling association mapping and interactomics.

In this article, we have reduced the search to SNPs belonging to gene pairs known to interact and referenced in protein databases. We apply this method to the data from the WTCCC and report the first genome-wide scan for epistasis based on biological networks. The significance level is evaluated with a Bonferroni-like procedure that accounts for the correlation between SNPs. We show that our correction is more powerful than a usual Bonferroni correction. We report significant interactions in susceptibility to CD, BD, HT and RA.

Materials and methods

The proposed method is made by a few steps that go from the Protein Interaction Database to the test of interaction between two SNPs in susceptibility to a complex disease. The main steps are summarized in a flowchart shown in the Supplementary Figure 1.

Protein interaction database

Among the large variety of protein interaction databases, we used the STRING database9 to guide the search for epistasis. STRING is one of the largest database of known and predicted protein–protein interactions. It combines reported interactions from dedicated interaction databases10 and multipurpose databases centred on specific model organisms.11 The interactions include direct (physical) and indirect (functional) associations derived from four sources: genomic context, high throughput, co-expression and previous knowledge. Although no distinction has been made between different types of interaction, more has been made on the confidence of the interaction. In the STRING database, each protein–protein interaction has a confidence score. We focused only on the high-confidence interactions (ie, interactions with a score larger than 0.7) and restricted the search to autosomal chromosomes. This selection leads to approximatively 71 000 potential protein–protein interactions that we wanted to test for epistasis.

For each relevant protein, we located the corresponding gene using the Ensembl database12 and identified all SNPs typed in a region of 100 kbp on either side of the gene. We extended the regions around the genes by 100 kbp to either side, as there may be regulatory variants or SNPs in significant linkage disequilibrium (LD) to the gene at this distance.

Data

We applied our approach to the recently released data from the WTCCC3 on BD, CAD, CD, HT, RA, T1D and T2D. For each disease, 2000 patients in the British population were genotyped using the Affymetrix GeneChip 500 k Mapping Array Set. The seven disease data sets share a set of 3000 controls.

We filtered the data in the following way: we masked genotypes with a posterior probability (or CHIAMO score) lower than 0.95 as ‘missing data'. Markers were then removed if the percentage of missing data was larger than 1%, the minor allele frequency lower than 10% or if they were not in Hardy–Weinberg equilibrium (P<0.05). Finally, to remove statistical interaction caused by LD rather than disease association, we excluded all SNP pairs located in linked gene pairs (ie, genes on the same chromosome and separated by less than 5 Mbp). After filtering, the number of SNP pairs for each disease was between 3 107 904 and 3 850 339.

Statistical analysis

In this study, we propose to test the interaction between a pair of SNPs by performing a likelihood ratio test. This test aims at comparing a logistic regression that takes into account only marginal effects of both SNPs with a full logistic regression model that includes pairwise interaction between the two SNPs. This statistical procedure was proposed by Cordell13 but has never been used for genome-wide data analysis. It can be formalized as follows. Let p be the probability of being affected. Let xji correspond to factors related to the underlying genotype j at locus i. The interaction model that incorporated interacting coefficients between the two SNPs can be written as

graphic file with name ejhg200915e1.jpg

where the coefficients β0, β1, β2, β3 and β4 represent genetic parameters that correspond to the mean effect and additive and dominance effects at the two loci. Parameters β5_8 correspond to epistatic effects. We propose to compare the interaction model with a null model where the interacting coefficients have been removed, which leads to

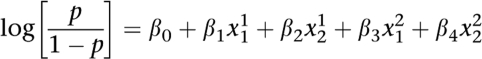graphic file with name ejhg200915e2.jpg

The model comparison is performed by a likelihood ratio test (with four degrees of freedom) between the above two models.

Population stratification

Similar to a previous study,3 we observe that the overall effect of population structure on our association results seems to be relatively small. We corrected for relatedness using the genomic control method. We estimated the inflation factor by adapting the procedure described in earlier studies.14, 15 We computed the mean and the median of our test statistic and divided them by 4 and 3.36, respectively, corresponding to the expected mean and median of the χ2 test statistics with four degrees of freedom. The corresponding inflation factors for each disease are 1.06–1.07 for BD, 1.02–1.02 for CAD, 1.08–1.09 for CD, 1.02–1.02 for HT, 1.04–1.05 for RA, 1.02–1.02 for T1D and 1.02–1.03 for T2D.

Correction for multiple testing

P-values have to be adjusted for multiple comparisons, to estimate the significance level of interaction. We propose to apply a Bonferroni-like correction based on the effective number of SNP pairs. In our network-based approach, there are two levels of dependencies. First, for a particular pair of genes, each SNP from the first gene is tested against each SNP from the second gene. Second, gene pairs are not independent, as one gene can belong to more than one gene pair. Although the second source of dependency might have an impact on the significance level, we accounted only for the multiple comparisons arising in a single gene pair test. If nGG is the number of gene pairs and nG1i and nG2i are the number of SNPs in the first and second gene, respectively, of the pair i, then the total number of tests, denoted by N, is

graphic file with name ejhg200915e3.jpg

To account for the dependency between tests, we propose to estimate the number of effective tests in a single gene pair i, denoted by neffi, and to use it in the above formula in place of nG1i × nG2i. The effective number of SNP pairs was calculated using the Eigen values of a correlation matrix,16 where the correlation between two pairs of SNPs can be measured with the entropy and the mutual information17 as follows:

graphic file with name ejhg200915e4.jpg

where H is the entropy measure and I is the mutual information measure. As described by Li and Ji,16 letting nGGi be the number of SNP pairs in the gene pair i, and λk (k=1…nGGi) the eigen values of the correlation matrix, the number of effective tests in the gene pair i neffi is given by

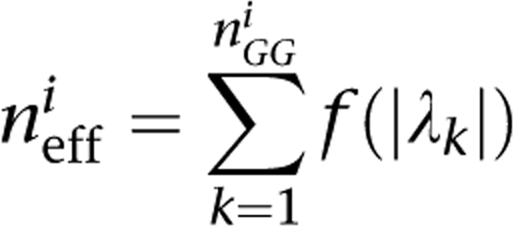graphic file with name ejhg200915e5.jpg

with f(x)=II(x≥1)+(x−⌊x⌋), where II is the indicator function and ⌊x⌋ is the floor of x. We estimate the number of effective SNP pairs as follows:

graphic file with name ejhg200915e6.jpg

A Bonferroni correction consists of multiplying the P-values by N, and an effective correction is made by multiplying the P-values by Neff. The use of our effective correction leads to a number of effective tests in the range of (506,173…600,010) for the seven diseases, leading to a globally nominal level in the range of (8.3 × 10−8, 9.9 × 10−8).

Quantile–quantile plots

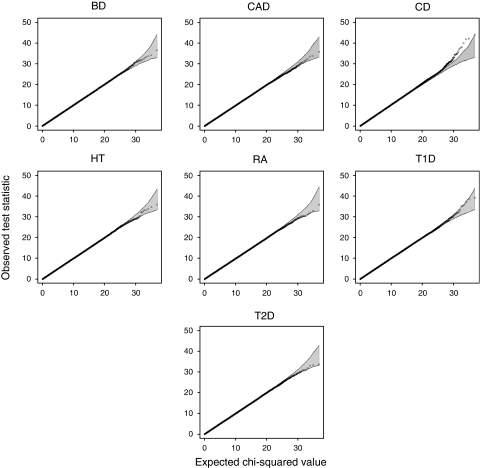
We constructed quantile–quantile (Q–Q) plots by plotting the order statistics from a set of values against their expected values obtained from the theoretical distribution under the null distribution. To make the interpretation easier, we adapted the idea developed by the WTCCC and calculated the 95% concentration bands (shaded grey in all Q–Q plots).18 The concentration band was calculated, with 10.000 simulations, assuming that SNP pairs are independent, and it does not reflect the effective level of significance.

SNPFile software

We performed all the analysis using a new binary file format for SNP data. SNPFile is a C++ library that stores genotype data together with any kind of additional data, using a flexible serialization mechanism. It is dedicated to the manipulation of genome-wide SNP data sets and is accessible through http://www.daimi.au.dk/~mailund/SNPfile/. Software that implements the proposed epistatic test is available (http://www.daimi.au.dk/~memily/BiRC/Software.html) and is compatible with the SNPFile format. As input of this code, one needs an interaction file referring to all gene pairs to be tested.

Results

A powerful statistical procedure to detect epistasis based on interactomics

To assess for the power of the proposed statistical procedure, described in the section on Statistical Analysis under Materials and methods, we looked at the distribution of the interaction statistics for 10 000 random SNP pairs, expected to follow the null hypothesis of non-interaction. We found that our interaction statistic, calculated as a likelihood ratio, followed a χ2 distribution with four degrees of freedom: type I error rate at 1, 5, 10 and 20% levels were 0.94, 4.8, 10 and 20%, respectively.

We then tested the efficiency of our correction for multiple comparisons (see Materials and methods) on simulated data sets based on the WTCCC data. Ten thousand gene pairs were generated in the set of genes from the STRING database. For each of the 10 000 gene pairs, the number of effective pairs was calculated with the procedure described in Materials and methods and compared with the total number of pairs that is used in the conventional Bonferroni correction. Type I error rate at the 5% level shows that a Bonferroni correction is overly conservative: we estimate that the probability of rejecting the null hypothesis of non-interaction to be 0.8%. It proves that LD structure within genes induces dependency between SNP pairs, lowering the power to detect epistasis. The use of the effective number of pairs gave a better correction, improving the power to detect interaction, and we estimate that the probability of rejecting the null hypothesis at a 5% level is 4.5%; still conservative but much less so than the Bonferroni correction. From this simulation study and the analysis of the seven case/controls data sets, we can conclude that the number of effective tests is approximatively six times lower than the total number of tests, which is in agreement with one previous investigation.19

Overall results from the WTCCC data analysis

After applying our data quality filter, as described in Materials and Methods, we were left with 3 107 904–3 850 339 tests per disease in the WTCCC data. Thus, as the total number of selected SNP pairs was equal to 10.700.176, approximatively two-thirds of SNP pairs were removed by the quality filter. The analysis of one data set took between 130 and 160 h, corresponding to an average of 25 000 tests per hour, on typical computer, showing the feasibility of our approach. In comparison, testing all possible pairs (125 billions pairs) would take 570 years on a single computer.

Figure 1 shows the quantile–quantile plots for the interaction test in the seven diseases using the 71 000 well-established protein–protein interactions in the STRING database.9 The shaded region in the plots corresponds to the 95% concentration band obtained from the null hypothesis of non-interaction (corresponding to a χ2 test with four degrees of freedom). The most interacting SNP pairs are reported in Table 1 for each disease.

Figure 1.

Figure 1

Open in a new tab

Overall analysis of the WTCCC data. Quantile–quantile plots of the test statistic observed in the seven studied diseases. The shaded region is the 95% concentration band, calculated assuming independent SNP pairs.

Table 1. Reports of the most interacting SNP pairs for the seven diseases from the WTCCC data.

Disease SNP1 Chr1 (position) Marginal effect 1 SNP2 Chr2 (position) Marginal effect 2 Interaction test Number of tests Number of effective tests
CD rs6496669 15 (88696269) Pval=0.86 RR=1.01 rs434157 5 (112219541) Pval=0.69 RR=1.02 1.13 × 10−9 3 334 147 530 071
BD rs2237091 5 (149529990) Pval=0.13 RR=1.12 rs1798011 12(87459093) Pval=0.28 RR=1.05 8.32 × 10−8 3 533 600 552 050
HT rs11208766 1 (66084927) Pval=0.44 RR=0.95 rs2859576 5 (76592073) Pval=0.42 RR=1.03 9.07 × 10−8 3 231 429 512 112
RA rs2830075 21 (26424313) Pval=0.59 RR=1.02 rs2163786 5 (139966674) Pval=0.54 RR=1.03 9.10 × 10−8 3 258 999 512 925
CAD rs4655797 1 (65913717) Pval=0.85 RR=1.01 rs10247918 7 (31627635) Pval=0.18 RR=1.06 2.33 × 10−7 3 107 904 506 173
T1D rs2771102 9 (90146698) Pval=0.46 RR=1.03 rs7150423 14 (76020264) Pval=0.90 RR=1.00 3.45 × 10−7 3 850 339 600 010
T2D rs2276549 2 (29452755) Pval=0.01 RR=0.89 rs10217742 9 (87198969) Pval=0.65 RR=1.02 5.21 × 10−7 3 395 047 528 824
Open in a new tab

The marginal effect of each SNP has been calculated using a standard allelic χ2 test. The corresponding marginal relative risks (RRs) is also reported. The number of effective tests has been obtained through the method described in the text.

The P-value yielding genome-wide significance at the 5% level after multiple comparisons depends on the disease and is in the range (8.3 × 10−8, 9.9 × 10−8). There are four cases of significance, one in each of CD, BD, HT and RA. Consistent with the quantile–quantile plots, CD shows the strongest interaction with a P-value of 1.13 × 10−9, yielding an overall P-value of 6.10−4 after correction. Despite the computational cost, we performed 10 re-analyses of CD data sets where individual phenotypes were permuted. Results shown in Supplementary Table 1 argue in favour of highly significant statistical interaction. The four significant interactions are individually discussed in the following paragraphs.

Crohn's disease

For CD, we observe an excess of points outside the 95% concentration band at the tail of the distribution. In total, eight SNP pairs show a significant interaction. All of them belong to the same putative biological interaction: the eight pairs are made by two SNPs from the first region and four SNPs from the second region. This interaction involves genes Adenomatous Polyposis Coli (APC) and the IQ-domain GTPase-activating protein 1 (IQGAP1). Removing all APC-IQGAP1 SNP pairs from the analysis completely eliminates the deviation from the expected Q–Q plot (see Figure 2).

Figure 2.

Figure 2

Open in a new tab

QQ plot for Crohn's disease (CD). Quantile–quantile plots of the test statistic observed for the CD. The black dots correspond to the entire data set. The blue dots result from the removal of SNP pairs included in APC-IQGAP1 regions. The shaded region shows the 95% concentration band for the non-interaction hypothesis.

The interaction pattern for the most significant SNP pair (rs6496669 on 15q26 and rs434157 on 5q22) is reported in Table 2. These SNPs have a minor allele frequency (MAF) of 0.20 and 0.33, and affected individuals show an excess of genotype pairs (AA, GG), (AG, GG) and (AA, GA), corresponding to epistatic model M11 proposed by Evans et al.6 Looking at SNP pairs in the neighbourhood of rs6496669 and rs434157 shows the same interaction pattern (data not shown). Risks, relative to the most common homozygote genotype (GG, AA), are reported in Table 2. For genotypes (AG, GG) and (GA, AA), the relative risks are significantly higher than 1:2.10 (95% CI: 1.33–3.34) and 1.67 (95% CI: 1.22–2.30). Although the risk for the genotype (AA, GG) does not reach the level of significance (1.34 with 95% CI: 0.55–3.24) possibly because of its low frequency, its value is larger than 1. The joint OR, that combined the three at-risk genotypes, is 1.85 (95% CI: 1.45–2.37) and this is significantly larger than 1 (Fisher's exact test, P=8.88 × 10−7), confirming that carrying at least three minor alleles combining rs6496669 and rs434157 elevates the risk for CD in the WTCCC data set. Interacting SNPs are in LD with genes APC and IQGAP1 (see Supplementary Figure 2). Biologically, β-catenin colocalizes with IQGAP1, APC and N-cadherin ruffles in NIH 3T3 fibroblasts, and APC/IQGAP1 has been identified to regulate cell migration.20 Furthermore, the two interacting regions have been related to the development of CD. First, APC located close to MCC (mutator in colorectal cancer) has been associated with CD.21, 22 Second, IQGAP1 is recognized as a negative regulator of cell–cell adhesion. Its role in carcinogenesis has already been reported,23 and it has been mentioned that IQGPA1 might be involved in gastric and colorectal cancers.24, 25

Table 2. Genotype counts for the SNP pair in Crohn's disease (rs6496669, rs434157) and odds ratio relative to the most common double homozygote genotype: (rs6496669, rs434157)=(GG, AA).

    rs6496669
  rs434157 AA AG GG
Controls GG 11 (13) 33 (48) 87 (70)
  GA 81 (103) 413 (399) 440 (434)
  AA 226 (195) 858 (879) 835 (840)
         
Crohn's disease GG 10 (8) 47 (31) 31 (47)
  GA 92 (69) 252 (265) 284 (289)
  AA 99 (129) 608 (586) 566 (560)
         
OR relative to GG/AA (95% CI) GG 1.34 (0.55–3.24) 2.10 (1.33–3.34) 0.53 (0.34–0.80)
  GA 1.67 (1.22–2.30) 0.90 (0.74–1.09) 0.95 (0.79–1.14)
  AA 0.65 (0.50–0.84) 1.05 (0.90–1.21) 1
Open in a new tab

Bipolar disorder

A statistical interaction was found between rs2237091 (chromosome 5q32) and rs1798011 (chromosome 12q22 located in the PDGFR-B gene and the KITLG gene, respectively). These SNPs have a MAF of 0.10 and 0.43, respectively (Table 3). The genotype pairs (GG, CT), (GA, TT) and (GG, TT) are overrepresented in affected individuals, resembling the interaction pattern M11 reported by Evans et al.6 Table 3 also shows the risks relative to genotype (AA, CC) and shows that the relative risk for (GA, TT) was 1.88 (95% CI: 1.31–2.71) and for (GG, CT) it was 1.34 (95% CI:0.58–3.05). The joint OR, which combined the three at-risk genotypes, has a value of 1.92 (95% CI: 1.4–2.64), significantly larger than 1 (Fisher's exact test P=5.68 × 10−5), confirming that carrying at least three minor alleles combining rs2237091 and rs1798011 is a risk predictor for bipolar disorder in the WTCCC data set. Biologically, the two genes can be linked to bipolar disorder as follows: PDGFR-B and KITLG are both member of the cytokine–cytokine receptor interaction pathway.25 Furthermore, they are both known to interact with the KIT tyrosine kinase receptor, which can be viewed as an indirect interaction between PDGFR-B and KITLG.

Table 3. Genotype counts for the SNP pair in bipolar disorder (rs2237091, rs1798011) and odds ratio relative to the most common double homozygote genotype: (rs2237091, rs1798011)=(AA, CC).

    rs2237091
  rs1798011 GG GA AA
Controls TT 0 (5) 59 (77) 509 (470)
  CT 13 (14) 242 (257) 1153 (1191)
  CC 9 (6) 173 (151) 820 (802)
         
Bipolar disorder TT 9 (3) 70 (51) 275 (313)
  CT 11 (9) 187 (171) 831 (792)
  CC 2 (4) 80 (101) 517 (534)
         
OR relative to AA/CC (95% CI) TT X 1.88 (1.31–2.71) 0.86 (0.71–1.03)
  CT 1.34 (0.58–3.05) 1.22 (0.98–1.53) 1.14 (0.99–1.32)
  CC 0.37 (0.05–1.49) 0.73 (0.55–0.97) 1
Open in a new tab

Hypertension

The analysis of the hypertension data set shows a significant statistical interaction between rs11208766 and rs2859576 placed within PDE4B gene (chromosome 1p31) and PDE8B gene (chromosome 5q13), respectively. Genotype pair (AA, GA) appeared to be underrepresented in affected individuals (see Table 4), leading to a protective epistasis model. The risk, relative to genotype (AA, GG), was equal to 0.42 (95% CI: 0.30–0.58), which is significantly lower than 1 (Fisher's exact test; P=7.63 × 10−8), confirming that carrying this genotype for the SNP pair (rs2237091, rs1798011) significantly protects from developing hypertension in the WTCCC data set. Genes PDE4B and PDE8B are connected to hypertension as members of phosphodiesterase-4, which have been recently reported to have protective effects in the early stage of pulmonary arterial hypertension in mice.26

Table 4. Genotype counts for the SNP pair in hypertension (rs11208766, rs2859576) and odds ratio relative to the most common double homozygote genotype: (rs11208766, rs2859576)=(AA, AA).

    rs11208766
  rs2859576 GG GA AA
Controls GG 7 (9) 19 (16) 7 (6)
  GA 130 (138) 248 (268) 184 (144)
  AA 605 (598) 1203 (1193) 599 (623)
         
Hypertension GG 9 (7) 8 (10) 3 (4)
  GA 101 (92) 199 (178) 57 (96)
  AA 392 (398) 784 (793) 440 (415)
         
OR relative to AA/AA (95% CI) GG 1.74 (0.63–4.99) 0.58 (0.23–1.30) 0.60 (0.12–2.23)
  GA 1.05 (0.79–1.41) 1.09 (0.87–1.37) 0.42 (0.30–0.58)
  AA 0.88 (0.74–1.05) 0.88 (0.76–1.03) 1
Open in a new tab

Rheumatoid arthritis

Analysis of the epistasis between APP and APBB3 genes, in susceptibility to RA, shows a significant interaction between rs2830075 (chromosome 21q21) and rs2163786 (chromosome 5q31.3). These two SNPs are common (MAFs of 0.34 and 0.49, respectively) and follow an epistatic model, labelled M2 by Evans et al.,6 where the genotype pair (TT, GA) is overrepresented in affected individuals (see Table 5). The risk, relative to genotype (CC, AA), for the specific genotype (TT, GA) was 1.60 (95% CI: 1.19–2.15), which is significantly larger than 1 (Fisher's exact test; P=3.6 × 10−4), confirming that carrying this genotype predisposes to RA in the WTCCC data set. Experimental evidence of biological epistasis between APP and APBB3 has been reported earlier.27, 28 Furthermore, amyloid precursors are associated with glycocorticoids sensitivity whose variations play an important role in susceptibility to many inflammatory diseases, such as RA.29

Table 5. Genotype counts for the SNP pair in rheumatoid arthritis (rs2830075, rs2163786) and odds ratio relative to the most common double homozygote genotype: (rs2830075, rs2163786)=(CC, AA).

    rs2830075
  rs2163786 TT TC CC
Controls GG 106 (79) 324 (335) 304 (310)
  GA 129 (158) 670 (690) 667 (648)
  AA 105 (101) 346 (331) 337 (334)
         
Rheumatoid arthritis GG 27 (53) 235 (223) 212 (206)
  GA 134 (105) 480 (459) 412 (430)
  AA 63 (67) 205 (220) 219 (222)
         
OR relative to CC/AA (95% CI) GG 0.39 (0.25–0.62) 1.16 (0.88–1.42) 1.07 (0.84–1.37)
  GA 1.60 (1.19–2.15) 1.10 (0.90–1.36) 0.95 (0.77–1.17)
  AA 0.92 (0.64–1.32) 0.91 (0.72–1.16) 1
Open in a new tab

Discussion

To identify interactions between SNPs in large-scale genome-wide association data, we introduced a new method, which uses information from known biological networks to limit the number of tests. Other existing methods propose either to test exhaustively all SNP pairs or to test only loci marginally significant. Our method is complementary to these approaches. First, by focusing on potentially good SNP pair candidates, which take part in a protein–protein interaction network, our method increases the significance level, and true findings, missed by testing all pairs exhaustively, may be picked up by our method. Second, by accounting for the correlation between SNP pairs, we control for multiple comparisons in a more efficient way than a Bonferroni correction. Moreover, the proposed statistical procedure can detect a large variety of epistatic models and allow for the detection of interaction between loci that do not display marginal effects.

We applied our approach on the seven data sets released by the WTCCC.3 The four potential cases of epistasis (for CD, BD, HT and RA) reported in this study would not have been found with any of the competing methods. Apart from four potential interactions, discussed in details, we did not find any evidence of interaction for the three other diseases (CAD, T1D and T2D). Although it might be due to the restriction of intragenic regions, this suggests that such interactions are either rare or that the statistical power is limited by the present sample sizes. Accordingly, the first attempts to screen for pairs of markers failed in finding any interaction effect.4

As the number of two-locus epistatic models is very large, it is not straightforward to evaluate the statistical power of our approach. Moreover, many other factors can affect our ability to detect interaction. Even with very large data sets made by 2000–3000 individuals, some genotypes will be represented by very few individuals. As a consequence, detecting interaction with a multiplicative underlying epistatic model is almost impossible for loci having an allelic frequency lower than 0.1. We used simulations to address the question of the allelic frequencies effect on the power of our proposed statistical procedure. We found that our test becomes conservative when minor allele frequencies decrease and marginal effects increase. Therefore, the approach is most powerful for identifying interaction of common SNPs with very limited marginal effects, which are exactly the types of interaction missed by other approaches based on marginal effects. Another limiting factor is the use of tag-SNPs, which considerably affects the statistical power of detecting interaction, in comparison with single marker association. Considering a pair of variants where none of the SNPs are on the chip, the use of tag-SNPs to detect the true interaction may fail, leading to a dramatic loss of power even with data sets with thousands of individuals.

Despite these power issues, we found four statistical significant interactions, in susceptibility to CD, between SNPs near the genes APC and IQGAP1, to bipolar disorder, involving genes PDGFR-B and KITLG, to hypertension with a protective effect implicating two phosphodiesterase-4, and to RA, between two amyloid beta A4 precursor. The statistical significance of the test was assessed by a Bonferroni-like correction for multiple comparisons. As the Bonferroni correction might be over-conservative, we accounted for the correlation within genes, due to LD. Following techniques developed by Li and Ji,16 we used a Bonferroni-like correction by multiplying the P-values by the effective number of independent comparisons. As correlation induced by non-independent gene pairs has been omitted, our correction is most likely to be overconservative. Even with a significant result, we cannot definitely state that this is a true interaction. Replication in other data sets, and preferably other populations, is necessary. Using simulations (see Supplementary Tables 2a and b), we estimate the power to replicate such interactions, at a nominal level of 5%, to 0.96 for CD, 0.94 for BD, 0.93 for HT and 0.91 for RA, with a typical data set with one thousand cases and controls. If the sample size of the replication cohort is divided by 2 (500 cases and 500 controls), power drops to 0.73 for CD, 0.56 for BD, 0.68 for HT and 0.63 for RA, whereas it reaches 100% for all diseases if the sample size is doubled (2000 cases and 2000 controls). Consequently, we can hope, with the current cohort's size, that our potential interaction can be replicated in another data set. Furthermore, with the upcoming of meta-analysis, data set sample sizes are boosted increasing the power to replicate findings.

The interaction pattern between rs6496669 and rs434157 indicates that carrying at least three of the four minor alleles of SNPs increases the risk for CD by a factor 1.85. The source of the interaction between APC and IQGAP120 relates to cell migration. The two genes have also been associated previously with colorectal cancer21, 25 and directly to CD.30 More precisely, germline mutations (in which gene APC) cause familial adenomatous polyposis (FAP), which is an autosomal dominant inherited disease characterized by the presence of adenomatous polyps in the colon and rectum, with the inevitable development of colorectal cancer.21 The link between colon cancer and CD is well established, with people affected by CD having a relative risk of 5.6 for developing colon cancer.31 In addition, experimental work has highlighted some association between CD and disorder of the APC gene.30 Recently, it has been suggested that APC might be involved in the apoptosis process implicated in colon cancer.22 As IQGAP1 is recognized as a negative regulator of cell–cell adhesion, this is consistent with the fact that IQGAP1/APC impacts on the regulation of cell migration as reported earlier.20

Analysis of epistasis in susceptibility to bipolar disorder reveals a significant interaction between rs2237091 and rs1798011: carrying at least three of the four minor alleles significantly increases the risk for bipolar disorder by a factor 1.81. Biological evidence has already emphasis on this interaction. A recent study has reported that a co-expression between KIT Ligand (KITLG) and PDGFR-B provides a good prognosis in neuroblastoma.32 In addition it has been reported that PDGF Receptor Beta (PDGFR-B) transcripts were significantly increased in schizophrenia brains,33 pointed out that PDGFR-B plays a role in bipolar disorder. Finally PDGFR-B and KITLG both belong to the cytokine-cytokine pathway, which is known to have an effect in schizophrenia.34 More precisely, growing evidence suggests an interplay between the immune and the nervous system, which might be reflected by the interaction between rs2237091 and rs1798011 in susceptibility to bipolar disorder.

Single-nucleotide polymorphism pair (rs11208766, rs2859576) shows an interaction pattern that protects for developing hypertension in the WTCCC data set. These two SNPs belong to two phosphodiesterase-4, and experimental evidence argues in favour of protective effects of these enzymes with hypertension.26 More precisely, phosphodiesterase-4 are enzymes that break a phosphodiester bond, and these enzymes have been identified as new potential therapeutics.35

The fourth SNP pair involves rs2830075 and rs2163786 in susceptibility to RA. These two SNPs are located in APP and APBB3 (Fe65L2) genes. Experimental evidence argues in favour of an interaction between Fe65L2 and APP.27 More precisely, Fe65L2 is a ligand of the cytoplasmic domain of APP. This interaction might play a role in the RA. First, Glucocorticoids (Gc) increase amyloid precursor proteins36 and may be linked to RA, as variation in Gc sensitivity is associated with inflammatory diseases. Second, many evidences support a negative association between Alzheimer and RA.37, 38, 39 This might be an explanation of the potential interaction found between rs2830075 and rs2163786.

To conclude, using biological knowledge to drive the search for interacting SNPs at the genome scale is complementary to existing methods. It allows for the detection of epistatic SNP pairs that do not show marginal effects and without any focus on a specific interaction model. A similar statistical procedure can be designed to detect higher-order interactions. However, such a test is most likely to be limited in terms of power because of a higher degree of freedom and, as one expects, very low counts for an n-tuplet SNPs.

Furthermore, our approach reduces the level of significance both by selecting candidate tests and by efficiently correcting for multiple comparisons. In addition, our method allows for a biological feedback of the findings, something lacking in many association studies. As an example, it provides candidate genes that might be involved in the interaction. These benefits are illustrated by the results reported for CD, BD, HT and RA.

Acknowledgments

We acknowledge two anonymous referees for useful comments. We thank Søren Besenbacher, Thomas Bataillon, Julien Dutheil, Carsten Wiuf, Garrett Hellenthal, Thorunn Rafnar and Patrick Sulem for fruitful discussions. This work has been funded by the EU project Polygene.

Footnotes

Supplementary Information accompanies the paper on European Journal of Human Genetics website (http://www.nature.com/ejhg)

Supplementary Material

Supplementary Figure 1
Click here for additional data file. (1.9MB, tiff)
Supplementary Figure 2
Click here for additional data file. (2.4MB, tiff)
Supplementary Table 1
Click here for additional data file. (2.3MB, tiff)
Supplementary Table 2a
Click here for additional data file. (1.3MB, tiff)
Supplementary Table 2b
Click here for additional data file. (1.5MB, tiff)

References

  1. Consortium International Human Genome Sequencing Initial sequencing and analysis of the human genome. Nature. 2001;409:860–921. doi: 10.1038/35057062. [DOI] [PubMed] [Google Scholar]
  2. HapMap The International HapMap Project. Nature. 2003;426:789–796. doi: 10.1038/nature02168. [DOI] [PubMed] [Google Scholar]
  3. The Wellcome Trust Case Control Consortium Genome-wide association study of 14 000 cases of seven common diseases and 3000 shared controls. Nature. 2007;447:661–678. doi: 10.1038/nature05911. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Curtis D. Allelic association studies of genome wide association data can reveal errors in marker position assignments. BMC Genetics. 2007;8:30. doi: 10.1186/1471-2156-8-30. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Marchini J, Donnelly P, Cardon LR. Genome-wide strategies for detecting multiple loci that influence complex diseases. Nat Genet. 2005;37:413–417. doi: 10.1038/ng1537. [DOI] [PubMed] [Google Scholar]
  6. Evans DM, Marchini J, Morris AP, Cardon LR. Two-stage two-locus models in genome-wide association. PLoS Genet. 2006;2:e157. doi: 10.1371/journal.pgen.0020157. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Wang K, Li M, Bucan M. Pathway-based approaches for analysis of Genomewide Association Studies. Am J Human Genet. 2007;81:1278–1283. doi: 10.1086/522374. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Pattin KA, Moore JH. Exploiting the proteome to improve the genome-wide genetic analysis of epistasis in common human dieases. Human Genet. 2008;124:19–29. doi: 10.1007/s00439-008-0522-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Von Mering C, Jensen LJ, Kuhn M, et al. STRING 7-recent developments in the integration and prediction of protein interactions. Nucleic Acid Res. 2007;35:D358–D362. doi: 10.1093/nar/gkl825. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Salwinski L, Miller CS, Smith AJ, Pettit FK, Bowie JU, Eisenberg D. The database of interacting proteins: 2004 update. Nucleic Acid Res. 2004;32:D449–D451. doi: 10.1093/nar/gkh086. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Mishra GR, Suresh M, Kumaran K, et al. Human protein reference database – 2006 update. Nucleic Acid Res. 2006;34:D411–D414. doi: 10.1093/nar/gkj141. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hubbard TJP, Aken BL, Beal K, et al. Ensembl 2007. Nucleic Acid Res. 2007;35:D610–D617. doi: 10.1093/nar/gkl996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Cordell HJ. Epistasis: what it means, what it doesn't mean, and statistical methods to detect it in humans. Human Mol Genet. 2002;11:2463–2468. doi: 10.1093/hmg/11.20.2463. [DOI] [PubMed] [Google Scholar]
  14. Devlin B, Bacanu S-A, Roeder K. Genomic control to the extreme. Nat Genet. 2004;36:1129–1130. doi: 10.1038/ng1104-1129. [DOI] [PubMed] [Google Scholar]
  15. Devlin B, Roeder K. Genomic control for association studies. Biometrics. 1999;55:997–1004. doi: 10.1111/j.0006-341x.1999.00997.x. [DOI] [PubMed] [Google Scholar]
  16. Li J, Ji L. Adjusting multiple testing in multilocus analyses using the eigenvalues of a correlation matrix. Heredity. 2005;95:221–227. doi: 10.1038/sj.hdy.6800717. [DOI] [PubMed] [Google Scholar]
  17. Cover TM, Thomas JA. Elements of Information Theory. John Wiley and Sons, Inc.: New York; 1991. [Google Scholar]
  18. Stirling WD. Enhancements to aid interpretation of probability plots. Statistician. 1982;31:211–220. [Google Scholar]
  19. Pickrell J, Clerget-Darpoux F, Bourgain C. Power of genome-wide association studies in the presence of interacting loci. Genet Epidemiol. 2007;31:748–762. doi: 10.1002/gepi.20238. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Sharma M, Henderson BR. IQ-domain GTPase-activating protein 1 regulates beta-catenin at membrane ruffles and its role in macropinocytosis of N-cadherin and adenomatous polyposis coli. J Biol Chem. 2007;282:8545–8556. doi: 10.1074/jbc.M610272200. [DOI] [PubMed] [Google Scholar]
  21. Fearnhead NS, Britton MP, Bodmer WF. The ABC of APC. Human Mol Genet. 2001;10:721–733. doi: 10.1093/hmg/10.7.721. [DOI] [PubMed] [Google Scholar]
  22. Huang X, Guo B. Adenomatous polyposis coli determines sensitivity to histone deacetylase inhibitor-induced apoptosis in colon cancer cells. Cancer Res. 2006;66:9245–9251. doi: 10.1158/0008-5472.CAN-06-0887. [DOI] [PubMed] [Google Scholar]
  23. Clark EA, Golub TR, Lander ES, Hynes RO. Genomic analysis of metastasis reveals an essential role for RhoC. Nature. 2000;406:532–535. doi: 10.1038/35020106. [DOI] [PubMed] [Google Scholar]
  24. Nabeshima K, Shimao Y, Inoue T, Koono M. Immunohistochemical analysis of IQGAP1 expression in human colorectal carcinomas: its overexpression in carcinomas and association with invasion fronts. Cancer Letts. 2002;176:101–109. doi: 10.1016/s0304-3835(01)00742-x. [DOI] [PubMed] [Google Scholar]
  25. Morris LE, Bloom GS, Frierson HFJ, Powell SM. Nucleotide variants within IQGAP1 gene in diffuse-type gastric cancers. Genes Chromosomes Cancer. 2005;42:280–286. doi: 10.1002/gcc.20150. [DOI] [PubMed] [Google Scholar]
  26. De Franceschi L, Platt OS, Malpeli G, et al. Protective effects of phosphodiesterase-4 (PDE-4) inhibition in the early phase of pulmonary arterial hypertension in transgenic sickle cell mice. FASEB J. 2008;22:1849–1860. doi: 10.1096/fj.07-098921. [DOI] [PubMed] [Google Scholar]
  27. Duilio A, Faraonio R, Minopoli G, Zambrano N, Russo T. Fe65L2: a new member of the Fe65 protein family interacting with the intracellular domain of the Alzheimer's beta-amyloid precursor protein. Biochem J. 1998;330:513–519. doi: 10.1042/bj3300513. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Chang Y, Tesco G, Jeong W, et al. Generation of the beta-amyloid peptide and the amyloid precursor protein C-terminal fragment gamma are potentiated by FE65L1. J Biol Chem. 2003;278:51100–51107. doi: 10.1074/jbc.M309561200. [DOI] [PubMed] [Google Scholar]
  29. Brugg B, Dubreuil YL, Huber G, Wollman EE, Delhaye-Bouchaud N, Mariani J. Inflammatory processes induce beta-amyloid precursor protein changes in mouse brain. Proc Natl Acad Sci. 1995;92:3032–3035. doi: 10.1073/pnas.92.7.3032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Fukushima K, Funayama Y, Shibata C, et al. Familial adenomatous polyposis complicated with Crohn's disease. Intl J Colorectal Dis. 2006;21:730–731. doi: 10.1007/s00384-006-0161-2. [DOI] [PubMed] [Google Scholar]
  31. Ekborn A, Helmick C, Zack M, Adami H. Increased risk of large-bowel cancer in Crohn's disease with colonic involvement. Lancet. 1990;336:357–359. doi: 10.1016/0140-6736(90)91889-i. [DOI] [PubMed] [Google Scholar]
  32. Shimada A, Hirato J, Kuroiwa M, et al. Expression of KIT and PDGFR is associated with a good prognosis in neuroblastoma. Pediatr Blood Cancer. 2008;50:213–217. doi: 10.1002/pbc.21288. [DOI] [PubMed] [Google Scholar]
  33. Prabakaran S, Swatton J, Ryan M, et al. Mitochondrial dysfunction in schizophrenia: evidence for compromised brain metabolism and oxidative stress. Mol Psychiatr. 2004;9:684–697. doi: 10.1038/sj.mp.4001511. [DOI] [PubMed] [Google Scholar]
  34. Drzyzgaa Ł, Obuchowicz E, Marcinowskaa A, Herman ZS. Cytokines in schizophrenia and the effects of antipsychotic drugs. Brain Behav Immun. 2006;20:532–545. doi: 10.1016/j.bbi.2006.02.002. [DOI] [PubMed] [Google Scholar]
  35. Growcott EJ, Spink KG, Ren X, Afzal S, Banner KH, Wharton J. Phosphodiesterase type 4 expression and anti-proliferative effects in human pulmonary artery smooth muscle cells. Resp Res. 2006;7:1–12. doi: 10.1186/1465-9921-7-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Green K, Billings L, Roozendaal B, McGaugh J, LaFerla F. Glucocorticoids increase amyloid-beta and tau pathology in a mouse model of Alzheimer's disease. J Neurosci. 2006;26:9047–9056. doi: 10.1523/JNEUROSCI.2797-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. McGeer P, McGeer E, Rogers G, Sibley J. Anti-inflammatory drugs and Alzheimer disease. Lancet. 1990;335:1037. doi: 10.1016/0140-6736(90)91101-f. [DOI] [PubMed] [Google Scholar]
  38. Myllykangas-Luosujarvi R, Isomaki H. Alzheimer's disease and rheumatoid arthritis. Brit J Rheumatol. 1994;33:501–502. doi: 10.1093/rheumatology/33.5.501. [DOI] [PubMed] [Google Scholar]
  39. McGeer P, Schulzer M, McGeer E. Arthritis and anti-inflammatory agents as possible protective factors for Alzeihmer's disease: a review of 17 epidemiologic studies. Neurology. 1996;47:425–432. doi: 10.1212/wnl.47.2.425. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Figure 1
Click here for additional data file. (1.9MB, tiff)
Supplementary Figure 2
Click here for additional data file. (2.4MB, tiff)
Supplementary Table 1
Click here for additional data file. (2.3MB, tiff)
Supplementary Table 2a
Click here for additional data file. (1.3MB, tiff)
Supplementary Table 2b
Click here for additional data file. (1.5MB, tiff)

Articles from European Journal of Human Genetics are provided here courtesy of Nature Publishing Group

RESOURCES