Coarse-grained stochastic processes for microscopic lattice systems

Abstract

Diverse scientific disciplines ranging from materials science to catalysis to biomolecular dynamics to climate modeling involve nonlinear interactions across a large range of physically significant length scales. Here a class of coarse-grained stochastic processes and corresponding Monte Carlo simulation methods, describing computationally feasible mesoscopic length scales, are derived directly from microscopic lattice systems. It is demonstrated below that the coarse-grained stochastic models can capture large-scale structures while retaining significant microscopic information. The requirement of detailed balance is used as a systematic design principle to guarantee correct noise fluctuations for the coarse-grained model. The coarse-grained stochastic algorithms provide large computational savings without increasing programming complexity or computer time per executive event compared to microscopic Monte Carlo simulations.

Scientific problems in diverse disciplines ranging from materials science (1, 2) to biomolecular dynamics (3) to atmosphere/ocean science and climate modeling (4, 5) involve the nonlinear interaction of physical processes across many length scales ranging from the microscopic to the macroscopic. In general, it is not feasible computationally to include all of these effects in detail in a model involving only the large scales. Thus there is a great need for developing systematic “noise” models for representing the interaction of the unresolved degrees of freedom in a coarse-grained framework that is computationally tractable.

For example, microscopic simulation methods such as molecular dynamics and Monte Carlo (MC) algorithms provide a fundamentally derived computational tool capable of describing complex, out-of-equilibrium interactions between atoms or molecules. With the current computing capabilities, these methods yield unprecedented insights into numerous problems ranging from physiochemical and biological processes to pattern recognition and imaging processing. Despite their widespread use and the substantial progress in related computational methods, molecular simulations are limited to short length and time scales, capable of simulating a relatively small number of atoms/molecules for quite short time periods, while device sizes and morphological features observed in experiments often involve much larger spatial and/or temporal scales. A major obstacle in addressing this multiscale modeling challenge is the lack of a rigorous mathematical and computational framework providing a direct link of microscopic scales to complex mesoscopic and macroscopic phenomena that are dictated by particle/particle interactions.

In this direction, the work presented here focuses on developing a stochastic modeling and computational framework capable of efficiently describing much larger length scales than conventional MC simulations while still incorporating microscopic details. Our main paradigm is a microscopic spin flip model for the adsorption and desorption of molecules between a surface and the overlying gas phase (1). Such types of microscopic, spin flip processes have also been proposed recently as providing paradigm models for unresolved features of moist atmospheric convection (6). Using the spin flip model as a starting point, we derive a coarse-grained stochastic birth-death process, describing the microscopic system at mesoscopic length scales. The stochastic process and the associated coarse-grained MC simulations can capture large-scale morphological structures while retaining microscopic information on intermolecular forces and particle fluctuations. It is shown numerically that the necessary computer time can be reduced by orders of magnitude for large systems and intermediate and long-range potentials.

Microscopic and Coarse-Grained Processes

To demonstrate the basic ideas, we consider as our microscopic model an Ising-type system set on a periodic lattice ℒ that is a discretization of the interval I = [0, 1]. We divide I in m coarse cells each with length 1/m (see Inset of Fig. 3). In turn, each coarse cell is subdivided into q (micro)cells of length 1/mq, hence I is divided in N = mq cells and ℒ = 1/mq ℤ ∩ I. Each coarse cell is denoted by D_k, k = 1, … , m. We define the coarse lattice corresponding to the coarse cell partition as ℒ_c = 1/m ℤ ∩ I, and consider the integers k = 1, … , m as the unscaled lattice points of ℒ_c; the coarse-grained stochastic processes defined below are set on ℒ_c. Throughout this article we concentrate on 1D models; however, our results extend easily to multiple dimensions.

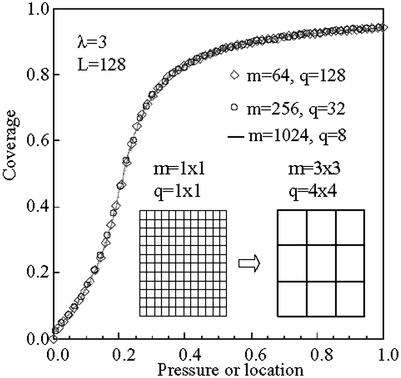
Figure 3.

Simulation results under a pressure gradient. (Inset) A schematic of the coarse-graining process in two dimensions.

The Ising model is defined on the lattice ℒ. At each lattice site x ∈ ℒ the order parameter σ(x) is allowed to take the values 0 and 1 describing vacant and occupied sites, respectively. A configuration σ = {σ(x):x ∈ ℒ} is an element of the resulting configuration space ∑. The energy H of the system, evaluated at σ, is given by the Hamiltonian,

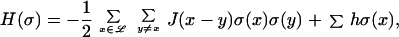where h = h(x), x ∈ ℒ, is the external field and J is the interparticle potential. Equilibrium states of the Ising model are described by the Gibbs states at the prescribed temperature T,

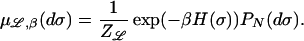where β = 1/kT and k is the Boltzmann constant and Z_ℒ is the partition function. Furthermore P_N(σ) = ∏_x∈ℒρ(σ(x)) is the prior distribution on ℒ, where ρ(σ(x)) is the distribution of a Bernoulli random variable with mean 1/2, for each x ∈ ℒ. The interparticle potentials J = J(x−y) are defined on the fine lattice ℒ. We consider symmetric potentials with finite range interactions whereby the integer 2L we denote the number of interacting neighboring sites of a given point on ℒ. The lattice size is 1/N, hence the actual potential radius is L/N. Since we consider periodic boundary conditions on ℒ, then for 2L + 1 = N we recover the case of long-range interactions, where each lattice site interacts with all N − 1 remaining sites on ℒ. Consequently the interaction potential J = J(x−y) can be written as

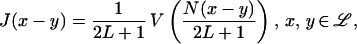1

where V(r) = V(−r), and V(r) = 0, |r| ≥ 1, accounting for possible finite range interactions. An additional condition required to obtain error estimates for the coarse-graining procedure is that V is smooth and ∫_R|∂_rV(r)|dr < ∞ (7). More general conditions are also possible. Note that for V summable, the choice of the scaling factor 1/2L + 1 in Eq. 1 implies the summability of the potential J, even when N, L → ∞.

The dynamics of Ising-type models considered in the literature consists of order parameter flips and/or exchanges that correspond to different physical processes. Here we focus on spin flip mechanisms and discuss other mechanisms elsewhere. More specifically a flip at the site x ∈ ℒ is a spontaneous change in the order parameter, 1 is converted to 0 and vice versa. Here, we consider it as a model for the desorption of a particle from a surface described by the lattice to the gas phase above and conversely the adsorption of a particle from the gas phase to the surface (1). This mechanism can describe phase transitions without order parameter conservation (8). Such a model has also been proposed recently for modeling certain unresolved features of tropical convection (6). If σ is the configuration before a flip at x, then after the flip the configuration is denoted by σ^x. When the configuration is σ, a flip occurs at x with a rate c(x, σ) i.e. the order parameter at x changes, during the time interval [t, t + Δt] with probability c(x, σ)Δt. The resulting stochastic process {σ_t}_t≥0 is defined as a continuous time jump Markov process with generator given by L_Nf(σ) = ∑_x∈ℤ^Nc(x, σ)[f(σ^x)], where f is a test function (9). The imposed condition of detailed balance implies that the dynamics leave the Gibbs measure invariant and is equivalent to

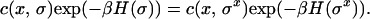For Metropolis-type dynamics, the energy barrier for desorption depends only on the energy difference between the initial and final states. In this article we focus on Arrhenius-type dynamics where the activation energy of surface desorption is the energy barrier a particle has to overcome in jumping from the surface to the gas phase. The Arrhenius rate is:

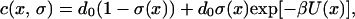2

where U(x) = ∑_{z≠x,z∈ℒ}J(x−z)σ(z) − h(x) is the total energy contribution from the particle interactions with the particle located at the site x ∈ ℒ, as well as the external field h. Typically a term U₀ corresponding to the energy associated with the surface binding of the particle at x can be absorbed in the external field h in U(x); finally, d₀ is a rate constant that mathematically can be chosen arbitrarily but physically is related to the pre-exponential of the microscopic processes.

Below we sketch how to replace the microscopic processes by a coarse-grained one with desirable mathematical properties as well as computational efficiency. The coarse-grained process {η_t}_t≥0 is defined on the coarse lattice ℒ_c by equivalently obtaining the corresponding semigroup generator, starting from the microscopic process. The coarse-grained random variable η_t is defined as an average of the microscopic process {σ_t}_t≥0 over each coarse cell D_k: η_t(k) = ∑_y∈Dkσ_t(y) and satisfies the constraint 0 ≤ η_t(k) ≤ q, since each coarse cell contains q microcells. Equivalently we may also consider the coverage η̄_t(k) = q⁻¹η_t(k). First, we define the coarse-grained Hamiltonian for the random variable η, corresponding to the microscopic Hamiltonian H:

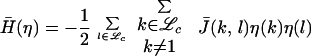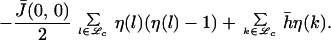The coarse-grained potential J̄ is defined by including the average of all contributions of pairwise microscopic interactions between coarse cells and within the same coarse cell,

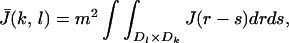3

where the area of D_l × D_k is equal to 1/m²; similarly we define V̄(k, l). Wavelets with vanishing moments can also be used in the construction of the coarse-grained potential (7). The coarse-grained external field h̄ is also defined as an average of the microscopic external field h,

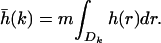If the corresponding continuum function h is smooth, then we have the error estimate h̄(k) = h(x) + 𝒪(1/m), for x ∈ D_k. In this case we can approximate the microscopic Hamiltonian by the coarse-grained one with errors of the order q/2L + 1.

Next we turn to the nonequilibrium problem and define the coarse-grained birth-death Markov process {η_t}_t≥0 on the configuration space ℋ_m,q = {0, 1, … , q}^ℒ_c, where η = {η(k):k ∈ ℒ_c} and η(k) ∈ {0, 1, … , q} in each coarse cell D_k. The generator of the process obtained from systematic coarse-graining is (7)

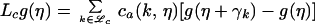4

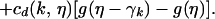Here γ_k ∈ ℋ_m,q is the configuration with a single particle at the site k ∈ ℒ_c. The update rate with which the value η(k) is increased by 1, i.e. the adsorption rate of a single particle in the coarse cell D_k is given by

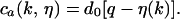5

Similarly the desorption rate with which the value η(k) is decreased by 1 is

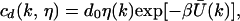6

where Ū is defined as the coarse-graining of U:

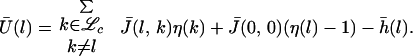Interactions within the same coarse cell, included in H̄(η) and Ū(l), are typically neglected in existing ad hoc models for coarse-grained variables (10–12). Indeed the microscopic derivation of our model shows (7) that same-cell interactions are lower order when 2L + 1 ≫ q; however, they cannot be ignored if the potential radius L is relatively short and/or the interactions are very strong. Furthermore by including same cell interactions we still obtain the global mean field theory when the coarse-graining is performed beyond the interaction radius L. As a result we obtain a complete “hierarchy” of MC models from nearest neighbor to mean field where the latter does not include interactions but includes noise, unlike the usual ordinary differential equation mean field theories. The proper addition of interactions within the cell in the coarse model is derived from the microscopics and η_t still obeys detailed balance, as established next.

Detailed Balance and Mesoscopic Limits

First, we derive the invariant measure for the coarse-grained process {η_t}_t≥0 and in particular we show it satisfies the detailed balance condition similarly to the original microscopic dynamics {σ_t}_t≥0. The product binomial distribution P_m,q(η) = ∏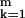ρ_q(η(k)), where ρ_q(η(k) = λ) = q!/λ!(q − λ! (1/2)^q is the prior distribution on the configuration space ℋ_m,q and arises naturally from the microscopic prior by including q independent sites. We define the canonical Gibbs measure on ℋ_m,q; here Z_m,q,β denotes the partition function:

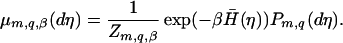The condition of detailed balance for {η_t}_t≥0 with respect to the measure μ_m,q,β is

We only verify the first relation; using that H̄(η + γ_k) − H̄(η) = −Ū(k) and the definitions of the rates (5, 6), we have (for d₀ = 1):

Since (q − λ)ρ_q(λ) = (λ + 1)ρ_q(λ + 1), the last curly bracket is equal to zero, hence detailed balance holds.

Next, we validate the approximation of the microscopic process {σ_t}_t≥0 by the coarse-grained process {η_t}_t≥0 by demonstrating that both share the same deterministic mesoscopic limit, in the limiting regime of long-range interactions N = 2L + 1. In this case the mesoscopic equation for Arrhenius dynamics derived from the microscopic process σ is

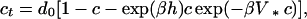7

where ∗ denotes a convolution. Furthermore in the same scaling regime the two processes have asymptotically the same fluctuations as a comparison of the respective probability distribution functions demonstrates, at least in the case of the Gibbs measures (see ref. 7 and the numerical comparisons in Fig. 1).

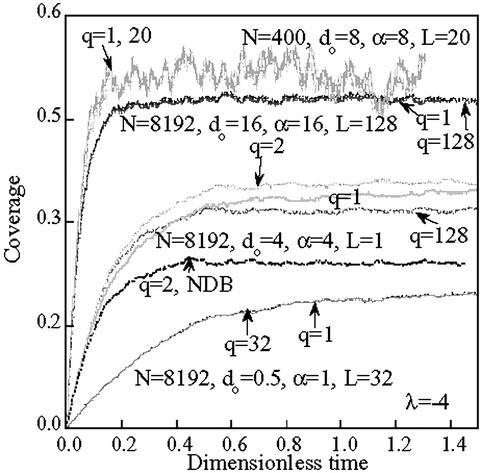
Figure 1.

Results of transient simulations from microscopic (q = 1) MC (solid lines) and coarse-grained MC (dotted lines) for a piecewise constant repulsive potential with parameters indicated. For N = 400 (uppermost curves) the noise is significant. For moderate and long-range potentials (e.g., L > 10), coarse-graining leads to excellent results in all expected equilibrium values, dynamics, and noise. Lack of detailed balance (NDB) leads to significantly wrong results, especially for short potentials and small coarse-grainings (e.g., q = 2).

Below we outline the derivation of Eq. 7 from the coarse-grained process. We consider as our observable the empirical measure μ^m(dy; t) = 1/mq ∑_l∈ℒcη_t(l)δ_l(dy), where δ_l is a Dirac measure centered at the point l/m ∈ T. Then we define f(η) = 〈μ^m, φ〉 = 1/mq ∑_l∈ℒcη_t(l)φ(l) for any test function φ and consider the martingale M_t = f(η_t) − f(η₀) − ∫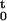L_cf(η_s)ds, with quadratic variation

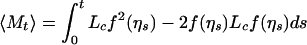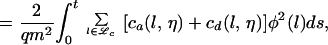and E〈M_t〉 = 𝒪(1/m). By Doob's maximal inequality we have that for any time horizon t₁, P(sup_t∈[0,t1]|M_t| > δ) ≤ 1/δ² 𝒪(1/m). Thus on a set of probability approximately one we have,

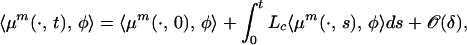8

were a short calculation shows that

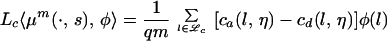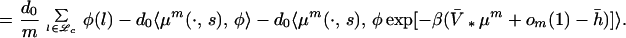We remark that the assumption of long-range interactions allowed us to rewrite the right side of Eq. 8 as a function of μ^m(dy, s) and thus obtain an approximate closed equation for the measure μ^m(dy, s). The relative compactness of the probability distributions of the random measures μ^m(dx, t) in the space D([0, T], ℳ₊) (the set of right continuous functions with left limits taking values in the space of positive finite measures ℳ₊) follows from the estimate on the quadratic variation 〈M_t〉. Passing to the m → ∞ limit in Eq. 8 we obtain Eq. 7 in weak form (for measure-valued solutions). It is not hard to see that the measure-valued solutions are absolutely continuous with respect to the Lebesgue measure thus Eq. 7 follows in the strong sense. We refer to ref. 9 for similar compactness and regularity arguments applied to other stochastic processes.

For the purpose of benchmarking simulations against mesoscopic theory in the next section we state some of the basic properties of Eq. 7. Steady-state solutions of Eq. 7 satisfy the algebraic equation α(1 − x) − xe^−λx = 0, where α = e^−βh and λ = V₀β, V₀ = ∫ V(r)dr. For a suitable parameter regime (12), Eq. 7 is bistable with stable roots (m₊, m₋) corresponding to the dense and the dilute phases of the system. One-dimensional standing and traveling waves for Eq. 7 connect high- and low-density phases (13). When the parameters (α, λ) satisfy α = e^−λ/2, the corresponding wave c is standing, i.e. has zero speed, and for V(x) = V₀χ_[−.5.,5] can be calculated explicitly:

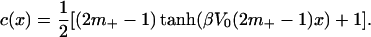9

As established in the next section, the proper inclusion of stochastic fluctuations inherited from the microscopics in the mesoscopic models is critical in simulating underresolved features that trigger phenomena such as nucleation, pattern selection, etc.

Coarse-Grained MC Simulations

Kinetic MC or continuous-time MC simulations (14) are performed where the transition probabilities are computed a priori and each event is successful. Coarse-grained MC codes are the same as microscopic MC ones with a few differences. First, the interparticle potential is coarse-grained at the beginning of a simulation to represent interactions between particles within each cell (a feature absent in microscopic MC) as well as interactions with neighboring cells. Second, the order parameter is still an integer but varies between zero and q, instead of zero and one that is typical for microscopic MC.

First, we present transient MC results in one dimension (trajectories) for the spatially average coverage in Fig. 1 under periodic boundary conditions, for four sets of adsorption-desorption parameters and potential length, to illustrate different points. The same random number generator seed is used in computing all these trajectories. Even though the simulations for N = 400 (Fig. 1, topmost curves) are slightly affected from finite size effects, we use these simulations to show enhanced noise compared to ones performed for a larger domain (N = 8,192). For moderately long potentials (L = 20, Fig. 1, uppermost curves and L = 32, bottommost curves), the coarse-grained MC (q = L) follows closely the dynamics of the microscopic MC (q = 1), and the noise level of the corresponding microscopic and coarse-grained simulations is comparable. This latter observation is theoretically supported by the fact that the Gibbs states of the coarse-grained process and the underlying microscopic process are asymptotically identical, at least in the case of long-range interactions (2L + 1 = N), as the large deviation principles for the coarse-grained and the microscopic processes are the same (see ref. 7 for details). For short-range potentials, such as L = 1 (Fig. 1, lower set of four curves), for which the asymptotics in ref. 7 do not apply, coarse graining (q = 2 and q = 128) results in larger, but still relatively small, errors in the equilibrium solution, as shown from the fluctuating coverage at long times in Fig. 1. All of these results show that the coarse-grained process is an accurate stochastic noise model for the microscopic process.

The detailed balance principle has been used as a design rule in deriving the coarse-graining processes. To elucidate its importance, we have also carried out simulations with the short-range interaction term in H̄, η(l)(η(l) − 1) replaced with the “intuitive” term η(l)², which does not satisfy detailed balance. The curve in Fig. 1 for q = 2 (labeled NDB) shows that nondetailed balance can lead to large discrepancies, especially for low q and low coverage. Therefore, the correct derivation of the coarse Hamiltonian and transition probabilities from the microscopics can be critical regarding numerical accuracy.

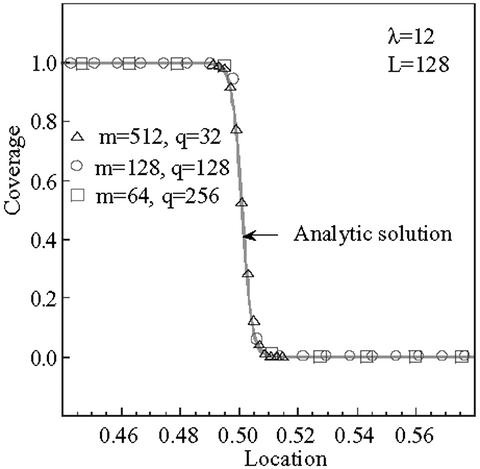
The above conditions lead to spatially uniform solutions for long times. Thus the numerical agreement between microscopic and mesoscopic MC is encouraging but not a strict test. To test the accuracy of the coarse-graining procedure, we have also performed simulations for conditions resulting in spatially varying solutions describing large-scale features of the microscopic model. In particular, we benchmark our coarse-grained MC simulations against an analytic solution, namely that of a standing wave (Eq. 9) for a piecewise constant potential, at relatively low temperatures where thermal fluctuations are reduced. To perform these simulations, two MC simulations were first carried out for each coarse-graining under periodic boundary conditions (infinite domain) to numerically evaluate m₊ and m₋. Virtual domains were next created on each side of the actual simulation domain of length L each. The boundary conditions were subsequently set in each virtual domain equal to m₊ on the left and m₋ on the right. With these Dirichlet boundary conditions, the standing wave was simulated for 5 × 10⁴ MC steps (each MC step corresponds to sampling each site once on the average) after steady state has been reached. The results are depicted in Fig. 2. It is seen that the numerical results (symbols) are in excellent agreement with the analytic solution (solid line), especially for the finest discretization shown. As expected from analogous deterministic simulations, the standing wave is not as well resolved for relatively coarse grids. Finally, in the aforementioned parameter regimes it is expected that the coarse-grained MC simulations can also be used to enhance the numerical bifurcation algorithms developed in ref. 15 for lattice MC algorithms.

Figure 2.

Standing wave for a piecewise constant potential from analytic solution (solid line) and various coarse-grainings indicated. Very good agreement between analytical and numerical solutions is obtained.

The previous simulations have been carried out under a uniform external field (pressure). In a variety of problems, kinetic MC simulations need to be coupled with macroscopic fluid-phase equations of change, where spatial variations in the external field occur typically over macroscopic scales. Representative examples include catalytic reactors, crystal growth, electrochemical systems, and stochastic modeling of atmospheric phenomena (1, 6). To mimic such situations, we have also performed simulations with a gradient in the external field. In the simulations conducted here, the external field varies linearly in space between zero at the left boundary and one at the right boundary. The linear choice is arbitrary. The steady-state solution obtained varies as a function of position. Since there is one-to-one map between position and pressure below we use these terms interchangeably.

First, we tested these simulations in the absence of interactions. In this case nodes are independent of each other (uncoupled nodes). Thus if one plots the solution (coverage) at each location as the function of position (or pressure), the Langmuir isotherm is obtained in a single run. Excellent agreement between the MC and the analytical isotherm was obtained (not shown). Next, we carried out simulations in the case of nontrivial interactions. For the gradient simulations, the boundary conditions were arbitrarily chosen to be Dirichlet. In particular, the coverage was set to zero at the left boundary and to value of the isotherm for the corresponding pressure (α = 1, d₀ = 1) at the right boundary. An example for attractive interactions is shown in Fig. 3. The value of interactions was chosen in the regime of a single-valued isotherm, but close to the critical point where the onset of multiplicity in 1D starts (λ_cr = 4).

Solutions from different discretizations depicted in the graph are practically indistinguishable. These simulations indicate that coarse-grained MC can allow for the coupling of microscopic-scale phenomena at an interface with continuum or stochastic simulations of a fluid in contact with the interface. A subtle point is that the solutions obtained for these conditions coincide with the isotherm obtained by using periodic boundary conditions at each pressure, i.e., simulations where nodes are decoupled. This result indicates that because of the large scales simulated partial equilibrium at each node is practically established.

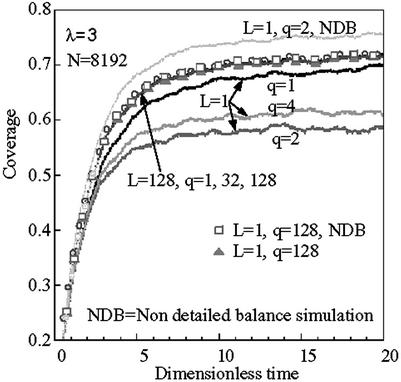
Fig. 4 shows the coverage vs. time for the above conditions of spatially varying external field for a long potential (L = 128) with different discretizations (q = 1, 32, 128) indicated. The conclusions are qualitatively similar to the ones under periodic boundary conditions discussed in Fig. 1. For long-range potentials, results are practically the same independent of coarse-graining. To explore the accuracy of coarse-graining beyond the asymptotic limit under external field gradients, we have also performed similar simulations for a very short potential (L = 1). The solution of the microscopic MC (q = 1) is close to the long-range potential (L = 128), as shown in Fig. 4. For q = 2 maximum deviations from the microscopic MC are seen. As q increases above approximately four, a hierarchy of solutions results that converges to the mean field limit of long potential for large-coarse grainings (e.g., q = 128, Fig. 4, triangles). Detailed balance plays an important role for small q, large coverage, and short potentials (see topmost line for q = 2, Fig. 4) but plays little role for large coarse grainings (e.g., q = 128, Fig. 4, squares) or long potentials (not shown).

Figure 4.

Spatially average coverage vs. time for the conditions of Fig. 3 and three discretizations (L = 128, q = 1, 32, 128) indicated. Short-range potential L = 1 results are also depicted for various values of q with and without (NDB) a detailed balance condition.

Finally, we should comment on the significant computational savings resulting from coarse-graining. For long-range potentials, the computer time in kinetic MC simulation with global update, i.e., searching the entire lattice to identify the chosen site, scales approximately as 𝒪(m³). For example, a 100-fold reduction in the number of sites (q = 100) results in reduced computer time by a factor of 10⁶. Therefore, coarse-graining can render MC simulation for the large-length scales feasible. Furthermore, coarse-grained potentials can be short and MC algorithms using local update based on lists of neighbors become amenable. Such a possible change in algorithms can lead to additional computer time savings by up to 2 orders of magnitude for typical MC simulation domains (16).

Conclusions

In this article we have introduced a class of coarse-grained stochastic processes and associated MC simulations that are derived directly from microscopic lattice systems and describe mesoscopic-length scales. Detailed balance is used as a systematic design principle to guarantee proper inclusion of noise fluctuations in the coarse-grained model. Numerical comparisons of coarse-grained and conventional (microscopic) MC simulations delineate the validity regimes of the proposed coarse-graining procedure. It is also demonstrated that the models result in significant computational savings by reducing the cost of the microscopic MC simulations by a factor of approximately q³, where q is the size of the coarse-graining. Consequently the proposed coarse-grained MC simulations are capable of capturing large-scale features, while retaining microscopic information on intermolecular forces and particle fluctuations.

The proposed algorithms have the potential for significant impact on numerous technologically relevant applications that are currently intractable with conventional MC simulations. Examples include pattern formation at mesoscopic-length scales on catalytic surfaces (17, 18), transport through microporous films (2), as well as growth processes of materials. Furthermore coarse-grained MC methods can provide a tool for the simulation of systems having a wide discrepancy of interrelated scales. One such process is chemical vapor deposition where microscopic interfacial phenomena typically simulated by MC methods affect the large-scale adjacent fluid flow (1). In the same broad multiscale context but in an entirely different direction, coarse-grained stochastic processes can be used as mesoscopic stochastic models for unresolved features in atmospheric phenomena. For example, such models and MC simulations can be directly derived from microscopic stochastic models for the parameterization of tropical convection developed recently in ref. 6.

Abbreviation

MC

Monte Carlo