Abstract
F1Fo-ATP synthase is the enzyme responsible for most of the ATP synthesis in living systems. The catalytic domain F1 of the F1Fo complex, F1-ATPase, has the ability to hydrolyze ATP. A fundamental problem in the development of a detailed mechanism for this enzyme is that it has not been possible to determine experimentally the relation between the ligand binding affinities measured in solution and the different conformations of the catalytic β subunits (βTP, βDP, βE) observed in the crystal structures of the mitochondrial enzyme, MF1. Using free energy difference simulations for the hydrolysis reaction ATP+H2O → ADP+Pi in the βTP and βDP sites and unisite hydrolysis data, we are able to identify βTP as the “tight” (KD = 10−12 M, MF1) binding site for ATP and βDP as the “loose” site. An energy decomposition analysis demonstrates how certain residues, some of which have been shown to be important in catalysis, modulate the free energy of the hydrolysis reaction in the βTP and βDP sites, even though their structures are very similar. Combined with the recently published simulations of the rotation cycle of F1-ATPase, the present results make possible a consistent description of the binding change mechanism of F1-ATPase at an atomic level of detail.
The enzyme F1Fo-ATP synthase is responsible for most of the ATP synthesis in living systems (1–3). It is a large multisubunit complex consisting of a proton-translocating membrane domain Fo attached via central and peripheral stalks to the catalytic domain F1, a spherical globular structure outside of the membrane (4–6). The F1 domain, called F1-ATPase, is made up of 3α and 3β subunits arranged in alternation around the α-helical coiled–coil structure of the γ subunit. The foot of the γ subunit is a more globular domain and makes extensive contacts with the ring of c subunits of the membrane portion, F0 (7). The γ subunit and the associated c ring are believed to rotate as an ensemble relative to the rest of the enzyme, the rotation being generated by the transmembrane proton-motive force via photosynthesis or respiration. The α-helical domain of the γ subunit is asymmetric and the rotation of this asymmetrical structure alters the conformations (4–6) and the binding affinities (8, 9) of the three catalytic β subunits for substrate and products. Each of them in turn is thought to go through three states known as open, loose, and tight (4), in accord with the “binding change” mechanism of ATP synthesis (1). The F1 domain can be separated from the membrane domain and it retains the ability to hydrolyze ATP. Hydrolysis of ATP leads to the rotation of the central stalk, although the detailed mechanism is not understood. By attaching an actin filament or a bead to the exposed foot of the central stalk, the rotation has been visualized in a microscope (10). The actin filament turns counterclockwise (as viewed from the membrane) in 120° steps. During the ATP synthesis cycle, the rotation of the central stalk is presumed to be in the opposite sense.
Of the three catalytic β subunits in the F1-ATPase (α3β3γδɛ) complex, two have very similar conformations in the crystal structures of the mitochondrial enzyme MF1 (4–6). In the first structure to be determined (4), one β subunit contained an ATP analogue, adenosine 5′-[β,γ-imido]triphosphate (AMP-PNP), and the other ADP; these two subunits have been referred to as the βTP and βDP subunits, respectively. The third site, called βE because it was empty in the structure, has a conformation that is significantly different from the other two. In the most recent structure (6), the βE site is not empty and has what is referred to as the half-closed conformation, βHC, which differs significantly from both βE and βTP,βDP.
Solution measurements (8, 9) have shown that there is a tight binding site for ATP (KD = 10−12 M in MF1; KD = 2 × 10−10 M in the Escherichia coli enzyme, EcF1), a loose site (KD = 5 × 10−7 M in EcF1), and a weak binding site (KD = 1.5 × 10−5 M in EcF1); a complete set of affinity measurements is not available for MF1, although the free energy of reaction 1 has been measured in both MF1 (8) and EcF1 (9). The measurements for the affinities other than the tight site are based on a Trp mutant of the E. coli enzyme (9); to describe his results, Senior (9) has used the notation H for high affinity, M for medium affinity, and O for open instead of tight, loose, and weak, respectively.
It has not been possible by experiment to identify the three measured binding constants with the three different conformations of the β subunits observed in the crystal structures; a crystal structure with a single ligand, such as AMP-PNP, would be suggestive in this regard. It is generally thought that βE (or βHC) is the weak binding site, but there is no consensus on whether βTP or βDP is the tight binding site. It has been suggested, based on the crystal structures, that the βDP site corresponds to the tight binding site for ATP (4, 6), but it also has been assumed, without specific justification, that the βTP site is the tight site (11). To understand the role played by each of the β subunits in the catalytic mechanism, it is essential to resolve the uncertainty concerning their binding affinities; that is, to make a connection (the “missing link”) between the microscopic (structural) and macroscopic (solution) data.
We report here “alchemical” free energy difference simulations (12–15) of the standard free energy change, ΔGo, of the balanced reaction,
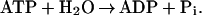 |
1 |
By combining the results of these simulations with solution data we are able to identify the βTP site as the tight site for ATP binding, and by elimination, the βDP site as the loose site. The recent crystal structures of Braig et al. (5) and Menz et al. (6) were used for the simulations (see Methods). For each site that was studied (βTP,βDP in ref. 5 and βTP,βDP,ΒHC in ref. 6), a stochastic boundary region with a radius of 25 Å centered on the γ-phosphate of ATP or on Pi was used in the simulations. The charge scaling procedure of Simonson et al. (13, 14) was employed for screening the long-range electrostatic interactions in an efficient way. The standard free energy of the balanced reaction shown in Eq. 1 was calculated for the various β sites and for the reaction in aqueous solution. Only the sites with bound ligands were used for simulations because it was possible to build ATP/H2O and ADP/Pi into the site by a straightforward procedure (see Methods). Calculations showed that the phosphate groups of ATP and ADP are unprotonated in the bound state and the same protonation states were used in solution for comparison with the data of George et al. (16); Pi is equal to H2PO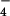 in both the enzyme and in solution at pH 7 with the protonated sites in the enzyme determined by Poisson–Boltzmann calculations (13, 17, 18); the identification of H2PO
in both the enzyme and in solution at pH 7 with the protonated sites in the enzyme determined by Poisson–Boltzmann calculations (13, 17, 18); the identification of H2PO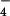 as the bound ligand is in accord with suggestions based on experiment (19). To obtain ΔGo for the reaction in the enzyme from the molecular dynamics free energy difference calculations, we use the ansatz:
as the bound ligand is in accord with suggestions based on experiment (19). To obtain ΔGo for the reaction in the enzyme from the molecular dynamics free energy difference calculations, we use the ansatz:
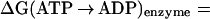 |
2 |
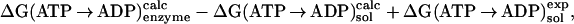 |
where ΔG(ATP → ADP) is the standard free energy change of the reaction; the subscripts indicate where the reaction takes place (bound to the enzyme or in solution), and the superscript indicates the source of the results (calculated or experimental). By introducing the measured free energy for the reaction in the absence of Mg2+, the condition of the solution simulation, ΔG(ATP → ADP)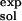 = −10.8 kcal/mol (16), we are able to avoid the inaccuracies that could arise from use of the calculated quantum-mechanical gas-phase free energy change of the reaction. This approach is analogous to the widely used method for estimating the pKa of a titrating site in a protein by introducing the reference pKa of a model system in solution (17, 18).
= −10.8 kcal/mol (16), we are able to avoid the inaccuracies that could arise from use of the calculated quantum-mechanical gas-phase free energy change of the reaction. This approach is analogous to the widely used method for estimating the pKa of a titrating site in a protein by introducing the reference pKa of a model system in solution (17, 18).
Methods
Structural Information.
There are three sets of similar structures of bovine mitochondrial F1-ATPase, which have different nucleotides bound in the catalyic β sites. The original F1-ATPase structure at 2.8 Å (4) has AMP-PNP,Mg2+ and ADP,Mg2+ in the βTP and βDP sites, respectively; the βE site is empty. A similar structure at 2.5-Å resolution (5) has AMP-PNP,Mg2+ in the βTP site and ADP,Mg2+ and AlF3 in the βDP site, and the βE site is empty. The more recent structure at 2 Å (6) has all three catalytic sites occupied with the βTP and βDP sites both containing ADP, Mg2+, and AlF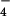 ; the third site, which is empty in the two other structures, adopts a so-called “half-closed” conformation (βHC), and is occupied by ADP and sulfate (mimicking phosphate). This alteration in conformation from βE to βHC is made possible by a rotation of the coiled–coil region of γ subunit by about 30° from its position in the ref. 5 structure to the ref. 6 structure.
; the third site, which is empty in the two other structures, adopts a so-called “half-closed” conformation (βHC), and is occupied by ADP and sulfate (mimicking phosphate). This alteration in conformation from βE to βHC is made possible by a rotation of the coiled–coil region of γ subunit by about 30° from its position in the ref. 5 structure to the ref. 6 structure.
The latter two structures [Protein Data Bank codes 1E1R (5) and 1H8E (6)] were used for the free energy simulations, because they are at a somewhat higher resolution than the original structure and contain ligands in configurations most useful for constructing the reactants and products of reaction 1 required for the simulations (see Fig. 5, which is published as supporting information on the PNAS web site, www.pnas.org). Also, the hexacoordination of Mg2+ ions, which involves several waters is clear from the x-ray structure; the results are generally in accord with the deductions from the mutagenesis studies of Weber et al. (20) for EcF1. ATP was directly overlapped with AMN-PNP and with ADP, AlF3, or ADP, AlF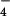 ; in the latter two, the γ-phosphate of ATP was superimposed on the Al atom. For ADP,Pi, the ADP was superimposed on the corresponding atoms of ATP and ADP and the phosphorous atom of Pi was placed at the γ-phosphate position of AMP-PNP and at Al of AlF3 and AlF
; in the latter two, the γ-phosphate of ATP was superimposed on the Al atom. For ADP,Pi, the ADP was superimposed on the corresponding atoms of ATP and ADP and the phosphorous atom of Pi was placed at the γ-phosphate position of AMP-PNP and at Al of AlF3 and AlF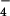 , and the S of the SO
, and the S of the SO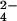 . Because the water between Glu-188 and the ligand is believed to be involved in the reaction, one oxygen of Pi was placed at the position of the oxygen of this water. In the βHC site, the reacting water was superimposed on one of the oxygens of SO
. Because the water between Glu-188 and the ligand is believed to be involved in the reaction, one oxygen of Pi was placed at the position of the oxygen of this water. In the βHC site, the reacting water was superimposed on one of the oxygens of SO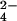 , which points away from ADP. Once the initial positions of the ligand atoms were modeled as described, the ligands were minimized with all other atoms of the system fixed to obtain chemically reasonable structures.
, which points away from ADP. Once the initial positions of the ligand atoms were modeled as described, the ligands were minimized with all other atoms of the system fixed to obtain chemically reasonable structures.
Continuum electrostatics calculations were used to determine the protonation states of the ligands (17, 18). For all protein residues, standard protonation states were obtained. The phosphate groups of ATP and ADP are deprotonated in the enzyme and the Pi complexed with ADP is doubly protonated (H2PO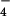 ), as it is in solution at pH 7. In the reference solution simulation, the same protonation states as found in the crystal structure were used with the experimental value (−10.8 kcal in ref. 16) corresponding to those protonation states.
), as it is in solution at pH 7. In the reference solution simulation, the same protonation states as found in the crystal structure were used with the experimental value (−10.8 kcal in ref. 16) corresponding to those protonation states.
Free Energy Calculations.
Each of the five occupied catalytic sites in the two structures used for the simulations was overlapped with a 25-Å stochastic boundary sphere centered on the γ phosphorous of ATP or on Pi. Several water overlays were made and ≈200 water molecules were added in addition to crystal waters; none of the additional waters interacted with the ligands. Solvent within the 25-Å sphere was treated explicitly. To account for the screening of long−range electrostatic interactions, charge scale factors were calculated for the ionic groups (all charged amino acid residues, Mg2+, ATP, ADP, and Pi) outside of the 25-Å sphere; these include, for example, ATP and Mg2+ in a neighboring α subunit.
The CHARMM 22 all-atom force field was used for the protein and the ligands (21), and the water was treated by a modified TIP3P model (22, 23); the charges on the ligands are shown in Fig. 6, which is published as supporting information on the PNAS web site. van der Waals interactions were switched to zero between 8 and 12 Å, and electrostatic interactions were treated by using a multipole approximation for groups >13 Å apart (24). The dielectric constant was set equal to 1, consistent with the charmm charges in a solvated environment.
Protein atoms more than 25 Å from the center of the sphere were fixed during the simulation and the atoms between 22 and 25 Å from the center were harmonically restrained to their initial positions. The force constants used were determined from the B factor of the appropriate residues in the crystal structures, multiplied by a scaling function that increases linearly from zero to one between 22 and 25 Å (25). The stochastic boundary method was used to restrain the water molecules within a 25-Å sphere (25–27). The internal geometries of the water molecules were constrained with the shake algorithm (28). Newtonian dynamics was used for all atoms inside the 22-Å radius and Langevin dynamics was used to simulate frictional and random forces experienced by protein and water heavy atoms located between 22 and 25 Å. The molecular dynamics simulations were done at 300 K with a 1-fs time step.
Free energy simulations were performed by using thermodynamic integration with the dual topology method in the block module (29) of the charmm program (30). The hybrid structure involving ATP and ADP was built from the bridging oxygen between the α- and β-phosphate of ADP and ATP. Bond and angle terms were not scaled during the free energy calculations (31). To avoid end point problems, the integrations were done by fitting to an analytic function of the form λ−1/4 (14). To determine the free energy of the reaction in solution, as required in Eq. 2, the differences of ATP versus ADP and H2O versus Pi were calculated individually in the absence of Mg2+. For each transformation, a cubic periodic water box 31 Å on a side was used; it contains the solutes and about 1,000 water molecules.
The free energy component analysis was performed as described (12–15, 29).
Thermodynamic Integration Windows and Convergence.
For the thermodynamic integration, linear scaling of the potential (12–15) was used with values for the scale parameter λ of 0.02, 0.05, 0.1, 0.15, 0.25, 0.35, 0.45, 0.55, 0.65, 0.75, 0.85, 0.9, 0.95, and 0.98. For each λ, the equilibration and production periods were determined by monitoring the convergence of the reverse cumulative average of the potential energy derivative with respect to λ. In this approach, simulations are done in 20-ps sets and monitored for convergence of the energy derivative by cumulative averaging beginning with the final value of the derivative and going backward in time. If the results are not well behaved, additional 20-ps sets are added. Convergence is achieved when a plateau value that lasts 20 ps or longer is present in the reverse cumulative average; the plateau is usually disrupted after a certain time by contributions from the initial equilibration portion of the trajectory. In this way, in contrast to standard methods, equilibration and convergence are treated separately. Equilibration was found to require 80–500 ps, longer than used previously in many simulations, and convergence required 50–100 ps. Detailed tests of this approach will be published separately (W.Y. and M.K., unpublished work).
Results
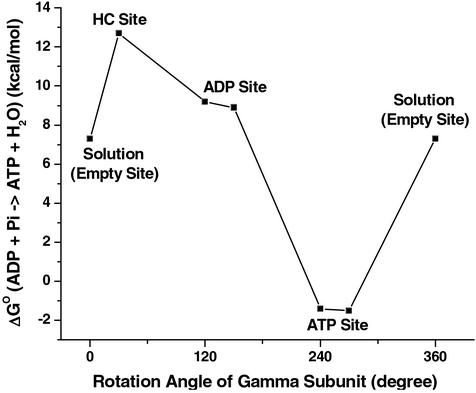
The results obtained for the catalytic β-subunit structures in refs. 5 and 6 are shown in Table 1. It can be seen that bound ATP/H2O has a free energy similar to that of ADP/Pi in the βTP site, whereas the free energy in the βDP site strongly favors ADP/Pi, relative to ATP. Experiments have shown that under unisite hydrolysis conditions, the free energies of ATP/H2O and ADP/Pi in the occupied site are nearly the same; i.e., the measured ΔGo values are 0.4 kcal/mol in the mitochondrial enzyme (MF1) (8) and −0.6 kcal/mol in the E. coli enzyme (EcF1) (9). Because unisite hydrolysis is expected to take place in the tight site, the above results identify the βTP and βDP subunits as the ones containing the tight and loose sites, respectively, for ATP binding. Synthesis of ATP is believed to involve clockwise rotation of the γ subunit, as viewed from the membrane (10), so that the changes in ATP binding affinity in a given site during the rotation cycle are βHC(loose′) → βDP (loose) → βTP (tight) → βE (weak), given the results of the calculations. The corresponding free energies of reaction 1 during the rotation cycle in the ATP synthesis direction are shown in Fig. 1. We consider the role of this sequence of steps in Discussion.
Table 1.
Standard free energy change (ΔG0) of the reaction ATP+H2O → ADP+Pi in the catalytic sites of F1-ATPase
The values are obtained by using Eq. 2. As an example we consider the βDP site of the ref. 6 structure for which ΔG(ATP → ADP)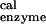 = 125.5 kcal/mol; the solution values are ΔG(ATP → ADP)
= 125.5 kcal/mol; the solution values are ΔG(ATP → ADP)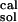 = 123.6 kcal/mol, and ΔG(ATP → ADP)
= 123.6 kcal/mol, and ΔG(ATP → ADP)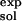 = −10.8 kcal/mol (16). The value ΔG(ATP → ADP)
= −10.8 kcal/mol (16). The value ΔG(ATP → ADP)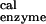 = 125.5 kcal/mol consists of the contributions of the protein, Mg2+ and H2O (it is equal to −21.0 kcal/mol for the βDP site in the ref. 6 structure) and the intrasubstrate and intersubstrate contributions of the bound reactants and products (146.5 kcal/mol, favoring the reactants).
= 125.5 kcal/mol consists of the contributions of the protein, Mg2+ and H2O (it is equal to −21.0 kcal/mol for the βDP site in the ref. 6 structure) and the intrasubstrate and intersubstrate contributions of the bound reactants and products (146.5 kcal/mol, favoring the reactants).
Figure 1.
Calculated free energies for the synthesis reaction ADP+Pi → ATP/H2O in the indicated sites obtained starting with the structures in refs. 5 and 6 as a function of the rotation angle of the γ subunit; the ref. 6 results are displaced by ≈30° with respect to the structure in ref. 6 based on the x-ray data. The free energy of the reaction given for that in solution (0° and 360°) is in the presence of Mg2+; the value of −10.8 kcal/mol used in Eq. 2 is without Mg2+ (16). The value for the βE subunit is thought to be similar to the solution value (see text).
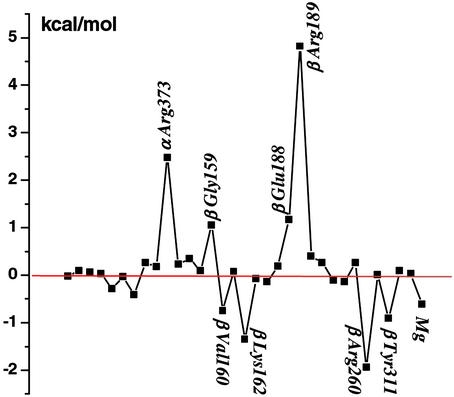
It is of interest to use the calculations to obtain information concerning the nature of the interactions that contribute to the free energy values obtained for reaction 1 in the various sites. Such an analysis is of particular importance for the βTP and βDP sites, since they are very similar in conformation and bind the ligands in a corresponding manner (see, for example, figure 2 of ref. 6); it has, in fact, been proposed in some mechanistic analyses of F1-ATPase that the two sites can be regarded as identical (32). The large electrostatic interactions between the nearby (mainly charged) residues of the enzyme and the charged reactant and product ligands lead to a balance of free energy contributions that is sensitive to the structural details. Figs. 2 and 3 show the important residues that interact with ATP/H2O or ADP/Pi in the βTP site of ref. 6; the βDP site looks similar. A component analysis of the free energy simulations (12–15) was used to estimate the essential interactions involved; applications of this type of approach to binding and catalysis include tyrosine t-RNA synthetase (33), triosephosphate isomerase (34, 35), and uracil DNA glycosylase (15). Fig. 4 shows the residue contributions to the difference in the free energies of reaction 1 between the βTP and βDP sites; this difference is an essential element of the binding change mechanism. The interactions with the protein, water and Mg2+ stabilize ADPi/Pi relative to ATP/H2O less in the βTP site than the βDP site; the calculated values are −12 (−14) and −21 (−21) kcal/mol, respectively, in the ref. 6 (ref. 5) structures (see Table 1 legend). Certain charged residues, which have been discussed based on the available structures (4–6) and mutagenesis data for F1ATPase of E. coli (3), are most important; they are Arg-373 in the corresponding α subunits (αTP for βTP and αDP for βDP; see ref 4) and Lys-162, Glu-188, Arg-189, Glu-192, and Arg-260 in the β subunits. In addition, β Tyr-311, and the main-chain NHs of β Gly-159 and β Val-160 in the P-loop, which is characteristic of nucleotide binding sites (36, 37), contribute significantly to the difference. The Mg2+ ion, which is essential for strong binding of ATP in the tight and loose sites (3), is also important in the differential binding (Fig. 4). Other residues contribute to the free energy difference in reaction 1, but their contributions in the two sites are nearly identical. Certain charged residues, such as α Asp-347 and β Arg-337 make only small contributions to the free energy differences, primarily because they are distant from the active site; this finding indicates that the size of the sphere used in the calculations (see above) is sufficient to obtain meaningful results.
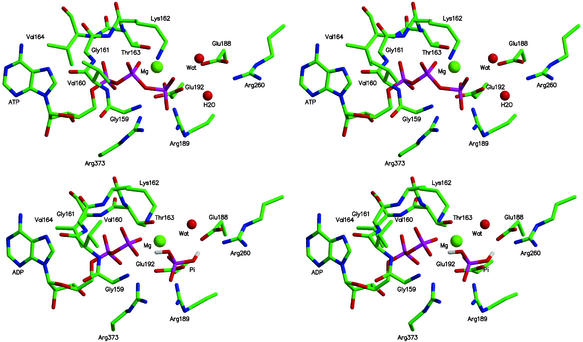
Figure 2.
Cross-eyed stereo images of the calculated geometries of the βTP site with ATP,H2O and ADP,Pi as ligands based on the structure in ref. 6. The results are close to those from the observed structures but show slightly shorter ligand–protein distances; this finding is in accord with expectations, given that ATP binds by a factor 103 times more strongly than the inhibitor AMP-PNP to the tight (βTP) site (3).
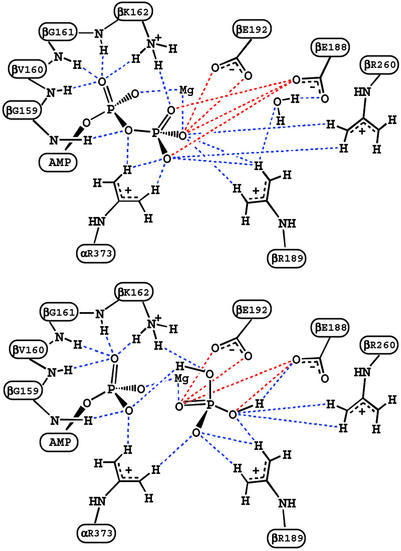
Figure 3.
Schematic diagrams corresponding to Fig. 2 to indicate the important interactions. The blue and red dashed lines correspond to attractive and repulsive interactions, respectively.
Figure 4.
Contributions (kcal/mol) of residues in order of sequence number (α subunit first and then the β subunit) and Mg2+ to the free energy difference for reaction 1 between the βTP and βDP sites; residues that contribute 0.5 kcal/mol or more are included and those making the largest contributions to the difference are labeled. Positive values correspond to the residues that stabilize (destabilize) the product ADP/Pi, relative to the reactants ATP/H2O, in the hydrolysis reaction in the βDP site more (less) than in the βTP site.
To go further in the analysis, we decompose the contributions of the important residues into those for the partial “reactions” ATP to ADP and H2O to Pi (see Fig. 7, which is published as supporting information on the PNAS web site). Although the values of the free energies of reaction 1 in each of the sites (Table 1) are the essential results of the simulations, their decomposition, which is based on a linear thermodynamic integration scheme (12–15), provides insights into the details of the interactions. The contributions to the half-reactions in the βTP and βDP sites are very close to each other in all cases. This finding is in accord with the structural data, which indicate that the two binding sites and the nature of the interactions are similar. Nevertheless, the overall free energies of the reaction are significantly different in the two sites, as already described above; i.e., there is approximately equal stability of ATP/H2O and ADP/Pi in the tight binding (βTP) site, where synthesis is expected to take place, whereas the βDP site has a reaction free energy similar to that in solution. For all positively charged residues, the half-reaction ATP → ADP is destabilized and the half-reaction H2O → Pi is stabilized by the protein; the negatively charged Glu-188 and Glu-192 show an inverse behavior. This difference corresponds to the expectation that the dominant interactions are attractive for the positively charged side chains and repulsive for the negatively charged ones.
To illustrate the nature of the interactions, we consider certain residues in detail; we present results based on the ref. 6 structure. For α Arg-373, which makes an important contribution to the calculated reaction free energy (see Fig. 4), we find that ATP is stabilized relative to ADP because one of the NH2 groups interacts strongly with two oxygens and the other with one oxygen of the γ-phosphate of ATP, whereas only one of the NH2 groups interacts strongly with an oxygen of β-phosphate in the ADP/Pi structure (see Fig. 3). This difference is counterbalanced, in part, by the stronger interaction of α Arg-373 with Pi than with H2O. Comparing the βTP and βDP sites, we find that the difference for the two sites is associated with the ATP to ADP half-reaction (see Fig. 7). There is a slightly larger stabilization of ATP vs. ADP caused by the stronger interaction with the γ-phosphate in the βTP than the βDP site.
We note that mutation experiments in EcF1 suggest that, although residue α Arg-376 (which corresponds to α Arg-373 in MF1) is important for catalysis, it has only a small effect on the ATP/H2O//ADP/Pi equilibrium (ref. 38 but see also ref. 39). This difference between the calculated contribution and that obtained from the mutation studies could be caused by several factors (13). One is that the mutant structure and interactions are significantly different from those in the wild type. The calculated contribution to differential binding corresponds to that made by the residue in the wild-type structure and not in the mutant structure. The possible importance of this difference is illustrated by an analogous example found in the analysis of mutations in aspartyl t-RNA synthetase (13). In that case, Lys-198 is calculated to make an important contribution to the binding of the Asp ligand in the wild-type enzyme, but the Lys-198 to Leu mutant has essentially the same binding free energy as the wild type. This cancellation arises from an adjustment of the position of other charged residues and the Asp substrate when the Lys-198 side chain is deleted in the mutant. Corresponding compensation could be taking place in F1-ATPase. It is possible also that the position of the corresponding Arg residue is different in the two enzymes, given its demonstrated 10-Å shift between two structures of the mitochondrial enzyme (40). A structure of EcF1 and its mutants would be very useful in this regard, as well as for the interpretation of other data available for this species.
For β Lys-162, the NH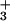 moiety interacts strongly with two phosphate oxygens and the main-chain NH with one phosphate oxygen in both ATP/H2O and ADP/Pi (see Figs. 2 and 3). The difference in the stabilization of the two half-reactions arises primarily from the fact that the charge on the γ-phosphate oxygen of ATP is −0.90, whereas that on the OH oxygen of Pi is only −0.72 (see Fig. 6). For Glu-188 and Glu-192, the repulsive interactions involve the carboxyl oxygens of the amino acids and the phosphate oxygens of the substrate or product. Kinetic measurements (3, 41) of mutants in EcF1 corresponding to β Lys-162 and β Glu-188 in MF1 yield results for the difference in the reaction free energy of Eq. 1 between the βTP and βDP sites of the same sign as in Fig. 4, but the experimental values are somewhat smaller in magnitude than the calculated ones, as expected (see above); there appear to be no data for β Arg-189.
moiety interacts strongly with two phosphate oxygens and the main-chain NH with one phosphate oxygen in both ATP/H2O and ADP/Pi (see Figs. 2 and 3). The difference in the stabilization of the two half-reactions arises primarily from the fact that the charge on the γ-phosphate oxygen of ATP is −0.90, whereas that on the OH oxygen of Pi is only −0.72 (see Fig. 6). For Glu-188 and Glu-192, the repulsive interactions involve the carboxyl oxygens of the amino acids and the phosphate oxygens of the substrate or product. Kinetic measurements (3, 41) of mutants in EcF1 corresponding to β Lys-162 and β Glu-188 in MF1 yield results for the difference in the reaction free energy of Eq. 1 between the βTP and βDP sites of the same sign as in Fig. 4, but the experimental values are somewhat smaller in magnitude than the calculated ones, as expected (see above); there appear to be no data for β Arg-189.
In the βHC site, there are significant differences in the individual amino acid contributions from those in the βTP and βDP sites, e.g., those from α Arg-373, β Arg-189, as well as that of Mg2+. Overall, the sum of the interactions with the environment contributes nearly zero to the reaction free energy in the βHC site. The major source of the strong stabilization of the product relative to the reactants in the βHC site arises from the fact that ADP and Pi are further apart than in the βTP and βDP sites. No free energy difference simulations were made for the βE site, because of the difficulty of obtaining a reliable model for the ligands in this site. However, given the identification of the tight and loose sites with βTP and βDP, respectively, βE is the weak binding site, as has been suggested (4–6), and it is likely to have a reaction free energy similar to, but somewhat less negative than that in solution (see Fig. 1).
Discussion
The present calculations make possible an association of the different catalytic sites in the x-ray structures with their measured binding affinities, the missing link in developing a microscopic description of the mechanism of F1-ATPase. The result that the tight binding site for ATP is the βTP site leads to a consistent model for ATP synthesis. Analysis of the calculated contributions demonstrates that there is a delicate balance between the interactions of a number of (mainly charged) residues with the ligands that modulate the binding free energies of the structurally similar βTP and βDP sites. The difference in the free energy of the reaction ATP/H2O → ADP/Pi is an essential aspect of the binding change mechanism.
Recent molecular dynamics simulations (42, 43) have demonstrated how rotation of the γ subunit during synthesis can drive the conformational change of the β subunits postulated from the x-ray data; although it does not give any indication of the forces involved, the interpolated pathway determined by Wang and Oster (44) is also of interest in this regard. Both steric and electrostatic interactions have been shown to contribute to the observed structural changes. The present results suggest that in ATP synthesis binding of the substrate occurs during the transition from βΕ to βHC, which has its binding free energy strongly biased toward ADP/Pi, relative to ATP/H2O (see Fig. 1). Rotation of the γ subunit transforms this site to the βDP site, which is less biased toward ADP/Pi, as compared with βHC, but it is only during the subsequent rotation and the change of βDP to βTP that the reaction free energy ADP,Pi → ATP,H2O is reduced to near zero and synthesis of ATP is expected to occur. The equalization of the reaction free energy lowers the activation free energy of the chemical step. The final release step takes place during the last portion of the rotation (βTP to βE or, possibly βHC), with the latter binding ATP only weakly.
The molecular dynamics simulations (42, 43) indicate that closing of βE to form βHC is spontaneous, once ligand is bound and the γ subunit has rotated by ≈30° as a result of the proton gradient. The next step, during which the γ subunit rotates by ≈90° and βHC changes to βDP is also expected to require little energy; the actual value depends on the absolute binding constants of ADP,Pi in the two sites (Y.Q.G., W.Y., R. A. Marcus, and M.K., unpublished work). The conformational change from βDP to βTP and synthesis of ATP is expected to be nearly spontaneous, given the reaction free energy of the two sites. The final product release step (βTP to βE), in which the strong affinity of βTP for ATP has to be overcome (the experimental value in MF1 is about −16.6 kcal/mol), requires the largest energy input in synthesis. It is here that the cooperativity embodied in the rotational catalysis plays an essential role; i.e., the rotation of the γ subunit and binding of substrate to the βHC site aids in the transformation of βTP to βE and the release of product. Given these results, one would expect all three sites to be occupied by ligands on average when the reactant concentrations are such as to obtain the optimum rate of synthesis.
Although we have focused on ATP synthesis, we note that the results are also of interest for the mechanism of the γ-subunit rotation during hydrolysis by F1-ATPase. The dissipation of the energy from an exothermic reaction (ATP/H2O to ADP/Pi), which is on the subnanosecond time scale in proteins (45), would be far too rapid to contribute directly to the γ-subunit rotation, which is on the millisecond time scale. The present analysis provides a detailed understanding of the origin of the differential affinities for the reactants and products, which are essential for making the energy available for driving the reaction. The results are in accord with the binding change mechanism for this “splendid molecular machine” (46, 47). An analogous binding change mechanism is likely to be the general basis of the energy transduction that drives a conformational change by ATP hydrolysis in molecular systems, such as GroEL and the molecular motors myosin and kinesin.
Supplementary Material
Acknowledgments
We thank A. Dinner and A. E. Senior for reading the manuscript and making many useful suggestions. We thank J. E. Walker and A. G. W. Leslie for providing some of the structures used in the simulations before publication. We thank I. Andricioaei, R. Bitetti-Putzer, P. Maragakis, and R. Petrella for advice concerning the calculations. We thank R. Yelle for his assistance with the local computing environment. Some of the computations were done at the National Energy Research Scientific Computing Center. The research was supported in part by a grant from the National Institutes of Health.
Abbreviation
- AMP-PNP
adenosine 5′-[β,γ-imido]triphosphate
References
- 1.Boyer P D. Angew Chem Int Ed Engl. 1998;37:2296–2307. doi: 10.1002/(SICI)1521-3773(19980918)37:17<2296::AID-ANIE2296>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
- 2.Walker J E. Angew Chem Int Ed Engl. 1998;37:2309–2319. [Google Scholar]
- 3.Weber J, Senior A E. Biochim Biophys Acta. 1997;1319:19–58. doi: 10.1016/s0005-2728(96)00121-1. [DOI] [PubMed] [Google Scholar]
- 4.Abrahams J P, Leslie A G W, Lutter R, Walker J E. Nature. 1994;370:621–628. doi: 10.1038/370621a0. [DOI] [PubMed] [Google Scholar]
- 5.Braig K, Menz R I, Montgomery M G, Leslie A G W, Walker J E. Structure (London) 2000;8:567–573. doi: 10.1016/s0969-2126(00)00145-3. [DOI] [PubMed] [Google Scholar]
- 6.Menz R I, Walker J E, Leslie A G W. Cell. 2001;106:331–341. doi: 10.1016/s0092-8674(01)00452-4. [DOI] [PubMed] [Google Scholar]
- 7.Stock D, Leslie A G W, Walker J E. Science. 1999;286:1700–1705. doi: 10.1126/science.286.5445.1700. [DOI] [PubMed] [Google Scholar]
- 8.Penefsky H S. Methods Enzymol. 1986;126:608–619. doi: 10.1016/s0076-6879(86)26064-4. [DOI] [PubMed] [Google Scholar]
- 9.Senior A E. J Bioenerg Biomembr. 1992;24:479–484. doi: 10.1007/BF00762365. [DOI] [PubMed] [Google Scholar]
- 10.Noji H, Yasuda R, Yoshida M, Kinoshita K., Jr Nature. 1997;386:299–302. doi: 10.1038/386299a0. [DOI] [PubMed] [Google Scholar]
- 11.Nakamoto R K, Ketchum C J, Al-Shawi M K. Annu Rev Biophys Biomol Struct. 1999;28:205–234. doi: 10.1146/annurev.biophys.28.1.205. [DOI] [PubMed] [Google Scholar]
- 12.Gao J, Kuczera K, Tidor B, Karplus M. Science. 1989;244:1069–1072. doi: 10.1126/science.2727695. [DOI] [PubMed] [Google Scholar]
- 13.Simonson T, Archontis G, Karplus M. Acc Chem Res. 2002;35:430–437. doi: 10.1021/ar010030m. [DOI] [PubMed] [Google Scholar]
- 14.Simonson T, Archontis G, Karplus M. J Phys Chem B. 1997;41:8347–8360. [Google Scholar]
- 15.Dinner A, Blackburn G M, Karplus M. Nature. 2001;413:752–755. doi: 10.1038/35099587. [DOI] [PubMed] [Google Scholar]
- 16.George P, Witonsky R J, Trachtman M, Wu C, Dorwart W, Richman L, Richman W, Shurayh F, Lentz B. Biochim Biophys Acta. 1970;223:1–15. doi: 10.1016/0005-2728(70)90126-x. [DOI] [PubMed] [Google Scholar]
- 17.Bashford D, Karplus M. Biochemistry. 1990;29:10219–10225. doi: 10.1021/bi00496a010. [DOI] [PubMed] [Google Scholar]
- 18.Schaefer M, Sommer M, Karplus M. J Phys Chem B. 1997;101:1663–1683. [Google Scholar]
- 19.Al-Shawi M K, Senior A E. Biochemistry. 1992;31:878–885. doi: 10.1021/bi00118a033. [DOI] [PubMed] [Google Scholar]
- 20.Weber J, Hammond S T, Wilke-Mounts S, Senior A E. Biochemistry. 1998;37:608–614. doi: 10.1021/bi972370e. [DOI] [PubMed] [Google Scholar]
- 21.MacKerell A D, Jr, Bashford D, Bellott R L, Dunbrack R L, Jr, Evanseck J D, Field M J, Fischer S, Gao J, Guo H, Ha S, et al. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 22.Jorgensen W L, Chandrasekhar J, Madura J D, Impey R W, Klein M L. J Phys Chem. 1983;79:926–935. [Google Scholar]
- 23.Neria E, Fischer S, Karplus M. J Chem Phys. 1996;105:1902–1921. [Google Scholar]
- 24.Stote R H, States D J, Karplus M. J Chim Phys. 1991;88:2419–2433. [Google Scholar]
- 25.Brooks C, III, Bržnger A T, Karplus M. Biopolymers. 1985;24:843–865. doi: 10.1002/bip.360240509. [DOI] [PubMed] [Google Scholar]
- 26.Brooks C, III, Karplus M. J Mol Biol. 1989;208:159–181. doi: 10.1016/0022-2836(89)90093-4. [DOI] [PubMed] [Google Scholar]
- 27.Brooks C, III, Karplus M. J Chem Phys. 1984;79:6312–6325. [Google Scholar]
- 28.Ryckaert J, Ciccotti G, Berendsen H. J Comput Phys. 1977;23:327–341. [Google Scholar]
- 29.Tidor B, Karplus M. Biochemistry. 1991;30:3217–3228. doi: 10.1021/bi00227a009. [DOI] [PubMed] [Google Scholar]
- 30.Brooks B R, Bruccoleri R E, Olafson B D, States D J, Swaminathan S, Karplus M. J Comp Chem. 1983;4:187–217. [Google Scholar]
- 31.Boresch S, Karplus M. J Phys Chem A. 1999;103:119–136. [Google Scholar]
- 32.Allison W S. Acc Chem Res. 1998;31:819–826. [Google Scholar]
- 33.Lau F T K, Karplus M. J Mol Biol. 1994;236:1049–1066. doi: 10.1016/0022-2836(94)90011-6. [DOI] [PubMed] [Google Scholar]
- 34.Bash P A, Field M J, Davenport R C, Petsko A, Ringe D, Karplus M. Biochemistry. 1991;30:5821–5832. doi: 10.1021/bi00238a002. [DOI] [PubMed] [Google Scholar]
- 35.Cui Q, Karplus M. J Am Chem Soc. 2001;123:2284–2290. doi: 10.1021/ja002886c. [DOI] [PubMed] [Google Scholar]
- 36.Walker J E, Saraste M, Runswick M J, Gay N J. EMBO J. 1982;1:945–951. doi: 10.1002/j.1460-2075.1982.tb01276.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Saraste M, Sibbald P R, Wittinghofer A. Trends Biochem Sci. 1990;15:430–434. doi: 10.1016/0968-0004(90)90281-f. [DOI] [PubMed] [Google Scholar]
- 38.Nadanaciva S, Weber J, Wilke-Mounts S, Senior A E. Biochemistry. 1999;38:15493–15499. doi: 10.1021/bi9917683. [DOI] [PubMed] [Google Scholar]
- 39.Le N P, Omote H, Wada Y, Al-Shawi M K, Nakamoto R K, Futai M. Biochemistry. 2000;39:2778–2783. doi: 10.1021/bi992530h. [DOI] [PubMed] [Google Scholar]
- 40.Gibbons C, Montgomery M G, Leslie A G W, Walker J E. Nat Struct Biol. 2000;7:1055–1061. doi: 10.1038/80981. [DOI] [PubMed] [Google Scholar]
- 41.Senior A E, Al-Shawi M K. J Biol Chem. 1992;267:21471–21478. [PubMed] [Google Scholar]
- 42.Bšckmann R A, Grubmüller H. Nat Struct Biol. 2002;9:198–202. doi: 10.1038/nsb760. [DOI] [PubMed] [Google Scholar]
- 43.Ma J, Flynn T C, Cui Q, Leslie A, Walker J E, Karplus M. Structure (London) 2002;10:921–931. doi: 10.1016/s0969-2126(02)00789-x. [DOI] [PubMed] [Google Scholar]
- 44.Wang H, Oster G. Nature. 1998;396:279–282. doi: 10.1038/24409. [DOI] [PubMed] [Google Scholar]
- 45.Henry E R, Eaton W A, Hochstrasser R M. Proc Natl Acad Sci USA. 1986;83:8982–8986. doi: 10.1073/pnas.83.23.8982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Boyer P D. In: Membrane Bioenergetics. Lee C P, Schatz C, Ernster L, editors. Waltham, MA: Addison–Wesley; 1979. pp. 461–477. [Google Scholar]
- 47.Boyer P D. Annu Rev Biochem. 1997;66:717–749. doi: 10.1146/annurev.biochem.66.1.717. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.