Comparing population structure as inferred from genealogical versus genetic information

Abstract

Algorithms for inferring population structure from genetic data (ie, population assignment methods) have shown to effectively recognize genetic clusters in human populations. However, their performance in identifying groups of genealogically related individuals, especially in scanty-differentiated populations, has not been tested empirically thus far. For this study, we had access to both genealogical and genetic data from two closely related, isolated villages in southern Italy. We found that nearly all living individuals were included in a single pedigree, with multiple inbreeding loops. Despite F_st between villages being a low 0.008, genetic clustering analysis identified two clusters roughly corresponding to the two villages. Average kinship between individuals (estimated from genealogies) increased at increasing values of group membership (estimated from the genetic data), showing that the observed genetic clusters represent individuals who are more closely related to each other than to random members of the population. Further, average kinship within clusters and F_st between clusters increases with increasingly stringent membership threshold requirements. We conclude that a limited number of genetic markers is sufficient to detect structuring, and that the results of genetic analyses faithfully mirror the structuring inferred from detailed analyses of population genealogies, even when F_st values are low, as in the case of the two villages. We then estimate the impact of observed levels of population structure on association studies using simulated data.

Introduction

Geographic isolates represent valuable resources for the dissection of complex genetic traits.^{1, 2, 3, 4} In principle, geographical isolation implies that genetic determinants and environmental factors contributing to complex traits are homogeneous across individuals. Unfortunately, undetected structuring within populations may bias association studies, and concerns about population stratification exist even in apparently homogeneous communities,⁵ essentially because their long-term demographic histories are generally unknown. The only way to ensure that isolates are not cryptically structured is through geneaological reconstruction.^{6, 7} In general, however, reconstructed pedigrees tend to span very few generations, and hence one has to resort to indirect evidence about structuring, typically obtained through analyses of genetic variation. To our knowledge, there has been no empirical comparison of genealogically and genetically inferred relationships in isolated populations.

A population is structured when it departs from panmixia because it is divided into sub-populations between which there is a certain degree of reproductive isolation. A number of Bayesian clustering algorithms have been developed in recent years that have proven effective in identifying genetic clusters of individuals in analyses of human populations.^{8, 9, 10, 11, 12, 13} Such populations were often distributed worldwide,^{14, 15, 16} but sometimes geographically close and isolated.¹⁷ Nonetheless, all populations investigated so far were well differentiated; values of Wright's genetic variance between sub-populations, F_st, were always >0.01. It is unknown whether and to what extent these methods can efficiently describe the structure of scanty-differentiated populations, such as those inhabiting small geographical regions. To date, this issue has only been addressed in simulated populations.¹⁸

Detection of population structure in genetic isolates is crucial because population stratification, ie, the existence of clusters of genetically non-independent individuals, is considered to be the main source of bias in association studies.^{19, 20, 21} Devlin and Roeder²² suggest that a common framework, termed genomic control, may be used to control for the effect of both population stratification and inter-individual relatedness on association tests using ‘null' markers. Where genealogical information is available, and inter-individual relatedness is considered the sole source of bias, this information is used directly in association tests without the need for genomic data.^{19, 23, 24}

In this study, we use genealogical and genetic data from Gioi²⁵ and Cardile, two isolated villages from southern Italy, close to a previously studied isolated village.^{26, 27} We investigated the extent of overlap between population structure inferred from genetic analyses and from detailed studies of genealogical relationships. We then develop a computer-simulation model incorporating observed levels of kinship to quantify the potential bias of observed levels of population structure on association studies.

Materials and methods

Study sample, genetic and genealogical data

The study sample comprises 1356 individuals from the villages of Gioi (n=882) and Cardile (n=474), corresponding almost completely to current residents. According to historical sources, the village of Gioi was settled in the ninth century BC by Greeks, and in the tenth century AD founders from Gioi settled Cardile 6 km away. High levels of reproductive isolation are reported for the two villages until the middle of the twentieth century.

We collected 20 383 birth records spanning the last four centuries from registry office and parish archives. These data were used to construct pedigrees spanning 350 years (15–17 generations). Kinship coefficients (Φ_ij) between individuals i and j were calculated as described in Karigl et al²⁸ and implemented in the KinInbCoeff module of the CC-QLS package.²³

A genome-wide scan of 1122 microsatellites (average marker spacing of 3.6 cM and mean marker heterozygosity of 0.70) was performed by the deCODE genotyping service on DNA extracted from peripheral blood from all study samples.

Genetic clustering analysis

Genetic clusters were inferred by the software Structure, under assumptions of admixture, correlated allele frequencies, and no prior population information.^{9, 29} For each number of clusters (K) from 1 to 8, 50 runs were performed using a burnin length of 20 000 iterations followed by 10 000 iterations. For each K, the posterior probability of clustering was estimated from the average logarithmic probability of data across runs. The second order rate of change of logarithmic probability of data between subsequent K values was estimated according to Evanno et al³⁰ to identify the optimal number of clusters in the data. Resulting membership coefficients generated by Structure were input into CLUMPP³¹ and analyzed using the LargeKGreedy algorithm. No genuine multimodality was found among runs with average similarity (G' values) of 0.99, 0.79, and 0.89% for K equals 2, 3 and 4, respectively. Graphical display of membership coefficients was obtained by Distruct.³²

Structure was run twice under the conditions described above. First, genotypes at 239 loci, a subset of the1122 loci available in our data, chosen to minimize the probability of linkage disequilibrium between adjacent markers on the chromosomes, were analyzed in all 1356 individuals. Then, we compared the 36 markers common to this study and to the HGDP-CEPH Human Genome Diversity Panel, using random subsamples of 37 and 22 individuals from Gioi and Cardile, respectively, and 161 European individuals available in the HGDP panel. Sizes of subsamples from the two villages were chosen to approximate sample sizes of European populations.

Spearman correlation coefficients were estimated using SPSS 13.0 (SPSS Inc., Chicago, IL, USA). F_st values were computed using the Arlequin 3.1 software.³³

Assessment of bias in association tests

Both population structure and relatedness among individuals contribute to non-independence of genotypes, which, in turn, inflates the variance of tests for allelic association, by a factor λ. For quantitative traits, Bacanu et al³⁴ proposed a method to quantify inflation of the variance of t² using null markers (ie, λ_GC). An alternative, generalized least squares approach, suitable for large, inbred pedigrees with high consanguinity and no population stratification, was proposed by Abney et al.¹⁹ Here, the genealogy-based variance inflation factor, λ_GB, is computed exactly while computing the t² statistic, and it corresponds to the ratio between non-corrected and corrected t² statistics at a given marker.

Simulations for comparing λ_GB and λ_GC were carried out using the Genedrop program from the MORGAN 2.6 package.³⁵ A quantitative trait was simulated for the 446 individuals in the largest pedigree of Cardile, and for a random sample of the same size in the largest pedigrees of Gioi and Gioi–Cardile (see Table 1) with heritability=0.3 and total phenotypic variance=0.0027. We then estimated λ_GC by simulating genotypes at 1122 null markers covering the whole genome for all individuals in the sample, as described in Ciullo et al.²⁷ To mimic a realistic situation, allele frequencies and inter-marker distances matched those of the 1122 microsatellite markers genotyped in the two villages.²⁶ A biallelic locus with a minor allele frequency of 0.3 was further simulated to estimate λ_GB. We considered four simulation schemes in which this locus had no effect on the trait (null model), additive, dominant, or recessive effects. For each model, the median values of λ_GB and λ_GC (expected values of λ_GB=1 and λ_GC=1) over 1000 simulations were estimated.

Table 1. Features of pedigrees reconstructed from sampled individuals using genealogical data.

All pedigrees	Gioi–Cardile	Gioi	Cardile
Sampled individuals included	1356	882	474
No. of pedigrees	63	45	19
No. of generations	Up to 15	Up to 15	Up to 15
Total members in pedigrees	5272	4190	2384
Largest pedigree
Sampled individuals included	1274	828	446
No. of pedigrees	1	1	1
No. of generations	15	15	15
Total members in the pedigree	5165	4113	2354

Results

Genetic clustering

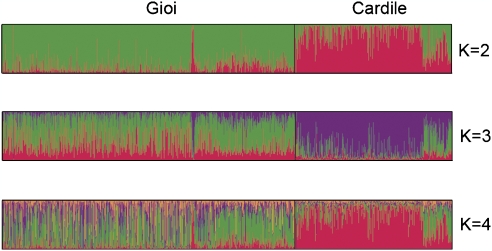
We analyzed population structure in Gioi and Cardile considering up to eight possible genetic clusters (K). Graphical representation of membership to clusters for K=2–4 is shown in Figure 1. The distribution of the logarithmic probability of the data between successive values of K showed no obvious peaks (Supplementary Figure 1); therefore, we inferred the number of clusters by Evanno's rate of change method³⁰ rather than computing the posterior probability of the data.³⁶ The most likely number of clusters was two, with clusters roughly corresponding to villages, despite the limited geographical distance. Individuals were clearly assigned to one of the two clusters, with 78% showing membership coefficients ≥0.75, 55%, ≥0.90 and 37%, ≥0.95 (Supplementary Table 1).

Figure 1.

Cluster membership according to analyses of genotypes at 239 markers in all individuals in the study sample, for K=2–4. Each inferred cluster is represented by a different color.

In comparison with other European populations, no population structure between the villages is apparent, as expected given the greater geographical scope of the analysis (Supplementary Figure 2). In fact, there was essentially no structure at all in the European plus Cilento data set, most likely because the limited degree of differentiation known to exist among European populations^{14, 37, 38} is likely to be undetectable with the low number of shared markers available for consideration. To better clarify this point, we analyzed the subsamples from Gioi and Cardile with the same 36 markers used for comparison with Europe and, again, we were unable to detect the same structure identified using 239 markers (data not shown). This suggests that comparisons across European populations are hardly informative when the number of markers is so small.

Validation of genetic clustering analysis by means of genealogical data

Kinship calculation

Using genealogical data, we backward reconstructed pedigrees starting from all contemporary individuals sampled in Gioi and Cardile (Table 1). In the same table, we report features of the largest reconstructed pedigree, comprising 5165 members and spanning 15 generations. As can be seen, for both individual villages and for the combined population a single pedigree includes nearly all individuals. This proved the presence of multiple relatedness links among individuals and confirmed, in the combined analysis, the common origin of the two villages.

Relatedness was quantified by pairwise kinship coefficients inferred from pedigree data. Summary kinship statistics are reported in Table 2, together with data on other isolated populations from the literature.^{7, 39, 40} Average kinship between individuals of the current generation is 0.004 in Gioi (equal to that between third cousins) and 0.009 in Cardile (approaching that between second cousins, ie, Φ_ij=0.015), showing a high degree of inbreeding in both villages.

Table 2. Kinship (Φ_ij) summary statistics of Gioi and Cardile compared with those of other isolated populations.

	Sample size	Average±SD	Median	25–75% percentiles
Gioi–Cardile	1356	0.003±0.015	0.001	0.000–0.002
Gioi	882	0.004±0.018	0.001	0.000–0.002
Cardile	474	0.009±0.024	0.004	0.001–0.008
Perdasdefogua	821	NA	0.007	0.004–0.011
Talanaa	875	NA	0.014	0.009–0.021
S-leut Hutteritesb	806	0.042±0.031	NA	NA
Icelandc	37762	0.008±NA	NA	0.000–0.001
1925–1949 cohort
Icelandc	38336	0.005±NA	NA	0.000–0.001
1950–1965 cohort

Note that estimates for Iceland were not obtained by comparing all possible pairs of individuals, but only for married couples. NA=not available.

^aFalchi et al.⁴⁰

^bAbney et al.¹⁹

^cHelgason et al.⁷

Membership and kinship

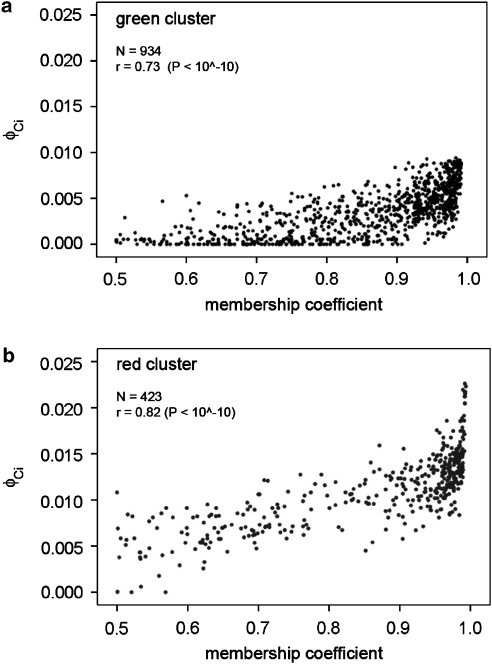
In determining the optimum clustering of the data, Structure estimates membership coefficients corresponding to the probability of an individual's genome belonging to each cluster. To investigate patterns of kinship as a function of group membership, we grouped individuals into clusters to which they had 50% or greater probability of belonging regardless of their village of origin. We compared membership coefficients for each individual with their estimated average kinship with all other members of the cluster, namely Φ_Ci, where C represents the cluster (C=1, 2, representing the green and red clusters in Figure 1) and i the individual considered (934 in the green and 423 in the red clusters). We found highly significant correlations between cluster membership coefficients and Φ_Ci, namely r=0.73 (P<10⁻¹⁰, N=934) and r=0.082 (P<10⁻¹⁰, N=423), respectively, for the green and red clusters in Figure 2.

Figure 2.

Relationship between average kinship of individuals with other cluster members (Φ_Cij; Y axis) and membership coefficients (X axis) for (a) green and (b) red clusters for K=2. Rank correlation coefficients (r) and number of observations (N) are also shown.

F_st and kinship

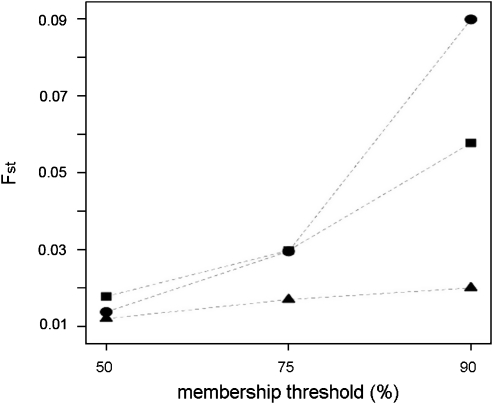
Pairwise F_st between samples from the two villages evaluated using genotypes at the 239 unlinked loci from all sampled individuals is a low 0.008. We investigated whether F_st calculations would be affected with subsamples of individuals with increasing relatedness. To this end, for K=2–4, individuals were clustered with increasing stringency of membership threshold requirements (threshold coefficient levels of 50, 75, 90, 95 and 99 percent; individuals in higher threshold clusters are also found in lower clusters). Regardless of the value of K considered, average kinship within clusters and F_st between clusters increases with increasing membership threshold (Supplementary Table 1, Figure 3). This is true especially for high levels of kinship; with 99% threshold and K=2, kinship in the two groups is between half-siblings (0.125) and first cousins (0.06) and F_st is 0.113.

Figure 3.

Genetic distances (overall F_st) among clusters for varying K values (triangles: K=2; circles: K=3; squares: K=4) and threshold levels of cluster membership. Individuals in higher threshold clusters are also found in lower clusters. Within each K, F_st increases with increasingly stringent threshold levels required for cluster membership (and thus kinship).

Substructure effect on association studies

The variance correction factor of the test for quantitative association was estimated by simulation, in Gioi and Cardile separately and in the combined Gioi–Cardile sample, using both genomic (λ_GC) and genomic/genealogical (λ_GB) approaches.

Genomic- and genealogy-based corrections performed similarly in our data with similar median values of λ_GC and λ_GB (Table 3), regardless of the model used for λ computation, in Gioi and Cardile, where no population structure is described. When the two populations were combined, λ_GC and λ_GB values remained close to those estimated in the two, unstructured, individual populations, and hence close to 1. This result suggests that existing population substructure does not substantially impact the simple association test for quantitative traits when Gioi and Cardile are analyzed together. Once inter-individual relatedness is correctly accounted for using either genomic or genealogical data, the impact of these levels of population substructure appears negligible.

Table 3. Comparison of λ_GC and λ_GB in Gioi–Cardile, Gioi, and Cardile samples.

Median λGC (95% CI)	Gioi—Cardile	Gioi	Cardile
Null	1.126 (1.015–1.262)	1.161 (1.035–1.322)	1.276 (1.103–1.487)
Additive	1.158 (1.043–1.301)	1.196 (1.060–1.363)	1.317 (1.133–1.567)
Dominant	1.149 (1.027–1.278)	1.193 (1.057–1.359)	1.310 (1.127–1.554)
Recessive	1.142 (1.021–1.274)	1.186 (1.054–1.353)	1.300 (1.121–1.549)
Median λGB (95% CI)
Null	1.123 (1.043–1.227)	1.168 (1.063–1.307)	1.275 (1.126–1.461)
Additive	1.136 (1.053–1.242)	1.183 (1.077–1.333)	1.304 (1.141–1.511)
Dominant	1.127 (1.043–1.241)	1.180 (1.073–1.327)	1.298 (1.134–1.507)
Recessive	1.126 (1.044–1.245)	1.177 (1.071–1.333)	1.295 (1.129–1.504)

Median values obtained from null distributions of the tests, considering different genetic effects, are reported.

Discussion

According to available historical data, the populations of Gioi and Cardile share a largely common origin, separating approximately 1000 years ago. Whether or not such a recent separation, combined with the close geographical distance and small population sizes (approximately 1000 for Gioi and 500 for Cardile), could result in significant differentiation was not obvious from the start. We found that genetic differentiation measured by F_st is an apparently low 0.8%. However, Rosenberg et al¹⁴ found that F_st between random (ie, non-isolated) European populations is even lower (namely 0.7%). Therefore, it is safe to conclude that small population sizes and even limited degrees of geographical isolation may rapidly lead to what can be considered a relatively sharp genetic divergence on a European scale. The high level of observed consanguinity confirms that these villages do represent genetic isolates, and hence are potentially useful for the study of complex traits.

Availability of genealogical records since the seventeenth century allowed us to calculate pairwise kinship as an estimator of relatedness between individuals. Strictly speaking, although kinship estimates based on genealogy path counting may not be as accurate as estimates based on genomic data, especially in populations with histories of consanguinity,^{41, 42} kinship inferred from genealogies allowed us to quantify relationships between individuals independently from data used to infer genetic clusters.

The average kinship in Gioi and Cardile is slightly lower than in other Italian genetic isolates⁴⁰ and one order of magnitude lower than in the highly inbred S-leut Hutterites.³⁹ A high correlation emerged between the two independent descriptors of population structure. This study confirms early findings in populations from New Guinea^{43, 44} that limited population size and nonrandom mate choice (resulting in genealogical structure in the population, and ultimately in inbreeding) are indeed reflected in distributions of allele frequencies. To our knowledge, our study represents the first empirical demonstration of that finding based on a thorough comparison of DNA and genealogical data.

Latch et al¹⁸ compared simulated data at 10 co-dominant loci in 100 individuals from five populations, assuming F_st values in the range of 1–10%. They concluded that available methods assign genotypes to clusters with accuracy >97% only if F_st is greater than 5%. Conversely, in this study we were able to identify two clusters and assign individuals almost consistently to their geographic origin, despite F_st being only 0.8%, probably due to the fact that Latch and colleagues considered lower numbers of markers and individuals.^{9, 45} We corroborated our result showing that: (a) individuals belonging to clusters are also genealogically related to other cluster members (by correlating membership coefficients inferred from genomic analysis and average kinship with other cluster members; Figure 2); and (b) the higher the average membership coefficient for a cluster, the greater the kinship between cluster members (as shown by the significant increase in average kinship with increasing membership stringency; Supplementary Table 1).

Population-based studies of complex traits are known to be sensitive to undetected structuring. When genealogical data are not available, genomic-based corrections represent the only viable alternative. By simulation, we estimated to what extent structuring may inflate measures of phenotype–genotype association. We expected that when Gioi and Cardile are treated as a single population, the differences between them, albeit limited, could lead to a poorer performance of genomic- versus genealogy-based corrections. To the contrary, the results show that the effects of the levels of structuring observed in Gioi and Cardile are unlikely to affect these measures to any substantial degree. Once inter-individual relatedness within each population is correctly handled, the effects of subtle differentiation between populations seem limited and indeed not large enough to significantly bias results of association studies.

In short, this study shows that populations may be structured even in geographically close localities whose inhabitants shared ancestors in the recent past. Furthermore, a limited number of neutral genetic markers (eg, 239 in our study) is sufficient to detect these low levels of structuring, and the results of genetic analyses reproduce faithfully the structuring inferred from detailed analyses of population genealogies. Therefore, when the complete genealogy of a study population cannot be reconstructed, which is more often the rule than the exception: (a) typing a few hundred polymorphisms allows one to recognize the effects of kinship and (b) the effects of kinship can be incorporated into models that predict possible biases in association studies. A still open question, which we plan to address soon, is the minimum number of polymorphisms necessary to recognize the population structure at this level of differentiation.