A quantitative structure–function relationship for the Photosystem II reaction center: Supermolecular behavior in natural photosynthesis

Abstract

Light-induced charge separation is the primary photochemical event of photosynthesis. Efficient charge separation in photosynthetic reaction centers requires the balancing of electron and excitation energy transfer processes, and in Photosystem II (PSII), these processes are particularly closely entangled. Calculations that treat the cofactors of the PSII reaction center as a supermolecular complex allow energy and electron transfer reactions to be described in a unified way. This calculational approach is shown to be in good agreement with experimentally observed energy and electron transfer dynamics. This supermolecular view also correctly predicts the effect of changing the redox potentials of cofactors by site-directed mutagenesis, thus providing a unified and quantitative structure–function relationship for the PSII reaction center.

Almost all of the earth's biomass originates from photosynthesis in plants and microorganisms. The vast majority of terrestrial photosynthesis depends on the ability of higher plants to use water as a source of protons and electrons, via a poorly understood water-splitting mechanism. A byproduct of water splitting is the release of molecular oxygen; thus water-splitting plants and bacteria are the origin of most of the oxygen in the atmosphere. The site of water splitting in oxygenic photosynthesis is a multicomponent assembly of proteins known as Photosystem II (PSII). PSII converts solar energy into a transmembrane potential, which is used to generate ATP. It also provides the electron supply for Photosystem I, which produces the reducing equivalents for the fixation of carbon as carbohydrate.

PSII comprises >20 identifiable polypeptides, most of which are membrane proteins. At the heart of PSII lies the reaction center, which undertakes the first energy conversion step of photosynthesis by using absorbed photons to drive a series of energy and electron transfer reactions, ultimately resulting in a separation of charge. This charge separation drives both water splitting and the creation of a transmembrane potential. The primary role of the PSII reaction center is therefore to receive excitation energy, either directly from the sun or indirectly from its extensive antenna system, and to use this to create an efficient charge separation. In PSII, however, unlike Photosystem I or purple bacterial systems, the reaction center has to comply with certain essential secondary functions. These secondary functions are all associated, either directly or indirectly, with the role of the PSII reaction center in driving the process of water splitting, and in protection from, or regulation of, the unstable and damaging photochemistry with which it is associated (1).

We have attempted to gain an understanding of the charge separation mechanism in PSII by a comparison of calculation and experiment. This helps to reveal any peculiarities of the process associated with the need to drive water splitting. These studies focused on the function of the isolated PSII reaction center (often called the D1/D2-Cyt b559 complex after its major subunits), which binds six chlorophyll molecules, two pheophytin molecules, one carotenoid, and one cytochrome. The quinone molecules, which are required for secondary electron transfer reactions in PSII, are found only in larger PSII complexes. Larger complexes also include extensive antenna proteins that bind numerous light-harvesting pigments. These antenna proteins have the effect of obscuring the dynamics of the reaction center itself, hence the need to study the isolated reaction center directly.

Spectroscopic analyses of the PSII reaction center have clearly shown that, unlike other reaction centers, PSII has excited states that are nearly, but not quite, degenerate (2, 3). In purple bacterial reaction centers, the electrons emerge from the lowest singlet state to initiate the process of charge separation. The absence of a low-lying excited state in PSII demonstrates that this configuration is not essential for efficient charge separation. The similarity in chlorin–chlorin coupling in the PSII reaction center complicates interpretation of the spectroscopic and kinetic data that are used to follow the rates and extents of the various electron transfer reactions (4, 5). This complication stems from extensive mixing between the inhomogeneously disordered transitions of the molecules comprising the chain of reactive cofactors.

Because the coupling between the chlorins is strong enough to cause significant delocalization of the excited states, it is natural to consider the reaction center as a supermolecular complex. This description of the PSII reaction center is known as the Multimer Model (2) and has been widely discussed (6, 7). This model has been shown, both by us and others, to predict correctly a wide range of spectroscopic properties of the PSII reaction center (3, 7).

The most striking example of the need to treat the reaction center as a supermolecular system is that the two redmost exciton states of the PSII reaction center have been shown experimentally to have an oscillator strength two to three times that of a single chlorophyll molecule (3), whereas the blue states are concomitantly weaker, because the oscillator strength of the system is conserved overall. Moreover, the orthogonal polarization of these high oscillator strength states was predicted by the Multimer Model and confirmed by experiment (3).

The Multimer Model has previously been used to calculate the dynamics of excitation energy transport between the delocalized exciton states of the PSII reaction center, and was shown to give good agreement with femtosecond transient absorption measurements of these processes (8).

The original parameters used in the Multimer Model were based on the structure of the Rhodopseudomonas viridis reaction center, with a reduced coupling between the putative “special pair chlorins” (2, 8). A medium resolution structure of the PSII core complex has, however, recently been published (9, 10), and in this work we apply the Multimer Model to these new structural data, to interpret a range of mechanistic observations. We also extend the Multimer Model to include electron transfer steps and find that the calculations produce results that recreate all observed rates of reaction and spectral features to within 20%.

Any valid calculational framework for the PSII reaction center should be able to predict the effects of modifying the energies of the cation and anion states of the complex. In this paper, we report tests of these predictions, via genetic engineering and time-resolved spectroscopy, and demonstrate that the altered kinetics in the mutant reaction centers are again reproduced by the Multimer Model with >20% accuracy. This reasonably stringent test of the Multimer Model suggests that it does indeed describe in a quantitative way the primary structure–function relationship of the PSII reaction center. Moreover, it suggests that the cofactors of the PSII reaction center do function to some extent as a single loosely coupled supermolecule.

Materials and Methods

Transient Absorption Spectroscopy.

Experimental details of the measurement methodology have been published elsewhere (4, 11, 12). The kinetics and yield of radical pair formation were monitored both by decay of stimulated emission from chlorin excited states and bleaching of chlorin (pheophytin and chlorophyll) Q_x absorption bands. For simplicity, we show here only the kinetics of total radical pair formation.

Calculations.

The calculations presented here are based on the supermolecular model we reported previously to describe vibration-induced exciton equilibration in the PSII reaction center. These calculations were shown to be in good agreement with experimental observations (2, 8). The model considers the dipole–dipole interactions between localized molecular excited states |n〉 to allow the delocalized exciton states |ψ_i〉 to be calculated. A Monte Carlo approach is used to simulate the effects of inhomogeneous broadening of molecular excited state energies. Earlier calculations indicated that this energetic disorder limited the exciton delocalization in the PSII multimer to two to three chlorins on average. Thermal equilibration of the excited state population is allowed for by consideration of exciton–phonon coupling and the application of detailed balance. In this paper, we extend the Multimer Model to include both energy and electron transfer dynamics. This is achieved by consideration of radical pair states as well as excited singlet states in our calculation of the delocalized states |ψ_i〉, which can now take on charge transfer character, as detailed below.

The 36 delocalized exciton/radical pair states |ψ_i〉 of the PSII Multimer were calculated by determination of the eigenstates and eigenvalues associated with the system hamiltonian defined by

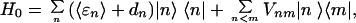1

where |n〉 are the 6 localized excited singlet and 30 radical pair states with average energies 〈ɛ_n〉 and inhomogeneous energy shifts d_n. V_nm is the coupling between states |n〉 and |m〉, calculated by using the dipole–dipole approximation for coupling between singlet excited states (13), and an empirical approximation for wavefunction overlap integrals for couplings involving radical pair states (14).

The calculations use cofactor separations and orientations based on a PSII crystal structure determined by x-ray crystallography (10). The coupling due to electron overlap was calculated by using V_nm = 1,600 exp(−0.7 r_nm), as determined empirically by Dutton and coworkers (14), where r_nm is the shortest edge–edge separation of the chlorin macrocycles; coupling strengths of <0.5 cm⁻¹ were neglected. Diagonalization of H₀ allows determination of each |ψ_i〉, corresponding to the ith mixed exciton/radical pair state comprising a linear combination of the localized chlorin excited states and radical pair states 〈n| such that:

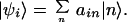2

Diagonalization also allows the associated transition energies ω_i to be determined.

Rate constants k_ij for vibrationally induced equilibration between the mixed states |ψ_i〉 were determined, as derived in ref. 8 from:

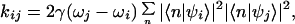3

where γ is the frequency-dependent electron–vibration coupling strength taken as previously to be

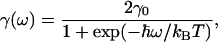4

with γ₀ taken to be 100 cm⁻¹.

Eq. 3 has a simple interpretation for the case of energy transfer dynamics (8). The summation term in Eq. 3 calculates the extent to which exciton states |ψ_i〉 and |ψ_j〉 share the occupation of an individual chlorin site. The transfer rate k_ij between exciton states therefore depends on the spatial overlap of these exciton states and the strength of the electron–vibration coupling at the site of overlap. In previous calculations, it was found that the assumption of dipole–dipole coupling between states, and of identical electron–vibration coupling at all sites, gave good agreement with the measured energy transfer dynamics of the PSII reaction center (8). In the calculations presented here, this model is extended to account for the electron transfer dynamics by including the radical pair states of the chlorins in |ψ_i〉 and allowing these to be coupled by electron overlap interactions.

Following determination of the rate constants k_ij, the population dynamics were determined by solution of the “master equation” (15):

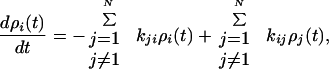5

where ρ_i is the population of the ith mixed state. The initial population distribution ρ_i(0) of the |ψ_i〉 states was taken to be proportional to their singlet excited state character determined from Eq. 2. Dynamics of localized states ρ_n were then determined from

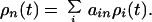6

Inhomogeneous disorder was included in the calculations by a Monte Carlo procedure in which the inhomogeneous shifts d_n of the localized excited/radical pair states were obtained from a random number generator using a Gaussian probability distribution (with full widths at half maximum Δ_es and Δ_rp for excited and radical pair states, respectively). For each particular realization of the disorder, the mixed states |ψ_i〉 and their corresponding energies ω_i were determined, the population transfer rate constants k_ij obtained by using Eq. 3, and the population dynamics then calculated by solution of Eqs. 5 and 6. Such calculations were repeated for 200 reaction centers (i.e., 200 different realizations of the inhomogeneous shifts d_i), and the resulting electron transfer dynamics ensemble averaged to allow comparison with experiment. Averaging over 200 reaction centers produces a statistical variation of ≈4%. This is better than the experimental precisions, which are of the order of 10–20% for most of the observable properties discussed here.

Model Parameters.

A crystal structure of the PSII core complex has recently been published by the Berlin Group (9, 10). The only significant difference between the results reported in these two papers (from the point of view of the primary function of the reaction center) is the separation of the two lower chlorophylls in the vicinity of the chlorophylls known as the “special pair” in the bacterial reaction center. The structure of Zouni et al. (9) has the chlorophylls separated by 10 Å, a configuration also allowed in the assumed structure of the original Multimer Model paper (2). Later refinement of the structure (10) suggests a center-to-center separation of 8.3 Å.

The orientation of the transition dipole moments is missing from all of the PSII structural data, because the precision of the structural data sets is too low to determine the orientation of the chlorophyll molecules, although the planes of the rings have been established. The dipole orientations presented in these structure papers are arbitrarily chosen within the plane of the chlorin ring (9, 10). The dipole couplings calculated by using the orientations and chlorin separations given in ref. 10 do not reproduce the spectroscopic observables. A large number of permutations of other dipole orientations within the chlorin rings do, however, reproduce the spectroscopic observables. We have arbitrarily chosen one of these orientation sets for this paper, but note that a number of arrangements are consistent with the experimental data. The dipole couplings used in our calculations are shown in Table 1 and come from one of the arbitrary dipole orientation sets consistent with the Vasil'ev et al. (10) data. Singlet excited state widths and energies were taken as Δ_es = 210 cm⁻¹ (full width half maximum) and 〈ɛ_es〉 = 14,860 cm⁻¹, which are the same as those used previously (8).

Table 1.

The dipole couplings (in cm⁻¹) between the chlorins in the PSII reaction center

	Ph(1)	Chl(1)	Chl(2)	Chl(3)	Chl(4)	Ph(4)
Ph(1)		101.5	22.9	−6.8	−7.0	4.7
Chl(1)			−86.8	−64.2	10.3	−5.4
Chl(2)				120	−27.4	−2.4
Chl(3)					−94.9	21.6
Chl(4)						81.7
Ph(4)

The values have been calculated by using the chlorin separations and plane orientations given in the PSII crystal structure (10). The labeling of the chlorins is shown in Fig. 3. 

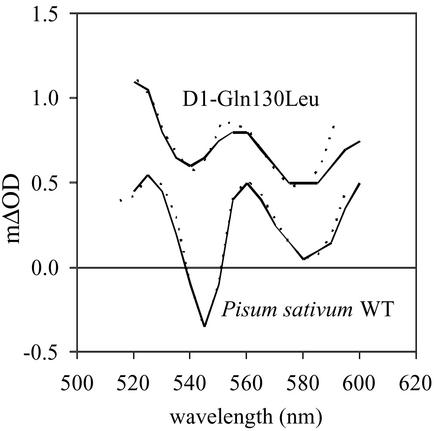
Relative radical pair energies were estimated from spectroscopic analysis of wild-type and genetically modified PSII reaction centers (11, 12, 16). The relative populations of these states were determined from previously published spectroscopic data, as described in ref. 16. In brief, the experimental transient absorption spectra, from wild-type and genetically modified PSII reaction centers, were compared with simulated spectra consisting of weighted contributions of excited singlet state, Chl⁺Ph⁻ state and Chl⁺Chl⁻ state spectra (11, 16). An example of this is given in Fig. 1, which compares simulated spectra with experimental spectra obtained at 60 ps from wild-type reaction centers isolated from Pisum sativum, and D1-Gln130Leu PSII reaction centers isolated from Synechocystis PCC 6803. Total radical pair concentration was deduced from stimulated emission or fluorescence up-conversion amplitudes (11, 16, 17).

Figure 1.

Experimental transient absorption spectra measured at 60 ps from wild-type reaction centers isolated from P. sativum and D1-Gln130Leu PSII reaction centers isolated from Synechocystis PCC 6803 (——) described in refs. 11 and 12. A comparison is made with the simulated spectrum (––––) obtained by using the following equation:

where ΔOD_RC* corresponds to the experimental change in the spectra's optical density (ΔOD) at 1 ps in wild-type pea reaction centers (i.e., before charge separation). ΔOD_RPpea was determined from the experimental ΔOD at 60 ps for P. sativum after subtracting contributions to the spectrum from excited states [25% excited states at this time delay (17)]. The transient ΔOD_{P680⁺Chl⁻} spectrum was calculated by subtracting spectral changes attributable to pheophytin reduction from the ΔOD_RPpea spectrum and then adding spectral changes observed for chlorophyll reduction in solution (32). Further details are presented in ref. 16.

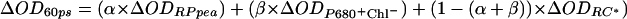Previous analyses determined that stable charge separation occurs only along one branch of the reaction center (12). This observation is crucial and allows us to put a lower limit on the radical pair energies of the inactive branch. Furthermore, in such engineered reaction centers, a significant population of Chl⁺Chl⁻ states can be observed (16), enabling the relative average energies of such radical pair states to be determined. Mean radical pair energies 〈ɛ_rp〉 were estimated by comparison of these experimentally determined populations with those calculated by the supermolecular model. This comparison yields 〈ɛ_rp〉 values of 14,440 cm⁻¹ for X⁺Phe(1)⁻ states in wild-type reaction centers (15,740 cm⁻¹ for the D1-Gln130Leu reaction centers) and 16,040 cm⁻¹ for other radical pair states.† Inhomogeneous broadening of the radical pair energies, Δ_rp, was taken as 850 cm⁻¹ from previous studies of both PSII and bacterial reaction centers (18, 19).

We also used the Multimer Model to predict energy transfer and trapping in the purple bacterial reaction center from Rhodobacter sphaeroides. There is more than one published value for the state energies in R. sphaeroides (20). We chose to use −330 cm⁻¹ and −730 cm⁻¹ as the values of the energies between the singlet states and P⁺B⁻H and P⁺BH⁻ (21), because the model used in that particular paper includes reverse electron transfer when determining the state energies, a necessity when energy gaps are relatively small.

Results

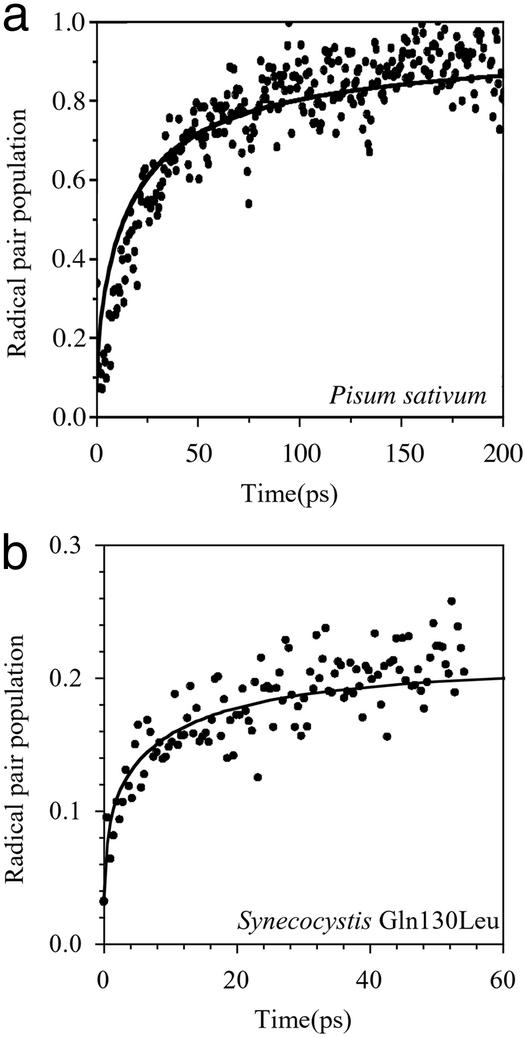
Femtosecond transient absorption spectroscopy was used to study the paths and rates of electron transport in the PSII reaction center. Fig. 2a shows both the calculated and measured rate of total radical pair formation. This reaction is known to be multiexponential, with components ranging from a few to a couple of hundred picoseconds (4, 5, 22–24).

Figure 2.

Comparison of experimental kinetics of radical pair formation with Multimer Model calculations for PSII wild-type reaction centers isolated from P. sativum (a) and D1-Gln130Leu genetically engineered reaction centers isolated from the cyanobacterium Synechocystis PCC 6803 (b).

The utility of the Multimer Model is further demonstrated in Fig. 2b, which shows the kinetics of total radical pair formation in the case of a mutant in which the terminal radical pair energy has been raised by increasing the redox potential of the pheophytin anion. The relative energy of this modified radical pair state is known from our previous measurements (11, 16). The most striking effect of this change in redox potential is the presence of a fast phase in the mutant kinetics, which is faithfully reproduced by the calculations. We thus conclude that the Multimer Model can be used to describe not only energy transfer but also electron transfer dynamics in both wild-type and PSII reaction centers in which radical pair energies have been modified by site-directed mutagenesis.

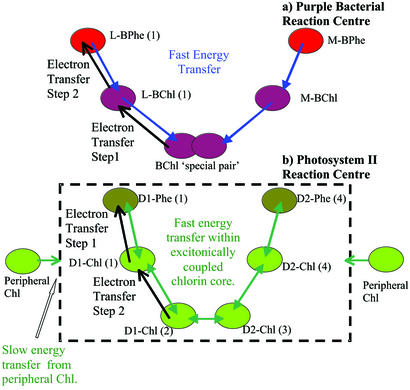
There have been speculations regarding the charge separation pathways in PSII. As these pathways cannot be directly observed in wild-type reaction centers, modifications of the reaction center in conjunction with calculations must be used to reveal them. State energies are a vital input to these calculations and are revealed only by genetic engineering. A key element of our modeling of the charge separation in PSII is that it includes all possible excitation energy and electron transfer pathways between the reaction center chlorins. We used the Multimer Model to investigate these pathways further by effectively switching off certain paths by raising state energies one by one and examining the net effect. The results indicate that the dominant pathway (>90%) for charge separation in PSII involves an initial electron transfer step from excited states on Chl(1) and Phe(1) to form the radical pair state Chl(1)⁺Phe(1)⁻, followed by electron transfer from Chl(2) to Chl(1)⁺, thereby producing the terminal radical pair state Chl(2)⁺Phe(1)⁻ (see Fig. 3). As an example, calculations in which this pathway was excluded, achieved by raising the energies of the Chl(1)⁺X⁻ states, yielded an ≈8-fold retardation of the kinetics of radical pair formation. In contrast, raising the energy of X⁺Chl(1)⁻ states, corresponding to the intermediate state observed for charge separation in bacterial reaction centers, had negligible influence on the calculated kinetics. The Chl(1)⁺X⁻ pathway for charge separation is dominant, because it avoids the formation of energetically unfavorable chlorophyll anion states, as previously noted (11, 16).

Figure 3.

Electron and energy transfer pathways in purple bacterial and PSII reaction centers. (a) In purple bacteria, the energy transfer is largely unidirectional. All electron transfer is thought to originate from the lowest singlet state of the excitonically coupled special pair and is strictly ordered with the BChl(1) anion being formed before formation of the BPhe(1) anion. (b) In PSII, there is no low-lying excited singlet state. Various elements have previously been identified as: multidirectional subpicosecond equilibration of the excitation energy within the excitonically coupled chlorin core (3, 27); slow energy transfer from the peripheral chlorophylls (33, 34); multiexponential charge transfer kinetics with lifetimes (and amplitudes) of 3 ps (0.19), 21 ps (0.57), 100 ps (0.14), and >100 ps (0.10) (4, 17, 23). (See also refs. 5, 22, and 24.) Both the experimental data and the Multimer Model are consistent with at least 90% of the charge separation originating via the radical pair state Chl(1)⁺Phe(1)⁻.

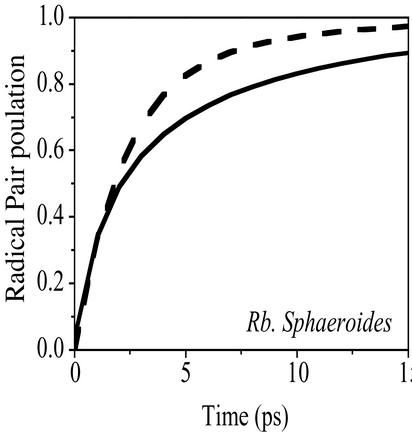
The Multimer Model may also be used to describe energy and electron transfer in other photosynthetic reaction centers where the dynamics are not so tightly intertwined, because supermolecular behavior should still be evident. To illustrate this point, we show a Multimer Model calculation of the rate of radical pair formation in the purple bacterial reaction center from R. sphaeroides and compare it with previously reported experimental data (Fig. 4). The result of the calculation can be only as accurate as the input parameters (i.e., state energies), and in this case, we used literature values for the radical pair states BChl(2)⁺BChl(1)⁻ and BChl(2)⁺BPhe(1)⁻ (21). We also had to take into account the higher electron–vibration coupling strength in bacteriochlorophyll compared with chlorophyll-a, which are found to occur in a ratio of 2.1:1 (25, 26). The tolerable agreement between calculation and experiment in Fig. 4 suggests that the supermolecular view can indeed be extended to other photosynthetic reaction centers.

Figure 4.

A comparison between experimentally determined kinetics obtained from R. sphaeroides in ref. 21 (dashed) and a Multimer Model calculation (solid). See Materials and Methods for details.

Discussion

The parameters used in the calculations presented here are based on a PSII crystal structure (10). Applying the Multimer Model to this structural data set successfully reproduces a number of experimental observables. For example: Rates of energy transfer: [Calculation: ≈450 and 250 fs time constants. Experimental: 400 ± 30 fs and 100 ± 50 fs (3, 27)]. Relative orientation of redmost exciton states: [Calculation: 90°. Experimental: 70 ± 10° (3)]. Relative oscillator strengths of redmost exciton states: [Calculation: 2.1-fold greater than a monomer. Experimental: 1.9 ± 0.5-fold greater (3)]; Absorption spectra: [Calculation: 70% of the total oscillator strength is found in a single band. Experimental 100% (2)]. Rates of electron transfer (this work). Effect of site-directed mutagenesis (this work). Space limitations preclude showing figures of all these comparisons.

A feel for the sensitivity of the chemistry to the structure of the reaction center can be gained by using the earlier assumed structure (2, 8). The results give a total radical pair population at 60 ps that is 88% of that observed experimentally. The calculations give the ratio of the excited singlet state to the chlorophyll anion state populations at 60 ps to be 13, which compares with the ratio of ≈6 obtained both experimentally (16) and from calculations using the Vasil'ev structure. It is at first sight surprising that the radical pair populations are not more sensitive to cofactor distance. Overall, however, the main reason for this insensitivity lies in the relatively large amount of inhomogeneity in the state energies and the central importance of the state energies themselves.

The Multimer Model (Eqs. 1, 3, and 4) assumes that the system is supermolecular, disordered, and driven by site local Markovian electron–vibration coupling. It explains why a given reaction center structure produces the chemistry that is observed experimentally. Knowing the energies of the key states is vital to this understanding. These energies were obtained from published studies of wild-type and genetically engineered PSII reaction centers (11, 16), which allowed the calculations to be conducted without the use of any variable fitting parameters. The Multimer Model is therefore directly predictive.

Implications of the Multimer Model.

In other photosynthetic reaction centers, a (bacterio)chlorophyll special pair creates a low-lying singlet state that functions as an energetic trap for excited states within the complex, and charge separation is thought to be constrained to being initiated from this state. The absence of a low-lying state in PSII manifestly removes this constraint and in principle allows charge separation to be initiated from any reaction center chlorin. The Multimer Model shows that the dominant pathway (>90%) for charge separation in PSII involves an initial electron transfer step from excited states on Chl(1) and Phe(1) to form the radical pair state Chl(1)⁺Phe(1)⁻, followed by electron transfer from Chl(2) to Chl(1)⁺, thereby producing the terminal radical pair state Chl(2)⁺Phe(1)⁻ (see Fig. 3). Studies of mutant reaction centers have previously shown that these chlorophyll anions have relatively high energies (16). Singlet state concentrations are found always to exceed chlorophyll anion concentrations, even when the free energy of the terminal radical pair state [Chl(2)⁺Phe(1)⁻] is raised by 100 meV (11, 16). It seems, therefore, that the majority of the charge separation process in PSII is produced via electron transfer steps that occur in the reverse order to that found in wild-type purple bacterial reaction centers. This reverse pathway could be deduced only by using the information retrieved from studies of mutants, because the pathway is otherwise totally hidden. The viability of a reversed-order electron-transfer pathway is supported by recent studies, which have reported that a similar charge separation pathway can be observed in genetically modified reaction centers of purple bacteria (28). The exact proportion of the forward and reverse order paths clearly depends on the precise energies of the states involved. The Multimer calculations and femtosecond measurements that we present here are commensurate in that they have an accuracy of 10–20%, limited on the one hand by accuracies with which the state energies are known and on the other hand by noise and by accuracy limits in quantification of the spectroscopic assignments. Bearing in mind these limitations on accuracy, it is still interesting to note that the degree of mixing of singlet and radical pair states allowed by the Multimer Model suggests that ≈5–10% of radical pairs are formed directly on absorption of a photon by the reaction center. In other words, the multimer singlet states do contain a degree of charge transfer character.

The Multimer Model allows a unification of energy and electron transfer theory by treating electron–vibration coupling in a consistent way. This is particularly crucial in PSII, where different spectroscopies at first sight appear to give contradictory information; the Multimer Model removes these paradoxes. To illustrate this point, we have also performed calculations using conventional nonadiabatic electron transfer theory. Although this conventional electron transfer theory also predicts the reverse electron transfer pathway, it cannot predict the degree of charge transfer character of the multimer and therefore cannot be reconciled with the results of, for example, Stark spectroscopy. Moreover, because the Multimer Model is a truly microscopic theory, it demonstrates the manner in which a Quantum Mechanical/Molecular Mechanical approach could now be applied to predict these reactions from first principles (25, 26). In addition, the Multimer Model should be applicable to all light reactions in all photosynthetic apparatus, including light-harvesting systems, as long as the various couplings can be deduced. Indeed, we have shown here that it does a passable job in predicting the electron transfer dynamics in reaction centers of R. sphaeroides. It is wise, however, to sound a note of caution at this point. The Multimer Model is not strictly valid in situations where activation energies are much higher than k_BT.

A corollary of the Multimer Model is that underdamped vibrations, which produce oscillatory behavior in some femtosecond transient absorption experiments, although interesting, are not relevant to this charge separation process. One should not, however, infer from this that underdamped vibrations are unimportant in proteins in general. Indeed, there is some evidence for their role in other membrane protein systems (29).

Biological Implications.

Finally, we address the biological implications of the supermolecular view of the PSII reaction center. One feature that distinguishes PSII from other systems is that PSII is highly regulated in response to fluctuating environmental conditions. This is a necessity due to the extreme sensitivity of PSII to photoinduced damage (30). One of the main regulatory mechanisms in PSII is the ability of the plant to form quenching centers in the PSII antenna to reduce the flow of excitation energy to the PSII reaction center (see, for example, ref. 1). This requires efficient competition with the charge separation process in the reaction center. The charge separation must be slow enough to allow this competition, yet still allow transmembrane electron transport with a high quantum yield. Indeed, a recent study of the antenna size dependence of energy transport and trapping in PSII has demonstrated that the predicted shallow equilibrium between antennae and reaction centers in PSII is a reality in closed particles (31).

The inverted charge separation pathway of PSII should be seen as a symptom of the small free energy gaps between the singlet, cation and anion states in PSII, due to the need to regulate radical pair formation and maintain oxidizing potential. This, in turn, means that the primary electron donor in PSII is not the molecule that drives the water-splitting process, and that the chlorophyll cation that drives water splitting is actually the one with the lowest oxidizing potential in the PSII reaction center, identified as Chl(2) in Fig. 3. This is not a very stringent requirement, however. For example, if the two cations Chl(2)⁺ and Chl(1)⁺ had identical redox potentials, then the cation transfer process would show an equilibrium constant of 1. In this case, reduction of reaction center cations via the active tyrosine of the water-splitting complex would simply occur at half the rate of that where the cation was located purely on Chl(2), and another factor of 1/e would accrue for every 25-meV difference in redox potentials.

The absence of a low-lying singlet state in PSII is also relevant to the issue of regulation via nonphotochemical quenching. R. sphaeroides has a special pair of particularly strongly coupled chlorophylls at the base of the reaction center. This leads to a relaxation of the excited state, which is greater than that found in uncoupled chlorophyll, and this lowering of free energy helps to trap excitation energy in the reaction center and speeds up the overall process of charge separation in the presence of an antenna system. If PSII did contain a pair of particularly strongly coupled chlorophyll molecules, then charge separation in vivo might well be faster, but it would be more difficult to turn off via the regulatory quenching centers in the PSII antenna.

Summary

• Treating reaction centers as supermolecular complexes via the Multimer Model allows the balance between energy and electron transfer to be calculated as long as the state energies are known. The Multimer Model is able to reproduce the energy/electron transfer rates and spectroscopic features in PSII, and also successfully predicts the effects of engineering the PSII reaction center via site-directed mutagenesis.

• The time scale of charge separation in the PSII reaction center is spread over two orders of magnitude due to a combination of inhomogeneous broadening of the cofactor energies and supermolecular behavior.

• Charge separation in PSII reaction centers is slow on average, because rapid excitation energy transfer between closely spaced states prevents the population of excited states accumulating on the primary electron donor.

• The absence of a pair of particularly strongly coupled chlorophyll molecules in PSII reflects the need for PSII to retain oxidizing power to drive water splitting and to avoid creating too deep a trap for excitation energy.

• The Multimer Model gives a reasonably good representation of charge separation in reaction centers from R. sphaeroides and should be applicable to all of the light reactions in photosynthesis.

• The primary structure–function relationship in the PSII reaction center is inherently supermolecular.

Abbreviation

PSII

Photosystem II