Abstract
γS-crystallin (γS) is an important human and bovine eye lens protein involved in maintaining the transparency of the eye. By adding small amounts of polyethylene glycol (PEG) to the binary aqueous bovine γS solutions, we have observed liquid–liquid phase separation (LLPS) at −8°C and revealed that, in the binary γS–water system, this phase transition would occur at −28°C. We have measured both the effect of PEG concentration on the LLPS temperature and protein/PEG partitioning between the two liquid coexisting phases. We use our measurements of protein/PEG partitioning to determine the nature and the magnitude of the γS-PEG interactions and to quantitatively assess the effectiveness of PEG as a crystallizing agent for γS. We use our measurements of LLPS temperature as a function of protein and PEG concentration to successfully determine the location of the critical point for the binary γS-water system. This phase transition cannot be observed in the absence of PEG because it is inaccessible due to the freezing of the system. Our findings indicate that the effective interactions between γS molecules in the binary γS–water system are attractive. We compare the magnitude of the attraction found for γS with the results obtained for the other γ-crystallins for which the critical temperature is located above the freezing point of the system. This work suggests that PEG can be used to reveal the existence of LLPS for a much wider range of binary protein–water systems than known previously.
Keywords: protein‖cataract‖polyethylene glycol‖phase transition‖partitioning
In protein condensation diseases the primary initial step in pathogenesis is the loss of solubility of the proteins, resulting in the formation of a condensed phase. Examples of such phases include a dense liquid phase, amorphous aggregates, or crystals that form in cataract (1, 2) or the formation of fibers that are responsible for sickle cell disease (3) and Alzheimer's disease (4). In all cases the attraction between proteins is the driving force for the onset of these pathologies. Thus, the characterization of the interactions between proteins is the first step for building strategies aimed at inhibiting such diseases (5).
Liquid–liquid phase separation (LLPS), which is induced by protein–protein attractive interactions, has been directly implicated in cataract. It has been shown that this is the mechanism for lens opacification in cold cataract and that it is also operative in galactosaemic and x-ray cataracts and in hereditary cataracts in mice (1, 6). The lens proteins primarily involved in phase separation are the γ-crystallins, a family of lens-specific monomeric proteins (1). Previous LLPS studies of binary aqueous solutions of four pure individual members of the bovine γ-crystallins have shown that these proteins fall into two groups: those that show an upper consolute point at ≈38°C (γE and γF) and those that show an upper consolute point at ≈5°C (γB and γD) (7, 8).
Another important member of the γ-crystallin family is γS-crystallin (γS). Although of approximately the same size (hydrodynamic radius ≈2.5 nm) and molecular mass (≈21 kDa), the expression of γS is different from that of the other proteins. γS is expressed after birth and its synthesis increases with age, whereas in bovine and human lenses the other γ-crystallins are expressed mainly prenatally and their synthesis sharply decreases after birth. It has also been found that the phase behavior of binary aqueous solutions of pure γS differs markedly from the other γ-crystallins. Specifically, γS solutions do not exhibit LLPS, even at temperatures as low as −10°C. Furthermore, the presence of γS in γB and γF aqueous solutions significantly lowers the phase separation temperatures of these proteins in the high concentration region. These facts suggest that the presence of γS in the lens helps to maintain transparency (9, 10).
We have experimentally and theoretically shown that polyethylene glycol (PEG) can be used to reveal LLPS in aqueous protein solutions (11). LLPS of binary protein–water systems may not be directly observable because it is inaccessible because of either the freezing of the system or the denaturation of the protein at high temperature (11, 12). The experiments with PEG can be used to deduce the location of the phase boundaries of the binary system. Here we show that LLPS of bovine γS aqueous solutions can be induced on adding a small amount of PEG. We have measured the phase boundaries for LLPS in the ternary γS–PEG–water system. These results are used to successfully locate the liquid–liquid phase boundary for the binary γS–water below the freezing point of the system. Therefore, we can determine that the interactions between γS molecules are attractive and compare the magnitude of the attraction with the other γ-crystallins.
The LLPS properties of the ternary protein–PEG–water system are described by a coexistence surface in the phase diagram. This coexistence surface represents the LLPS temperature, Tph, as a function of protein concentration, c1, and PEG concentration, c2. At a fixed temperature, the LLPS properties of the system are described by an isothermal coexistence curve, which gives the concentrations (c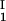 , c
, c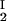 ) and (c
) and (c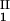 , c
, c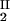 ) of the coexisting phases, I and II. The partitioning of the components in the two coexisting phases is described by tie lines connecting the points (c
) of the coexisting phases, I and II. The partitioning of the components in the two coexisting phases is described by tie lines connecting the points (c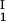 , c
, c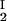 ) and (c
) and (c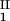 , c
, c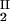 ) of the coexistence curve. The critical point, (c
) of the coexistence curve. The critical point, (c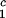 , c
, c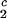 ), is defined as the point on the coexistence curve where the condition (c
), is defined as the point on the coexistence curve where the condition (c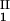 , c
, c ) = (c
) = (c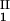 , c
, c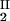 ) occurs. The location of this point as a function of the temperature is described by a critical line on the coexistence surface (11).
) occurs. The location of this point as a function of the temperature is described by a critical line on the coexistence surface (11).
Materials and Methods
Bovine γS, which has a molecular weight of 20,800 g/mol, was isolated from 1- to 6-week-old calf lenses, obtained by overnight express from Antech (Tyler, TX). Pure γS was isolated and purified from these lenses by standard procedures as described (7–10). The purity of the native sample was at least 98%, based on both ion-exchange and size-exclusion HPLC. To suppress aggregation of γS, the purified protein was stored at 4°C in acetate buffer (0.2 M, pH 5) that contained DTT (0.02 M) and sodium azide (0.02%) (10, 13). PEG with average molecular weight of 1,450 g/mol (PEG1450) was purchased from Sigma-Aldrich and used without further purification.
Protein–PEG aqueous solutions were prepared as follows. The purified γS was dialyzed exhaustively into sodium phosphate buffer (0.1 M, pH 7.1) that contained sodium azide (0.02%). Solutions containing dilute γS in phosphate buffer were concentrated by ultrafiltration. When the desired protein concentration was reached, a known weight of PEG was added to the protein solution. The concentration of γS in the samples was determined by UV absorption at 280 nm, using the extinction coefficient value of 1.85 mg−1⋅ml⋅cm−1 calculated from the sequence (www.expasy.ch). The concentration of PEG in the samples was calculated by using the mass of PEG and the total volume of the solution. The volumetric contribution of each component was obtained by multiplying the mass of the component by the corresponding specific volume, i.e., 0.71 ml/g (14) for the protein, 0.84 ml/g for PEG (15), and 0.992 ml/g for the buffer (11).
The LLPS temperature for a given protein–PEG aqueous solution was determined by gradually lowering the temperature of the sample until clouding was observed. The cloud point was determined by the examination of the transmitted intensity-temperature profile as described by Liu et al. (9).
The coexisting phases were obtained by quenching the sample at fixed temperature below the coexistence surface. If after about 24 h the two coexisting phases had not separated by gravity, centrifugation was used for the separation. The protein concentration in each phase was determined by UV absorption. To determine the PEG concentration in each of the coexisting phases, an aliquot of known weight was taken from each phase, and the PEG was separated from the protein by ultrafiltration (Amicon Microcon YM-10). The concentration of PEG in the filtrate of known volume was determined by using a standardized refractive index detector (Perkin–Elmer LC-30 RI). Thus, the concentration of PEG in each aliquot could be calculated from its measured value in the filtrate. To account for the small effects of the two buffer salts (dibasic and monobasic sodium phosphate), the refractive index measurements were performed after isocratic elution of the filtrate solution on a size exclusion HPLC column (10 × 300 mm, Superdex 75 HR 10/30 from Amersham Pharmacia). The procedure was verified with protein–PEG aqueous solutions of known composition. In all cases, the measured protein and PEG concentrations in the two coexisting phases were consistent with the protein and PEG concentrations in the original, homogeneous samples.
Results
Our protein–PEG–buffer solutions can be described essentially as ternary protein–PEG–water systems. This approximation is justified by the insignificant difference in buffer concentration measured between the two coexisting phases.
We have previously shown that it is convenient to present our results in terms of the protein (component 1) concentration c1, and the PEG (component 2) concentration c2s inside the protein-free volume. If v is the protein specific volume and φ = c1v is the protein volume fraction, then c2s is equal to c2/(1 − φ). The choice of c2s (instead of c2) is convenient because of the following argument. We consider as a reference system one in which the particles of component 2 have a negligible size and do not introduce specific chemical interactions in the system. In this reference case, the different values of c2 between the two coexisting phases are entirely determined by the exclusion of component 2 from the volume occupied by component 1. Here, the condition of chemical equilibrium is expressed by the relation c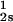 = c
= c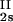 . Thus, in our systems, any observed difference in c2s between two coexisting phases is related to the finite size and specific chemical properties of the PEG molecules (11).
. Thus, in our systems, any observed difference in c2s between two coexisting phases is related to the finite size and specific chemical properties of the PEG molecules (11).
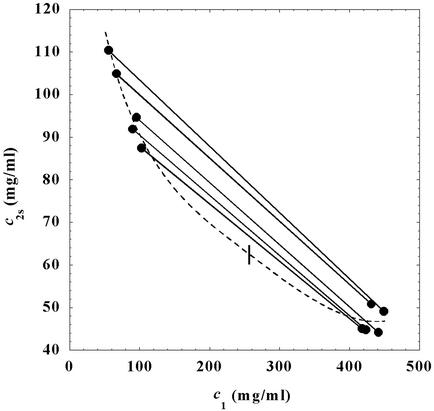
In Fig. 1, we present our experimental data (solid circles) of the coexisting values (c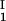 , c
, c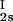 ) and (c
) and (c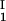 , c
, c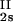 ) for the γS–PEG1450–water solutions at 265.1 K. The pairs of points representing the coexisting phases are connected by straight lines (tie lines). The dashed curve is an eye guide representing the coexistence curve. The coexisting phases were obtained by quenching samples with the same initial protein concentration of ≈300 mg/ml but with different initial PEG concentrations. Because the protein critical concentration, c
) for the γS–PEG1450–water solutions at 265.1 K. The pairs of points representing the coexisting phases are connected by straight lines (tie lines). The dashed curve is an eye guide representing the coexistence curve. The coexisting phases were obtained by quenching samples with the same initial protein concentration of ≈300 mg/ml but with different initial PEG concentrations. Because the protein critical concentration, c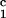 , is equal to the average concentration (c
, is equal to the average concentration (c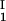 + c
+ c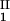 )/2 in the limit of c
)/2 in the limit of c − c
− c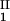 = 0, we determined c
= 0, we determined c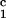 by plotting (c
by plotting (c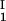 + c
+ c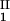 )/2 as a function of c
)/2 as a function of c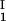 − c
− c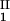 . The resulting value of the critical concentration (vertical bar in Fig. 1) is 260 ± 10 mg/ml, which corresponds to a critical protein volume fraction: φc = 0.18 ± 0.01. To quantify PEG partitioning, we consider the normalized slope of the tie lines at the critical point (∂c2s/∂c1)
. The resulting value of the critical concentration (vertical bar in Fig. 1) is 260 ± 10 mg/ml, which corresponds to a critical protein volume fraction: φc = 0.18 ± 0.01. To quantify PEG partitioning, we consider the normalized slope of the tie lines at the critical point (∂c2s/∂c1)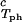 /c
/c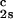 . This quantity was obtained by plotting the incremental ratio (ln c
. This quantity was obtained by plotting the incremental ratio (ln c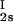 − ln c
− ln c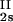 )/(c
)/(c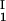 − c
− c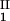 ) as a function of c
) as a function of c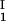 − c
− c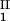 and considering the limit of c
and considering the limit of c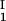 − c
− c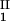 = 0. We found (∂c2s/∂c1)
= 0. We found (∂c2s/∂c1)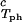 /c
/c = (−2.1 ± 0.1) 10−3⋅mg−1⋅ml.
= (−2.1 ± 0.1) 10−3⋅mg−1⋅ml.
Figure 1.
Coexisting surfaces at constant temperature for the ternary γS–PEG1450–water system. The pairs of points representing the coexisting phases (circles) are connected by the tie lines (solid lines). The dashed curve is a guide for the eye and the vertical bar locates the critical point at c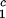 = 260 mg/ml. The normalized slope of the tie lines at the critical point is (∂c2s/∂c1)
= 260 mg/ml. The normalized slope of the tie lines at the critical point is (∂c2s/∂c1)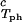 /c
/c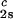 = (−2.1 ± 0.1)10−3 mg−1⋅ml.
= (−2.1 ± 0.1)10−3 mg−1⋅ml.
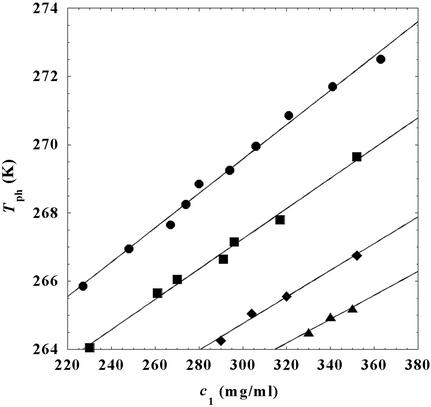
In Fig. 2, we present our measurements of the LLPS temperature, Tph, for the ternary γS–PEG1450–water solutions at constant PEG concentration of c2s = 74 mg/ml (circles), c2s = 66 mg/ml (squares), c2s = 60 mg/ml (diamonds), and c2s = 53 mg/ml (triangles). In all cases, the PEG concentration is smaller than the semidilute crossover concentration c2s = 80 mg/ml (16). In Fig. 2, we can see that Tph linearly increases as c1 increases. We can fit each experimental data set with the linear function Tph = Tc(c2s) + (∂Tph/∂c1)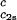 (c1 − c
(c1 − c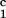 ) (solid lines in Fig. 2). Using c
) (solid lines in Fig. 2). Using c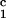 = 260 mg/ml we obtained the values for both the critical temperatures, Tc(c2s), and the slopes (∂Tph/∂c1)
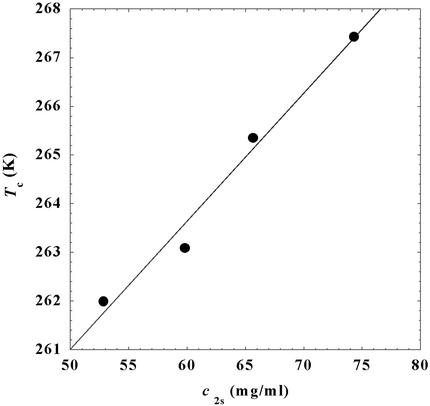
= 260 mg/ml we obtained the values for both the critical temperatures, Tc(c2s), and the slopes (∂Tph/∂c1)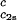 . In Fig. 3, we plot Tc(c2s) as a function of c2s. We observe that Tc is approximately a linear function of c2s with (∂Tph/∂c2s)c1 = (0.27 ± 0.03) K⋅mg−1⋅ml. In Fig. 4, we plot (∂Tph/∂c1)
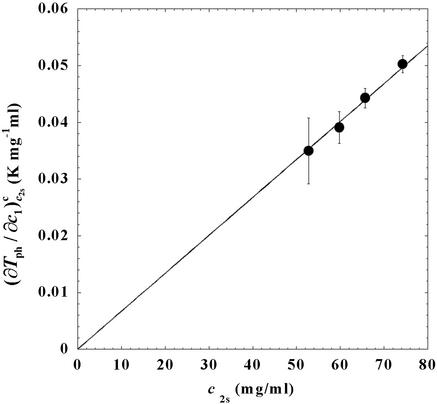
. In Fig. 3, we plot Tc(c2s) as a function of c2s. We observe that Tc is approximately a linear function of c2s with (∂Tph/∂c2s)c1 = (0.27 ± 0.03) K⋅mg−1⋅ml. In Fig. 4, we plot (∂Tph/∂c1) as a function of c2s. We see that (∂Tph/∂c1)
as a function of c2s. We see that (∂Tph/∂c1)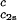 increases linearly with c2s and starts at zero when c2s = 0 as it is required for a binary protein–water system (9). We found (∂Tph/∂c1)
increases linearly with c2s and starts at zero when c2s = 0 as it is required for a binary protein–water system (9). We found (∂Tph/∂c1)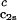 /c
/c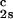 = (0.674 ± 0.004)10−3 K⋅mg−2⋅ml2.
= (0.674 ± 0.004)10−3 K⋅mg−2⋅ml2.
Figure 2.
LLPS temperature, Tph, at constant PEG1450 concentration of c2s = 74 mg/ml (circles), c2 = 66 mg/ml (squares), c2s = 60 mg/ml (diamonds), and c2s = 53 mg/ml (triangles). The solid lines are linear fits to the experimental data. The protein critical concentration is c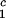 = 260 mg/ml.
= 260 mg/ml.
Figure 3.
Critical temperature, Tc, for the ternary γS–PEG1450–water system as a function of c2s. The dashed line is a linear fit to the experimental data with slope (∂Tph/∂c2s)c1 = (0.27 ± 0.03) K⋅mg−1⋅ml.
Figure 4.
Slope of the critical temperature, (∂Tph/∂c1)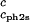 /c2s, for the ternary γS–PEG1450–water system as a function of c2s. The dashed line is a linear fit to the experimental data with slope (∂Tph/∂c1)
/c2s, for the ternary γS–PEG1450–water system as a function of c2s. The dashed line is a linear fit to the experimental data with slope (∂Tph/∂c1)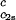 /c2s = (0.674 ± 0.004) 10−3 K⋅mg−2⋅ml2.
/c2s = (0.674 ± 0.004) 10−3 K⋅mg−2⋅ml2.
The behavior of the coexistence surface is described by the three slopes (∂c2s/∂c1)Tph, (∂Tph/∂c2s)c1, and (∂Tph/∂c1)c2s, which are related to each other by the mathematical relationship (9, 11):
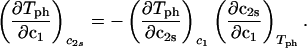 |
1 |
We apply Eq. 1 on the critical line and use the measured values of (∂c2s/∂c1)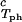 /c
/c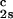 and (∂Tph/∂c1)
and (∂Tph/∂c1)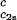 /c
/c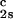 to determine that (∂Tph/∂c2s)
to determine that (∂Tph/∂c2s)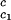 = 0.320 ± 0.013 K⋅mg−1⋅ml. This value is in satisfactory agreement with the value obtained by the direct analysis of the dependence of Tc on c2s shown in Fig. 3 [i.e., (∂Tph/∂c2s)c1 = (0.27 ± 0.03) K⋅mg−1⋅ml].
= 0.320 ± 0.013 K⋅mg−1⋅ml. This value is in satisfactory agreement with the value obtained by the direct analysis of the dependence of Tc on c2s shown in Fig. 3 [i.e., (∂Tph/∂c2s)c1 = (0.27 ± 0.03) K⋅mg−1⋅ml].
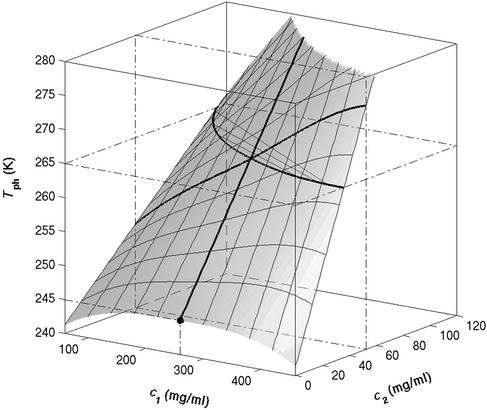
It is also convenient to describe the essential features of the coexistence surface within our experimental domain in terms of the variables c1 and c2 as shown in Fig. 5. All our data are taken in the vicinity of the point on the coexistence surface specified by the coordinates c1 = 260 mg/ml, c2 = 53 mg/ml, and Tph = 265 K. At this point, the values of the two principal slopes are (∂Tph/∂c2)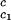 = (0.38 ± 0.04) K⋅mg−1⋅ml and (∂c2/∂c1)
= (0.38 ± 0.04) K⋅mg−1⋅ml and (∂c2/∂c1)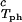 /c
/c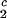 = (−3.0 ± 0.1)10−3 mg−1⋅ml.
= (−3.0 ± 0.1)10−3 mg−1⋅ml.
Figure 5.
Coexistence surface, Tph(c1,c2), for the ternary γS–PEG1450–water system. Our measurements of Tph(c1,c2) reported in Fig. 2 cover the range 220 < c1 (mg/ml) < 360, 40 < c2 (mg/ml) < 60. A representative solid curve at constant PEG concentration is generated by the intersection of the coexistence surface and the plane at c2 = 53 mg/ml. Our concentration measurements on the coexisting phases reported in Fig. 1 are represented by the isothermal coexistence curve (solid curve) generated by the intersection of the coexistence surface with the plane at Tph = 265 K. The three tie lines at Tph = 265 K are calculated from Eq. 4 by using q = 0.36. The circle at c2 = 0 locates the critical point for the binary γS–water system. The location of the critical point as a function of temperature is described by the critical line (solid curve at c1 = 260 mg/ml).
We can estimate the critical temperature, T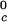 , for the binary γS–water system by using the relationship T
, for the binary γS–water system by using the relationship T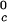 = Tc − (∂Tph/∂c2)
= Tc − (∂Tph/∂c2)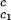 c2 to the critical line. This expression assumes that both the protein critical concentration, c
c2 to the critical line. This expression assumes that both the protein critical concentration, c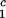 , and the slope, (∂Tph/∂c2)
, and the slope, (∂Tph/∂c2)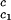 , are not functions of PEG concentration. This assumption was demonstrated to be correct for the ternary γD–PEG–water systems when PEG concentration is ≈50 mg/ml (11). We obtain T
, are not functions of PEG concentration. This assumption was demonstrated to be correct for the ternary γD–PEG–water systems when PEG concentration is ≈50 mg/ml (11). We obtain T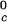 ≈ 245 K for the binary γS–water system. In Fig. 5, the critical point for the binary γS–water system is located by the circle at c2 = 0.
≈ 245 K for the binary γS–water system. In Fig. 5, the critical point for the binary γS–water system is located by the circle at c2 = 0.
In Table 1, we report the value of the critical temperature, T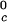 , and the critical volume fraction, φc, for the binary γS–water system. We also report the corresponding values for the high T
, and the critical volume fraction, φc, for the binary γS–water system. We also report the corresponding values for the high T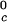 γ-crystallins (γE and γF) and the low T
γ-crystallins (γE and γF) and the low T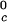 γ-crystallins (γB and γD) (8). All of the proteins in Table 1 have essentially the same critical volume fraction (φc ≈ 0.2), indicating that the range of the inter-protein interactions is essentially the same for all five γ-crystallins (17). However, the difference in critical temperature of ≈66 K between the high T
γ-crystallins (γB and γD) (8). All of the proteins in Table 1 have essentially the same critical volume fraction (φc ≈ 0.2), indicating that the range of the inter-protein interactions is essentially the same for all five γ-crystallins (17). However, the difference in critical temperature of ≈66 K between the high T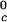 proteins and γS, and the difference of ≈33 K between the low T
proteins and γS, and the difference of ≈33 K between the low T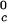 proteins and γS is the result of a corresponding difference between the magnitudes of the attraction energy. We therefore conclude that the magnitude of the attraction between γS molecules is, respectively, ≈20% and ≈10% smaller than the molecular attraction found for the high T
proteins and γS is the result of a corresponding difference between the magnitudes of the attraction energy. We therefore conclude that the magnitude of the attraction between γS molecules is, respectively, ≈20% and ≈10% smaller than the molecular attraction found for the high T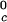 and the low T
and the low T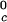 proteins.
proteins.
Table 1.
Critical points for the bovine γ-crystallins
| γ-Crystallins | φc |
T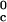 , K , K |
|---|---|---|
| γE | 0.22 ± 0.01 | 313 |
| γF | 0.22 ± 0.01 | 309 |
| γB | 0.19 ± 0.01 | 278 |
| γD | 0.20 ± 0.01 | 278 |
| γS | 0.18 ± 0.01 | 245 |
Discussion
The experimentally observable feature of the coexistence surface, (∂c2/∂c1)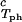 /c
/c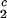 , is fully determined by the effective protein and PEG chemical potentials μ1 and μ2 (11). If PEG concentration is relatively small, these two chemical potentials can be expressed in the following way (11):
, is fully determined by the effective protein and PEG chemical potentials μ1 and μ2 (11). If PEG concentration is relatively small, these two chemical potentials can be expressed in the following way (11):
 |
2a |
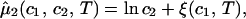 |
2b |
where μ̂i ≡ (μi − μ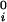 )/RT (with i = 1,2), μ
)/RT (with i = 1,2), μ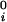 is the standard part of the chemical potential, T is the temperature, and R is the ideal gas constant. The quantity μ̂′1(c1, T) ≡ μ̂1(c1, 0, T) corresponds to the binary protein–water system and ξ(c1, T) is the first term in a series expansion describing the contribution to μ̂2 over and above the ideal mixing entropy. The two cross-derivatives of the chemical potentials, (∂μ̂1/∂c2)c1,T and (∂μ̂2/∂c1)c2,T, are both equal to (∂ξ/∂c1)T. This quantity characterizes the protein–PEG interactions (11).
is the standard part of the chemical potential, T is the temperature, and R is the ideal gas constant. The quantity μ̂′1(c1, T) ≡ μ̂1(c1, 0, T) corresponds to the binary protein–water system and ξ(c1, T) is the first term in a series expansion describing the contribution to μ̂2 over and above the ideal mixing entropy. The two cross-derivatives of the chemical potentials, (∂μ̂1/∂c2)c1,T and (∂μ̂2/∂c1)c2,T, are both equal to (∂ξ/∂c1)T. This quantity characterizes the protein–PEG interactions (11).
The Slope of the Tie Lines.
If we differentiate Eq. 2a with respect to c2 at constant c1 and T, and Eq. 2b with respect to c1 at constant μ̂2 and T, we obtain
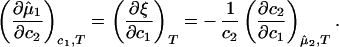 |
3 |
The normalized derivative, (∂c2/∂c1)μ̂2,T coincides with the limiting value of the slope of the tie lines at the critical point and has been experimentally measured. This quantity determines the effectiveness of PEG as a crystallizing agent for γS. Indeed, if protein crystals (the solid phase) are in thermodynamic equilibrium with the liquid phase, μ̂1 must be equal to its value in the solid phase, μ̂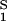 . For relatively low protein concentrations, μ̂′1(c1, T) ≈ ln c1. Thus, using the equality of chemical potentials and Eq. 2a, we find ln c1 ≈ μ̂
. For relatively low protein concentrations, μ̂′1(c1, T) ≈ ln c1. Thus, using the equality of chemical potentials and Eq. 2a, we find ln c1 ≈ μ̂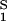 − (∂ξ/∂c1)Tc2. This relationship gives the protein solubility, c1, as a function of PEG concentration, c2. The dependence of μ̂
− (∂ξ/∂c1)Tc2. This relationship gives the protein solubility, c1, as a function of PEG concentration, c2. The dependence of μ̂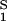 on c1 and c2 is expected to be very weak. Thus the fractional decrease of protein solubility with PEG concentration is fully determined by the value of (∂ξ/∂c1)T, which is provided by the slope of the tie line (see Eq. 3) (11). Thus, PEG1450 reduces the solubility of γS. We therefore believe that PEG is a useful tool not only for inducing LLPS of γS solutions but also for favoring the formation of γS crystals by solubility reduction.
on c1 and c2 is expected to be very weak. Thus the fractional decrease of protein solubility with PEG concentration is fully determined by the value of (∂ξ/∂c1)T, which is provided by the slope of the tie line (see Eq. 3) (11). Thus, PEG1450 reduces the solubility of γS. We therefore believe that PEG is a useful tool not only for inducing LLPS of γS solutions but also for favoring the formation of γS crystals by solubility reduction.
The Excluded Volume Model of Protein–PEG Interactions.
We now analyze the experimental coexisting values (φI, c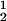 ) and (φII, c
) and (φII, c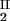 ) to gain insight into the physical factors that are responsible for the γS–PEG1450 interactions. We apply a simple excluded volume model that directly relates PEG partitioning to the difference in free volume fractions between the two coexisting phases. If we assume that PEG molecules can be described as ideal polymer coils and that protein molecules have a spherical shape, then due to steric hindrance, each protein will be surrounded by an adjacent region where the centers of mass of the coils are excluded, and the width, δ, of the resulting depletion layer will be proportional to the gyration radius, Rs, of the polymer coil (18–23). If α is the volume fraction available to the centers of mass of the coils, the condition of chemical equilibrium becomes c
) to gain insight into the physical factors that are responsible for the γS–PEG1450 interactions. We apply a simple excluded volume model that directly relates PEG partitioning to the difference in free volume fractions between the two coexisting phases. If we assume that PEG molecules can be described as ideal polymer coils and that protein molecules have a spherical shape, then due to steric hindrance, each protein will be surrounded by an adjacent region where the centers of mass of the coils are excluded, and the width, δ, of the resulting depletion layer will be proportional to the gyration radius, Rs, of the polymer coil (18–23). If α is the volume fraction available to the centers of mass of the coils, the condition of chemical equilibrium becomes c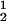 /αI = c
/αI = c /αII, where c2/α is the polymer concentration in the free volume (21). An approximate expression for the free volume fraction, α, as a function of the hard sphere volume fraction, φ, is given by the well-established scaled particle theory (24–26):
/αII, where c2/α is the polymer concentration in the free volume (21). An approximate expression for the free volume fraction, α, as a function of the hard sphere volume fraction, φ, is given by the well-established scaled particle theory (24–26):
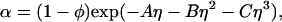 |
4 |
where η = φ/(1 − φ), A = 3q + 3q2 + q3, B = 9q2/2 + 3q3, C = 3q3, and q = δ/R is the depletion layer thickness normalized with respect to the hard sphere radius, R. The prefactor, 1 − φ, in Eq. 4, is the volume fraction not occupied by the spheres, whereas the exponential factor describes the effect of the depletion layers.
Because c /c
/c = α(q, φII)/α(q, φI), we substitute the expression for α provided by Eq. 4 into the ratio of the free volume fractions and thereby can determine an apparent q value for each experimental tie line. We find that, within the experimental error, this quantity does not depend on the tie-line position in the coexistence curve and report the average apparent value of q̄ = 0.36 ± 0.01. On the other hand, theoretically we expect that q = k(Rg/R) where k, in the case of hard sphere-ideal chain interactions, is a known function of Rg/R (23). For PEG1450, Rg = 1.56 nm (14), whereas R = 1.80 nm is estimated from the molecular weight and specific volume of γS. Because Rg/R = 0.87, the theoretical value of k is 1.03 (23) and the theoretical value of q is 0.89. Therefore, the apparent value of q is numerically ≈2.5 times smaller than the corresponding theoretical values. This significant discrepancy between the apparent and the theoretical q was also observed in the case of ternary γD–PEG water systems. It appears that weak attractive interactions between PEG and γS induce a flattening of the polymer coils near the protein surface and a corresponding reduction of the depletion layer thickness (11).
= α(q, φII)/α(q, φI), we substitute the expression for α provided by Eq. 4 into the ratio of the free volume fractions and thereby can determine an apparent q value for each experimental tie line. We find that, within the experimental error, this quantity does not depend on the tie-line position in the coexistence curve and report the average apparent value of q̄ = 0.36 ± 0.01. On the other hand, theoretically we expect that q = k(Rg/R) where k, in the case of hard sphere-ideal chain interactions, is a known function of Rg/R (23). For PEG1450, Rg = 1.56 nm (14), whereas R = 1.80 nm is estimated from the molecular weight and specific volume of γS. Because Rg/R = 0.87, the theoretical value of k is 1.03 (23) and the theoretical value of q is 0.89. Therefore, the apparent value of q is numerically ≈2.5 times smaller than the corresponding theoretical values. This significant discrepancy between the apparent and the theoretical q was also observed in the case of ternary γD–PEG water systems. It appears that weak attractive interactions between PEG and γS induce a flattening of the polymer coils near the protein surface and a corresponding reduction of the depletion layer thickness (11).
Summary and Conclusions
We have experimentally observed the liquid–liquid phase transition in ternary γS–PEG–water ternary systems. We have used the experimental coexisting values (φI, c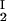 ) and (φII, c
) and (φII, c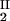 ) together with the slope, (∂c2/∂c1)
) together with the slope, (∂c2/∂c1)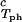 /c
/c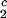 , to determine the γS–PEG interactions. We have used the experimental observable feature of the coexistence surface, (∂Tph/∂c2s)c1, to successfully determine the location of the upper consolute point for the binary γS–water system. This phase transition could not previously be observed in absence of PEG because it is inaccessible due to the freezing of the system.
, to determine the γS–PEG interactions. We have used the experimental observable feature of the coexistence surface, (∂Tph/∂c2s)c1, to successfully determine the location of the upper consolute point for the binary γS–water system. This phase transition could not previously be observed in absence of PEG because it is inaccessible due to the freezing of the system.
It is possible to argue that liquid–liquid transitions have not been observed for many binary protein–water systems because they fall outside the accessible experimental temperature range (from ≈−10°C to ≈40°C). If this is the case, PEG can be used to reveal the existence of LLPS for a much wider range of proteins than known previously.
Acknowledgments
We acknowledge Neer Asherie, Ajay Pande, Jayanti Pande, Alexander Chernov, and Seth Fraden for useful comments. This work was supported by National Aeronautics and Space Administration Grant NAG8-1659 and National Institutes of Health Grant EY05217.
Abbreviations
- PEG
polyethylene glycol
- LLPS
liquid–liquid phase separation
- γS
γS-crystallin
References
- 1.Benedek G B. Invest Ophthalmol Visual Sci. 1997;38:1911–1921. [PubMed] [Google Scholar]
- 2.Pande A, Pande J, Asherie N, Lomakin A, Ogun O, King J, Benedek G B. Proc Natl Acad Sci USA. 2001;98:6116–6120. doi: 10.1073/pnas.101124798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Steinberg M H, Forget B G, Higgs D R, Nagel R L. Disorders of Hemoglobin: Genetics, Pathology, Clinical Management. Cambridge, U.K.: Cambridge Univ. Press; 2000. [Google Scholar]
- 4.Selkoe D J. J Neuropathol Exp Neurol. 1994;53:438–447. doi: 10.1097/00005072-199409000-00003. [DOI] [PubMed] [Google Scholar]
- 5.Benedek G B, Pande J, Thurston G M, Clark J I. Prog Ret Eye Res. 1999;18:391–402. doi: 10.1016/s1350-9462(98)00023-8. [DOI] [PubMed] [Google Scholar]
- 6.Benedek G B. In: Human Cataract Formation. Nugent J, Whelan J, editors. London: Pitman; 1984. pp. 237–247. [Google Scholar]
- 7.Thomson J A, Schurtenberger P, Thurston G M, Thomson J A, Benedek G B. Proc Natl Acad Sci USA. 1987;84:7079–7083. doi: 10.1073/pnas.84.20.7079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Broide M L, Berland C R, Pande J, Ogun O, Benedek G B. Proc Natl Acad Sci USA. 1991;88:5660–5664. doi: 10.1073/pnas.88.13.5660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Liu C, Asherie N, Lomakin A, Pande J, Ogun O, Benedek G B. Proc Natl Acad Sci USA. 1996;93:377–382. doi: 10.1073/pnas.93.1.377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Liu C, Pande J, Lomakin A, Ogun O, Benedek G B. Invest Ophthalmol Visual Sci. 1998;39:1609–1619. [PubMed] [Google Scholar]
- 11.Annunziata O, Asherie N, Lomakin A, Pande J, Ogun O, Benedek G B. Proc Natl Acad Sci USA. 2002;99:14165–14170. doi: 10.1073/pnas.212507199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Galkin O, Chen K, Nagel R L, Hirsch R E, Vekilov P G. Proc Natl Acad Sci USA. 2002;99:8479–8483. doi: 10.1073/pnas.122055299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Skouri-Planet F, Bonneté F, Prat K, Bateman O A, Lubsen N H, Tardieu A. Biophys Chem. 2001;89:65–76. doi: 10.1016/s0301-4622(00)00216-7. [DOI] [PubMed] [Google Scholar]
- 14.Schurtenberger P, Chamberlin R A, Thurston G M, Thomson J A, Benedek G B. Phys Rev Lett. 1989;63:2064–2067. doi: 10.1103/PhysRevLett.63.2064. [DOI] [PubMed] [Google Scholar]
- 15.Bhat R, Timasheff S N. Protein Sci. 1992;1:1133–1143. doi: 10.1002/pro.5560010907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kulkarni A M, Chatterjee A P, Schweizer K S, Zukoski C F. J Chem Phys. 2000;113:9863–9873. [Google Scholar]
- 17.Lomakin A, Asherie N, Benedek G B. J Chem Phys. 1996;104:1646–1656. [Google Scholar]
- 18.Asakura S, Oosawa F. J Chem Phys. 1954;22:1255–1256. [Google Scholar]
- 19.Vrij A. Pure Appl Chem. 1976;48:471–483. [Google Scholar]
- 20.Gast A P, Hall C K, Russell W B. J Colloid Interface Sci. 1983;96:251–267. [Google Scholar]
- 21.Lekkerkerker H N W, Poon W C K, Pusey P N, Stroobants A, Warren P B. Europhys Lett. 1992;20:559–564. [Google Scholar]
- 22.Ilett S M, Orrock A, Poon W C K, Pusey P N. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Top. 1995;51:1344–1352. doi: 10.1103/physreve.51.1344. [DOI] [PubMed] [Google Scholar]
- 23.Tuinier R, Vliegenthart G A, Lekkerkerker H N W. J Chem Phys. 2000;105:10768–10775. [Google Scholar]
- 24.Widom B. J Chem Phys. 1963;39:2808–2812. [Google Scholar]
- 25.Lebowitz J L, Helfand E, Praestgaard E. J Chem Phys. 1965;43:774–779. [Google Scholar]
- 26.Lekkerkerker H N W. Colloids Surf. 1990;51:419–426. [Google Scholar]