On the use of sibling recurrence risks to select environmental factors liable to interact with genetic risk factors

Abstract

Gene–environment interactions are likely to be involved in the susceptibility to multifactorial diseases but are difficult to detect. Available methods usually concentrate on some particular genetic and environmental factors. In this paper, we propose a new method to determine whether a given exposure is susceptible to interact with unknown genetic factors. Rather than focusing on a specific genetic factor, the degree of familial aggregation is used as a surrogate for genetic factors. A test comparing the recurrence risks in sibs according to the exposure of indexes is proposed and its power is studied for varying values of model parameters. The Exposed versus Unexposed Recurrence Analysis (EURECA) is valuable for common diseases with moderate familial aggregation, only when the role of exposure has been clearly outlined. Interestingly, accounting for a sibling correlation for the exposure increases the power of EURECA. An application on a sample ascertained through one index affected with type 2 diabetes is presented where gene–environment interactions involving obesity and physical inactivity are investigated. Association of obesity with type 2 diabetes is clearly evidenced and a potential interaction involving this factor is suggested in Hispanics (P=0.045), whereas a clear gene–environment interaction is evidenced involving physical inactivity only in non-Hispanic whites (P=0.028). The proposed method might be of particular interest before genetic studies to help determine the environmental risk factors that will need to be accounted for to increase the power to detect genetic risk factors and to select the most appropriate samples to genotype.

Introduction

If gene–environment (G × E) interactions are expected to be important in multifactorial disease susceptibility,¹ genetic and environmental factors are most often evaluated independently rather than jointly. Joint analysis and G × E interaction testing is usually performed in a second step once the observed effects of each factor have been evidenced.^{2, 3, 4} Using such a strategy, we are likely to miss important genetic or environmental factors whose effects could only be detected when accounting for the other factor.^{5, 6} This was clearly evidenced in the study by Selinger-Leneman et al⁶ where it was shown that the power to detect a genetic risk factor interacting with an environmental risk factor might be considerably reduced when the environmental exposure of individuals is not accounted for. However, this was very dependent on the environmental risk factor prevalence, on its effect on the disease and on its interaction with the genetic factor. In some situations, accounting for the environmental exposure was even detrimental in terms of power. This first study called for the need to develop methods to select environmental factors that might be involved in G × E interaction and should therefore be accounted for in genetic studies.

The problem of selecting environmental exposures to account for in genetic studies becomes even more crucial when performing genome-wide association studies with hundreds of thousands of markers. Indeed, in this context, for each exposure to study, there are such a huge number of tests to perform that one wants to make sure that only relevant exposures are accounted for. The development of methods to select these relevant environmental factors will probably be the first step to test for G × E interactions at the genome-wide levels.

In their previous work, Selinger-Leneman et al⁶ have shown that selecting environmental factors based solely on their observed effects is not an efficient strategy and it might be useful to find a statistical tool to determine if they are likely to interact with genetic risk factors. This, however, should be carried out before the genetic analysis and thus involves the use of methods that do not require genotyping data. One such method was proposed by Purcell⁷ for twin data and relies on variance component modeling. Apart from the fact that it requires twin data, the method also requires exposure status of both sibs, which is not always easy to obtain. Our proposed method also uses familial aggregation of the disease as a surrogate for the genetic factors but exposure in indexes only. Indeed, as suggested by Stücker et al,⁸ familial aggregation of disease would be different for exposed and unexposed indexes if the environmental factor studied is involved in G × E interaction. A rational for this property is that in presence of G × E interaction exposed indexes have not the same distribution of genotypes as unexposed indexes. Their sibs will consequently have a different probability of having the disease from those of unexposed indexes.

In this paper, we used this idea of difference in sibling recurrence risks based on index's exposure to propose a test aimed at selecting environmental factors that are prone to interact with the genetic component of a multifactorial disease and propose a simple statistical test. We study the statistical properties of this test under different models and apply it on a type 2 diabetes (T2D) sample.

Materials and methods

To evidence a difference in the recurrence risk for siblings of exposed and unexposed individuals, we need data on a sample of sib pairs ascertained through an affected index (sib 1). The variable of interest is the affection status of the other sib (sib 2) and the explicative variable is the exposure status of sib 1. The data can be presented in a contingency table such as Table 1.

Table 1. Distribution of the sample of sib pairs in cross table according to exposure of sib 1 and disease status of sib 2.

	Sib 1 (affected)
Sib 2	Exposed	Unexposed
Affected	a	b	a+b
Unaffected	c	d	c+d
	a+c	b+d	N
	KSE=a/(a+c)	KSĒ=b/(b+d)	KS=(a+b)/N

The sibling recurrence risk over the whole sample (K_S) and sibling recurrence risks stratified on sib 1's exposure (K_SE and K_SĒ) can be derived from the observed numbers (a, b, c and d). The odds ratio of recurrence (ORR) is equal to:

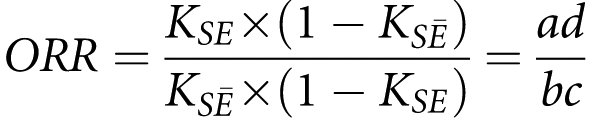Odds ratio of recurrence and Exposed versus Unexposed Recurrence Analysis

Let K_S be the sibling recurrence risk defined as the probability of sib 2 being affected given sib 1 is affected⁹. Let K_SE (K_SĒ) be the risk when sib 1 is affected and exposed (unexposed) to a given environmental factor E. To measure the difference between these two stratified risks, an odds ratio of recurrence (ORR) can be calculated by analogy with an odds ratio (OR):

Deriving the above recurrence risks as a function of observed numbers in the contingency table (Table 1), the ORR can be expressed as:

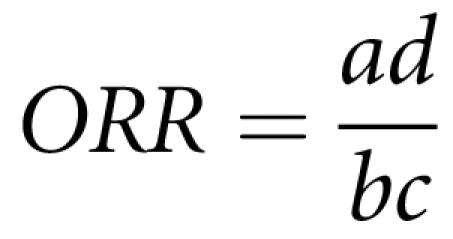In contrast to the OR of an environmental factor where exposure and disease statuses are measured in the same individual, in the ORR, exposure is measured in the affected index and the disease status is measured in the sib.

In the presence of a G × E interaction involving environmental factor E, we expect the ORR to be different from 1. To test for ‘ORR=1', we propose to perform a 1 degree of freedom (d.f.) χ²-test on the contingency table crossing sib 1's exposure with sib 2's affection status (Table 1) or the asymptotically similar Wald test based on the logistic regression parameter estimate and its variance. This test will be referred to as the Exposed versus Unexposed Recurrence Analysis (EURECA) test.

Properties of the ORR and of the EURECA test under different models

To study the behavior of the ORR and the statistical properties of EURECA, we considered a model of interaction involving a single gene (G) and a single environmental factor (E) even though the method practically only uses environmental information. We computed the expected numbers in each cell of the contingency table and derived the different recurrence risks (Table 1) under the different models of G × E interaction defined by the parameters presented in Table 2. A disease D with population prevalence f_D is considered. It is assumed that D is causally associated only with E and G.

Table 2. Probability of disease given exposure and genotype statuses according to genetic and environmental model parameters.

	Genotype
Exposure	G− (1–fG)	G+ (fG)
E− (1–fE)	B	B.RRG
E+ (fE)	B.RRE	B.RRG.RRE.I

Abbreviations: E+, exposed; E−, unexposed; f_E, proportion of exposed individuals in population; G+, carrier of the predisposing genotype(s); G−, noncarrier of the predisposing genotype(s); f_G, proportion of carriers of the predisposing genotype(s) in population; B, baseline risk; RR_E, exposure relative risk; RR_G, genotypic relative risk; I, multiplicative interaction coefficient for individuals both exposed and carrier of the predisposing genotype.

The E factor is dichotomous with population frequency f_E and a main effect size on D measured by the exposure relative risk, RR_E. To model the possibility for a familial clustering of E, as in Khoury et al,¹⁰ we define the conditional probability of sib 2 being exposed given the exposure status of sib 1 as:

where Y₁ is a dummy variable that takes the value 1 when sib 1 is exposed and 0 otherwise, and C_E is the environmental correlation between the sibs. Thus, when C_E=0, sib 2's exposure status is independent from sib 1's exposure status and its probability is always equal to the prevalence of E in the general population, f_E. When C_E=1, correlation between sibs for exposure is complete and sib 2's exposure probability is equal to 1 when sib 1 is exposed and 0 when sib 1 is unexposed.

The G factor corresponds to a predisposing genetic factor localized on an autosomal biallelic genetic locus. The allele that confers predisposition to disease is noted A and has a population frequency of q, whereas the other allele a has a population frequency of 1–q. Frequencies of the different possible genotypes (AA, Aa and aa) are supposed to follow Hardy–Weinberg proportions in the population (ie, q², 2q(1–q) and (1–q)², respectively). The main effect of the G factor is measured by the genotypic relative risk (RR_G) that corresponds to the ratio of the disease risk in carriers of the predisposing genotype(s) to the risk in noncarriers of the predisposing genotype(s) among unexposed individuals. In all situations, we compared dominant and recessive genetic models for a given frequency f_G of predisposing genotype(s), with f_G=q² under a recessive model and f_G=q²+2q(1–q) under a dominant model.

Let B designate the baseline risk, that is, the probability of disease for a noncarrier and unexposed individual. The interaction between E and G is measured by an interaction coefficient I, which corresponds to a departure from a multiplicative model when both E and G are present. In the absence of interaction, the risk of an individual exposed and carrier of the predisposing genotype is the product of B, RR_E and RR_G. In the presence of interaction, this risk is multiplied by the interaction coefficient I (Table 2). The conditional risks of disease given genotype and exposure status and the numbers of the contingency table cells were derived using the ITO matrix method of Li and Sacks¹¹ modified to account for the environmental factor. Computations were performed with the Maple 10 software¹² and explanations are given in the Supplementary materials.

Type I error and power of the EURECA test were asymptotically estimated considering a sample of 1000 sib pairs by use of 1 d.f. noncentral χ²-distributions. Alternatively, we calculated the required number of sib pairs to reach a power of 0.80 with a type I error rate of 0.05.

Application to type 2 diabetes

The Gene ENvironment Interactions (GENI) study¹³ collected phenotypic and environmental data of type 2 diabetic subjects and their families living in the San Luis Valley and the Denver metropolitan area in Colorado (USA). Among 452 pedigrees (3090 nuclear families) ascertained through one index sib affected with T2D, we extracted 2699 index sib pairs for which data were available in the index for at least one of the two studied exposures: obesity and physical inactivity. Of those pairs, 1734 were Hispanics (H) and 965 were non-Hispanic whites (NHW). Subjects previously diagnosed by a physician as having T2D and treated with oral hypoglycemic agents or insulin were considered affected. For subjects that did not report having T2D or subjects untreated for T2D, diabetic status was determined by an oral glucose tolerance test using American Diabetes Association criteria (1997). For diabetic subjects, self-reported body mass index (BMI) at the time of diagnosis was used. BMI was calculated at recruitment time for other subjects. Individuals having a BMI value exceeding 30 kg/m² were classified as obese. Physical activity assessment was carried out once during the study using a previously validated questionnaire self-administered by the subjects.¹⁴ Energy expenditure was assessed as metabolic equivalent task (MET) units. The MET is the ratio of the metabolic rate during exercise to the metabolic rate at rest.¹⁵ The average MET per week (before the diagnosis of T2D for affected individuals) was calculated for each study participant. The MET variable was divided into sex-specific tertiles, and a dichotomous variable was created distinguishing individuals in the lower tertile (‘low physical activity') from those in the upper two tertiles.

We carried out all the analysis separately for the two population strata (H and NHW) because the two exposures distributions were significantly heterogeneous. We first evaluated the observed main effect of each exposure using conditional logistic regression applied on discordant sib pairs for the T2D affection status. The numbers of available subjects were 198 H and 116 NHW for obesity and 458 H and 309 NHW for physical inactivity. Exposure frequency was measured in the control samples (unaffected sibs) and used as an estimate of exposure prevalence in population.

For each exposure, we randomly selected one sib for each index to compute contingency table numbers and global and stratified recurrence risks (K_S, K_SE and K_SĒ). The numbers of available pairs were 267 H and 321 NHW for obesity and 246 H and 268 NHW for physical inactivity. We derived an ORR for each exposure and applied the EURECA test of interaction using a logistic regression model. To account for correlated pairs belonging to the same pedigree, we computed the standard error of the logistic regression parameter using a robust sandwich estimator clustered by family as implemented in Stata/SE 10.1.¹⁶ When exposure of the random sib was available, the pairs were also used to calculate a correlation coefficient between sib pairs for each exposure variable using Equation 2.

Results

Behavior of the odds ratio of recurrence under different disease models

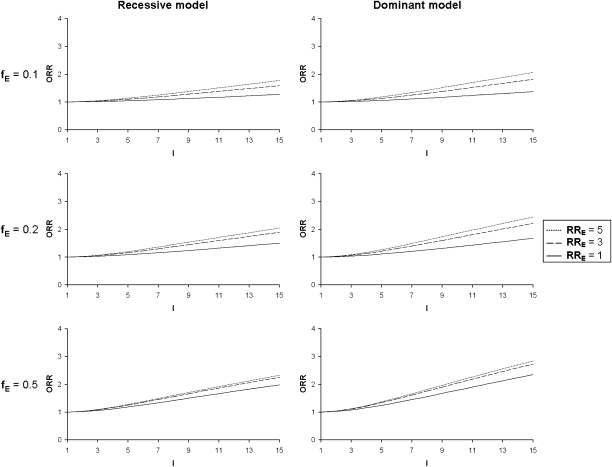
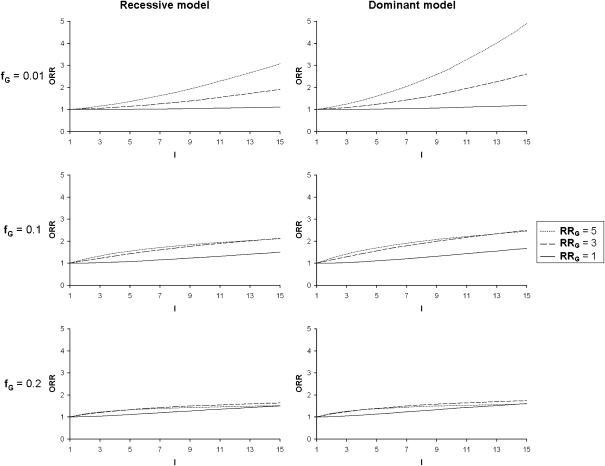
To evaluate the pertinence of using the ORR as an indicator of the presence of a G × E interaction, we investigated the variations of the ORR under different models first without correlation between siblings for E (C_E=0). As expected, we observe that in the presence of an interaction the values of the ORR increase with increasing values of the interaction coefficient I, but they also depend on the other model parameters. Impacts of these parameters are shown in Figure 1 for the exposure parameters (f_E and RR_E) and in Figure 2 for the genetic parameters (f_G and RR_G). For a given value of I, ORR is greater for high values of f_E and RR_E (Figure 1) and small values of f_G. When prevalence of the predisposing genotype(s) increases (f_G=0.2), the changes in ORR seen with varying RR_G tend to disappear and even reverse when interaction values are elevated (Figure 2). ORR is higher for a dominant as compared to a recessive model at fixed f_G.

Figure 1.

Odds ratio of recurrence (ORR) as a function of the gene–environment interaction coefficient (I) for varying exposure prevalences (f_E), varying exposure relative risks (RR_E) and for a recessive and a dominant genetic model. Fixed parameters: disease prevalence, f_D=0.1; frequency of predisposing genotype(s), f_G=0.1; genotypic relative risk, RR_G=1; sibling correlation for the environmental factor, C_E=0.

Figure 2.

Odds ratio of recurrence (ORR) as a function of the gene–environment interaction coefficient (I) for varying frequencies of predisposing genotype(s) (f_G), varying genotypic relative risks (RR_G) and for a recessive and a dominant genetic model. Fixed parameters: disease prevalence, f_D=0.1; frequency of exposure, f_E=0.2; exposure relative risk, RR_E=1; sibling correlation for the environmental factor, C_E=0.

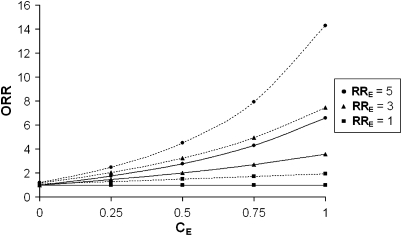
Because environmental correlation between sibs might induce a possible confusion with a G × E interaction, we looked into variations of ORR values for different values of C_E, when I=1 and I=5 (Figure 3). We observe that under the null hypothesis (I=1), the ORR value (referred to as ORR₀) is always equal to 1 in situations where there is no correlation of the E factor (C_E=0) or when there is no effect of E (RR_E=1). On the other hand, in the presence of an effect of E (ie, RR_E≠1) associated with a correlation between sibs for this factor (ie, C_E≠0), the ORR₀ values are inflated. In presence of a sibling correlation for E, the estimates obtained with a G × E interaction (I=5, Figure 3) should thus be tested against the value of ORR₀ rather than against 1. The null hypothesis of the test becomes ‘ORR=ORR₀'. The value of ORR₀ depends on the disease prevalence, on the environmental parameters and to a lesser extent on the genetic parameters. To estimate ORR₀, we thus need to obtain some estimates these different parameters. Disease prevalence is often known from previous studies in similar populations. The environmental parameters (C_E, f_E, RR_E) can be estimated using the studied sample when data on the environmental exposure of siblings are available (see the T2D example here). If this is not the case, results from previous studies on the effect of the environmental can be used. Only the genetic model is not known. We propose to calculate ORR₀ for different genetic model parameters (f_G, RR_G) and then to use as ORR₀ the value the closest to the observed ORR. This ‘worst-case scenario' ensures a robust inference on the test (see example in the Results section, Application to type 2 diabetes). To compute the expected ORR₀, the Maple source code of ‘EURECA' is available from the corresponding author on request. More theoretical derivation of the ORR₀ computation is also given in the Supplementary materials.

Figure 3.

Odds ratio of recurrence (ORR) as a function of the sibling correlation for the environmental factor (C_E) and the environmental factor relative risk (RR_E). Fixed parameters: disease prevalence, f_D=0.1; frequency of exposure, f_E=0.2; frequency of predisposing genotype(s), f_G=0.1; genotypic relative risk, RR_G=1. Solid curves represent null hypothesis scenarios and dotted curves represent corresponding situations with a gene–environment interaction (I) of 5.

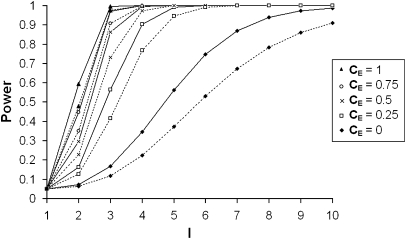
Properties of the Exposed versus Unexposed Recurrence Analysis test

In Figure 4, the power of the EURECA test of ‘ORR=ORR₀' is reported for varying levels of interaction and C_E under dominant and recessive models. As expected, the power increases with increasing value of I but more interestingly, this increase depends on C_E and is larger for high C_E values than for low C_E values. Alternatively, Table 3 reports the number of sib pairs that are needed to reach a power of 0.80 with a type I error rate of 0.05 for increasing values of I and C_E under a plausible disease model (frequent factors, f_G=0.1 and f_E=0.2; with moderate effects, RR_G=2 and RR_E=2). In situations with no C_E and small I, sample sizes are very high and thus unlikely to be recruited. But considering situations with elevated interaction coefficients (I>3) and with high correlation for exposure in sibs (C_E>0), sample sizes are more reasonable.

Figure 4.

Power of the EURECA test as a function of the interaction coefficient I and the sibling correlation for exposure C_E, after accounting for inflated type I error rates due to C_E, considering a sample size of 1000 sib pairs. Fixed parameters: disease prevalence, f_D=0.1; frequency of exposure, f_E=0.2; exposure relative risk, RR_E=2; frequency of predisposing genotype(s), f_G=0.1; genotypic relative risk, RR_G=2. Dotted curves represent computations for recessive models and solid curves for dominant models.

Table 3. Sample size (number of sib pairs) required to obtain a power of 0.80 with a type I error rate of 0.05 as a function of the interaction coefficient (I) and the environmental correlation between sibs (C_E).

	Recessive model					Dominant model
CEI	1	2	3	5	10	1	2	3	5	10
0	∞	72 417	13 885	2946	720	∞	41 516	8061	1754	448
0.25	∞	12 250	2568	619	181	∞	8418	1745	423	126
0.5	∞	5371	1182	307	99	∞	3875	841	219	70
0.75	∞	3172	725	199	67	∞	2345	529	145	47
1	∞	2163	511	147	51	∞	1625	379	108	35

Fixed parameters: disease prevalence, f_D=0.1; frequency of predisposing genotype(s), f_G=0.1; genotypic relative risk, RR_G=2; frequency of exposure, f_E=0.2; exposure relative risk, RR_E=2.

Considering the same frequencies with a sibling correlation of 0.25 and varying values of RR_E and RR_G, the required sample sizes are shown in Supplementary Figure S1. As expected, these sizes are smaller when G and E have strong effects, but they seem to be more sensitive to G than to E.

All the previous results considered a disease prevalence (f_D) of 0.10. Variations in power as a function of interaction and disease prevalence are presented in the Supplementary Figure S2. In summary, it shows that the best performances of this test are obtained with common rather than with rare diseases. When the disease is rare, the sibling recurrence risk (K_S) is low and the difference between the exposed and unexposed index strata due to the G × E interaction is harder to detect.

Application to type 2 diabetes

The results of the T2D application are presented in Table 4. For each population strata (H and NHW) and each studied exposure, we show first the environmental parameter estimates: OR_E (exposure's OR), f_E and C_E, and then the proposed G × E interaction analysis: ORR and EURECA test. To account for C_E, we calculated the ORR expected under the null hypothesis (ORR₀). The Center for Disease Control and Prevention 2001 diabetes data for the state of Colorado provided diabetes prevalence (f_D=4.5%).¹⁷ On the basis of this estimate and using the environmental parameters calculated previously on the T2D data, we computed expected ORR₀ values for a wide range of genetic parameters (f_G=0.01–0.5, RR_G=0.5–10). An interval of variation of ORR₀ was obtained in this way. To ensure robustness of the test, we considered the ‘worst-case scenario' and compared the observed ORR to the value of ORR₀ that was the closest to the observed ORR.

Table 4. Results of the application on T2D data.

Environmental factor	Obesity		Low physical activity
Stratum	H	NHW	H	NHW
ORE	2.48	3.87	1.13	0.93
95% CI of ORE	1.18, 5.22	1.54, 9.65	0.72, 1.77	0.53, 1.65
fE	0.29	0.37	0.31	0.23
CE	0.22	0.14	−0.02	0.07
ORR0	1.25a, 1.27	1.22a, 1.25	0.99, 1.00a	0.99, 1.00a
ORR	0.67	1.03	1.14	2.13
95% CI of ORR	0.40, 1.11	0.53, 1.99	0.62, 2.08	1.08, 4.19
EURECA	4.03	0.25	0.15	4.78
P-value	0.045	0.617	0.70	0.028

Abbreviations: H, Hispanics; NHW, non-Hispanic whites; OR_E, odds ratio estimate of the environmental factor; f_E, estimated frequency of the environmental factor; C_E, estimated sibling correlation for the environmental factor; ORR₀, interval of variation of the expected odds ratio of recurrence under the null hypothesis; ORR, odds ratio of recurrence; CI, confidence interval; EURECA, Exposed versus Unexposed Recurrence Analysis.

^aClosest bounding value used to perform the test.

In H, obesity has an ORR equal to 0.67 (95% CI 0.40, 1.11). Remarkably, in this stratum, obesity has a strong significant observed effect of 2.48 (95% CI 1.18, 5.22), which, associated with a C_E of 0.22 and an f_E of 0.29, gives an expected ORR₀ varying between 1.25 and 1.27. In this example, we used 1.25 (closest value to the observed ORR of 0.67) to perform the EURECA test and obtained a P-value of 0.045. In NHW, obesity has also a significant observed effect with an OR of 3.87 (95% CI 1.54, 9.65) but the interaction test is not significant.

Considering physical inactivity, the interaction test is significant in the NHW sample only (P=0.028) and the ORR is 2.13 (95% CI 1.08, 4.19). This exposure has no significant observed effect and does not aggregate in sib pairs, which is a situation where the proposed test usually lacks power to detect the G × E interaction (as shown in Table 3 and Supplementary Figure S1).

Because the sex distributions of indexes and of sibs were homogenous between the groups of exposed and unexposed indexes, this variable should not interfere with the EURECA test.

Discussion

Contrasting the sibling recurrence risks based on the exposure status of the index is a simple and attractive approach to select environmental factors involved in a G × E interaction. We propose to measure this contrast by computing an ORR and show that the ORR is a good indicator of a G × E interaction. This ORR is not a direct measure of interaction but rather a measure of the difference between recurrence risks in exposed and unexposed indexes. For example, using the low physical activity in NHW result in Table 4, the risk of T2D in an NHW individual is multiplied on average by a factor of 2.13 when his affected index sib has a low physical activity compared to an individual whose affected index sib has a high physical activity. At this level of information, discriminating between an underlying genetic component interacting with the exposure and the familial clustering of this exposure associated to the disease is quite difficult,¹⁸ but our results show that it is possible, provided that the effect and familial correlation of the environmental factor is well documented.

In the context of a dichotomous environmental variable, the interest of using the ORR, instead of the ratio of recurrence risks, resides in applying a logistic regression as done in most epidemiologic studies, but the same approach can be easily extended to multiclass or continuous environmental factors using the classic general linear models. The use of continuous variables when available would probably increase the power but would also make the assumption of a linear relation. To test for the difference of the ORR with a null hypothesis value (ORR₀), we derive a statistical test, the EURECA test. To use this test, we need to define the value of ORR₀. We have derived analytically a formula to compute ORR₀ based on exposure parameter and disease prevalence estimates. These estimates are often easily obtained from the data sample and from the literature. To ensure robustness of the test, we suggest accounting for the impact on ORR₀ of possible variations in these estimates by deriving a range of variation of ORR₀ and to consider in the test the ORR₀ value the closest to the observed ORR. Note that the loss of power due to the uncertainty of the genetic parameters should be minimal because the ORR₀ variations would usually be small as in the illustrative example (from 0.01 to 0.03). Interestingly in our example, we found even under this ‘worst-case scenario', it is possible to show that observed ORR for some exposure significantly differs from ORR₀. This is in good agreement with the results of Khoury et al¹⁰ showing that the degree of familial aggregation of most common diseases cannot be entirely explained by a familial clustering of environmental risk factors even if we assume an extreme clustering of the environmental factor.

The study of the statistical properties of EURECA has shown that the test is appropriate to test for common diseases rather than rare ones (Supplementary Figure S2). Interestingly, even when the tests are corrected for the exposure correlation in siblings, powers were found to be higher for elevated values than for lower values of C_E. We hypothesize that the sibling correlation actually has a confounding effect on one part, but also emphasizes the existing difference in recurrence risks between strata of indexes due to the G × E interaction. We only tested positive correlation coefficients between siblings for exposure because it is probably the most common situation in familial studies.

Gene–environment interactions are difficult to detect and often require very large sample sizes. In an effort to increase the power to detect G × E interaction, new methods have been developed that are based on particular sampling designs. Among these methods are the log-linear modeling method that uses case–parent trio data and compares genotype distribution of exposed and unexposed cases conditional on parental genotypes,¹⁹ methods that use countermatching designs to enrich the sample with rare exposure or genetic factors²⁰ or case–control combined designs with both population and familial controls.²¹ A common feature of all these different methods to detect G × E interactions is their need to have a complete knowledge of the exposure statuses and genotypes of the studied subjects. Among the methods that use familial aggregation of the disease as a surrogate for the latent genetic factor, Purcell⁷ proposed to apply variance components models in twin studies to evidence G × E interactions with an environmental factor measured in both twins. What distinguishes the method we propose here is the type of information used to assess the G × E interaction. This method relies on the exposure of the index case and information on the familial recurrence of the disease. There is no need to have a measure of exposure in the sibs and for easily recognizable diseases, their affection status might be obtained from indexes. Large sample sizes can thus be obtained at a minimal cost. It is true however that if sibs could also be examined, familial recurrence will certainly be better estimated. It will also be possible to assess, directly from the data rather than from the literature, potential environmental correlation between sibs.

The use of the sib recurrence information as surrogate for genetic risk factors has the advantage of requiring no a priori hypothesis on the genetic model underlying disease susceptibility. It also permits to test for the involvement in the disease of genetic factors located anywhere on the genome at no cost in terms of multiple testing. This is an important point as the issue of multiple testing in G × E interaction studies considering thousands of genetic markers coupled with tens of exposures remains to be resolved. On the contrary, this approach only stipulates a specific environmental factor and tests for its interaction with the genetic component implicated in disease risk increase. As compared to other methods that use both genotypic and environmental information, this method could lack power to detect some interaction with a specified genetic factor. But it provides an easy way to screen for environmental factors potentially implicated in G × E interactions when genotypes are not available.

Association between T2D and obesity was significant both in H and NHW, as previously evidenced in many cross-sectional and longitudinal studies.²² Concerning interaction, EURECA was significant only in H (P=0.045) with a particular model of interaction where the interaction effect is in opposite direction compared to the main exposure effect. In an earlier study of recurrence risk estimation in T2D families, analogous results were found and elevated recurrence risk ratios were found in siblings of nonobese as compared to obese patients.²³ This kind of interaction illustrates the situations where the G × E interaction is a nuisance element that has to be accounted for to better detect a main effect.^{5, 6} Regarding low physical activity that had no significant observed effect in any of the two populations, the interaction test was significant in NHW (P=0.028) but not in H. A previous study that applied family-based association tests and generalized estimating equations models showed a G × E interaction between the peroxisome proliferator-activated receptor-γ gene and low physical activity in H too.¹³ Ascertainment of indexes through multiplex families as in the case of the GENI study could make it difficult to extrapolate results to the general population of diabetic patients. Indeed, an enrichment in disease susceptibility alleles is expected in these families and thus sibling recurrence risk estimates are likely to be increased as compared to those expected in the general population.²³ However, it should not create an erroneous heterogeneity between exposed and unexposed indexes strata unless there is a correlation between sibs for the environmental factor that is not correctly accounted for. In this example, the results are likely to encourage further studies to select nonobese subjects in H populations, to search for genetic factors implicated in T2D, whereas studying NHW populations, we would be more interested in searching for an interaction with low physical activity. This illustrates how one can use the ORR point estimates, their confidence intervals and corresponding P-values to rank among many environmental factors those that should be selected in priority to test for a G × E interaction in following genetic studies.

In conclusion, this paper demonstrates that valuable amount of familial information can be exploited toward detecting G × E interactions that underpin multifactorial disease susceptibility. This method is proposed as a strategy that can be used before genetic studies to help plan these studies. It can help investigators identify environmental factors liable to interact with genetic factors and that will need to be accounted for in the analysis but could also be used in the study design to select subcategories of the population to enhance genetic factor detection.