Genetic biases for showy males: Are some genetic systems especially conducive to sexual selection?

Abstract

Male secondary sexual characters (conspicuous ornaments, signals, colors) are among nature's most striking features. Yet, it is unclear why certain groups of organisms are more likely than others to evolve these traits. One explanation for such taxonomic biases is that some genetic systems may be especially conducive to sexual selection. Here, we present theory and simulation results demonstrating that rare alleles encoding either male ornaments or female preferences for those ornaments are better protected against random loss in species with ZZ/ZW or ZZ/ZO sex chromosome systems (male homogamety) than in species with XX/XY or XX/XO systems (male heterogamety). Moreover, this protection is much stronger in diploid than haplodiploid species. We also present empirical data showing that male secondary sexual characters are better developed in diploid than haplodiploid species and in diploid species with male homogamety than in those with male heterogamety. Thus, taxonomic biases for showy males may stem from differences in sex chromosome systems.

Darwin's theory of sexual selection clarifies why males, and not females, often evolve elaborate secondary sexual traits (1). Sexual selection arises from differences in reproductive success caused by competition for acquisition of mates, and this competition is typically stronger among males than females (2). In support of Darwin's predictions, abundant evidence indicates that weapons evolve through sexual selection by contests over females, whereas male ornaments evolve through sexual selection by female choice of mate (2). Yet, the question of why species differ in propensity to express such elaborate male secondary sexual traits remains unresolved. For instance, Darwin noted (1) that, “secondary sexual characters are more diversified and conspicuous in birds . . . than in any other class of animals.” Here, we suggest that such taxonomic biases for showy (ornamented) males may stem from differences in sex chromosome systems.

To understand how such taxonomic biases for ornamented males may arise, consider that during Fisherian sexual selection (3) an allele encoding a male secondary sexual trait increases in frequency when showy males gain a mating advantage with females that prefer that trait. Offspring of matings between males possessing the trait allele and females possessing the preference allele will tend to inherit both alleles. Thus, as the trait allele increases in frequency owing to enhanced mating success of trait-bearing sons, the preference allele increases in frequency also, causing a positive feedback that promotes the spread of both alleles (2–6).

Consider new mutant trait and preference alleles that result in marked exaggeration of their corresponding phenotypes (7–9) and thus are unlikely to have been initially present via mutation-selection balance (10). We initially consider only alleles that are sex-limited in effect, as did other models of sexual selection (4–6), because Fisherian male ornaments expressed in females (or Fisherian female preferences expressed in males) will be costly without compensating benefits, and thus alleles lacking sex-limited expression will be especially unlikely to experience positive selection (we discuss the consequences of relaxing this assumption later). Mutant alleles can produce sex-limited effects upon first appearance if they modify the response of structural or regulatory genes to circulating sex hormones or other signals for sexual development. Such newly arisen alleles are vulnerable to chance loss because of genetic drift when rare, even in large populations and when positively selected (3, 11, 12). However, the greater the magnitude of selection compared with genetic drift, the greater the likelihood that the phenotype encoded by the alleles will spread to fixation (13).

The sex chromosome system can ultimately reduce the chance that a rare mutant allele will be lost through genetic drift by increasing the probability that such an allele will occur in the genotype most strongly favored by selection (12, 14). Even small decreases in the probability of random loss necessarily boost the long-term probability of fixation by the allele (12, 14). Moreover, the results of a Markovian model of phenotypic evolution (12, 14) reveal that small differences in these fixation probabilities can be magnified into large differences in long-run probabilities of observing a rare mutant allele's phenotypic effect, e.g., an extravagant male secondary sexual character.

In the first part of our paper, we present a model of mate-preference evolution showing that rare alleles encoding either male ornaments or female preferences for those ornaments are better protected against random loss in species with ZZ/ZW or ZZ/ZO sex chromosome systems (male homogamety) than in species with XX/XY or XX/XO systems (male heterogamety). Moreover, we show that this protection is much stronger in diploid than haplodiploid species.

In the second part of the paper, we present results of simulations demonstrating that different genetic systems do indeed differ in their tendency to yield male ornaments as predicted by the model. Finally, we present empirical data showing that some genetic systems may indeed be especially conducive to sexual selection. Our results suggest that taxonomic biases for showy males may stem from differences in sex chromosome systems.

Model

To evaluate which genetic systems minimize the probability of random loss of rare trait and preference alleles, we first determined, for each genetic system, the most frequent mating type involving a preference-bearing female and a trait-bearing male, when the latter is rare. Then, we determined the fraction of sons inheriting both trait and preference alleles. As the proportion of sons carrying both alleles increases, the likelihood of chance loss of the male trait allele decreases, for two reasons. First, these males' traits will yield enhanced mating success through the mating preferences of preference-bearing females (2–6). Second, the greater number of offspring produced by these sons will increase the frequency of the preference allele in the next generation, thereby strengthening positive selection on the trait allele (2–6). Therefore, male trait and female preference alleles are best protected against chance loss in genetic systems that increase the proportion of sons carrying both alleles.

Consider, for example, when trait and preference alleles are diploid, unlinked, and autosomal. Let “P” and “T” represent alleles for female preference and male trait, respectively, and “p” and “t” represent lack of preference and trait, respectively. When T is rare, the most frequent mating type involving a P-bearing female will be (the dash signifies a nonspecified preference allele):

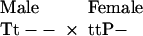Male offspring will exhibit four equally frequent genotypes: TtP-, ttP-, Tt--, and tt--. Thus, in a diploid autosomal system, at least 1/4 of the males will carry both T and P alleles.

By contrast, when T and P are X-linked (male heterogamety) and T is rare, the most frequent mating type involving a P-bearing female will be:

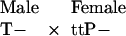Here, male offspring will exhibit two equally frequent genotypes (tP and t-), because the father does not contribute genetically to the female's sons. In this case, no sons possess both T and P alleles, so a rare T allele is especially vulnerable to chance loss in an X-linked system. (Although half of the daughters will possess both P and T alleles, these daughters will have fewer offspring than sons possessing both alleles, because they cannot benefit from the mating advantage accruing to T-bearing sons. Daughters also pay any costs of being choosy; reviewed in ref. 15.)

Next, consider when T and P are Z-linked (male homogamety) and T is rare. Here, the most frequent mating type involving a P-bearing female will be:

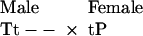Because the female transmits her P allele to all of her sons, they exhibit the genotypes TtP- and ttP- with equal frequency. In this case, half of the sons possess both T and P alleles, so the protection afforded the T allele from chance loss is the highest for any genetic system.

Thus, two important predictions emerge from our model. First, in diploid systems, the protection from chance loss is greater when T and P are Z-linked than when autosomal, but the protection is greater when T and P are autosomal than when X-linked. Second, this protection is greater in diploid than in haplodiploid species (e.g., ants, bees, and wasps), because the latter essentially possess a completely X-linked genome (16).

We tested the above model predictions in two ways. First, we conducted Monte Carlo simulations of the coevolution of P and T alleles to determine whether different genetic systems do indeed differ in their theoretical tendency to yield male ornaments, in accordance with the model. Second, we conducted a comparative metaanalysis to ascertain whether, as suggested by both our model and the simulation results (see below), secondary sexual characters are better developed in diploid than haplodiploid species and in diploid species with male homogamety than in those with male heterogamety.

Materials and Methods

Monte Carlo Simulations.

We simulated coevolution of P and T alleles by using a MATHEMATICA V.4.0 program available from the authors. A population with a low frequency of the P allele was seeded with a single T-bearing male mutant, and the frequency of the T-allele was measured after 100 nonoverlapping generations, averaged across each of 10 blocks of 100 replicate evolving populations. The population consisted of 2,000 members divided equally between the sexes and initially consisted of a single T-bearing mutant male and a starting allele frequency of 0.10 for the P allele.

In each generation, each female scanned N different males in the population. If the female had a P allele, she mated either with a single, randomly chosen T-bearing male that appeared in her scan (dominant T allele) or was twice as likely to mate with TT males as with Tt males (additive T allele). A P-bearing female mated randomly with males in her scan if no T-bearing males appeared in her scan. PP females either behaved exactly like Pp females (dominant P allele) or were twice as likely to prefer T-bearing males when the latter appeared in her scan (vs. mate randomly) as were Pp females (additive P allele).

In accordance with recent data (17), both X- and Z-linked loci were assumed to be dosage compensated. Each female produced two offspring randomly drawn from the appropriate pool of offspring genotypes. A female produced a son with probability = 1/2. Before the next round of mating, males suffered either no viability cost (neutral case) or a 5% reduction in survival (costly ornament case). Coevolution was simulated for 100 generations in each run, for a total of either 100 runs (for the costly ornament case) or 1,000 runs (for the neutral case), and the mean population frequencies of the T and P alleles were computed at the end of the 100 generations. In the neutral case, we correlated the mean frequencies of the T and P alleles after 100 generations for each genetic system across each of the 10 blocks of 100 replicate populations.

Comparative Analyses.

To test the predictions of our model empirically, we evaluated the association between the degree of sexual dimorphism, a measure of the strength of sexual selection (2), and the observed sex chromosome system across various insect and vertebrate taxa. First, we developed an ordinal variable representing the predicted strength of selection favoring extravagant male traits. This ordinal scale, which was ranked according to the relative strength of selection on additive T alleles (Figs. 1 and 2), was −4 for haplodiploid systems, −3 for XX/XY (or XO) systems with highly heteromorphic sex chromosomes, −2 for XX/XY systems with slightly heteromorphic sex chromosomes, −1 for XX/XY systems with homomorphic sex chromosomes, +1 for ZZ/ZW systems with homomorphic sex chromosomes, +2 for ZZ/ZW systems with slightly heteromorphic sex chromosomes, and +3 for ZZ/ZW (or ZO) systems with highly heteromorphic sex chromosomes. This scale takes into account the possibility that alleles may arise on Y or W chromosomes in species with relatively little or no sex chromosome heteromorphism (7). In particular, it takes into account that Y-linked T alleles are strongly protected from random loss, but W-linked T alleles cannot be. For this reason, XX/XY genetic systems with greater sex chromosome homomorphism (= more active genes on the Y chromosome), and ZZ/ZW genetic systems with lesser sex chromosome homomorphism (= fewer active genes on the W chromosome), should be more prone to the evolution of male ornamentation. The maximally protected combination in an XX/XY system would be an autosomal P allele and a Y-linked T allele, and the maximally protected combination in a ZZ/ZW system (and the most potent combination overall) would be a Z-linked P allele and an autosomal or Z-linked T allele. (Future analyses ideally will take into account the relative sizes of the sex chromosomes in relation to autosomes, as discussed in ref. 14.)

Figure 1.

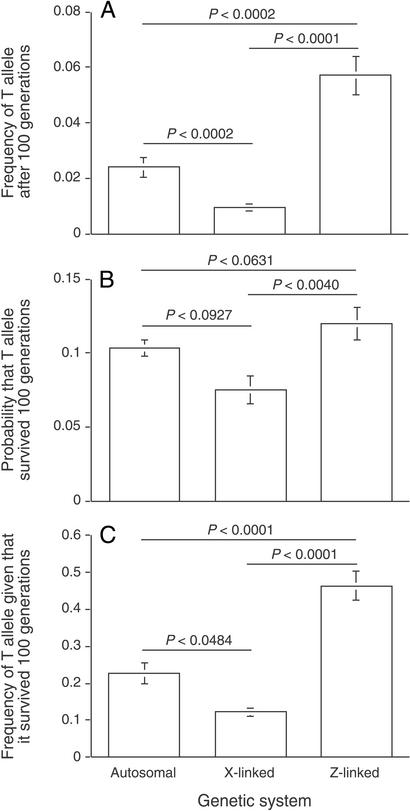
Results of Monte Carlo simulations when T and P alleles were assumed to be additive and when males suffered no viability cost for expressing the ornament encoded by the T allele (neutral case). (A) Frequency of T allele after 100 generations. (B) Probability that T allele survived 100 generations. (C) Frequency of T allele given that it survived 100 generations, when the T allele was autosomal, X-linked, and Z-linked. For all three response measures, P < 0.004; ANOVA on arcsine square root transformed data. P values above bars refer to pairwise comparisons using a Scheffé's test.

Figure 2.

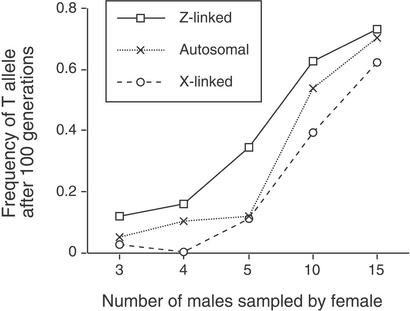
Results of Monte Carlo simulations when T and P alleles were assumed to be additive and when males suffered a 5% reduction in survival for expressing the ornament encoded by the T allele (costly ornament case), showing frequency of T allele after 100 generations as a function of the number of males that females sampled (a measure of the strength of the female preference) when the T allele was autosomal, X-linked, and Z-linked. The three different chromosome systems were significantly different from one another (P < 0.01; Friedman's nonparametric two-way ANOVA).

Next, we calculated the Spearman rank order correlation coefficient between the sex chromosome scores and a measure of the degree of sexual dimorphism exhibited by species within seven major taxonomic groups: insects, fish, anurans, salamanders, lizards, snakes, and birds (mammals were excluded because of extreme homogeneity in sex chromosome scores; birds vary in the degree of ZZ/ZW sex chromosome heteromorphism. We used a Spearman rank order correlation coefficient for our analyses, because this coefficient is not sensitive to outlying data points.)

The degree of sexual dimorphism was estimated for insects from the percentage of species within an order reported to exhibit male courtship (18). For fish, salamanders, anurans, reptiles, snakes, and birds, we estimated the degree of sexual dimorphism by using field guides and the primary literature to score for each species the number of visual and auditory traits reported as more exaggerated in mature males than in mature females. For example, if for a given species, only males possessed a call, a long tail, and bright plumage, three traits would be more exaggerated in males than in females, yielding a sexual dimorphism score of 3. We excluded olfactory traits from the analysis, because such traits are difficult to characterize. We did, however, include traits that have not necessarily been implicated in female choice, because the selective basis of many male secondary sexual traits remains unclear (19) and excluding a subset of such traits might have introduced subjective bias into our data set.

For all groups, the correlation between sex chromosome scores and the degree of sexual dimorphism was computed across the highest-level taxonomic units that had highly homogeneous sex chromosome systems [i.e., species (fish), genera (anurans, salamanders), families (lizards, snakes), or orders (insects, birds), with species averaged within higher-level taxonomic units]. For insects (n = 103 species analyzed), fish (n = 29 species), anurans (n = 51 species), salamanders (n = 38 species), and lizards (n = 96 species), we included only species for which we had both sexual dimorphism and sex chromosome data. For snakes (n = 142 species) and birds (n = 854 species), we included additional species for which we had only sexual dimorphism data (using ref. 20 for snakes and refs. 21–24 for birds), because families and orders in snakes and birds, respectively, have uniform sex chromosome systems, differing only in the degree of chromosomal heteromorphism (25–27).

Our model predicted a positive association between sex chromosome score and degree of sexual dimorphism. We did not test for the significance of correlation coefficients within the seven higher-level taxonomic groups because of possible phylogenetic nonindependence of chromosome scores and dimorphism data within these groups (28). Instead, we treated each correlation as a single data point and tested statistically whether our sample of seven correlation coefficients (for insects, fish, anurans, salamanders, lizards, snakes, and birds) was drawn from a distribution with a mean of zero (no association). As before, we used a nonparametric test that was not sensitive to outliers. These correlations are phylogenetically independent from each other, because each describes associations between the traits arising from evolution only within the clades corresponding to the major groups (28); thus, the analysis can be thought of as a correlational equivalent of an independent contrast test.

Results

Monte Carlo Simulations.

As expected from Fisherian coevolution, when T alleles increased in frequency, P alleles generally increased also, but the strength of the correlation between the two depended on the chromosome system. In particular, the frequencies of T and P after 100 generations were highly positively correlated across replicate populations when each allele was autosomal (r = 0.910; P < 0.0001) and Z linked (r = 0.685; P = 0.0265), but not when they were X linked (r = −0.082; P = 0.8276). Thus, Fisherian coevolution occurred frequently when T and P were either autosomal or Z linked, but rarely when they were X linked.

We then measured the mean frequency of the T allele after 100 generations to evaluate which systems were most likely to protect rare T alleles from loss. When we assumed that T and P were additive (as in most models of sexual selection; e.g., see ref. 4), we found that Z-linked systems were significantly most likely to protect rare T alleles from loss, autosomal systems were the next most likely to do so, and X-linked systems were the least likely (Fig. 1). These differences among chromosome systems in degree of protection held, regardless of whether the male trait was neutral (Fig. 1) or deleterious to male survival (Fig. 2) and regardless of the strength of the female preference (Fig. 2).

In contrast to the additive case, when P and T alleles were completely dominant, the mean frequency of the T-allele after 100 generations was significantly higher in autosomal (0.115) than in X-linked (0.077) or Z-linked (0.055) systems (P < 0.001, ANOVA on arcsine square root transformed data; P < 0.0059, Scheffé's post hoc tests), but this mean frequency did not differ between the latter two systems (P = 0.158). We did not simulate the case of fully recessive T and P alleles, because of the extreme infrequency with which T would survive loss, but here it must be that Z-linked systems will confer much greater protection than autosomal systems, and that X-linked systems will confer almost no protection: For Z-linked systems, a recessive P allele will be expressed phenotypically at low frequency, but a recessive T allele will not be expressed until the T alleles drift up to the point to which TT homozygotes are no longer rare. For autosomal systems, neither a recessive P allele nor a recessive T allele will be expressed until both alleles drift up to the point to which homozygotes are no longer rare. For X-linked systems, a recessive P allele will not be expressed when rare, but the T alleles will be expressed when rare, and thus selection will act to eliminate the T allele because of ornament costs, without any compensating positive selection generated by the female preference. Recent data on the degree of dominance of adaptive new mutations suggests that such mutants can range from completely recessive to completely dominant, but are on average close to additive in effect (29), which would entail that Z-linked systems should usually be most potent for sexual selection. {If new mutant alleles are not entirely sex limited in effect, and cause suboptimal phenotypes in the opposite sex, the genetic biases predicted are unaffected. For example, X-linked rare ornament genes would have the same mean expression in females as would autosomal rare ornament genes [the X-linked alleles would occur twice as frequently (14), but be half as expressed, in females]}.

To summarize our simulation results, Z-linked systems are generally more likely to protect T alleles than are X-linked systems (the latter also always conferring less protection than autosomal systems) across the continuum of allelic dominance. Thus, as the fraction of all genes on the X chromosome increases, and, hence, as the probability that a mutant allele will arise on the X chromosome increases, the propensity for sexual selection should decrease. By contrast, as the fraction of genes on the Z chromosome increases, the propensity for sexual selection should increase.

Comparative Analysis.

A list of taxa used in the comparative analyses along with each taxon's sexual dimorphism score (i.e., the number of secondary sexual traits that were reported as more exaggerated in males than in females) and sex chromosome score are shown in Tables 1–6, which are published as supporting information on the PNAS web site, www.pnas.org.

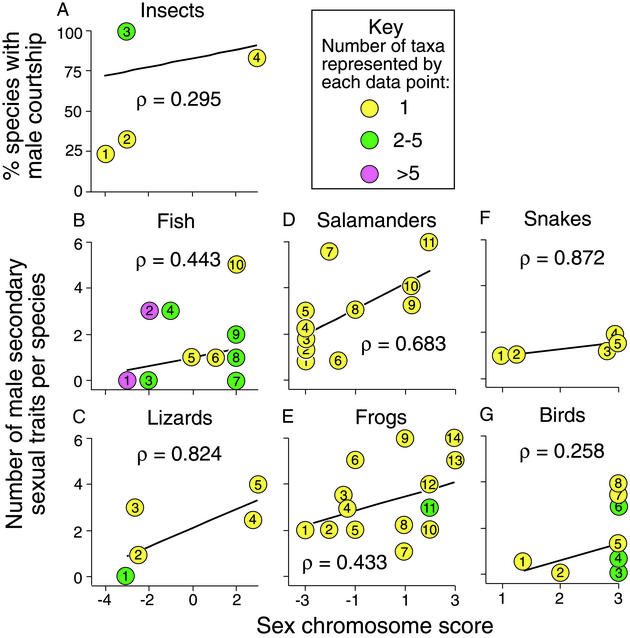
Correlations between the degree of sexual dimorphism and sex chromosome scores measuring the predicted strength of selection were positive across all seven major groups examined (Fig. 3). Indeed, the overall mean within-group (± SEM) Spearman rank order correlation coefficient (0.544 ±0.094) was significantly greater than zero (P < 0.016; two-tailed Wilcoxon signed-rank test). Thus, as predicted, male secondary sexual characters were more exaggerated in ZZ/ZW systems than in XX/XY systems and in diploid species than in haplodiploid species.

Figure 3.

Relationship between number of male secondary sexual characters per species (i.e., the number of secondary sexual traits that were reported as more exaggerated in males than in females) and sex chromosome score of those species for various major taxonomic groups. Each data point is the mean value across the species scored (number of species scored indicated below in parentheses) within the following orders. (A) Insect orders: 1, Hymenoptera (N = 30); 2, Diptera (N = 49); 3, Coleoptera (N = 4), Hemiptera (N = 1), Homoptera (N = 4), and Orthoptera (N = 1); 4, Lepidoptera (N = 14). (B) Fish species: 1, Brevoortia aurea, Coregonus sardinella, Gobiodon citrinus, Oncorhyncus nerka, Rhinobatos productus, Symphurus plagiusa; 2, Carcharodon carcharinus, Charcharhinus limbatus, Rhizoprionodon terraenova, Salmo gairdneri, Scopeloberyx mizolepis, Scopeloberyx robustus, Xenentodon cancila; 3, Fundulus diaphanus, Parasalmo mykiss; 4, Cichlosoma nigrofasciatum, Poecilia reticulata; 5, Xiphophorus maculatus; 6, Poecilia sphenops; 7, Clarias gariepinus, Dasyatis americana, Saurida undosquamis, Scardinius erythrophthalmus; 8, Eleotris pisonis, Gambusia affinis, Gambusia holbrooki; 9, Apeltes quadracus, Colisa fasciatus; 10, Poecilia latinpinna. (C) Lizard families: 1, Gekkonidae (N = 1) and Pygopodidae (N = 1); 2, Phrynosomatidae (N = 73); 3, Polychrotidae (N = 6); 4, Lacertidae (N = 13); 5, Agamidae (N = 2). (D) Salamander genera: 1, Bolitoglossa (N = 5); 2, Oedipina (N = 3); 3, Thorius (N = 4); 4, Necturus (N = 5); 5, Nototriton (N = 1); 6, Hydromantes (N = 5); 7, Triturus (N = 6); 8, Siren (N = 1); 9, Aneides (N = 4); 10, Ambystoma (N = 3); 11, Pleurodeles (N = 1). (E) Frog genera: 1, Eupsophus (N = 2); 2, Physalaemus (N = 1); 3, Rana (N = 14); 4, Gastrotheca (N = 4); 5, Bombina (N = 1); 6, Hyperolius (N = 1); 7, Leiopelma (N = 3); 8, Xenopus (N = 17); 9, Bufo (N = 1); 10, Discoglossus (N = 1); 11, Crinia (N = 1) and Tomopterna (N = 1); 12, Buergeria (N = 1); 13, Hyla (N = 2); 14, Pyxicephalus (N = 1). (F) Snake families: 1, Tropidophiidae (N = 1); 2, Boidae (N = 2); 3, Colubridae (N = 79); 4, Viperidae (N = 31); 5, Elapidae (N = 29). (G) Bird orders: 1, Struthioniformes (N = 8); 2, Tinamous (N = 45); 3, Apodiformes (N = 7), Ciconiiformes (N = 260), Columbiformes (N = 15), and Gruiformes (N = 15); 4, Coraciiformes (N = 3), Cuculiformes (N = 8), Piciformes (N = 22), Psittaciformes (N = 7), Strigiformes (N = 27); 5, Passeriformes (N = 334); 6, Anseriformes (N = 57) and Trochiliformes (N = 20); 7, Trogoniformes (N = 2); 8, Galliformes (N = 24). In each panel, the least squares regression line is given (for illustrative purposes only) along with the Spearman rank order correlation coefficient (ρ).

Discussion

We predicted that some genetic systems might be especially conducive to sexual selection, because, in these systems, rare alleles encoding either male ornaments or female preferences for those ornaments are better protected against random loss. In particular, our model and simulations predicted that male secondary sexual characters would be better developed in diploid than haplodiploid species and in diploid species with male homogamety than in those with male heterogamety (Figs. 1 and 2). In accordance with these predictions, our comparative analysis revealed an association between sexual dimorphism and genetic system (Fig. 3). Hence, taxonomic biases for showy males (1) may stem from differences in sex chromosome systems (see also ref. 30).

Our model extends “protected invasion” theory (12, 14) to sexual selection. This theory postulates that, by affecting the exposure of rare alleles to natural selection, and therefore the resistance of these alleles to chance loss through genetic drift, the genetic architecture of a population can profoundly affect the probability that the population will express phenotypes encoded by these alleles (12, 14). Although this theory was originally developed to explain female biases in (allo)parental care in haplodiploid vs. diploid species (12), it has been generalized to explain variation in allo(parental) care sex biases among diploid species with varying sex chromosome organization (14), because the pattern of selection on sex-linked loci in diploid organisms parallels that on loci in haplodiploid organisms (16). Thus, the protected invasion hypothesis applies to any case in which a population moves from a previously sexually monomorphic phenotypic optimum to a distant, sex-conditional phenotypic optimum (14).

The association between sex chromosome systems and extravagant male traits (Figs. 1–3) is predicted to have resulted from male ornamentation having evolved in response to the genetic system, and not vice versa. This result is almost certainly true for birds (Fig. 3) and is predicted to be true for the other taxa as well. Origin of the sex chromosome system before male ornamentation is suggested by the fact that male ornamentation typically occurs in a small fraction of related taxa sharing a sex-chromosome system.

A critical prediction of our model is that sexually selected characters, particularly female mating preferences, will often be Z-linked. In fact, there is evidence for such Z-linkage in birds (7) and butterflies (31). Thus, the model generates a new theory of how the genes encoding male and female secondary sexual characters will be distributed throughout the genome. The latter theory supplies a new conceptual framework for studies of genome structure through karyotyping and techniques of gene localization and thereby interconnects genomics, behavioral ecology, and evolutionary biology.

Genetic biases for showy males should occur whenever Fisherian sexual selection operates (i.e., whenever male trait and female preference alleles spread because of their correlation). Moreover, because such a Fisherian process should inevitably arise (2, 32), even when females target males that possess “good genes” or that provide direct benefits (2), genetic biases for showy males should occur whenever females choose their mates. Given the widespread occurrence of female choice (2), such biases provide a general explanation for why certain taxa are predisposed to evolve extravagant male traits.