Linkage disequilibrium and age of HLA region SNPs in relation to classic HLA gene alleles within Europe

Abstract

The HLA region on chromosome 6 is gene-rich and under selective pressure because of the high proportion of immunity-related genes. Linkage disequilibrium (LD) patterns and allele frequencies in this region are highly differentiated across broad geographical populations, making it a region of interest for population genetics and immunity-related disease studies. We examined LD in this important region of the genome in six European populations using 166 putatively neutral SNPs and the classical HLA-A, -B and -C gene alleles. We found that the pattern of association between classic HLA gene alleles and SNPs implied that most of the SNPs predated the origin of classic HLA gene alleles. The SNPs most strongly associated with HLA gene alleles were in some cases highly predictive of the HLA allele carrier status (misclassification rates ranged from <1 to 27%) in independent populations using five or fewer SNPs, a much smaller number than tagSNP panels previously proposed and often with similar accuracy, showing that our approach may be a viable solution to designing new HLA prediction panels. To describe the LD within this region, we developed a new haplotype clustering method/software based on r², which may be more appropriate for use within regions of strong LD. Haplotype blocks created using this proposed method, as well as classic HLA gene alleles and SNPs, were predictive of a northern versus southern European population membership (misclassification error rates ranged from 0 to 23%, depending on which independent population was used for prediction), indicating that this region may be a rich source of ancestry informative markers.

The HLA region on chromosome 6 is an important region of interest for both population genetics and immunity-related disease studies. Owing to the selective pressure associated with immune functions, linkage disequilibrium patterns and allele frequencies are highly differentiated across populations. As HLA typing of classic HLA gene alleles is expensive and time-consuming, although necessary for transplantation matching and detailed analysis of disease associations, we assessed whether a simple new method could ascertain SNPs that were informative of HLA allele carrier status. One important consideration in finding such SNPs is the age of the SNP in question, and whether it is likely that it arose before or after the origin of classic HLA gene alleles. SNPs that arose on a particular classic HLA gene allele haplotype background may be more informative for the prediction of carrier status for that allele than SNPs that predate the origin of the allele. It is also of interest to examine the linkage disequilibrium (LD) structure of the HLA region, especially within closely related populations. Previous approaches for the creation of haplotype blocks have generally relied on the LD metric D', which may not be as sensitive within these high LD regions as the alternative LD metric r². We developed a new haplotype blocking strategy based on r², and applied this method to SNP data in the HLA region across six European populations. Finally, we tested whether haplotype blocks, HLA alleles and SNPs were useful for differentiating European populations using logistic regression and unsupervised clustering algorithm approaches. Using these approaches, we identified new SNPs in the HLA region that may be useful as ancestry informative markers (AIMs) for European populations.

Materials and methods

Populations sampled

The project involved genotyping 657 DNA samples from unrelated representatives of nine European populations: English (n=77, mainly from Birmingham), Orcadians from the Orkney Islands, UK (n=88), Catalans (n=66), Italians from Bergamo (n=82), Piedmont (n=59) and Sicily (n=59), French Basques (n=76), Finns (n=71) and unrelated individuals from the CEPH reference families in Utah (n=79). Nine European populations were available for study, of which we used six populations for logistic regression and clustering analyses. These populations were collapsed into northern European (Orkney and English) and southern European (Bergamo, Piedmont, Sicily and Catalan). This choice was based on the assumption that the Basques and the Finns are generally considered to be outlier populations, whereas the European CEPH are an unknown mixture, although retrospectively they are mostly northern European. This is a limited sample of European populations, but serves to illustrate methods of analysis and does reveal major differences between northern and southern European populations.

SNP selection

Two sets of markers were selected:

1. A total of 188 SNPs within the HLA region defined as putatively neutral by the following criteria: their presence in introns, pseudogenes, intergenic regions or by synonymous changes. The SNPs were selected on the basis of their chromosome position to provide, as far as possible, an even distribution across the 3.9 Mb HLA region (chromosome 6, 29587512–33516520, National Center for Biotechnology Information, Build 36.3) at an average density of 1 SNP per 18 kb. In addition, extra SNPs were chosen to cover areas around presumed recombination hotspots.¹ Only SNPs with minor allele frequency reported on NCBI as being greater than 0.05 were included.

2. A total of 78 SNPs in exons 2 and 3 of the HLA-A, B and C genes providing a low-to-medium resolution HLA Class I allele typing with a total of 69 alleles (locus A – 18, B – 31 and C – 20), all with frequencies greater than 0.05 in Caucasians in the Allele^*Frequencies in World Populations Database (http://www.allelefrequencies.net).

Genotyping

A total of 35 SNPs were successfully genotyped in house using ARMS-PCR (amplification refractory mutation system) with KCl buffer and 15 ng of DNA in a 6.5 μl PCR reaction. Detection of the product was carried out using AMDI (alkaline-mediated differential interaction). In all, 153 SNPs were typed by the Centre National de Genotypage (Ivry, France), using a customised Illumina Beadarray Platform.² Of these, 131 gave successful results and were included in the analysis, resulting in a total of 166 SNPs. HLA class I allele typing was carried out based on the 12th International Histocompatibility Workshop Protocol.³ The 78 ‘diagnostic' SNPs were typed by ARMS-PCR with MgCl₂ buffer and 15 ng of DNA in 6.5 μl PCR reaction, followed by AMDI detection.⁴ All typing results were checked for Hardy–Weinberg equilibrium using a cutoff P-value of 0.05 to exclude abberrant results. Internal quality control with 94 duplicates gave 100% concordance. A total of 14 individuals had five or more missing genotypes and were removed from further analysis, thus the available N was 643.

Statistical methods

Prediction of classic HLA alleles by SNPs

We tested whether the 166 SNPs predicted individual classic HLA-A, B and C gene alleles by deriving a binary variable for each HLA allele and each SNP. The binary variable represented the presence or absence of the haplotype or minor allele, respectively, in an individual: thus, if an individual carried the haplotype or minor allele, they were assigned a 1, otherwise a 0. We then used Fisher's exact test to test the 2 × 2 associations between each SNP and HLA allele. We corrected for multiple testing using a Bonferroni correction for the total number of tests (166 SNPs × 56 observed HLA alleles = 9296 tests). We ranked pairwise associations between SNPs and HLA alleles by −log₁₀(P-value), and, using all SNPs passing Bonferroni's correction, obtained counts of the number of SNPs in which minor alleles were present in HLA allele carriers and noncarriers. In addition, we formally tested whether these SNPs were able to predict HLA carrier status using a split-half cross-validation approach. We estimated a logistic regression model on the training set containing the five most strongly associated SNPs (with the exception of HLA-B^*44, which only had four SNPs in the Bonferroni-corrected set) to predict HLA allele carrier status. We used only the top five most strongly associated SNPs instead of the full set because of multicollinearity. We then used the test set to predict the HLA allele carrier status. We validated the ability of this model built on the training data to predict the HLA allele carrier status using the independent CEPH population. The logistic regression model was of the following form:

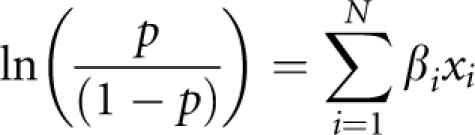where the probability of carrying a particular HLA allele was the outcome to be predicted by the linear combination of x_i of N markers in the equation, which were binary coded as the presence or absence of the minor frequency allele carried by that individual. We then calculated the sensitivity (number of predicted carriers/number of true carriers) and specificity (number of predicted noncarriers/number of true noncarriers) of the test set; as the association between SNPs and HLA alleles was calculated using the full set of six populations, this may overestimate both sensitivity and specificity. We therefore also calculated the same quantities for the independent CEPH population.

r2blocks: a haplotype blocking algorithm based on r²

We implemented a new algorithm to define correlated clusters or blocks of SNPs based on the LD metric r² (r2blocks) and compared this algorithm with blocks defined by the programme Haploview,⁵ which are based on the evidence for historical recombination using D'.⁶ D' is less sensitive in tightly correlated LD regions than r². The clustering algorithm of r2blocks accepts genotype-level data or phased haplotypes as input and allows users to impute missing genotypes, set an r² threshold for defining blocks and set a maximum number (M) of SNPs to skip that do not pass the threshold while continuing to build a block. Briefly, starting with the highest r² value for all pairs of SNPs that are separated by the most M SNPs, it calculates pairwise r² measures for all SNPs within M SNPs of the first pair and continues to grow the block in either direction as long as one pairwise r² value within M SNPs of any SNP within the current block is above the threshold, omitting SNPs that do not pass the threshold (Figure 1). It then considers the next SNP within the block and all pairwise r² values for SNPs within M SNPs, growing the block until no additional SNPs remain or until no additional SNPs pass the threshold value. We evaluated two threshold values for the creation of haplotype blocks: r²≥0.70 and r²≥0.5 with M set to 4. The blocking algorithm is implemented in a freely available contributed package r2blocks for the R statistical computing environment (www.r-project.org).

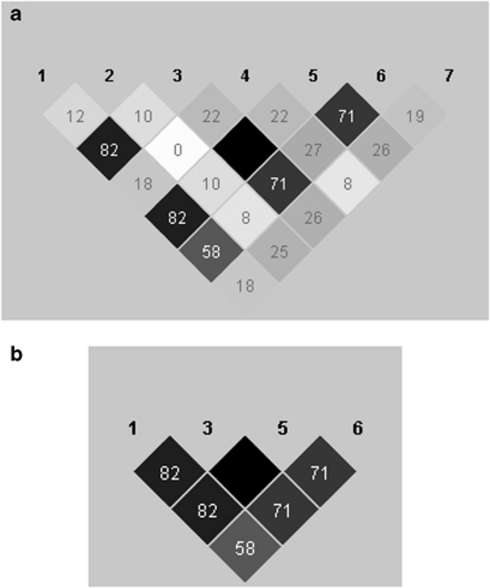
Figure 1.

Schematic of the r2blocks algorithm. HAPLOVIEW plot of pairwise r² values between a set of seven simulated SNPs; the block shading shows the strength of correlation. (a) Assuming a window size (M) of 4 and an r² threshold of 0.70, the r2blocks algorithm begins with the highest pairwise LD value, here between SNPs 3 and 5, which are in perfect LD (r²=1.0). Starting with SNP 3, consider r² values with SNPs 1, 2 and 4. Only SNP 1 passes the r² threshold; add SNP 1 to the block. Discontinue growing the block to the left. Consider r² values between SNP 5 and SNPs 4, 6 and 7 and add SNP 6. Move to SNP 6, consider r² values between SNP 6 and 7, which is below the threshold. Terminate growing block to the right, creating block 1 of SNPs 1, 3, 5 and 6. Now consider r² values between SNPs not assigned to blocks: SNPs 2, 4 and 7; none of the pairwise r² values are above the threshold, hence the algorithm terminates, leaving these three SNPs as singletons. (b) The resulting haplotype block from (a).

Population differentiation: HWE, F_ST, association, prediction and clustering

As population differentiation can cause departures from the Hardy–Weinberg equilibrium (HWE), we tested for departures from HWE in the pooled population and in the northern and southern populations separately using Fisher's exact test.

We used Weir and Cockerham's⁷ estimate of F_ST as implemented in the R package Geneland⁸ to assess genetic differentiation using the 166 SNPs and the top 20 SNPs, individual r2blocks blocks or two-locus HLA haplotypes that were most strongly associated with the north–south status. In addition, we calculated F_ST for individual SNPs, r2blocks haplotype blocks, HLA alleles and HLA haplotypes. Three-locus HLA haplotypes were estimated using PHASE v.2.1.1^{9, 10} with parent-independent mutation; two-locus HLA haplotypes were derived from those estimates.

Allele- and genotype-based associations were tested between individual SNPs, r2blocks-defined haplotypes, HLA alleles and 2- and 3-locus HLA-A, B and C haplotypes, and the north–south status using χ² tests or Fisher's exact test, when appropriate. Allele-based tests tested the association between each allele and the north–south status (sample size = 2N); genotype-based tests tested the number of minor alleles versus the north–south status (sample size = N). We set the P-value threshold to 0.05.

We ranked association tests between north–south status and SNPs, haplotype blocks and 2-loci HLA haplotypes by −log₁₀(P-value) and considered the top 20 most strongly associated predictors in a leave-one-population-out approach to validate predictive ability on an independent southern population. We could not carry out leave-one-out analyses with the northern set because of small sample size; instead, we used the CEPH sample for prediction. The logistic regression model used was as follows:

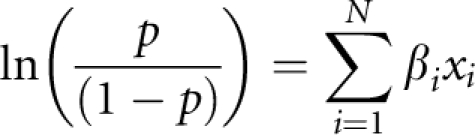where the probability of population membership is the outcome predicted by the linear combination of x_i of N markers/haplotypes in the equation, which are coded as the presence or absence of particular alleles/haplotypes carried by that individual. Prediction of individual population assignment for the CEPH population and for the removed southern population was carried by calculating the probability of being northern European using each individual's observed genotypes in the model. Misclassification rates were calculated by taking the number of individuals misclassified given their ‘true' north/south label/total number of individuals in the independent population.

Current approaches to population differentiation detection using genome-wide sets of biallelic markers often apply unsupervised clustering algorithms, such as principal components analysis (PCA, eg, EIGENSTRAT,¹¹ KPCA from the R package kernlab¹²) or Bayesian methods such as implemented in STRUCTURE^{13, 14} or BAPS.^{15, 16} We applied EIGENSTRAT, KPCA and BAPS to data from the 166 SNPs.

Results

Association of classic HLA alleles by genotyped SNPs

Nearly all of the classic HLA-A, B and C gene alleles were strongly associated with at least one SNP. Table 1 lists the top 20 most strongly associated SNP–HLA allele pairs and Figure 2 shows the −log₁₀(P-values) for those SNPs passing Bonferroni correction (see Supplementary Table 1 for a full list of all pairs passing Bonferroni correction). As expected, most SNPs in strong LD with one or more alleles at a particular HLA locus are physically proximal to the corresponding locus, with peaks observed close to the physical location of each gene, although LD patterns extended across most of the region (see Figure 2). Only a few very low-frequency HLA alleles (4 HLA-A alleles; 10 HLA-B alleles; and 2 HLA-C alleles) were not observed to show Bonferroni-corrected association with genotyped SNPs. A total of 55 (33.1%) SNPs did not show corrected association with HLA alleles; of the 111 significantly associated SNPs, 72 (64.8%) showed association with ≤3 alleles. One SNP showed strong association with seven HLA alleles: rs1265059 (HLA-A^*29, HLA-B^*07, HLA-C^*0702, ^*06, ^*16, ^*0302 and ^*0303). The HLA-A^*29/C^*16 haplotype has a frequency of 2.8% in Northern Ireland and the HLA-B^*07/C^*0702 haplotype is frequent in the same population (17.0%) (frequencies from allelefrequencies.net), indicating that this SNP may be tagging common haplotypes. Note that the position of HLA-DRA1 is between SNPs 122 and 123 and that of HLA-DRB1, HLA-DQA1 and HLA-DQB1 are between SNPs 129 and 130, possibly explaining the strong association observed on the far right hand side of Figure 2.

Table 1. Counts, odds ratios (ORs) and –log₁₀(p-values) for association tests for the top 20 pairs of Bonferroni-corrected significantly positively associated ‘tagging' pairs of HLA alleles and SNPs.

HLA allele	SNP	+ +a	+ −	− +	− −	OR	−log10 (P-value)b
HLA-A*03	rs3121593	82	9	3	337	946.2	73.74
HLA-A*02	rs6909253	202	14	64	151	33.66	59.8
HLA-C*06	rs10484554	72	0	52	307	425.1	48.92
HLA-C*05	rs2524160	67	3	37	324	191.1	47.44
HLA-A*03	rs6921921	88	3	74	266	104.2	43.41
HLA-A*01	rs1150741	105	8	82	236	37.43	43.18
HLA-B*08	rs3094014	68	7	57	299	50.23	36.76
HLA-A*03	rs2734925	89	2	102	238	102.9	36.2
HLA-C*06	rs2523619	72	0	110	249	163	33.25
HLA-A*03	rs1737043	88	3	116	224	56.2	31.14
HLA-A*24	rs2394186	66	17	63	285	17.4	29.88
HLA-B*51	rs2523685	69	3	107	252	53.71	28.93
HLA-C*06	rs3130473	72	0	128	231	129.9	28.46
HLA-A*24	rs1150741	79	4	108	240	43.53	28.06
HLA-A*11	rs2076177	50	7	58	316	38.41	27.98
HLA-B*08	rs3094216	66	9	80	276	25.06	27.95
HLA-A*11	rs29226	50	7	62	312	35.5	27.64
HLA-C*1203	rs10484554	46	0	78	307	181.1	27.56
HLA-B*07	rs3093993	87	12	88	244	19.94	27.3
HLA-A*01	rs404240	46	67	4	314	53.25	26.9

^a+ +, Refers to counts of co-occurrence of the HLA haplotype indicated and a minor allele at the SNP indicated; + −, refers to the presence of the HLA haplotype but no copies of the minor allele at the SNP; − +, refers to no copies of the HLA haplotype and at least one copy of the minor allele at the SNP; − −, refers to no copies of the HLA haplotype indicated or the minor allele at the SNP.

^b−log₁₀(P-value) is for the association test between copies of HLA alleles and minor alleles carried.

Figure 2.

Association of HLA-A, B and C alleles by genotyped SNPs. Plot shows −log₁₀(P-values) of Fisher's exact tests for association between classic HLA gene alleles and genotyped SNPs passing Bonferroni correction. Association with classic HLA gene alleles only are plotted in primary colours (HLA-A = blue, HLA-B = dark yellow and HLA-C = red); association with two classic HLA gene alleles are shown as secondary colours (HLA-A (blue) and HLA-B (yellow) = green; HLA-A (blue) and HLA-C (red) = violet; HLA-B (yellow); and HLA-C (red) = orange); association with all three classic HLA gene alleles = black. The position of HLA-DRA1 is between SNPs 122 and 123 and that of HLA-DRB1, HLA-DQA1 and HLA-DQB1 are between SNPs 129 and 130.

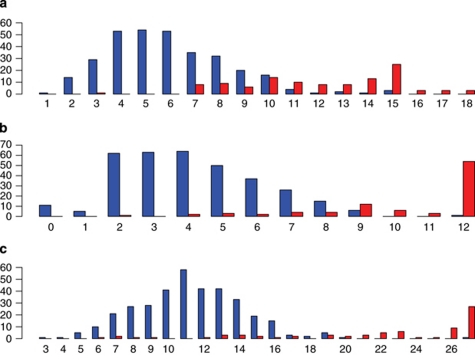
Histograms of counts of the number of minor alleles carried at SNPs passing Bonferroni's correction in HLA allele carriers and noncarriers clearly showed a bimodal distribution (Figure 3; also see Supplementary Figures S1-S10). Using the top five most strongly associated SNPs and the HLA haplotypes observed with >1% frequency in either northern or southern European populations (Supplementary Table 2), we observed high sensitivity and specificity in predicting whether an individual carried a particular classic HLA allele in both the test set and in the independent CEPH set for most HLA alleles tested (Table 2). In particular, the overall misclassification rate for HLA-A^*29 in the independent CEPH set was <0.01, with sensitivity near 1.0 (0.997) and 94.3% specificity. In addition, HLA-A^*01 showed <5% misclassification rate in the CEPH population (4.5%) and had 93.5% sensitivity and 99.9% specificity, indicating that genotyping even a small number of SNPs can provide information about the HLA allele carrier status, although not as complete information as direct HLA typing.

Figure 3.

Histograms of the number of minor allele carriers at associated SNPs by HLA allele carrier status. (a) HLA-A^*01 (18 SNPs), (b) HLA-A^*03 (12 SNPs), (c) HLA-B^*08 (27 SNPs); y-axis = frequency, x-axis = number of SNPs in which individuals carry at least one minor allele. Blue = HLA allele noncarrier; red = HLA allele carrier.

Table 2. Sensitivity, specificity and misclassification rates for five SNP logistic regression models predicting HLA allele carrier status.

HLA allele	Mean test set sensitivity (95% CI)	Mean test set specificity (95% CI)	Number of CEPH carriers (%)	Mean CEPH sensitivity (95% CI)	Mean CEPH specificity (95% CI)	Mean CEPH misclassification (95% CI)
HLA-A*01	0.953 (0.901, 1.00)	0.869 (0.745, 0.989)	23 (35.4)	0.935 (0.925, 0.944)	0.999 (0.996, 1.00)	0.0453 (0.0385, 0.0521)
HLA-A*02	0.878 (0.770, 0.987)	0.762 (0.695, 0.829)	40 (61.5)	0.937 (0.765, 1.00)	0.823 (0.776, 0.882)	0.147 (0.124, 0.170)
HLA-A*03	0.974 (0.953, 0.996)	0.949 (0.867, 1.00)	18 (27.7)	0.936 (0.875, 0.997)	0.982 (0.924, 1.00)	0.0540 (0.00501, 0.103)
HLA-A*29	0.977 (0.945, 1.00)	0.826 (0.677, 0.976)	3 (4.6)	0.997 (0.978, 1.00)	0.943 (0.678, 1.00)	0.00748 (0.000201, 0.0351)
HLA-B*07	0.907 (0.863, 0.952)	0.793 (0.656, 0.930)	19 (29.2)	0.863 (0.923, 0.903)	0.834 (0.730, 0.937)	0.147 (0.124, 0.168)
HLA-B*08	0.952 (0.921, 0.983)	0.859 (0.702, 1.00)	17 (26.2)	0.882 (0.850, 0.913)	0.914 (0.785, 1.00)	0.114 (0.0862, 0.142)
HLA-B*44a	0.818 (0.726, 0.910)	0.686 (0.508, 0.863)	23 (35.4)	0.722 (0.590, 0.853)	0.938 (0.758, 1.00)	0.265 (0.135, 0.394)
HLA-B*57	0.954 (0.926, 0.982)	0.708 (0.496, 0.920)	0 (0)	—	—	—
HLA-C*0701	0.828 (0.784, 0.873)	0.818 (0.690, 0.946)	22 (33.8)	0.828 (0.812, 0.843)	0.765 (0.687, 0.844)	0.191 (0.161, 0.220)
HLA-C*0702	0.889 (0.840, 0.938)	0.753 (0.608, 0.898)	3 (4.6)	0.972 (0.949, 0.995)	0.106 (0.0347, 0.177)	0.225 (0.178, 0.272)
HLA-C*05	0.964 (0.928, 1.00)	0.773 (0.638, 0.908)	4 (6.2)	0.924 (0.922, 0.927)	0.0 (0.0, 0.0)	0.247 (0.221, 0.273)
HLA-C*06	0.997 (0.992, 1.00)	0.946 (0.829, 1.00)	0 (0)	—	—	—
HLA-C*16	0.977 (0.955, 0.999)	0.870 (0.375, 1.00)	3 (4.6)	0.972 (0.960, 0.985)	0.828 (0.275, 1.00)	0.0405 (0.00680, 0.0742)

Abbreviation: CI, confidence interval.

^aThis model contains four SNPs.

Comparison of haplotype blocking algorithms

Using an r² threshold of 0.70 and a window size (M) of 3, r2blocks creates 12 blocks across the HLA region in the pooled sample of European populations. Reducing the r² threshold to 0.50 leads to an additional 7 blocks and 14 additional SNPs being assigned to blocks (Figure 4; Supplementary Table 3). The Gabriel block method using default parameters (lower bound D' confidence interval ≥0.7 and upper bound confidence interval ≥0.98) defines 18 blocks. The two additional blocking methods (the four gamete rule (FGR) and solid spine of LD with default D' threshold of 0.7) both create twice as many blocks over the region compared with r2blocks and the Gabriel method, and assign nearly half of the HLA genomic region to haplotype blocks. In northern European populations, r2blocks using an r² threshold of 0.50 creates 20 blocks over the HLA region and 19 blocks in southern European populations; block regions were generally consistent across the two sets of European populations. Using r2blocks with an r² threshold of 0.50 leads to a similar number of blocks and SNPs assigned to blocks as the Gabriel method, although the block boundaries are often different. Not surprisingly, the use of r2blocks with a higher r² (0.70) threshold leads to a more similar percentage of genome covered as the Gabriel method than the lower r² threshold. r2blocks with both r² thresholds and the Gabriel method show that LD is slightly lower in southern versus northern European populations, but with similar average block size, number of SNPs assigned to blocks and percentage of the genome assigned to blocks in northern Europeans. Of the 20 blocks assigned using r2blocks with an r² threshold of 0.50, more than half (11; 55%) are in genic regions.

Figure 4.

HLA region haplotype blocks in European populations defined by r2blocks and the Gabriel, four-gamete rule and solid spine of LD methods. Plots show the LD heatmap of pairwise r² values for SNPs. Top bar represents physical spacing of SNPs. Triangles show the location of haplotype blocks defined by each method. Methods are indicated on the left hand side of each plot. (a) Pooled European populations; red triangles show blocks added by reducing the r² threshold from 0.7 to 0.5 using r2blocks. (b) Blocks obtained using r2blocks with an r² threshold of 0.70 in northern European populations (top) and southern European populations (bottom); (c) blocks obtained using r2blocks with an r² threshold of 0.50 in northern European populations (top) and southern European populations (bottom). (d) Blocks obtained using the Gabriel method in northern European populations (top) and southern European populations (bottom).

HWE, F_ST, association tests and clustering of markers/haplotypes, and northern–southern European status

Excess deviations from HWE versus expected numbers of deviations can be induced by population structure. Of the 166 SNPs tested, 15 (9.0%) were out of HWE at the α=0.05 level, almost double the number expected by chance alone (8.3) (Supplementary Table 4 shows HWE, association test results and F_ST for all markers). In separate analyses of northern/southern populations, the number of SNPs out of HWE was much nearer the expected value (8 and 10, respectively), suggesting that the excess when using the combined populations is probably because of population structure.

Overall, F_ST values using the 20 SNPs, haplotypes and classic HLA gene alleles most strongly associated with north–south status were modest, as expected within European populations (Supplementary Table 5; see Supplementary Table 3 for the full list of markers). The largest F_ST value (0.056) was observed between northern and southern populations using this panel of 20 alleles/markers/haplotypes, which were selected to highlight north–south differences; similarly, the second largest F_ST value (0.050) was observed between southern populations and the CEPH sample. The smallest F_ST value (0.0024) was found between northern populations and the CEPH sample. Single SNP F_ST values were strongly negatively correlated with both allelic (r=−0.41, −log₁₀(P-value)=7.42) and genotypic (r=−0.42, −log₁₀(P-value) =7.81) association test P-values for north–south status, indicating that the allelic/genotypic tests are similar measures to F_ST (Supplementary Table 4). We note that single SNP F_ST estimates are approximately distributed as χ²₁ and thus have large variances. The largest single SNP F_ST for differentiation between northern and southern European populations was for rs411136 in SYNGAP1 (F_ST=0.29); interestingly, this same SNP showed the largest pairwise F_ST between any two populations, namely, for southern Europeans versus CEPH (F_ST=0.51). However, the same comparison between northern Europeans and CEPH produced an F_ST value of 0.015, suggesting that rs411136 may be an important AIM within European populations.

Of the 166 SNPs, 74 (44.6%) were significantly associated with north–south status using the uncorrected allelic or genotypic test, and, after Bonferroni correction for the 332 allelic and genotypic tests, 25 (15.1%) still showed significant associations (Table 3; see also Supplementary Table 4). The strongest association was observed with rs411136 in SYNGAP1, with an allelic test −log₁₀(P-value) of 32.42. As expected, the largest 3-locus haplotype frequency difference between northern and southern European populations was for haplotype HLA-A^*01-HLA-B^*08-HLA-C^*0701 with frequencies of 0.097 versus 0.034, respectively (−log₁₀(P-value)=4.16; Supplementary Table 2).¹⁷

Table 3. Association tests for Hardy–Weinberg equilibrium (HWE), minor allele frequencies and F_ST for 20 most strongly associated HLA alleles, blocks and haplotypes with north–south status.

Marker	Location	Gene symbol	Function	Combined MAF	Combined HWE −log10 P-value	North–south single SNP association –log10 P-value1	North–south single block association −log10 P-value (r2≥0.5)	North–south FST	North MAF	North HWE −log10 P-value	South MAF	South HWE −log10 P-value
rs411136	33516520	SYNGAP1	Ser556Ser	0.15	4.00	32.42 (28.57)	—	0.29	0.33	0.37	0.034	0.00
rs1265160	31246350	POU5F1	Phe3Phe	0.070	0.66	11.15 (11.55)	—	0.099	0.15	1.44	0.023	0.00
rs3096702	32300309	NOTCH4	5' region	0.29	0.08	9.20 (8.29)	—	0.087	0.42	0.39	0.22	0.02
rs2256328	31489616	MICA	Intron	0.24	0.33	8.87 (9.10)	—	-0.0021	0.12	0.93	0.31	0.24
rs2256594	32294850	NOTCH4	Intron	0.13	0.00	8.46 (8.11)	—	0.078	0.21	0.36	0.073	0.10
rs2535318	31159367	—	—	0.49	0.06	7.48 (6.66)	—	0.070	0.37	0.00	0.44	0.19
rs659445	31972283	EHMT2	Intron	0.28	0.57	7.07 (5.91)	—	0.066	0.39	0.16	0.22	0.03
Block 20	33438959–33454164	—	1–1 haplotype	0.40	0.23	—	6.36 (3.96)	0.030	0.42	0.35	0.60	0.09
Block 10	31159367–31186474	C6orf15	2–1 haplotype	0.42	0.51	—	5.65 (4.83)	0.037	0.51	0.71	0.34	0.19
rs389883	32055439	STK19	Intron	0.23	0.10	5.49 (4.87)	—	0.050	0.31	0.07	0.17	0.33
rs2855453	33242370	COL11A2	Intron	0.31	0.97	5.44 (4.51)	—	0.047	0.40	0.00	0.25	0.88
Block 8	30832409–30847883	—	1–1 haplotype	0.16	0.15	—	5.4 (4.15)	0.031	0.72	0.00	0.85	0.10
HLA-B*07/ C*0702
Haplotype	—	HLA-B/C	—	—	—	—	5.32 (5.32)	0.050	0.16	—	0.060	—
rs1800684	32259972	AGER, PBX2	Ala3Ala, 3' region	0.087	0.16	5.29 (5.07)	—	0.042	0.14	0.20	0.053	0.03
rs1810472	33191099	—	—	0.32	0.23	5.14 (4.74)	—	0.048	0.23	0.00	0.38	0.65
rs4713505	32212979	—	—	0.31	1.58	5.13 (4.01)	—	0.045	0.22	0.59	0.37	0.70
HLA-B*08/ C*0701 Haplotype	—	HLA-B/C	—	—	—	—	4.47 (4.82)	0.042	0.13	—	0.049	—
rs8512	30819336	IER3	3' UTR	0.19	4.39	2.34 (4.74)	—	0.017	0.14	0.00	0.22	6.64
rs211452	33438959	—	—	0.40	0.23	4.69 (4.11)	—	0.039	0.31	0.35	0.46	0.090
Block 17	32331236–32345991	—	2–1 haplotype	0.32	0.13	—	4.31 (4.64)	0.024	0.21	0.00	0.11	0.00

SNPs shown are associated with north–south status after Bonferroni correction for all allelic and genotypic tests.

P-values for association tests are shown as allele-based first, genotype-based in parentheses.

Association tests between the 20 haplotype blocks defined using r2blocks with an r² threshold of 0.50 and the north–south status showed that, in nearly all cases, the haplotype block was more strongly associated than the individual SNPs comprising the block. Of the 20 haplotype blocks, 15 were associated with a north–south status. Six of the significantly associated blocks did not contain any individual SNPs that were significantly associated with north–south status. Of the 9 blocks containing at least 1 significantly associated SNP, 6 showed stronger association with the haplotype block containing that SNP than with all individual SNPs (Supplementary Table 4; Supplementary Figure 11). In fact, of the 20 most strongly associated HLA allele haplotypes, SNPs or block-based haplotypes, four were haplotypes created using our new methodology (Table 3).

KPCA and EIGENSTRAT analyses of single SNPs did not reveal tight clustering by north–south designation (Supplementary Figure 12). Clustering of individuals using BAPS on single SNPs resulted in a best-fitting solution of 11 clusters; an inspection of the proportion of individuals from northern and southern European populations in each cluster revealed a mixture of both; none of the clusters were comprised of purely northern or southern European samples (data not shown). However, BAPS clustering of the six population samples, instead of individuals, led to a best-fitting solution of two clusters exactly matching our northern and southern designations, confirming our a priori clustering of individuals.

Population membership prediction using HLA alleles, SNPs and blocks

We used logistic regression to test the predictive ability of the 20 most significantly associated HLA SNPs by using leave-one-population-out validation to predict north–south population membership on the independent population and on the CEPH population. To avoid multicollinearity induced by LD, we removed predictors that were strongly correlated with other predictors, retaining the predictor that was more strongly associated with north–south status, to reduce the model containing 20 variables to a model containing 7 predictors: rs411136, rs1265160, rs3096702, rs2256328, rs2855453, block 8 and HLA-B^*08/C^*0701. Even using such a limited number of predictors provided a perfect prediction for the Piedmont population and a low prediction error for the Sicily population (8.5%), although the error rates for the Bergamo (13.0%) and Catalan (18.0%) populations were higher (Table 4). The CEPH population prediction error rate was steady across all models at ∼22% however, given that the genetic background of this population is not clearly defined, this may indicate some evidence for southern European admixture.

Table 4. North–south population membership prediction error for logistic regression models using the most associated SNPs, blocks and HLA-A/B and HLA-B/C haplotypes.

Population removed	Population predicted	Misclassification rate
Catalan	Catalan	0.18
Catalan	CEPH	0.23
Bergamo	Bergamo	0.13
Bergamo	CEPH	0.22
Piedmont	Piedmont	0.00
Piedmont	CEPH	0.22
Sicily	Sicily	0.085
Sicily	CEPH	0.22

Discussion

Owing to the time-consuming and expensive process needed to carry out full classic HLA allele typing, we developed a simple strategy to identify inexpensively and easily genotyped SNP combinations that could predict classic HLA gene allele carrier status in a leave-one-population-out cross-validation using logistic regression models. We have also described a new haplotype blocking method and software based on r², which is probably more appropriate than a D'-based method in regions of strong linkage disequilibrium. In addition, we have shown that haplotype blocks created using the new haplotype blocking method, classic HLA gene alleles and neutral HLA region SNPs were useful for the differentiation of northern versus southern European populations, in agreement with previous work,¹⁸ and suggested particular SNPs that may be useful as AIMs.

An examination of the 15 associations in Supplementary Table 1 that show the opposite classic HLA allele-SNP pattern to that observed in the other 304 associations, namely the frequency of individuals carrying the HLA allele but not carrying the minor allele at the SNP is greater than the frequency of individuals not carrying the HLA allele but carrying the minor allele at the SNP, shows that the four SNPs associated with >1 HLA allele are associated with known HLA haplotypes of high frequency in Europeans. rs404240 shows this pattern with HLA-A^*01, HLA-B^*08 and HLA-C^*0701, which is the most frequent 3-locus haplotype in northern Europeans (0.034 in southern Europeans and 0.097 in northern Europeans); two additional SNPs, rs2001009 and rs2249099, also show this pattern with HLA-A^*01 and HLA-C^*0701. rs1800684 shows this pattern with HLA-B^*07 and HLA-C^*0702, a high-frequency haplotype in Europe (0.060 in southern Europeans and 0.16 in northern Europeans). rs404240 and rs1800684 are both synonymous, and rs404240 and rs2249099 are physically proximal to the HLA-A gene, whereas rs2001099 is physically proximal to HLA-DRA. The fact that the opposite pattern is much more frequently observed, namely that, for a given SNP, there are many individuals who do not carry the associated classical HLA allele but do carry the minor SNP allele, implies that most of these SNPs are older than the classical HLA alleles. We searched dbSNP build 36.3 (http://www.ncbi.nlm.nih.gov/projects/SNP/) for presumed ancestral (Pan troglodytes) alleles for these polymorphisms and found 26 out of 166 (15.7%) were in regions that could not be aligned with the chimpanzee sequence (indicated in Supplementary Table 4). Most of these SNPs were unassociated with the north–south status, although 3 of the 26 were strongly associated with the north–south status (rs2256328, rs2857205 and rs2747479). However, of these 26 SNPs, only 6 (23.1%) did not show Bonferroni-corrected association with at least one classic HLA gene allele, a smaller percentage than in the full set of 166 SNPs (31.1%), suggesting the existence of human-specific SNPs that probably arose on a particular HLA allele haplotype background, and which might be more informative of the classic HLA gene allele carrier status. The fact that these data suggest that most SNPs are older than the classic HLA gene alleles, most of which are common to humans and chimpanzees, implies that they are not likely to be good markers for LD-based associations. It seems likely that this is a problem shared by a high proportion of SNPs in the commonly used SNP databases, as the SNPs used in this study were selected only by location. The age of SNPs could account for the emphasis on building haplotype blocks using very high LD thresholds. Only in those cases in which LD is very high and SNPs are very closely linked will such blocking give meaningful results for relatively old SNPs, given that the average rate of decay of LD between two SNPs is 1–r per generation, where r is the recombination fraction between SNPs. For example, for a distance of 1000 bp, corresponding, on an average, to r=10⁻⁵, the LD would decay by a factor of 0.0034 in 500 000 generations, and thus to negligible levels in the separation time between humans and chimpanzees. The SNPs may show associations with more recent variation, as with HLA alleles, but these associations will be incomplete.

We show that, even with highly AIMs, unsupervised clustering algorithms were unable to detect substructure with our limited number of SNPs. Clustering algorithms should be used with caution when genome-wide data are unavailable, even if the SNPs selected are informative of ancestry.

The bimodal distribution of minor allele carriers of sets of SNPs that are strongly associated with classic HLA gene alleles and the use of logistic regression to predict HLA allele carrier status are computationally efficient and simple methods that do not require particular ‘tag SNPs'¹⁹ or previous database-based information,²⁰ and thus may be preferred when no previous data exist on a particular population. Even though our method and previously described methods show relatively high sensitivity and specificity for the prediction of a classic HLA gene allele carrier status, none of the proposed methods, including ours, is as accurate as HLA allele typing. Even with this caveat, our method may be helpful in preselecting a subset of individuals for full classic HLA gene allele typing in disease association studies, thus reducing genotyping time and costs.

Higher-order associations, such as associations between blocks of SNPs, may more accurately describe genetic diversity and historical recombination patterns of a particular region of the genome, and may be helpful for the assignment of classic HLA gene allele carrier status than previously reported approaches.^{17, 19, 20} Future work will develop a new meta-blocking algorithm to carry out higher-level blocking using blocks created by r2blocks, to be used as input in unsupervised and/or supervised clustering algorithms for the detection of population stratification based on the example of the HLA region in closely related populations. This meta-blocking algorithm may also be useful in predicting classic HLA gene allele carrier status.

The authors declare no conflict of interest.