Sporadic cases are the norm for complex disease

Abstract

The results of genome-wide association studies have revealed that most human complex diseases (for example, cancer, diabetes and psychiatric disorders) are affected by a large number of variants, each of which explains a small increase in disease risk, suggesting a pattern of polygenic inheritance. At the same time, it has been argued that most complex diseases are genetically heterogeneous because many sporadic cases are observed, as well as cases with a family history. In this study, under the assumption of polygenic inheritance, we derive the expected proportion of sporadic cases using analytical methods and simulation. We show how the proportion of sporadic cases depends on disease prevalence (K) and heritability on the underlying liability scale (h_L²). We predict the underlying heritability and the proportion of sporadic cases for a range of human complex diseases, and show that this proportion is typically large. For a disease with h_L²=63% and K=0.4%, such as schizophrenia, >83% of proband cases are predicted to be sporadic (no affected first-, second- and third-degree relatives) in typical families (on an average, two children per couple). For the majority of these diseases, a large proportion of sporadic cases is expected under the polygenic model, implying that the observed large proportion of sporadic cases is not informative to the causal mechanism of a complex genetic disease.

Introduction

Large-scale, high-density genome-wide association studies (GWAS) have greatly facilitated the discovery of genetic variants that affect the predisposition to human complex diseases.¹ The results of recent GWAS suggest that the majority of susceptible loci have small contributions to phenotypic variation, which indicates that there should be a large number of susceptibility loci involved in the genetic basis of complex disease.^{2, 3, 4, 5, 6, 7, 8} These findings are consistent with the polygenic model, proposed almost a century ago,⁹ underlying the genetic etiology of complex diseases. At the same time, on the basis of the knowledge of family history, differentiation is often made between sporadic and familial cases. This differentiation implies some sort of genetic heterogeneity, either that environmental factors are more important in sporadic cases or that sporadic cases arise from new mutations of large effect size. Integrating this differentiation into an understanding of the genetic architecture of complex disease depends on the frequency of sporadic cases, consistent with the polygenic model.

In this study, we investigate the relative proportion of sporadic and familial cases expected under the polygenic threshold model. We assume that disease susceptibility is genetically homogeneous in the population and the observed illness results from the accumulative effect of multiple common genetic and environmental effects that exceeds a certain threshold.^{10, 11, 12, 13} We conducted a simulation study to calculate the probability of a proband case without family history. Furthermore, we investigated the relationship of disease prevalence, heritability of liability, recurrence risk (RR) and family size, and analytically predicted heritability of liability and the proportion of sporadic cases in human complex diseases under the polygenic model.

Methods and results

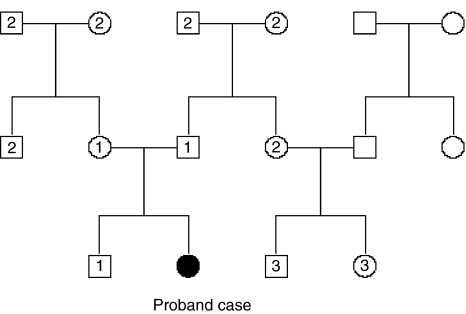
We simulated pedigrees with three generations. For each pair of parents in the first and second generations, the number of offspring was independently drawn from a Poisson distribution, as in Cui and Hopper.¹⁴ The structure of the simulated pedigree is illustrated in Figure 1. The disease liability (y) of each individual in the pedigree was simulated by a simple genetic model y=a+e, where a is the additive genetic effect; e is the environmental effect; e ∼ N(0, h²_L); and h_L² is the narrow sense heritability of liability. The additive effects of the individuals in the first generation were drawn from a ∼ N(0, h²_L), whereas those in the second and third generations were generated by a=0.5a_F+0.5a_M+m, where a_F and a_M are the additive effects of parents, and m is the effect due to Mendelian segregation, m ∼ N(0, 0.5h²_L) (Appendix). A range of heritability levels (h_L²=0, 10,…100%), along with three levels of disease prevalence (K=10, 1 and 0.1%), was considered to be representative of human complex diseases. An individual was considered to be diseased if y>T, where T is the threshold on the normal distribution truncating the proportion K. A total of 100 000 pedigrees with at least one disease case (proband) in the third generation were generated for each of combinations of h_L², K and S, where S is the mean family size per couple. A proband case was considered to have a family history of disease on the basis of two different definitions: (I) at least one first-degree relative with disease, and (II) at least one first-, second- or third-degree (1°, 2° or 3°, illustrated in Figure 1) relative is affected, and the probability of a sporadic case was defined accordingly.

Figure 1.

Structure of the simulated pedigree. The number of children for each pair of parents is distributed as a Poisson variable. The numerical labels ‘1', ‘2' and ‘3' represent the first-, second- and third-degree relatives of the proband case.

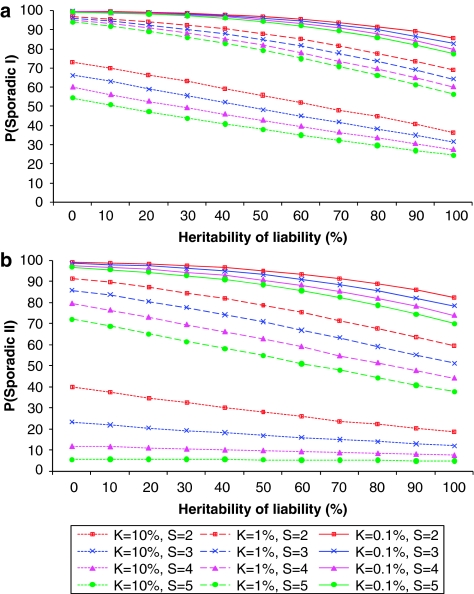
It is shown in Figure 2 that P(sporadic) depends mainly on disease prevalence K. It increases markedly with decreasing K, and gradually increases with decreasing h_L² and S. For a disease with a prevalence of 0.1%, a proband case has a probability of ∼78% (definition I) or ∼70% (definition II) to be sporadic, even if the heritability of disease is 100% and family size is large (S=5). We investigated the relationship between the underlying and observed scale. 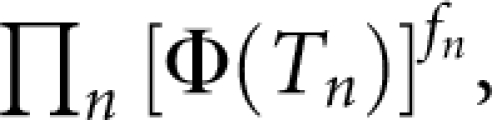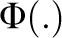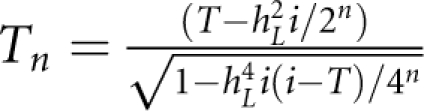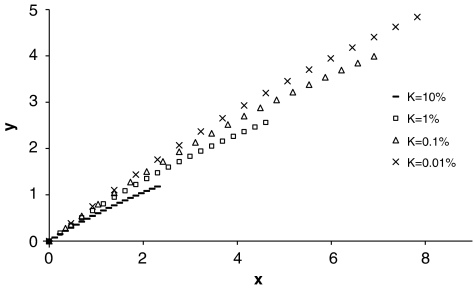In theory, P(sporadic) is approximately equal to where is standard normal cumulative distribution function; f_n is the number of n^th-degree relatives; with i=z/K; and z is the height of the standard normal curve at the truncation point T (Appendix). For example, when S=2 and for diseases with prevalence ranging from 0.1 to 1%, P(sporadic) will range from 66 to 99% (definition I) or from 52 to 99% (definition II), with h_L² from 100 to 0%. Therefore, for these diseases, the proband cases observed in typical families will more likely seem to be sporadic no matter how heritable the disease is. By contrast, a large proportion of probands would present with a family history for a disease with a high prevalence (K=0.1); even if the heritability is extremely low (h_L²=10%), there are 31% (definition I) or 65% (definition II) of probands having a family history. In addition, the nth-degree RR can be calculated analytically as 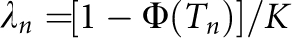(Appendix). The RRs for relatives from this equation were verified by simulations and are listed in Table 1. In line with the results for P(sporadic), RRs largely depended on disease prevalence K. Although the relationship of h_L², K and λ_n is theoretically nonlinear, the relationship between log(λ₁) and −h_L² log(K) is approximately linear for each K (Figure 3), and is roughly log(λ₁)=−0.62 h_L² log(K) with regression R²=99.4% for K from 0.01 to 10%.

Figure 2.

Proportion of sporadic cases under different combinations of disease prevalence (K), heritability on underlying scale (h_L²) and mean family size per couple (S). (a) and (b) refer to the two definitions of family history, respectively.

Table 1. Recurrence risks for relatives under different combinations of heritability of liability and disease prevalence (K) by our analytical derivation.

	Heritability of liability (%)
	0	10	20	30	40	50	60	70	80	90	100
K=10%
λ1	1.0	1.2	1.3	1.5	1.7	1.9	2.2	2.4	2.7	2.9	3.2
λ2	1.0	1.1	1.2	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9
λ3	1.0	1.0	1.1	1.1	1.2	1.2	1.2	1.3	1.3	1.4	1.4
K=1%
λ1	1.0	1.4	1.9	2.6	3.4	4.4	5.6	7.0	8.7	11	13
λ2	1.0	1.2	1.4	1.7	1.9	2.2	2.6	3.0	3.4	3.9	4.4
λ3	1.0	1.1	1.2	1.3	1.4	1.5	1.7	1.8	1.9	2.1	2.2
K=0.1%
λ1	1.0	1.7	2.8	4.5	6.9	10	15	21	29	40	54
λ2	1.0	1.3	1.7	2.2	2.8	3.6	4.5	5.6	6.9	8.4	10
λ3	1.0	1.2	1.3	1.5	1.7	2.0	2.2	2.5	2.8	3.2	3.6

λ₁, λ₂ and λ₃ represent the first-, second- and third-degree recurrence risks, respectively.

Figure 3.

Empirical relationship of disease prevalence (K), heritability on underlying scale (h_L²) and first-degree recurrence risk (λ₁). In the figure, y=log(λ₁) and x=−h_L² log(K).

An analytical method to calculate h_L² using K and λ₁ is provided in the Appendix. We used this method to predict heritability of liability for a range of common complex diseases using the observable parameters, namely, disease prevalence and first-degree RR (Table 2). Given h_L² and K of disease, we also predicted P(sporadic) from our analytical approximation and checked all our analytic results by simulation. The predictions of P(sporadic) for these diseases are presented in Table 2. The predictions of P(sporadic) from simulation agreed well with those from approximation, with a correlation of 0.998.

Table 2. Prediction of the heritability of liability (h_L²) and proportion of sporadic cases in human complex diseases.

					P(sporadic I) (%)		P(sporadic II) (%)
Disease	K (%)	λ1	hL2 (%)	Sa	Theor.b	Simu.c	Theor.b	Simu.c
Prostate cancer27	2.40	2.8	44	2	81	82	63	66
				3	76	78	49	55
Colon cancer27	1.50	5.1	64	2	79	80	64	67
				3	73	76	51	58
Breast cancer27	3.60	2.5	44	2	75	77	53	57
				3	69	72	37	45
Lung cancer27	1.70	6.1	76	2	72	74	55	61
				3	65	69	41	51
Stomach cancer27	1.00	6.0	63	2	83	84	71	74
				3	78	80	60	65
Bladder Cancer27	1.00	1.7	16	2	95	95	88	88
				3	93	93	81	82
Schizophrenia28, 29	1.00	8.6	80	2	76	78	63	67
				3	70	74	51	59
Schizophrenia22	0.40	9.0	63	2	90	90	83	85
				3	86	88	76	79
Bipolar disorder30	1.00	6.8	69	2	81	82	69	72
				3	75	78	57	64
Bipolar disorder22	0.45	7.9	60	2	90	90	83	84
				3	87	88	76	79
Unipolar disorder31	10.0	1.7	39	2	60	57	31	25
				3	52	47	18	11
Type I diabetes32	0.54	13.7	86	2	81	79	73	69
				3	77	73	66	59
Type II diabetes33	3.00	3.5	60	2	72	73	50	55
				3	64	68	35	44
Crohn's disease1	0.10	26	76	2	92	93	89	90
				3	90	91	85	87
Asthma34	2.00	2.6	38	2	85	86	70	72
				3	81	82	57	62
Coronary artery disease35	5.60	3.2	72	2	55	59	29	38
				3	45	53	15	26
Systemic lupus erythematosus36	0.03	30	65	2	97	97	96	96
				3	96	96	95	95
Rheumatoid arthritis16	0.75	8.0	70	2	83	84	73	75
				3	78	80	62	68

The disease prevalence (K) and first-degree recurrence risk (λ₁) are obtained from the literature and may include averaging over sexes. h_L² is calculated from its analytical relationship with K and λ₁ (Appendix).

^aS is the mean family size per couple.

^bTheor. represents the predictions of P(sporadic) by analytical approximation.

^cSimu. represents the predictions of P(sporadic) by simulation.

Discussion

Using the relationship between underlying and observed scale parameters under a polygenic inheritance model, we predicted h_L² for a list of human complex diseases, using K and λ₁ collected from literature. The proportion of sporadic cases and RRs for relatives depends mainly on disease prevalence. If we consider three-generation pedigrees with S=2, then for diseases with a low prevalence (K<1%), even if they are highly heritable (h_L²=90%), the disease cases will seem more likely to be sporadic, P(sporadic II) >63% (Figure 2b). On the other hand, for a disease with a high prevalence (K >10%), a large proportion of disease cases seems to have a family history, P(sporadic II) <37% (Figure 2b), even when disease heritability is extremely low (h_L²=10%). Kendler¹⁵ modeled familial versus sporadic schizophrenia and major depression using simple genetic and environment etiology models. He showed that family history had a high positive predictive value, but a low negative predictive value. Under the liability threshold model, these results still apply, that is, a positive family history implies a high genetic liability to disease and a negative family history implies very little about genetic liability to disease.

Our results necessarily reflect our assumptions in modeling complex genetic disease. First, we assumed that the causes of familiality of complex disease reflect only genetic rather than family environment factors. As more distant relatives are less likely to share the same environmental risk factors, this assumption can be tested by comparing RRs for different types of relatives with their expected values under a genetic etiology model. Second, we used idealized family history assuming that the true disease status of all relatives is known, ignoring recall errors and age of onset factors. This implies that our estimates of proportion of sporadic cases are conservative and in practice may be even higher than our prediction. Moreover, in some diseases, family history reflects increased severity of the disease,¹⁶ which, although not inconsistent with a polygenic model, may imply genetic heterogeneity. Finally, we assumed that a liability threshold model is representative of complex genetic diseases. The model assumes a normally distributed liability to disease, with disease occurring in those who exceed a liability threshold. A normal distribution of liability would be achieved if there are multiple genetic and environmental factors, each making a small contribution to the risk of disease. Comparison of the prediction frequency of familial versus sporadic cases provides some benchmark for the validity of our assumptions. For example, a Swedish population study investigated breast cancer in 1 732 775 sisters from 763 963 families (S=2.3) before the age of 70 years.¹⁷ A total of 16 505 proband cases and 714 sisters of probands were identified with breast cancer, which provides the estimates of K=1% and λ_s=3 for breast cancer before the age of 70 years. We predicted an h_L² of 35% by our analytical equation. Given K and h_L², we simulated 1 million nuclear families with S=2.3, and estimated a multiplex proportion of siblings (the number of families with at least two affected siblings divided by the number with at least one sibling) of 4.6%, with 95% CI of 4.2% ∼5.0%, which is consistent with the observed proportion of 4.3%.

We consider the example of schizophrenia. The prevalence of sporadic versus familial cases has been considered in detail under a range of genetic models^{15, 18} in the context of etiological heterogeneity of schizophrenia. The latest evidence from GWAS for schizophrenia points to a large polygenic component.¹⁹ At the same time, significantly increased rates of de novo copy number variant (CNV) mutations have been reported in sporadic (but not familial) cases of schizophrenia,²⁰ together implying genetic heterogeneity. In combination, these results point to many risk alleles that have a range of frequencies and effect sizes but that are still consistent with a normally distributed underlying liability to disease. Genetic epidemiology parameters of schizophrenia are classically quoted to be K=1%, λ₁=8.6 and h_L²=81%,²¹ but results from a Swedish population sample of >9 million have revised these estimates to K=0.4%, λ₁=9 and h_L²=64%.^{22, 23} For K=0.4% and λ₁=9, we predict h_L² to be 63%, and for K=1% and λ₁=8.6, we predict h_L² to be 80%, reflecting that under a threshold liability model, the lower disease prevalence forces a lower estimate of h_L² for the same λ₁. For K=0.4% and h_L²=63%, we predict the proportion of sporadic schizophrenia cases to be 90% (definition I) and 83% (definition II) in three-generation pedigrees with S=2 (Table 2). The Swedish population study observed a multiplex proportion of 3.8% (the number of families with at least two affected members divided by the number with at least one affected member)¹⁷ from nuclear families with ∼3.8 members per family.¹⁶ We simulated 1 million nuclear families with S=1.8, and estimated the multiplex proportion as 4.0% (95% CI of 3.7–4.4% from 100 simulation replicates) and P(sporadic I) as 90.6% (95% CI of 89.7–91.5%).

In conclusion, although sporadic cases can arise from nongenetic risk factors and from new mutations with large effects, a large proportion of sporadic cases is expected under the polygenic model, a result that reflects the relatively low prevalence rates (<5%) that are typical of common complex genetic diseases. Therefore, it is not possible to make any inference with regard to the causal mechanism of a complex disease from the observed proportion of sporadic cases alone.

Appendix Relationship of additive genetic effects between parents and offspring under a polygenic model

Following Lynch and Walsh,²⁴ under the assumption of a polygenic inheritance for a quantitative trait, the additive genetic effect of a parent (a_p) and its gamete (a_g) is

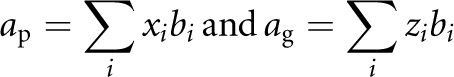where x_i is coded as 0, 1 or 2 if the genotype at locus i is qq, Qq or QQ (alleles are arbitrarily called Q or q); z_i is coded as 0 or 1 if the genotype of locus i is q or Q; and b_i is the allelic effect at locus i.

Although the parent passes half of the genome to its gamete, a_g is not necessarily equal to ½a_p because of random segregation of alleles.

Assuming that all of the loci are independent, the additive genetic variance equals

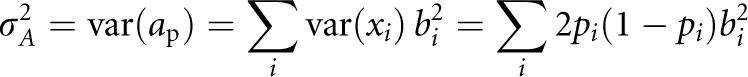where p_i is the frequency of allele Q at locus i.

As

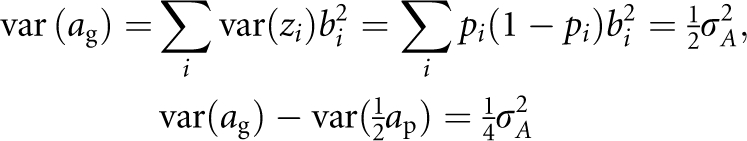Therefore, we can express the additive effect of a gamete as

Consequently, we can express the additive effect of offspring as

where a_F and a_M are the additive effects of two parents, m is the effect due to Mendelian segregation,

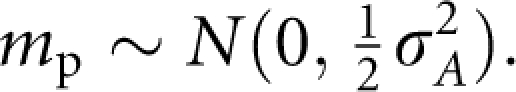Relationship between underlying and observed scales under a threshold liability model

Consider a disease on the basis of a threshold liability model with population prevalence K. The liability of the n^th-degree relatives of the proband case follows the normal distribution of Falconer and Mackay¹¹

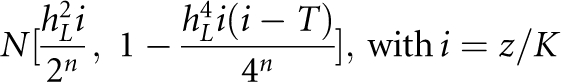where h_L² is the heritability of liability and z is the height of the standard normal curve at the truncation point T pertaining to a disease prevalence of K.

Given a proband case, the probability of the n^th-degree relative being is

where 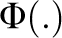is standard normal cumulative distribution function and

Therefore, the nth-degree RR is 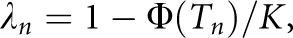, which provides a link between the underlying liability scale and the observed risk scale. In particular, the RR to MZ twin is 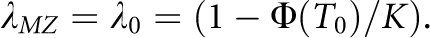Following James,²⁵ the n^th-degree RR can also be expressed as 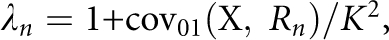where 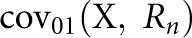is the covariance between the proband case and its nth-degree relatives on the observed 0–1 scale, hence 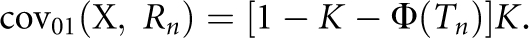Therefore, the heritability on the observed 0–1 scale is

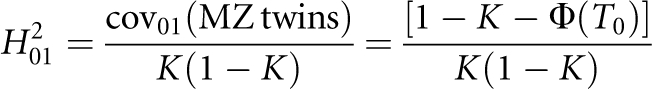In addition, if there are f_n number of n^th-degree relatives, the probability of a proband case without family history is approximately

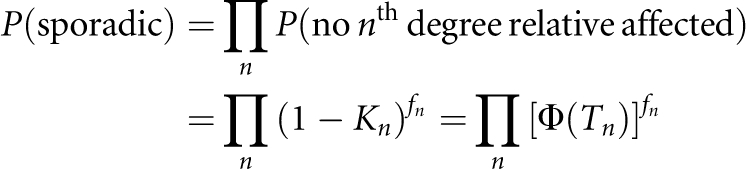This approximation is a conservative prediction of P(sporadic) because the probabilities of affected relatives are not independent, especially when both K and h_L² are high and lots of relatives are included.

All the derivations above begin with K and h_L² being known parameters; in practice, however, only λ_n and K are observable. Given λ₁ and K, h_L² can be predicted by rearranging Eq. A1 for n =1 and solving for h_L².^{24, 26}

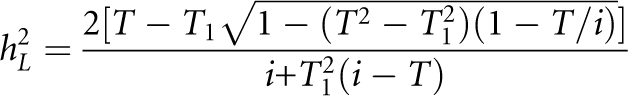where T₁ is truncation point pertaining to the accumulative probability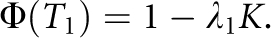

The authors declare no conflict of interest.