Are Different Rhythms Good for Different Functions?

Abstract

This essay discusses the relationship between the physiology of rhythms and potential functional roles. We focus on how the biophysics underlying different rhythms can give rise to different abilities of a network to form and manipulate cell assemblies. We also discuss how changes in the modulatory setting of the rhythms can change the flow of information through cortical circuits, again tying physiology to computation. We suggest that diverse rhythms, or variations of a rhythm, can support different components of a cognitive act, with multiple rhythms potentially playing multiple roles.

Introduction

It has been known since the work of E. D. Adrian (Adrian, 1950) that cognitive states can be associated with brain rhythms and that specific spectral content can be localized to specific areas of the brain. Since then, there have been numerous studies linking a variety of cognitive tasks to more detailed data about brain rhythms and their interactions. However, a fundamental issue is still mysterious: what roles, if any, do rhythms play in cognition?

Two themes will be stressed in this paper. The first is that “function” is tightly tied to physiological and dynamical properties of a given rhythm, not just its frequency. The second is that the connection between rhythms and function can be better understood if the latter is construed in terms of “useful computation” rather than the end-product of that computation, such as attention, memory, learning, etc. For example, as discussed below, physiology matters to the creation and manipulation of cell assemblies (Harris et al., 2003). Since different rhythms are associated with different underlying physiology, they can participate differently in the computation of cell assembly creation. As a second example, we consider interactions of different brain regions via oscillations (Fries, 2005). As discussed more fully below, changes in the modulatory setting of the rhythms can change the flow of information through cortical circuits, again tying physiology to computation.

Cell Assembly Formation Via Gamma Rhythms

By “cell assemblies”, we will mean subsets of pyramidal cells that fire approximately synchronously in a transient manner, whether or not those cells have recurrent excitatory connections. Models show that gamma rhythms, especially the so-called “pyramidal-interneuron network gamma” (PING; 40–90 Hz; Whittington et al., 1997) are especially good at creating cell assemblies (Olufsen et al., 2003). The PING rhythm is fundamentally an interaction between fast spiking (FS) interneurons and excitatory pyramidal cells. The zeroth order description of the mechanism is straightforward: the pyramidal cells excite the FS cells, which then inhibit both the pyramidal cells and themselves; when the inhibition wears off, the pyramidal cells fire again. Thus, the period of the gamma rhythm is tightly tied to the decay time of the inhibition, though it is also affected by the level of excitatory drive to the pyramidal cells.

There is another kind of gamma rhythm that is important in function: the persistent gamma rhythm (Traub et al., 2000), which can be obtained in vitro by exposing neuronal networks to the neuromodulators kainate or carbachol. In this version of the gamma rhythm, pyramidal cells fire sparsely, and the rhythm is maintained by the FS cells, which fire on almost every cycle. Persistent gamma requires noisy activation of the pyramidal cells, which is believed to be provided by ectopic spiking of pyramidal cells and amplification by an axonal plexus (Traub et al., 2000, 2003). Inhibition is critical in both kinds of in vitro gamma (Whittington et al., 2000). The role of the inhibition in gamma rhythms was discovered in vitro, but has been corroborated in vivo (Atallah and Scanziani, 2009; Cardin et al., 2009).

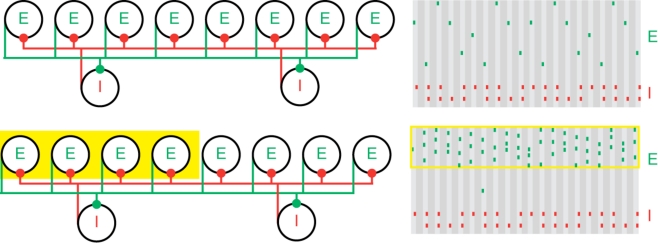
The physiology of PING provides an excellent setting for the creation and protection of cell assemblies. Increased tonic input to a subset of pyramidal cells (either not previously activated or participating in persistent gamma) can create (approximately) synchronous firing in that subset in a PING rhythm, while other pyramidal cells in the network are suppressed (Figure 1). Models suggest that the essential reason for this competition is that the stronger input defines the firing rate of the inhibitory cells and entrains the target network; the stronger input then arrives just before the next bout of inhibition, when the inhibition is lowest, while the weaker input, which excites its targets more slowly, arrives when inhibition is higher (Borgers et al., 2005, 2008). We think of the persistent gamma as a background state in which further inputs can create a PING rhythm (Borgers et al., 2005).

Figure 1.

Population gamma activity and competition among excitatory cells. Upper left: A cartoon representation of two interacting cell populations that generate a persistent gamma rhythm; circles labeled “E” represent pyramidal cells and “I” represent FS cells. The two cell populations are reciprocally connected with excitatory (green) and inhibitory (red) synapses from each cell to all other cells. Upper right: Cartoon example of the spiking activity of the two cell populations during persistent gamma activity. Each tick mark represents an action potential (or spike) of an E (green) or I (red) cell. In each cycle of the persistent gamma rhythm, a single pyramidal cell spikes and delivers excitation to the FS cells. The FS cells then spike and inhibit the pyramidal cells. When the inhibition decays sufficiently, one of the pyramidal cells generates another spike, and the rhythm continues. Lower: Increased depolarizing input to a subset of pyramidal cells (yellow box on the left) increases their spiking activity. The population gamma rhythm continues with the “driven” pyramidal cells (yellow box on the right) dominating the excitatory activity.

The physiology underlying the PING rhythms has immediate implications for attention. It has been shown via modeling that the windowing of inhibition in the persistent gamma oscillation makes it easier for a weak input to create a cell assembly than if the same level of inhibition is more spread out in time (Borgers et al., 2005). Another connection to attention is the ability of a coherent oscillatory source with a gamma frequency to create and lock to a gamma oscillation in the target network, locking out the effects of other input sources, even when the latter have somewhat greater amplitude (Borgers et al., 2008). The lock-out effect comes from the fact that the feed-forward inhibition produced by the more coherent input is active during the less coherent other input; the importance of the gamma frequency input is that the frequency of the rhythm in the target is tied to the decay time of inhibition, and hence a gamma frequency input produces feed-forward inhibition at an optimal frequency to keep all but the most coherent input locked out. Since attention is associated with more coherence in the gamma range in most reports (Tiitinen et al., 1993; Fries et al., 2008; Jung et al., 2008; Dockstader et al., 2010; but see Chalk et al., 2010), it can bias competition in the input at a downstream structure. Finally, results about firing rate changes associated with selective attention (Reynolds et al., 1999) can be understood via changes in gamma-producing networks in response to cholinergic modulation (Borgers et al., 2008). For other observations about gamma and attention, see Buia and Tiesinga (2006) and Ardid et al. (2007).

The physiology of the gamma rhythm supports the ability of the networks of excitatory and inhibitory neurons to produce gamma. However, the properties of this rhythm, including the tendency of cell assemblies to compete instead of cooperate, makes it difficult to use the PING rhythm to coordinate and manipulate multiple cell assemblies, as needed for some higher-order processing. We suggest below that other rhythms may play these roles, and how the specific physiological properties of other rhythms may contribute to that function.

Different Rhythms Allow Temporal Segregation of Multiple Assemblies

That other possible computations involving cell assemblies might be done with other rhythms is suggested by close study of the beta1 rhythm (15 Hz) in the rodent secondary somatosensory association cortex (S2) (Roopun et al., 2008). This rhythm can appear in vivo after the stimulation that induces a gamma rhythm is over (Tallon-Baudry et al., 1999; Haenschel et al., 2000). To mimic the basic features of this phenomenon in vitro, Roopun et al. (2006) first produced a gamma rhythm in S2 evoked by a bath application of kainate; subsequently, after 1 h, the kainate-mediated excitation is reduced using a kainate antagonist. In the initial, higher excitation regime, only the superficial layers produce the gamma; the deep layer (Layer V) produced a beta2 rhythm (25 Hz). The gamma oscillation is the standard persistent gamma described above; the beta2 oscillation is produced by intrinsic currents timed by the kinetics of the M-current (a subthreshold potassium current modulated by muscarinic receptors) and synchronized by gap junctions. When the kainate antagonist was added, the two independent rhythms both changed to the beta1 rhythm in a manner that was coordinated between the superficial and deep layers. This required some plasticity in the network, since an immediate removal of kainate did not produce the switch to beta1.

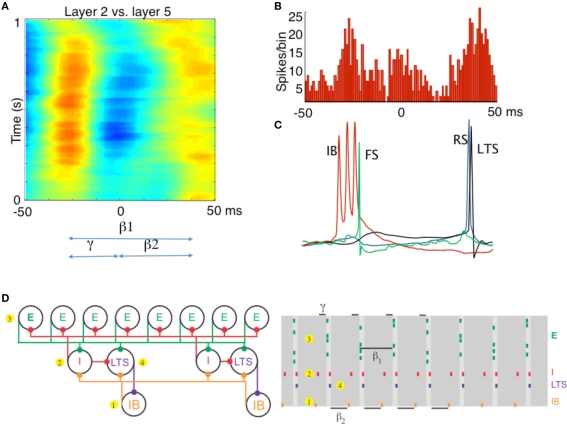
Experiments and modeling have shown (Kramer et al., 2008; Roopun et al., 2008) that the coordination between the layers is mediated by inhibitory rebound: excitation in Layer V intrinsic bursting neurons (IB cells) excite superficial FS cells, which inhibit regular spiking (RS) superficial pyramidal cells, which respond by rebound and initiate a gamma cycle in the superficial layers. The spiking of the RS cells excites the low-threshold spiking interneurons (LTS cells), another population of inhibitory cells in the superficial layers, which inhibit the apical dendrites of the IB cells. The IB cells then respond by inhibitory rebound and start another beta2 cycle. The result is that the beta1 rhythm is a “concatenation” of one superficial layer gamma cycle followed by one deep layer beta2 cycle; the period of the beta1 is indeed a sum of the periods of the gamma and beta2 (Figure 2). Thus, assemblies composed of superficial RS cells can co-exist with assemblies composed of deep layer IB cells, and fire at different times in the beta1 cycle. The fact that the beta1 operates through inhibitory rebound makes it possible for this rhythm to continue in the absence of continuing input, unlike the PING rhythm.

Figure 2.

Different rhythms allow period concatenation. (A) Cross-correlogram showing stable phase relationship between layer 2/3 and layer 5 field potentials in association cortex (S2). When excitation is high, layer 2/3 generates a gamma rhythm (c. 40 Hz) and layer 5 a beta2 rhythm (c. 25 Hz). Reducing excitation then concatenates these two rhythms to generate a beta1 (c. 15 Hz) frequency oscillation in both layers. (B) The asymmetric phase relationship seen for field potentials in (A) is also seen when comparing the timing of layer 2 units with layer 5 units. (C) Intracellular recordings, relative to an on-going beta1 frequency field potential, show the sequence of outputs from different neurons. Each beta1 period begins with a brief burst from layer 5 intrinsically bursting (IB) neurons. This triggers single spikes in superficial fast spiking interneurons (FS). Superficial regular spiking pyramids (RS) spike on the rebound of the resulting IPSP, triggering superficial low-threshold spiking interneurons (LTS) to fire. (D) A cartoon representation of the important cell types in the beta1 rhythm. To the PING model in Figure 1, we add a population of low-threshold spiking (LTS) interneurons and intrinsically bursting (IB) pyramidal cells. We note that the LTS cells inhibit the IB cells, and that the IB cells form excitatory synapses onto all inhibitory cells. A cartoon rastergram is on the right. The beta1 rhythm results from a process of period concatenation. Briefly, the beta1 rhythm propagates through the different cell types as follows. First, the IB cells spike (1) and cause the basket cells to spike (2). The basket cells inhibit the superficial pyramidal cells (3), which recover and spike after one gamma cycle. The superficial pyramidal cell spikes cause the basket and LTS cells to spike (4) which inhibit the IB cells. The IB cells then recover and spike after one beta2 cycle (interval indicated with beta2 label at bottom of this panel) and the rhythm repeats. (A–C) Adapted from Roopun et al. (2008).

In hippocampus, where there is only a single pyramidal cell lamina, theta rhythms may work to both coordinate and separate cell assemblies formed within the gamma rhythm. For this we consider the nesting of gamma rhythms in the theta rhythm in the hippocampus (Bragin et al., 1995). The latter is believed to make use of the so-called oriens-lacunosum moleculare (O-LM) cell (Gillies et al., 2002; Goutagny et al., 2009), whose physiology has been studied (Saraga et al., 2003; Lawrence et al., 2006; Goldin et al., 2007). It is known experimentally that a theta rhythm can be produced in purely inhibitory networks including the O-LM cells (Gillies et al., 2002), and modeling has suggested that the inhibitory interactions among O-LM cells alone do not produce a coherent theta rhythm because of the interaction of the inhibition with intrinsic currents in the O-LM cells, especially the mixed cation, hyperpolarization-activated, inward h-current (Rotstein et al., 2005). However, the interaction of the O-LM cells with FS cells can produce a coherent rhythm (Rotstein et al., 2005), with fast IPSPs produced by the FS cells coordinated with the slow IPSPs produced by the O-LM cells, as in (Gillies et al., 2002). When AMPA transmission is not blocked, the CA1 network in vitro is capable of producing gamma, theta, or a nesting of the two (Gloveli et al., 2005), depending on how well the O-LM neuronal processes are preserved in the slice (determined by the angle of cut during tissue preparation). Modeling (Gloveli et al., 2005; Tort et al., 2007) reveals that the nesting of the gamma in the theta rhythm can be explained from the O-LM – FS interneuronal interaction to form theta, and the overlapping network of pyramidal – FS cell interaction to form the gamma.

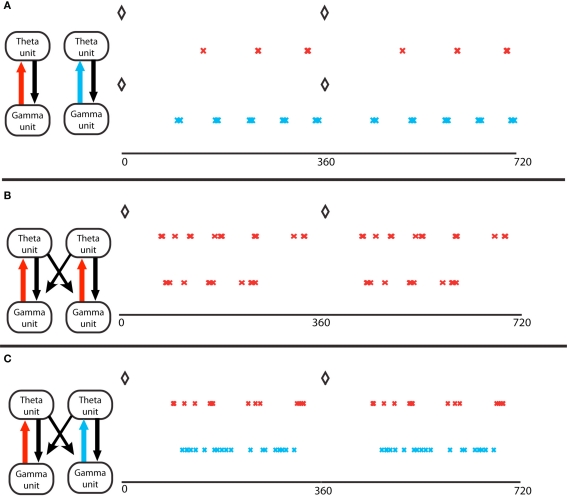
The coordination of cell assemblies in the nesting of these rhythms depends on the underlying physiology. Cell assemblies are formed when a subset of pyramidal cells is given more input. Gamma rhythms can form in transverse slices, in which the O-LM axons project fairly locally. We considered multiple transverse slices (“modules”) connected only by O-LM axons projecting to pyramidal cells of other modules. Modeling using multiple compartment (Tort et al., 2007) or single compartment (Kopell et al., 2010) biophysical neurons showed that the O-LM input, with its long-lasting IPSPs, can synchronize cell assemblies created by the pyramidal – FS interaction in different modules; for synchronization of subsets of pyramidal cells to happen, it is necessary that those subsets be involved in the gamma oscillation (Tort et al., 2007). More recent work (Malerba, 2010) has shown that the phases of the gamma rhythm within the theta oscillation can depend on the connections within a module: if the synapses from the pyramidal cells to the O-LM cells are relatively stronger than those from the FS cells to the O-LM cells (excitation-dominated or ED regime), the phases of the pyramidal cells cluster more highly than if the reverse is true (inhibition-dominated or ID regime), leading to more coordination of cell assemblies (Figure 3A). Modules in the ED regime can be well-synchronized if they are not too far apart in drive (Tort et al., 2007); if they are sufficiently far apart in drive, separate cell assemblies co-exist (Figure 3B). There can be coordination of cell assemblies in the ID regime, but cell assemblies formed in the ED regime do not easily coordinate with those in the ID regime, providing a mechanism to separate cell assemblies (Figure 3C). We note that there is a similar dichotomy in firing patterns of pyramidal cells in hippocampal slices (Senior et al., 2008). These computational results suggest an alternative to the idea of sequential gamma slots within a theta cycle, each corresponding to a separate cell assembly (Jensen and Lisman, 1996). Instead, the cell assemblies can be separated, while each one participates in multiple gamma cycles within a theta cycle.

Figure 3.

Gamma assemblies prefer different theta phases depending on local synapses. (A) Theta phase of gamma spikes, for a single module. Top, a module in the excitation-dominated (ED) regime; red crosses mark the pyramidal cell spikes. The black diamonds mark the O-LM spikes at zero theta phase in all panels. Bottom, a single module in inhibition dominated (ID) regime; light blue crosses mark the pyramidal cell spikes. Theta phases of gamma spikes cluster more in ED regimes. (B) Two coupled modules, in identical ED regimes, receiving different gamma drives. The spike phases on top are for the pyramidal cell of the module that receives stronger gamma drive. The two cell assemblies do not synchronize (Tort et al., 2007). (C) Two coupled modules, receiving identical gamma drive, in different excitation regimes. The red crosses mark activity of the module in ED regime, the light blue marks report activity of the module in ID regime. The theta phases of the gamma spikes in the ID regime do not cluster, so the two gamma signals in the two different modules have the same frequency but have different theta phases.

Time-Variant Assembly Modification

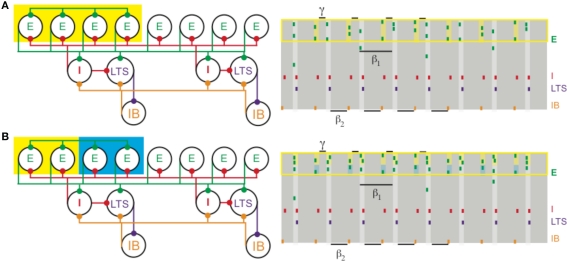
The physiology of concatenated gamma and beta2 rhythms (see Different Rhythms Allow Temporal Segregation of Multiple Assemblies) has important consequences for the formation and manipulation of cell assemblies in the context of the beta1 rhythm (Kopell et al., 2009). For example, if a subset of superficial pyramidal cells already participating in the beta1 rhythm is given more input, those cells can form a gamma-frequency cell assembly nesting inside the beta1 rhythm, without affecting the deep-layer cell assemblies (Figure 4A). Thus, there are cell assemblies existing simultaneously that code for past and current input: the past is represented by the cell assemblies formed in the beta1 oscillation, and the present by the cell assembly nesting inside the superficial layer beta1 assembly. If two such subsets are given different amounts of input, they can form synchronizing assemblies with reduced competition (Figure 4B) when compared to PING (Borgers et al., 2005, 2008). Thus, the beta1 rhythm is, in principle, suitable for higher-order processing in which it is necessary to compare new and old information, or put together information arriving from different modalities (Tallon-Baudry et al., 2001; Weiss et al., 2005; Buschman and Miller, 2007; Lalo et al., 2007; Pesaran et al., 2008). Models suggest that the beta1 rhythm also allows assemblies of deep layer cells firing at beta1 to build up over time as more input becomes available (Kopell et al., 2009), useful for tasks in which information must be temporally integrated before a decision can be made (Donner et al., 2009). We note that these roles for beta band oscillations are consistent with the suggestion (Engel and Fries, 2010) that beta is a frequency useful for holding in place certain signals; indeed, the beta1 rhythm discussed above persists by virtue of interacting inhibitory rebound, without need for further input. We suggest here that the beta1 oscillations can also be used to manipulate the signals that have been held in place, to facilitate further processing.

Figure 4.

(A) Increased depolarization of a subset of superficial pyramidal cells (yellow box on the left) produces a gamma rhythm nested in the beta1 activity. The depolarized pyramidal cells, which are connected by all-to-all excitatory synapses, receive enough excitation to generate two bouts of spikes: once after recovering from basket cell input (matching Figure 1) and a second time before receiving basket cell input (yellow shaded regions on the right). (B) Different levels of excitation to subsets of superficial pyramidal cells still produces gamma activity nested in beta1. A population of superficial pyramidal cells, with all-to-all excitatory synapses, receives two levels of increased input, one stronger (yellow) and the other weaker (blue). Both subsets of cells merge to create a gamma rhythm nested in beta1. The subset receiving larger input (shaded yellow on the right) tends to spike more, while the subset receiving weaker input (shaded blue) continues to spike, unlike in PING.

Dynamical Routing with Multiple Rhythms

The interaction of different substructures of the brain depends on both the dynamics in the different regions and how they react to neuromodulators. The rest of this paper describes two interactions that depend on the modulatory context.

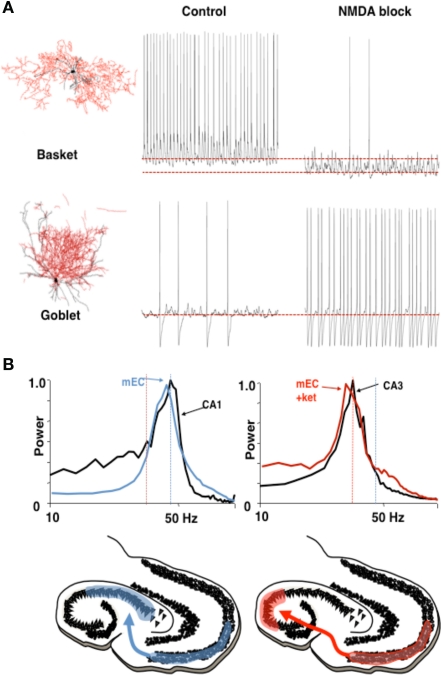
The first of these concerns coordination between hippocampal CA3/CA1 and the entorhinal cortex (EC). It has been shown (Middleton et al., 2008) that the EC is capable of two physiologically different gamma rhythms. In normal ACSF, with some kainate-mediated activation, the EC produces a persistent gamma rhythm, using a subnetwork of pyramidal cells and FS cells (Cunningham et al., 2003). These FS cells, predominantly located in layer 2, require NMDA currents to be active (Jones and Buhl, 1993); addition of an NMDA-receptor blocker eliminates these cells from the network. This uncovers a different gamma rhythm, with a lower frequency (25–35 Hz), created from a subnetwork of pyramidal cells and another kind of interneuron, called a “goblet cell” (Middleton et al., 2008). The NMDA-receptor blockade changes the subset of interneurons that dominates the full network, and thereby determines the frequency generated by the local circuit.

Functional implications of this mechanism make use of observations concerning the frequencies of neural rhythms in CA3 and CA1: In the same ACSF that produces the higher frequency gamma rhythm, the natural frequency of the active CA3 local circuit in hippocampus is very similar to that of the NMDA-blocked gamma, while the frequency of CA1 local circuits is very similar to the normal higher frequency of persistent gamma in EC. Models have shown that, when a phasic input (driver) to an oscillator (target) has approximately the same frequency as that oscillator, the two can phase-lock, creating coherent oscillations at which the relative phases of the input and output stay constant (Kopell and Ermentrout, 2002). Although networks need not behave like single oscillators, the results for the single oscillators suggest that the higher frequency, NMDA receptor-dependent gamma rhythm in medial EC (mEC) can drive that of CA1, and the slower, NMDA receptor-independent gamma rhythm can drive that of the CA3. For single oscillators, if the frequencies are too different, it takes a much larger drive to lock phasic inputs to the target region's intrinsic frequency, if at all; in the absence of locking, the relative phases of the driver and target change cycle by cycle, implying that the effects of the driver on the target are also not reproducible cycle by cycle. Thus, modulation of the NMDA drive to EC during gamma rhythm generation may serve to change the path of information flow from EC through the hippocampal circuit; the two physiologically different gamma rhythms support different pathways for processing (Figure 5). A more recent report shows a similar phenomenon in vivo (Colgin et al., 2009).

Figure 5.

Different rhythms may allow routing of cortical information flow. (A) Medial entorhinal cortex (mEC) generates two different frequencies of gamma rhythm depending on the degree of NMDA receptor-mediated excitation present. In control conditions a c. 40 Hz gamma rhythm is mediated by activity in layer 2 basket cells. In the absence of NMDA receptor-mediated excitation these interneurons become relatively hyperpolarized. The reduction in this source of phasic inhibition allows a second type of interneuron (layer 3 goblet cells) to become active, mediating a lower frequency (c. 30 Hz) gamma rhythm. Examples of reconstructed interneurons of both types and 1 s epochs of intracellularly recorded activity during local gamma rhythm generation are shown. (B) The two gamma rhythms in mEC have modal peak frequencies which correspond to the main resonant frequency of either the hippocampal CA1 or CA3 subnetworks during gamma generation. Spectra show that, in control conditions (NMDA present), mEC frequency matches that of area CA1. In the absence of NMDA drive mEC frequency matches that of area CA3. Below are cartoons illustrating the possible consequences for information flow into hippocampus. Figure from Middleton et al. (2008).

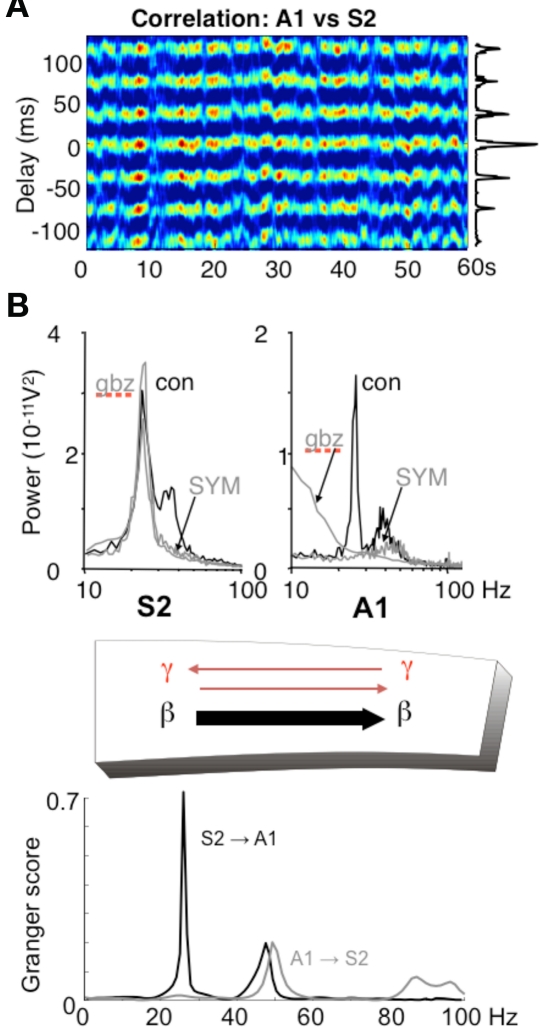
In addition to the possibility of choosing the direction of information flow from a single source, it is possible for different rhythm mechanisms to dictate the direction of information between pairs of sources. However, in some cases there is a clear directionality to this communication (e.g., Supp et al., 2007; Williams et al., 2009). Using an in vitro model of dynamical interactions between association cortex and primary auditory cortex (Roopun et al., 2010) it is possible to see how different mechanisms underlying the same frequency of local network rhythm may impart directionality in communication. We have discussed above the mechanism underlying gamma and beta2 frequency rhythms in S2 (an association area in rodent). In adjacent primary auditory cortex (A1) an almost spectrally identical pair of frequencies is also generated in superficial and deep layers but by a very different physiological and dynamical mechanism. While glutamatergic excitation generates only a superficial gamma rhythm in A1, the presence of cholinergic excitation reproduces the gamma/beta2 rhythms seen in adjacent S2. This differential response to mode of excitation is even more marked when considering the converse: cholinergic drive alone, while generating gamma/beta2 in A1, produces no rhythm generation in S2. In auditory cortex the cholinergic beta2 rhythm is highly sensitive to blockade of GABAergic and glutamatergic fast synaptic neurotransmission, whereas the glutamate receptor driven S2 beta2 rhythm is almost completely inert to such manipulations (Roopun et al., 2010). This differential sensitivity to synaptic input for two spectrally identical rhythms results in highly directed coherence estimates favoring information flow from layer 5 of S2 to layer 5 of A1 via long-range cortico-cortical synaptic connections (Figure 6).

Figure 6.

Different rhythms allow for directionality in functional connectivity. (A) Cross-correlogram showing a highly stable phase relationship between association cortex (S2) and primary auditory cortex (A1) when both generate beta2 frequency (c. 25 Hz) oscillations driven by kainate in the presence of cholinergic neuromodulation. (B) While the beta2 frequency rhythms in each area are spectrally the same, the mechanisms underlying them at the local network level are not. S2 beta2 rhythms are almost completely resistant to blockade of fast glutamatergic (SYM = SYM2206, 20 μM) or GABAergic (gabazine, 500 nM) synaptic transmission, whereas the same frequency generated by A1 requires both these components of synaptic transmission. The resulting combination of a rhythm dependent on chemical synaptic activity and one resistant to it results in highly significant partial directed coherence estimates (Granger scores) within the beta2 frequency band: The relatively synaptically inert S2 beta2 rhythm is able to dominate over the synaptically labile A1 beta2 rhythm. Note that in both regions, the accompanying superficial layer gamma rhythm is abolished by synaptic blockade and that, for the gamma rhythm, interactions are bi-directional. Figure from Roopun et al. (2010).

In the above in vitro model, more subtle changes in directionality of interactions are seen for the coexistent gamma rhythms in superficial layers. With kainate receptor-mediated drive alone, both A1 and S2 superficial layers generate gamma. However, there is a small but robust difference in frequency of a few Hz, with S2 gamma being faster than A1 gamma. This results in a coherence estimate directed in favor of S2 influencing A1 (Roopun et al., 2010). When both kainate and cholinergic drive are present, the additional drive from cholinergic receptors increases the frequency of A1 gamma selectively, and gamma frequencies match. In this situation directionality is lost and information flow, at gamma frequencies, is mutual (Figure 6).

Conclusions and Further Directions

It is not clear if any of the dynamical mechanisms described above are pertinent to the physiology of other rhythms, such as the alpha rhythm or delta rhythm, both of which support nesting with other rhythms (Palva and Palva, 2007; Schroeder and Lakatos, 2009). The gamma/theta nesting appears to depend on the overlap of cell types participating in the related rhythms. We do not know enough about the physiology of the alpha or delta rhythm to understand the mechanisms of nesting or cell assembly formation. As in other frequency bands, there are likely to be multiple mechanisms that produce the rhythms. For the gustatory cortex (Tort et al., 2010), there are (at least) two different rhythms in the alpha band associated with different temporal stages of the taste process, plus another associated with lack of engagement in the task. They lie in different sub-bands of the alpha range, and may have different mechanisms. It has been suggested that some kinds of alpha-band rhythms may be a product of single-cell dynamics in the LGN (Lorincz et al., 2008) while others may be network phenomena involving both the neocortex and the thalamus (Lopes da Silva et al., 1980; Contreras et al., 1996); such differences have implications for how the rhythm may be deployed functionally.

The recent enthusiasm for measuring cross-frequency coupling (Bruns and Eckhorn, 2004; Lakatos et al., 2005; Palva et al., 2005; Canolty et al., 2006; Jensen and Colgin, 2007; Tort et al., 2008, 2009) has begun to reveal the subtlety of the relationship between function and rhythms. These studies demonstrate that the sub-bands within the theta, gamma and very high frequency bands used to communicate between brain structures vary for different pairs of structures (Tort et al., 2008), and that the strength of the coupling can change in the course of a task. The discovery of such structure lends further weight to the hypothesis that rhythms are functionally important, and that subtle differences among rhythms in both frequency and physiology may provide important clues to function. We suggest here that diverse rhythms, or variations of a rhythm, can support different components of a cognitive act, with multiple rhythms potentially playing multiple roles.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.