Contrasting roles of axonal (pyramidal cell) and dendritic (interneuron) electrical coupling in the generation of neuronal network oscillations

Abstract

Electrical coupling between pyramidal cell axons, and between interneuron dendrites, have both been described in the hippocampus. What are the functional roles of the two types of coupling? Interneuron gap junctions enhance synchrony of γ oscillations (25–70 Hz) in isolated interneuron networks and also in networks containing both interneurons and principal cells, as shown in mice with a knockout of the neuronal (primarily interneuronal) connexin36. We have recently shown that pharmacological gap junction blockade abolishes kainate-induced γ oscillations in connexin36 knockout mice; without such gap junction blockade, γ oscillations do occur in the knockout mice, albeit at reduced power compared with wild-type mice. As interneuronal dendritic electrical coupling is almost absent in the knockout mice, these pharmacological data indicate a role of axonal electrical coupling in generating the γ oscillations. We construct a network model of an experimental γ oscillation, known to be regulated by both types of electrical coupling. In our model, axonal electrical coupling is required for the γ oscillation to occur at all; interneuron dendritic gap junctions exert a modulatory effect.

Electrical coupling occurs in mammalian telencephalon, between interneurons (primarily dendritic; refs. 1–6) and also between principal cell axons (7). Blockade of interneuron gap junctions has been shown, pharmacologically, to reduce synchrony of γ oscillations in isolated interneuron networks (8). In addition, through analysis of a connexin36 knockout mouse, in which coupling between interneurons is drastically reduced (9, 10), it has been shown that loss of interneuron gap junctions exerts a similar negative effect (that is, γ-power-reducing) on kainate-induced γ oscillations in vitro (9). In contrast, axon electrical coupling (presumably gap-junction-mediated) in this knockout appears unaffected, as ultrafast (>100 Hz) oscillations have properties similar to ultrafast oscillations in hippocampus from wild-type animals (9, 11).

Gap junctions play a critical role in the patterning of neuronal network oscillations in a variety of neural systems. Examples of such systems include central pattern-generating networks in the digestive system of crustaceans, in which gap junctions and chemical synapses often cooperate (12), and the medullary pacemaker nucleus of weakly electric fish, which appears not to depend on chemical synapses, and in which many of the gap junctions are located between axons (13–15). In mammals, gap junctions and chemical synapses can cooperate in producing a patterned circuit output. One example is the respiratory central pattern generator (16, 17); another example may be the supraoptic neurons that are thought to generate circadian rhythms (18, 19). What pattern-generating role is played by electrical coupling between different neuronal types (principal cells vs. interneurons) and between different sites (axons vs. dendrites), however, remains to be clarified. The connexin36 knockout mouse provides an opportunity to analyze the respective roles of axonal and dendritic gap junctions.

Persistent γ oscillations induced in vitro by carbachol and kainate depend on chemical synapses, specifically α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) and γ-aminobutyric acid (GABA_A) receptors (20, 21), but they depend on gap junctions as well (9, 22). In the transgenic mouse in which the neuronal connexin36 (23), which is predominantly expressed in interneurons (9, 10), was knocked out, the incidence of electrical coupling between interneurons was greatly reduced; despite this, persistent γ oscillations could still be evoked, albeit with reduced power compared with wild-type mice (9). This result suggested that interneuron (predominantly dendritic; refs. 2 and 6) gap junctions modulated the strength of the oscillation, but were not necessary for the oscillation's occurrence. Hormuzdi et al. (9) additionally noted that >100 Hz neuronal oscillations in low [Ca²⁺]_o appeared the same in the connexin36 knockout as in the wild type. Because the latter sort of oscillation has been attributed to electrical coupling between axons of pyramidal neurons (7, 11, 24), the data of Hormuzdi et al. (9) suggest the hypothesis that axonal principal cell electrical coupling could also act as a driver of the persistent kainate-induced γ oscillation, in addition to being the driver of neuronal oscillations >100 Hz (24). This hypothesis is examined in this paper. An earlier model of carbachol γ (22) is consistent with this hypothesis, but that model did not include interneuron gap junctions, so that no comparison could be made of the respective roles of the two types of electrical coupling.

Materials and Methods

Our computer-simulated network structure was similar (in essentials) to that used in ref. 25, with the addition of dendritic gap junctions and other modifications as noted below. The present network had, as before, 3,072 pyramidal cells and 384 interneurons (96 basket cells, 96 chandelier cells, and 192 dendrite-contacting interneurons). Each pyramidal cell was multicompartment (26) but with the axon extended from 5 to 10 compartments (each 75 μm long). g_Ca and g_K(AHP) densities were halved, compared with the original paper (27). Each interneuron was also multicompartment (28), but with reduced active conductance densities in the dendrites. There was a random current bias of −0.15 to −0.05 nA to pyramidal cells, and a tonic excitation of 5.5 nS to each of seven compartments in the apical dendrites (reversal 60 mV positive to resting potential). Each interneuron received a randomly chosen tonic excitatory conductance of 1–2 nS to each of four compartments in the proximal dendrites. In addition, Poisson-distributed ectopic axonal action potentials occurred, averaging 1 Hz per axon in pyramidal cells and 0.2 Hz per axon in interneurons. Kainate has been shown to induce ectopic spikes in axons (29).

Chemical Synaptic Connectivity.

Each principal cell received inputs from 30 principal cells and 80 interneurons (20 basket cells, 20 chandelier cells, 40 dendrite-contacting cells). Each interneuron was excited by 150 pyramidal cells and inhibited by 60 interneurons (20 basket cells, 40 dendrite-contacting cells). Excitatory connections were to mid-basilar and apical dendrites of pyramidal cells and mid-dendrites of interneurons. Chandelier cells inhibited the first axonal compartment of pyramidal cells; basket cells inhibited the soma and proximal dendrites of principal cells. Inhibitory connections were in the dendrites of interneurons. AMPA and GABA_A receptors were simulated. Unitary pyramidal EPSCs were (in nS, and t in ms) 2.1 × t exp (−t/2), and interneuron EPSCs were 0.5 × t exp (−t). Unitary IPSCs decayed with time constant of 10 ms and peaked at 1 nS for pyramidal cells, 1 nS for basket-to-interneuron connections, 0.1 nS for other interneuron–interneuron connections.

Gap Junctions.

Gap junctions were located in pyramidal cell axons in the compartment centered 187.5 μm from the soma and on interneuron dendrites in a compartment centered 85 μm from the soma (8). Gap junctions (axonal or dendritic) could only form between neurons with soma <200 μm apart. Each pyramidal axon contacted, on average, 1.6 other axons. Each interneuron contacted, on average, two other interneurons, subject to constraints: no junctions could form between basket cells (or chandelier cells) and dendrite-contacting interneurons (4, 8). Axonal gap junction conductance was 2.33 nS. For interneurons, we used values of 0.00–1.97 nS.

We illustrate average activity of the network with a rough approximation to a field potential, minus the average somatic potential of 224 nearby pyramidal cells. Power spectra of γ oscillations were computed with a fast-Fourier transform algorithm applied to 16,384 (2¹⁴) points, ≈3.1 s, of this local average signal.

Programs were written in FORTRAN augmented with instructions for parallel computing, and were run under AIX by using 12 processors of two different IBM SP2 parallel computers. In the computer with power-2 processors, it took ≈6.2 h to simulate each second of network activity. With power-3 processors, the figure was ≈3.1 h (contact the authors for programming and other details).

Results

We have recently shown that the gap junction blocker carbenoxolone suppresses γ oscillations evoked by kainate in the in vitro hippocampal CA3 region in connexin36 knockout mice (30). As interneuron electrical coupling has already been severely reduced by the genetic knockout manipulation itself (9), this result suggests that electrical coupling between the axons of pyramidal cells is critical for the γ oscillation. (It had previously been shown that gap-junction blockade suppresses low [Ca²⁺]_o-induced oscillations of >100 Hz both in wild-type and in connexin36 knockout animals (9, 11); this is consistent with the notion that electrical coupling between pyramidal cell axons is required for oscillations >100 Hz.) We suspect that the action of carbenoxolone (as used in refs. 11 and 30) is specifically to reduce electrical coupling rather than to reflect nonspecific actions, given the near superimposability of action potentials recorded with and without the drug (7).

To study further the respective roles of different types of electrical coupling in γ oscillations, we constructed a detailed network model, with 3,072 principal neurons and 384 interneurons (22). There were chemical synaptic interactions (via simulated AMPA and GABA_A receptors), as well as gap junctions, both between the axons of principal cells (7) and between the dendrites of interneurons (3–6). The network was activated by small tonic depolarizations of the respective cell types (not enough in themselves to induce oscillations), and the network was activated also by spontaneous ectopic spikes in axons that occurred at low frequency (mean = 1 Hz per axon for pyramidal cells; mean = 0.2 Hz per axon for interneurons). Ectopic spikes were able to cross from pyramidal axon to pyramidal axon, resulting in barrages of orthodromic and antidromic stimulation. This network model is the first one which, to our knowledge, incorporates both axonal (principal cell) and dendritic (interneuron) electrical coupling into the same system. It is not a priori obvious, from a theoretical point of view, how the two forms of coupling will influence one another.

Fig. 1 demonstrates that such a network model (robustly) generates a γ oscillation that exhibits many features in common with experimental persistent γ: interneurons fire at higher rates than pyramidal cells; the oscillation is associated both with γ-frequency excitatory postsynaptic potentials and inhibitory postsynaptic potentials in pyramidal cells; and the γ component of the oscillation requires both AMPA and GABA_A receptors to occur (data not shown; cf. refs. 20 and 21).

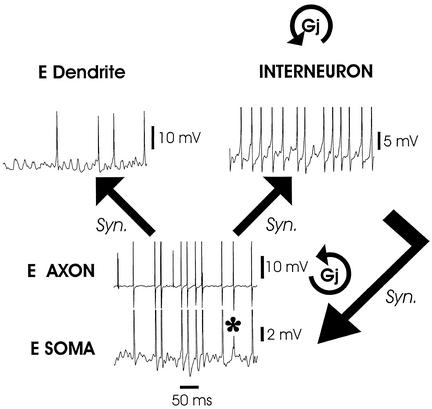
Figure 1.

Network model of kainate oscillations involves gap junctions between the axons of pyramidal cells (excitatory or “e” cells), gap junctions between dendrites of interneurons (0.525 nS in this case), and chemical synapses. In the latter category are AMPA-receptor-mediated excitation of pyramidal cell and interneuron dendrites, as well as GABA_A-receptor-mediated inhibition of pyramidal cells (on axon initial segments, somata, and dendrites; GABA_A-receptor-mediated inhibition of interneurons was also included but is not shown in the figure). Typical firing patterns are illustrated for a simulation of kainate-induced γ activity. Randomly occurring spikes in excitatory axons pass across gap junctions to other axons; they also occasionally propagate antidromically to produce a spikelet (*); axonal spikes propagate orthodromically to excite pyramidal cells (E Dendrite, Upper Left) and interneurons (Upper Right). In turn, interneurons inhibit each other and the pyramidal cells. Inhibition in pyramidal cells not only hyperpolarizes the latter but also interferes with the ability of axonal spikes to propagate to other axons, thereby phasically diminishing the gain of the system.

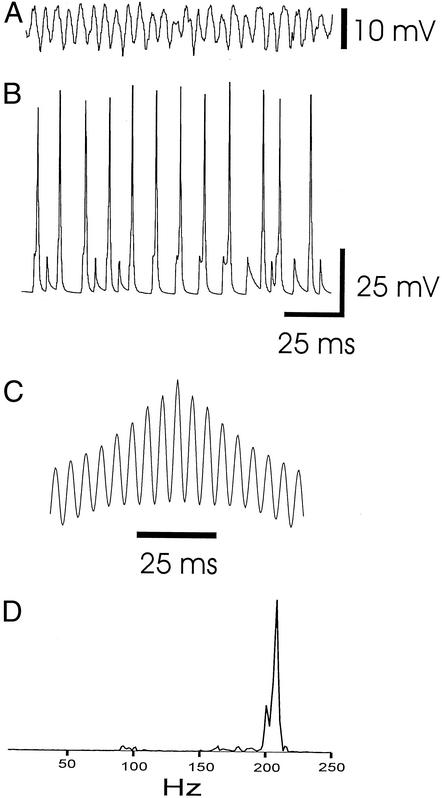
This model is in agreement with previous data (9, 11) on very fast oscillations, as well as with previous simulation data (24). Specifically, when all chemical synapses are blocked in the network of Fig. 1, a very fast oscillation is uncovered. As shown in Fig. 2, the very fast oscillation occurs at ≈200 Hz. It is mediated by electrical coupling between pyramidal cell axons.

Figure 2.

Blockade of chemical synapses in the model uncovers a −200 Hz (ultrafast) population oscillation in pyramidal cells, corresponding to experimental ultrafast oscillations in low [Ca²⁺]_o media (9, 11, 24). The only interaction between pyramidal cells under these model conditions is via axonal gap junctions. Other parameters were as in Fig. 1. (A) Average (inverted) somatic potential of 224 nearby pyramidal cells. (B) Simultaneous trace of pyramidal cell soma (hyperpolarized with 1.0-nA current). Note the numerous spikelets and action potentials with notched rising phases (cf. refs. 7 and 11). (C) Autocorrelation of the signal in A. (D) Power spectrum of 768 ms of data from the signal in A. The spectral peak is at 208 Hz.

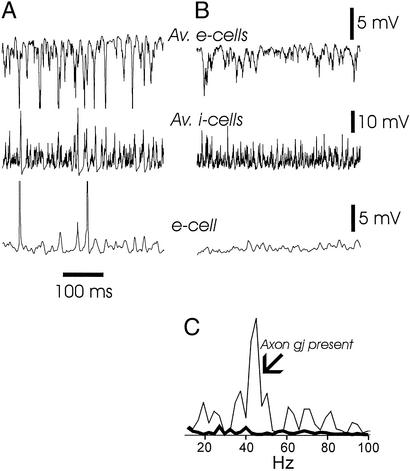
On the other hand, although the “full” model (with chemical synapses and gap junctions all present, Fig. 1) can generate γ oscillations, the data in Fig. 3 demonstrate that complete blocking of axonal electrical coupling, even with dendritic gap junctions present, abolishes γ oscillatory activity. The result is virtually identical in the case when axon electrical coupling is blocked, and dendritic gap junctions are also absent (data not shown).

Figure 3.

Blocking axonal electrical coupling between pyramidal cells abolishes γ oscillations in the model. (A) Simulation with axon gap junctions present (and dendritic gap junctions, 1.05 nS). Signals are the average (inverted) somatic potential of 224 nearby pyramidal cells, the average somatic potential of 28 nearby interneurons, and the somatic potential of a single pyramidal cell (hyperpolarized with −1.0 nA current). (B) The simulation of A was repeated, but with axonal gap junctions blocked. (C) Superimposed power spectra (10–100 Hz) of the local average pyramidal signals from A and B. The power spectrum of A (thin line, axon gap junctions present) reveals a clear peak at 44 Hz. The power spectrum of B (thick line, axon gap junctions blocked) plotted on the same scale shows virtually no γ power.

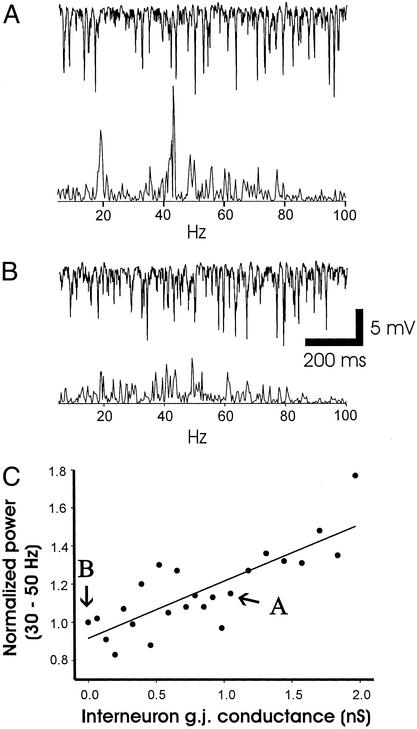
Finally, we examined whether the model could replicate the results of ref. 9 on the reduction of γ oscillatory power with reduction of the electrical coupling between interneurons. As the mean conductance of interneuron gap junctions is not known in the hippocampus, we did not know which precise conductance value to assign to “wild type.” Therefore, we examined a range of 24 different conductance values that encompasses experimental estimates of the coupling conductance for cortical interneurons [0.66 ± 0.18 nS (3); 1.6 ± 1.3 nS (4)]. We assigned a constant conductance to all coupled interneuron pairs in any given simulation. The model data (Fig. 4C) demonstrate a highly significant (R > 0.8) correlation between interneuron dendritic gap junction conductance and γ oscillatory power, in agreement with the experimental result.

Figure 4.

Dendritic gap junctions, between interneurons, enhance the power of γ oscillations in the model (as shown experimentally; ref. 9). (A) Inverted local average pyramidal cell activity (Upper) and power spectrum (5–100 Hz) of 3.1 s of this activity (Lower) from a simulation with interneuron gap junction conductance 1.05 nS. (B) The same signals, from a simulation with interneuron gap junction conductance 0.00 nS. (C) Scatter plot of data from 24 simulations, each with a different value of interneuron gap junction conductance. The ordinate shows integrated power from 30 to 50 Hz (in power spectra of 3.1 s of local average e-cell activity), expressed relative to the 30- to 50-Hz power when interneuron gap junctions are blocked. The linear regression fit has a positive slope (30% increase in power/nS conductance) with P < 0.0001 and R = 0.81. The slope was also positive with P < 0.002, R = 0.61, when we plotted normalized power from 15 to 60 Hz.

One reason that γ power is correlated with interneuron gap junction conductance could be that mean interneuron firing rate increases with the gap junction conductance. We fixed a particular interneuron and calculated its firing rate in 21 simulations, each with a different interneuron gap junction conductance (rate = 28–36 Hz in different simulations). The rate was positively correlated both with interneuron gap junction conductance (R = 0.72) and also with γ power (R = 0.68; data not shown).

Discussion

Our experimental and simulation data suggest a dual role for axonal (between pyramidal cells) and dendritic (between interneurons) electrical coupling, in generating persistent γ oscillations. Axonal electrical coupling sites, if endowed with enough conductance to allow action potentials to cross from axon to axon, and in the presence of background spontaneous firing, can generate a very fast network oscillation with synapses blocked (11, 24); but with synapses intact, the orthodromic effects of the axonal activity drive interneurons and pyramidal cells. Within a range of time constants and peak values for the synaptic conductances, a network γ oscillation can then result, even with limited tonic excitation of the neurons. (Of course, if strong tonic excitation is present, a γ oscillation can also result; ref. 31.) Without tonic excitation and without the axonal electrical coupling, however, the data suggest that a γ oscillation will not occur at all. In particular, in kainate or in carbachol, in which strong tonic depolarizations of the neurons are absent, a γ oscillation is not expected without the axonal electrical coupling between pyramidal cells.

Once the persistent γ oscillation is in place, our data suggest that the dendritic interneuron gap junctions act to tighten the organization of the rhythm. Such a tightening action is superficially similar to what happens in γ rhythms expressed in pharmacologically isolated networks of interneurons, in which carbenoxolone also suppressed γ synchronization (8); but in persistent γ oscillations, the interneurons are not pharmacologically isolated, and, indeed, the rhythm collapses after blockade of AMPA receptors (9, 11). Therefore, the precise mechanisms underlying the tightening of synchronization need not be identical in persistent γ, as compared with γ in isolated interneuron networks.

Our interpretation of the data can be tested in mice in which the putative axonal gap junction protein has been knocked out: we predict that persistent γ oscillations will not occur in such mice. We propose the following principle regarding the function of electrical coupling in cortical circuits: that axonal electrical coupling can be used to generate oscillations, and that dendritic gap junctions can be used to sharpen them.

Abbreviations

AMPA

α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid

GABA_A

γ- aminobutyric acid