Power assessment for genetic association study of human longevity using offspring of long-lived subjects

Abstract

Recently, an indirect genetic association approach that compares genotype frequencies in offspring of long-lived subjects and offspring from random families has been introduced to study gene-longevity associations. Although the indirect genetic association has certain advantages over the direct association approach that compares genotype frequency between centenarians and young controls, the power has been of concern. This paper reports a power study performed on the indirect approach using computer simulation. We perform our simulation study by introducing the current Danish population life table and the proportional hazard model for generating individual lifespan. Family genotype data is generated using a genetic linkage program for given SNP allele frequency. Power is estimated by setting the type I error rate at 0.05 and by calculating the Armitage’s chi-squared test statistic for 200 replicate samples for each setting of the specified allele risk and frequency parameters under different modes of inheritance and for different sample sizes. The indirect genetic association analysis is a valid approach for studying gene-longevity association, but the sample size requirement is about 3–4 time larger than the direct approach. It also has low power in detecting non-additive effect genes. Indirect genetic association using offspring from families with both parents as nonagenarians is nearly as powerful as using offspring from families with one centenarian parent. In conclusion, the indirect design can be a good choice for studying longevity in comparison with other alternatives, when relatively large sample size is available.

Introduction

As a complex trait, human longevity involves a large number of both genetic and non-genetic factors together with their interactions [1]. In the recent years, high throughput genotyping for the single nucleotide polymorphisms (SNPs) is enabling the genetic association analysis in fine mapping genes that contribute to human complex traits. In longevity studies, genetic association analysis using the popular case–control design has been conducted frequently for which genotypic information from centenarians or nonagenarians (cases) and young subjects (controls) are collected and genotype frequency compared to infer the association. Similar to the genetic association study of human diseases, the case–control design in longevity study requires that the two groups be well matched for potential confounding factors. However, the case–control design for longevity study failed to account for the important birth cohort effect, because of the constantly improving living standard and healthcare, which have largely helped to extend human lifespan [2]. Moreover, similar to any complex disease phenotype, the multi-factorial nature of human longevity also means that complex interaction between genes and the environment can be an important contributor to extreme survival. In this case, the changing environment reflected by the birth cohort effects could result in a biased estimate of the true genetic model.

Instead of directly comparing the long-lived subjects with young controls, which are taken from different birth cohorts, Barzilai et al. [3] introduced an indirect genetic association analysis on the cholesteryl ester transfer protein gene by comparing genotype frequencies between centenarian offspring and their age-matched controls. Their analysis detected significant increase of the homozygote genotype of the 405 valine allele in the centenarian offspring with similar pattern also revealed by a direct comparison between centenarians and young controls. Similar indirect analyses had been done on health outcomes by Barzilai [3] and by Adams et al. [4]. The merits in offspring of long-lived subjects in studying exceptional longevity have been demonstrated in the literature [5–13]. For example, a very recent study reported that centenarian offspring are more likely to age in better cardiovascular health and with a lower mortality than their peers [11]. In another study, Rose et al. [12] reported that centenarians and their offspring show significantly higher level of heteroplasmy in the mtDNA control region than the controls. All these observations indicate that offspring of the long-lived subjects could be ideal samples for studying human longevity.

In this paper, we are going to validate the indirect genetic association approach for studying longevity using computer simulation. Efficiency of the approach will be examined by power estimation for given parameters (allele relative risk, frequency, mode of inheritance) and for given sample sizes under two sampling schemes (LP1: at least one centenarian parent; LP2: both parents over age 90) when type I error rate is fixed to α = 0.05. Individual lifespan data are generated according to the current population survival to ensure the simulated lifespan distribution complies with the observed population data. Power estimates for the indirect association will be compared with our published power estimates for the direct association approach [14] and advantages and disadvantages will be discussed.

Materials and methods

The Danish population survival data

We introduce the latest life table for Denmark in our data simulation. With the observed population survival from the Danish life table, we are able to generate our data that follow the current mortality rate in the Danish population, without imposing any parametric function for the survival distribution. The Danish life table was taken from the Human Life-Table Database maintained at the Max-Planck Institute for Demographic Research in Rostock, Germany under http://www.lifetable.de/data/MPIDR/DNK_2005-2006.pdf. According to the life table, life-expectancy at birth for males is 76 years and for females 80 years. The mean survival for the two sexes was taken for the simulation.

Generating individual lifespan

For a given SNP allele with frequency p and relative risk r (r < 1beneficial and r > 1 harmful to survival; the other allele is defined as the baseline allele), we decompose the observed population survival at age x from the Danish life table s̄(x) into genotype specific survivals,

$$\overline{s}(x)=p^2{s}_2(x)+2p(1-p)s_1(x)+{(1-p)}^2{s}_0(x)$$ (1)

where s₂(x), s₁(x) and s₀(x) are genotype-specific survival functions for individuals carrying 2, 1 and 0 copies of the allele. Genotype-specific survivals are dependent on the relative risk parameter, the number of risky alleles carried by the genotype, and the mode of inheritance. In a simple proportional hazard model, we assume that the risk of an allele is constant over the ages (for example, the effect of apolipoprotein E gene as reported by Gerdes et al. [15]) so that the hazard function corresponding to a genotype-specific survival function, for example s₁(x), can be written as μ₁(x) = rμ_o(x). Here we can see that, for carriers of one allele with r < 1, the hazard of death can be reduced by 100*(1 − r) percent. Given the existence of multiple unobserved factors or hidden frailty that also contribute to individual survival by increasing or reducing the hazard of death, we introduce a gamma-frailty model [16] (mean of frailty = 1, variance = σ²) for defining the genotype-specific survival functions so that we have

$$\begin{array}{l}{s}_2(x)={[1-r^2{\sigma }^{2}ln{s}_o(x)]}^{-{\sigma }^2},\\ s_1(x)={[1-r{\sigma }^{2}ln{s}_o(x)]}^{-{\sigma }^2},\\ s_0(x)={[1-{\sigma }^{2}ln{s}_o(x)]}^{-{\sigma }^2}.\end{array}$$ (2)

Here s_o(x) is the baseline survival function and σ² is set to 0.1 according to our experience in fitting frailty models to the Danish life table data [17]. Introducing (2) into (1), we can numerically solve Eq. (1) to obtain a non-parametric baseline survival function s_o(x) for given risk and frequency parameters [18] and consequently obtain the genotype-specific survival functions in (2). Individual lifespan can then be generated for given genotypes.

Generating family data

Family data and individual genotypes are simulated using the linkage program Merlin [19]. The program first randomly generates parental genotypes based on the specified allele frequency and then offspring genotypes are assigned based on their parental genotypes. Both parental and offspring genotypes are used for simulating their lifespan data. However, only offspring genotypes are used for indirect association analysis by frequency comparison between offspring of long-lived parents (probands) and their age-matched controls who are offspring from random families. The maximum age gap between the long-lived parents and their offspring is set to 35 years.

Power calculation

We choose the Armitage’s trend test given by Sasieni [20] as the test statistic for comparing genotype frequency between offspring of probands and of random families. Following Sasieni, the Armitage’s test statistic ${\chi }_G^2$ is calculated using the following formula,

$${\chi }_G^2=\frac{N{(N(2R_2+R_1)-R(N_1+2N_2))}^2}{(N-R)R\left(N(N_1+4N_2)-{(N_1+2N_2)}^2\right)}\sim {\chi }_1^2$$ (3)

Here, N₁ and N₂ are the number of heterozygous and homozygous allele carriers in the total sample of size N, R₁ and R₂ are the number of heterozygous and homozygous allele carriers in the R offspring of the long-lived parents (Table 1).

Table 1.

Genotype frequency table for calculating the Armitage’s test statistic

Offspring	Genotypes			Totals
	0/0	0/1	1/1
Proband families	R0	R1	R2	R
Random families	S0	S1	S2	S
Totals	N0	N1	N2	N

In our simulation, an equal number of samples are drawn for offspring from long-lived parents and from random families. So we have R = S = 0.5*N. The test statistic ${\chi }_G^2$ follows a chi-squared distribution with 1 degree of freedom. Power of the test is calculated as the proportion of significant tests among all the tests performed on 200 replications generated in the simulation. By setting the type I error rate to α = 0.05, we can calculate the power as

$$\text{Power}(\alpha =0.05)=\frac{{\displaystyle \sum _{j=1}^B}I\left[{\chi }_G^2(j)\ge {\chi }_{0.05(1)}^2\right]}{B}.$$ (4)

In (4), B is the total number of replicates set to B = 200, ${\chi }_G^2(j)$ is the test statistic for the jth replicate, and ${\chi }_{0.05(1)}^2=3.84$.

Results

In Fig. 1, we show the frequency of a beneficial allele in 1,500 offspring with at least one centenarian parent (LP1 offspring) with an allele frequency at birth of 0.2 in the simulated samples. Each of the 95% confidence intervals (CIs) is estimated from an independent simulation with an assigned risk of the allele (0.7, 0.75, 0.8, 0.85, and 0.9). We can see that the allele frequency estimates significantly deviate from 0.2 and the deviation increases rapidly with the percentage of hazard reduction (from the lowest reduction of 10% for r = 0.9 to the highest reduction of 30% for r = 0.7). The message from Fig. 1 is that, frequency of gene alleles that contribute to human longevity is higher in the offspring of centenarians than in the general population. This phenomenon also means that offspring of the long-lived can be used for indirect genetic association analysis of human longevity.

Fig. 1.

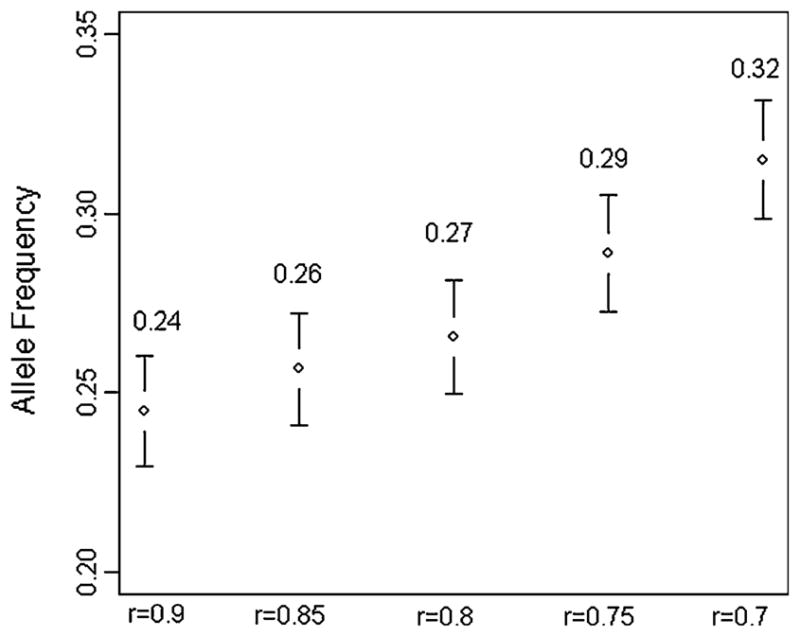
Allele frequency estimates with 95% CIs from offspring of long-lived parents (at least one centenarian) for a beneficial allele with frequency at birth set to 0.2 and risk of the allele varies from 0.7 to 0.9. Each frequency estimate is obtained from an independent simulation

Next we examine the power for the indirect approach using different settings of allele risk (from 0.6 to 0.9) and frequency parameters (from 0.05 to 0.8) for various sample sizes (from 200 to 3000) under different modes of inheritance (multiplicative or log additive, dominant and recessive). Table 2 has the power estimates for comparing genotype frequency of LP1 offspring with offspring from random families for additive SNP alleles. For a sample size of 3,000 (i.e. 1,500 centenarian offspring), the power for detecting an allele of r = 0.9 (10% hazard reduction) is 82% when allele frequency is 0.2, 96% when frequency is 0.5 and 72% when frequency is 0.8. When the sample size is reduced to 1,600, the model still has high power (>81%) in capturing common SNP alleles that reduces hazard by 15% (r = 0.85). For a sample size of 1,000, only common alleles of big effect (r = 0.8 or 20% hazard reduction) can be mapped with enough power (>81%). For large effect alleles (>20% hazard reduction), a sample size of 400–600 can be used. A small sample of 200 subjects does not have enough power unless extremely large effect genes exist which is unlikely.

Table 2.

Power in detecting additive effects: LP1 vs control offspring

Allele relative risk	Total sample size
	200	400	600	1,000	1,600	3,000
Allele frequency = 0.05
0.60	0.92	1.00	1.00	1.00	1.00	1.00
0.70	0.58	0.94	0.99	1.00	1.00	1.00
0.80	–*	0.54	0.61	0.81	0.92	1.00
0.85	–	–	–	–	0.51	0.91
0.90	–	–	–	–	–	0.50
Allele frequency = 0.20
0.60	1.00	1.00	1.00	1.00	1.00	1.00
0.70	0.90	1.00	1.00	1.00	1.00	1.00
0.80	0.59	0.87	0.94	0.99	1.00	1.00
0.85	–	0.72	0.80	0.83	0.94	1.00
0.90	–	–	–	–	0.69	0.82
Allele frequency = 0.50
0.60	1.00	1.00	1.00	1.00	1.00	1.00
0.70	0.97	1.00	1.00	1.00	1.00	1.00
0.80	0.66	0.92	0.98	1.00	1.00	1.00
0.85	–	0.72	0.87	0.93	1.00	1.00
0.90	–	–	0.58	0.63	0.74	0.96
Allele frequency = 0.80
0.60	0.70	0.92	1.00	1.00	1.00	1.00
0.70	0.54	0.78	0.88	1.00	1.00	1.00
0.80	–	–	0.56	0.83	0.97	1.00
0.85	–	–	–	0.56	0.81	0.98
0.90	–	–	–	–	–	0.72

^*Power estimates lower than 0.50 are not shown

As shown in Tables 3 and 4, sufficient power (>80%) can only be achieved with large samples of centenarian offspring in testing strong effect SNP alleles having over 15% hazard reduction for dominant alleles with frequency <0.5 and for recessive alleles with frequency >0.5. These results indicate that, the indirect association is actually a weak approach for studying genes with non-additive effects.

Table 3.

Power in detecting dominant effects: LP1 vs control offspring

Allele relative risk	Total sample size
	200	400	600	1,000	1,600	3,000
Allele frequency = 0.05
0.60	0.76	0.99	1.00	1.00	1.00	1.00
0.70	–*	0.81	0.97	1.00	1.00	1.00
0.80	–	–	0.68	0.70	0.79	1.00
0.85	–	–	–	–	–	0.82
Allele frequency = 0.20
0.60	0.89	1.00	1.00	1.00	1.00	1.00
0.70	0.62	0.94	1.00	1.00	1.00	1.00
0.80	–	0.69	0.84	0.91	0.96	1.00
0.85	–	–	–	0.59	0.71	0.95
0.90	–	–	–	–	–	0.65
Allele frequency = 0.50
0.60	–	0.81	0.85	0.95	0.99	1.00
0.70	–	0.69	0.77	0.81	0.89	1.00
0.80	–	–	–	0.51	0.52	0.93
0.85	–	–	–	–	–	0.69

^*Power estimates lower than 0.50 are not shown

Table 4.

Power in detecting recessive effects: LP1 vs control offspring

Allele relative risk	Total sample size
	200	400	600	1,000	1,600	3,000
Allele frequency = 0.20
0.60	–*	0.75	0.85	0.85	0.98	1.00
0.70	–	–	0.50	0.56	0.56	0.82
Allele frequency = 0.50
0.60	0.92	1.00	1.00	1.00	1.00	1.00
0.70	0.63	0.92	0.97	0.99	1.00	1.00
0.80	–	0.61	0.72	0.78	0.81	1.00
0.85	–	–	–	0.51	0.53	0.86
Allele frequency = 0.80
0.60	0.73	0.93	0.98	1.00	1.00	1.00
0.70	–	0.71	0.88	0.98	1.00	1.00
0.80	–	–	–	0.76	0.93	1.00
0.85	–	–	–	–	0.67	0.90
0.90	–	–	–	–	–	0.50

^*Power estimates lower than 0.50 are not shown

Instead of sampling centenarian offspring, we also simulated another sampling scheme that collects genotype information for offspring, whose parents both lived past 90 years (LP2 offspring). Power estimates indicate that such a sampling scheme has high power (>86%) in identifying common SNP alleles with over 15% hazard reduction for large sample sizes (>3,000) (Table 5). For a smaller sample size of 1,000, the approach has acceptable power in detecting common SNP alleles with over 20% hazard reduction. Comparing power estimates in Table 5 with that in Table 2, one can see that although the LP2 offspring are generally less informative than the LP1 offspring, the major difference is only for the rare SNPs (frequency of 0.05). For very high frequency alleles, power estimates are very close, especially for large sample sizes.

Table 5.

Power in detecting additive effects: LP2 vs control offspring

Allele relative risk	Total sample size
	200	400	600	1,000	1,600	3,000
Allele frequency = 0.05
0.60	–*	0.74	0.96	0.97	1.00	1.00
0.70	–	–	0.82	0.78	0.89	1.00
0.80	–	–	–	0.52	0.53	0.88
0.85	–	–	–	–	–	0.57
Allele frequency = 0.20
0.60	0.86	1.00	1.00	1.00	1.00	1.00
0.70	0.53	0.96	0.99	0.99	1.00	1.00
0.80	–	0.73	0.86	0.91	0.92	1.00
0.85	–	0.51	0.64	0.68	0.77	0.86
0.90	–	–	–	–	–	0.65
Allele frequency = 0.50
0.60	0.99	1.00	1.00	1.00	1.00	1.00
0.70	0.87	1.00	1.00	1.00	1.00	1.00
0.80	0.56	0.87	0.96	1.00	1.00	1.00
0.85	–	0.61	0.84	0.88	0.95	1.00
0.90	–	–	0.52	0.56	0.56	0.88
Allele frequency = 0.80
0.60	0.84	1.00	1.00	1.00	1.00	1.00
0.70	0.80	0.83	0.96	0.99	1.00	1.00
0.80	–	–	0.61	0.78	0.97	1.00
0.85	–	–	–	0.50	0.81	0.88
0.90	–	–	–	–	–	0.62

^*Power estimates lower than 0.50 are not shown

Discussion

We have shown, through computer simulation that indirect genetic association analysis is a valid method for studying genetic association with human longevity. The estimated power is highly dependent on the parameters specified (frequency, risk, mode of inheritance) and sampling schemes (size of study, selection of proband). A relatively large sample size (over 1,000 centenarian offspring) is required for mapping genes with low to modest additive effects. For non-additive effect genes, the power is generally low. The power is especially low for detecting high frequency dominant and low frequency recessive genes. The low power can be due to the high presence of risky genotypes that overwhelm the population, p² + 2p(1 − p), for high frequency dominant alleles, and to the low presence of risky genotype that is very rare in the population, p², for low frequency recessive alleles in offspring from both proband and random families.

As shown in Tables 2 and 5, except for rare SNP alleles, the power in testing common SNPs using offspring from LP1 (centenarian as proband) and LP2 (nonagenarian as proband) families is comparable. This means, according to our power estimates that, offspring from LP2 families are nearly equally as useful as those from the LP1 families and thus can be sampled and analyzed jointly. The joint sampling can help researchers to achieve larger sample sizes and thus more power for their studies.

It is necessary to compare our power estimates for the indirect approach with that from the direct approach [14]. For any fixed parameter and sample size, the indirect genetic association exhibits lower power, compared to the direct approach and thus larger sample sizes are needed in order to obtain comparable power as in the direct association studies. In general, there is a 3 to fourfold difference in sample size requirement between the two approaches. Note that, the reported power for the direct association does not take into account the birth cohort effect that constantly reduces mortality over time. However, we emphasize the following two points.

First, the offspring from both proband and random families, who are genotyped in the indirect association studies, are of relatively younger ages (over age 65 in LP1 families and 55 in LP2 families). Their genotype information can be re-used when these individuals are followed up to conduct cohort studies on, for example, aging related diseases or longevity. According to Hjelmborg et al. [21] the genetic influences on lifespan are minimal prior to age 60 but increase thereafter. This means that the follow-up studies on the offspring from the indirect approach can be highly informative. As offspring of centenarians or long-lived subjects reported to inherit significantly better health [11], important results can be expected from follow-up studies on these already genotyped samples.

Second, most of the genetic association studies using centenarians are of small scale, because centenarians are rare samples. However, the indirect design genotypes centenarian offspring instead of the centenarians themselves. Since the indirect design does not require genotypic data from centenarians, the sampling scope can be largely expanded.

Third, because of the rarity of centenarians, many case–control association analyses have been done using nonagenarians or even octogenarians as cases instead of centenarians. Tan et al. [14] reported that the case–control association using nonagenarians requires a more than fivefolds increase in the sample size, compared to using centenarians. In this case, a better alternative would be conducting the indirect genetic association analysis given the above mentioned advantages.

Obtaining sufficient samples has been a major obstacle in longevity studies. The small sample sizes used resulted in the lack of power and accounts for the inconsistent results in gene-longevity association studies [14]. In this aspect, the indirect association design offers a good alternative although it requires larger sample sizes. It is encouraging that international consortia have been established for collecting data on long life families (for example, the Long Life Family Study at https://dsgweb.wustl.edu/llfs/, the Genetics of Healthy Aging Project at http://www.geha.unibo.it/). Large scale genotype data will be collected for performing both direct and indirect genetic association analyses for identifying or replicating genetic variations that affect human longevity.

Our simulation focuses on nuclear families with only one offspring. In practice, multiple siblings from each family of long-lived parents can be sampled. In this case, inference on statistical significance in frequency differences needs to take into account of the genetic correlation among siblings within each family. Statistical models able to handle correlated data are available, for example the generalized estimation equation model that treats siblings in each family as one cluster with exchangeable correlation structure [22].

Conclusions

Our computer simulation has shown that the indirect case–control association design, using centenarian offspring, is a valid approach for studying human longevity. Compared with the direct design that is based on centenarians, a three to fourfolds increase in samples size is required to achieve comparable power. However, given the rarity of centenarians and the usefulness of genotype data of centenarian offspring, the indirect design can be a good choice for studying longevity in comparison with other alternatives.