Abstract
Synthetic biology is a rapidly expanding discipline at the interface between engineering and biology. Much research in this area has focused on gene regulatory networks that function as biological switches and oscillators. Here we review the state of the art in the design and construction of oscillators, comparing the features of each of the main networks published to date, the models used for in silico design and validation and, where available, relevant experimental data. Trends are apparent in the ways that network topology constrains oscillator characteristics and dynamics. Also, noise and time delay within the network can both have constructive and destructive roles in generating oscillations, and stochastic coherence is commonplace. This review can be used to inform future work to design and implement new types of synthetic oscillators or to incorporate existing oscillators into new designs.
Keywords: synthetic biology, gene regulatory networks, oscillators
1. Introduction
The aim of synthetic biology is to design and synthesize biological networks or devices that perform a desired function in a predictable manner (Endy 2005; Andrianantoandro et al. 2006; Serrano 2007; Haseloff & Ajioka 2009). Achieving this goal requires a combination of in silico and in vivo analysis, and combines approaches from the fields of engineering, mathematics and biology. Much attention has focused on the synthesis of gene regulatory networks. Since the early papers (Becskei & Serrano 2000; Elowitz & Leibler 2000), two paradigmatic types of networks have been of interest to the scientific community: switches and oscillators (Tyson et al. 2008).
Over the past few years, numerous designs have been proposed for both types of networks in prokaryotic and eukaryotic cells. Because of the highly interdisciplinary nature of synthetic biology, results are published in a plethora of different journals ranging from dynamical systems and mathematics journals to computational biology and mainstream biological journals. Moreover, while some papers focus on the design of an oscillator of interest, others derive its model and analyse its features, while yet other journals report the in silico or in vivo validation. A subset of the current networks have been discussed in existing reviews (e.g. Hasty et al. 2001b; Novák & Tyson 2008). However, these have focused on different aspects of the oscillators and with various degrees of detail. They also differ in their structure and approach. Hence, when studying the problem of synthesizing a new network, it is difficult to find a coherent description of the various existing oscillators in a unified framework.
The aim of this paper is to address this gap in the literature by expounding the features of the main synthetic oscillators proposed so far in a unified, coherent framework. In so doing, we review and compare the characteristics of the various oscillating networks available in the literature, highlighting advantages and disadvantages. Starting from the simplest Goodwin oscillator (Goodwin 1963), we will consider repressilators (Fraser & Tiwari 1974; Elowitz & Leibler 2000), several types of activator–repressor networks and the very recent oscillators constructed in mammalian cells (Tigges et al. 2009, 2010). The aim is to present a review of the features of each network, the models used for their in silico design and validation and the main in vivo data available in the literature. The comparative analysis of these existing oscillators can be used to inform the modelling, design and in vivo implementation of future synthetic oscillators, but also as a guideline to synthetic biologists and engineers wishing to use existing models and designs.
For brevity and clarity, this review focuses solely on the analysis of synthetic oscillators. However, the study of natural genetic oscillators is itself a large and established field, with results that are relevant to the study of synthetic oscillators in their wider context (e.g. Lewis 2003; Pomerening et al. 2005).
The rest of the paper is organized in the following sections, each devoted to a different class of oscillators, giving details on the network, the mathematical analysis presented in the literature and the results of the in silico and, if available, in vivo implementation of the design:
— Goodwin oscillator (§2);
— Repressilators (§3);
— Amplified negative feedback oscillators (§4), focusing on networks obtained by using either transcriptional repression, repression by sequestration or repression by proteolysis;
— Fussenegger oscillators (§5);
— Smolen oscillator (§6);
— Variable link oscillators (§7); and
— Metabolator (§8).
2. Goodwin oscillator
The Goodwin oscillator, conceived over 40 years ago (Goodwin 1963), was the first synthetic genetic oscillator to be studied. It is also the simplest oscillator, comprising a single gene that represses itself (figure 1a). Early theoretical work was extensive, but noted for its conflicting results on the existence of oscillations. Relevant references to this early work can be found within Banks & Mahaffy (1978a) and Smith (1987), while discussion of the early work can be found in Tyson (1975), Banks & Mahaffy (1978a) and Smith (1987).
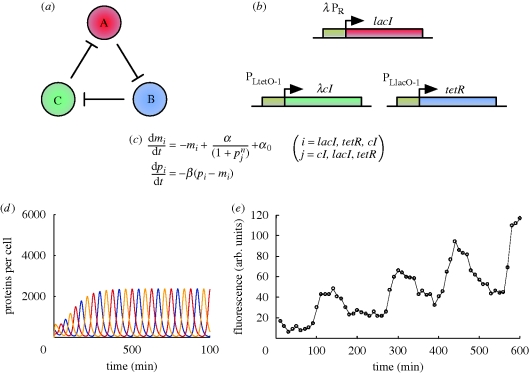
Figure 1.
(a) Goodwin oscillator topology. It comprises a single gene that represses itself. Throughout the text, the convention used is that a solid line indicates direct transcriptional control, while dotted lines indicate an alternative or indirect regulatory mechanism. (b) Gillespie simulation of a Goodwin oscillator model. (c) In vivo implementation. The PLlacO-1 promoter (Lutz & Bujard 1997; also employed in the construction of Elowitz's repressilator, see §3.3), active in the absence of LacI, was used to control LacI expression. (d) In vivo time series of GFP fluorescence. Figure (b) and (d) are adapted from Stricker et al. (2008).
More recently, different types of models have been proposed in the literature including ordinary differential equations (ODEs; Müller et al. 2006; electronic supplementary material, §S2.1), delay differential equations (DDEs; Smith 1987 (using a model from Banks & Mahaffy (1978b)); Bratsun et al. 2005; Stricker et al. 2008; electronic supplementary material, §S2.3 and S1) and discrete stochastic simulations using the Gillespie algorithm (Bratsun et al. 2005; Gillespie 2007; Stricker et al. 2008).
2.1. Mathematical analysis
Both ODE (Müller et al. 2006) and DDE (Bratsun et al. 2005) models suggested that oscillations in the Goodwin network arise through a Hopf bifurcation, if repression is modelled by a nonlinear Hill function with a sufficiently high cooperativity coefficient (Smith 1987; Bratsun et al. 2005). The presence of a time delay in the negative feedback loop was also suggested to have a constructive role. In particular, the region in parameter space where oscillations are detected can be expanded by increasing the value of the time delay within the feedback loop (Stricker et al. 2008). Moreover, as shown in Mallet-Paret & Smith (1990), oscillations can be proved to be associated with a unique limit cycle and hence to be globally asymptotically stable.
2.2. In silico experiments
The presence of oscillations was confirmed via in silico experiments using a number of different techniques. Early discrete, Boolean-like simulations (Fraser & Tiwari 1974; Tiwari & Beckman 1974) suggested only damped oscillations were possible under biologically realistic parameters. However, oscillations for biologically plausible parameters could be obtained using stochastic simulations with parameters drawn randomly1 from either an exponential (Tiwari & Beckman 1974) or normal distribution (Fraser & Tiwari 1974). Recent studies support this early finding, with increased parameter ranges associated with oscillatory behaviour being observed under stochastic simulations (Lewis 2003; Bratsun et al. 2005; Stricker et al. 2008).
In one of these examples, a biologically detailed simulation allied to in vivo work (Stricker et al. 2008), it is shown that while oscillations are predicted to decay with a deterministic model, they can persist under Gillespie simulations (figure 1b). However, this was only observed under certain conditions, suggesting that the constructive role for noise may be parameter dependent. These simulations also suggested that a robust period appears to be a feature of the Goodwin oscillator, an observation also made elsewhere (Lewis 2003). Period was of the order of between 10 and 20 min in simulations and was relatively insensitive to inhibition of repression (Stricker et al. 2008). Further in accordance with these results, a separate study found that for certain parameter values, period is resistant to temperature, displaying temperature compensation (Ruoff & Rensing 1996), a common feature of natural oscillators (Pittendrigh & Caldarola 1973).
Early simulations also found that a time delay between transcription and translation, characteristic of a eukaryotic system, could improve the regularity of oscillations (Tiwari & Beckman 1974). However, recent Gillespie simulations incorporating delay conversely suggested that increasing delay within the feedback loop reduces regularity (Bratsun et al. 2005). Together with the mathematical results demonstrating the role of time delay in the negative feedback in improving oscillatory capacity, studies suggest a trade-off between an increased oscillatory capacity and noisy oscillations may exist with regard to time delay.
2.3. In vivo implementation
Given the controversial nature of some of the findings of the theoretical work, it was important that an in vivo construction was performed. Construction of the Goodwin oscillator used the PLlacO-1 promoter (Lutz & Bujard 1997), repressed by LacI, but capable of driving transcription at a sufficiently high level when unrepressed. By using this promoter to control LacI expression (Stricker et al. 2008; figure 1c), a negative feedback loop was formed. The same promoter also controlled expression of the fluorescent reporter protein yemGFP (monomeric yeast-enhanced green fluorescent protein), allowing observation of dynamics. LacI and yemGFP contained sequences termed ssrA ‘tags’, which are recognized by Escherichia coli proteases, and are used to increase the degradation rates of LacI and yemGFP to achieve faster dynamics. Each gene was constructed on a different plasmid. The system was introduced into E. coli deficient in the lac operon, minimizing host genome interference.
Consistent with simulations (Stricker et al. 2008), oscillations were relatively irregular, often failing to return to a zero level (figure 1d). Period was of the order of 30 min, slightly longer than corresponding simulations. However, in agreement with simulations, the period of the oscillations was largely unaffected by IPTG (an inducer molecule that binds to LacI and inhibits repression), varying less than 5 per cent over the range examined (Stricker et al. 2008). The percentage of oscillatory cells was not reported, meaning a proper assessment of robustness is not possible.
In addition to the agreement with simulations, an in vivo implementation has also validated the mathematical results on the requirement for sufficient nonlinearity in repression to obtain oscillations. The implementation here used LacI, which is a tetramer. However, an earlier implementation used TetR (Becskei & Serrano 2000), which is dimeric. Repression by TetR will therefore be described by a lower Hill coefficient than LacI, and subsequently there will be less nonlinearity in repression. In agreement with the mathematical results, the implementation using TetR did not oscillate, but instead exhibited highly stable dynamics.
2.4. Discussion
The insensitivity of period to IPTG and (theoretically) temperature (Ruoff & Rensing 1996) are potentially useful features of the Goodwin oscillator. However, oscillations observed thus far have been quite irregular, which may limit its utility.
We now move to discussing multi-gene oscillators, starting with one of the most widely known genetic oscillators presented in the literature: the repressilator.
3. Repressilators
A repressilator can be thought of as an extension of the Goodwin oscillator. It is defined as a regulatory network of one or more genes, with each gene repressing its successor in the cycle (Müller et al. 2006). The term was first used to describe a cycle of three genes (Elowitz & Leibler 2000; figure 2a). A one-gene repressilator is the previously discussed Goodwin oscillator (§2).
Figure 2.
(a) Three-gene repressilator topology. Each gene represses its successor in the cycle. (b) In vivo implementation of a three-gene repressilator. LacI represses tetR through PLlacO-1, tetR represses λ cI through PLtetO-1 and cI represses lacI through λ PR, completing the cycle. All genes contain an ssrA sequence tag to promote rapid degradation. (c) ODE model equations for the in vivo implementation. mi and pi represent mRNA and protein concentrations, respectively, i and j paired order-wise, resulting in six ODEs. α0 and α + α0 are the number of protein copies produced per cell with saturating repressor levels (promoter ‘leakyness’) and without repressor, respectively. β is the ratio of the protein decay rate to the mRNA decay rate and n the Hill coefficient. (d) Time series obtained by in silico simulation of ODEs for a particular set of parameters (see Elowitz & Leibler (2000) for details). (e) In vivo time series of GFP fluorescence. Figure (d) and (e) are adapted from Elowitz & Leibler (2000).
Repressilators were first studied over 30 years ago as a logical extension to the Goodwin oscillator, using the same discrete, Boolean-like simulations (Fraser & Tiwari 1974). Continuous models were subsequently studied using DDEs (Smith 1987; electronic supplementary material, §S2.3), and more recently ODEs (Elowitz & Leibler 2000; El-Samad et al. 2005; Müller et al. 2006; figure 2c; electronic supplementary material, §S2.1 and 2.2), other DDE models (Wang et al. 2005a) (electronic supplementary material, §S2.4), discrete stochastic simulations using the Gillespie algorithm (Yoda et al. 2007; Rajala et al. 2010) and hybrid stochastic schemes (Tuttle et al. 2005) have been used. The repressilator topology is also observed in other fields. In electronics, a cycle of an odd number of NOT gates is termed a ‘ring oscillator’, and in neuroscience, cyclic networks of neurons are referred to as ‘neural ring networks’ (Pasemann 1995).
3.1. Mathematical analysis
The mathematical results on the Goodwin oscillator are an invocation of results developed for repressilators in general. As with the Goodwin oscillator, oscillations arise through a Hopf bifurcation (Müller et al. 2006), results on DDEs also suggesting a common requirement of sufficiently nonlinear repression (Smith 1987). Results proving oscillations as a global attractor of the system are also applicable, while a complementary theory developed for DDEs, not yet applied to the Goodwin oscillator (Mallet-Paret & Sell 1996), demonstrates that, at least for three genes, time delay can have a constructive effect, creating oscillations (Wang et al. 2005a).
Repressilators comprising an even number of genes were initially found to exhibit multi-stability (Smith 1987; Müller et al. 2006). More recently, it has been shown that repressilators with six or more genes actually possess a quasi-stable periodic solution (all but one Floquet multipliers less than 1), generated through a Hopf bifurcation (Strelkowa & Barahona 2010). The stability of the periodic solution increases for increasing gene number (Strelkowa & Barahona 2010), the magnitude of the multiplier corresponding to the unstable direction decreasing. This finding potentially expands the oscillatory capacity of the repressilator class. Indeed, only the two- and four-gene repressilators have not been shown to oscillate, the two-gene version demonstrated in vivo to function as a bi-stable switch (Gardner et al. 2000).
Bifurcation analysis of a three-gene repressilator ODE model allied to in vivo work (Elowitz & Leibler 2000; figure 2c) showed oscillations were favoured by strong promoters (high maximal transcriptional rate), efficient ribosome-binding sites (high average number of proteins per transcript), low levels of transcription when fully repressed and cooperative repression characteristics. It was also important that genes in the system all had comparable mRNA and protein decay rates.
The studies of Müller et al. (2006) and Elowitz & Leibler (2000) considered symmetrical networks possessing identical parameter sets for each gene. In vivo implementation of such a balanced network is likely to be impossible. Non-symmetric networks can also display oscillations, although the analysis of these has not been extensive (El-Samad et al. 2005; Strelkowa & Barahona 2010).
3.2. In silico experiments
Early discrete simulations (Fraser & Tiwari 1974) demonstrated oscillations in three-gene repressilators over a small parameter range, requiring a high repression efficiency, in agreement with mathematical results. Simulations of ODEs by Elowitz (Elowitz & Leibler 2000) also exhibited oscillations, with a period of the order of 150 min, using parameters suggested by their analytical work (figure 2d). While mathematical analysis had demonstrated the ability for time delay to generate oscillations, simulations showed that it could also be used to tune oscillation characteristics. Increasing the total time delay in the system increased the amplitude and period of oscillations linearly (Wang et al. 2005a). Recent work also suggests the rate and duration of transcriptional pausing can affect the period (Rajala et al. 2010).
Deterministic simulations also confirmed the existence of quasi-stable oscillations in even gene-number repressilators (Strelkowa & Barahona 2010). Although oscillations eventually decay, it was observed that the lifetime of oscillations improves for higher gene numbers, as predicted by the mathematics. It was also suggested that this ‘quasi-stability’ can be exploited to switch oscillations on and off in a controlled way (Strelkowa & Barahona 2010).
The constructive role for noise observed in the Goodwin oscillator (Tiwari & Beckman 1974) was also confirmed for repressilators. The inclusion of stochasticity into the initial discrete simulations, this time by drawing parameters randomly from a normal distribution, significantly decreased the dependence on repression efficiency for oscillations (Fraser & Tiwari 1974). Furthermore, while the quasi-stability eventually stopped oscillations in deterministic simulations of even gene-number networks, the stochasticity in Gillespie simulations allowed oscillations to continue indefinitely (Strelkowa & Barahona 2010). However, as observed for the Goodwin oscillator, a constructive role for noise can depend on system parameters. In the adiabatic regime (a significantly higher DNA-protein binding rate relative to the rate of change in protein number) of a model presented in Yoda et al. (2007), oscillations occurred in Gillespie simulations but not in a corresponding ODE representation, suggesting a constructive role for noise. Yet, the opposite was observed in a strongly non-adiabatic regime, where noise destroyed the correct ordering of oscillations, or phase coherence, observed for the ODEs. A destructive role for noise was also present in Gillespie simulations by Elowitz (Elowitz & Leibler 2000), in which oscillations exhibited significant amplitude variability. The property of stochastic coherence, a maximum in the regularity of the oscillations (measure on the distance between peaks) as a function of the system size (average number of components; Hilborn & Erwin 2008), has been documented (Yoda et al. 2007). This has not yet been observed in the Goodwin oscillator specifically, in this case, it is the dependence of phase coherence on noise, phase coherence depending nonlinearly on noise strength (Yoda et al. 2007).
Finally, the sensitivity to the level of parameter symmetry observed mathematically persists under stochastic simulations; oscillations are suppressed above some level of asymmetry (Tuttle et al. 2005).
3.3. In vivo implementation
Based on the suggestions of their mathematical analysis (see §3.1), Elowitz & Leibler (2000) constructed a three-gene repressilator in vivo (figure 2b) using LacI from E. coli, TetR from the Tn10 transposon and cI from the λ phage (Elowitz & Leibler 2000). In their network, LacI represses transcription of tetR, TetR represses transcription of cI and cI represses transcription of lacI, completing the cycle of repression. Owing to the mathematical results, strong, tightly repressible hybrid promoters were employed to control tetR and cI, combining the λ PL promoter with LacI and TetR operators, respectively (Lutz & Bujard 1997; Elowitz & Leibler 2000). The λ PR promoter, which contains cI operators, was used to control lacI. To increase protein decay rates closer to that of the mRNA, another suggestion of the mathematical work, ssrA tags were inserted at the 3′ end of each gene, targeting the repressilator proteins for rapid destruction (Elowitz & Leibler 2000). The repressilator was constructed on a low copy-number plasmid and introduced into E. coli deficient in the lac operon, minimizing interference from the host genome on dynamics. Additionally, a high copy-number plasmid containing a reporter gene that encoded an intermediate stability green fluorescent protein (GFP) and that was repressed by TetR was introduced, allowing monitoring of network dynamics by fluorescence.
At least 40 per cent of cells exhibited oscillations, with a period of 160 ± 40 (mean ± s.d.) min, of the order of deterministic simulations, and a significant variation in amplitude, as predicted by stochastic simulations (Elowitz & Leibler 2000). While protein levels in simulations returned to zero between oscillations, fluorescence by GFP increased over time (figure 2e). This is probably due to the higher stability of the GFP relative to the rapidly degraded repressilator proteins. However, it was not explicitly accounted for in modelling, and hence not predicted. Despite the variability in amplitude, oscillations in progeny were correlated for a significant amount of time after cell division, demonstrating that network state is passed to progeny (Elowitz & Leibler 2000). The timing of oscillations was not correlated with cell division, suggesting repressilator dynamics were decoupled from the cell-division cycle (Elowitz & Leibler 2000). However, the entry of E. coli into stationary phase arrested oscillations, indicating that dynamics are coupled to the global regulation and effects of cell growth and division (Elowitz & Leibler 2000). Observation time for oscillations was limited by this entry into stationary phase to approximately 10 h, allowing three to four oscillations to occur (Elowitz & Leibler 2000). A potential source of interference may be the increased concentration of the σ38 transcription initiation factor that occurs during stationary phase. This would compete with σ70 (the initiation factor responsible for specifying RNA polymerase binding to the repressilator promoters) for available RNA polymerase and may significantly affect dynamics. Designing repressilators that function with both types of σ factor may allow oscillations to continue into stationary phase.
3.4. Discussion
Although conceived after the Goodwin oscillator, the three-gene repressilator was the first synthetic genetic oscillator to be successfully implemented in vivo (Elowitz & Leibler 2000). However, less than half of observed cells exhibited oscillations, suggesting it lacks robustness. The role of noise is not yet well understood, and may be partly responsible. Furthermore, although the repressilator can function with some parameter asymmetry, significant asymmetry could contribute to the fact that the majority of cells did not oscillate. Interference from native cellular systems may also play a role, with the oscillations decaying to an equilibrium value. The limited studies on time delay suggest the repressilator may function in eukaryotes, although there are indications that temporal differences in how DNA is duplicated in eukaryotes may affect the repressilator dynamics (Chen et al. 2004).
Regarding improvements, it has been observed that the addition of a positive feedback loop to any of the repressilator genes expands the region in parameter space over which the core repressilator oscillates, enhancing robustness (Tsai et al. 2008). This addition also allows the repressilator to exhibit a far greater range of frequencies for a given amplitude (Tsai et al. 2008), increasing its potential utility as a component of more complex synthetic networks (Tsai et al. 2008). Finally, the controllable oscillatory capacity of even-gene repressilators may significantly expand the utility of the topology. More generally, this highlights the potential for transient dynamics and in particular quasi-stability, used elsewhere in flight and fluid control (Strelkowa & Barahona 2010), in gene network function.
The presence of a positive self-feedback loop is a feature of the class of oscillators presented in the next section, the amplified negative feedback oscillators.
4. Amplified negative feedback oscillators
The Goodwin oscillator and the repressilators are formed from solely repressive links. The logical next step in oscillator design was to explore oscillators also incorporating activating links between genes. The amplified negative feedback oscillator comprising two genes is possibly the simplest type of amplified negative feedback oscillator. Here, one gene promotes (amplifies) its own transcription via a positive self-feedback loop and also activates transcription of the other gene. At the same time, the second gene represses transcription of the first gene, forming a negative feedback loop (figure 3a). Three different versions of this topology have been considered; repression by transcriptional control, repression through sequestration by dimerization and repression by proteolysis. In what follows, we will describe the features of each of these three main realizations of the network.
Figure 3.
(a) Amplified negative feedback topology, with repression by transcriptional control. Gene A activates its own transcription and that of gene B, while B represses transcription from A. (b) In vivo implementation. Details provided in the main text. (c) ODE model equations for the in vivo implementation. xi represent concentrations of network components (normalized with respect to their steady-state values), odd and even numbered variables describe mRNA and protein concentrations, respectively. The model comprises six ODEs, two describing the reporter LacZ. fi are tri-phasic transcriptional rates (see electronic supplementary material, §S3.2), while βi are constants describing numerous rates. (d) In vivo (squares) and simulation (solid lines) time series for the three-cycle implementation. β-Galactosidase is encoded by the lacZ reporter encoded as part of the lacYZA operon on the E. coli chromosome, but under the control of the oscillator. (e) In vivo and simulation time series for the four-cycle implementation. Figure (d) and (e) are adapted from Atkinson et al. (2003).
4.1. Case I: repression by transcriptional control
ODE models and Gillespie-based stochastic simulations of these networks have been presented in the literature (Atkinson et al. 2003; Guantes & Poyatos 2006; Conrad et al. 2008 (uses model from Guantes & Poyatos (2006)); figure 3c; electronic supplementary material, §S3.1).
4.1.1. Mathematical analysis
The analysis of the models proposed in the literature suggests two alternative bifurcation mechanisms to explain the presence of oscillations in the network. In Guantes & Poyatos (2006), the occurrence of oscillations is explained in terms of a saddle-node bifurcation on an invariant circle (SNIC), while under different parameter values Conrad et al. (2008) show oscillations can arise from either a SNIC or a subcritical Hopf bifurcation. Furthermore, in Atkinson et al. (2003), a Hopf bifurcation is also proposed as causing the onset of oscillatory behaviour. The discrepancies are presumably due to both model and parameter differences. However, in all cases, the bifurcation can occur because of significantly faster activator than repressor dynamics, either through faster activator degradation and translation rates (Guantes & Poyatos 2006; Conrad et al. 2008), or activator mRNA degradation rates (Atkinson et al. 2003). This has the effect of causing the activator concentration to reach a significant amplitude before the repressive effect gets too great (Guantes & Poyatos 2006), encouraging sustained oscillations. The Hopf bifurcation in Atkinson et al. (2003) can also arise through changes in activator and repressor cooperativity.
4.1.2. In silico experiments
The simulations reported in Guantes & Poyatos (2006) suggest that oscillations emerging from a SNIC do so at almost zero frequency, as the trajectories are still influenced by the slow trajectories of the region where the stable equilibrium was present before the bifurcation. This slow region corresponds to the saturated part of the repressor-response curve, where repressor concentration is little affected by small activator changes. This translates into oscillations with an extended region of high activator and repressor concentrations and therefore large periods (Guantes & Poyatos 2006). Immediately after the bifurcation, a further increase in the ratio of the activator to repressor degradation rates decreases the period rapidly, which quickly plateaus. Repression is via a homodimer, requiring a significant concentration to achieve strong repression, permitting relatively large amplitudes (Guantes & Poyatos 2006). Finally, while the Hopf bifurcations generate sinusoidal oscillations, the SNICs produce ‘relaxation’ oscillations, which rise sharply but decay slowly.
Undamped oscillations owing to the Hopf bifurcation in Atkinson et al. (2003) have been observed, although for biologically realistic parameters only damped oscillations were found (figure 3d). A period of 20 h was observed for a cell doubling time of 2 h, a considerably longer period than the three -gene repressilator. Period and amplitude were shown to depend on cell doubling time, and while halving the doubling time halved the period, it approximately doubled the amplitude (Atkinson et al. 2003). The suggestion from mathematical work that increasing activator cooperativity on its own transcription could shift dynamics towards an undamped regime was implemented by increasing activator gene copy number. Higher gene copy number leads to higher activator concentration, allowing the activator to get further along its sigmoidal activation curve, better realizing the cooperative dynamics manifested in the rapidly changing ‘switch’ section of the curve (Atkinson et al. 2003). Although undamped oscillations were still not obtained, the number of damped oscillations could be improved from three to four (figure 3e).
Gillespie simulations confirmed the presence of oscillations from the SNIC bifurcation in Guantes & Poyatos (2006), demonstrating weak stochastic coherence when the parameters are such that the network dynamics are close to the bifurcation point. By modifying transcription and translation rates such that the average number of mRNA molecules could be varied while keeping average protein levels unchanged, mRNA number could be seen to contribute significantly to noise and its effect on the regularity of oscillations. Specifically, the effect of the average mRNA number on regularity was comparable to the effect of the average number of all other molecules combined (Guantes & Poyatos 2006).
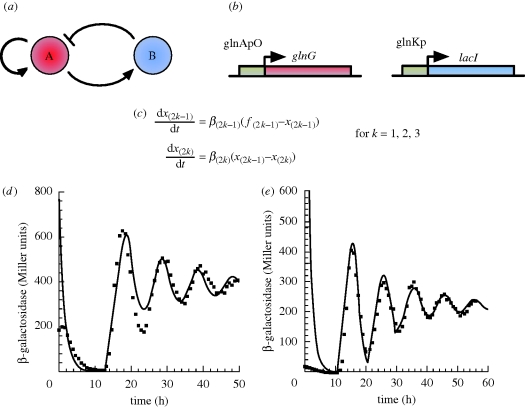
4.1.3. In vivo implementation
Only the Hopf-driven oscillator in Atkinson et al. (2003) has been implemented in vivo. The network consists of two modules, one encoding the activator, NRI, and the second encoding the repressor LacI. The activating module of the oscillator was constructed by fusing glnG, encoding NRI, to a control region based on a glnA promoter (glnAP2; figure 3b). The promoter was regulated by two upstream adjacent high-affinity binding sites for phosphorylated NRI (NRIp), which formed an ‘enhancer’, and two ‘perfect’ LacI operators, one downstream of the promoter, and one immediately upstream of the enhancer (Atkinson et al. 2003). The design intended to make use of DNA looping; during activation, NRIp interacts with promoter-bound RNA polymerase via a DNA loop, while during repression, LacI bound to the two operators also forms a loop, ensuring stable repression. The two loops act antagonistically, as formation of the loops is mutually exclusive (Atkinson et al. 2003). The repressor module was constructed by fusing lacI to a control region comprising the glnK promoter and an upstream enhancer formed of adjacent high-affinity and low-affinity NRIp binding sites (Atkinson et al. 2003). Consequently, the glnK promoter is only fully activated at high NRIp levels (Atkinson et al. 2003). The modules were incorporated into the E. coli chromosome as a single copy within regions flanked by transcription termination sequences, ensuring transcriptional isolation (Atkinson et al. 2003). E. coli were mutated such that the only LacI source was the repressor module, and mutant NRI phosphatase ensured NRI phosphorylation under all conditions (Atkinson et al. 2003). LacI dynamics were assayed on a population level with β-galactosidase encoded by lacZ present in the lacYZA operon (under the control of the oscillator) on the E. coli chromosome, and on a single-cell level using CFP fused to an LacI repressible promoter present as a single chromosomal copy (Atkinson et al. 2003).
In vivo dynamics of β-galactosidase closely matched modelling predictions both qualitatively and quantitatively. Initially, three damped oscillations were observed (figure 3d) as predicted by simulation. This could be increased to four (figure 3e) by moving the activator module next to the replication origin where copy numbers exist approximately fourfold higher than at the replication terminus (Atkinson et al. 2003), again, a prediction of simulations (Atkinson et al. 2003). Furthermore, amplitude and period were comparable between simulation and experiment, experiments also matching predicted effects of doubling time, controlled using growth media, on period and amplitude (Atkinson et al. 2003). Single-cell observations agreed with those at the population level, demonstrating damping is not due to individual cells oscillating out of phase (Atkinson et al. 2003). The percentage of oscillating cells was not reported, so it is not possible to assess robustness.
4.1.4. Discussion
Although only damped oscillations have been obtained in vivo, the significant agreement between simulations and experiment shows relatively simple models can capture both qualitative and quantitative behaviour. However, this quantitative agreement is only relevant at the population level and further analysis is required to ascertain the applicability of the model at a single-cell level. Such an analysis would also help define the role of noise, so far suggested by Guantes & Poyatos (2006) to be of little importance.
4.2. Case II: repression by sequestration
An alternative implementation of the amplified negative feedback oscillator is based on repression occurring through sequestration of proteins from the first gene, by dimerization with proteins from the second gene (figure 4a). This implementation was first considered in Barkai & Leibler (2000). ODEs have been used to study this network (Vilar et al. 2002; Hilborn & Erwin 2008; figure 4b; see electronic supplementary material, §S4.1, and §S4.2), SDEs (Hilborn & Erwin 2008; electronic supplementary material, §S4.3) and also Gillespie simulations (Barkai & Leibler 2000; Vilar et al. 2002; Steuer et al. 2003; Hilborn & Erwin 2008). The network has never been implemented in vivo.
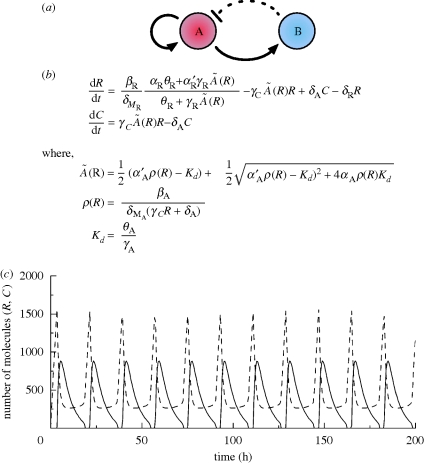
Figure 4.
(a) Amplified negative feedback topology, with repression by dimerization. This topology is identical to that of §4.1. However, rather than repression occurring at the level of transcription, repression occurs through sequestration of the protein encoded by the first gene, by dimerization with the protein encoded by the second gene. Solid lines represent direct transcriptional control, while the dotted line represents the repression by dimerization. (b) ODE model equations describing this network. R and C are the number of repressor molecules and activator–repressor complexes, respectively, Ã(R) is the quasi-equilibrium value of the number of activator molecules and MA and MR are the number of activator and repressor mRNAs, respectively. αi and αi′ are the basal and activated rates of transcription, βi the translation rates, δi the degradation rates, γi and θi the rates of binding and unbinding, respectively, of A to other components. (c) In silico simulation of the ODEs. Solid lines and dashed lines represent R and C, respectively. Figure (c) adapted from Vilar et al. (2002). Copyright © National Academy of Sciences, USA.
4.2.1. Mathematical analysis
The existence of oscillations can be proved using the Poincaré–Bendixon theorem on a simplified model (figure 4b) describing only the evolution of the repressor and the activator–repressor complex. Such a model has been observed in silico to capture qualitatively the main features of a more complete model (reported in the electronic supplementary material, §S4.1; Vilar et al. 2002). Oscillatory behaviour was detected over a broad range of parameter values, suggesting robustness, but requires an intermediate repressor degradation rate (Vilar et al. 2002), a potential point of fragility.
4.2.2. In silico experiments
In addition to their importance in determining the existence of oscillations, deterministic and stochastic simulations highlighted the significant effect of the repressor degradation rate on the period of the oscillations; the lower the rate, the longer the period (Vilar et al. 2002). The amplitude of the oscillations was found to be sensitive to transcription and translation rates (Barkai & Leibler 2000). Period is predicted to be of the order of 20 h (Vilar et al. 2002), comparable to the Hopf-driven transcriptionally controlled network in Atkinson et al. (2003).
In addition to oscillations existing (figure 4c) over a broad parameter range, simulations suggested oscillations could exist even at very low average mRNA levels (Barkai & Leibler 2000; Vilar et al. 2002), oscillations persisting even when the number of mRNA molecules mainly alternates between zero and one (Vilar et al. 2002). This is in contrast to the sensitivity seen with transcriptional repression, and is a consequence of the fact that average protein levels appear to be the important factor in permitting oscillations, which can be maintained at low mRNA levels by increasing the translation rate (Vilar et al. 2002). A constructive role for noise is also apparent, with oscillations occurring over a wider range of parameter values in stochastic simulations than in deterministic simulations (Vilar et al. 2002; Hilborn & Erwin 2008). Furthermore, stochastic coherence is also a feature of the network, with maximum oscillation regularity being observed for an intermediate system size in Gillespie simulations (Steuer et al. 2003; Hilborn & Erwin 2008).
However, the details of the stochastic coherence are dependent on where noise exists. Under an SDE model the regularity of oscillations exhibits a very different dependence on noise subject to whether noise is added to activator or repressor concentrations (Hilborn & Erwin 2008). This dependence can probably be attributed to the difference in dynamics of the components (Hilborn & Erwin 2008). Strikingly, the ability to observe stochastic coherence at all in these simulations is dependent on the model used. Under Gillespie simulations of a reduced model (electronic supplementary material, §S4.2), using steady-state assumptions on fast variables, stochastic coherence is not observed, even though deterministic simulations of the full and reduced model are very similar (Hilborn & Erwin 2008). The model reduction has therefore obscured the stochastic coherence.
4.2.3. Discussion
The ability to function over a relatively broad parameter range confers a level of robustness to parameter fluctuations, suggesting an in vivo implementation may be successful. Period is comparable to repression by transcriptional control. However, in contrast, low mRNA levels appear to be less consequential, and noise plays a more significant role, expanding the oscillatory parameter region, and generating stochastic coherence. Finally, it is worth emphasizing that low-dimensional approximate models can indeed yield information on whether a network can oscillate, but might fail to capture more subtle features of the system of interest such as stochastic coherence.
4.3. Case III: repression by proteolysis
A third implementation of the amplified negative feedback topology where repression is obtained by degradation of the protein from the first gene by a protease encoded by the second gene was studied by Guantes & Poyatos (2006) and Conrad et al. (2008) (figure 5a). The network has been studied using ODEs (Guantes & Poyatos 2006; figure 5b; Conrad et al. 2008; uses the same model as Guantes & Poyatos (2006)) and Gillespie simulations (Guantes & Poyatos 2006), but never implemented in vivo.
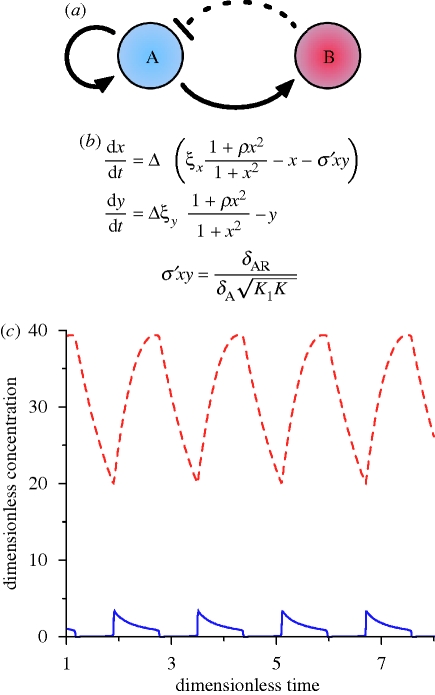
Figure 5.
(a) Amplified negative feedback topology, with repression by proteolysis. This topology is identical to that of §4.1 and 4.2. However, repression is instead by degradation of the protein encoded by the first gene by a protease encoded by the second gene. Solid lines represent direct transcriptional control, while the dotted line represents the repression by proteolysis. (b) ODE model equations describing this network. x and y are dimensionless concentrations of A and B, respectively. All other parameters are identical to those defined for electronic supplementary material, §S3.1. Repression by protease action is captured by the term σ′xy. (c) In silico simulation of the ODEs. The blue solid line and red dashed line correspond to x and y, respectively. Figure (c) adapted from Guantes & Poyatos (2006).
4.3.1. Mathematical analysis
Oscillations in Guantes & Poyatos (2006) were found to arise through a subcritical Hopf bifurcation, requiring the activator to have significantly faster dynamics than the repressor, achieved by considerably faster activator degradation and translation rates. This is a requirement in common with repression by transcriptional control. The existence of a subcritical Hopf bifurcation was confirmed by Conrad et al. (2008) who also demonstrated, as with the transcriptionally repressed oscillator, that oscillations could additionally arise through a SNIC. Oscillations exist for a significant range of values of the ratio between the activator and repressor degradation rates (Guantes & Poyatos 2006).
4.3.2. In silico experiments
Under the Hopf bifurcation, oscillations appear possessing a finite frequency, which increases as activator dynamics become increasingly faster than repressor dynamics. Frequency reaches a plateau approximately fourfold higher than oscillations generated by the transcriptionally repressed SNIC-driven oscillations (§4.1.2). In addition to existing for a significant variation of the activator to repressor degradation rate, oscillations are observed for a larger parameter range than for the SNIC-driven oscillations (Guantes & Poyatos 2006). This suggests a certain level of robustness to parameter variations. The subcritical nature of the bifurcation can also permit damped oscillations for a brief window in the degradation ratio (Guantes & Poyatos 2006). Repression in the transcriptionally repressed SNIC-driven oscillator occurs with homodimers, whereas repression here occurs via monomeric proteases. As such, the required level of repression is reached much sooner, resulting in significantly lower activator amplitudes (figure 5c; Guantes & Poyatos 2006).
Stochastic coherence is observed under Gillespie simulations, and is notably stronger than in the transcriptionally repressed SNIC oscillator (Guantes & Poyatos 2006). However, as for that oscillator, the mRNA number contributes significantly to noise and its effect on oscillation regularity (Guantes & Poyatos 2006).
4.3.3. Discussion
The subtle change from nonlinear transcriptional repression via homodimers, to linear repression via monomeric proteases, can produce an oscillator with higher frequency, lower amplitude oscillations and stronger stochastic coherence. This is a clear demonstration of how relatively small changes in the repression mechanism can actually have large effects on dynamics, and therefore function.
4.4. Remarks
The amplified negative feedback oscillators discussed so far do not demonstrate sustained oscillations in vivo, or demonstrably robust dynamics. However, they are valuable for their ability to inform on the relationship between topology and dynamics. Three of the four networks described here require the same condition for bifurcation, significantly faster activator than repressor dynamics. However, despite this commonality, they display a wide range of bifurcation mechanisms. The period of the oscillations is comparable between the Hopf-driven transcriptionally repressed oscillator in Atkinson et al. (2003) and the dimerization repressed oscillator. However, the period of the oscillations exhibited by the proteolytically repressed oscillator driven by the subcritical Hopf is instead approximately four times shorter than the SNIC-driven transcriptionally controlled oscillator.
5. Fussenegger oscillators
The requirement of relatively faster activator than repressor dynamics for oscillations is present in three out of the four oscillator topologies based on amplified negative feedback discussed so far. This has the same effect as that of adding a delay in the negative feedback loop. Both allow the activator concentration to reach a significant level before repression becomes too great, encouraging sustained oscillations. It is therefore expected that increasing the delay in the negative feedback loop may increase the likelihood of observing undamped oscillations in vivo, as opposed to the damped oscillations obtained in vivo for the amplified negative feedback oscillators reviewed so far.
This is precisely the idea behind the oscillators presented in Tigges et al. (2009, 2010) that we shall refer to, for the sake of brevity, as the Fussenegger oscillators. The Fussenegger oscillators are the only oscillators to have been implemented in a eukaryotic system. This is an important step towards using eukaryotic cells as hosts for more complex networks and for exploiting the powerful but often subtle regulatory mechanisms they possess. The original Fussenegger oscillator (Tigges et al. 2009) comprises two genes, with both sense and antisense transcription occurring from one of them. The sense transcript is translated, the resulting protein feeding back to itself by promoting transcription, and also activating the second gene. In a first for a synthetic genetic network, this second gene activates antisense transcription from the first gene, the transcript not translated, instead hybridizing with the sense transcript, repressing sense protein production at translation. This completes a negative feedback loop (figure 6a). The Fussenegger oscillator is therefore an amplified negative feedback oscillator (figure 6b). However, importantly, in comparison to the previous negative feedback oscillators, it contains an additional step in the negative feedback loop that ‘delays’ the repressive effect.
Figure 6.
(a) Fussenegger oscillator topology. A promotes its own transcription, while also activating gene C. C promotes transcription of B (antisense A), which, through hybridization, represses A at the level of translation. B is represented by a square to signify that it is an RNA not a protein. Solid lines represent direct transcriptional control, while the dotted line represents the repression by sense–antisense hybridization. (b) The Fussenegger oscillator topology in (a) is an example of an amplified negative feedback topology; the combination of the link from C to B and B to A effectively forms one repressive link from C to A. (c) In vivo implementation. Details provided in the main text. (d) ODE model equations for the in vivo implementation are given in electronic supplementary material, §S5. (e) In silico simulation of ODEs for (1:1:1) plasmid ratios and no antibiotics. The black and blue lines are tTA and PIT, respectively, while the dashed and solid green lines are unfolded and active GFP, respectively. These are the results of an initial qualitative model, intended to demonstrate the capacity for oscillations. The timescale does not agree with the final model or the in vivo results. (f) Single-cell fluorescence trajectory, equimolar plasmid ratios (100 ng each), no antibiotics. Figure (e) and (f) are adapted from Tigges et al. (2009).
The biological implementation of the Fussenegger oscillator was modelled using ODEs (electronic supplementary material, §S5) and Gillespie simulations (modified τ-leap). Models considered the potential interactions of RNA polymerases transcribing sense and antisense strands simultaneously, a significant consequence of the sense–antisense repression mechanism. The final model was obtained after rounds of improvement using extensive parameter estimation from in vivo data as detailed in Tigges et al. (2009), but so far no mathematical analysis of its dynamics or bifurcations have been presented.
5.1. In silico experiments
Simulations demonstrated the occurrence of oscillations robust to variations in mRNA and protein degradation rates, but highly sensitive to absolute and relative gene dosage (Tigges et al. 2009; figure 6e). Gene dosage also affected period and amplitude nonlinearly, exposing a potential method of tuning the oscillator. Further control was available by inhibiting activation by the sense protein, allowing oscillations to be switched on or off. Oscillations were insensitive to inhibition of antisense transcription.
Stochastic simulations showed significant variability at low gene levels, while at high gene levels, low-amplitude oscillations not present in ODE simulations were observed, suggesting a constructive role for noise under certain conditions.
5.2. In vivo implementation
The sense–antisense construct used for the in vivo implementation comprised the gene encoding the tetracycline-dependent transactivator protein (tTA), controlled in the sense direction by the tTA activated promoter PhCMV*-1, forming the positive feedback loop. tTA also promoted production of pristinamycin-dependent transactivator protein (PIT) through PhCMV*-1. PIT promoted production of antisense tTA RNA through a PPIR promoter (figure 6c). Rapidly degraded GFP controlled by tTA through PhCMV*-1 reported on dynamics. Interactions between tTA and PhCMV*-1 could be inhibited by tetracycline, while the PIT–PPIR interaction could be inhibited by pristinamycin. The tTA, PIT and gfp genes were each placed on different plasmids, and introduced into Chinese hamster ovary (CHO-K1) cells (Tigges et al. 2009).
Undamped oscillations were observed with periods of 170 ± 71 (mean ± s.d.) min (Tigges et al. 2009; figure 6f), confirming the effectiveness of considering a delay in the negative feedback. However, the fact that the implementation is eukaryotic may also play a yet undetermined role. Significant cell–cell variability was also observed, as predicted by stochastic simulations. The sensitive and nonlinear relationship between period and amplitude, and relative gene dosage, also matched predictions by simulations, demonstrating that network output can be predictably tuned. Further in accordance with simulations, inhibition by tetracycline of transcriptional activation by the sense protein could abolish oscillations. However, in contrast to simulations, inhibition of antisense transcription by pristinamycin also had a marked effect, fluorescence continually growing rather than oscillating.
A ‘low-frequency’ variant of the Fussenegger oscillator has recently been constructed (Tigges et al. 2010) using direct interference by siRNAs in place of the indirect repression by production of an antisense mRNA. Although a step in repression has been removed, the time delay for the repressive process is still adequate to support sustained oscillations. The oscillations possess a period of approximately 26 h, the longest of any synthetic oscillator. In contrast to the tunability of the original Fussenegger oscillator, and in agreement with theoretical predictions, the period is insensitive to relative plasmid dosages. However, the oscillator is not robust, at most only approximately 18 per cent of cells exhibiting oscillations.
5.3. Discussion
In contrast to the damped oscillations displayed in the previous amplified negative feedback in vivo implementation (Atkinson et al. 2003), the Fussenegger oscillator and the recent low-frequency variant produce sustained, undamped oscillations, probably owing to the additional time delay in the negative feedback loop. They are the only eukaryotic synthetic oscillators to date, and the first to incorporate sense–antisense and siRNA-mediated regulation, potential mechanisms available for exploitation by synthetic biologists. The results provide an insight into the non-intuitive relationship between gene dosage and dynamics, and suggest that this can be used to fine-tune network output. In both implementations, a full mathematical study would help link the underlying mechanisms, together with the implications for time delay of a eukaryotic implementation, to the behaviour observed. This would provide a valuable and experimentally verified first insight into the dynamics of eukaryotic oscillators.
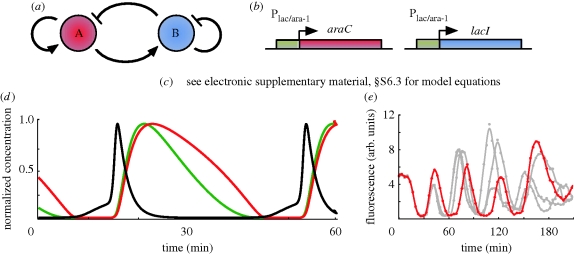
6. Smolen oscillator
None of the preceding oscillators are demonstrably robust. In particular, the percentage of oscillating cells is either low, or not reported. However, robustness is vital if synthetic oscillators are to become components of larger synthetic systems, or interface with and regulate natural systems (Lu et al. 2009).
The Smolen oscillator2 (Smolen et al. 1998) comprises two genes (figure 7a). The first gene (gene A) promotes its own transcription and that of the other gene, while the second gene (gene B) represses its own transcription and that of the first gene. The self-repression loop acting on the second gene is the extra link that differentiates the topology of this oscillator from the amplified negative feedback oscillators (§4). Different types of models have been proposed to characterize the dynamics of the Smolen oscillator. In particular, ODE models can be found in Smolen et al. (1998) (electronic supplementary material, §S6.2), Hasty et al. (2002) (electronic supplementary material, §S6.1) and Stricker et al. (2008) (electronic supplementary material, §S6.3), this latter model being far more detailed and higher dimensional than the previous two. DDE models were also proposed in Smolen et al. (1998, 1999) (electronic supplementary material, §S6.4); Smolen et al. (1999) also considering a spatial component. Finally, SDE-based models were discussed in Wang et al. (2005b; electronic supplementary material, §S6.5) and Gillespie simulations were used to study the oscillator dynamics (Wang et al. 2005b; Stricker et al. 2008).
Figure 7.
(a) Smolen oscillator topology. Gene A activates its own transcription and that of gene B, while gene B represses its own transcription and that of gene A. (b) In vivo implementation. Details provided in the main text. (c) ODE model equations for the in vivo implementation are given in electronic supplementary material, §S6.3. (d) In silico simulation of ODEs for 0.7% arabinose and 2 mM IPTG. There red and green lines are LacI tetramers and AraC dimers, respectively. The black line is LacI mRNA. (e) Single-cell fluorescence trajectories, with 0.7% arabinose and 2 mM IPTG. Figure (d) and (e) are adapted from Stricker et al. (2008).
6.1. Mathematical analysis
Oscillations were first demonstrated mathematically using a simple model and shown to arise from either a supercritical or subcritical Hopf bifurcation (Hasty et al. 2002). It was shown that such a bifurcation is more likely to occur when the activator degradation rate is two or three times faster than that of the repressor. A similar requirement was also suggested for amplified negative feedback oscillators and might be due to the similarity between the topologies. The existence of a subcritical Hopf bifurcation is dependent on the degree to which the activator promotes the transcription of the activator and repressor genes upon binding to a specific site. Its occurrence yields narrow regions in parameter space where the coexistence of oscillations and a stable equilibrium state is detected (see Hasty et al. (2002) for further details).
More complex dynamical behaviour was detected in more recent work. For example, using a higher dimensional, detailed model allied to experiments (§6.3), it was shown that two limit cycles can exist simultaneously (Stricker et al. 2008). Specifically, a long-period limit cycle at low arabinose (an enhancer of activating links) levels can coexist with a limit cycle characterized by a smaller period with a very small basin of attraction. As the arabinose level increases, this latter limit cycle coalesces onto a stable equilibrium via a Hopf bifurcation, resulting in the presence of damped oscillations whose basin of attraction expands for increasing arabinose concentration (Stricker et al. 2008).
6.2. In silico experiments
All the ODE models studied in the literature predicted the existence of oscillations with periods of approximately 40 min (Smolen et al. 1998; Stricker et al. 2008; figure 7d). Such a period is far shorter than the period of oscillations detected in the Hopf-driven transcriptionally controlled amplified negative feedback oscillator in Atkinson et al. (2003) or the Fussenegger oscillators. Relative amplitudes of the activator and the repressor differ between models (Smolen et al. 1998; Stricker et al. 2008), although Gillespie simulations (Stricker et al. 2008) agree with the earlier ODE model in Smolen et al. (1998), suggesting activators achieve a significantly higher concentration. This is a characteristic of the Smolen oscillator shared with the SNIC-driven transcriptionally controlled amplified negative feedback oscillator.
The effects of time delays have also been considered in the literature. Namely, it was shown that the inclusion of delays in the models of greater than 2 h, accounting for transcription factor diffusion, eliminated oscillations observed in Smolen et al. (1998), but created a new stable (delay-induced) limit cycle with a period of the same order as the delay (Smolen et al. 1999). Also, when spatial diffusion models for mRNA were considered, oscillations were made to disappear by a narrow region of low diffusivity representing a nuclear membrane (Smolen et al. 1999). Conversely, effectively increasing delay by decreasing reaction rates in the detailed model increased the region in parameter space associated to oscillatory behaviour and hence increased robustness to parameter variations (Stricker et al. 2008). It is clear that the effects of delay are not yet fully understood.
A certain degree of tunability of the oscillation period was observed. In particular, IPTG that inhibits repressive links or arabinose that enhances activating links had differing effects on period in the detailed ODE model (Stricker et al. 2008). At low concentrations, period rapidly increases for increasing IPTG concentration to a peak, after which it decreases as IPTG concentration increases further, while period increases monotonically to a plateau for increasing arabinose (Stricker et al. 2008). Using a parameter relating E. coli cell cycle time to temperature in place of the Arrhenius constant, period was observed to decrease almost linearly for increasing temperature (Stricker et al. 2008). In general, oscillations appear to be tunable over a wide range of conditions (Stricker et al. 2008), and could possibly be tuned over a still greater range by using one or more of these tuning parameters in conjunction.
The simultaneous existence of a long-period limit cycle and a stable equilibrium with damped oscillations (§6.1) manifests itself as a bimodal distribution of period lengths in Gillespie simulations (Stricker et al. 2008). The majority of oscillations correspond to the long-period limit cycle, far fewer small-amplitude oscillations occurring by noise-induced incursions into the basin of attraction of the stable equilibria (Stricker et al. 2008). As the basin of attraction expands, the number of small-amplitude oscillations increases (Stricker et al. 2008). This is a novel behaviour, directly attributable to noise.
Surprisingly, oscillations have higher regularity when the Goodwin oscillator subnetwork itself (B with its self-repressing feedback only) generates weak, low-amplitude oscillations with the repressor not reaching zero (Mather et al. 2009), rather than more regular oscillations that reach zero (Stricker et al. 2008). This finding is undoubtedly a consequence of the nonlinearity of genetic networks, and highlights the potential pitfalls of taking a modular approach to gene network design.
Stochastic coherence has so far only been observed in the simple model (Wang et al. 2005b). By positioning the Chemical Langevin Equation (CLE) and Gillespie representations of the model (Hasty et al. 2002) close to the subcritical Hopf bifurcation, a peak in the signal-to-noise ratio for oscillations occurs for an intermediate system size (Wang et al. 2005b).
6.3. In vivo implementation
In vivo construction (figure 7b) based on the detailed model used the hybrid promoter Plac/ara-1 (Lutz & Bujard 1997) that contained two adjacent AraC binding sites upstream of the promoter (at a position from which bound AraC will activate transcription) and three LacI operators (two upstream of the promoter and one downstream; Stricker et al. 2008). Plac/ara-1 is activated by AraC in the presence of arabinose and repressed by LacI. Repression can be inhibited by IPTG (Stricker et al. 2008). The araC and lacI genes were each placed independently under the control of Plac/ara-1 promoters. yemGFP, also under the control of Plac/ara-1, reported on dynamics. All proteins contained ssrA tags, promoting rapid degradation. The activator and repressor genes were placed on separate plasmids and transformed into E. coli deficient in araC and lacI, minimizing host genome interference (Stricker et al. 2008).
Over 99 per cent of cells displayed oscillations, with a period of approximately 40 min (Stricker et al. 2008; figure 7e), in accordance with simulations, and a clear demonstration of robustness. Oscillatory state was transmitted to progeny and synchrony lost after a few periods (Stricker et al. 2008). In agreement with theoretical results, oscillations were highly tunable, oscillating over a wide range of IPTG and arabinose concentrations, temperatures and media sources, allowing period tuning between 13–58 min (Stricker et al. 2008). Modelling also closely captured the effects of arabinose and IPTG on period, and accurately predicted the relationship between temperature and period, from 25°C to 37°C. However, individual cells showed an unexpected gradual increase in period, possibly owing to the dynamics of the reporter used. As with the three-gene repressilator, this was not accounted for in the model. Although cell doubling time in minimal media and Luria Broth differed by approximately 1 h, period lengths were comparable, demonstrating that dynamics are de-coupled from the cell cycle (Stricker et al. 2008). The bi-modality of period lengths predicted by Gillespie simulations has not yet been observed (Stricker et al. 2008), this novel behaviour remaining theoretical for the time being.
6.4. Discussion
The Smolen oscillator is robust and highly tunable, able to display periods over a fivefold range, down to a rapid 13 min. These are both characteristics observed in natural oscillators; robustness provides reliability, while tunability provides utility. This is encouraging for the future construction of synthetic oscillators. The rapidity of the oscillations appears to be due to the addition of a negative feedback loop to what would otherwise be an amplified negative feedback topology. It probably also contributes towards robustness and tunability. Predicted bi-modality is a novel and potentially desirable attribute that also appears to be tunable. If realized in vivo, this may expand the future applications of the oscillator. Studies on time delays are inconclusive, but the construction of the Fussenegger oscillators suggests a eukaryotic implementation may be successful.
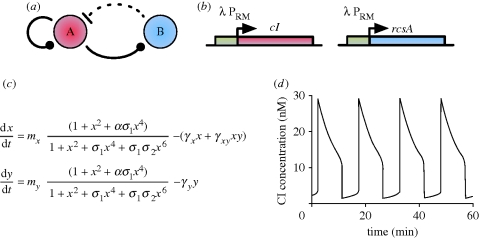
7. Variable link oscillators
A gene regulatory network is generally abstracted as a topology comprising a number of nodes connected by activating or repressing links. However, not all networks can be described in this way. For instance, the PRM promoter of the λ phage is controlled by cI at three operators: OR1, OR2 and OR3. Binding affinities are such that binding typically proceeds sequentially, OR1 before OR2, and OR2 before OR3 (Hasty et al. 2001a). Transcription is enhanced by cI binding to OR2, but repressed by binding to OR3; therefore, at low to medium cI concentrations, OR2 will be bound and transcription enhanced, while at high concentrations OR3 will also be bound, repressing transcription (Hasty et al. 2001a). The link formed by the regulation of this promoter is therefore variable.
This promoter has been used in an amplified negative feedback-like topology (figure 8a; Hasty et al. 2001a). The first gene regulates itself and a second gene, through the variable promoter, while repression by the second gene is via a protease acting on the product of the first gene. To study the network in silico, an ODE-based model was proposed in Hasty et al. (2001a) (figure 8c).
Figure 8.
(a) Variable link oscillator topology. At low concentrations of protein A, gene A promotes its own transcription and that of gene B, while at high A concentrations, A represses its own transcription and that of gene B. B is a protease and represses A by degradation. The variable links are denoted by a ball. Solid lines represent direct transcriptional control, while the dotted line represents the repression by proteolysis. (b) Possible in vivo implementation using the PRM promoter of the λ phage. Details provided in main text. (c) ODE model equations. x and y are dimensionless quantities of cI and RcsA, respectively, t is dimensionless time (see Hasty et al. (2001a) for details) and mi are the respective plasmid copy numbers. σi represents the relative affinities of cI dimer binding to OR1 relative to OR2 (σ1) and OR3 (σ3) binding. α is the degree to which transcription is enhanced by dimer occupation of OR2, while γx and γy capture degradation of cI and RcsA, respectively, and γxy represents the rate of cI degradation by RcsA. (d) In silico simulation of ODEs demonstrates oscillations. Figure (d) adapted from Hasty et al. (2001a).
The implementation relies on the fact that a single gene regulating itself through the variable promoter acts as a bi-stable switch (Hasty et al. 2001a), displaying hysteresis with respect to its degradation rate. The remainder of the topology exists to effectively move the degradation rate back and forward, pushing the system round the hysteric loop, generating oscillations. Oscillations are favoured with smaller protein degradation rates and lower protease activity (Hasty et al. 2001a). Gene copy number also plays a role (Hasty et al. 2001a).
Oscillations were found to exhibit periods of the order of tens of minutes via in silico simulations of the topology (figure 8d). This is comparable to the Smolen oscillator and significantly more rapid than either the Hopf-driven amplified negative feedback oscillator in Atkinson et al. (2003) or the Fussenegger oscillators. In addition to their importance in determining the existence of oscillations, degradation rates and gene copy number were also found to affect the period (Hasty et al. 2001a).
Although no in vivo implementation has yet been undertaken, it has been proposed that it might be possible to use the repressor cI as gene A, and the protease RcsA as gene B (Hasty et al. 2001a), both controlled by the PRM promoter (figure 8b).
In conclusion, simulations seem to suggest that the use of variable promoters in an amplified negative feedback topology will increase the frequency of oscillations, to a level comparable with that exhibited by the Smolen oscillator. A pressing open problem is the lack of an in vivo implementation of variable link oscillators. This is required to assess to what extent the in silico predictions can be matched in vivo, and to ascertain whether such an implementation can also match the robustness properties of the Smolen oscillator. The promoter structure discussed has also been used in another, more complex transcriptional level controlled oscillator reported in Wang et al. (2007).
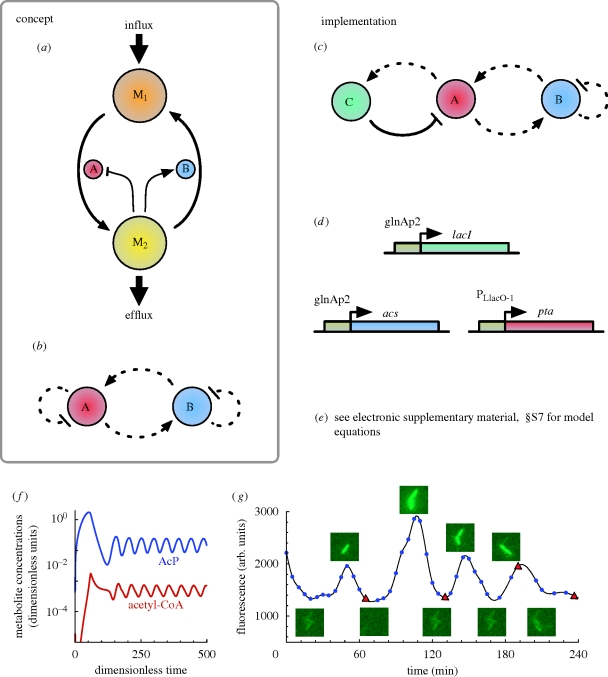
8. Metabolator
The metabolator (Fung et al. 2005) is the first oscillator to be reported in the literature that incorporates metabolites as a core component. Conceptually, it comprises two genes. One gene produces an enzyme that converts one metabolic pool (M2) to another (M1); its transcription being activated by M2. At the same time, the other gene produces an enzyme that converts M1 to M2; its transcription being repressed by M2. Additionally, there is an influx into M1, and an efflux from M2 (figure 9a). To facilitate comparison with other oscillators, the topology of the metabolator can be represented schematically as a gene regulatory network (figure 9b). Here, two genes, A and B, activate each other and are self-repressed by increasing/decreasing the metabolic pool M2. A particular implementation of this concept (figure 9c) was modelled with ODEs (electronic supplementary material, §S7) and CLEs, which explicitly represent a GFP reporter (Fung et al. 2005). All following discussion refers to this model.
Figure 9.
(a) Metabolite-centric conceptual view of the metabolator. Gene A produces an enzyme that converts one metabolic pool (M1) to another (M2), its transcription repressed by M2, while gene B produces an enzyme that converts M2 to M1, its transcription activated by M2. In addition, there is an influx into M1 and an efflux from M2. (b) Schematic GRN diagram. Gene A represses itself (as it increases the level of M2, which represses it), while promoting gene B (it is activated by M2). Gene B also effectively represses itself (as it decreases the level of M2, which activates it), while effectively activating gene A (as M2 represses gene A). (c) Implementation topology. Three genes were used in the implementation. The negative feedback link from gene A to itself via gene C, is equivalent to gene A repressing itself in (b). Solid lines represent direct transcriptional control, while the dotted lines represent indirect repression. (d) In vivo implementation. Details are provided in the main text. (e) ODE model equations for the in vivo implementation are given in electronic supplementary material, §S7. (f) In silico simulation of ODEs with a relatively high glycolytic flux. (g) Single-cell fluorescence trajectories. Figures (a), (f) and (g) are adapted from Fung et al. (2005).
8.1. Mathematical analysis and in silico experiments
Mathematical analysis showed oscillations arise through a Hopf bifurcation, dependent on a number of factors. It was observed that a high-enough influx rate is essential for the presence of oscillations which can be instead suppressed by high M2 concentrations. Oscillations were also found to be sensitive to relative gene copy numbers. Simulations predicted the oscillation period to be approximately 40 min and confirmed the requirement of an adequate in flux rate (figure 9f), while CLE simulations, as per many of the other oscillators, showed the addition of noise created significant amplitude variation.
8.2. In vivo implementation
The E. coli acetate pathway was exploited for in vivo implementation. Acetyl coenzyme A (acetyl-CoA) was used as M1, and acetyl phosphate was used as M2. Acetyl-CoA is converted to acetyl phosphate by phosphate acetyltransferase (Pta), which corresponds to gene A in the network (figure 9c,d). Acetyl phosphate represses transcription indirectly: it results in the phosphorylation of Nitrogen Regulator I (NRI), which stimulates production of LacI by activating a glnAp2 promoter. LacI represses pta expression through promoter PLlacO-1 (Lutz & Bujard 1997). Acetyl-CoA synthetase (AcS—synthesises acetyl-CoA) served as gene B in the network (figure 9c,d). Its expression was also under the control of a glnAp2 promoter, and was thus upregulated by acetyl phosphate via NRI. Acetyl-CoA is a metabolic product of sugars, fatty acids and amino acids. Sugars present in growth media served as the influx to the network. Acetyl phosphate is converted to acetate by acetate kinase (AcK), and after protonation is permeable across the cell membrane, serving as the efflux. The lacI gene was incorporated into the E. coli chromosome in single copy, with pta and acs genes placed on a single plasmid. A reporter gene encoding GFP, under the control of LacI, was placed on a separate plasmid. All proteins contained ssrA tags, ensuring rapid degradation. E. coli contained non-functioning pta and lacI mutants, ensuring minimal host genome interference, and a glnL knockout, allowing phosphorylation of NRI by acetyl phosphate.
Oscillations were observed in approximately 60 per cent of cells, with a period of 45 ± 10 min (mean ± s.d.; figure 9g), of the order of in silico predictions, and lasted at least 4 h. As predicted by stochastic simulations, amplitudes varied significantly. Cell divisions appeared uncorrelated with oscillations, suggesting dynamics are de-coupled from the cell cycle.
In agreement with the mathematical analysis, influx rates from media containing glucose, fructose and mannose were high enough to support oscillations, while a lower rate from glycerol was not. Furthermore, addition of high concentrations of acetate, which maintains a high acetyl phosphate (M2) concentration through AcK, suppressed oscillations. Oscillations can therefore be easily controlled externally through metabolites. Natural accumulation of acetate also suppressed oscillations, suggesting removal could support longer term oscillations (Fung et al. 2005).
8.3. Discussion
Theoretical models of the metabolator account for in vivo observations, and dynamics can be predictably controlled by external metabolite sources. Sensitivity of oscillations to gene copy number, which will vary temporally, may account for the relatively low percentage of oscillating cells. Although a GRN representation has been proposed here, the metabolator naturally lends itself to a metabolite-centric representation (i.e. figure 9a; Fung et al. 2005). This raises the question of whether GRNs are always the most useful way of representing biological networks containing genes.
9. Conclusions
Synthetic genetic oscillators, both constructed in vivo and studied theoretically, have been reviewed and presented, where possible, in a coherent unified framework. A path has been taken from the early theoretical work of Goodwin, to the recent construction of the robust Smolen oscillator, and the more sophisticated Fussenegger oscillators. A summary of oscillator features can be found in tables 1 and 2, collating oscillators using solely transcriptional regulation and at least one non-transcriptional regulation mechanism, respectively.
Table 1.
A summary of the oscillators using soley transcriptional control. Period is recorded as mean ± s.d.; n.a., not applicable.
| name | gene number/total link number | link type | bifurcation mechanism | noise effects | in vivo implementation (oscillating cell percentage) | oscillation characteristics | robust aspects | tunable aspects | key reference(s) |
|---|---|---|---|---|---|---|---|---|---|
| repressilator | N/N | N negative | Hopf | significant amplitude variation. Enlarged oscillatory parameter range. Stochastic (phase) coherence. | 3 gene. prokaryotic (approx 40%) | period: 160 ± 40 min. Significant amplitude variation | dynamics decoupled from cell cycle | dynamics coupled to global regulation of cell growth | Elowitz & Leibler (2000), Müller et al. (2006) and Strelkowa & Barahona (2010) |
| Goodwin | 1/1 | 1 negative | Hopf | enlarged oscillatory parameter region | prokaryotic (n.a.) | period: ∼30 mins. Irregular. Rarely reach zero | period resistant to IPTG conc. | n.a. | Stricker et al. (2008) and Müller et al. (2006) |
| Amp. Neg. F.Back. Transc. | 2/3 | 2 positive, 1 negative | Hopf/sub-Hopf or SNIC | weak stochastic coherence for SNIC driven oscillator | prokaryotic (n.a.) | oscillations damped. Period: 10/20 h | n.a. | period and amplitude via cell doubling | Atkinson et al. (2003) and Guantes & Poyatos (2006) |
| Smolen | 2/4 | 2 positive, 2 negative | super/sub-Hopf, undefined for in vivo implementation model | bi-modal oscillations (in vivo implementation). Stochastic coherence. | prokaryotic (>99%) | period: 13–58 min | decoupled from doubling time/cell cycle | period, by IPTG, arabinose and temperature | Stricker et al. (2008) |
| metabolator | 3/5 | 3 positive, 2 negative | Hopf | significant amplitude variation | prokaryotic (60%) | period: 45 ± 10 min. Lasted ∼4 h. Significant amplitude variation | decoupled from cell cycle | oscillations switched on/off by influx and efflux rates | Fung et al. (2005) |
Table 2.
A summary of the oscillators using a least one regulatory mechanism that does not act at the level of transcription. Period is recorded as mean ± s.d.; n.a., not applicable.
| name | gene number/total link number | link type | bifurcation mechanism | noise effects | in vivo implementation (oscillating cell percentage) | oscillation characteristics | robust aspects | tunable aspects | key reference(s) |
|---|---|---|---|---|---|---|---|---|---|
| Fussenegger | 2/4 | 3 positive, 1 negative | n.a. | significant variability at low gene dosage, additional oscillations at high dosage | eukaryotic (n.a.) | period: 170 ± 71 min. Significant cell–cell variability | n.a. | period and amplitude via gene dosage | Tigges et al. (2009) |
| low-frequency Fussenegger | 2/3 | 2 positive, 1 negative | n.a. | n.a. | eukaryotic (∼18%) | period: 26 ± 8.5 h. Longest period of any synthetic oscillator | period insensitive to relative plasmid dosage | n.a. | Tigges et al. (2010) |
| Amp. Neg. F.Back. Dim. | 2/3 | 2 positive, 1 negative | loss of equilibrium stability | enlarged oscillatory parameter region. Stochastic coherence | no (-) | period: ∼20 h | oscillations possible at very low average mRNA levels | period by degradation rate. Amplitude by transcription/translation rate | Vilar et al. (2002) |
| Amp. Neg. F.Back. Prot. | 2/3 | 2 positive, 1 negative | sub-Hopf or SNIC | stochastic coherence | no (-) | higher frequency and lower amplitude than transc. repressed SNIC. Damped oscillations possible | larger oscillatory parameter region than with SNIC driven transc. controlled oscillator | period by relative degradation rates | Guantes & Poyatos (2006) and Conrad et al. (2008) |
| variable link | 2/3 | 2 variable, 1 negative | loss of equilibrium stability | n.a. | no (-) | period: tens of minutes | n.a. | period via degradation rates and gene dosage | Hasty et al. (2001a) |
Although outside the scope of this review, there is an increasing amount of investigation into coupled genetic oscillators. The focus has been on coupled repressilators (Garcia-Ojalvo et al. 2004; Ullner et al. 2007; Zhou et al. 2008), although coupling of other networks has also been studied (McMillen et al. 2002; Li et al. 2006). The analysis has almost exclusively been theoretical, but coupling has recently been used in vivo to generate a population of cells displaying synchronized oscillations (Danino et al. 2010).
Comparisons between oscillators are hindered by the fact that, despite the drive towards a standardized characterization of synthetic biological components and devices (The BioBricks Foundation, http://bbf.openwetware.org/), there currently exists no characterization standard for published synthetic oscillators. Reported characteristics vary significantly between oscillators in both type and detail, for instance, the percentage of oscillating cells, a vital measure of robustness, is only reported in approximately half of the in vivo implementations of the oscillators described in this paper.
In vivo implementations have almost exclusively been in prokaryotes, the eukaryotic Fussenegger oscillators being a recent exception. The prokaryotic systems exploited thus far are generally easy to manipulate and their mechanisms of gene regulation are generally simpler than those of eukaryotes. This relative simplicity means models are more likely to capture the systems essential features and hence be more predictive.
Oscillatory periods vary between 13 min and 26 h (Smolen and the low-frequency Fussenegger oscillator, respectively), a significant range. The reason for this variation is not yet clear, and period can be tuned through a number of different means in different oscillators. For instance, period is tuned by temperature, and small-molecule concentrations affecting transcription regulation, in the Smolen oscillator, and by relative plasmid dosage in the original Fussenegger oscillator. Noise is likely to also play a role in determining period. Amplitude can be tuned through similar means. In the original Fussenegger oscillator, this is again through relative plasmid dosage. In terms of reported oscillating cell percentages, only the Smolen oscillator can be termed robust.
Simulations suggest a dual role for intrinsic noise in dynamics. On the one hand, noise accounts for amplitude variations, but on the other, it enlarges oscillatory parameter regions, enhances access to regions of phase space and generates stochastic coherence. These constructive effects of noise will probably be exploited in future oscillators through copy number control. However, the ability to observe these effects in silico, in particular stochastic coherence, depends on the parameters and representation used. Stochastic coherence is abolished in the non-adiabatic regime of the repressilator, and by quasi-equilibrium assumptions in the dimerization-controlled amplified negative feedback oscillator. It should be noted that as of yet, there appears to have been no in vivo validation of stochastic coherence within genetic oscillators.
This review found that modelling has been significantly predictive and often in agreement with in vivo observations, but model parameters were often identified by heuristic procedures. Generally, simpler models have been used to determine the network potential for oscillations, with more detailed models subsequently being developed to obtain better qualitative and quantitative predictions of the network behaviour. Detailed models can also uncover more complex behaviour as, for instance, the coexistence of multiple limit cycles observed in the Smolen oscillator. However, where more complex behaviour has not yet been observed in vivo, it is important to check that such behaviours are not just an artefact of the increased model detail and the subsequent higher dimensionality, which might serve to distract from the main dynamical behaviour.
Surprisingly, not all models explicitly take into account the dynamics of the reporter, usually a fluorescent protein, as the means of assessing dynamics. For example, the models proposed for both the repressilator and the Smolen oscillator do not, and both show unexpected effects that might be explained by the reporter characteristics, specifically, the continually growing fluorescence of the repressilator, and the gradually increasing period of the Smolen oscillator.
Both mathematical analysis and in silico simulations confirmed that the most common source of oscillations is the presence of a Hopf bifurcation in the model, although other bifurcation scenarios, such as a saddle-node of limit cycles or homoclinic bifurcation, are also potential mechanisms. Despite the importance of these mechanisms, their implications are only marginally discussed in the literature. This is rather surprising as they can have dramatic effects on the dynamics exhibited by the oscillators. Good examples are the transcriptionally and proteolytically controlled amplified negative feedback oscillators where in both cases oscillations can be generated either through a SNIC or a subcritical Hopf bifurcation (Guantes & Poyatos 2006; Conrad et al. 2008). In the transcriptionally repressed oscillator, the SNIC leads to oscillations with arbitrarily low frequencies and large periods, while in the proteolytically repressed oscillator, the subcritical Hopf bifurcation yields higher frequencies and damped oscillations. Differences are further apparent when responses to external stimuli are considered. In both oscillators, the SNIC causes the respective oscillator to act as an integrator of signals, while the subcritical Hopf bifurcation causes it to act as a frequency-sensitive resonator, both behaviours directly attributable to the underlying bifurcation mechanism (Guantes & Poyatos 2006; Conrad et al. 2008).
There is an interesting relationship between topology and dynamics. Although bifurcation mechanisms varied significantly across the amplified negative feedback implementations, the bifurcation requirement of a significant difference in the speed of activator and repressor dynamics was well conserved. This requirement even extended through to the Smolen oscillator, presumably owing to the similarity between the two topologies. Previous studies demonstrated correlation between topology and the frequency–amplitude relationship of oscillators (Tsai et al. 2008). Together with the findings here, it appears that correlations between topology and dynamics exist within certain levels of classification, and over certain ranges of topologies.
Time delay has both constructive and destructive effects. In the Goodwin oscillator, it increases the oscillatory parameter space, but also reduces regularity, while under one representation of the Smolen oscillator, it probably increases robustness, yet under another oscillations are abolished when it is too great, or in a manner representing a nuclear membrane. However, increased time delay is the likely reason why the Fussenegger oscillators display undamped oscillations while the earlier amplified negative feedback implementation does not.
Even in light of the apparent robustness of the Smolen oscillator, robustness is still a significant issue for synthetic oscillators. Although current oscillators generally appear decoupled from the cell cycle, networks exist in cellular environments that are not fully characterized or understood. Interference from the host cell is likely, possibly accounting for the low percentages of oscillating cells reported. The halting of oscillations in the three-gene repressilator by entry into the stationary phase is an indication of such interference (Elowitz & Leibler 2000). With the exception of the Fussenegger oscillators, all in vivo implementations used mutation or removal of particular host genes to mitigate against interference. However, as networks become larger, the number of potentially interfering host components will increase. Unknown components will form interactions and known components will form unknown interactions. Both of these are more likely in lesser characterized and larger eukaryotic systems into which networks will increasingly be placed. These issues also extend to purely synthetic components. A measure of how likely network function is to be compromised if subjected to reasonable levels of host cell interactions is required. In this direction, two empirical rules have been developed for the repressilator (Goh et al. 2008). Generally, non-specific interactions forming coherent couplings (couplings preserving regulatory signs between nodes) are more likely to maintain oscillations than those forming incoherent couplings, and non-specific interactions having higher regulatory homogeny (a greater fraction of their interactions with the network positive or negative) are also more likely to preserve oscillations (Goh et al. 2008). Effects of the cell cycle, through changes in volume, component levels at division (Chen et al. 2004; Yoda et al. 2007) and levels of host cell components required for network function e.g. RNA polymerase and ribosomes (Tuttle et al. 2005), are also starting to be considered. Together, these should aid the design and implementation of new types of reliable, robust, tunable biological oscillators, and their incorporation into new synthetic genetic regulatory network designs.
Acknowledgements
We acknowledge funding from the UK EPSRC via the Bristol Centre for Complexity Sciences. We thank Matthew R. Bennett for providing model details.
Footnotes
This was one of the first demonstrations of a constructive role for noise in GRN dynamics.
This is sometimes referred to as the Hasty oscillator.
References
- Andrianantoandro E., Basu S., Karig D. K., Weiss R. 2006. Synthetic biology: new engineering rules for an emerging discipline. Mol. Syst. Biol. 2, 2006.0028 ( 10.1038/msb4100073) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atkinson M. R., Savageau M. A., Myers J. T., Ninfa A. J. 2003. Development of genetic circuitry exhibiting toggle switch or oscillatory behavior in Escherichia coli. Cell 113, 597–607. ( 10.1016/S0092-8674(03)00346-5) [DOI] [PubMed] [Google Scholar]
- Banks H. T., Mahaffy J. M. 1978a Global asymptotic stability of certain models for protein synthesis and repression. Q. Appl. Math. 36, 209–221. [Google Scholar]
- Banks H. T., Mahaffy J. M. 1978b Stability of cyclic gene models for systems involving repression. J. Theor. Biol. 74, 332–334. [DOI] [PubMed] [Google Scholar]
- Barkai N., Leibler S. 2000. Circadian clocks limited by noise. Nature 403, 267–268. ( 10.1038/35002258) [DOI] [PubMed] [Google Scholar]
- Becskei A., Serrano L. 2000. Engineering stability in gene networks by autoregulation. Nature 405, 590–593. ( 10.1038/35014651) [DOI] [PubMed] [Google Scholar]
- Bratsun D., Volfson D., Tsimring L. S., Hasty J. 2005. Delay-induced stochastic oscillations in gene regulation. Proc. Natl Acad. Sci. USA 102, 14 593–14 598. ( 10.1073/pnas.0503858102) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L., Wang R., Kobayashi T. J., Aihara K. 2004. Dynamics of gene regulatory networks with cell division cycle. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 70, 011909 ( 10.1103/PhysRevE.70.011909) [DOI] [PubMed] [Google Scholar]
- Conrad E., Mayo A. E., Ninfa A. J., Forger D. B. 2008. Rate constants rather than biochemical mechanism determine behaviour of genetic clocks. J. R. Soc. Interface 5, S9–S15. ( 10.1098/rsif.2008.0046.focus) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danino T., Mondragón-Palomino O., Tsimring L., Hasty J. 2010. A synchronized quorum of genetic clocks. Nature 463, 326–330. ( 10.1038/nature08753) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elowitz M. B., Leibler S. 2000. A synthetic oscillatory network of transcriptional regulators. Nature 403, 335–338. ( 10.1038/35002125) [DOI] [PubMed] [Google Scholar]
- El-Samad H., Vecchio D. D., Khammash M. 2005. Repressilators and promotilators: loop dynamics in gene regulatory networks. Proc. Am. Control Conf., Portland, OR, 8–10 June 2005, pp. 4405–4410. NJ: IEEE. ( 10.1109/ACC.2005.1470689) [DOI] [Google Scholar]
- Endy D. 2005. Foundations for engineering biology. Nature 438, 449–453. ( 10.1038/nature04342) [DOI] [PubMed] [Google Scholar]
- Fraser A., Tiwari J. 1974. Genetical feedback-repression II. Cyclic genetic systems. J. Theor. Biol. 47, 397–412. [DOI] [PubMed] [Google Scholar]
- Fung E., Wong W. W., Suen J. K., Bulter T., Gu Lee S., Liao J. C. 2005. A synthetic gene-metabolic oscillator. Nature 435, 118–122. ( 10.1038/nature03508) [DOI] [PubMed] [Google Scholar]
- Garcia-Ojalvo J., Elowitz M. B., Strogatz S. H. 2004. Modeling a synthetic multicellular clock: repressilators coupled by quorum sensing. Proc. Natl Acad. Sci. USA 101, 10 955–10 960. ( 10.1073/pnas.0307095101) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner T. S., Cantor C. R., Collins J. J. 2000. Construction of a genetic toggle switch in Escherichia coli. Nature 403, 339–342. ( 10.1038/35002131) [DOI] [PubMed] [Google Scholar]
- Gillespie D. T. 2007. Stochastic simulation of chemical kinetics. Annu. Rev. Phys. Chem. 58, 35–55. ( 10.1146/annurev.physchem.58.032806.104637) [DOI] [PubMed] [Google Scholar]
- Goh K.-I., Kahng B., Cho K.-H. 2008. Sustained oscillations in extended genetic oscillatory systems. Biophys. J. 94, 4270–4276. ( 10.1529/biophysj.107.128017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodwin B. C. 1963. Temporal organization in cells. A dynamic theory of cellular control processes. London, UK: Academic Press. [Google Scholar]
- Guantes R., Poyatos J. F. 2006. Dynamical principles of two-component genetic oscillators. PLoS Comput. Biol. 2, e30 ( 10.1371/journal.pcbi.0020030) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haseloff J., Ajioka J. 2009. Synthetic biology: history, challenges and prospects. J. R. Soc. Interface 6, S389–S391. ( 10.1098/rsif.2009.0176.focus) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasty J., Isaacs F., Dolnik M., McMillen D., Collins J. J. 2001a Designer gene networks: towards fundamental cellular control. CHAOS 11, 207–220. ( 10.1016/j.jtbi.2008.03.012) [DOI] [PubMed] [Google Scholar]
- Hasty J., McMillen D., Isaacs F., Collins J. J. 2001b Computational studies of gene regulatory networks: in numero molecular biology. Nat. Rev. Genet. 2, 268–79. ( 10.1038/35066056) [DOI] [PubMed] [Google Scholar]
- Hasty J., Dolnik M., Rottschäfer V., Collins J. J. 2002. Synthetic gene network for entraining and amplifying cellular oscillations. Phys. Rev. Lett. 88, 148101 ( 10.1103/PhysRevLett.88.148101) [DOI] [PubMed] [Google Scholar]
- Hilborn R. C., Erwin J. D. 2008. Stochastic coherence in an oscillatory gene circuit model. J. Theor. Biol. 253, 349–354. ( 10.1016/j.jtbi.2008.03.012) [DOI] [PubMed] [Google Scholar]
- Lewis J. 2003. Autoinhibition with transcriptional delay: a simple mechanism for the zebrafish somitogenesis oscillator. Curr. Biol. 13, 1398–1408. ( 10.1016/S0960-9822(03)00534-7) [DOI] [PubMed] [Google Scholar]
- Li C., Chen L., Aihara K. 2006. Synchronization of coupled nonidentical genetic oscillators. Phys. Biol. 3, 37–44. ( 10.1088/1478-3975/3/1/004) [DOI] [PubMed] [Google Scholar]
- Lu T. K., Khalil A. S., Collins J. J. 2009. Next-generation synthetic gene networks. Nat. Biotechnol. 27, 1139–1150. ( 10.1038/nbt.1591) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lutz R., Bujard H. 1997. Independent and tight regulation of transcriptional units in Escherichia coli via the lacr/o, the tetr/o and arac/i1-i2 regulatory elements. Nucleic Acids Res. 25, 1203–1210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mallet-Paret J., Sell G. 1996. The Poincaré–Bendixon theorem for monotone cyclic feedback systems with delay. J. Diff. Eqns 125, 441–489. ( 10.1006/jdeq.1996.0037) [DOI] [Google Scholar]
- Mallet-Paret J., Smith H. L. 1990. The Poincaré–Bendixon theorem for monotone cyclic feedback systems. J. Dyn. Dif. Eqns 2, 367–421. ( 10.1007/BF01054041) [DOI] [Google Scholar]
- Mather W., Bennett M. R., Hasty J., Tsimring L. S. 2009. Delay-induced degrade-and-fire oscillations in small genetic circuits. Phys. Rev. Lett. 102, 068105 ( 10.1103/PhysRevLett.102.068105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMillen D., Kopell N., Hasty J., Collins J. J. 2002. Synchronizing genetic relaxation oscillators by intercell signaling. Proc. Natl Acad. Sci. USA 99, 679–684. ( 10.1073/pnas.022642299) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller S., Hofbauer J., Endler L., Flamm C., Widder S., Schuster P. 2006. A generalized model of the repressilator. J. Math. Biol. 53, 905–937. ( 10.1007/s00285-006-0035-9) [DOI] [PubMed] [Google Scholar]
- Novák B., Tyson J. J. 2008. Design principles of biochemical oscillators. Nat. Rev. Mol. Cell. Biol. 9, 981–991. ( 10.1038/nrm2530) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pasemann F. 1995. Characterization of periodic attractors in neural ring networks. Neural Netw. 8, 421–429. ( 10.1016/0893-6080(94)00085-Z) [DOI] [Google Scholar]
- Pittendrigh C. S., Caldarola P. C. 1973. General homeostasis of the frequency of circadian oscillations. Proc. Natl Acad. Sci. USA 70, 2697–2701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pomerening J. R., Kim S. Y., Ferrell J. E. 2005. Systems-level dissection of the cell-cycle oscillator: bypassing positive feedback produces damped oscillations. Cell 122, 565–578. ( 10.1016/j.cell.2005.06.016) [DOI] [PubMed] [Google Scholar]
- Rajala T., Hakkinen A., Healy S. Y.-H. O., Riberio A. S. 2010. Effects of transcriptional pausing on gene expression dynamics. PLoS Comput. Biol. 6, 1–12. ( 10.137/journal.pcbi.1000704) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruoff P., Rensing L. 1996. The temperature-compensated Goodwin model simulates many circadian clock properties. J. Theor. Biol. 179, 275–285. ( 10.1006/jtbi.1996.0067) [DOI] [Google Scholar]
- Serrano L. 2007. Synthetic biology: promises and challenges. Mol. Syst. Biol. 3, 158 ( 10.1038/msb4100202) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith H. 1987. Oscillations and multiple steady states in a cyclic gene model with repression. J. Math. Biol. 25, 169–190. ( 10.1007/BF00276388) [DOI] [PubMed] [Google Scholar]
- Smolen P., Baxter D. A., Byrne J. H. 1998. Frequency selectivity, multistability, and oscillations emerge from models of genetic regulatory systems. Am. J. Physiol. 274, C531–C542. [DOI] [PubMed] [Google Scholar]
- Smolen P., Baxter D. A., Byrne J. H. 1999. Effects of macromolecular transport and stochastic fluctuations on dynamics of genetic regulatory systems. Am. J. Physiol. 277, C777–C790. [DOI] [PubMed] [Google Scholar]
- Steuer R., Zhou C., Kurths J. 2003. Constructive effects of fluctuations in genetic and biochemical regulatory systems. BioSystems 72, 241–251. ( 10.1016/j.biosystems.2003.07.001) [DOI] [PubMed] [Google Scholar]
- Strelkowa N., Barahona M. 2010. Switchable genetic oscillator operating in quasi-stable mode. J. R. Soc. Interface 7, 1071–1082. ( 10.1098/rsif.2009.0487) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stricker J., Cookson S., Bennett M. R., Mather W. H., Tsimring L. S., Hasty J. 2008. A fast, robust and tunable synthetic gene oscillator. Nature 456, 516–519. ( 10.1038/nature07389) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tigges M., Marquez-Lago T. T., Stelling J., Fussenegger M. 2009. A tunable synthetic mammalian oscillator. Nature 457, 309–312. ( 10.1038/nature07616) [DOI] [PubMed] [Google Scholar]
- Tigges M., Dénervaud N., Greber D., Stelling J., Fussenegger M. 2010. A synthetic low-frequency mammalian oscillator. Nucleic Acids Res. 38, 2702–2711. ( 10.1093/nar/gkq121) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tiwari A. F. J., Beckman R. 1974. Genetical feedback repression I. Single locus models. J. Theor. Biol. 45, 311–326. ( 10.1016/0022-5193(74)90117-9) [DOI] [PubMed] [Google Scholar]
- Tsai T., Choi Y., Ma W., Pomerening J., Tang C., Ferrell J. E. 2008. Robust, tunable biological oscillations from interlinked positive and negative feedback loops. Science 321, 126–129. ( 10.1126/science.1156951) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuttle L., Salis H., Tomshine J., Kaznessis Y. 2005. Model-driven designs of an oscillating gene network. Biophys. J. 89, 3873–3883. ( 10.1529/biophysj.105.064204) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyson J. 1975. On the existence of oscillatory solutions in negative feedback cellular control processes. J. Math. Biol. 1, 311–315. ( 10.1007/BF00279849) [DOI] [Google Scholar]
- Tyson J. J., Albert R., Goldbeter A., Ruoff P., Sible J. 2008. Biological switches and clocks. J. R. Soc. Interface 5, S1–S8. ( 10.1098/rsif.2008.0179.focus) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ullner E., Zaikin A., Volkov E. I., García-Ojalvo J. 2007. Multistability and clustering in a population of synthetic genetic oscillators via phase-repulsive cell-to-cell communication. Phys. Rev. Lett. 99, 148103 ( 10.1103/PhysRevLett.99.148103) [DOI] [PubMed] [Google Scholar]
- Vilar J., Kueh H., Barkai N., Leibler S. 2002. Mechanisms of noise-resistance in genetic oscillators. Proc. Natl Acad. Sci. USA 99, 5988–5992. ( 10.1073/pnas.092133899) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang R., Jing Z., Chen L. 2005a Modelling periodic oscillation in gene regulatory networks by cyclic feedback systems. Bull. Math. Biol. 67, 339–367. ( 10.1016/j.bulm.2004.07.005) [DOI] [PubMed] [Google Scholar]
- Wang Z., Hou Z., Xin H. 2005b Internal noise stochastic resonance of synthetic gene network. Chem. Phys. Lett. 401, 307–311. ( 10.1016/j.cplett.2004.11.064) [DOI] [Google Scholar]
- Wang Z., Hou Z., Xin H., Zhang Z. 2007. Engineered internal noise stochastic resonator in gene network: a model study. Biophys. Chem. 125, 281–285. ( 10.1016/j.bpc.2006.09.006) [DOI] [PubMed] [Google Scholar]
- Yoda M., Ushikubo T., Inoue W., Sasai M. 2007. Roles of noise in single and coupled multiple genetic oscillators. J. Chem. Phys. 126, 115101 ( 10.1063/1.2539037) [DOI] [PubMed] [Google Scholar]
- Zhou T., Zhang J., Yuan Z., Chen L. 2008. Synchronization of genetic oscillators. CHAOS 18, 037126 ( 10.1063/1.2978183) [DOI] [PubMed] [Google Scholar]