Skip to main content
PMC home page
Journal of the Royal Society Interface logoLink to Journal of the Royal Society Interface
. 2010 Apr 28;7(53):1745–1752. doi: 10.1098/rsif.2010.0075

Extensive collection of femtolitre pad secretion droplets in the beetle Leptinotarsa decemlineata allows nanolitre microrheology

Bérengère Abou 1,*, Cyprien Gay 1, Bastien Laurent 1, Olivier Cardoso 1, Dagmar Voigt 2,3, Henrik Peisker 3, Stanislav Gorb 2,3
PMCID: PMC2988262  PMID: 20427331

Abstract

Pads of beetles are covered with long, deformable setae, each ending in a micrometric terminal plate coated with secretory fluid. It was recently shown that the layer of the pad secretion covering the terminal plates is responsible for the generation of strong attractive forces. However, less is known about the fluid itself because it is produced in an extremely small quantity. We present here the first experimental investigation of the rheological properties of the pad secretion in the Colorado potato beetle Leptinotarsa decemlineata (Coleoptera, Chrysomelidae). Because the secretion is produced in an extremely small amount at the level of the terminal plate, we first developed a procedure based on capillary effects to collect the secretion for rheological experiments. In order to study the collected fluid (less than 1 nl) through passive microrheology, we managed to incorporate micrometric probes (melamine beads) that were initially in the form of a dry powder. Finally, the bead thermal motions were observed optically and recorded to determine the mechanical properties of the surrounding medium. We achieved this quantitative measurement with the collected volume, which is much smaller than the usual 1 µl sample volume required for this technique. Surprisingly, the beetle secretion was found to behave as a purely viscous liquid, of high viscosity (about 100 times that of water). This suggests that no specific complex fluid behaviour is needed by this adhesive system during beetle locomotion. We describe a scenario for the contact formation between the spatula at the setal tip and a smooth substrate, during the insect walk. We show that the attachment dynamics of the insect pad computed from the high measured viscosity is in good agreement with the observed insect pace. We finally discuss the consequences of the viscosity of the secretion on the insect adhesion.

Keywords: adhesive secretion, insect, microrheology

1. Introduction

Among few other animal groups, insects possess a fascinating ability to walk on smooth vertical surfaces and even on ceilings. Such ability is robust, fault tolerant and resistant to contamination. Insects can stick well to both hydrophobic and hydrophilic surfaces and detach in a very fast manner. The comparative data show that the evolution of attachment mechanisms in insects has developed along two distinctly different mechanisms: smooth flexible pads and hairy (setose, fibrillar) surfaces (Beutel & Gorb 2001, 2006; Gorb 2001). In cockroaches, grasshoppers and bugs, the pads are soft deformable structures with a relatively smooth surface, whereas in flies, beetles and earwigs they are covered with long deformable setae. Because of the flexibility of the material in both mechanisms—soft attachment pads or fine surface microstructures—the possible contact area with the wide range of substrate profiles is maximized despite the surface roughness of the substrates, and the high proximity between contacting surfaces ensures strong attachment forces between the pads and the substrata.

Hairy attachment systems are typical for evolutionarily younger and successful insect groups, such as flies and beetles, and have a huge diversity of forms. There are several geometrical effects, such as multiple contact formation, high aspect ratio of single contact structures or peeling prevention using spatula-like tips of single contact elements, that are responsible for the generation of a strong pull-off force. These effects, which are found in attachment devices of insects, are an important source of information for further development of biomimetic patterned adhesives. One may speculate about the different physical mechanisms that are able to generate sufficient adhesion despite variation in the physico-chemical properties of the surface (hydrophobic, hydrophilic), surface profile (rough, smooth) and environmental condition (dry, wet). The theoretical background pertaining to these physical effects has been intensively theoretically discussed in several publications (Arzt et al. 2003; Persson 2003; Persson & Gorb 2003; Chung & Chaudhury 2005; Gao et al. 2005).

Even though hairy attachment systems have been under investigation for more than 300 years (Leeuwenhoek 1690), the attachment mechanism of animals walking on smooth walls or ceilings is still under debate. Different hypotheses for attachment, such as sticky fluid, microsuckers or the action of electrostatic forces, have been proposed (Dewitz 1884; Simmermacher 1884; Gillett & Wiggleswort 1932). It is now well known that hairy attachment pads of reduviid bugs (Edwards & Tarkanian 1970), flies (Bauchhenss 1979; Walker et al. 1985) and beetles (Ishii 1987; Kosaki & Yamaoka 1996; Eisner & Aneshansley 2000) secrete fluid into the contact area, whereas others, such as spiders or geckos, do not. Based on experimental data, adhesion has been recently attributed to molecular interactions and capillary attractive forces mediated by secretion (reduviid bugs, flies, beetles; Stork 1980) or van der Waals interactions (spiders, geckos; Autumn et al. 2000, 2002).

2. Motivation

In hairy wet attachment systems, the role of the secretion still remains unclear. It has already been shown that the presence of the fluid is required for generating adhesion in insect adhesive pads. For example, as shown in 1970, attachment was impaired when hairy pads of the bug Rhodnius prolixus were treated with organic solvents (Edwards & Tarkanian 1970). In 1980, experiments with beetles on various substrates also strongly suggested that cohesive forces, surface tension and molecular adhesion, mediated by pad secretion, may be involved in the mechanism of attachment (Stork 1980). It was inferred from experiments (Wallentin et al. 1999; Gorb 2001) that the secretion induces a viscous resistance to detachment of the pad from the substrate and a capillary attraction that applies both before and during detachment (static and dynamic processes). Later, on the scale of individual seta terminal plates, experiments conducted on the fly Calliphora vicina using multiple local force–volume atomic force microscopy (AFM) measurements indicated that the adhesion between the AFM tip and the seta (used to estimate the local seta adhesive properties) is approximately two times stronger in the centre of the terminal plate, where the thickness of the fluid is higher, than on its border (Langer et al. 2004): adhesion was shown to strongly decrease as the volume of the secretion decreases, indicating that a layer of pad secretion, covering the terminal plates, is crucial for generation of the strong attractive force.

However, by measuring the attachment forces on a smooth glass using a centrifuge technique, recent experiments demonstrated two apparently contradictory results (Dreschler & Federle 2006): (i) both friction and adhesion of insect pads on smooth surface are greater when less secretion is present and (ii) the adhesive force on rough substrates decreases when the pad secretion is depleted through multiple consecutive pull-off motions. From a physiological point of view, these results seem to indicate that the most important function of the secretion is to provide attachment on rough substrates. Indeed, most of the substrates encountered by insects are not smooth but rough. From a physical point of view, these results closely reproduce two complementary requirements well known for adhesive substances, whether natural or manufactured: they must (i) establish a good contact with the substrate even in the presence of surface roughness and (ii) resist separation, i.e. dissipate a significant amount of energy during separation (Gay & Leibler 1999).

The usual pressure-sensitive adhesive materials such as those included in adhesive tapes or stickers, which are solids, manage to establish a good contact (point (i)) as a result of their high deformability, as recognized by Dahlquist (1969) more than 40 years ago. A fortiori, a liquid secretion is suitable for establishing an intimate contact with a rough substrate and helps in maximizing the contact area.

Concerning the strong resistance during separation (point (ii)), it implies that the secretion is a very dissipative material, at least over the relevant time scale for the insect. But if the secretion deformation during separation dissipates energy, then it also does so during the reverse deformation, i.e. during contact formation. Thus, if dissipation is too high, the contact formation will not be completed within a time scale compatible with the insect walk. Hence, in the presence of a high dissipation, only indirect contact (mediated by the secretion fluid) will be achieved between the insect and the substrate: no good initial, solid contact will then be established and adhesion will tend to be weak. For this reason, it is crucial to determine the rheology of the secretory material to assess whether the insect can develop a good contact while walking. That issue is the central goal of the present work.

3. Known relevant secretion properties

Secretion is known to contain a non-volatile, lipid-like substance in diverse insects, but in some other groups, such as flies and ants, it is a two-phase microemulsion presumably containing water-soluble and lipid-soluble fractions (Gorb 2001; Federle et al. 2002; Vötsch et al. 2002). Concerning its mechanical properties, up to now, measurements were interpreted assuming that secretion was purely viscous. The secretion dissipation has been shown to be large, although a quantitative evaluation of its rheological properties could not be conducted because the exact geometries of the droplets, capillary bridges and contact areas were unknown (Wallentin et al. 1999; Langer et al. 2004). The dewetting velocity of ants' secretion droplets, observed through interference reflection microscopy, was interpreted in terms of viscosity and provided an estimate of 40–150 mPa s (Federle et al. 2002). In this experiment, because the dewetting velocity was constant, the mechanical properties of the material were probed at a fixed frequency, and no inference can be made about the response at other frequencies and hence about the possibly viscoelastic properties.

4. Our mechanical measurements

In the present paper, we quantitatively evaluate the rheological properties of the attachment pad secretion in the beetle L. decemlineata for the first time and we relate them to the attachment dynamics of the insect.

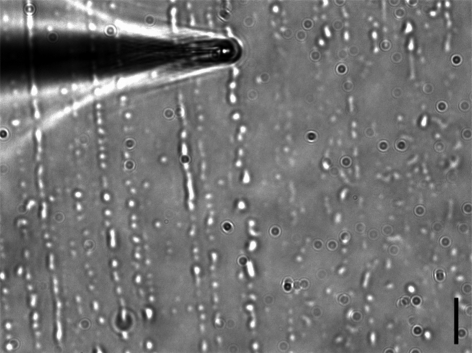
The essential difficulty of such a rheological measurement resides in the extremely tiny amount of secreted fluid: it totally excludes the use of standard rheology techniques, which require at least a few millilitres of material. Microrheology, by contrast, typically requires less than 1 µl of sample and is thus suitable for performing rheological measurements in situations where the available volume of material is a limiting factor. This issue is particularly significant for insect secretion: the typical volume of a secretory droplet of the Colorado potato beetle L. decemlineata, collected on a glass slide and shown in figure 1, is 1 µm3, which corresponds to 10−9 µl. At first sight, in order to obtain the required volume of 1 µl, it would be necessary to collect a discouragingly large number of droplets: typically 109 droplets! In the present work, as we shall see, we achieve a reliable microrheological measurement with a much smaller sample volume, namely 10−4 µl (0.1 nl).

Figure 1.

Figure 1.

Open in a new tab

Secretion droplets from adult beetles L. decemlineata on a glass slide. The beetles' legs are rubbed against the slide, which results in a strong shear that is able to deposit the secretion on the surface. The typical size of the droplets is a few microns. A home-made microneedle, mounted on a three-axis micromanipulator, was used to draw up the secretion droplets spread on the glass slide. The tip was moved onto the slide surface to collect the largest amount of secretion. Owing to capillary effects, the rise of the liquid takes place spontaneously inside the capillary tube. Scale bar, 10 µm.

The microrheology technique involves using micrometric beads to measure the relation between stress (probe force) and deformation (probe position) in materials, at the microscopic scale. The driving force applied on the probes is thermal, with an energy scale corresponding to kT. Measurements of the particles' mean-squared displacement (MSD) give access to the possibly viscoelastic properties of the fluid material. Because the driving force is small, only the linear viscoelastic response of the material is probed. From the stress–deformation relation, the viscoelastic properties of the surrounding medium can be derived (Mason & Weitz 2005; Waigh 2005).

In the following, we first propose a procedure to collect the secretion, in a sufficiently large amount, by using capillary effects taking place in a home-made microneedle. We then describe how micrometric probes were immersed in the collected volume, and their Brownian motion recorded. We then validate our measurements performed on the secretion (statistical accuracy and geometry) with additional tests in a calibrated Newtonian oil. We finally suggest a scenario for the contact formation between a single seta and the substrate in such a fluid. Using this scenario, together with the rheological data, we then estimate the attachment dynamics of the setae, and therefore of the insect pads.

5. Collecting the secretion using capillarity

A home-made microneedle, with a tip size of a few microns, was used to draw up the secretion droplets (1–10 µm in diameter) spread on a glass slide (figure 1). The procedure used to collect the secretion from insects is described in appendix A. The microneedles were pulled from thin-wall borosilicate glass capillaries with a 1 mm outer diameter and a 0.78 mm inner diameter (Harvard Apparatus, France) with a Narishige PB-7 double-stage puller (Narishige Instruments, Tokyo, Japan). By adjusting the puller settings, microneedles with a tip size of a few microns were produced. The microneedle was then mounted on a three-axis piezo micromanipulator (Burleigh), and attached to an inverted microscope (Leica DMI3000).

Owing to capillary effects, the rise of the wetting secretion takes place spontaneously in the tube as the tip is maintained in contact with the support and the droplet. The microneedle tip was moved onto the slide surface in order to collect the largest possible amount of secretions. Owing to its high flexibility, it could be maintained in contact with the slide without breaking, thus optimizing the collection of the secretion. The microneedle tip was connected to a syringe, allowing us to apply a positive or negative pressure to the microneedle. Spontaneous suction—due to surface tension—could possibly be assisted by applying slight negative pressure to the microneedle. After an entire day (approx. 8 h) collecting the secretions, the final volume of fluid represented a drop which was about 100 µm in diameter and 30 µm in height (figure 2).

Figure 2.

Figure 2.

Open in a new tab

The collected volume is ejected on dry 0.74 µm diameter melamine beads. (a) Before the ejection (the dry beads have been deposited on a glass slide) and (b) during the ejection. The final volume of the collected secretion is a drop of 100 µm in diameter and 30 µm in height. Scale bar, 10 µm.

6. Brownian motion measurements

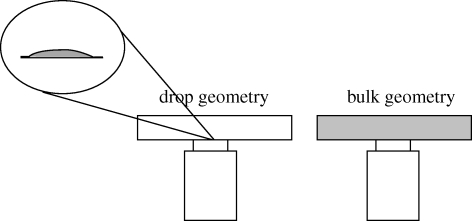
A dry powder of melamine beads (Acil, France) was deposited on a clean glass slide. The collected secretion volume was then ejected on the dry beads, which were 0.740 ± 0.005 µm in diameter, by applying a positive pressure to the microneedle (figure 2). During the ejection, the microneedle was slightly pulled away, in order to avoid the secretion rising along the outer side of the microneedle tube. After ejection, the microneedle tip was moved along the glass slide to unstick any beads from the surface. The secretory fluid was then drawn up again and ejected several times in order to mix the beads with the secretion. The final mixture was then ejected in a square chamber (10 × 10 mm2) made of a microscope plate and a cover-slip separated by a thin adhesive spacer (100 µm thickness). The container was sealed to avoid contamination or possible evaporation of the secretion drop (figure 4).

Figure 4.

Figure 4.

Open in a new tab

Scheme of ‘bulk’ and ‘drop’ geometries used to perform microrheological measurements. The bulk geometry (1 cm × 1 cm × 100 µm) is the usual geometry for performing microrheological measurements. The ‘drop’ geometry was used with the secretion in the present work, owing to the extremely small amount of fluid available. The drop size was 100 µm in diameter and 30 µm in height. The ‘drop’ geometry was shown to provide the same viscosity results as the usual bulk geometry, which shows that it is reliable.

The fluctuating motion of the tracer beads immersed in the secretory fluid was recorded with a fast charge-coupled device camera (Kodak motion) mounted on an inverted Leica microscope, with an oil immersion objective (63×). The fast camera was typically sampling at 125 Hz, for 8 s. For reliable analysis of the Brownian motion, particular attention was paid to recording the motion far from the rigid wall formed by the glass slide and the drop edges. Home-made image analysis software allowed us to track the beads' positions x(t) and y(t) close to the focus plane of the objective (see appendix A for more details). For each bead, the time-averaged MSD 〈Δr2(t)〉t′ = 〈[x(t′ + t) − x(t′)]2 + [y(t′ + t) − y(t′)]2〉t′ = 2〈Δx2 (t)〉t′ was calculated, improving the statistical accuracy. To maintain reliable statistics, the data from the MSD were kept in the range below t < 2 s (Abou et al. 2008). The quantity 〈Δr2 (t)〉t′ was then averaged over several beads (about 20), and identified as the ensemble-averaged MSD. The resolution on the bead position, determined with a sub-pixel accuracy in the image analysis detection, was about 0.3 pixel, corresponding to δ = 30 nm. This resolution determined the lowest accessible MSD in these experiments, and corresponded to about 2 × 10−3 µm2.

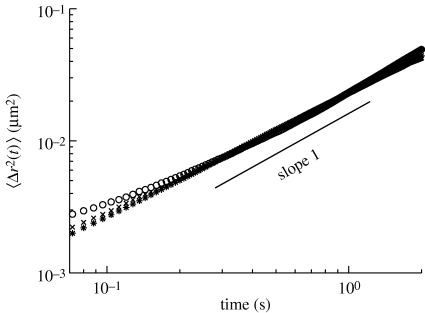
Figure 3 shows the ensemble-averaged MSD 〈Δr2(t)〉E (MSD) of the tracer beads, as a function of the lag time t. As can be seen, the diffusive behaviour of the tracers, characterized by a linear dependency of the MSD with time, 〈Δr2(t)〉 = 4Dt, is measured. This linear dependency implies that the beetles' pad secretion simply behaves in a purely viscous manner in the investigated time window. The viscosity of the material was then directly deduced from the diffusion coefficient according to the Stokes–Einstein relation D = kT/6πRη0, where R is the bead radius and T the bath temperature (see appendix A.3). The secretory fluid viscosity corresponds to 110 ± 5 mPa s at a room temperature of T = 21 ± 1oC. This value corresponds to approximately 100 times the viscosity of water.

Figure 3.

Figure 3.

Open in a new tab

Mean-squared displacement (MSD) of 0.74 µm melamine beads immersed in: the beetle secretion (asterisks), the calibrated 100 BW Newtonian fluid in the bulk geometry (unfilled circles), and 100 BW in the drop geometry (crosses), as a function of time. In all cases, the fluctuating motion of the tracers is purely diffusive, characterized by a linear dependency of the MSD with time. The secretion was found to behave as a purely viscous fluid on the time scales investigated, with a viscosity approximately 100 times that of water.

In order to test the reliability of the Brownian motion measurements in the ‘drop’ geometry used for secretion, microrheological tests were also performed in a calibrated Newtonian fluid (100 BW, ZMK-Analytic-GmbH), in two different geometries. The first one—bulk geometry—corresponds to the usual geometry used in microrheology (10 mm × 10 mm × 100 µm), while the second one—drop geometry—corresponds to a drop approximately 100 µm in diameter and 30 µm in height spread on a glass slide (figure 4). In both experiments, the Brownian motion of the tracers was recorded, far from the glass slide walls and the drop edges. Also, in both experiments, the MSD was averaged on approximately the same number of beads, of the order of 20. The experimental results were found to be in good agreement in both geometries, in the time range investigated (7 × 10−2 < t < 2.0 s) (figure 3). In both cases, the MSD increased linearly with time, indicating a purely viscous behaviour, characterized by a viscosity of the order of 100 mPa s, which is in excellent agreement with standard rheological measurements in the calibrated oil. The ‘drop geometry’ as well as the statistical accuracy were then confirmed to be reliable in our microrheological measurements.

The beads' chemistry is known to be a relevant parameter in microrheological experiments. The choice of melamine beads was driven by the necessity to use dry bead powder, because of the small quantity of secretion. Tests that we performed in different oils, such as the BW oil glycerol, with the same melamine beads gave us very good agreement with bulk rheological measurements. Here, we believe that the beads' chemistry is neutral to the surrounding fluid and does not influence the rheological measurements.

7. Insect pad attachment dynamics

Let us now focus on the modelling of the attachment dynamics of the insect in the presence of secretion. The spatula at the setal tip is assumed to be initially covered by a thin film of secretion (thickness H), as shown in figure 5a. We will now estimate the duration of the attachment process of the spatula onto the substrate, and hence of the insect pads, on the basis of the above rheological measurements.

Figure 5.

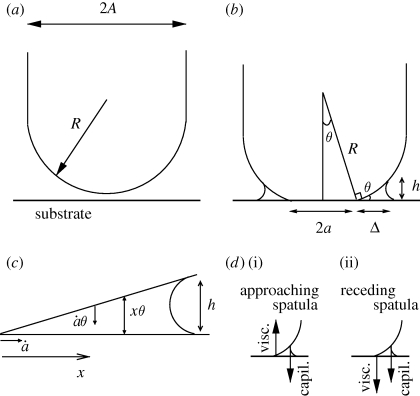
Figure 5.

Open in a new tab

Geometry of the setal tip. The seta consists of a tip of diameter 2A and curvature 1/R located at the end of a long fibre (a). The tip of the seta is covered by a thin film of viscous secretion. When the seta contacts substrate, the contact region expands laterally (b). The meniscus (outer diameter 2(a + Δ)) still represents a small portion of the tip surface (a ≪ A) (c). As the contact broadens (ȧ > 0), because the liquid is within a sharp wedge with angle θ ≪ 1, the tip surface approaches the substrate at velocity ȧ tan(θ) ≃ ȧθ. The viscous dissipation in the meniscus then determines the velocity ȧ > 0. This is calculated (see appendix A.5) by integration over the distance x from the edge of the solid contact and over the local thickness x tan(θ) ≃ xθ (d). Upon contact formation d(i), the driving force is the capillary force (at the edge of the meniscus) and is opposed by viscous dissipation in the corner. Upon separation d(ii), the motion is reversed; hence, the viscous force is reversed and the insect must overcome both the capillary force and the viscous dissipation.

We here consider the spatula to be a portion of a hemisphere, with a radius of curvature R and a diameter 2A. As it approaches the substrate, the contact region of radius a rapidly expands laterally. As a result, a capillary force Fcapil ≃ 4πRγ arises between the spatula at the setal tip and a smooth substrate, and promotes the contact (see figure 5d(i)). This is calculated in appendix A.4.

Without any active effort from the insect, this capillary force spontaneously drives the formation of the contact between the spatula and the solid substrate, as fast as allowed by the opposing viscous force (see figure 5d(i)): 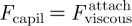Inline graphic. Later, upon detachment, the viscous force now opposes detachment (see figure 5d(ii)) and the insect must exert a tensile force that exceeds the capillary force: 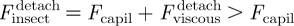Inline graphic. For detachment to occur at the same rate as attachment, which seems reasonable, it is required that 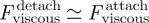Inline graphic; hence, 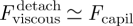Inline graphic. 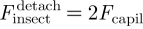As a result, during detachment, the insect must exert a tensile force typically equal to twice the capillary force: Inline graphic.

Let us now focus on the attachment dynamics. The viscosity η extracted from the above Brownian motion measurements now allows us to derive a prediction for the duration of the attachment/detachment process of a spatula on a substrate. The flow in the meniscus dissipates energy and leads to the following estimate (see appendix A.5) for the viscous force: Fviscous ≈ ηR2ȧ/a. Equating Fviscous and Fcapil, we find that the contact widens at velocity ȧ ≈ aγ/Rη. The corresponding time needed to establish the equilibrium contact is 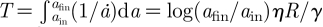Inline graphic. Considering that the final contact radius afin is not tremendously bigger than the initial radius Inline graphic, the quantity log(afin/ain) will be at most a few units; hence, the attachment process can be estimated to scale as T ≈ ηR/γ. Using the viscosity η = 10−1 Pa s extracted from the above Brownian motion measurements and assuming γ ≈ 10−2 Nm−1 and R ≈ 1 µm, we obtain T ≈ 10 ms.

This therefore predicts, on the basis of the measured viscosity, a total duration T of the contact (attachment and detachment) and thus a pace rate, as well as a detachment force 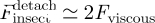Inline graphic. It turns out that the estimate T ≃ 10 ms obtained for the contact duration is compatible with the duration observed in video recordings of walking beetles (S. Gorb 2010, personal observation).

With regard to detachment, the insect must provide active effort. Hence, low or moderate viscous dissipation is preferable to high dissipation, although perhaps this is not crucial: we speculate that beetles, like geckoes (Autumn et al. 2000) and flies (Niederegger & Gorb 2003), adopt a leg motion suitable for easing detachment significantly. This may imply bending or rolling of the spatulae in such a way that the local curvature becomes stronger at the contact with the substrate.

8. Discussion and conclusion

Our passive microrheology nanolitre procedure is innovative in two respects: (i) the material under investigation is initially available as an assembly of 1 femtolitre droplets deposited on a glass slide and (ii) the 0.1 nl collected volume used to perform the microrheological measurement was significantly less than the usual 1 µl.

These measurements show that the secretion behaves as a purely viscous fluid of high viscosity over the range of frequencies investigated. This is the first experimental indication that beetle locomotion might not need a specifically viscoelastic behaviour. Let us emphasize, however, that, owing to the resolution (30 nm) of our particle tracking set-up, we could not explore frequencies above 15 Hz, which is slightly below the beetle pace rate (around 100 Hz). It is therefore not to be excluded that the secretion response could depart from a purely viscous behaviour at higher frequencies. In future studies, we intend to extend our measurements to the secretions of other animals over a wider range of frequencies.

Our model provides the expression T ≈ ηR/γ for the duration of the pad/substrate contact formation. This implies that the secretion viscosity η sets an upper bound of the order of 1/T for the insect's pace rate. This formula is only an estimate since (i) the exact spatula geometry and dimensions are not precisely known and vary within one single animal (Voigt et al. 2008) and (ii) numerical prefactors were omitted. Nevertheless, using this expression with the measured viscosity provides a time scale for attachment which is compatible with live observations. The high secretion viscosity should therefore not prevent the insect from forming good contacts.

One might wonder, however, why the secretion viscosity is so high (100 times the viscosity of water). A lower viscosity would ease the insect's locomotion and speed up its pace. It is not unreasonable to suggest that high viscosity, and correspondingly high molecular weight, ensures slow evaporation—a crucial issue at such small length scales. Additionally, high viscosity ensures that the adhesion is robust under unexpected and rapidly varying conditions. It is interesting to note that some insect adhesive pads use emulsions with non-Newtonian properties, providing a mechanism that prevents insects from slipping on smooth substrates (Dirks et al. 2009). This non-slip property probably results from the existence of a yield stress for such an emulsion: if the emulsion consists of small enough droplets, the weight of the insect is too weak to trigger shear. This indicates that secretions may serve various insect strategies.

Acknowledgements

This work was supported by the Programmes Interdisciplinaires de Recherche from the CNRS to B.A. This work as part of the European Science Foundation EUROCORES Programme FANAS was supported by the German Science Foundation DFG (contract no. GO 995/4-1) and the EC Sixth Framework Programme (contract no. ERAS-CT-2003-980409) to S.N.G.

Appendix A

A.1. Insects and preparation of the footprints

Adult L. decemlineata (Chrysomelidae) beetles were collected from various species of annual plants from the family Solanaceae in the Botanical Garden of Dresden University of Technology, Germany. The tarsi were cut off the body using small scissors and used to prepare footprints on the substrate by pressing the ventral side of the tarsi against a clean glass slide. Pressure was applied on the foot in order to have strong contact with the glass slide and to force the secretion out through the pore channels. At the same time, the leg was rubbed against the slide, which resulted in a strong shear that deposited the secretion on the surface. This produced a collection of small droplets of various sizes, from a few microns to 10 microns for the largest ones (figure 1). In all cases, the droplets were spread with their height never exceeding a few microns. Interestingly, evaporation of the secretions was not observed within the experiment time.

A.2. Particle tracking algorithm

Two-dimensional analysis of the particle motion was performed using a home-made algorithm, implemented as an ImageJ plugin (Rasband 1997–2007). A classical cross-correlation method was used to determine the bead displacements. In order to achieve sub-pixel spatial resolution, the computed correlation was interpolated using a paraboloid approximation. With this algorithm, several beads could be tracked at the same time.

A.3. MSD analysis

Passive, or thermally driven, microrheology is based upon the generalized Einstein relation (GER), which is valid in a viscoelastic stationary medium in thermal equilibrium at temperature T. It relates the frequency-dependent MSD of the diffusing particle to its frequency-dependent mobility, according to the relation s2〈Δx̂2(s)〉 = 2kTμ̂(s), where k is the Boltzmann constant and s is the frequency in the Laplace domain (Mason & Weitz 2005; Waigh 2005; Abou et al. 2008). As can be seen, measuring the particles' MSD at equilibrium leads to the indirect measurement of the particle mobility. The bulk frequency-dependent viscosity of the fluid can then be deduced assuming that the Stokes relation μ̂(s) = 1/6πRη̂(s) remains valid in the viscoelastic material. In the particular case of a purely viscous fluid, the MSD increases linearly with time and the GER can be written as 〈Δr2(t)〉 = 4Dt, where D is the diffusion coefficient. The viscosity of the material is directly deduced from the diffusion coefficient according to the Stokes–Einstein relation D = kT/6πRη0, where R is the bead radius and T the bath temperature.

A.4. Capillary attachment force

We shall now estimate the capillary force between the spatula at the setal tip and a smooth substrate in the case of partial contact (a < A). Immediately outside the contact region of radius a, the surface of the spatula is expected to depart from the substrate with a weak slope θ, with θ ≃ a/R (figure 5b). Considering that there is very little secretion at the tip, the meniscus width Δ is much smaller than a. The meniscus height (which is also twice its radius of curvature, i.e. h = 2r) is then typically equal to h ≃ θΔ. Integrating the capillary (Laplace) pressure −γ/r (Wikipedia 2010) over the contact surface area between the meniscus and the spatula, which is approximately 2πaΔ, provides the capillary force 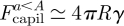Inline graphic. Interestingly, this capillary force turns out to be independent of both the radius a of the contact and the amount of liquid in the meniscus. Note that, depending on the curvature and rigidity of the spatula, the surface tension of the secretion and the force applied by the insect, the contact—of final radius afin—remains either partial (afin < A) or total (afin = A). In both cases, the dynamics of the attachment/detachment process remains identical and is described in the next section.

A.5. Dissipation in the secretion meniscus

As the spatula approaches the substrate at velocity vz, the contact radius widens at velocity ȧ > 0 (where vz ≃ ȧθ ≃ ȧa/R), as shown in figure 5c, and the fluid in the meniscus moves outwards. The zero-velocity condition at the substrate and the spatula surfaces implies a dissipation of order η(ȧ/h(x))2 per unit volume, where the local gap is h(x) = θx, with x the horizontal position along the meniscus width. The total power dissipated in the meniscus is thus approximately Pviscous ≈ ∫η(ȧ/θx)2 2πaθxdx ≈ ηȧ2a/θ. Hence, the viscous force can be written as Fviscous = Pviscous/vz ≈ ηȧR2/a. Note that the above calculation of the dissipation in the meniscus overlooks the detailed shape of the spatula as deformed dynamically by the meniscus (to the best of our knowledge, such a calculation is not currently available). It is likely that the spatula surface does not locally make a sharp (although small) angle with the substrate, and that the true dissipated power is in fact larger than the above estimate.

Besides the dissipation in the meniscus, some dissipation also occurs within the spatula, if it is viscoelastic, particularly in the vicinity of the interface with the solid substrate. In other words, during detachment, the opening of an interfacial crack between the spatula and the substrate requires some energy by itself. Here, we assume that the spatula is almost purely elastic and that such viscoelastic dissipations are negligible. Besides, the thermodynamic energy required to break the contact with the substrate (balance of surface tensions) is presumably comparable to or weaker than the capillary interaction, and is also neglected here.

References

  1. Abou B., Gallet F., Monceau P., Pottier N. 2008. Generalized Einstein relation in an aging colloidal glass. Physica A 387, 3410 ( 10.1016/j.physa.2008.02.034) [DOI] [PubMed] [Google Scholar]
  2. Arzt E., Gorb S., Spolenak R. 2003. From micro to nano contacts in biological attachment devices. Proc. Natl Acad. Sci. USA 100, 10 603–10 606. ( 10.1073/pnas.1534701100) [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Autumn K., Liang Y. A., Hsieh S. T., Wai W., Kenny P. C., Fearing T. W., Full R. J. 2000. Adhesive force of a single gecko foot-hair. Nature 405, 681–685. ( 10.1038/35015073) [DOI] [PubMed] [Google Scholar]
  4. Autumn K., et al. 2002. Evidence for van der Waals adhesion in gecko setae. Proc. Natl Acad. Sci. USA 99, 12 252–12 256. ( 10.1073/pnas.192252799) [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bauchhenss E. 1979. Die Pulvillen von Calliphora erythrocephala Meig. (Diptera, Brachycera) als Adhäsionsorgane. Zoomorphologie 93, 99–123. ( 10.1007/BF00994125) [DOI] [Google Scholar]
  6. Beutel R. G., Gorb S. N. 2001. Ultrastructure of attachment specializations of hexapods (Arthropoda): evolutionary patterns inferred from a revised ordinal phylogeny. J. Zool. Syst. Evol. Res. 39, 177–207. ( 10.1046/j.1439-0469.2001.00155.x) [DOI] [Google Scholar]
  7. Beutel R. G., Gorb S. N. 2006. A revised interpretation of attachment structures in Hexapoda with special emphasis on Mantophasmatodea. Arthropod. Syst. Phyl. 64, 3–25. [Google Scholar]
  8. Chung J. Y., Chaudhury M. K. 2005. Roles of discontinuities in bio-inspired adhesive pads. J. R. Soc. Interface 2, 55–61. ( 10.1098/rsif.2004.0020) [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Dahlquist C. A. 1969. Proc. Nottingham Conf. on adhesion, 1966. Fundamentals and practice. London, UK: MacLaren. [Google Scholar]
  10. Dewitz H. 1884. Über die Fortbewegung der Tiere an senkrechten glatten Flächen vermittels eines Secretes. Arch. Ges. Physiol. 33, 440–481. ( 10.1007/BF01628473) [DOI] [Google Scholar]
  11. Dirks J. H., Clemente C. J., Federle W. 2009. Insect tricks: two-phasic foot pad secretion prevents slipping. J. R. Soc. Interface 7, 587–593. ( 10.1098/rsif.2009.0308) [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Dreschler P., Federle W. 2006. Biomechanics of smooth adhesive pads in insects: influence of tarsal secretion on attachment performance. J. Comp. Physiol. A 192, 1213–1222. ( 10.1007/s00359-006-0150-5) [DOI] [PubMed] [Google Scholar]
  13. Edwards J. S., Tarkanian M. 1970. The adhesive pads of Heteroptera: a re-examination. Proc. R. Entomol. Soc. Lond. A 45, 1–5. [Google Scholar]
  14. Eisner T., Aneshansley D. J. 2000. Defence by foot adhesion in a beetle (Hemisphaerota cyanea). Proc. Natl Acad. Sci. USA 97, 6568–6573. ( 10.1073/pnas.97.12.6568) [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Federle W., Riehle M., Curtis A., Full R. 2002. An integrative study of insect adhesion: mechanics and wet adhesion of pretarsal pads in ants. Integr. Comp. Biol. 42, 1100–1106. ( 10.1093/icb/42.6.1100) [DOI] [PubMed] [Google Scholar]
  16. Gao H., Wang X., Yao H., Gorb S., Arzt E. 2005. Mechanics of hierarchical adhesion structures of geckos. Mech. Mater. 37, 275–285. ( 10.1016/j.mechmat.2004.03.008) [DOI] [Google Scholar]
  17. Gay C., Leibler L. 1999. On stickiness. Phys. Today 52, 48–52. ( 10.1063/1.882884) [DOI] [Google Scholar]
  18. Gillett J. D., Wiggleswort V. B. 1932. The climbing organ of an insect. Rhodnius prolixus (Hemiptera, Reduviidae). Proc. R. Soc. Lond. B 111, 364–376. ( 10.1098/rspb.1932.0061) [DOI] [Google Scholar]
  19. Gorb S. N. 2001. Attachment devices of insect cuticle. Dordrecht, The Netherlands: Kluwer Academic Publishers. [Google Scholar]
  20. Ishii S. 1987. Adhesion of a leaf feeding ladybird Epilachna vigintioctomaculata (Coleoptera: Coccinellidae) on a vertically smooth surface. Appl. Entomol. Zool. 22, 222–228. [Google Scholar]
  21. Kosaki A., Yamaoka R. 1996. Chemical composition of footprints and cuticula lipids of three species of lady beetles Japan. J. Appl. Entomol. Zool. 40, 47–53. [Google Scholar]
  22. Langer M. G., Ruppersberg J. P., Gorb S. N. 2004. Adhesion forces measured at the level of a terminal plate of the fly's seta. Proc. R. Soc. Lond. B 271, 2209–2215. ( 10.1098/rspb.2004.2850) [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Leeuwenhoek A. 1690. The select works of Antony van Leeuwenhoek: containing his microscopical discoveries in many of the works of nature, vol. 2 (transl. Hoole S. 1800). London: G. Sidney. [Google Scholar]
  24. Mason T. G., Weitz D. A. 2005. Optical measurements of frequency dependent linear viscoelastic moduli of complex fluids. Phys. Rev. Lett. 74, 1250 ( 10.1103/PhysRevLett.74.1250) [DOI] [PubMed] [Google Scholar]
  25. Niederegger S., Gorb S. 2003. Tarsal movements in flies during leg attachment and detachment on a smooth substrate J. Insect Physiol. 49, 611–620. ( 10.1016/S0022-1910(03)00048-9) [DOI] [PubMed] [Google Scholar]
  26. Persson B. N. J. 2003. On the mechanism of adhesion in biological systems. J. Chem. Phys. 118, 7614–7621. ( 10.1063/1.1562192) [DOI] [Google Scholar]
  27. Persson B. N. J., Gorb S. 2003. The effect of surface roughness on the adhesion of elastic plates with application to biological systems. J. Chem. Phys. 119, 11 437–11 444. ( 10.1063/1.1621854) [DOI] [Google Scholar]
  28. Rasband W. S. 1997–2007 ImageJ. Bethesda, MD: US National Institutes of Health. See http://rsb.info.nih.gov/ij/ . Source code for the plugin is available at http://www.msc.univ-paris-diderot.fr/~olivier/ImageJ/ . [Google Scholar]
  29. Simmermacher G. 1884. Haftapparate bei Wirbeltieren. Zool. Gart. 25, 289–301. [Google Scholar]
  30. Stork N. E. 1980. Experimental analysis of adhesion of Chrysolina polita (Chrysomelidae, Coleoptera) on a variety of surfaces. J. Exp. Biol. 88, 91–107. [Google Scholar]
  31. Voigt D., Scuppert J. M., Dattinger S., Gorb S. 2008. Sexual dimorphism in the attachment ability of the Colorado potato beetle Leptinotarsa decemlineata (Coleoptera: Chrysomelidae) to rough substrates. J. Insect Physiol. 54, 765–776. ( 10.1016/j.jinsphys.2008.02.006) [DOI] [PubMed] [Google Scholar]
  32. Vötsch W., Nicholson G., Müller R., Stierhof Y., Gorb S., Schwarz U. 2002. Chemical composition of the attachment pad secretion of the locust Locusta Migratoria. Insect Biomech. Mol. Biol. 32, 1605–1613. ( 10.1016/S0965-1748(02)00098-X) [DOI] [PubMed] [Google Scholar]
  33. Waigh T. A. 2005. Microrheology of complex fluids. Rep. Prog. Phys. 68, 685–742. ( 10.1088/0034-4885/68/3/R04) [DOI] [PubMed] [Google Scholar]
  34. Walker G., Yule A. B., Ratcliffe J. 1985. The adhesive organ of the blowfly, Calliphora vomitoria: a functional approach (Diptera: Calliphoridae). J. Zool. Lond. 205, 297–307. [Google Scholar]
  35. Wallentin J., Mondon M., Stadler H., Gorb S. N., Ziegler Ch. 1999. The secrets of fly secretes: adhesion properties probed by force–distance curves. In Proc. Workshop on Scanning-probe microscopes and organic materials VIII, Basel, Switzerland, 4–6 October 1999 (eds Müller D. J., Knapp H. F.), p. 14. [Google Scholar]
  36. Wikipedia. 2010. Young–Laplace equation. See http://en.wikipedia.org/wiki/Young-Laplace_equation. [Google Scholar]

Articles from Journal of the Royal Society Interface are provided here courtesy of The Royal Society

RESOURCES