Nanostructure and molecular mechanics of spider dragline silk protein assemblies

Abstract

Spider silk is a self-assembling biopolymer that outperforms most known materials in terms of its mechanical performance, despite its underlying weak chemical bonding based on H-bonds. While experimental studies have shown that the molecular structure of silk proteins has a direct influence on the stiffness, toughness and failure strength of silk, no molecular-level analysis of the nanostructure and associated mechanical properties of silk assemblies have been reported. Here, we report atomic-level structures of MaSp1 and MaSp2 proteins from the Nephila clavipes spider dragline silk sequence, obtained using replica exchange molecular dynamics, and subject these structures to mechanical loading for a detailed nanomechanical analysis. The structural analysis reveals that poly-alanine regions in silk predominantly form distinct and orderly beta-sheet crystal domains, while disorderly regions are formed by glycine-rich repeats that consist of 3₁-helix type structures and beta-turns. Our structural predictions are validated against experimental data based on dihedral angle pair calculations presented in Ramachandran plots, alpha-carbon atomic distances, as well as secondary structure content. Mechanical shearing simulations on selected structures illustrate that the nanoscale behaviour of silk protein assemblies is controlled by the distinctly different secondary structure content and hydrogen bonding in the crystalline and semi-amorphous regions. Both structural and mechanical characterization results show excellent agreement with available experimental evidence. Our findings set the stage for extensive atomistic investigations of silk, which may contribute towards an improved understanding of the source of the strength and toughness of this biological superfibre.

1. Introduction

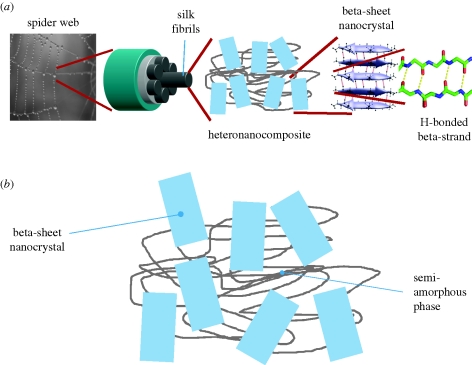
Chemistry and nanoscale features of biological materials are crucial to understand the source of their mechanical properties such as strength, failure mechanisms and elasticity (Fratzl & Weinkamer 2007). In protein materials, the primary structure of macromolecules, consisting of a linear sequence of individual amino acids, describes the chemical specificity of the interactions at the molecular level, which give rise to formation and failure characteristics of the material (LeDuc & Robinson 2007; Buehler & Yung 2009). Spider silk is an extraordinary material that surpasses most synthetic fibres in terms of toughness through a balance of ultimate strength and extensibility (Termonia 1994; Simmons et al. 1996; Vollrath & Knight 2001; Shao & Vollrath 2002; Becker et al. 2003). The source of spider silk's unique properties has been attributed to the specific secondary structures of proteins found in the repeating units of spider silk (Hayashi et al. 1999), which assemble into a hierarchical structure shown in figure 1a,b.

Figure 1.

(a) Hierarchical structure of spider silk. The work reported here is focused on the scale of the nanocomposite structure, (b) where beta-sheet nanocrystals are immersed in a matrix of semi-amorphous protein. The focus of the present study is on a simple model system that contains a single beta-sheet nanocrystal embedded in the semi-amorphous matrix.

Experimental studies have thus far primarily focused on developing a mapping between the repeating sequence units of spider silk and the basic structural building blocks of fibrils. Two distinct proteins are typically found in dragline silks with similar sequences across species (Gatesy et al. 2001). One of the most studied silk from spiders, Nephila clavipes dragline silk, contains MaSp1 and MaSp2 proteins, with different repeat units and possibly distinct mechanical functions (Hayashi & Lewis 1998; Hayashi et al. 1999; Brooks et al. 2005; Holland et al. 2008). MaSp1 contains glycine (Gly or G)-rich Gly–Gly–X (GGX) repeats with poly-alanine (Ala or A) and GA domains, where X typically stands for alanine, tyrosine, leucine or glutamine. Whereas MaSp2 also contains poly-Ala domains, it has a repeat unit with high proline content in the form of (GPGQQ/GPGGY). The proline-rich segments are intrinsically twisted, which inhibits edge-to-edge aggregation of strands, thereby controlling the location and size of beta-sheet nanocrystals in silk. These segments, bearing sequence resemblance to elastin, are thought to form beta-spiral or type II beta-turn structures that provide extensibility through hidden length formation, and control the unique thermomechanical properties of spider silk (Hayashi et al. 1999; Gosline et al. 2002; Savage & Gosline 2008). Earlier studies have suggested that MaSp1 is more dominant in the composite morphology of the spider dragline silk than MaSp2, with a ratio of approximately 3 : 2 or higher, depending on the species (Hinman & Lewis 1992; Guerette et al. 1996; Brooks et al. 2005; Sponner et al. 2005). Recent investigations revealed that anti-parallel beta-sheet crystals at the nanoscale, consisting of highly conserved poly-(Gly[G]–Ala[A]) and poly-Ala repeats found in both commercial and spider silk (Hayashi et al. 1999), play a key role in defining the mechanical properties of silk by providing stiff orderly cross-linking domains embedded in a semi-amorphous matrix with less orderly structures (Thiel et al. 1997; van Beek et al. 2002; Lefevre et al. 2007). Earlier studies have shown that the hydration level and solvent conditions such as ion content and pH play a role in the structure and mechanical properties of silk proteins (Dicko et al. 2004; Rammensee et al. 2008). For instance, a unique aspect of silk fibres is their capacity to exhibit a dramatic reduction in length upon hydration; a phenomenon known as supercontraction (Shao & Vollrath 1999; van Beek et al. 1999).

Beta-sheet nanocrystals that employ a dense network of hydrogen bonds (Keten & Buehler 2008a,b) have dimensions of a few nanometres and constitute at least 10–15% of the silk volume, while, with less orderly extended structures, the beta-sheet content can be much higher for most silks (Grubb & Jelinski 1997; Rousseau et al. 2004; Du et al. 2006). The existence of 3₁ helices, and beta-turn or beta-spiral conformations has been suggested for the amorphous domains (Cunniff et al. 1994; Thiel et al. 1997; van Beek et al. 2002; Lefevre et al. 2007); however, no definite atomistic-level structural model has yet been reported. It is anticipated that novel statistical mechanics approaches (Porter et al. 2005), experimental methods, such as X-ray diffraction and scattering (Riekel & Vollrath 2001; Trancik et al. 2006), solid-state nuclear magnetic resonance (NMR; Simmons et al. 1996; van Beek et al. 1999; Holland et al. 2008; Jenkins et al. 2010) and Raman spectroscopy (Rousseau et al. 2004, 2009; Lefevre et al. 2007), combined with pioneering multiscale atomistic-modelling methods such as those based on density functional theory (Porter & Vollrath 2008; Keten et al. 2010) or molecular dynamics (Brooks 1995; Ma & Nussinov 2006; Buehler et al. 2008; Keten & Buehler 2010), will provide more insight into the atomic resolution structure for complex materials such as spider silk. An earlier study of silk using replica exchange molecular dynamics (REMD; Keten & Buehler 2010) has yielded interesting results in comparison with experiments (Kummerlen et al. 1996; van Beek et al. 2002; Holland et al. 2008). However, this study was focused solely on the case of MaSp1 and did not encompass any mechanical characterization. Owing to the lack of current large-scale atomic resolution models, the links between genetic make-up, chemical interactions and structure, as well as the associated macroscale mechanical properties, remain obscure for silk. Earlier atomistic studies have focused solely on the well-defined crystalline regions consisting of poly-Ala (spider silk) or poly-Gly–Ala repeats (silkworm silk; Xiao et al. 2009; Keten et al. 2010), and studies on the links between structural and nanomechanical features of the nanocomposite structure of silk have remained a challenge.

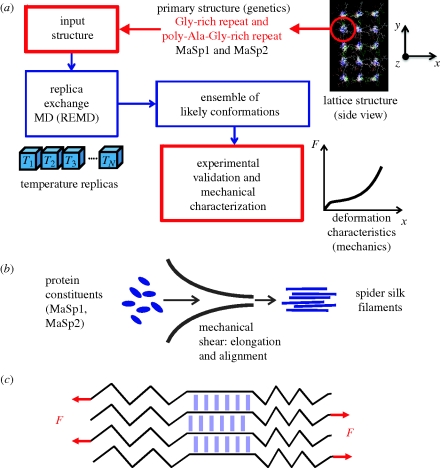
Here, we carry out atomistic simulations to identify nanostructural models of spider silk proteins, with the goal of developing a link between genetic sequence and resulting mechanical properties. The challenges of reaching native (equilibrium) structures within the time scales accessible to conventional molecular dynamics simulation require enhanced sampling methods such as REMD (Sugita & Okamoto 1999). Here, we employ REMD to investigate the structures formed by assemblies of short segments of MaSp1 and MaSp2 proteins. Along with other protein structure prediction approaches (Bradley et al. 2005; Zhang 2008), REMD is considered to be an effective tool for investigating folding and aggregation of proteins, as it reduces the likelihood of kinetic trapping at non-native states (Sanbonmatsu & Garcia 2002). Through a fast search of the conformation space at high temperatures and more detailed investigation at low temperatures, it allows the system to overcome energy barriers and local minima corresponding to non-native structures (Feig et al. 2003; Rao & Caflisch 2003; Rhee & Pande 2003; Miyashita et al. 2009) of proteins and facilitates identification of native protein structures from the amino acid sequence with atomistic resolution. The overall approach is summarized in figure 2a.

Figure 2.

Simulation protocol and representative molecular structure results. (a) Summary of the approach taken to identify the nanostructure of spider silk proteins, here focused on the MaSp1 and MaSp2 silk sequences from the N. clavipes spider. Monomers representing sections of the MaSp1 and MaSp2 proteins (containing a poly-alanine repeat in the centre) are used as the basic building block. Replica exchange simulations are carried out at multiple temperatures, and an ensemble of most likely, final low-temperature structures are compared with experimental evidence. (b) Illustration of the natural process of silk assembly (and fibre formation) during which silk proteins are subject to shear. The natural process of shearing and alignment of protein monomers motivates our choice of the initial geometry shown in (a). (c) The mechanical loading condition employed in our simulations in line with the shear topology of beta-sheet crystals in spider silk.

2. Material and methods

The computational approach used here consists of two steps, (i) structure identification with validation against experimental results and (ii) mechanical loading of the resulting structures, with subsequent analysis of material properties and deformation mechanisms.

2.1. Structure identification

Primary protein structures (polypeptide sequences) are created with the amino acid sequence of the N. clavipes MaSp1 and MaSp2 proteins, which constitute the majority of the silk's core (Holland et al. 2008). The MaSp1 sequence is (in one-letter amino acid codes): GGAGQGGYGGLGSQGAGRGGLGGQGAGAAAAAAGGAGQGGYGGLGSQGAGRGGLGGQGAG. The MaSp2 sequence is: GPGQQGPGGYGPGQQGPGGYGPGQQGPSGPGSAAAAAAAAGPGQQGPGGYGPGQQGPGGYGPGQQGPSGPGS.

The monomers consist of two glycine-rich repeating units surrounding a poly-alanine segment to represent a single monocrystal. MaSp1 protein consists primarily of GGX type repeats followed by a GA and poly-Ala region. MaSp2, on the other hand, has proline-rich GPGQQGPGGY repeats, and a poly-Ala region. The starting configuration is a lattice structure consisting of an anti-parallel arrangement in one direction and a parallel arrangement in the other. Previous findings on poly-alanine aggregation suggest that anti-parallel orientation in the hydrogen-bonding direction and parallel stacking in the side-chain direction leads to stable beta-sheets (Ma & Nussinov 2002), and hence such an arrangement is considered here to be a good starting point for obtaining assembled structures by silk proteins. In the initial set-up, each strand is separated by 10 Å in a square lattice (figure 2a). The simulations start from an extended conformation, which is very relevant in the processing of silk where elongational flow in the spinning duct leads to stretching and alignment of monomers in the concentrated dope, as shown in recent experimental work (Rammensee et al. 2008; see figure 2b for a schematic). We note that higher temperature replicas can allow wide sampling around this basic orientation, where chains can rearrange in anti-parallel or parallel orientations as the strands can diffuse within the lattice. At high-temperature replicas, weak interactions between the strands can be broken; that is, the system ‘melts’ and reforms in a wide range of structures that can be investigated in detail at lower temperatures. A key hypothesis here for using an initial orderly lattice arrangement is that edge-to-edge aggregation of strands—similar to amyloids (Kenney et al. 2002)—is the driving force for formation of mono-crystals, rather than local folding of the backbone onto itself through short turn structures. This is supported by recent experiments, which suggest that large extensional forces during spinning and high concentration of the dope are requirements for crystal formation (Rammensee et al. 2008). This assumption is reasonable in the context of a monocrystal study as pursued here, and does not rule out the possibility of the formation of folded intramolecular contacts at longer length scales. Experimental evidence also suggests that strand orientation in the proximity of the crystals is aligned more or less parallel to the fibre axis, also supporting this initial configuration (van Beek et al. 2002; Rousseau et al. 2009).

For structure identification, we carry out simulations with Langevin dynamics using CHARMM (Brooks et al. 1983) and the EEF1.1 force field with a Gaussian effective solvent energy function (Lazaridis & Karplus 1999). The REMD protocol is set up using the MMTSB toolset (Feig et al. 2004). A simulation time step of 2 fs is used by employing the SHAKE algorithm for hydrogen atoms. Solvent friction is added via a Langevin friction term that allows for high mobility and conformational sampling. While the EEF1.1 model has some particular modifications and simplifications on solvent, side-chain and hydrogen bond interactions, it has the benefit of being orders of magnitude faster than other implicit or explicit solvent models, and the solvent volume exclusion model is particularly attractive for large-scale assembly processes as in the case of spider silk. Since force fields are generally parameterized for room temperature calculations, we only pick ensemble structures from the lowest temperature replica and use higher temperatures only for overcoming kinetic trapping and fast conformational search in the REMD scheme.

Initial structures are oriented along the main chain axis using built-in functions in CHARMM (see geometry shown in figure 2). We perform long initialization runs to obtain distinct starting configurations to enhance better sampling in the production run. This is followed by a production run starting from the final configurations of the replicas from the initialization run and using an exchange time step of 2 ps to allow the relaxation of the system. Starting from the final configurations of the initial run, we run simulations on 64 replicas distributed over the 300–650 K temperature range (the high-temperature replicas ensure that the protein can sample a wide range of conformations). Each replica is simulated for a total of 10 ns, corresponding to a total simulation time of 640 ns for each sequence.

An ensemble of structures is analysed from the last 1000 exchanges of the production run from the lowest temperature replica, and is used to extract the lowest energy structures (coordinates of all structures generated from our simulations are available from the authors upon request). Representative final structures are selected based on a clustering algorithm grounded on mutual similarity according to root mean square deviation for each structure. We use the K-means clustering algorithm in the MMTSB toolset (Feig et al. 2004) to identify the largest clusters that have approximately 10 per cent or more presence in the selected set, corresponding to the top five clusters. From the selected clusters, we present structures closest to the cluster centre as the representative models. Analyses on dihedral angles and alpha-carbon distances are carried out using the complete dataset to achieve better statistical representation. The secondary structure content is calculated in visual molecular dynamics (VMD; Humphrey et al. 1996) using the STRIDE algorithm.

2.2. Nanomechanical analysis

Mechanical stretching tests are done using a constant loading rate of 2 pN applied every 20 ps, that is, a loading rate of 0.2 N s⁻¹. Half of the chains are randomly selected to be pulled in the +z direction while the other half is pulled in –z, to impose the characteristic lateral loading of the crystals as experienced in the native silk structure (see schematic shown in figure 2c).

Force–extension plots are based on the forces applied, and the measured distance between the centre of mass of pulled atoms. The analysis on hydrogen bond dynamics is computed using .tcl scripts.

3. Results

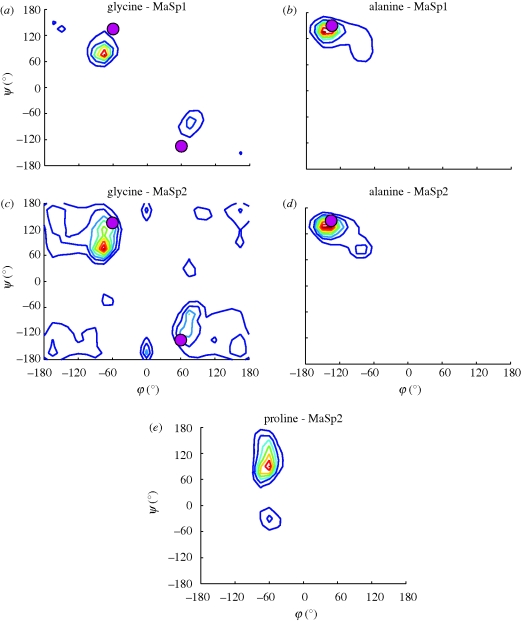
Here, we present our structural predictions and compare the results with experimental evidence. We focus primarily on torsion angles and secondary structures of most common amino acids, since this approach allows for a direct quantitative comparison that is independent of the size of the system studied. Since the majority of silk consists of glycine and alanine amino acids, we directly compare the dihedral angles of glycine and alanine residues with experimental data on spider silk proteins. For MaSp1 alanine residues (figure 3a), we observe that the most common φ–Ψ angle value is around (−150, 135), in excellent agreement with experimental findings that suggested (−135, 150), corresponding to a beta-sheet structure. For glycine (figure 3b), our results show a symmetry around the origin, where we observe a wide distribution around approximately (+/−75, −/+75), in agreement with experimental findings around (+/−60, −/+135; van Beek et al. 2002) that also have symmetry. Similar results are observed for MaSp2 (figure 3c–d); however, a wider distribution of glycine dihedral angles is evident from the Ramachandran plot.

Figure 3.

Comparison of resulting structures for MaSp1 and MaSp2 with experimental data for validation. (a–d) For alanine residues, we observe that the most common φ–Ψ angle value is around (−150, 135), in excellent agreement with experimental findings that suggested (−135, 150), corresponding to a beta-sheet structure. For glycine residues, we observe a wide distribution around approximately (+/ − 75, − / + 75) with symmetry around the origin, in line with experimental findings around (+/60, − / + 135) that also show symmetric distribution. The wider distributions in MaSp2 may be due to a more amorphous structure caused by high proline content. (e) Dihedral angle distribution of proline residues cluster around (−60, −30) and (−60, 120), which correspond to type I and type II beta-turn conformations, respectively.

While mapping of the poly-alanine regions to beta-sheet conformation is straightforward from the data on alanine residues for both structures, the glycine regions require more data to be able to distinguish them within common protein structures. A close look at proline residues in MaSp2 shows peaks around (−60, −30) and (−60, 120), corresponding to type I and type II beta-turns that would incorporate adjacent Gly residues. From the ensemble of structures obtained from MaSp1 replica exchange simulations, we consider the alpha-carbon atom distances between glycine residues that are three residues apart, to characterize the basic repeat unit length of the GGX domains. The probability distribution of Cα(i)–Cα(i + 3) distances measured from atomic coordinates has a distinct peak around 9 Å. This value is greater than most known beta-turn structures and falls short of the anti-parallel beta-sheet conformations that typically exceed 10 Å. These domains have interchain hydrogen bonding that is less oriented and sparser. Based on these observations, we conclude that these disorderly structures in MaSp1 resemble the characteristics of 3₁-helices, which are the most probable conformations taken by Gly-rich domains, supporting earlier hypotheses reported in the literature (Kummerlen et al. 1996; van Beek et al. 2002). The density of hydrogen bonding in these regions is significantly reduced compared with the orderly network in beta-sheet nanocrystals, suggesting that moderating the number and orientation of intermolecular interactions leads to the characteristic heterogeneous structural arrangement observed in silks.

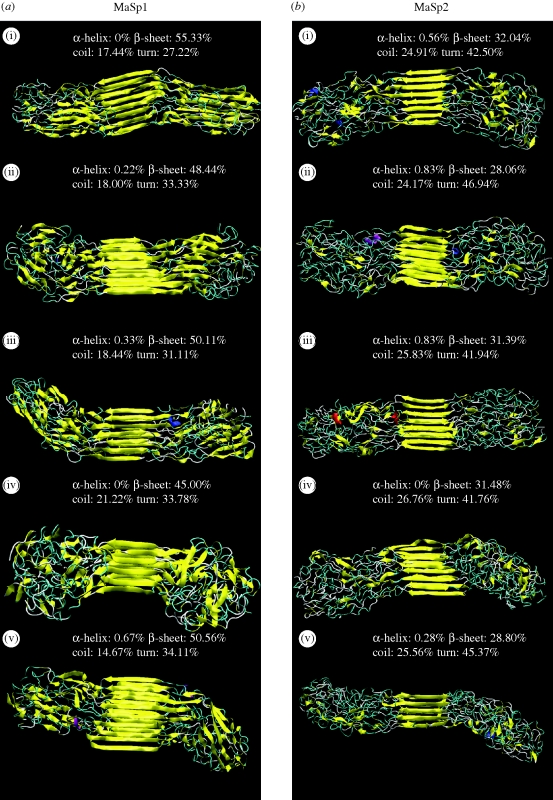
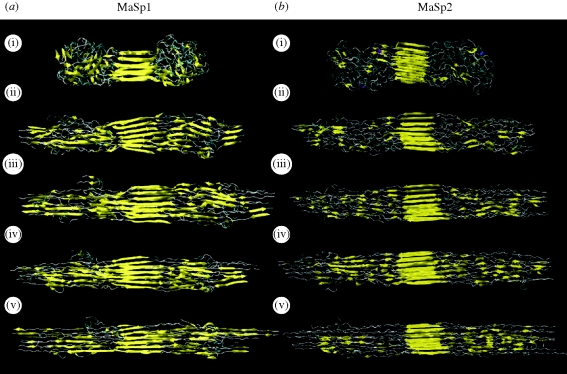
For illustrative purposes, a representative collection of selected structures (see §2) obtained from the simulations is shown in figure 4, where percentages of different secondary structures are illustrated in each subpanel (i–v). For both MaSp1 and MaSp2, a significant percentage of residues are found to be in semi-extended, disorderly conformations in agreement with the discussion put forth based on experimental studies (Rammensee et al. 2008). Our results suggest that poly-alanine regions have an extremely high propensity for aggregating into crystalline beta-sheet structures by inter-strand hydrogen bond formation and inter-sheet stacking in the side-chain direction. Along with glycine regions that also form extended regions, the beta-sheet percentage ranges from 28 to 55 per cent for the sequences studied in this work. These results compare well with recent NMR studies on dragline silk, which have indicated 34 per cent beta-sheet content (Jenkins et al. 2010). This highly orderly domain is dispersed within the glycine-rich repeat units, which are still fairly oriented but much less orderly, forming more amorphous structures. A key finding from the secondary structure content analysis is the lack of any alpha-helix conformation of the MaSp1 and MaSp2 silk constituents, supporting a wide range of experimental evidence that ruled out this conformation (Jelinski 1998; van Beek et al. 2002; Holland et al. 2008; Jenkins et al. 2010). Instead, our results suggest that disorderly structures resembling 3₁-helices and beta-turns dominate non-beta-sheet conformations in these proteins. The higher content of proline in MaSp2 leads to more disorderly structures in amorphous regions and well-defined beta-sheet crystal regions. This is evident from both the lower ratio of beta-sheets in this sequence, and also the shorter lengths of beta-strands when comparing MaSp1 structures in figure 4a with those of MaSp2 in figure 4b.

Figure 4.

Secondary structure distribution of selected protein assemblies. We select the most representative structures from the lowest temperature replica, and calculate the secondary structure distribution for (a) MaSp1 and (b) MaSp2 protein assemblies. (i–v) The five most likely structures selected for each sequence. The colouring is based on structural configuration, in which yellow represents beta-sheet and extended structures. (a) The selected structures for MaSp1. The majority of the structures are observed to be in beta-sheet or beta-turn conformation, and, for MaSp1 (a), the beta-sheet content is higher than for MaSp2 (b) owing to the lack of proline residues that reduce chain aggregation into sheets. The relative content of secondary structure controls the mechanical properties of protein assemblies, in which greater crystallinity typically means greater strength, whereas turn structures provide hidden length required for extensibility and toughness. (b) Representative structures for MaSp2. The results consistently show that poly-Ala regions form highly orderly beta-sheet crystals whereas the glycine-rich repeat units are less orderly, forming more amorphous domains.

Altogether, the structure identification and comparison with available experimental results suggest that the models obtained from our simulations resemble those found in native spider silk. Overall, crystal structures consisting of poly-Ala repeats have the size of 2–3 nm in the chain direction, with partial beta-sheet domains in semi-crystalline regions, particularly for MaSp1. Stacks of 2–4 sheets (1–2 nm) and up to eight strands per sheet (2–4 nm) are observed in simulations (but these values may increase if the number of chains considered is increased). The amorphous domains are semi-extended, and the average lateral length per residue for both structures emerges as around 2–3 nm, which is shorter than fully extended structures that would require more than 3 nm length. We do not observe larger folds where sheets are formed by polypeptide strands through self-interactions, but such morphologies cannot be ruled out considering that actual spider silk sequences are much longer and therefore more flexible than the short segments we have studied here. In this regard, this study sets the stage now to explore the mechanical properties of both the MaSp1 and MaSp2 structures using ultra-large-scale molecular dynamics simulations.

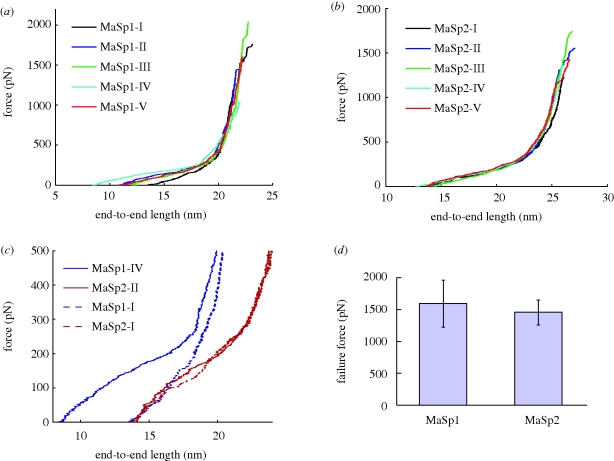
We proceed with carrying out constant loading rate mechanical shear simulations on the selected structures, where randomly selected strands are pulled in opposite directions to mimic the relevant lateral (shear) loading conditions of small crystals in spider silk. The resulting force–displacement curves from these simulations are shown in figure 5a,b. Both MaSp1 and MaSp2 show a characteristic smooth curve with three regimes, where the relative moduli of these regimes depend on the secondary structure content. For molecules with high turn ratio and low beta-sheet content (see MaSp1-IV and MaSp2-II), we observe an initial stiff regime, followed by a softer regime, followed by a very stiff regime leading to failure. On the other hand, systems with very high beta-sheet content (MaSp1-I, MaSp2-I) show a monotonically stiffening force–extension response. This suggests that the characteristic yielding behaviour at the molecular level of the hierarchy of silk is controlled by the ratio of turn to beta-sheet structures, where a higher turn ratio leads to the emergence of this phenomenon. This is an alternative means of achieving high initial stiffness in comparison with, for instance, the MaSp1-I structure, which has more beta-sheet content and therefore exhibits high initial stiffness as well, but provides much less extensibility. We find that MaSp1 generally exhibits a larger deviation in the initial end-to-end length, owing to the wider secondary structure distribution. The effect of this is evident from the analysis displayed in figure 5c, which illustrates the yielding behaviour of both structures and much larger variation in response in MaSp1, where increasing the turn content and inter-chain hydrogen bonding increases the initial stiffness and extensibility of the assembly, thereby improving the toughness as well. The failure strengths of MaSp1 and MaSp2 seem to be similar in our simulations, as shown in figure 5d.

Figure 5.

Force–displacement curves for selected structures. Figure shown illustrates the response of selected structures to shear forces applied to alternating strands. Force values shown are the loads applied per polypeptide strand. Illustration of the plots obtained from MaSp1 (a) and MaSp2 (b). The forces cause tensile stretching of the strands, in which a strain stiffening behaviour is evident once the chain reaches a certain length, independent of the chain's initial stretch state. The responses are similar for MaSp1 and MaSp2; however, it depends on the secondary structure content of the system. MaSp1 structures have a large variation on beta-sheet versus turn content, which leads to distinctly different mechanical responses (c). Solid lines indicate cases having the largest turn content, whereas dashed lines indicate structures with more beta-sheets. As the turn ratio increases, an initial stiff regime, followed by softening, followed by a stiff bond stretching regime is observed. For extended structures, the initial stiff regime disappears and the typical strain stiffening behaviour of polypeptide chains can be observed. The source of this difference is the existence of denser hydrogen bonding in amorphous regions owing to turn formation, which leads to higher stiffness and energy dissipation for structures containing more turns. The lower variation of turn and beta-sheet content in MaSp2 leads to the reduced variation of the mechanical response for this structure. As can be inferred from (d), the failure strength of both structures is more or less the same, as expected from the sequence similarity of the alanine-rich crystalline regions controlling the onset of failure.

The force–extension curves obtained here also show minor deviations from the inextensible chain models commonly used for polymer materials. At low forces, this is due to the rearrangement and rupture of H-bonds in the amorphous domains. At high force, the crystal morphology can change owing to large shear stresses as well as transverse compression, where the latter causes buckling and collapse of the sheet into a smaller, more compact formation.

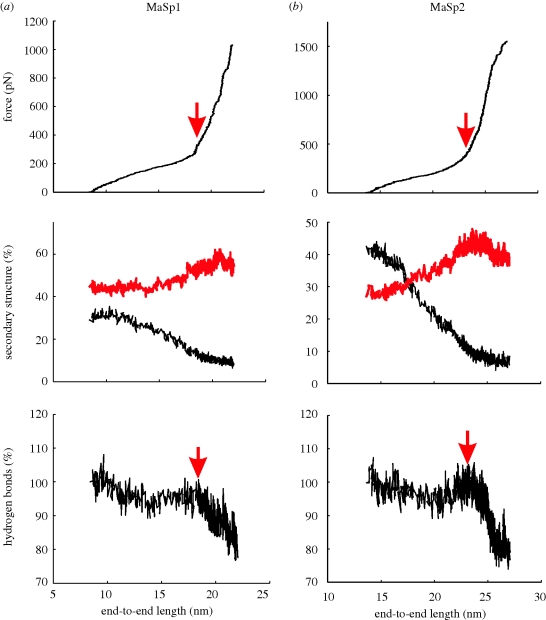
Some of the structural transformations and failure mechanisms can be observed from the trajectories obtained from stretching simulations of the spider silk assemblies. Figure 6a,b(i–v) shows snapshots of deformation from MaSp1 and MaSp2 stretching simulations. As evident from the snapshots and the analysis presented in figure 7a,b, amorphous domains stretch significantly with applied force, and a transition from turn to beta-sheet structures can be observed for both MaSp1 and MaSp2 (the regime just before the point is marked by a red arrow in figure 7). The per cent change seems to be larger for MaSp2, since in their unstretched configuration proline residues act as beta-sheet breakers. A key observation is that failure of the system happens by sliding of strands with respect to each other, which can occur only upon breaking of the hydrogen bonds in the crystalline domain. In our simulations, failure occurs at the interface region with solvent at the boundary of the crystal, leaving part of the crystal intact even after failure.

Figure 6.

Stretching and structural transformation of the proteins. The figure illustrates the stretching behaviour of the amorphous domains and crystals under shear forces for (a) MaSp1 and (b) MaSp2. (i–v) The time sequence of events during the stretching simulations. As evident from the time sequence of snapshots (i–v), amorphous domains stretch significantly, and a transition from turn to beta-sheet structures is observed. The GGX repeats in MaSp1 are capable of forming beta-sheets during stretching, whereas this is observed to a lesser extent in MaSp2, in particular at low extension. A key observation is that failure of the system happens by sliding of strands with respect to each other upon breaking of the hydrogen bonds and side-chain contacts in the crystalline domain. This typically occurs at the interface region with solvent at the boundary of the crystal, leaving part of the crystal intact even after failure of the structure.

Figure 7.

Representative plots are shown from MaSp1 and MaSp2 structures with the highest turn content. Comparison of (a) and (b) shows the strain softening behaviour that occurs when the turn/beta-sheet ratio is high in the initial structures. Upon initial yielding, the number of hydrogen bonds in the system and also the turn content decreases; however, further stretching leads to a slight increase in the number of H-bonds and formation of beta-sheet structures in the amorphous region. This is followed by a final stiff regime dominated by the stretching of covalent bonds, which ultimately leads to rapid rupture of many hydrogen bonds (shown with a red arrow) in the non-crystalline domains. The system fails upon breaking of hydrogen bonds in the crystal, and sliding of beta-strands. The characteristic sigmoidal force–extension behaviour observed here for both structures shows resemblance to the macroscale response of spider silk. (a,b) Black line, turn; red line, beta-sheet.

Representative plots from MaSp1 and MaSp2 structures with highest turn content are shown in figure 7. A comparison of figure 7a and b shows the strain-softening behaviour that occurs when the turn/beta-sheet ratio is high in both structures. Upon initial yielding, the number of hydrogen bonds in the system and also the turn content decrease, as shown in figure 7a,b, respectively, for MaSp1 and MaSp2. Further extension leads to a slight increase in the number of H-bonds and formation of beta-sheet structures in the amorphous region. This is followed by a final stiff regime dominated by the stretching of covalent bonds, which ultimately leads to rapid rupture of many hydrogen bonds (shown with a red arrow) in the non-crystalline domains. Eventually, a final stiff regime is reached where covalent bonds in the peptide backbone are stretched out (regime after the point marked by a red arrow in figure 7), which initiates rapid rupture of many hydrogen bonds in the amorphous domains. The system fails upon breaking of hydrogen bonds in the crystal and the subsequent sliding of strands. The constitutive sigmoidal behaviour of the force–displacement graphs observed here for both structures agrees qualitatively with the macroscale response of spider silk.

4. Discussions and conclusion

We have presented results from atomistic simulations on MaSp1 and MaSp2 protein segments of the spider dragline silk from N. clavipes. We have illustrated that the REMD simulation method establishes an atomistic basis for a wide variety of findings from experimental studies of the silk nanostructure. Key findings from secondary structure and dihedral angle analyses have shown that poly-Ala regions in MaSp1 and MaSp2 form beta-sheet crystals, whereas the glycine-rich regions form semi-extended 3₁ helix type structures as well as beta-turns (figure 3). Our simulations show no evidence for the existence of alpha-helix or beta-helix structures in MaSp1 and MaSp2 repeating units.

Our results confirm that MaSp1 and MaSp2 form different nanostructures. MaSp1 tends to form more orderly extended structures with beta-sheet domains, whereas turn structures and a greater level of amorphousness are observed in MaSp2, owing to the natural twist of the proline segments, which limits the crystalline fraction of the protein assemblies (figures 3 and 4). The existence of semi-extended domains in the amorphous matrix may be the molecular source of the large semi-crystalline fraction observed in silks, and also form the basis of the so-called ‘pre-stretched’ molecular configuration (Ene et al. 2009). The presence of less dense hydrogen bonding in glycine-rich regions compared with alanine-rich regions indicates at least a two-phase system with complementary mechanical functions: extensibility and fracture strength. This is more evident in MaSp2, which has apparent features resulting from the proline-rich sequence, such as higher disorder and well-defined crystal regions. Of particular importance for this effect is the lack of amide bonds and the torsional twisting at proline sites, which control morphology development as the proline residues have varying capacity to form hydrogen bonding at different extension states. In the actual morphology of dragline silk, both proteins can be observed at varying amounts depending on the species (Hinman & Lewis 1992; Guerette et al. 1996; Brooks et al. 2005; Sponner et al. 2005). The current study focused on isolated systems of MaSp1 and MaSp2, but the same simulation protocol can be applied to understand the structure and behaviour of mixed systems, and the possible role of proline in controlling intermolecular contacts between MaSp1 and MaSp2. Overall, the results reported here are strongly supportive of experimental findings on the spider dragline silk that suggest similar structural characteristics, in particular the existence of a Gly-rich amorphous phase and Ala-rich crystalline phase (Thiel et al. 1997; van Beek et al. 2002).

The mechanical stretching simulations hint towards a sigmoidal constitutive behaviour as observed in the macroscale response of spider silk, as shown in figure 5c. Our results provide insight into the nanoscale deformation mechanisms, as shown in the simulation snapshots in figure 6 and the detailed analysis in figure 7. We find that the initial softening of the system is governed by hydrogen bond breaking in the amorphous domain. Strain stiffening is observed once the covalent chains are highly extended after rupture of a large number of hydrogen bonds in the non-crystalline domains. The eventual failure of the system occurs when strands begin to slide across each other owing to severed hydrogen bonds and side-chain interactions in the crystal. Considering that the initial end-to-end length of the systems studied ranges from 8 nm to 14 nm and failure occurs at around 25 nm or more, the failure strains observed here seem to be much larger than that of experimental studies that show failure strains around 40 per cent (Du et al. 2006). The source of this discrepancy may be several factors in our simulations that differ from experiments. First, the results for strain will depend on sequence; here, we study two amorphous domains and one crystal domain, hence our system is likely to be more extensible. The second reason is that, in the actual morphology of silk, there will be heterogeneity and defects, and orientation of the forces with respect to chains will not be perfect. Hence, the extensibility of the chains will be further reduced, as they will slide across each other more easily in non-uniform loading. A third possible reason is that current simulations correspond to hydrated systems with no control on prestretching. Prestretching of the strands during silk synthesis may contribute to the lower failure strain of the actual systems. More analysis and upscaling of our results will have to be done to make a rigorous link between nanoscale results and macroscale experiments. The failure strength of the molecular assembly shows less variation between sequences; rather, it is observed to depend more on the morphology of the crystal and the amorphous structures. Based on our simulations, we note that mechanical stretching of the strands may play a role in controlling crystal size, where compression in the transverse direction causes collapse of the crystals into a more compact formation. This may be an important consideration for the influence of mechanical strain on the morphology of the silk crystals (Grubb & Jelinski 1997).

In summary, we have developed and applied a framework for predicting the nanostructure of spider silk using atomistic principles that could be widely applicable not only to different types of silks but also to other biopolymers, and thereby provide a link between genetics and material properties. This materiomics framework provides a powerful tool to explore fundamental structure–property relationships of complex biological materials such as spider silk. Our atomistic calculations resolve some of the controversies regarding the structure of the amorphous domains in silk by shedding light on the semi-extended, well-oriented and more sparsely hydrogen-bonded structures in amorphous domains. To the best of our knowledge, the results reported here—combining REMD structure identification with experimental validation and a subsequent detailed nanomechanical analysis with a study of fundamental deformation mechanisms—is the first of its kind for spider silk, and only the beginning. We expect that future studies could be focused on improved structure prediction and a wide variation of conditions during mechanical analysis.

Our findings may set the stage for more extensive full-atomistic mechanics studies on silk domains that will contribute towards an improved understanding of the source of the strength and toughness of this biological superfibre, where the structures identified here could be subjected to mechanical loading under varying conditions, such as changes in solvent or pH, and even under variations of the amino acid sequence of the constituting protein domains. Future investigations could also focus on much larger, mixed MaSp1/MaSp2 systems in a variety of conditions or on the impact of mechanical constraints on the assembly and initial structure formation.