Skip to main content
PMC home page
Journal of the Royal Society Interface logoLink to Journal of the Royal Society Interface
. 2010 Jul 14;7(53):1753–1758. doi: 10.1098/rsif.2010.0292

Bridging the gulf between correlated random walks and Lévy walks: autocorrelation as a source of Lévy walk movement patterns

Andy M Reynolds 1,*
PMCID: PMC2988271  PMID: 20630882

Abstract

For many years, the dominant conceptual framework for describing non-oriented animal movement patterns has been the correlated random walk (CRW) model in which an individual's trajectory through space is represented by a sequence of distinct, independent randomly oriented ‘moves’. It has long been recognized that the transformation of an animal's continuous movement path into a broken line is necessarily arbitrary and that probability distributions of move lengths and turning angles are model artefacts. Continuous-time analogues of CRWs that overcome this inherent shortcoming have appeared in the literature and are gaining prominence. In these models, velocities evolve as a Markovian process and have exponential autocorrelation. Integration of the velocity process gives the position process. Here, through a simple scaling argument and through an exact analytical analysis, it is shown that autocorrelation inevitably leads to Lévy walk (LW) movement patterns on timescales less than the autocorrelation timescale. This is significant because over recent years there has been an accumulation of evidence from a variety of experimental and theoretical studies that many organisms have movement patterns that can be approximated by LWs, and there is now intense debate about the relative merits of CRWs and LWs as representations of non-orientated animal movement patterns.

Keywords: correlated random walks, non-orientated movements, Lévy walks

1. Introduction

For many years, the dominant conceptual framework for describing non-oriented animal movements has been the correlated random walk (CRW) model in which an individual's trajectory through space is regarded as being made up of a sequence of distinct, independent randomly oriented ‘moves’ (Kareiva & Shigesada 1983; Turchin 1998 and references therein). Turning angles are drawn at random from a unimodal distribution that is typically peaked around zero degrees. Because small turns are much more likely than large ones, the models can mimic the observed tendency of many animals to move forward, a tendency known as ‘directional persistence’.

It has long been recognized that the transformation of the animal's continuous movement path into a broken line is necessarily arbitrary and that probability distributions of move lengths and turning angles are model artefacts (see Turchin 1998 and references therein). Dunn & Brown (1987) and Alt (1988, 1990) were perhaps the first to address the problem. They formulated ‘continuous-time’ CRW models. In these models, velocities evolve as a Markovian process and are exponentially autocorrelated. Integration of the velocity process gives the position process. The approach pioneered by Dunn & Brown (1987) and by Alt (1988, 1990) has recently been developed by Johnson et al. (2008) who demonstrated its utility in an analysis of telemetry data for harbour seals (Phoca vitulina) and northern fur seals (Callorhinus ursinus). All of these models are founded on the classic Langevin equation

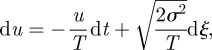1. 1.1

where dξ(t) is an incremental Wiener process with autocorrelation 〈dξ(t)dξ(t′)〉 = δ(t − t′)dt. This stochastic equation describes how velocity, u, changes by an amount du in a time increment of size dt. Modelled velocities, u, are Gaussian distributed with mean zero and variance σ2. Velocities are also exponentially correlated, 〈u(t + τ)u(t)〉 = σ2 exp(−τ/T). Discrete versions of the Langevin equation are first-order autoregressive AR(1) processes, and these correspondences allow for statistical inferences of model parameter values from discrete telemetry records (Johnson et al. 2008). Two-dimensional movements can be simulated using two independent Langevin equations for movements in the x- and y-directions, and such a model has been shown to represent faithfully the movement patterns of harbour and northern fur seals (Johnson et al. 2008). At short times, t < T, mean-squared displacements evolve according to 〈x2〉 = σ2t2 and movements are said to be ‘ballistic’. At long times, 〈x2〉 = 2σ2Tt and movements are diffusive (Doob 1942). At long times (t >T), the Langevin equation reduces to the simplest discrete-time CRW model. This can be seen by first multiplying both sides of the Langevin equation by T and then taking the long-time limit (equivalent to letting T → 0 while σ2T → K, where K is the diffusivity). This procedure gives T du =−u dt + 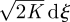Inline graphic. The term T du vanishes because velocity increments are bounded. The quantity u dt is just the incremental change in position, dx. The Langevin equation thus reduces to the discrete CRW model, dx = 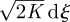Inline graphic, at long times. A more general argument developed by Thomson (1987), in the context of atmospheric dispersal modelling, shows that any continuous-time CRW model with fixed parameters will reduce to dx = 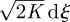Inline graphic at long times.

In parallel with these developments, there has been an accumulation of empirical and theoretical evidence that many animals have movement patterns that can be approximated by Lévy walks (LWs) (see Raposo et al. 2009; Reynolds & Rhodes 2009 and references therein). LWs first entered the literature on animal movement patterns when it was proposed that they may be observed in foraging ants (Shlesinger & Klafter 1986). LWs have subsequently been found to represent accurately the movement patterns of a diverse range of animals that includes microzooplankton (Bartumeus et al. 2003), honeybees (Reynolds et al. 2007a,b, 2009), fruitflies (Reynolds & Frye 2007) and many marine predators (Edwards 2008; Sims et al. 2008).

LWs comprise clusters of short move step lengths with longer moves between them. This pattern is repeated across all scales, with the resultant scale-free clusters creating fractal patterns. Directions of movement are uniformly distributed between 0° and 360°. Distributions of individual movement lengths, l, have power-law tails, pl(l) ∼ l−μ, where 1 < μ ≤ 3. Distributions of total displacements (i.e. sums of individual lengths) tend to Lévy stable distributions by virtue of a generalized central limit theorem owing to Gnedenko and Kolmogorov. For μ > 3, total displacements eventually become Gaussian distributed by virtue of the central limit theorem and so these motions are effectively Brownian at long times. The cases of μ ≤ 1 do not correspond to normalizable distributions with probabilities that sum to unity. Mean-squared displacements of μ ≤ 2 Levy walks grow ballistically as 〈x2〉 ∼ t2 (Klafter et al. 1996) just as they do for continuous-time CRWs at short times.

LWs have not met with acceptance in some quarters. This is in part because of a perceived lack of biological realism. It is one thing to explain large-scale movements with Gaussian, space-filling CRW but quite another to do so with fractal, superdiffusive LWs. But this common and perfectly reasonable viewpoint is shown here to be erroneous. An exact mathematical analysis reveals that the distances travelled between successive ‘turns’ in movement patterns produced by the Langevin equation are μ = 4/3 power-distributed. Such power-law scaling is the defining characteristic of a μ = 4/3 LW movement pattern and illustrates that the CRW and LW paradigms are not mutually incompatible. The connection between CRWs and LWs therefore runs far deeper than their appearing to have similar superdiffusive characteristics in some situations (Viswanathan et al. 2005). The new analysis draws upon the previous work of Kearney & Majumdar (2005) who obtained exact μ = 4/3 power-law scaling for the area under continuous-time Brownian motion. The approach developed by Kearney & Majumdar (2005) is rigorous and is the simplest one known for the establishment of such power-law scaling. Here, this approach is used to establish an exact power-law scaling for the area under velocity records produced by the Langevin equation. The area under a velocity record is a net displacement and the area under a velocity record between successive zero-crossings is a net displacement made between successive turns in a one-dimensional movement pattern. So while the physical content of the results presented here has previously appeared in other contents, the results are interesting in a biological context because they provide a straightforward connection between CRWs and LWs. The connection is a priori relevant in real animal trajectories.

In the next section, it is proved that one-dimensional μ = 4/3 LW movement patterns arise from the Langevin equation. A simple, more accessible but approximate scaling argument is then given for the production of μ = 4/3 LW movement patterns by other one-dimensional continuous-time CRW models. The theoretical predictions are supported by the results of numerical simulations. One dimensionality is not an unrealistic scenario as terrestrial ecotones such as riparian forests, dune systems or rocky shores with strong depth-environmental gradients force ‘edge’-foraging (one dimensionality; Bartumeus et al. 2008). Two-dimensional movement patterns produced by two independent Langevin equations for movements in the x- and y-directions do not seem to be amenable to analytic analysis and are examined later with the aid of numerical simulations. This analysis uncovers the presence of LW movement patterns. A discussion of the findings and their connection with recent observations is presented in §3.

2. Autocorrelation as a source of lw movement patterns

2.1. Exact analytic analysis of one-dimensional movement patterns

Here, through an exact mathematical analysis and a general scaling argument it is shown that the distances, x, travelled between successive turns in one-dimensional movement patterns produced by the Langevin equation are power-law distributed over an extended range of scales and are indicative of μ = 4/3 LW movement patterns.

Let P(x|u0) be the distribution of distances x given the initial condition, u(0) = u0. The Laplace transform of P(x|u0) is

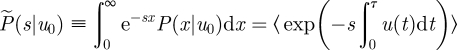2.1. 2.1

where s is the Laplace transform variable and where the angular brackets denote an ensemble average over of all possible velocity records that begin with u(0) = u0 and end with u(τ) = 0, i.e. end immediately prior to a change in direction (Kearney & Majumdar 2005). Following Kearney & Majumdar (2005), the time interval [0, τ] is now split into two parts: a left interval [0, Δt] where according to the Langevin equation (equation (1.1)) the velocity proceeds from u0 to 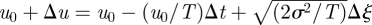Inline graphic in a time Δt and a right interval [Δt, τ] in which the process starts at u0+Δu0 at time Δt and reaches 0 at time τ. Equation (2.1) can then be rewritten in the form of a recurrence relation

2.1. 2.2

where we have used the fact that for the right interval [Δt, τ], the starting position is u0 + Δu0, which itself is random. The ensemble average in equation (2.2) is over all velocity increments Δu. Substituting 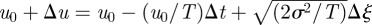Inline graphic into equation (2.2), expanding in powers of Δt, averaging over the noise Δξ and then collecting together terms of order Δt yields the celebrated Feynman–Kac equation (Kac 1949)

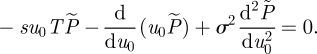2.1. 2.3

Appropriate boundary conditions for equation (2.3) follow from equation (2.1). When u0/σ → 0, the time τ till u = 0 must also tend to zero. The integral 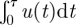Inline graphic in equation (2.1) then vanishes and 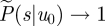Inline graphic. When u0/σ →∞, the time τ till u = 0 must diverge. The integral 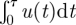Inline graphic in equation (2.1) then diverges and 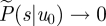Inline graphic. Normalization requires that 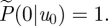Inline graphic For small speeds (|u0| < σ), the solution to equation (2.3) satisfying these conditions is

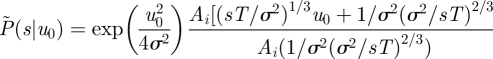2.1. 2.4

where Ai(x) is the Airy function.

In the short time limit (equivalent to T → ∞), equation (2.4) reduces to

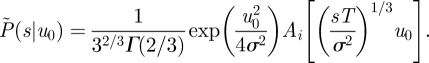2.1. 2.5

The inversion of the Laplace transform of equation (2.5) gives the distribution P(x|u0) of distances travelled between consecutive turning points made over short times. The inversion is achieved by noting that

2.1.

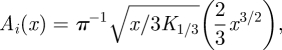where K1/3 is a modified Bessel function, and by noting that

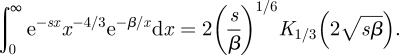2.1. 2.6

This gives

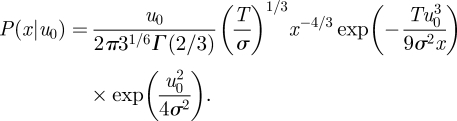2.1. 2.7

This distribution P(x|u0) has a power-law tail

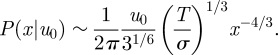2.1. 2.8

Equation (2.8) is indicative of μ = 4/3 LW movement patterns. This finding can be explained using a simple but approximate scaling argument. Integration of the Langevin equation (1.1) gives 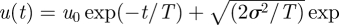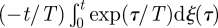Inline graphic Inline graphic. Velocities therefore grow diffusively like u ∼ t1/2 at short times (t/T < 1) after a turn (u0/σ < 1). And so distances travelled between consecutive turns, 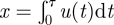Inline graphic, will typically scale as τ3/2 where the distribution of times, τ, between consecutive turns, pτ(τ) ∼ τ−3/2 (Wang & Uhlenbeck 1945). The result of Wang & Uhlenbeck (1945) is an example of the continuous-time analogue of the Sparre Andersen theorem according to which any discrete-time random walk process with each step chosen from a continuous, symmetric but otherwise arbitrary jump length distribution produces a first passage time density governed by the universal long-time decay n−3/2 (Sparre Andersen 1953, 1954). It follows that distances travelled between consecutive turns are distributed according to a power law p(x) ∼ x−4/3. The generality of the scaling argument suggests that μ = 4/3 LW movement patterns are a ubiquitous characteristic of continuous-time CRW models. This possibility is supported by an exact analysis (not presented) of the continuous-time CRW model for exponentially distributed velocities.

It can be shown that in the long-time limit (equivalent to T → 0), 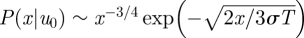Inline graphic. LW characteristics are therefore truncated at large scales.

2.2. Analysis of simulation data for one- and two-dimensional movement patterns

One-dimensional movement patterns were simulated by numerical integration of the Langevin equation. The Akaike information criterion was used to test whether simulation data provided more evidence for distances, l, travelled between successive turns being power-law p1(l) = (μ − 1)aμ−1l−μ (l > a) or exponentially distributed p2(l) = λe−λ(l− a) (l > a). The Akaike weight for a power-law distribution can be considered as the weight of evidence in favour of a power-law distribution being the better model of the simulation data, i.e. the Akaike weight for a power law can vary from 0 (no support) to 1 (complete support; Edwards 2008). Plots of the survival function (the complement of the cumulative distribution function) were also used to further examine the form of the tails and to determine the extent of power-law scaling: an approach that is more reliable than probability density function plots (White et al. 2008). To construct the survival function, the simulation data {li} is first ranked from largest to smallest {i = 1, … , n}. The probability that a length is greater than or equal to li (the survival function) is then estimated as i/n.

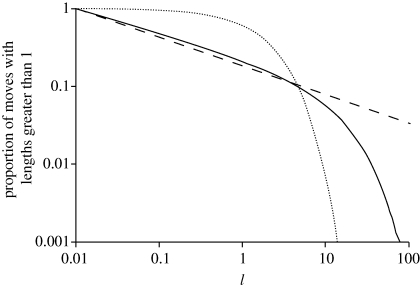
For one-dimensional movements, the Akaike weights for power laws are 1.00, indicating that power-law distributions are convincingly favoured over exponential distributions. And the maximum-likelihood estimate μ = 1.33 (a = 0.01) coincides with the analytically-determined scaling for one-dimensional movements (e.g. figure 1). Power-law scaling extends over about two decades but breaks down when lengths are comparable with σT (figure 1). The lower cut-off length a = 0.01 is comparable with the mean distance during the time step of numerical integration. The Akaike weights and the maximum-likelihood estimates μ are not sensitively dependent upon a.

Figure 1.

Figure 1.

Open in a new tab

The survival function (the complement of the cumulative distribution) of ‘move’ lengths travelled between consecutive turns (solid line). Shown for comparison are the maximum-likelihood power-law (dashed line) and exponential (dotted line) distributions. A straight line on this log–log plot is indicative of power-law scaling. Here, approximate power-law scaling is seen to extend over about two decades. Data are shown for one-dimensional movement patterns produced by the Langevin equation with σ = 1 and T = 10. The Langevin equation was integrated numerically with a time step Δt = 0.01 arbitrary time units.

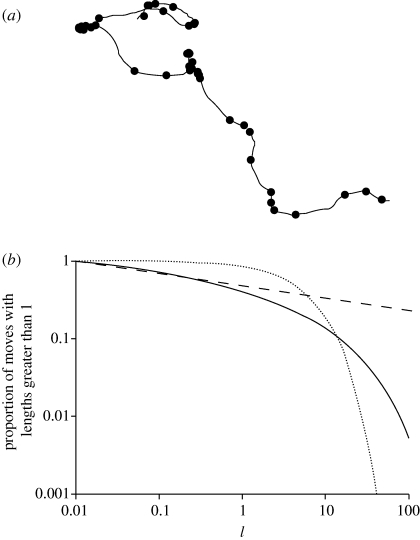
Two-dimensional movement patterns were simulated using two independent Langevin equations for movements in the x- and y-directions. Whereas the notion of a turn is clear in one dimension (turns arise whenever the velocity changes sign), the definition of a turn is ambiguous in two dimensions. Here the first turn in a movement pattern is deemed to have arisen when the absolute difference between the current and initial directions of travel, θ1 and θ0, differed by a critical amount, Δθc, i.e. when the direction of travel had changed by an amount Δθc. The next change turn arises when |θ2 − θ1| = Δθc, where θ2 is the new current direction of travel (figure 2a).

Figure 2.

Figure 2.

Open in a new tab

(a) An example of a simulated movement pattern produced by two independent Langevin equations (σ = 1, T = 10) for the x- or y-components of velocity. The Langevin equations were integrated numerically with a time step Δt = 0.01 arbitrary time units. The turning points where the direction of travel changed by an amount Δθc = 45° are indicated (filled circle). (b) The survival function (the complement of the cumulative distribution) of ‘move’ lengths travelled between consecutive turns (solid line). Shown for comparison are the maximum-likelihood power-law (dashed line) and exponential (dotted line) distributions. A straight line on this log–log plot is indicative of power-law scaling. Here, approximate power-law scaling is seen to extend over about two decades.

Analysis of simulation data for two-dimensional movements revealed that straight-line distances (rather than travelled distances) between consecutive turns are power-law distributed to good approximation. The Akaike weights for power-law distributions are typically 1.00 and are not sensitively dependent upon Δθc. Maximum-likelihood estimates for μ are dependent upon Δθc and values for μ range between about 1.1 and about 1.4. For Δθc = 45°, maximum-likelihood estimate for μ = 1.16 (a = 0.01) and power-law scaling extends over about two decades (figure 2b). Akaike weights and maximum-likelihood estimates for μ do not change significantly when instead of the aforementioned definition, a two-dimensional turn is deemed to have arisen when the angle between two successive moves (i.e. between three successive positions) is less than some critical angle. Whether or not LWs characteristics are identified in discretely sampled data is dependent upon the sampling protocol (Plank & Codling 2009).

3. Summary

Whether individual movement patterns are better described by CRW or LW models has been long debated, leading to two streams of thought in the model development of an organism's movement behaviour (Bartumeus 2009). The present study attempts to unify these two directions of model development by showing that continuous-time CRW produce LW movement patterns. This was done by adapting an exact analytic approach developed earlier by Kearney & Majumdar (2005) within a purely theoretical probabilistic context to determine the area under a continuous-time Brownian motion till its first passage time. When applied to the classical Langevin equation, the simplest possible continuous-time CRW model for one-dimensional movement patterns, this approach revealed μ = 4/3 power-law scaling of the distances travelled between successive turns. Such power-law scaling is the hallmark of μ = 4/3 LW movement patterns. A simple, approximate but general scaling argument showed that μ = 4/3 LW movement patterns are not specific to the Langevin equation but will arise from almost any one-dimensional continuous-time CRW model. Analysis of simulation data (figure 2) suggests that this correspondence between continuous-time CRW and LW extends to two dimensions. LW movement patterns were found to provide a good representation of simulation data for two-dimensional movement patterns produced by two independent Langevin equations for movements in the x- and y-directions.

The new results open up new perspectives for understanding and predicting the movement patterns of the enormous variety of animals whose movement patterns can be well represented by discrete CRW (see Turchin 1998 and references therein) and which are likely to be better modelled by more realistic continuous-time CRW.

This advance has resonance with recent developments in the understanding of cell mobility. Most models of cell motility as random motion are founded on generalizations of the Langevin equation (Selmeczi et al. 2005). Model components are, however, ad hoc as they are inspired by fits to experimental data. As a consequence, model agreement with experimental data does not add much to our understanding of spontaneous movements of these cells beyond demonstrating that they can be modelled phenomenologically. However, a slight re-parametrization and re-interpretation of the driving noise lead to the model of Lubashevsky et al. (2009) which realizes LW as Markovian stochastic processes (Reynolds 2010). The distinction between CRW and LW therefore appears to be superficial one, in the context of cell mobility modelling.

The new results do not account for the μ ≈ 2 LW movement characteristics of microzooplankton, honeybees, fruitflies and many marine predators (Bartumeus et al. 2003; Reynolds & Frye 2007; Reynolds et al. 2007a,b, 2009; Sims et al. 2008) that have been attributed to optimal searching. Nonetheless, the findings do suggest that LW movement patterns are ubiquitous because they are an inevitable by-product of autocorrelation. Autocorrelation must be present in all movements but is not captured in discrete CRW modelling. Autocorrelation has been quantified in cell motility studies (see Selmeczi et al. 2005 and references therein) but until recently it has received scant attention in the literature on the movement patterns in ‘higher’ animals. A notable exception to this is the analysis by Johnson et al. (2008) of harbour seal (P. vitulina) and northern fur seal (C. ursinus) telemetry data. Johnson et al. (2008) reported that autocorrelation timescales are several hours long. LW movement patterns on these scales should be evident but have not been reported on. LW movement patterns with μ = 1.25 (1.07, 1.43, 95% CI) and so consistent with model expectations have, however, been found in grey seals (Halichoerus grypus; Edwards 2008).

The fact that LW movement patterns have not so far been uncovered in movement data well described by CRW models can be attributed, at least in part, to the data analysis techniques that tend to mask behavioural intermittency (i.e. turns and bouts of relatively straight-line motion) that is indicative of LW movement patterns (Bartumeus 2009). Recent observations (Mashanova et al. 2010) of the movement patterns of black bean aphids (Aphis fabae) are an exception to this and may provide the first empirical evidence for the synthesis of CRW and LW characteristics. Mashanova et al. (2010) reported that the movement patterns of starved aphids are nearly ballistic at short times and nearly Brownian at long times. This is consistent with a continuous-time CRW. Mashanova et al. (2010) also reported that the durations of ‘fast phases’ during which speed remains continually above a threshold value were distributed according to a truncated power law. Such a truncated power-law distribution was uncovered by Wang & Uhlenbeck (1945) in their analysis of the Langevin equation and underlies the occurrence of LW movement patterns reported on here.

It is hoped that the present study will change the nature and tone of the debate about whether CRW models of animal movement patterns are more or less realistic than LW models.

Acknowledgements

Rothamsted Research receives grant aided support from the Biotechnology and Biological Sciences Research Council. I thank five anonymous referees for constructive remarks that led to a much improved manuscript.

References

  1. Alt W. 1988. Modelling of motility in biological systems. In ICIAM '87: Proc. of the First Int. Conf. on Industrial and Applied Mathematics (eds McKenna J., Temam R.), pp. 15–30. Philadelphia, PA: SIAM. [Google Scholar]
  2. Alt W. 1990. Correlation analysis of two-dimensional locomotion paths. In Biological Motion: Proc. of a Workshop held in Königswinter Germany (eds Alt W., Hoffman G.). Lecture Notes in Biomathematics, pp. 254–268. Berlin, Germany: Springer-Verlag. [Google Scholar]
  3. Bartumeus F. 2009. Behavioral intermittence, Lévy patterns, and randomness in animal movement. Oikos 118, 488–494. [Google Scholar]
  4. Bartumeus F., Peters F., Pueyo S., Marrase C., Catalan J. 2003. Helical Lévy walks: adjusting searching statistics to resource availability in microzooplankton. Proc. Natl Acad. Sci. USA 100, 12 771–12 775. ( 10.1073/pnas.2137243100) [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bartumeus F., Fernández P., da Luz M. G. E., Catalan J., Solé R. V., Levin S. A. 2008. Superdiffusion and encounter rates in diluted, low dimensional worlds. Eur. Phys. J. Spec. Top. 157, 157–166. ( 10.1140/epjst/e2008-00638-6) [DOI] [Google Scholar]
  6. Doob J. L. 1942. The Brownian movement and stochastic equations. Ann. Math. 43, 351–369. ( 10.2307/1968873) [DOI] [Google Scholar]
  7. Dunn G. A., Brown A. F. 1987. A unified approach to analyzing cell motility. J. Cell Sci. Suppl. 8, 81–102. [DOI] [PubMed] [Google Scholar]
  8. Edwards A. M. 2008. Using likelihood to test for Lévy flight search patterns and for general power-law distributions in nature. J. Anim. Ecol. 7, 1212–1222. [DOI] [PubMed] [Google Scholar]
  9. Johnson D. S., London J. M., Lea M. A., Durban J. W. 2008. The continuous-time correlated random walk model for animal telemetry data. Ecology 89, 1208–1215. ( 10.1890/07-1032.1) [DOI] [PubMed] [Google Scholar]
  10. Kac M. 1949. On distributions of certain Wiener functionals. Trans. Am. Math. Soc. 65, 1–13. ( 10.2307/1990512) [DOI] [Google Scholar]
  11. Kareiva P. M., Shigesada N. 1983. Analysing insect movement as a correlated random-walk. Oecologia 56, 234–238. ( 10.1007/BF00379695) [DOI] [PubMed] [Google Scholar]
  12. Kearney M. J., Majumdar S. N. 2005. On the area under a continuous time Brownian motion till its first-passage time. J. Phys. A 38, 4097–4104. ( 10.1088/0305-4470/38/19/004) [DOI] [Google Scholar]
  13. Klafter J., Shlesinger M. F., Zumofen G. 1996. Beyond Brownian motion. Phys. Today 49, 33–39. ( 10.1063/1.881487) [DOI] [Google Scholar]
  14. Lubashevsky I., Friedrich R., Heuer A. 2009. Realization of Levy flights as continuous processes. Phys. Rev. E 79, 011110. ( 10.1103/PhysRevE.79.011110) [DOI] [PubMed] [Google Scholar]
  15. Mashanova A., Oliver T. H., Jansen V. A. A. 2010. Evidence for intermittency and a truncated power law from highly resolved aphid movement data. J. R. Soc. Interface 7, 199–208. ( 10.1098/rsif.2009.0121) [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Plank M. J., Codling E. A. 2009. Sampling rate and misidentification of Levy and non-Levy movement patterns. Ecology 90, 3546–3553. ( 10.1890/09-0079.1) [DOI] [PubMed] [Google Scholar]
  17. Raposo E. P., Buldyrev S. V., da Luz M. G. E., Viswanathan G. M., Stanley H. E. 2009. Levy flights and random searches. J. Phys. 42, 434003 ( 10.1088/1751-8113/42/43/434003) [DOI] [Google Scholar]
  18. Reynolds A. M. 2010. Can spontaneous cell movements be modelled as Lévy walks? Physica A 389, 273–277. ( 10.1016/j.physa.2009.09.027) [DOI] [Google Scholar]
  19. Reynolds A. M., Frye M. A. 2007. Free-flight odor tracking in Drosophila is consistent with an optimal intermittent scale-free search. PLoS ONE 4, e354 ( 10.1371/journal.pone.0000354) [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Reynolds A. M., Rhodes C. J. 2009. The Lévy flight paradigm: random search patterns and mechanisms. Ecology 90, 877–887. ( 10.1890/08-0153.1) [DOI] [PubMed] [Google Scholar]
  21. Reynolds A. M., Smith A. D., Menzel R., Greggers U., Reynolds D. R., Riley J. R. 2007a. Displaced honeybees perform optimal scale-free search flights. Ecology 88, 1955–1961. ( 10.1890/06-1916.1) [DOI] [PubMed] [Google Scholar]
  22. Reynolds A. M., Smith A. D., Reynolds D. R., Carreck N. L., Osborne J. L. 2007b. Honeybees perform optimal scale-free searching flights when attempting to locate a food source. J. Exp. Biol. 210, 3763–3770. ( 10.1242/jeb.009563) [DOI] [PubMed] [Google Scholar]
  23. Reynolds A. M., Swain J. L., Smith A. D., Martin A. P., Osborne J. L. 2009. Honeybees use a Lévy flight search strategy and odour-mediated anemotaxis to relocate food sources. Behav. Ecol. Sociobiol. 64, 115–123. ( 10.1007/s00265-009-0826-2) [DOI] [Google Scholar]
  24. Selmeczi D., Mosler S., Hagedorn P. H., Larsen N. B., Flyvbjerg H. 2005. Cell motility as persistent random motion: theories from experiments. Biophys. J. 89, 912–931. ( 10.1529/biophysj.105.061150) [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Shlesinger M. F., Klafter J. 1986. Lévy walks versus Lévy flights. In On growth and form (eds Stanley H. E., Ostrowsky N.), pp. 279–283. Dordrecht, The Netherlands: Nijhoff. [Google Scholar]
  26. Sims D. W., et al. 2008. Scaling laws of marine predator search behaviour. Nature 451, 1098–1102. ( 10.1038/nature06518) [DOI] [PubMed] [Google Scholar]
  27. Sparre Andersen E. 1953. On the fluctuations of sums of random variables. Math. Scand. 1, 263–285. [Google Scholar]
  28. Sparre Andersen E. 1954. On the fluctuations of sums of random variables II. Math. Scand. 2, 195–223. [Google Scholar]
  29. Thomson D. J. 1987. Criteria for the selection of stochastic models of particle trajectories in turbulent flows. J. Fluid Mech. 180, 529–556. ( 10.1017/S0022112087001940) [DOI] [Google Scholar]
  30. Turchin P. 1998. Quantitative analysis of movement: measuring and modelling population redistribution in animals and plants. Sunderland, MA: Sinauer Associates. [Google Scholar]
  31. Viswanathan G. M., Raposo E. P., Bartumeus F., Catalan J., da Luz M. G. E. 2005. Necessary criterion for distinguishing true superdiffusion from correlated random walk processes. Phys. Rev. E 72, 011111. ( 10.1103/PhysRevE.72.011111) [DOI] [PubMed] [Google Scholar]
  32. Wang M. C., Uhlenbeck G. E. 1945. On the theory of Brownian motion II. Rev. Mod. Phys. 17, 323–342. ( 10.1103/RevModPhys.17.323) [DOI] [Google Scholar]
  33. White E. P., Enquist B. J., Green J. L. 2008. On estimating the exponent of power-law frequency distributions. Ecology 89, 905–912. ( 10.1890/07-1288.1) [DOI] [PubMed] [Google Scholar]

Articles from Journal of the Royal Society Interface are provided here courtesy of The Royal Society

RESOURCES