Image-Guided Radio-Frequency Gain Calibration for High-Field MRI

Abstract

High-field (≥ 3T) MRI provides a means to increase the signal-to-noise ratio, due to its higher tissue magnetization compared with 1.5T. However, both the static magnetic field (B₀) and the transmit radio-frequency (RF) field (B₁⁺) inhomogeneities are comparatively higher than those at 1.5T. These challenging factors at high-field strengths make it more difficult to accurately calibrate the transmit RF gain using standard RF calibration procedures. An image-based RF calibration procedure was therefore developed, in order to accurately calibrate the transmit RF gain within a specific region-of-interest (ROI). Using a single-shot ultra-fast gradient echo pulse sequence with centric k-space reordering, a series of “saturation-no-recovery” images was acquired by varying the flip angle of the preconditioning pulse. In the resulting images, the signal null occurs in regions where the flip angle of the preconditioning pulse is 90°. For a given ROI, the mean signal can be plotted as a function of the nominal flip angle, and the resulting curve can be used to quantitatively identify the signal null. This image-guided RF calibration procedure was evaluated through phantom and volunteer imaging experiments at 3T and 7T. The image-guided RF calibration results in vitro were consistent with standard B₀ and B₁⁺ maps. The standard automated RF calibration procedure produced approximately 20% and 15–30% relative error in the transmit RF gain in the left kidney at 3T and brain at 7T, respectively. For initial application, a T₂ mapping pulse sequence was applied at 7T. The T₂ measurements in the thalamus at 7T were 60.6 ms and 48.2 ms using the standard and image-guided RF calibration procedures, respectively. This rapid, image-guided RF calibration procedure can be used to optimally calibrate the flip angle for a given ROI and thus minimize measurement errors for quantitative MRI and MR spectroscopy.

Introduction

High-field (≥ 3T) MRI provides a means to increase the signal-to-noise ratio (SNR) due to its higher tissue magnetization compared with 1.5T, as well as to achieve better spectral separation. The relaxation times are also altered at high-field (i.e., typically higher T₁; slightly lower T₂) (1), and this can be further exploited to achieve high SNR. With pulse sequence and radio-frequency (RF) coil development, these advantages can be realized to achieve higher spatiotemporal resolution, faster imaging, and improved spectroscopy. These advantages have been demonstrated in previous brain studies (2,3) and in body studies, including coronary angiography (4,5), carotid MRI (6), peripheral angiography (7), prostate MRI (8), cardiac MRI (9,10), pancreas MRI (11), and musculoskeletal MRI (12,13), and in MR spectroscopy (14,15).

At high-field strengths, however, both the static magnetic field (B₀) and the transmit RF field (B₁⁺) inhomogeneities are comparatively higher than those at 1.5T (11,16–21). These challenging factors make it more difficult to achieve uniform RF excitation, as well as to accurately calibrate the transmit RF gain. Non-uniform excitation flip angle can produce regional signal and image contrast variations, as well as measurement errors for quantitative MRI and MR spectroscopy. Typically, B₁⁺ mapping pulse sequences are needed to compensate for the underlying B₁⁺ variations. However, these sequences are generally time consuming and require off-line image reconstruction and analysis, rendering them impractical for routine clinical MRI.

In conventional MRI, an automated RF calibration procedure is performed as a pre-scan to calibrate the RF excitation. However, it may not necessarily produce the expected flip angle within a given region-of-interest (ROI). An incorrect calibration of the transmit gain will produce the wrong flip angle and consequently altered image contrast and an incorrect specific absorption rate (SAR) estimation. Thus, it is highly desirable to design a rapid, image-guided RF calibration procedure in order to avoid the aforementioned problems. The purpose of this study, therefore, was to develop a rapid, image-guided RF gain calibration procedure for high-field MRI and evaluate its performance through phantom and in vivo experiments at 3T and 7T.

Experimental

Standard RF Calibration Procedure

The standard RF transmitter calibration procedure implemented on the scanner (MAGNETOM Tim Trio and MAGNETOM 7T, Siemens Healthcare, Erlangen, Germany) uses a train of 3 rectangular RF pulses (90°-180°-90°) with magnetic gradient along the slice-select direction, in order to excite and receive signal from a 1cm-thick transversal slice at magnet isocenter. The duration of the 90° pulse is 0.5 ms, and the duration of the 180° pulse is 1.0 ms. The amplitude of the spin echo produced by the first 2 pulses is maximal for a 90°-180° pulse pair, while the stimulated echo amplitude is minimal for a 90°-180°-90° pulse train. The ratio of the echo amplitudes is proportional to the cosine of the flip angle.

Pulse Sequence

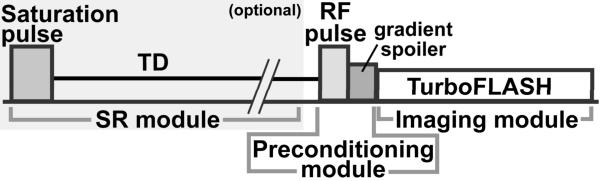
Figure 1 shows the pulse sequence diagram of the proposed image-guided RF calibration procedure. The pulse sequence used in this study is similar to the sequence proposed by Klose for B₁⁺ mapping (22), but with two key different features: i) the targeted RF transmitter gain is for a 90° excitation, and ii) the preconditioning pulse is a slice-selective sinc pulse. Using a turbo fast low angle shot (TurboFLASH) pulse sequence with centric k-space reordering, a series of “saturation-no-recovery” images is acquired by varying the flip angle of the preconditioning pulse. In the resulting images, the signal null occurs in regions where the preconditioning pulse excitation is 90°. This region is, by definition, the accurately calibrated excitation region. The signal null region is seen to move across the field of view (FOV) as the flip angle of the preconditioning pulse is adjusted. The user can thus choose the RF transmitter amplitude that corresponds to the flip angle which produces the best signal null within a desired ROI.

Figure 1.

Pulse sequence diagram for the proposed image-guided RF gain calibration procedure. The basic components are the preconditioning RF module and the TurboFLASH imaging sequence. The preconditioning RF pulse was designed as a slice-selective sinc pulse (see Materials for more details). The optional component is the SR module, which is used to achieve consistent M_z prior to the preconditioning module.

The preconditioning RF pulse was designed as a slice-selective sinc pulse with variable flip angle, fixed pulse duration = 2.8 ms, time-bandwidth product = 6, and transmitter bandwidth = 2.1 kHz. The slice thickness of the preconditioning pulse was set to 6 times that of the image slice. This thickness factor was empirically determined to minimize the effects of imperfect slice profile and chemical shift (see the Discussion section). Immediately following the sinc pulse, 3-ms-long spoiler gradients were applied, with the magnitude of net zeroth gradient moment = 135mT/m·ms, in order to spoil the transverse magnetization. Right after the spoiler gradients (i.e., “no recovery”), a TurboFLASH sequence with centric k-space reordering was performed to image the residual longitudinal magnetization (M_z) left behind by the preconditioning RF pulse. As suggested by Cunningham et al. (23), a saturation-recovery (SR) module can be optionally used to achieve a constant M_z prior to the preconditioning RF pulse module. For this purpose, a hybrid adiabatic-rectangular pulse train (24) was used to achieve effective saturation of magnetization, followed by approximately 850 ms of saturation-recovery time delay (TD) for adequate SNR. This pulse sequence was implemented on a 3T whole-body MR scanner (MAGNETOM Tim Trio, Siemens Healthcare, Erlangen, Germany) and on a 7T whole-body MR scanner (MAGNETOM 7T, Siemens Healthcare, Erlangen, Germany), both equipped with a gradient system capable of achieving a maximum gradient strength of 45 mT/m and a slew rate of 200T/m/s. For the 3T scanner, the body coil was used for RF excitation, and phased array coils were used for MR signal reception. For the 7T scanner, a transmit/receive (transmit birdcage; 24 receive elements) head coil (Nova Medical, Inc., Wilmington, MA) was used to image phantoms and the brain.

Relevant imaging parameters include: FOV = 250–340mm in the frequency-encoding direction (81.3% FOV in the phase-encoding direction), acquisition matrix = 128 × 104, slice thickness = 8 mm, echo time (TE)= 1.2 ms, repetition time (TR) = 2.4 ms, image acquisition time ~ 150ms, flip angle = 10°, TD ~ 850ms, generalized autocalibrating partially parallel acquisitions (GRAPPA) with an effective acceleration factor = 1.6, receiver bandwidth = 1565Hz/pixel, total scan time per measurement = 1000 ms, and repetition = 10. The relevant properties of the slice-selective excitation pulse include: pulse duration = 0.4 ms, time-bandwidth product = 1.6, and transmitter bandwidth = 4 kHz. Note that the initial flip angle scale factor (κ) of the preconditioning pulse, the increment step of κ for repeated acquisitions, and the repetition number were made adjustable through the pulse sequence user interface. By definition, κ is the ratio of the nominal flip angle and nominal 90°.

For phantom MRI at 3T, the image acquisition was repeated with κ ranging from 0.9–1.12 (0.02 steps). For phantom MRI at 7T, the image acquisition was repeated with κ ranging from 0.8–1.25 (0.05 steps). For kidney MRI at 3T, the image acquisition was repeated with κ ranging from 0.8–1.7 (0.1 steps). For brain MRI at 7T, the image acquisition was repeated with κ ranging from 0.5–0.9 (0.05 steps).

Phantom Imaging

A head-sized spherical phantom filled with oil was imaged in an axial plane at magnet isocenter, in order to evaluate the accuracy of the image-guided RF calibration procedure. The first experiment was performed at 3T to qualitatively evaluate the agreement between the image-guided RF calibration procedure and the standard B₀ and B₁⁺ mapping pulse sequences. Specifically, after performing standard automated B₀ shimming and RF calibration procedures, standard B₀ and B₁⁺ maps were acquired with the same spatial resolution as the image-guided RF calibration sequence. The B₀ map was acquired using a standard double-echo phase difference sequence (25) with a flip angle of 30°, and the B₁⁺ map was acquired using the double angle method (26) with excitation flip angles of 60° and 120°. At on-resonance, a “saturation-no-recovery” image was acquired with nominal 90° excitation. After full recovery of M_z, the image acquisition was repeated at 100-, 300-, and 500-Hz off-resonance, in order to evaluate the sensitivity of the preconditioning pulse to off-resonance.

The second experiment was performed at 7T to quantitatively evaluate the influence of off-resonance on the image-guided RF calibration. The same oil phantom was imaged in a coronal plane at magnet isocenter. After performing standard automated B₀ shimming and RF calibration procedures, a standard B₁⁺ map was acquired. The image-guided RF calibration experiment was repeated with κ ranging from 0.8–1.25 (0.05 steps) and with B₀ offset ranging from −300 to 300 Hz (50 Hz steps). The standard B₁⁺ map and the image-guided RF calibration results were analyzed to evaluate their agreement.

The third experiment was performed at 3T, using the same oil phantom, in order to evaluate the effects of the imaging excitation flip angle and the incomplete magnetization recovery after the SR module on the image-guided RF calibration procedure. After performing standard automated B₀ shimming and RF calibration procedures, the image acquisition was repeated with κ ranging from 0.9–1.12 (0.02 steps), for three different cases: a) imaging flip angle = 10° with full M_z recovery between image acquisitions, b) imaging flip angle = 5° with full M_z recovery between image acquisitions, and c) imaging flip angle = 10° and partial M_z recovery between image acquisitions, using a SR module with TD = 850 ms. A small increment of κ (0.02 steps) was used to evaluate the sensitivity of the image-guided RF calibration sequence to B₁⁺.

In Vivo Imaging

Two human subjects were examined to evaluate the performance of the image-guided RF calibration procedure. In one subject (female, 69 years old), we examined the kidneys in an axial plane at 3T. In another subject (male, 23 years old), we examined the brain in a sagittal plane at 7T. Human imaging was performed in accordance with protocols approved by the Human Investigation Committee at our institution; all subjects provided written informed consent.

Image Analysis

For qualitative analysis of the image-guided RF calibration data, the series of images was scrolled through to identify the signal null in the ROI. For quantitative analysis, the mean signal intensity was plotted as a function of κ, in order to more accurately identify the signal null in the ROI. For larger ROI with relatively large B₁⁺ variation, the mean signal vs. κ curve may not produce a clear minimum because of signal variation within the ROI. As such, the resulting mean signal intensity curve may produce a broad global minimum as a function of κ. In such a case, the standard deviation (SD) of the signal was used to identify the κ value that produces minimum signal dispersion within the ROI, and this κ value that coincides with a minimum of the mean signal vs. κ curve was determined to be the best value for RF calibration.

Initial Application: T₂ Mapping

The influence of the RF calibration on T₂ measurements was evaluated in an agarose phantom and in the brain at 7T. We used an optimal multi-echo fast spin echo (ME-FSE) sequence with reverse centric k-space reordering (27), using the following set of relevant imaging parameters: spatial resolution = 1.3 mm × 1.7 mm × 8 mm, echo spacing = 6.2 ms, turbo factor = 4, and number of images = 8.

For the same subject at 7T, the T₂ mapping sequence was performed in the same sagittal plane as the RF calibration experiment. The T₂ mapping sequence was performed twice, first using the transmit RF gain calculated by the standard automated calibration procedure, and second using the correct transmit RF gain calculated by the image-guided RF calibration procedure.

For phantom imaging, after performing standard automated B₀ shimming procedure and RF calibration, the image-guided RF calibration image acquisition was repeated with κ ranging from 0.7 to 1.1 (0.05 steps). Correspondingly, T₂ mapping was repeated with the transmit RF gain ranging from 0.6 to 1.2 (0.1 steps).

For image analysis, the corresponding pixel-by-pixel T₂ map was calculated by non-linear least square fitting of the mono-exponential relaxation curve using the MATLAB® R2008a software (Mathworks, Natick, MA).

Results

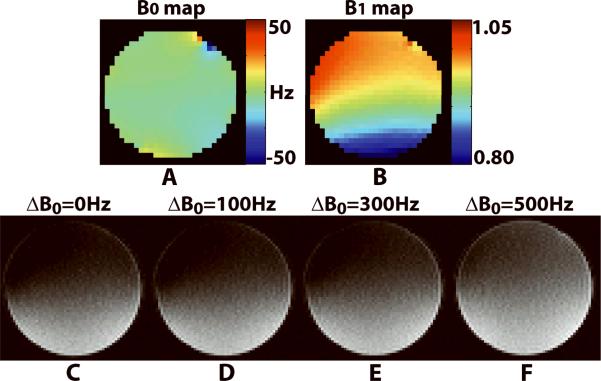
Figure 2 shows a qualitative comparison of the standard B₀ and B₁⁺ maps and the image-guided RF calibration images of the phantom acquired with nominal 90° at on-resonance and 100-, 300-, and 500-Hz off-resonance. Within the whole phantom, B₀ ranged from −56 to 24 Hz, while B₁⁺ scale ranged from 0.79 to 1.02. The RF calibration images were consistent with the standard B₁⁺ map up to 300Hz off-resonance. Note that the dark regions correspond to locations where the RF excitation was approximately 90°.

Figure 2.

Comparison of the standard B₀ and B₁⁺ maps and the RF transmitter calibration images of the phantom acquired with nominal 90° at on-resonance and 100-, 300-, and 500-Hz off-resonance. Standard B₀ map (A) and B₁⁺ map (B) acquired in an axial plane at magnet isocenter. Image-guided RF calibration images at on-resonance (C) and 100-, 300-, and 500-Hz off-resonance (D–F) are shown. The image-guided RF calibration sequence is relatively insensitive to off-resonance up to 300 Hz. Note that the dark regions correspond to locations where the RF excitation is approximately 90°.

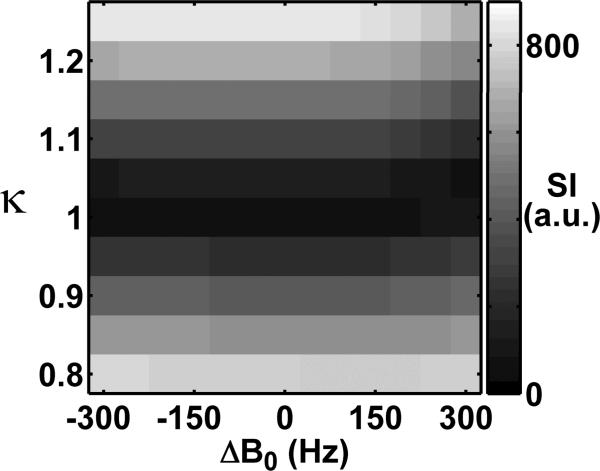
Figure 3 shows a 2D display of the mean signal of the phantom acquired at 7T, as a function of κ and B₀ offset. This display shows the mean signal calculated from the ROI, which was defined as the region in the standard B₁⁺ map with B₁⁺ scale (normalized by 60°) ranging from 0.975 to 1.025. Consistent with the pulse sequence design and the standard B₁⁺ map, the minimum signal occurred at flip angle scale = 1.0 throughout the B₀ offset values.

Figure 3.

A representative 2D display of the mean signal intensity (SI, in arbitrary unit) of the phantom at 7T, as a function of κ and B₀ offset. This display shows the mean signal calculated from the ROI, which was defined as the region in the standard B₁⁺ map with B₁⁺ scale (normalized by 60°) ranging from 0.975 to 1.025. Consistent with the pulse sequence design and the standard B₁⁺ map, the minimum of the signal occurred at κ = 1.0 throughout the range of B₀ offset values.

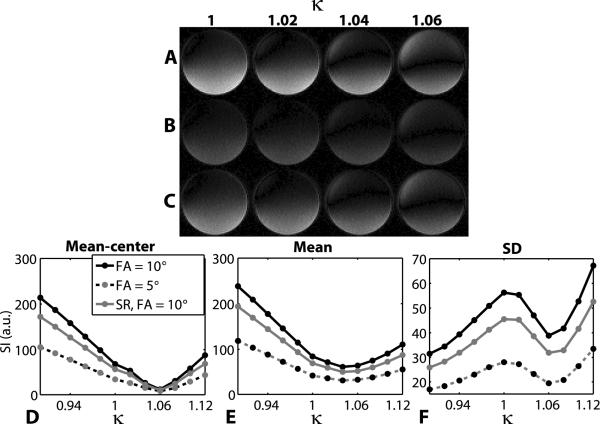
Figure 4 shows representative images of the phantom acquired using the image-guided RF calibration procedure with κ ranging from 1 to 1.06 (0.02 steps). These images represent 3 different image acquisition settings: imaging flip angle 10°, imaging flip angle 5°, and imaging flip angle 10° with the SR module. Consistent with the pulse sequence design (e.g., cosine function is sensitive to flip angle near 90°), these images show that the image-guided RF calibration sequence is sensitive to B₁⁺. The mean signal intensity measured in the inner area, as defined as the area encircled by one-half radius, of the phantom produced the same signal minimum at κ = 1.06 for all 3 acquisition settings. For the whole phantom analysis, the mean signal vs. κ curve produced a broad global minimum, and the local minimum of the SD of the signal vs. κ curve occurred at κ = 1.06 for all 3 acquisition settings. Incidentally, these results showed that the automated RF calibration produced approximately 6% relative error in the transmit RF gain and that the center of the phantom is relatively bright at nominal 90° excitation.

Figure 4.

Representative phantom images at 3T (A–C) illustrating the effects of the choice of the imaging flip angle and the SR module on the RF calibration images. Three different sets of acquisition parameters were used: imaging flip angle 10° (A), imaging flip angle 5° (B), and imaging flip angle 10° with the SR module (C). For all three acquisition settings, mean signal intensity measured in the inner area of the phantom (D), as well as the mean signal intensity in the whole phantom (E) coupled with the SD of the signal measured in the whole phantom (F), resulted in the correct RF calibration at κ = 1.06. Note that the automated RF calibration (κ = 1.00) did not produce the expected RF flip angle in the center of the phantom.

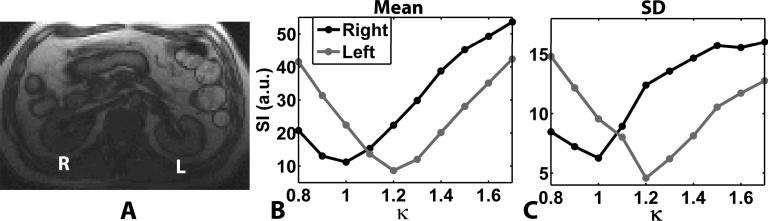
Figure 5 shows representative RF calibration curves obtained in the right and left kidneys at 3T, acquired with κ ranging from 0.8 to 1.7 (0.1 steps). In the right kidney, the automated RF calibration (κ = 1.0) produced signal nulling, whereas κ = 1.2 produced the best signal nulling in the left kidney, suggesting that the automated RF calibration produced approximately 20% relative error in the transmit RF gain for the left kidney.

Figure 5.

Representative abdomen results at 3T (A). The right (R) and left (L) kidneys are shown in an anatomical proton density-weighted image (A). The mean signal intensities measured in the kidneys are plotted as a function of κ (B), as well as the corresponding SD of the signal intensity as a function of κ (C). While the automated RF calibration was correct in the right kidney, it did not produce the expected flip angle in the left kidney.

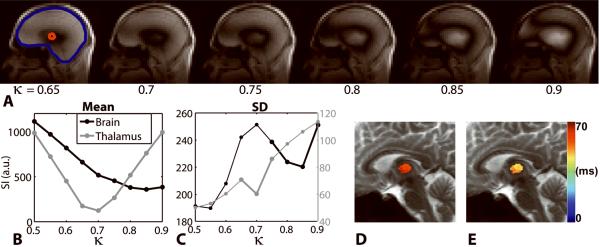
Figure 6 shows representative brain results at 7T. Using both the mean and SD of signal of the whole brain, the correct transmitter gain was determined to be at κ = 0.85, suggesting that the automated RF calibration yielded 15% overall error in the transmitter gain. For the thalamus, however, κ = 0.7 produced the best signal nulling, which suggests 30% relative error in the transmitter gain for the thalamus. Note that the SD of the signal is much smaller for the thalamus than for the whole brain, for which the SD analysis was necessary to determine best signal null value. Figure 6 also shows the influence of the RF transmitter gain on the corresponding T₂ maps of the thalamus. The mean T₂ measurements of the thalamus, using the transmitter gain calculated with the standard automated RF calibration procedure and the correct transmitter gain calculated with the image-guided RF calibration procedure, were 60.6 ms and 48.2 ms, respectively. These results suggest that the standard RF calibration resulted in 25.7% error in T₂.

Figure 6.

Representative brain results at 7T. An anatomical proton density-weighted image (A) is displayed, as well as the curves representing the mean (B) and SD (C) of the signal intensity measured in the ROI plotted as a function of κ. Two ROIs were considered: whole brain and thalamus (arrow head). The SD curve aided in determining the RF transmitter gain for the whole brain, whereas it is unnecessary for the thalamus. Note that the automated RF calibration (κ = 1.00) did not produce the correct transmit gain for the whole brain, as well as for the thalamus. The influence of the RF transmitter calibration on T₂ measurements of the thalamus is also shown. The mean T₂ measurements using the transmit RF gain calculated by the standard RF calibration (D) and using the correct RF gain calculated by the image-guided RF calibration (E) (κ = 0.7) were 60.6 ms and 48.2 ms, respectively. These results suggest that the standard RF calibration resulted in 25.7% error in T₂.

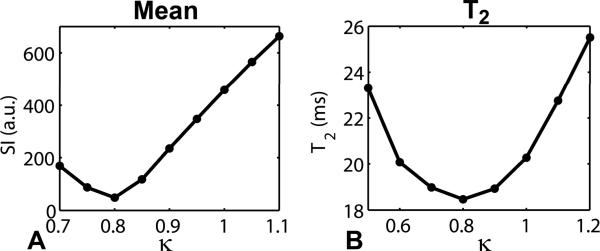
Figure 7 shows a plot of the mean signal as a function of κ and a plot of the mean T₂ as a function of κ. Both the signal intensity and T₂ measurements were made from the inner area, as defined as the area encircled by one-half radius, of the agarose phantom. As observed in the brain, T₂ measurements vary with the RF transmitter gain. The minimum T₂ value coincides with the minimum signal in the RF calibration curve, suggesting that the correct RF calibration is at κ = 0.8.

Figure 7.

Influence of the RF transmitter calibration on T₂ measurements of the agarose phantom at 7T. Plots of mean signal (A) and mean T₂ (B) as a function of κ. Both the signal intensity and T₂ measurements were made in the inner area of the phantom. Both the minimum signal intensity and minimum T₂ occurred at κ = 0.8, suggesting that the correct flip angle calibration occurred at κ = 0.8. These results show the importance of correct RF transmitter calibration for T₂ mapping when using a ME-FSE pulse sequence.

Both the in vitro and in vivo T₂ measurements demonstrate the importance of correct RF calibration for T₂ mapping when using a ME-FSE pulse sequence. These findings are consistent with previous multi-echo spin echo studies (28,29) which showed that stimulated echoes generated by non-ideal 180° refocusing RF pulses can cause overestimation of T₂.

Discussion

This study has described a rapid image-guided RF gain calibration procedure for high-field MRI. This rapid RF calibration sequence can be performed within 10s and, therefore, can be easily added to existing clinical protocols. The RF calibration images can be analyzed either visually for signal null or quantitatively using descriptive statistics. Conveniently, a simple quantitative analysis based on mean signal intensity can be performed using the image viewing tools available on commercial scanners. For larger ROI with relatively large B₁⁺ variation, the SD of the signal curve can be combined with the mean signal curve to find the best transmitter gain factor. This practical procedure can be used to calibrate the RF excitation within a desired ROI, and to minimize measurement errors for quantitative MRI and MR spectroscopy, since these applications will be improved with correct RF calibration. The correct RF calibration is also important to avoid excessive RF power deposition, particularly for 7T applications. The image-guided RF calibration pulse sequence is also useful for RF coil development, as the localized RF transmitter calibration can be used to fine tune the RF coil performance.

The image-guided RF calibration procedure was able to show that the standard automated RF transmitter calibration procedure does not necessarily produce the expected RF excitation field within a given ROI. It is worth noting the key differences between the standard RF calibration and proposed RF calibration procedures. First, the standard automated RF transmitter calibration procedure acquires the signal from a 1cm-thick transversal slice at magnet isocenter, whereas the image-guided RF calibration pulse sequence can acquire signal from any arbitrary imaging plane. Second, the standard automated RF transmitter calibration procedure receives the signal from the whole transversal slice and calculates a global value for RF calibration. In contrast, the image-guided RF calibration procedure can be used to locally adjust the transmit RF gain for a given ROI.

There are several limitations that warrant discussion. First, the proposed RF calibration pulse sequence is relatively sensitive to very large off-resonance settings. However, the phantom results at 7T (Figure 3) showed that the preconditioning pulse is relatively insensitive to B₀ offset up to ± 300 Hz. We note that clinically relevant B₀ variation within the body at 3T is on the order of ±150 Hz (18), and our preliminary measurement of B₀ variation within the brain at 7T, excluding regions near the sinus, is on the order of ±250 Hz. As such, the proposed image-guided RF calibration procedure is applicable for most 3T and 7T applications, except for body MRI at 7T. Second, the proposed procedure does not account for the receive coil sensitivity. However, the receive coil sensitivity is secondary in importance to B₁⁺ and should simply result in an offset of local signal intensity that will drop out during the quantitative evaluation. A proton density image can be acquired without the preconditioning RF pulse, in order to correct for the receive coil sensitivity, as previously described (30). Third, it should be noted that the proposed RF calibration is not equivalent to B₁⁺ mapping. As such, the results can not be used to perform B₁⁺ correction to quantitative measures. Sixth, different vendors use different automated RF calibration procedures. Therefore, the benefit with using the image-guided RF calibration procedure may be different for different MR scanners.

There are two types of chemical shift artifact that warrant discussion. First, the chemical shift artifact with the gradient echo readout can produce signal voids in voxels with both fat and water. We used a high receiver bandwidth (1565Hz/pixel) to minimize this chemical shift artifact. Any residual chemical shift artifact is not expected to influence the quantitative analysis for RF calibration, because the signal void during readout is constant as a function of κ. Second, the chemical shift of fat and water (e.g, 434 Hz and 1013 Hz at 3T and 7T, respectively) will result in differential spatial shifts of fat spins between the preconditioning pulse (transmitter bandwidth = 2.1 kHz) and excitation pulse (transmitter bandwidth = 4.0 kHz). Specifically, the relative spatial shift, as a percentage of the slice thickness, of fat for the preconditioning pulse is on the order of 21% at 3T and 48% at 7T, whereas the relative spatial shift of fat for the excitation pulse is on the order of 10% at 3T and 25% at 7T. We had designed the slice thickness of the preconditioning pulse to be six times that of the excitation pulse, in order to compensate for the differential spatial shifts of fat between the preconditioning and excitation pulses. For example at 3T, assuming imaging at magnet isocenter, the upper and lower limits of the slice position of fat are 33.9 to −14.1 mm and 4.9 to −3.1 mm for the preconditioning (slice thickness = 48 mm) and excitation (slice thickness = 8 mm) pulses, respectively. Note that the imaged slice of fat resides within the “preconditioned” slice of fat. Correspondingly at 7T, the upper and lower limits of the slice position of fat are 47.2 to −0.8 mm and 6.0 to −2.0 mm for the preconditioning and excitation pulses, respectively. Note that 15% of the imaged slice of fat is outside the “preconditioned” slice of fat. In the imaged slice the untipped fat spins will contribute a constant signal bias as a function κ, and, therefore, do not affect the quantitative analysis for RF calibration. Nonetheless, the non-ideal slice profile of the preconditioning pulse can produce differential excitation of the fat and water spins, particularly at 7T, and introduce a systematic error for RF calibration. One potential solution to further minimize this error is to improve the slice profile of preconditioning pulse, either by increasing the time-bandwidth product of the sinc pulse at the expense of increasing the pulse duration, or by exploring other RF envelopes that better approximate an ideal slice profile. An alternative solution is to increase the transmitter bandwidth using a variable-rate selective excitation (VERSE) pulse (31), while maintaining the same pulse duration.

Conclusion

The proposed rapid image-guided RF calibration procedure permits local adjustment of the RF transmit gain for a specific area within the FOV. This procedure can easily be added to existing clinical protocols. The quantitative analysis of the RF calibration images can be performed on commercial scanners using simple descriptive statistics provided by the scanners. This rapid image-guided RF transmitter calibration can be used to optimally calibrate the RF transmit gain for a given ROI, avoid excessive RF power deposition, and minimize measurement errors for quantitative MRI and spectroscopic applications.

List of Abbreviations

FOV

field of view

GRAPPA

generalized autocalibrating partially parallel acquisitions

RF

radio-frequency field

B₀

static magnetic field

B₁⁺

transmit RF field

T₁

spin-lattice relaxation constant

T₂

effective spin-spin relaxation constant

SNR

signal-to-noise ratio

TE

echo time

TR

repetition time

TD

saturation-recovery time delay time

M_z

longitudinal magnetization

TurboFLASH

turbo fast low-angle shot

SAR

specific absorption rate

ROI

region of interest

SD

standard deviation

TurboFLASH

Turbo fast low angle shot

VERSE

variable-rate selective excitation