Modulation of Energy Transfer Pathways between Mitochondria and Myofibrils by Changes in Performance of Perfused Heart

Abstract

In the heart, the energy supplied by mitochondria to myofibrils is continuously and finely tuned to the contraction requirement over a wide range of cardiac loads. This process is mediated both by the creatine kinase (CK) shuttle and by direct ATP transfer. The aim of this study was to identify the contribution of energy transfer pathways at different cardiac performance levels. For this, five protocols of ³¹P NMR inversion and saturation transfer experiments were performed at different performance levels on Langendorff perfused rat hearts. The cardiac performance was changed either through variation of external calcium in the presence or absence of isoprenaline or through variation of LV balloon inflation. The recordings were analyzed by mathematical models composed on the basis of different energy transfer pathway configurations. According to our results, the total CK unidirectional flux was relatively stable when the cardiac performance was changed by increasing the calcium concentration or variation of LV balloon volume. The stability of total CK unidirectional flux is lost at extreme energy demand levels leading to a rise in inorganic phosphate, a drop of ATP and phosphocreatine, a drop of total CK unidirectional flux, and to a bypass of CK shuttle by direct ATP transfer. Our results provide experimental evidence for the existence of two pathways of energy transfer, direct ATP transfer, and PCr transfer through the CK shuttle, whose contribution may vary depending on the metabolic status of the heart.

Introduction

In highly organized intracellular environment, the creatine kinases are distributed next to ATP-producing or ATP-consuming sites. Through such localization and functional coupling between participating enzymes, the creatine kinase (CK)² system forms a shuttle, which is able to convert ATP to PCr in mitochondria or next to glycolytic systems and use PCr to supply ATP to ATPases (1–9). Because of the close vicinity of mitochondria to the sites of ATP utilization, mitochondrial ATP has been shown to be directly transferred to myofibrillar and SR ATPases (9–11). The CK shuttle has been studied on several levels: organ, cellular and organelle. The main difficulty in studying CK shuttle at the organ level and thus be able to determine its role in the system which is closest to in vivo, is to take into account intracellular compartmentation (12). Recently, a new technique for NMR-inversion transfer analysis has been developed and applied to identify the intracellular energy transfer pathways (4, 13, 14). It has been shown, that the role of the CK shuttle may depend on the metabolic state of the cell (4). At mid-work level, the energy is transferred from mitochondria to ATPases through PCr diffusion. However, when ATP synthesis was inhibited by cyanide, a model with a single CK functioning at equilibrium was sufficient to reproduce all data (4). The mechanism behind such change in energy transfer is not clear. It could be induced by the inhibition of ATP synthesis. Alternatively, it could be some general property of cardiac metabolism that is evidenced at high energy demand.

The aim of this study is to identify the energy transfer pattern at different cardiac performance levels. For this, NMR inversion transfer experiments were performed at different cardiac performance levels. The cardiac performance was changed either through variation of external Ca ([Ca]_o) in the presence or absence of isoprenaline or through variation of LV balloon inflation. The recordings were analyzed by mathematical models composed on the basis of different energy transfer pathway configurations.

MATERIALS AND METHODS

Physiology

Hearts of Wistar male rats (350 g) were perfused by the Langendorff technique at a constant flow. A thin latex balloon inserted in the left ventricle (LV) allowed recording of contractile parameters as previously described (15). The HEPES-buffered phosphate-free perfusate contains sodium pyruvate (10 mm) as oxidative substrate to minimize the activity of glycolysis. Cardiac performance was characterized by the mean coronary pressure (CP), LV systolic (LVDP), end diastolic pressure (EDP), spontaneous heart rate, and rate pressure product (RPP in 10⁴ mmHg × beats × min⁻¹) mmHg. For each heart the oxygen consumption, VO₂ (expressed in μmol O₂ × min⁻¹ × g wet weight⁻¹) was inferred from the relationship between RPP and VO₂ determined in parallel experiments out of the magnet.

All hearts were initially perfused in isovolumic condition (LV balloon inflated by about 80 μl) with a solution containing 1.8 mm of external Ca ([Ca]_o) at a coronary flow of either 13 ml/min or 20 ml/min resulting in medium contractility. Low cardiac performance was achieved by a decrease in [Ca]_o to 0.5 mm at 13 ml/min (n = 16). To increase the performance, hearts initially perfused at a flow of 20 ml/min, were submitted to either high [Ca]_o ([Ca]_o = 4 mm, n = 17) or β-stimulation (isoprenaline, 5 × 10⁻⁸ m) in low ([Ca]_o = 0.5 mm, n = 20) or high [Ca]_o ([Ca]_o = 4 mm, n = 16). These groups underwent the whole magnetization transfer analysis.

In an additional series of experiments, performance was modified by mechanical load to test whether the protocol of altering the energy demand would influence CK kinetics. Time dependent saturation transfer was used to probe CK flux in this series. Energy demand was altered by changing the volume of the LV balloon in random order (n = 8). To minimize the influence of individual heart variations, 3 to 5 changes in balloon volume (1 − 60 μl) were applied stepwise to each heart ([Ca]_o 1.8 mm, coronary flow = 13 ml/min), and data were analyzed in each individual heart. We originally planned to probe a wider range of energy demand by perfusing the heart at high [Ca]_o (4 mm, as performed by Bittl and Ingwall (16)). However, in our hands, in 4 pilot hearts, reducing the volume of the LV balloon in high [Ca]_o induced numerous arrhythmias or even fibrillation periods artificially reducing CK flux.

At the end of the NMR experiments all hearts were freeze clamped. Part of the frozen hearts were used to measure ATP, PCr, and creatine contents (in nmol × mg prot⁻¹) to calculate the metabolite concentrations during magnetization transfer. All metabolite data are expressed in mmol/liter of intracellular water assuming 2.72 μl of H₂O × mg protein⁻¹ and 160 mg prot × g ww⁻¹. Another part was used to measure mitochondrial content by tissue fractionation using density gradient centrifugation in non aqueous media as previously described (14, 17). Briefly, 6–8 fractions were collected from each gradient. In each fraction the activity of marker enzymes for mitochondrial (citrate synthase) and extra-mitochondrial space (phosphoglycerate kinase) were determined as well as the protein and metabolite contents. From the distribution of marker enzymes in each fraction, protein, and metabolite contents were extrapolated to contents in the mitochondrial space. Any heart having more than 10% change in ATP or PCr before and after the flux detection by magnetization transfer was excluded from the analysis.

NMR Protocols

³¹P NMR spectra were acquired at 161.93 MHz on a INOVA Varian wide bore magnet in a 20 mm diameter tube as previously described (13). Control spectra were obtained with 80° pulse angle, 4K data points acquisition, a spectral width of 10,000 Hz and a line broadening of 20 Hz. Fully relaxed spectra (repetition time 10 s) were acquired before and after each magnetization transfer experiments to evaluate the metabolite concentration and their stability. Each heart underwent one inversion transfer and one saturation transfer protocol (either before or after the inversion transfer). For each inversion protocol 4–5 hearts in similar metabolic and contractile steady state conditions were used. For each physiological condition the full analysis groups five experimental protocol of magnetization transfer: a selective saturation of γATP and four selective inversion protocols as previously described (4, 13).

Briefly, time-dependent saturation transfer (TDST) included a nonsaturated spectrum allowing an absolute quantification of PCr and ATP content averaged during the whole saturation procedure and 8 spectra saturated at the frequency of γATP for a duration ranging from 0.3 to 9 s (16 scans for each spectrum). The delays between pulse were adjusted to achieve in each spectra a constant rate of recurrence of 10 s.

Selective inversion of either PCr (invPCr), or γATP (invATP) was achieved by a sync pulse of 15 ms followed by a variable delay (0 to 10 s) before the sampling pulse and a 10 s delay for complete relaxation. InvPCr and InvATP protocols were additionally performed with a continuous saturation of P_i resonance by a selective pulse to mask the contribution of ATP-P_i exchange. Free induction decays (FID) were acquired by trains of 4 scans cycling through the whole transfer protocols (a total of 24 scans for each spectra in the inversion protocols) in both inversion and saturation transfer protocol to minimize eventual time evolution of energetic parameters. In all groups, the hearts were in metabolic steady state as checked on control spectra obtained before and after the inversion protocol.

The investigation was conducted in accordance with our institutional guidelines defined by the European Community guiding principles in the care and use of animals and French decree no. 87/848 of October 19, 1987. Authorizations to perform animal experiments according to this decree were obtained from the French Ministry of Agriculture, Fisheries, and Food (no. 7475, May 27, 1997).

Statistics

All data are presented as mean and standard deviation. The group of hearts perfused at [Ca]_o 1.8 mm under isovolumic conditions (80 μl in the LV balloon) was considered as control, and statistical difference was analyzed by variance analysis and the Bonferroni test.

Data Analysis

Forward CK Flux on the Basis of satATP Experiment

The total unidirectional CK flux PCr → ATP (F_f, expressed in mm/s), was classically determined as the product of the apparent rate constant of the reaction, k_f, and the steady state PCr concentration in a three-site exchange model (scheme 1 in Fig. 4). We first checked by TDST in at least 5 hearts of each group that T₁^PCr value was unaffected by a change in [Ca]_o or by β-stimulation. The average value T₁^PCr of 3.43 ± 0.44 s (n = 22), was then used to estimate the CK flux by steady state γATP saturation protocol (satATP). This time-saving protocol included one control spectrum to determine M₀^PCr and 2 spectra saturated for 9 s for M_∞^PCr, the apparent rate constant was in this case calculated as (M₀/M_∞ − 1)/ T₁^PCr.

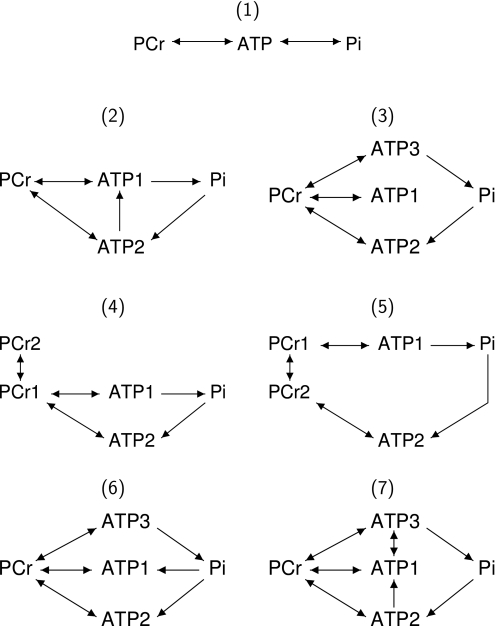
FIGURE 4.

Kinetic schemes analyzed in this work. All the unidirectional fluxes considered in the work are shown by arrowheads. See the text for the description of the schemes.

Analysis using Kinetic Schemes

The list of the schemes used in the analysis is shown in Fig. 4. For each kinetic scheme, a mathematical model was developed based on the Bloch-McConnell equations. For the three-site scheme (scheme 1 in Fig. 4), the equations are as follows,

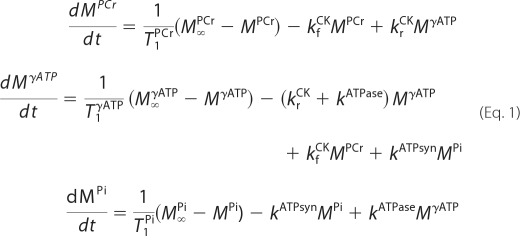where k values are pseudo-first-order rate constants of the reactions, M^Met and M_∞^Met are the magnetization of the metabolite Met during the experiment and at steady state, respectively. The intrinsic relaxation parameter for the metabolite Met was denoted by T₁^Met.

The model parameters were found by fitting the model solution to experimental measurements using the least squares method. For this, the set of the model parameters was varied until the best fit was obtained through minimization of χ²,

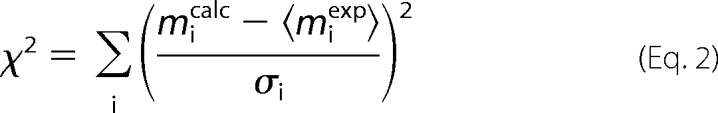where m_i^calc, 〈m_i^exp〉, and σ_i are calculated, mean measured value, and standard deviation for magnetization (ATP or PCr) at the time-moment i, respectively. The values of model parameters were considered the same for all experimental protocols under the same conditions (14). The description of the parameters optimized for each of the schemes is given in supplemental materials.

Evaluation of the Spread of the Measurements

As a basis of our analysis, we compared the deviation of the model solution from the measured mean value with the spread of the measurements. In correspondence with the least-squares method, the deviation of the model solution from the measured mean value was given by χ² (Equation 2). Similarly, the spread of the measurements can be described by χ²,

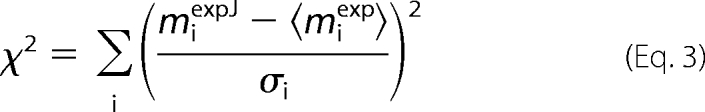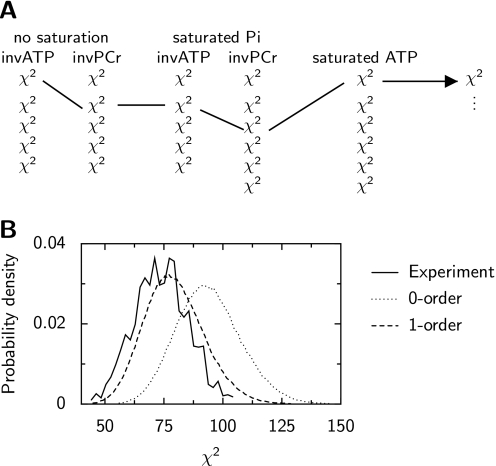
where m_i^expJ is the measured magnetization (ATP or PCr) at the time-moment i for the heart No J. On the basis of 4–6 individual recordings, we tried to estimate the distribution of χ² for each experimental protocol reflecting the spread of the measurements. For this, two types of stochastic processes were evaluated. For the first process, the deviation of measured magnetization at each time-moment is considered to be independent from the measurements at the previous time-moments. In this case, the data dispersion is assumed to result mainly from the error of each measurement. Thus, it is a 0-order process. In this process, the magnetization of PCr and ATP was assumed to be completely described by a normal distribution with the standard deviation and the mean value at each time-moment estimated from the measurements. For the second process, we assumed that the deviations of ATP and PCr magnetization at each time-moment were, in addition to estimated standard deviation and the mean value, dependent on the deviations at the previous time-moment. In this hypothesis, the data dispersion is partially attributed to the variability of parameters between the hearts. This process is a 1-order process. The detailed description of the 1-order process construction algorithm is given in supplemental materials. To compare the two types of processes, the distribution of total χ² (χ² corresponding to all protocols summed together as shown in Fig. 1A) was computed and compared with the distribution of total χ² estimated on the basis of the measurements (Fig. 1B). In all studied conditions, the total χ² distribution calculated using the 0-order process had a tendency to overestimate the spread of the experiments (larger than measured χ² were predicted). When 1-order process is used, the calculated total χ² spread is closer to the one, estimated from the measurements. For further analysis, the 1-order process was used.

FIGURE 1.

Characterization of the variation of the experimental measurements. Subplot A, Because all the five different types of experiments (protocols) were performed independently from each other, the distribution of total χ² can be estimated by finding all possible combinations of the individual experiments. Here, one of such combinations is shown. Subplot B, probability density function showing the variation of the experimental data acquired with 0.5 mm [Ca]_o in the presence of isoprenaline (solid line). To imitate the variation of experimental data, two stochastic processes were constructed (0-order and 1-order) as explained in the text. Note that 1-order stochastic process is able to reproduce experimental χ² variation rather well. The 0-order process has a tendency to overestimate the experimental variation leading to the higher χ² values.

Sensitivity Analysis

To estimate the sensitivity of the model parameters found by the fit to the variation of experimental data, the following procedure was used. Virtual experiments (5 protocols) were generated, ∼7000 times, using the 1-order stochastic process. Each experiment was fitted by the model. From the ∼7000 fitting results, a probability density function for each parameter was obtained. Using the probability density functions we were able to assess the stability of each of the model parameters. Additionally, from the spread of the fitted model parameters the S.D. was calculated. This S.D. was presented in some of our simulation results.

Numerical Methods

The system of ordinary differential equations was solved by the backward differentiation formula that is able to treat stiff equations (18). The accuracy of the solution was tested by varying the tolerance of the ordinary differential equation solver. The required optimization was performed using the Levenberg-Marquardt algorithm (19). In addition to the numerical libraries mentioned above, the following was used: Universal Non-Uniform Random Number generator (20); Pseudo-Random Number Generator; LAPACK, and BLAS.

RESULTS

In this study, isolated rat hearts were exposed to several conditions altering their performance and tested using five magnetization protocols. The experimental results were analyzed by seven high-energy phosphate kinetic schemes using rigorous statistical analysis. First, the physiological data are presented. Next, the analysis of the data is described.

CK Flux and Cardiac Performance

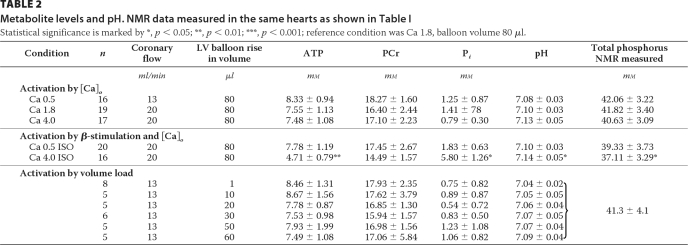
The cardiac contractile and respiratory responses to a change in calcium and to β-adrenergic stimulation are shown in Table 1. Rising [Ca]_o from 0.5 to 4 mm together with an increase in flow of perfusion from 13 to 20 ml/min increased RPP from 1.3 to 6.3 10⁴ mmHg × beats × min⁻¹ leading to about 3-fold increase in oxygen consumption. This occurred without significant alteration in energetic parameters (pH or ATP, PCr, and P_i concentrations) as shown in Table 2. Further enhancement in cardiac energy demand induced by β-stimulation under low [Ca]_o also occurred without energetic balance alteration. Under those conditions, the increase in energy demand was mainly caused by acceleration in heart rate. In contrast, β-stimulation under high [Ca]_o resulted in a new metabolite quasi steady state characterized by a significant rise in P_i, drop in ATP and PCr (by 37 and 11%, respectively) and a significant although moderate leak in total NMR visible phosphorus species (by about 10%, Table 2). Mitochondrial ATP content expressed as a percentage of total cellular contents were similar in Ca 0.5, Ca 1.8, and Ca 4 mm groups (6.4 ± 2.6%; 12.5 ± 2.6%, 10.2 ± 2.8%, respectively, n = 3–4) and increased to 24.5 ± 8% (n = 4, p < 0.05) in the Ca 4 mm under β-stimulation series.

TABLE 1.

Cardiac performance

Note that in this table, oxygen consumption VO₂ was calculated on the basis of RPP-VO₂ relationship (significance not shown). RPP-VO₂ relationship was determined outside of the magnets in heart submitted to activation by [Ca]_o and β-stimulation (n = 6) and hearts activated by volume load (n = 6). RPP-VO₂ relationship was similar in both protocols: the average slope was described by VO₂ = 1.5329 RPP + 2.759 (same units as shown in the table). EDP was similar in all groups (range 5–8 mmHg, not shown). Hearts corresponding to data shown in Fig. 3. Statistical significance is marked by *, p < 0.05, **, p < 0.01, ***, p < 0.001; reference condition was Ca 1.8, balloon volume 80 μl.

Condition	n	Coronary flow	LV balloon volume	LVDP	Half time of relaxation	Heart rate	Coronary pressure	RPP	VO2
		ml/min	μl	mmHg	ms	beats/min	mmHg	104 mmH g× beats/min	μmol O2/g wet weigh t× min
Activation by [Ca]o
Ca 0.5	16	13	80	52 ± 9***	55 ± 10*	252 ± 57*	75 ± 7	1.30 ± 0.41***	4.75 ± 0.63
Ca 1.8	19	20	80	154 ± 23	46 ± 3	296 ± 27	68 ± 11	4.58 ± 0.90	9.79 ± 1.38
Ca 4.0	17	20	80	225 ± 27***	45 ± 5	282 ± 33	123 ± 21**	6.33 ± 0.99**	12.46 ± 1.52
Activation by β-stimulation and [Ca]o
Ca 0.5 ISO	20	20	80	201 ± 21**	32 ± 2**	407 ± 32**	83 ± 7*	8.19 ± 1.21***	15.31 ± 1.85
Ca 4.0 ISO	16	20	80	234 ± 22***	29 ± 1**	373 ± 21**	81 ± 4*	8.69 ± 1.00***	16.08 ± 1.24
Activation by volume load, [Ca]o = 1.8 mm
	8	13	1	6 ± 3***	49 ± 14	276 ± 69	63 ± 9	0.17 ± 0.07***	3.02 ± 0.11
	5	13	10	24 ± 6***	52 ± 5	266 ± 31	68 ± 14	0.61 ± 0.08***	3.70 ± 0.12
	5	13	20	36 ± 5***	47 ± 15	279 ± 10	65 ± 10	1.00 ± 0.16***	4.29 ± 0.24
	6	13	30	61 ± 10**	35 ± 3*	259 ± 18	72 ± 17	1.57 ± 0.22***	5.16 ± 0.34
	5	13	50	80 ± 9**	38 ± 7	261 ± 20	76 ± 17	2.06 ± 0.15**	5.92 ± 0.23
	5	13	60	108 ± 6*	34 ± 3*	276 ± 26	72 ± 13	2.96 ± 0.24*	7.29 ± 0.37

TABLE 2.

Metabolite levels and pH. NMR data measured in the same hearts as shown in Table I

Statistical significance is marked by *, p < 0.05; **, p < 0.01; ***, p < 0.001; reference condition was Ca 1.8, balloon volume 80 μl.

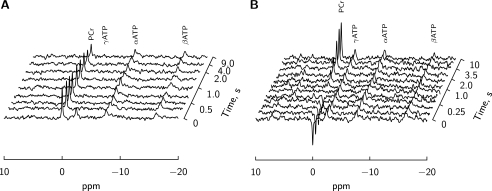
Typical magnetization transfer protocols are shown in two representative hearts for a time-dependent saturation (TDST) of γATP (Fig. 2A) and for an inversion of PCr (Fig. 2B). If a significant adenylate kinase AK flux (2ADP ⇆ ATP + AMP) had contributed to the energy transfer it would have been detected as a transfer from the magnetization of γATP to the βATP peak. However no evidence of a significant AK unidirectional flux could be observed in any of the physiological conditions. CK unidirectional forward flux was determined from the TDST protocol assuming a simple three-site exchange model (scheme 1 in Fig. 4). The total unidirectional CK flux was not significantly different from Ca 1.8, in group Ca 0.5, Ca 4 and Ca 0.5 under β-stimulation (6.5 ± 1.0, 5.3 ± 1.2, 5.6 ± 1.1, 4.5 ± 1.1, mm × s⁻¹, respectively). As shown in Fig. 3A, the flux was not positively correlated to energy demand. Moreover the flux significantly decreased to 3.8 ± 0.8 mm × s⁻¹, p < 0.05 in the [Ca]_o 4 mm under the β-stimulation group that developed the highest energy demand.

FIGURE 2.

Sample NMR spectra showing response to γATP peak saturation (subplot A) and PCr inversion (subplot B). Spectra were acquired at [Ca]_o 0.5 mm with (subplot B) and without (subplot A) the presence of isoprenaline.

FIGURE 3.

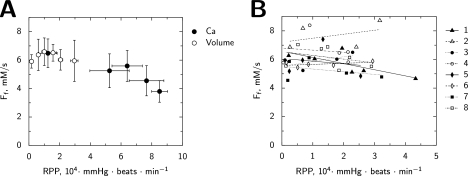
Total unidirectional flux of creatine kinase in the direction of ATP synthesis. This flux represents the sum of all CK isoforms activities. It was calculated using the drop of PCr magnetization in response to the γATP saturation. The work of the heart was changed either by variation of [Ca]_o and isoprenaline (Ca) or by variation of the balloon volume in the left ventricle (volume). In subplot A, the average values are shown for both types of stimulation. In subplot B, the cardiac work was varied only by changing the balloon volume. In this subplot, the individual measurements performed in n = 8 hearts are shown together with the linear regressions (number of the heart is shown in label). Note that the x-axis scale is different in the subplots.

To minimize individual heart variations and confirm the stability of CK flux, the total unidirectional CK flux was further analyzed in hearts undergoing several step-changes in the LV balloon volume to determine the slope of the relationship of CK flux to RPP in each individual heart (n = 8, [Ca]_o 1.8 mm). The functional and energetics parameters show the range of cardiac performance and the metabolic stability (Tables 1 and 2). The independence between the total unidirectional CK flux and RPP is clearly shown in the individual hearts (Fig. 3B). The average relationship is described by F_f (in mm × s⁻¹) = a + b × (RPP in 10⁴ mmHg × beats × min⁻¹) where a = 6.0 ± 0.8 and the slope b is nonsignificantly different from zero (b = 0.23 ± 0.70). As summarized in Fig. 3A, except for the highest energy demand, total unidirectional forward CK flux was constant and independent of energy demand during both activation by load and by calcium.

Detailed Analysis of the Fluxes

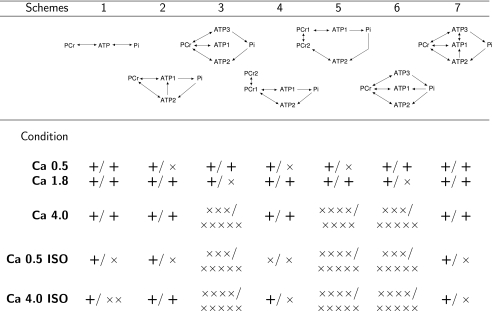
Schemes

Whereas total CK flux remained constant in most of the conditions, because of CK isoenzyme compartmentation, local subcellular fluxes could vary with cardiac performance. In our analysis, we considered seven different schemes describing energy fluxes within the cardiac muscle cell (Fig. 4). The schemes describe the average energy fluxes within repeating units of mitochondria and adjacent ATP consumers (myofibrils, sarcoplasmic reticulum, and sarcolemma). In adult rat cardiomyocytes, such units are distributed regularly over the cell (21, 22). We assume that those units work uniformly and there is a minimal interaction induced by diffusion of metabolites between the units. Thus, the influence of intracellular diffusion restrictions between the units (11, 23, 24) was not considered.

The simplest, non-compartmentalized case, is shown in scheme 1. This scheme considers both directions of the CK reaction (all isoforms together), ATPase (link from ATP to P_i), and ATP synthesis in mitochondria (link from P_i to ATP). All other schemes take into account ATP compartmentation in the cell. The schemes 2, 4, and 5 consider two ATP compartments: mitochondrial matrix (ATP2) and the rest of the cell (ATP1). Schemes 3, 6, and 7, partition ATP into three compartments: mitochondrial matrix (ATP2), ATP next to ATPases (ATP3), and the rest of the cell (ATP1). PCr was partitioned into two compartments in schemes 4 and 5. The fluxes in compartmentalized schemes were as follows. The unidirectional fluxes of cytoplasmic and myofibrillar CK link PCr pools with ATP1 and ATP3 (all schemes). Mitochondrial CK (MiCK) coupled to adenine nucleotide translocase (ANT) link PCr with ATP2 (all schemes). Because of the possible free energy profile of coupled MiCK-ANT reaction (25), both directions of the reaction were considered. The direct transfer of ATP from mitochondrial matrix to cytoplasm is shown by a link between ATP2 and ATP1 (schemes 2 and 7). This transfer is considered as unidirectional due to the large membrane potential difference in the mitochondrial inner membrane. Diffusion of ATP between cytoplasm and ATP compartment next to ATPases is shown by a link between ATP1 and ATP3 (scheme 7). Diffusion between two PCr compartments (PCr1 and PCr2) is considered in schemes 4 and 5. All the other processes were considered as unidirectional. ATP synthesis and ATPase activity is shown by linking P_i with ATP2 or ATP(1,3), respectively (all schemes). Glycolysis is considered in scheme no. 6 and is shown by linking P_i to ATP1.

Tests

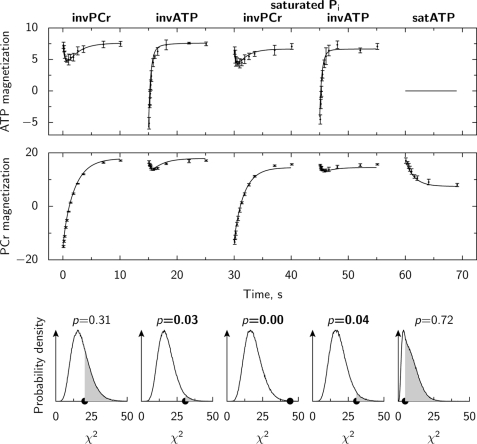
Each scheme was evaluated by two different tests. These tests were performed to check the ability of the model to fit the measurements (test 1) and whether the model contained too many parameters (test 2). In the first test, the model solution was fitted to the experimental data (example in Fig. 5). To estimate whether the scheme is able to fit all the data uniformly and not just a subset of the used protocols, the deviation of the model solution from the mean value was compared with the estimated spread of the measurements. If the deviation from the mean of the individual experiment was larger than the deviation of the model solution with a chance higher than p = 0.05 then the model passed the test. As it is shown in the bottom row of Fig. 5, the model poorly fits (p < 0.05) three protocols indicating that scheme no. 3 (Fig. 4) cannot reproduce the measurements performed at 4.0 mm [Ca]_o.

FIGURE 5.

Example of the model fit to the experimental data. In the two upper subplots, the model fit (solid line) is plotted against measured mean and S.D. values (points with error bars) of ATP and PCr magnetization. The model parameters were found by simultaneously fitting all five types of experiments (see the top of the figure for experiment types). On the bottom row, the deviation of model solution from the mean values (χ² is marked by solid dots on the x-axis) is compared with the estimated spread of the measurements in each type of the experiments. Each subplot on the bottom row corresponds to the type of the experiment plotted above it. The probability values p, shown on the bottom row subplots, indicate the chance to have the deviation from the mean of the individual measurement larger than the one for the model solution. This probability is found by integration of the probability density function at χ² values higher than the one obtained during the model fit. The integration is demonstrated by shaded area in the bottom row subplots. Note, that the model is rather poorly fitting measured PCr and ATP magnetization after inversion of PCr in the presence of P_i saturation leading to a very low p value. In this example, kinetic scheme no. 3. (Fig. 4) was used, and the measurements were performed at 4.0 mm [Ca]_o without isoprenaline.

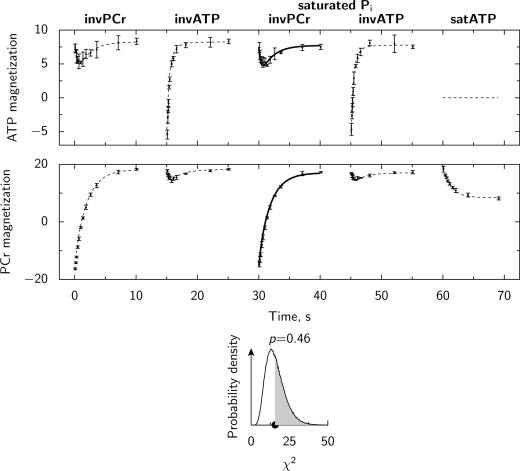
In the second test, the model was used to reconstruct data obtained by one protocol on the basis of the measurements with the other protocols (Fig. 6). This test was performed to check the model sensitivity and whether the model has too many parameters (26). If the model is too sensitive or there are too many model parameters then data acquired with each protocol contributes to the fit. In this case, if one of the protocols is omitted (for example inversion of PCr with P_i saturation in Fig. 6) then the model parameters found on the basis of other protocols would be considerably different from the values found using all experimental data. As a result, if the model is used to predict the omitted data then the deviation from the mean experimental measurements could be too large. In the example shown at Fig. 6, the model is able to reproduce the omitted data using the model parameters found by fitting the data from the other four protocols.

FIGURE 6.

Model validation procedure used in this work (same notation as in Fig. 5). In the test, model parameters were obtained by fitting data obtained in four protocols (solution is shown by dashed lines in the two upper subplots). From the resulting parameters, the omitted data (the fifth protocol) was predicted by the model (solution is shown by a thick solid line) and this prediction was compared with the mean experimental data. As is shown in the lower subplot, the omitted data were successfully reconstructed (p > 0.05). In this example, kinetic scheme no. 3 (Fig. 4) was used and the measurements were performed at 0.5 mm [Ca]_o.

Comparison of the Schemes

The results of the test of the schemes are shown in Fig. 7. In the first two studied conditions ([Ca]_o equal to 0.5 mm or 1.8 mm), all models passed almost all the tests: they were able to fit the data and at most one protocol failed the predictive test. Thus, in these conditions, it is impossible to discriminate between the schemes. However, at higher level of energy demand (high [Ca]_o or in the presence of isoprenaline), schemes 3 and 6 (Fig. 4) failed in all the tests (Fig. 7). Such problems were not detected for the schemes which allow a direct link between ATP next to the ATPases and ATP synthase (schemes 1, 2, and 7). The models composed on the basis of these schemes were able to fit the measurements in all conditions (test 1). Most of the protocols were well predicted from the fit to the other ones as well (test 2). Thus, on the basis of analysis of schemes 1–3, 6, and 7, at least in some conditions, the energy export from the mitochondrial matrix to the cytosol is carried via direct diffusion of ATP in addition to CK shuttle system.

FIGURE 7.

Validation of the kinetic schemes at different work conditions. The schemes were tested by fitting the data and comparing the obtained χ² value to the spread of the experimental data as illustrated in Figs. 5 and 6. The minimal probability p required to consider the model fit as a successful one was taken p > 0.05. The results of both tests are presented in the form test1/test2 for each of the model in each condition. If the test was successful, it was shown by + symbol; if both tests were successful, it was shown as +/+. If one of the protocols was either not fitted with the sufficient precision or not predicted, it was marked by ×. The number of × indicates the number of protocols which have been not sufficiently reproduced by the model. For example, the scheme 1 at Ca 0.5 ISO is able to pass the test 1, but was not able to reproduce the data recorded on one of the protocols on the basis of the other data. Note that the schemes with the direct transfer between mitochondrial and cytosolic ATP pools are able to fit the data in all conditions. The models assuming that CK shuttle is an exclusive connection providing the link between ATP production and consumption cannot fit the data obtained at higher energy demands (except if PCr compartmentation was considered).

In the schemes 4 and 5 (Fig. 4), PCr is partitioned into two compartments and the energy transfer from matrix ATP to cytosol is carried out through the CK shuttle only. In both cases the model degenerates into a four sites scheme by either reducing the compartment PCr1 to the lower limit (scheme 4) or increasing infinitely the exchanges between the two compartments, making the two compartment fuse (scheme 5). Thus, PCr compartmentation is not required to simulate our data. The detailed description of all simulation results with the obtained model parameters under all studied conditions is presented in supplemental materials.

Total Unidirectional Flux of CK Reaction

The total unidirectional CK flux was estimated using several schemes (Fig. 8). According to our estimations, the flux is rather stable when the energy demand is changed through variation of [Ca]_o only. However, if [Ca]_o is changed in the presence of isoprenaline, the total unidirectional CK flux drops significantly. The estimate of CK flux was only slightly dependent on the used model. Namely, if the schemes, which assume that CK shuttle is an exclusive link between ATP synthase and ATPases, were used then the total unidirectional CK flux was slightly larger than the one predicted with the other schemes (Fig. 8).

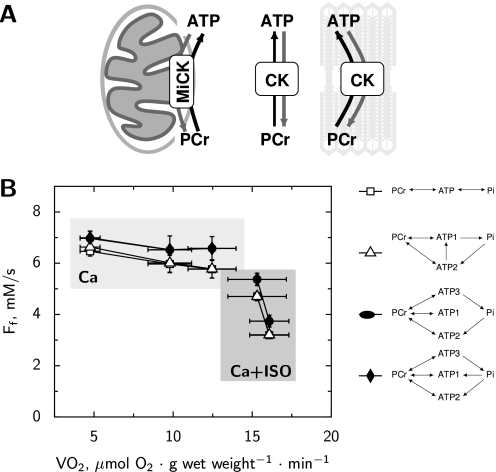
FIGURE 8.

The total unidirectional flux F_f of creatine kinase. The estimated flux is a sum of activities of all CK isoforms in the direction of ATP synthesis as shown in subplot A by black arrows. Note that CK reactions are considered bidirectional, as indicated in subplot A. In subplot B, the mean value of the flux with its S.D. is estimated using the kinetic schemes. Note that our estimation does not depend significantly on the scheme. Additionally, unidirectional CK flux is kept relatively stable if the cardiac work is changed through variation of [Ca]_o only (shaded box marked by Ca). As soon as isoprenaline is added, the unidirectional CK flux drops with the increase of cardiac work (shaded box marked by Ca+ISO).

Energy Transfer from Mitochondria

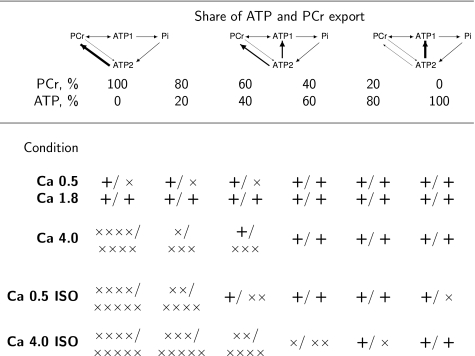
We estimated the proportion of ATP exported from mitochondria to ATPases bypassing CK shuttle using the model based on scheme 2 (Fig. 4). This scheme, considering both PCr and direct ATP exchange between subcellular compartments, is the simplest unified metabolic scheme that allows to analyze the measurements in all studied conditions. The proportion of ATP export from mitochondria to ATPases bypassing CK shuttle was not distributed in a bell-shaped manner around the average value, but was either zero or one (see supplemental materials). To get further insight in the distribution of energy export from mitochondria, we adopted the strategy of fixing the proportion of energy exported as ATP or PCr and then optimized all the other model parameters. The results of our simulations are shown in Fig. 9. In those simulations, the specific proportion of ATP export through the CK shuttle system cannot be predicted, thus only the range of possible solutions is determined. Note that at lower energy demand levels ([Ca]_o 0.5 mm and 1.8 mm), we were not able to discriminate between the model solutions (the model was able to fit the data with PCr export ranging from 0 to 100%). However, with increasing energy demand, the model assuming that CK shuttle is the only link providing ATP from ATP synthase to ATPases is not in agreement with the measurements (energy transport by PCr ranged from 0 to 60% for both Ca 4 mm and Ca 0.5 mm in presence of isoprenaline). With further increase in energy demand, up to the extreme case ([Ca]_o 4.0 mm in the presence of isoprenaline), a fit was only possible if the majority of ATP synthesized in mitochondria bypassed CK shuttle system (PCr direct export ranged from 0 to 20% of the total energy export). The same conclusion can be drawn if scheme 7 (Fig. 4) is used (results not shown). As it is clear from our simulations, the maximal possible share of CK shuttle system in the export of ATP decreased gradually with the increase of energy demand.

FIGURE 9.

Modulation of energy export pathways from mitochondria to cytoplasm by mechanical activity. In these simulations, the proportion of ATP and PCr export from mitochondria to cytoplasm was fixed as shown in the table. The other model parameters were optimized to fit the data. The results are shown using the same notation as in Fig. 7. As in Fig. 7, the minimal probability p required to consider the model fit as a successful one was taken as p > 0.05. Note that the proportions of ATP export that are consistent with the measurements vary depending on the conditions.

Minimal Set of Experiments

Finally, we tested whether some of the protocols can always be predicted on the basis of the data collected using the protocols. According to our simulations, it is possible to reduce the number of measurements by two inversion experiments. Namely, the inversion of PCr magnetization without saturation of P_i and inversion of ATP magnetization with saturation of P_i can be predicted simultaneously using the three other protocols. Such prediction of the two protocols was possible in all studied conditions with any of the schemes as long as the scheme was able to fit the data in this condition. As shown in detail in supplemental materials, the precision of the prediction was relatively high (p > 0.2, p calculated as in Fig. 6). Alternative pair of the inversions which can be predicted quite well on the basis of other protocols is inversion of ATP magnetization without saturation of P_i and inversion of PCr magnetization with saturation of P_i. The predictions were almost as good as for the first pair of the protocols proposed above, except in the extreme conditions ([Ca]_o 4.0 mm in the presence of isoprenaline). In the extreme conditions, none of the models was able to predict the omitted pair with a significant precision (p > 0.01). Such difference between the proposed pairs can be caused by relatively large standard deviations in one of the protocols in these conditions. Namely, at some time-moments, the recorded magnetization of ATP after inversion of ATP in the presence of P_i saturation had relatively large dispersion. As a result, this inversion is easier to predict on the basis of other protocols.

DISCUSSION

According to our results, the total CK unidirectional flux is relatively stable in the heart when the cardiac energy demand is changed through variation of [Ca]_o, β-stimulation, or LV volume. The stability is lost at extreme energy demand leading to the drop of total CK unidirectional flux and to a bypass of CK shuttle by the export of ATP from mitochondria to ATPases. Such shift from one metabolic state to the other one under extreme conditions is consistent with the earlier analysis of the respiration in cyanide-inhibited hearts (4).

Comparison with Earlier Studies

In this work, we extended the analysis method used earlier (4, 13, 14) to better discriminate between the possible schemes. The aim of our analysis was not only to choose a scheme fitting the five protocols for each experimental condition, but to find a unique scheme able to fit the all conditions, in order to describe the pathways modifications resulting from the change of energy demand. For that, rigorous testing was applied to each of the studied schemes. The tests were derived from proposed neural-network construction and selection procedures (26). To our knowledge, it is the first time such approach has been applied in modeling of biological systems. In contrast to earlier studies where overall χ² was used (4, 13, 14), we assessed the quality of the fit by checking whether the scheme was able to reproduce all the experiments and whether the number of parameters was too large. The tests greatly benefited from the stochastic model of the experiment, which was able to reproduce the statistical properties of the measurements well (Fig. 1) and allowed us to account for non-normal distribution of model parameters (supplemental materials). As a result of this new type of testing, we were able to identify a unique scheme that was able to reproduce all studied experiments and is relatively simple (scheme 2). Additionally, we were able to test which protocols are always reproducible on the basis of the other protocols. According to our simulations, the inversion of PCr magnetization without saturation of P_i and inversion of ATP magnetization with saturation of P_i can be predicted simultaneously using the three other protocols. Thus, it is sufficient to perform the following measurements: inversion of ATP magnetization without saturation of P_i, inversion of PCr magnetization with saturation of P_i, and response of PCr magnetization to saturation of P_i.

Our results show that the total CK unidirectional flux was stable if the energy demand was changed either by variation of [Ca]_o or by LV balloon volume. This conclusion was reached using two different methods for estimation of the flux: Time Dependent Saturation Transfer method (Fig. 3) and fitting all five protocols of saturation and inversion transfer (Fig. 8). Because the dispersion of CK flux value measured by NMR is rather high (Fig. 3A, see also (16, 27)), we looked into regression between CK flux and energy demand in individual hearts undergoing several steps of balloon change (Fig. 3B). No significant change in CK flux was identified using individual heart measurements either.

The relationship of CK unidirectional flux to cardiac energy demand has been a subject of a controversy for some time. Some studies using the perfused rat heart reported that the total CK unidirectional flux increases with energy demand, either linearly or following a Michaelis-Menten relationship (16, 27). On the opposite, as also observed here, the total CK unidirectional flux was shown to be independent of energy demand over a wide range of performance, both in the isolated perfused beating adult heart (28–30) and in vivo (31, 32). The reason for such divergent results is not fully understood but could result from different experimental models. First, KCl-arrested hearts were used as the minimal working condition in several studies (16, 27). However this artificial condition perturbs ionic intracellular homeostasis and intracellular energy transfer (33). Indeed, except study (29), the transition from arrest in KCl to beating heart is associated with a marked increase in CK flux (16, 27, 33), sometimes as drastically as by 3 fold. Second, the increase in CK forward flux together with energy demand was observed when glucose was the only myocardial substrate available (16, 27), a condition known to increase the value of CK flux (28, 34). Such an exclusive dependence on glycolytic substrate does not prevail in the heart in vivo.

Compared with other NMR studies, our study explored a large variation in cardiac energy demand in the beating heart resulting in a 4-fold increase in VO₂. The highest performance, obtained under β-stimulation in high calcium may reflect the limit of the used model (the isovolumic perfused heart). Although, under these conditions the levels of phosphorylated metabolites reached a new steady state (i.e. there is no imbalance between energy production and demand), the decrease in CK flux found here did not occur in vivo in the adult heart submitted to dobutamine stress (31). However the results of our approach could be relevant for the understanding of the energetics of the pathological myocardium (see below).

Physiological Implications

Does the stability of total CK unidirectional flux mean that the CK shuttle system is bypassed and CK is in equilibrium (12)? No. The adult heart, as opposed to the neonatal cardiac muscle or to the fast glycolytic skeletal muscle, is characterized by high compartmentation of CK isoforms, localized close to the sites of ATP production and utilization. Compartmentation of CK isoforms generates local fluxes that all contribute to the total CK unidirectional flux. According to our simulations, the increase of energy demand by changing [Ca]_o from 0.5 mm to 1.8 mm can be very well modeled by the schemes, which supply ATP to ATPases by CK shuttle exclusively (scheme 3, for example in Fig. 7). This indicates that net CK shuttle flux could increase significantly without any increase of total CK unidirectional flux (Fig. 8). Indeed, the increase of unidirectional mitochondrial CK flux at the expense of the unidirectional cytosolic CK in direction of synthesis of PCr would be consistent with our data and would lead to increase of net PCr flux at higher energy demand.

Using scheme 2, we estimated the fraction of ATP exported from mitochondria to cytoplasm directly (Fig. 9). There is a clear difference between energy pathways at lower and high energy demand levels. At lower energy demand, we were not able to distinguish the pathway of ATP export from mitochondria. Indeed, all solutions fitted the measured data rather well (Fig. 9). The situation is different at extreme energy demand ([Ca]_o 4.0 mm in the presence of isoprenaline). Only by assuming that ATP is mainly exported directly from mitochondria bypassing CK shuttle, we were able to fit the measurements with the model. Such difference in energy transfer pathways at extreme conditions is accompanied with changes in metabolite concentrations (Table 2) and a reduction in total CK unidirectional flux (Fig. 8). However, this occurred without significant increase of mitochondrial membrane proton leak (RPP and VO₂ relationship was the same as for the lower cardiac performance levels). Bypassing the CK shuttle at extreme cardiac performance, as identified in this work, is similar to our previous results obtained upon inhibition of respiration (4). Namely, in the presence of cyanide, the concentrations of metabolites changed and the best fit to the measured data were obtained by the model which assumed that ATP is bypassing CK shuttle during its export from mitochondria (4). The results obtained in this work and in our earlier studies suggest that CK shuttle is bypassed by direct diffusion of ATP when the energy requirement becomes close to the maximum ATP synthesis capacity. The possible mechanism leading to such ATP export from mitochondria at extreme energy demand is not clear and requires further study. At present, we cannot state whether the changes in the mechanism of ATP export from mitochondria are gradual with the increase of energy demand or occur abruptly. Both hypotheses would be consistent with our results. Our results show that the maximal share of CK shuttle system in export of ATP from mitochondria which is consistent with our data is reducing gradually with the increase of energy demand (Fig. 9). However, taking into account a wide range of CK shuttle contributions consistent with the data, this does not necessarily mean that ATP export is changing gradually. On the basis of our results, we suggest that the relative contribution of CK shuttle and direct ATP export from the mitochondria is a finely tuned variable. The contribution of both PCr export by CK and direct ATP export from mitochondria might represent a safety mechanism allowing the rapid and efficient adaptation in energy transfer required by large changes in cardiac energy demand.

Application to Pathologies

Several cardiac pathologies (such as cardiac insufficiency, heart failure, cardiomyopathy, diabetes) impair energy synthesis and/or utilization together with the marked alteration in the CK system (35–37). The implication of CK system to energy transfer is highlighted by showing that the ratio of PCr to ATP concentrations can be used as a predictive indicator of mortality in human heart failure patients (38, 39). Depending on the pathologies, decreased total CK activity, and/or alterations in the expression of CK specific isoforms have been observed (40, 41). Alterations in the functional coupling of CK to ATPases (myosin, SERCA, or sarcolemmal ATPases) were also demonstrated in subcellular preparations of skinned fibers (36, 40) together with direct energy transfer between mitochondria and ATPases (42). What is the relative importance of these subcellular alterations for the alteration of the whole heart function remains presently unknown. We think that our method of analysis of energy transfer is a valuable tool to evaluate the consequences of these subcellular alterations in the global energy transfer of the whole heart in a pathological state. Application of such analysis should give further insight in the existence of adaptive mechanisms and of the transition toward heart failure. In addition, information obtained using the ³¹P-NMR inversion transfer and saturation transfer protocols can be used to analyze the regulation of metabolism when combined with the kinetic mathematical models. Usually, kinetic models are used to analyze changes in concentrations induced by variation of the workload or inducing ischemia (43–45). The inversion transfer and saturation transfer analysis results can be used to verify the predictions obtained by kinetic models and, as a result, would allow us to learn more about the cardiac regulation in health and disease.