Experimental Validation of the Predicted Binding Site of Escherichia coli K1 Outer Membrane Protein A to Human Brain Microvascular Endothelial Cells

Abstract

Escherichia coli K1, the most common cause of meningitis in neonates, has been shown to interact with GlcNAc1–4GlcNAc epitopes of Ecgp96 on human brain microvascular endothelial cells (HBMECs) via OmpA (outer membrane protein A). However, the precise domains of extracellular loops of OmpA interacting with the chitobiose epitopes have not been elucidated. We report the loop-barrel model of these OmpA interactions with the carbohydrate moieties of Ecgp96 predicted from molecular modeling. To test this model experimentally, we generated E. coli K1 strains expressing OmpA with mutations of residues predicted to be critical for interaction with the HBMEC and tested E. coli invasion efficiency. For these same mutations, we predicted the interaction free energies (including explicit calculation of the entropy) from molecular dynamics (MD), finding excellent correlation (R² = 90%) with experimental invasion efficiency. Particularly important is that mutating specific residues in loops 1, 2, and 4 to alanines resulted in significant inhibition of E. coli K1 invasion in HBMECs, which is consistent with the complete lack of binding found in the MD simulations for these two cases. These studies suggest that inhibition of the interactions of these residues of Loop 1, 2, and 4 with Ecgp96 could provide a therapeutic strategy to prevent neonatal meningitis due to E. coli K1.

Introduction

Neonatal bacterial meningitis is one of the most serious infections of the central nervous system, resulting in significant neurological sequelae (such as hearing loss, convulsive disorders, abnormal speech patterns, cortical blindness, and mental retardation) in half of the survivors (1–4). The incidence of bacterial meningitis in infants is about five cases per 100,000 live births per year in developed countries but can be 10 times higher in underdeveloped countries (5).

Escherichia coli K1 is the predominant pathogen causing neonatal meningitis and septicemia (6). The mortality and morbidity due to E. coli K1 has remained significant in the last few decades, despite the use of effective antimicrobial therapy. This poor outcome is due to increased antibiotic resistance of E. coli, possibly due to their use in food stock (7) and the high adaptive mutation ability of E. coli (shown to be on the order of 10⁻⁵ per genome per generation) (8).

Our previous experimental studies in the newborn rat model of hematogenous meningitis demonstrated that a high degree of bacteremia is required for the onset of meningitis (9). We showed that the entry of E. coli K1 into human brain microvascular endothelial cells (HBMEC),³ which comprise the lining of the blood-brain barrier, requires the expression of a 35-kDa OmpA (outer membrane protein A) in E. coli K1 (10).

In addition, we and others (9–12) showed that OmpA expression is important for entry of monocytes, macrophages, and dendritic cells, indicating the important role of this protein in the pathogenesis of neonatal meningitis by E. coli K1. We also showed that the interaction of OmpA with Ecgp96 (a homologue of Hsp90 that specifically expresses on HBMEC) is critical for the invasion of E. coli (13, 14). Indeed, we showed that Ecgp96 contains two N-glycosylation sites at the N-terminal region whose N-acetyl-d-glucosaminyl-β(1–4)-N-acetyl-d-glucosamine (chitobiose) moieties that interact with OmpA during the invasion process (11, 12).

Our previous studies using synthetic peptides representing portions of loops 1 and 2 of OmpA showed that these loops might be involved in E. coli K1 interaction of HBMEC for invasion (13). This was supported by our previous computational studies that identified two binding sites: the outer site, involving loops 1 and 2 and the inner site, involving loops 3 and 4.

However, our previous computational studies were restricted to rigid ligand docking approaches, with no consideration for the phospholipid membrane or the solvent environment (14). Additionally, we ignored considerations of entropy, due to the enormous computational cost (15) associated with exact methods, such as free energy perturbation and Widom-particle insertion (16–20). This is a major potential source of error, as entropy is generally believed to play a critical factor in protein folding (21, 22), in binding of various proteins to DNA, (23) and in the hydrophobic effect (24).

To overcome these limitations, we now apply our two-phase thermodynamics (2PT)⁴ (25) method to extract the entropies, quantum effects (zero-point energies), and free energies from Molecular Dynamics (MD) simulations of the OmpA/chitobiose. With 2PT, the thermodynamic properties are obtained directly from the velocity autocorrelation function, derived from short (20 ps) MD simulations.

Here, we used 2PT simulations to characterize the interaction of chitobiose moieties with OmpA. We find that the initial recognition involves a specific loop site, which is followed by cooperative binding to the barrel site, leading to a new proposed mechanism: the loop-barrel pathway model. The critical residues on OmpA suggested from these predicted binding studies were then mutated to alanines computationally to predict the effect on the free energy of binding for comparison to the experimental invasion efficiency of E. coli.

These same mutations were generated experimentally in a double-blind study in which the computational and experimental results were not revealed until both studies were complete. Most exciting is that the predicted free energies correlate with experimental invasion efficiency with 90% accuracy. This indicates that these methods might be useful in search for therapeutic candidates.

We find that two mutations in OmpA completely inhibit the E. coli invasion of HBMEC and that the MD simulations on these cases indicate no binding. Based on the functional groups identified by mutational analysis, we suggest pharmacophore models of the binding sites that might be useful in designing new therapeutics. The current work is the first attempt to obtain free energies of binding for OmpA/ligand complexes as it related to bacterial meningitis.

EXPERIMENTAL PROCEDURES

Molecular Dynamics Simulations

To predict the binding sites and affinities for the OmpA-chitobiose complex for both WT OmpA and 11 mutants, we started by embedding the OmpA (26) receptor (Protein Data Bank code 1QJP) in the center of a pre-equilibrated box of 200 1,2-dipalmitoyl-sn-phosphatidylcholine (DPPC) molecules in 0.1 m KCl salt solution (a total of 13,875 water molecules). We removed any overlapping lipid and solvent molecules, leaving a total of 53,614 atoms for the WT. We generated the DPPC lipid system using the CHARMM-GUI (27) internet portal and performed the MD using the TIP3P (28) water model and the CHARMM36 (29) force field, shown to reproduce the experimental surface area per lipid in the isobaric isothermal (NPT) ensemble. OmpA was described using the CHARMM force field for proteins (30).

We equilibrated this system with 30 ns of annealing dynamics, cycling from 300 to 500 Kelvin (K) in three 10-ns intervals, using the NPT ensemble (pressure maintained at 1 atm). Annealing dynamics achieves faster equilibration in condensed phased systems because the system is given sufficient energy to overcome barriers on the potential energy surface and then allowed to relax to a lower energy valley. The complex was then subjected to a further 25-ns NPT dynamics at 300 K and 1 atm. All simulations were performed using the LAMMPS (31) open source MD package.

The 11 mutants (Fig. 1) were generated, reminimized with the membrane and solvent present, and simulated for a further 10 ns of NPT dynamics. The structures were well equilibrated (supplemental Table S1) after 4 ns of MD. Chitobiose units were then docked into the two binding sites, determined by unbiased scanning of the OmpA receptor (see supplemental Methods) using our GenDock procedure (32). GenDock has been validated to predict accurate binding sites in previous studies (33–38). Here, we generated >2,000,000 ligand poses and selected the best pose based on the ligand interaction energy with the binding pocket. The solvent and DPPC molecules were not considered in our docking procedure.

FIGURE 1.

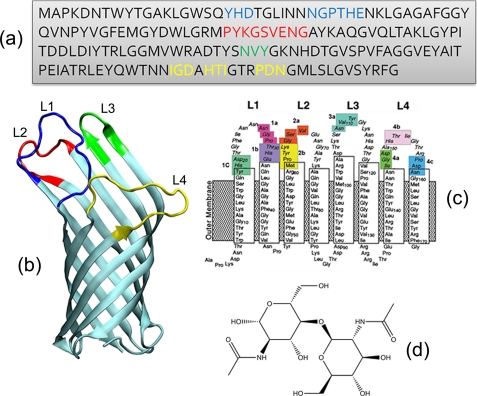
Overview of OmpA structure used in this study. a, amino acid sequence with the three sets of amino acid residue mutations (always to alanine) color-coded as follows: loop 1 (blue): 1a, Asn-28–Gly-29–Pro-30; 1b, Thr-31–His-32–Glu-33; 1c, Tyr-19–His-20–Asp-21. Loop 2 (red): 2a, X-66–X-67–X-68; 2b, Pro-63–Tyr-64–Lys-65; 2c, Glu-69–Asn-70–Gly-71. Loop 3 (green): 3a, Asn-110–Val-111–Tyr-112. Loop 4 (yellow): 4a, Ile-148–Gly-149–Asp-150; 4b, His-152–Thr-153–Ile-154; 4c, Pro-158–Asp-159–Asn-160. b, OmpA crystal structure (Protein Data Bank code 1QJP, 2.5 Å resolution) with the individual loops numbered and color-coded as in a. c, schematic of OmpA structure showing each of the 10 mutation set, plus the transmembrane and loop regions. d, the chitobiose ligand.

The best pose for each binding site was placed in the equilibrated protein-solvent-membrane system (again removing any overlapping solvent molecules) for 10-ns NPT dynamics. For consistency, the chitobiose was described using the CHARMM carbohydrates force field (39, 40), validated to give good performance over a range of carbohydrate-protein complexes.

Free Energy Calculations

To obtain the standard molar entropy S⁰, quantum corrections to the internal energy U⁰, and the Helmholtz free energy,

we used the 2PT method (25). We then calculated the relative binding free energy as the energy required to bring the chitobiose units from solution into the two binding pockets.

The chitobiose solvation free energy is obtained from a 10-ns MD simulation in a box with 512 TIP3P waters.

During the final 10 ns of the NPT simulations outlined above, we selected snapshots of the system (coordinates and velocities) every 2 ns. Each of the five snapshots was then simulated for 20 ps of MD using the Gibbs ensemble. The velocities and coordinates were saved every 4 fs (must be shorter than the fastest vibrational levels, which have periods of ∼10 fs for the 3000 cm⁻¹ C–H vibrations).

From these trajectories, we calculated the velocity autocorrelation function,

where v_j^k(t) is the k-th component of the velocity of atom j at time t (For illustration, supplemental Fig. S1 shows the velocity autocorrelation function for WT obtained from a 20-ps MD trajectory). From the velocity autocorrelation function, we obtained the density of states (DoS) by a Fourier transform of Equation 3.

Here, DoS(v) is the number of modes of the system at frequency v, including both vibrational and diffusional components. Indeed, DoS(0) measures the diffusion coefficient D₀,

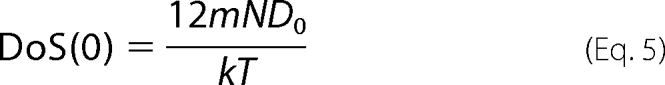where m is the mass, N is the number of atoms, k is the Boltzmann's constant, and T is the temperature.

A finite DoS(0) would lead to infinite entropy for standard quantum statistical formula (25). 2PT overcomes this limitation by partitioning DoS(v) into two components (supplemental Fig. S2). For DoS_diff(v), the diffusional component is described as a hard sphere diffusing gas, for which the velocity autocorrelation function decays exponentially with time, leading to,

where N_diff = 3Nf is the total diffusional degrees of freedom.

The diffusional contributions to the thermodynamics, S_diff, U_diff, and A_diff, are obtained from the Chapman-Enskog hard sphere theory as explained in Ref. 25. For the systems considered here, we find N_diff = 29,610, which is 18.4% of the 160,839 total modes of the WT.

DoS_solid(v) goes smoothly to zero as v → 0 (no diffusion), representing a vibrating Debye crystal. Here, we evaluate the partition function Q using the standard harmonic oscillator expressions from statistical mechanics (41).

Because DoS_solid(v) → 0 as v → 0, there are no singularities in Equation 7 at v = 0.

The system thermodynamics of the solid component are then obtained by integrating over the DoS_solid(v). Thus, the standard molar entropy S⁰ is as follows,

where β = 1/kT. The internal energy U⁰ is as follows,

where UMD is the internal energy from MD. Here, U⁰ is the reference energy of the system with all vibrations are in their lowest (zero) vibrational level, explicitly including zero-point energies. Finally, the Helmholtz free energy A⁰ is as follows in Equation 10.

Cell Culture and Invasion Assays

Human brain capillaries were isolated from small fragments of cerebral cortex, which were obtained from surgical resections of 4- to 7-year-old children with seizure disorders at Children's Hospital Los Angeles. HBMECs were isolated from these capillaries and cultured as described previously (13). These HBMECs were maintained at 37 °C in a humidified atmosphere of 5% CO2 in a medium containing M-199/Ham F-12 (1:1 v/v) supplemented with 10% fetal bovine serum, sodium pyruvate, and 2 mm glutamine and then cultivated in a cell culture incubator at 5% CO₂ and 37 °C. The HBMEC used for all experiments were between 12 and 16 passages.

For invasion assays, HBMEC grown in 24-well cell culture plates to 95% confluence were infected with 10⁷ cfu of E. coli in experimental medium (1:1 mixture of Ham F-12 and M-199 containing 5% heat-inactivated fetal bovine serum) and incubated for 90 min at 37 °C in an atmosphere containing 5% CO₂. The monolayers were washed three times with RPMI 1640 medium followed by addition of gentamicin (100 μg/ml) and further incubated for 1 h at 37 °C. The cells were then washed three times with RPMI 1640 and lysed with 0.5% of Triton X-100. The released bacteria were diluted with saline and enumerated by plating on blood agar. Results were expressed as an average of four independent determinations ± S.D. of the mean.

Generation of ompA Mutants in E. coli

Primer pairs (supplemental Table S2) containing the desired mutations were synthesized and cartridge-purified. PCR for the plasmid mutation was carried out using PfuTurbo DNA polymerase and pKE325 as the template, which is a 4-kb plasmid containing the complete E. coli ompA gene.

The reaction mix was heated at 96 °C for 90 s before the enzyme was added and followed by 18 cycles at 95 °C for 30 s, 55 °C for 1 min, 68 °C for 5 min, and a 5-min extension at the end. A faint band was visualized on agarose gel when the amplification succeeded. The DNA was then digested with DpnI and transformed into E. coli DH5α, selecting for kanamycin resistance. Plasmids were isolated, and the mutation was verified by sequencing.

The correct plasmids were introduced into the ΔompA strain E98, and the growth pattern of the bacteria was examined. The expression of OmpA in each strain was examined by Western blotting using an anti-OmpA antibody.

RESULTS

The Nature of Chitobiose Binding in Loop Region Differs across Mutants

In general agreement with our previous studies (14), we find two important binding sites for chitobiose on OmpA: one site consisting of the 1-2-3 loop regions (region L for loop) and the other site closer to the barrel of the OmpA and loop 4 (region B for barrel) (Fig. 2a).

FIGURE 2.

Structure of the chitobiose-OmpA (WT) complex after 70 ns of MD in explicit solvent, counter ions, and membrane. The binding sites are indicated by the electrostatic surface plots. These MD studies started with the two structures from docking: pose L (for loops) with chitobiose bound to loops 1, 2, and 3) and pose B (for barrel) with chitobiose bound to loop 4. Upper right panel, L binding site, showing all residues within 4 Å. Here three of the four HBs are shown, two of which are removed upon mutation (1a and 2c mutants). The average interaction distance is indicated in angstroms. The average deviation is 0.2 Å. Red arrows, hydrogen bond between chitobiose and protein; chitobiose is proton donor. Green arrows, hydrogen bond; chitobiose is proton acceptor. Lower right panel, B binding site, showing all residues within 4 Å. There is a strong HB to Thr-153, which is removed in the 4b mutant. Trp-103 has three strong electrostatic interactions with the C5 alcohol and O6 motifs of chitobiose. Thr-145 has two weak hydrogen bond interactions.

Our new ligand docking procedure (supplemental Fig. S3) (32, 42) finds the binding to region B to be consistently stronger than to region L (Table 1). Furthermore, the new predicted binding sites lead to vastly improved chitobiose binding energies (cf. −85.6 kcal/mol versus −15.0 kcal/mol for region L and −148.8 versus −20 kcal/mol for region B).

TABLE 1.

The cavity analysis of the chitobiose interaction with the WT OmpA in loop region L (1-2-3 loops) and region B (loop 4), ordered by total contribution to the binding energy

Residues affected by various mutations are indicated.

^‡ The residues on the OmpA were selected to be within 10 Å of the chitobiose.

^† The total binding energy includes contributions from residues not listed with binding energies < 1 kcal/mol.

^§ The individual components of the energy (van der Waals, coulombic, and hydrogen bonding) are shown in kcal/mol.

^ζ The residues to be alanized in a specific mutant are labeled.

The chitobiose in region L makes strong hydrogen bonds (HBs) with Asn-26 (−2.5 kcal/mol) and Asn-27/28 (−4.0 kcal/mol), as reported previously (14). We observe new HBs to Arg-61 (−3.2 kcal/mol) and Asn-70 (−1.0 kcal/mol). We consider these four interactions to be critical for binding. Indeed, the loss of the HB for the N28A mutation in the 1a mutant (N28A/G29A/P30A) dramatically decreases the binding energy of chitobiose in region L by 83%. Similarly, the binding energy in the 1b mutant (T31A/H32A/E33A) decreases by 84% (Table 2), due primarily to the loss of a favorable interaction with Glu-33 (−7.66 kcal/mol). As we show below that these mutants completely abrogate E. coli invasion, we conclude that region L binding energies < 20% of the WT could represent a lower bound on the energy required for the pathogenesis of bacterial meningitis. This hypothesis could be exploited for rapid screening of new ligands.

TABLE 2.

Chitobiose binding energy (kcal/mol) to critical residues in region L of the WT, compared with the 10 mutants considered in this study (negative indicates binding)

The residues selected form strong HBs to the chitobiose or had interaction energy >5 kcal/mol or was alanized. Residues affected by the specific mutations are in boldface and italicized.

	WT	1a	1b	1c	2a	2b	3a	4a	4b	4c
Asp-21	−1.47	0.78	0.79	0.00	−0.44	1.62	0.67	−0.56	−4.69	3.70
Asn-26	−4.49	−0.40	−0.20	−0.17	−0.14	−0.08	−0.24	−1.29	−0.22	−0.50
Asn-28	−2.25	0.15	0.12	−0.67	−0.50	−0.04	−0.63	−12.78	−0.51	−4.91
Glu-33	−7.67	0.56	0.00	1.11	−1.16	0.81	0.54	−0.89	−2.57	−0.23
Arg-61	−4.01	−0.94	−1.59	−1.92	0.61	−1.93	−0.68	0.37	−0.08	−9.00
Pro-63	−1.12	−0.04	−0.10	−0.22	0.00	−0.38	−0.05	0.05	0.10	−0.80
Ser-67	−5.81	−0.23	−0.64	0.03	−0.42	0.00	−0.02	0.36	0.17	−9.95
Glu-69	−1.33	−0.44	1.77	−2.43	−21.92	−7.77	0.34	−4.40	−4.02	−0.37
Asn-70	−8.37	−0.61	−0.13	−5.73	−4.08	−3.23	−0.19	−0.77	−3.42	−10.29
Tyr-108	−8.04	−0.63	−1.17	−1.15	−7.24	−0.68	−16.67	−0.23	−10.42	−1.82
Tyr-112	−2.72	−3.29	−0.67	−0.12	−0.13	−0.14	0.00	−0.07	−1.36	−0.49
Lys-114	−6.37	−0.73	−1.22	0.14	−3.69	0.00	0.42	2.29	−4.16	−3.07
Asn-115	−7.87	−0.24	−0.11	−0.06	−0.03	−0.01	−0.14	−0.10	−0.12	−0.21
Total	−85.63	−14.43	−13.54	−32.60	−73.70	−22.99	−35.36	−76.28	−83.44	−89.45

The 1c (Y19A/H20A/D21A), 2b (P63A/Y64A/K65A) and 3a (N110A/V111A/Y112A) mutations also affect the binding energy of chitobiose in region L, with 62, 73, and 59% reductions observed compared with the WT. The 2a (G66A/S67A/V68A) mutant is not as affected (14% to reduction), due to the presence of a new, very strong and largely electrostatic interaction with Glu-69 (−21.9 kcal/mol). Finally, the three mutations in loop 4 did not affect the chitobiose binding in region L (no more than 11% reduction).

In region B, we find four important HBs in the WT structure: Met-101, Ser-121, Thr-145 and Thr-153. The loss of these HBs leads to decreased binding in the 4a (I148A/G149A/D150A), 4b (H152A/T153A/I154A), and 4c (P158A/D159A/N160A) mutants of 36, 26, and 38% respectively (Table 3). Specifically, only the Ser-121 HB is conserved in the 4a–c mutants; whereas Thr-124 forms a weak HB in the 4a and 4b mutants, this HB is completely abrogated in 4c.

TABLE 3.

Chitobiose binding energy (kcal/mol) to critical residues in region B of the WT, compared with the 10 mutants considered in this study

	WT	1a	1b	1c	2a	2b	3a	4a	4b	4c
Arg-61	−5.82	−0.85	−0.60	−0.76	0.43	−0.86	2.16	−1.34	−4.51	0.13
Val-78	−9.33	−0.52	−0.42	−0.34	0.02	−0.31	−0.16	−0.34	−0.52	−0.19
Met-101	−9.36	−5.79	−6.36	−7.96	−9.11	−7.34	−6.59	−6.42	−8.06	−2.60
Trp-103	−12.65	−13.96	−13.31	−10.15	−19.02	−22.06	−19.72	−16.61	−15.69	−13.80
Thr-118	−6.83	−1.10	−1.12	−0.69	−0.68	−1.30	−0.76	−0.58	−0.06	−0.44
Ser-121	−9.16	−13.96	−4.88	−9.36	−17.37	−13.27	−19.78	−9.47	−5.63	−1.81
Thr-145	−1.03	−15.84	−14.38	−20.94	−5.92	−10.08	−5.29	−10.80	−13.84	−10.90
Ile-148	−13.91	−1.32	−0.99	−1.24	−2.10	−0.29	−1.44	−0.05	0.24	0.04
Asp-150	−1.71	−1.37	1.79	−0.05	2.19	0.89	0.88	0.10	−0.23	0.66
Thr-153	−15.14	−0.08	−1.28	−13.39	−6.92	0.11	−5.85	−1.21	0.02	0.82
Total	−148.83	−133.03	−145.00	−137.93	−150.69	−155.80	−128.29	−94.83	−109.59	−91.64

Thermodynamics of Chitobiose Binding

We first tested the ability of our simulation protocol and the 2PT method to capture the thermodynamics of the WT/chitobiose structure. Here, we evaluated the thermodynamics every 500 ps during the 30 ns of annealing dynamics and the 40-ns NPT simulation (a total of 70 ns simulation in explicit solvent and DPPC membrane). The separated chitobiose and WT structures were taken as the reference state.

During the three annealing cycles, the free energy tracks the temperature (supplemental Fig. S4), rising monotonically up to 4000 kcal/mol at 500 K and then decreasing to −200 kcal/mol at 300 K. After annealing, the free energy rapidly converges to the average value of −206 ± 5.6 kcal/mol after only 4 ns. The fluctuations in the free energy (4.1%) are similar to those observed in equilibrated condensed phase systems (43).

Comparing the binding free energy of the mutants with WT, we find that all mutants have a reduced internal energy compared with the WT: ranging from the 1b mutant (less stable by 281.5 kcal/mol) to the 3a mutant (less stable by 12.5 kcal/mol or 4.4%) (supplemental Table S3). The correspondence in the entropy is not as straightforward, however. We would have expected the entropy to increase (be more favorable) for each of the mutants relative to the WT, because mutating the bulky group to alanines should increase the available space (and mobility) of the chitobiose unit. This is indeed the case for all but the 3a (Δ(TΔS) = −6.6 kcal/mol or −8.4%) and 4b (Δ(TΔS) = −21.26 kcal/mol or −27.2%) mutants.

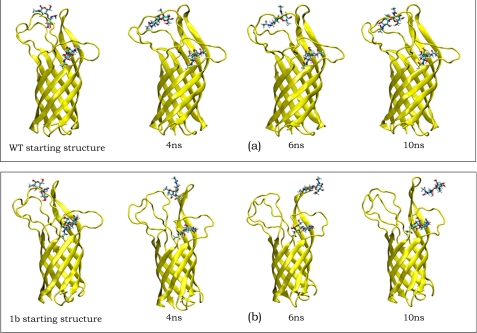
We find two distinct binding modes of chitobiose in region L, as illustrated in Fig. 3 for the WT where the chitobiose is bound during the entire dynamics (Fig. 3a) and the 1b mutant, where the chitobiose unit becomes unbound after 6 ns (Fig. 3b).

FIGURE 3.

Snapshots of OmpA-chitobiose complexes during the MD. a, WT OmpA. The chitobiose in both L and B regions are flexible but remain strongly bound. The largest change in free energy is <5% of the total. b, 1b mutant. The chitobiose in region L gets ejected from the structure after 6 ns; the calculated internal energy is less favorable than for WT by 282 kcal/mol, but the total entropy (TΔS) is more favorable by 79 kcal/mol, due mainly to the increased motions of the unbound chitobiose. The free energy is thus 206 kcal/mol less favorable than the WT. Similar results are found for the 1a mutant (less favorable free energy of 208 kcal/mol compared with the WT, becoming unbound after 6.7 ns). Indeed, our experiments show no invasion of the bacteria for mutants 1b and 1a.

For the 1b mutant, we observe a reorientation of the chitobiose unit in region L after 4 ns of MD (after annealing dynamics and equilibration), allowing the chitobiose unit to become more solvent-exposed, thus increasing the free energy (becoming more negative: more stable). This is due to an increase in internal energy ΔU⁰ of 1.0% and an increase of 0.4% in the total entropy (TΔS⁰). The more mobile chitobiose unit is calculated to be the major contributor to the increased entropy, although we also calculate an appreciable increase in the entropy of the loop region due to the mutation.

After 6 ns, the chitobiose unit is completely ejected from the binding pocket in the 1b mutant. The free energy further increases during the transition, compared with the value at 2 ns. After 10 ns, the final binding free energy is only 0.15% more favorable than the value at 2 ns, however. Here, the internal energy is decreased (more positive) by 0.5% as the chitobiose is no longer interacting with the protein. The loss of internal energy is compensated by a gain in total entropy (1.6%) arising from the unbound, more mobile chitobiose unit. This is direct computational evidence of the entropy-enthalpy compensation effect (44–46).

Interestingly, the 0.5% difference in the internal energy of the bound (2 ns) and unbound (10 ns) states is smaller than the gas-phase binding energy (1.3%) of the chitobiose in region L. This indicates that although the internal energy of the unbound state becomes less attractive as the chitobiose becomes unbound, the magnitude of this change is mitigated by the increased interactions between the hydrophilic chitobiose sugar and nearby water molecules (the solvation effect).

The 1a mutant shows a profile similar to 1b: an increase in free energy of 1.2% after 4 ns, a further increase to 1.5% during the transition at 6 ns and a final increase of only 0.04% after 10 ns, compared with the value at 2 ns. Because 1a and 1b are unique from the other mutants, we conclude that the 2PT method is sensitive enough to accurately capture the thermodynamics in the OmpA-chitobiose complex arising from subtle structural changes.

Conversion of Small Stretches (Three to Four) of Amino Acids to Alanines in Loops 1 and 4 of OmpA Significantly Reduced the Invasion of E. coli K1 in HBMEC

Subsequent to the theoretical predictions, we carried out all 10 sets of mutations in the various loops of OmpA experimentally to assess the critical interaction necessary for invasion; however, the 2c mutation produced lethal consequences to the bacteria. The growth characteristics of the other mutants were all similar to that of wild type E. coli K1. In addition, all mutants express similar amounts of OmpA as examined by Western blotting with an anti-OmpA antibody (supplemental Fig. S5).

Invasion assays using the OmpA mutant strains revealed the following: 1) mutations 1a and 1b abrogated the invasion of E. coli K1 in HBMEC by 98% compared with wild type E. coli K1; 2) mutations 1c and 2b reduced the invasion by 60%; 3) mutations 2a and 3a had very little effect on the invasion and 4) loop 4 mutations reduced the invasion by 60–80%. These results confirm that regions 1a and 1b are critical while region 2b and loop 4 also contribute significantly to OmpA/Ecgp96 interactions, as predicted by the MD simulations.

Quantitative Comparison between Theory/Experiment and Theoretical Prediction of E. coli Invasion

Ignoring entropy and zero-point energy corrections and using only the MD potential energy of the system, we found a 31% correlation with the experimental invasion activities. After including the zero-point energy corrections, the correlation increased dramatically to 75% (supplemental Table S4). This means that the vibrational modes of the OmpA and the chitobiose are strongly dependent on the mode of binding. Upon including entropies to obtain the free energy, the correlation further increased to 90% (Fig. 4a). Thus, we conclude that including entropic contributions is necessary for accurate predictions of the invasion of the 2b, 3a, 4b, and 4c mutants. For the 2c mutant (not yet experimentally measured), we predict an invasion rate of 7.85%.

FIGURE 4.

a, correlation between free energies from theory and experimental invasion activity. Abscissa, experimental invasion activities (% relative to WT) of the ten OmpA mutants. Ordinate, filled blue squares indicate relative Helmholtz free energies (kcal/mol). The lines are fitted to the 9 cases for which there are experimental data. The 1a and 1b mutants are predicted not to invade because the chitobiose in region L becomes unbound during dynamics. This is consistent with observation. We find excellent correlation of the binding free energy to the experimental invasion (90%). The uncertainties are shown by black error bars; theoretical error bars are smaller than the symbols unless otherwise indicated. b, comparison between experimentally (exp) observed invasions (red bars) and those predicted from Helmholtz free energy (calc) (blue) best-fit line. The error bars are shown in black.

The predicted binding free energy of mutants 1a and 1b mutants (before the chitobiose becomes unbound) is 1.8 and −0.4 kcal/mol, respectively. There is reduced total entropy TΔS (−7.2 and −2.3 kcal/mol, respectively) but increased internal energy (−5.5 and −2.6 kcal/mol), compared with the separated chitobiose and protein. As there should be no binding, we conclude that our 2PT simulation protocol calculates free energies to within 2.2 kcal/mol.

OmpA Interacts with Ecgp96 by Cooperative Binding, the Loop-Barrel Pathway Model

Based on these results, we now propose a two-step mechanism for OmpA interaction with the HBMEC protein Ecgp96, an etiological factor in the pathogenesis of bacterial meningitis in neonates. In this loop-barrel pathway model, the solvent exposed region L binding site on OmpA acts as the primary recognition element for the sugar moieties present in the glycosylation sites on Ecgp96. After recognition, there is a subsequent binding event to region B, with binding to both regions being necessary for invasion. Analysis of the Ecgp96 sequence reveals two possible glycosylation sites (NASD, residues 142–145; and NDSQ, 251–254) with geometric dimensions consistent with the OmpA loop structure.

Pharmacophores for OmpA-Ecgp96 Interaction

We performed further, long term (>40 ns) dynamics on the WT structure with chitobiose attached, from which we developed a pharmacophore model of the two binding sites, analyzed using the LigandScout program (47, 48), with further optimization using the Phase module in the Jaguar (version 7.0) (49) software package. Here, the distances between the relevant functional group were calculated every 100 ps of MD for a total of 300 data points.

The distribution of distances obeyed a single normal distribution; the average distance was taken as the center of the Gaussian, and the S.D. was taken as 67% of the width. The plane of the chitobiose unit was defined by three unique points for simplicity, with any additional, critical interactions included as necessary.

In region L, we find that the plane of the chitobiose unit is best defined by three residues (Fig. 5, a and c): 1) the primary amine of Asn-27, 2) the secondary amine of Ala-72, and 3) the primary amine of Asn-110. The amine groups on these three residues form nearly an equilateral triangle, with edge lengths of 9.62, 10.20, and 10.34 Å. The chitobiose rotates freely about the plane defined by these residues, with the chitobiose showing large (>2.5 Å) fluctuations during dynamics, compared with the <0.2 Å fluctuation seen in these residues.

FIGURE 5.

Pharmacophores for L and B binding sites. The residues and functional groups on the protein that interact critically with the chitobiose are shown. The average distance between the functional groups on the protein is given; the average deviation is 0.25 Å for the loop site and 0.15 Å for the barrel site. a, three-dimensional pharmacophore for loop binding site. Three interactions define a plane for the chitobiose unit. The two-dimensional pharmacophore is shown in c. All three residues interact with chitobiose through hydrogen bonds. b, projection of three-dimensional pharmacophore for the barrel binding site. The two-dimensional pharmacophore is shown in d. Trp-103, Thr-145, and Thr-153 define a plane for the chitobiose unit, whereas Asp-159 and Asp-117 are out of the plane, in a boat configuration. Thr-145, Thr-153, and Asp-159 all interact with the chitobiose through hydrogen bonds, Asp-117 through electrostatic interactions while an alcohol on chitobiose interacts with the aromatic ring of Trp-103.

The plane of the chitobiose unit in the region B is defined completely and consistently by Trp-103, Thr-145, and Thr-153, with edge lengths of 9.5, 9.62, and 10.25 Å. The chitobiose interaction with Trp-103 is proton aromatic in nature, whereas Thr-145 is through hydrogen bonds and Thr-153 is through electrostatics. Unlike the loop binding site, the chitobiose unit does not rotate freely about this plane. Instead, the ends are locked in a boat conformation by Asp-117 (electrostatic interaction) and Asp-159 (hydrogen bond). The three-dimensional and two-dimensional pharmacophores of the B site are shown in Fig. 5, b and d.

We propose that the pharmacophores presented here might facilitate the search for small molecules that block invasion. The Phase program enables this through database matching of the constraints and functional groups.

DISCUSSION

This study is the first complete theoretical characterization of protein-protein interactions that relates directly to a transition in disease dynamics. OmpA has generally been described as a structural protein with porin activity, however studies from the Prasadarao lab have shown that OmpA binds to HBMEC via Ecgp96 during E. coli invasion (13, 14). We investigated these interactions computationally with all-atom MD simulations, including explicit treatment of the membrane and solvent, leading to three significant conclusions that support the experimental data.

First, we show that the initial configuration of OmpA incorporated into the membrane environment is sufficient to generate a model in which the binding of chitobiose moieties correlates with experimental invasion efficiency. The 90% correlation of the calculated binding free energy of the OmpA-chitobiose complex with the experimentally observed invasion rate mediated by OmpA and nine of its mutants supports the hypothesis that E. coli meningitis is facilitated by OmpA interacting with the glycosylation sites on Ecgp96. The experimental result that mutants 1a and 1b of loop 1 prevent invasion is consistent with our previous studies in which synthetic peptides representing the loop 1 regions significantly blocked invasion (13).

It might have been expected that mutations to three or four residues of OmpA might result in misfolded structures, destroying protein function. However, we showed computationally that these specific three to four residue mutations to the loop regions maintain the structure fidelity of OmpA, despite the dramatic alteration in the system thermodynamics.

Second, we propose the loop-barrel pathway model, which explains the mechanism of E. coli invasion in terms of our theoretical findings. The loop-barrel pathway model assumes that the first step is for the loop region L on OmpA to recognize and bind to a glycosylation site on Ecgp96. This is followed by cooperative binding of loop region B on OmpA to the second glycosylation site. Interactions in the buried region B are predicted to be much stronger than the solvent exposed region L. Strong HB interactions are removed in region B by the 4b and 4c mutants, but the chitobiose remains bound during dynamics. Both the calculated free energy and the experimentally observed invasion rates are reduced, suggesting that the strength of binding of chitobiose in region B is important to invasion.

Finally, we find that the 2PT method provides a practical method for extracting accurate thermodynamics of condensed phase systems. 2PT is sensitive enough to capture the thermodynamics resulting from subtle changes in the protein structure. This sensitivity is particularly evident in the 1a and 1b mutants, where we find similar structural fluctuations in the protein unit as in the WT, but dramatically worse free energies of binding, thereby accounting for the experimentally observed loss of invasion. Because 2PT leads to accurate entropies with just 20 ps of sampling, it is orders of magnitude more efficient than perturbation and umbrella sampling methods (50). Although the current study considers binding only to the chitobiose ligand, we expect that the minimum threshold in binding for invasion might also apply to other ligands, providing an energy criterion for rapid screening to find lead molecules most likely to prevent invasion.

Finally, as very few amino acids in OmpA are critical for interacting with Ecgp96 to facilitate invasion of HBMEC, targeting those areas for inhibition by small molecules might provide a therapeutic strategy to preventing neonatal bacterial meningitis. We provide a pharmacophore model that we hope will spur further investigations aimed at identifying small molecule inhibitors of invasion.